06 classification 2 bayesian and instance based classification

สอนโดย ดร.หทัยรัตน์ เกตุมณีชัยรัตน์
ภาควิชาการจัดการเทคโนโลยีการผลิตและสารสนเทศ
บทที่ 6: การจาแนกประเภทข้อมูล 2
(Classification 2)
1
Bayesian Classification & Instance-Based Classification

การจาแนกประเภทโดยใช้กฎของเบย์
 เป็นการจาแนกประเภทโดยใช้หลักสถิติในการพยากรณ์ความน่าจะ
เป็นของสมาชิก
 เรียกว่า ทฤษฎีของเบย์(Bayesian theorem)
 เป็นการเรียนรู้เพิ่มได้: ตัวอย่างใหม่ที่ได้มาถูกนามาปรับเปลี่ยนการแจกแจง
ซึ่งมีผลต่อการเพิ่ม / ลดความน่าจะเป็น ทาให้มีการเรียนรู้ที่เปลี่ยนไป
วิธีการนี้ตัวแบบจะถูกปรับเปลี่ยนไปตามตัวอย่างใหม่ที่ได้โดยผนวกกับ
ความรู้เดิมที่มี
 การทานายค่าคลาสเป้าหมายของตัวอย่างใช้ความน่าจะเป็นมากที่สุดของทุก
สมมติฐาน
3

ทฤษฎีของเบย์ (Bayesian theorem)
 ให้ D แทนข้อมูลที่นามาใช้ในการคานวณการแจกแจงความน่าจะเป็น
posteriori probability ของสมมติฐาน h คือ P(h|D) ตามทฤษฎี
P(h) คือ ความน่าจะเป็นก่อนหน้าของสมมติฐาน h
P(D) คือ ความน่าจะเป็นก่อนหน้าของชุดข้อมูลตัวอย่าง D
P(h|D) คือ ความน่าจะเป็นของ h เมื่อรู้ D
P(D|h) คือ ความน่าจะเป็นของ D เมื่อรู้ h
4

ตัวอย่าง:: การพยากรณ์อากาศ
 การพยากรณ์อากาศ (Weatherforecast)
 ความน่าจะเป็นที่เกิดเฮอร์ริเคนในชิคาโก้คือ 0.008
 ทอมมีทักษะในการพยากรณ์ถูกต้องประมาณ 98% ของการทานายทั้งหมด (Predict-hur)
 แต่ทอมก็มีการทานายถูกว่าไม่เกิดเฮอร์ริเคนถูกต้อง 97% เช่นกัน (Predict-nohur)
P(hurricane) = 0.008
P(~hurricane) = 1 – P(hurricane)
= 0.992
P(~h)
P(h)
P(~h) = 1- P(h)
P(h) + P(~h) = 1
5

 การพยากรณ์อากาศ (Weather forecast)
 แต่ทอมก็มีการทานายถูกว่าไม่เกิดเฮอร์ริเคนถูกต้อง 97% เช่นกัน (Predict-nh)
P(predict-hur | hurricane) = 0.98
P(predict-nohur | hurricane) = 0.02
P(~hurricane) = 0.992
P(hurricane)
P(predict-h)
= 0.98
P(predict-nh)= 0.02
6

 การพยากรณ์อากาศ (Weatherforecast)
 แต่ทอมก็มีการทานายถูกว่าไม่เกิดเฮอร์ริเคนถูกต้อง 97%
(Predict-nohur)
P(predict-h|hurricane) = 0.98
P(predict-nh|hurricane) = 0.02
P(predict-h|~hurricane) = 0.03
P(predict-nh| ~hurricane) = 0.97
P(~hurricane)
P(predict-h)
= 0.03
P(predict-nh) = 0.97
7

ตัวอย่าง:: มะเร็ง (Cancer)
 คนไข้คนหนึ่งไปตรวจหามะเร็ง ผลการตรวจเป็นบวก(+) อยากทราบว่า เราควร
วินิจฉัยโรคคนไขคนนี้ว่าเป็นมะเร็งจริงหรือไม่? ความเป็นจริง คือ
 ผลการตรวจเมื่อเป็นบวกจะให้ความถูกต้อง98% กรณีที่มีโรคนั้นอยู่จริง
 ผลการตรวจเมื่อเป็นลบจะให้ความถูกต้อง 97% กรณีที่ไม่มีโรคนั้น
 0.008 ของประชากรทั้งหมดเป็นโรคมะเร็ง
 จากความน่าจะเป็นข้างต้น เราจะทราบว่าความน่าจะเป็นต่อไปนี้
P(cancer)= P(~cancer) =
P(+ | cancer) = P(- | cancer) =
P(+ |~ cancer) = P(- |~ cancer) =
9

ตัวอย่าง:: มะเร็ง (Cancer)
 เราสามารถคานวณค่าความน่าจะเป็นของสมมติฐานว่าคนไข้เป็น / ไม่เป็น
โรคมะเร็ง เมื่อทราบผลตรวจเป็นบวก โดยใช้กฎของเบย์ ดังนี้
ความน่าจะเป็นที่คนไข้คนนี้จะเป็นโรคมะเร็งเมื่อผลตรวจเป็นบวก เท่ากับ
P(cancer |+) =
ความน่าจะเป็นที่คนไข้คนนี้จะไม่เป็นโรคมะเร็งเมื่อผลตรวจเป็นบวก เท่ากับ
P(~cancer |+) =
P(+|cancer)P(cancer) =
P(+|~cancer)P(~cancer) =
10

วิธีการเรียนรู้เบย์อย่างง่าย (Naïve Bayesian Learning)
 วิธีการของ Naïve Bayesian คือการใช้วิธีการของเบย์พร้อมสมมติฐานของการ
เป็นอิสระต่อกันของตัวแปรอิสระทุกตัว
 โดยแต่ละ instance x มี n แอททริบิวต์ หรือ x= {A1, …, An} และมี Ci เป็น
class label
Naïve Bayes Classifier = Max (P(Ci)  P(Aj |Ci) )
P(A1,…, An)
C = Max P’(Ci)  P’(Aj |Ci)
n
i=1
m
j=1
11

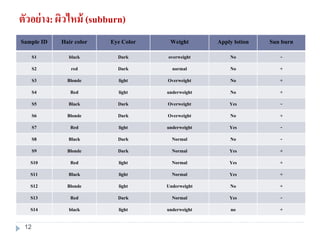
ตัวอย่าง: ผิวไหม้ (subburn)
Sample ID Hair color Eye Color Weight Apply lotion Sun burn
S1 black Dark overweight No -
S2 red Dark normal No +
S3 Blonde light Overweight No +
S4 Red light underweight No +
S5 Black Dark Overweight Yes -
S6 Blonde Dark Overweight No +
S7 Red light underweight Yes -
S8 Black Dark Normal No -
S9 Blonde Dark Normal Yes +
S10 Red light Normal Yes +
S11 Black light Normal Yes +
S12 Blonde light Underweight No +
S13 Red Dark Normal Yes -
S14 black light underweight no +
12

ตัวอย่าง: ผิวไหม้ (subburn)
 Instance x = <hair color=red, eye color = dark, weight= overweight, apply lotion = no>
เพราะฉะนั้น เมื่อ instance ใหม่เข้ามาถามว่าผิวจะไหม้หรือไม่
 C1 : sun burn is + :
P(+).P(red|+).P(dark|+).P(overweight|+).P(applylotion|+)
 C2 : sun burn is - :
P(-).P(red|-).P(dark|-).P(overweight|-).P(applylotion|-)
01.0
9
6
9
2
9
3
9
3
14
9

018.0
5
2
5
2
5
4
5
2
14
5
  X belongs to class (“sunburn = -”)
13

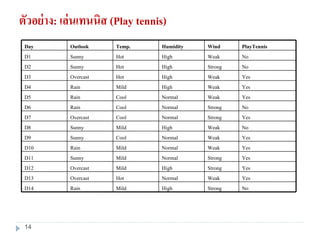
ตัวอย่าง: เล่นเทนนิส (Play tennis)
NoStrongHighMildRainD14
YesWeakNormalHotOvercastD13
YesStrongHighMildOvercastD12
YesStrongNormalMildSunnyD11
YesWeakNormalMildRainD10
YesWeakNormalCoolSunnyD9
NoWeakHighMildSunnyD8
YesStrongNormalCoolOvercastD7
NoStrongNormalCoolRainD6
YesWeakNormalCoolRainD5
YesWeakHighMildRainD4
YesWeakHighHotOvercastD3
NoStrongHighHotSunnyD2
NoWeakHighHotSunnyD1
PlayTennisWindHumidityTemp.OutlookDay
14

วิธีการเรียนรู้เบย์อย่างง่าย (Naïve Bayesian Learning)
 ข้อดี
 ง่ายต่อการนาไปใช้เพราะใช้การคานวณที่ง่าย
 ได้ผลลัพธ์ที่สามารถนาไปประยุกต์ใช้ได้ดี
 ข้อเสีย
 ใช้ได้กับ attribute ที่เป็นอิสระกันเท่านั้น
17

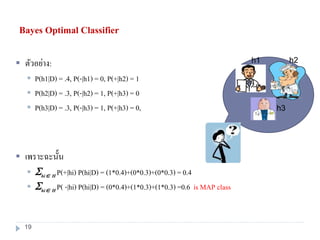
ตัวจะแนกประเภทที่ดีที่สุดแบบเบย์ (Bayes Optimal Classifier)
 พิจารณา
 จากความน่าจะเป็น 3 สมมติฐาน
P(h1|D) = 0.4, P(h2|D) = 0.3, P(h3|D) = 0.3
 ถ้าให้new instance x เข้าไปถาม จะตอบว่า
h1(x) = +, h2(x) = -, h3(x) = -
 What’s hMAP(x) ?
 What's most probable classification of x?
18

Bayes Optimal Classifier
 ตัวอย่าง:
 P(h1|D) = .4, P(-|h1) = 0, P(+|h2) = 1
 P(h2|D) = .3, P(-|h2) = 1, P(+|h3) = 0
 P(h3|D) = .3, P(-|h3) = 1, P(+|h3) = 0,
 เพราะฉะนั้น
 hi H P(+|hi) P(hi|D) = (1*0.4)+(0*0.3)+(0*0.3) = 0.4
 hi H P( -|hi) P(hi|D) = (0*0.4)+(1*0.3)+(1*0.3) =0.6 is MAP class
h1 h2
h3
19

Instance-Based Classification
20

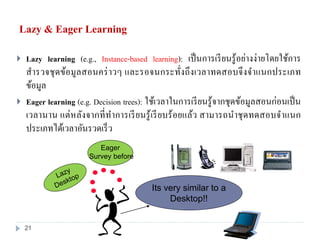
Lazy & Eager Learning
 Lazy learning (e.g., Instance-based learning): เป็นการเรียนรู้อย่างง่ายโดยใช้การ
สารวจชุดข้อมูลสอนคร่าวๆ และรอจนกระทั่งถึงเวลาทดสอบจึงจาแนกประเภท
ข้อมูล
 Eager learning (e.g. Decision trees): ใช้เวลาในการเรียนรู้จากชุดข้อมูลสอนก่อนเป็น
เวลานาน แต่หลังจากที่ทาการเรียนรู้เรียบร้อยแล้ว สามารถนาชุดทดสอบจาแนก
ประเภทได้เวลาอันรวดเร็ว
Its very similar to a
Desktop!!
Eager
Survey before
21

Lazy Learner: Instance-Based Methods
 เทคนิคที่ใช้สาหรับ Instance-Based Methods มีชื่อว่า
 k-nearest neighbor
 การหาประเภทของข้อมูลโดยให้การวัดการระยะห่างที่เรียกว่า
Euclidean Distance
 Locally weighted regression
 หาสมการเชิงเส้นตัดเพื่อวัดจุดใกล้เคียง
22

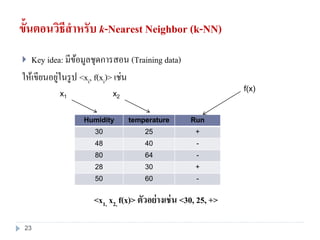
ขั้นตอนวิธีสาหรับ k-Nearest Neighbor (k-NN)
 Key idea: มีข้อมูลชุดการสอน (Training data)
ให้เขียนอยู่ในรูป <xi, f(xi)> เช่น
Humidity temperature Run
30 25 +
48 40 -
80 64 -
28 30 +
50 60 -
x1 x2
f(x)
<x1, x2, f(x)> ตัวอย่างเช่น <30, 25, +>
23

ขั้นตอนวิธีสาหรับ k-Nearest Neighbor (k-NN)
 Discrete-valued หมายถึง ค่าป้ ายบอกฉลากเป็นที่แบ่งประเภทชัดเจน เช่น วิ่ง หรือ ไม่วิ่ง ใช่
หรือ ไม่ใช่ เป็นต้น
 ดังนั้นหาชุด xq, ที่ใกล้เคียงที่สุดสาหรับชุดข้อมูลสอนมาเป็นตัวประมาณค่าสาหรับ xn
 Real-valued หมายถึง ค่าป้ ายบอกฉลากเป็นตัวเลขทศนิยม เช่น การพยากรณ์ปริมาณน้าฝน
อุณหภูมิ เป็นต้น
24

ตัวอย่าง
• ในการตัดสินผลไม้ที่ไม่เคยเห็นนั่นคือ แอปเปิ้ล นั่นคือเลือกพิจารณาภาพผลไม้จานวน K ที่ใกล้เคียงมาก
ที่สุด ดังนั้น การจาแนกประเภทผลไม้ที่ไม่ทราบจะใช้จานวนผลโวตของผลไม้แต่ละประเภทว่าคือ แอปเปิ้ล
25

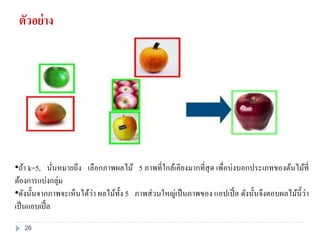
ตัวอย่าง
•ถ้า k=5, นั่นหมายถึง เลือกภาพผลไม้ 5 ภาพที่ใกล้เคียงมากที่สุด เพื่อบ่งบอกประเภทของต้นไม้ที่
ต้องการแบ่งกลุ่ม
•ดังนั้นจากภาพจะเห็นได้ว่า ผลไม้ทั้ง 5 ภาพส่วนใหญ่เป็นภาพของ แอปเปิ้ล ดังนั้นจึงตอบผลไม้นี้ว่า
เป็นแอบเปิ้ล
26

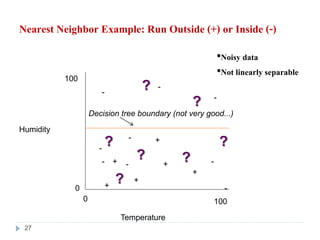
Nearest Neighbor Example: Run Outside (+) or Inside (-)
Humidity
Temperature
0
100
0 100
+
+
+
+
-
-
-
-
-
-
-
+
+
•Noisy data
•Not linearly separable
Decision tree boundary (not very good...)
?
?
?
?
-
-
?
?
?
27

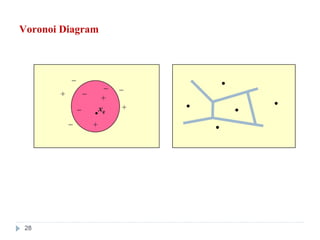
Voronoi Diagram
.
_
+
_ xq
+
_ _
+
_
_
+
.
.
.
. .
28

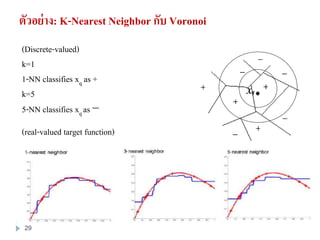
ตัวอย่าง: K-Nearest Neighbor กับ Voronoi
(Discrete-valued)
k=1
1-NN classifies xq as +
k=5
5-NN classifies xq as −
(real-valued target function)
29

เมื่อไหร่ถึงจะใช้ k-Nearest Neighbor
 เมื่อชุดข้อมูลสามารถแปลงให้อยู่ระนาบของมิติได้ ℜn
 มี Attribute น้อยว่า 20 ตัว
 มีข้อมูลชุดการสอน (Training data) เป็นจานวนมาก
 ข้อดี
 สอน (training) เร็วมาก
 สามารถเรียนรู้กับฟังก์ชันที่ซับซ้อนได้
 ไม่สูญเสียข้อมูลอื่น
 ข้อเสีย
 ช้าเวลาจาแนกประเภทข้อมูล
 จะโง่เมื่อมีการคิด attribute ที่ไม่เกี่ยวข้อง
30

การกาหนดตัวแปร K
 ไม่ควรเลือก K เล็กเกินไป เพราะจะทาให้เบี่ยงเบนสูง
 ไม่ควรเลือก K ใหญ่เกินไป เพราะจะทาให้ข้อมูลเกินความลาเอียง
 เพราะฉะนั้นการเลือกค่า K ขึ้นอยู่กับข้อมูล ต้องมีการปรับค่าการประเมินเช่น Cross-validation
 ระยะทางที่ใช้วัด คือ
 ถ้า x ประกอบไปด้วย Attribute <a1(x), a2(x), …, an(x)> ดังนั้น ar(x) ดังกล่าวจึงแทนด้วยค่าในด้วย x
ค่าระยะทางที่ใช้เรียกว่า Euclidean Distance


n
r
jrirji xaxaxxd
1
2
))()((),(
31

Euclidean Distance
30 25 +
48 40 -
80 64 -
28 30 +
50 60 -
x = <humidity, temperature>
New instance xq = <40, 30, run=?? > We can run inside(+)or outside (-)


n
r
jrirji xaxaxxd
1
2
))()((),(
18.11)2530()3040(),( 22
1 xxd q
80.12)4030()4840(),( 22
2 xxd q
5.52)6430()8040(),( 22
3 xxd q
1-NN (x1) Answer run inside (+)
2-NN (x1,x4) Answer run inside (+)
3-NN (x1,x2,x4)Answer run inside (+)
4-NN (x1,x2,x4,x5)Answer run inside (+)
5-NN Answer run inside (-)
12)3030()2840(),( 22
4 xxd q
62.31)6030()5040(),( 22
5 xxd q
Discrete values
32

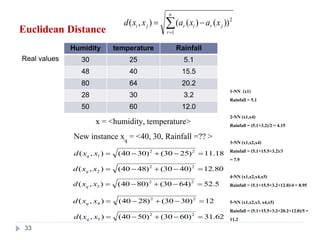
Euclidean Distance
Humidity temperature Rainfall
30 25 5.1
48 40 15.5
80 64 20.2
28 30 3.2
50 60 12.0
New instance xq = <40, 30, Rainfall =?? >


n
r
jrirji xaxaxxd
1
2
))()((),(
18.11)2530()3040(),( 22
1 xxd q
80.12)4030()4840(),( 22
2 xxd q
5.52)6430()8040(),( 22
3 xxd q
1-NN (x1)
Rainfall = 5.1
2-NN (x1,x4)
Rainfall = (5.1+3.2)/2 = 4.15
3-NN (x1,x2,x4)
Rainfall = (5.1+15.5+3.2)/3
= 7.9
4-NN (x1,x2,x4,x5)
Rainfall = (5.1+15.5+3.2+12.0)/4= 8.95
5-NN (x1,x2,x3, x4,x5)
Rainfall = (5.1+15.5+3.2+20.2+12.0)/5=
11.2
12)3030()2840(),( 22
4 xxd q
62.31)6030()5040(),( 22
5 xxd q
Real values
33

Distance-Weighted kNN (แบบละเอียด)
 ถ้าต้องการให้มีการประมาณค่าได้รายละเอียดมากขึ้น ดังนั้นจึงต้องคานวณค่า
น้าหนักสาหรับการแบ่งประเภท ดังต่อไปนี้
34

ตัวอย่าง:
30 25 1
48 40 0
80 64 0
28 30 1
50 60 0
New instance xq = <40, 30> We can run inside(+) or outside (-) , by k=3
1 1 2 2 3 3
1 2 3
( ) ( ) ( )ˆ( )q
w f x w f x w f x
f x
w w w
 

 
168.0
)
12
1
()
8.12
1
()
18.11
1
(
)1(*)
12
1
()0(*)
8.12
1
()1(*)
18.11
1
(
)(
222
222



qxf

35

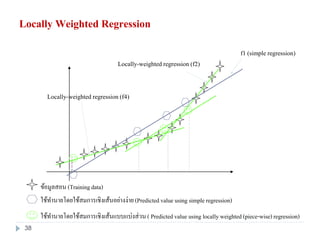
Locally Weighted Regression
 แนวความคิด:
 มาจาก k-NN ที่ค้นหาการประมาณค่าโดยใช้พื้นที่ใกล้เคียงในการประมาณ
 ทาไมต้องอยู่ในรูปการใช้สมการเชิงเส้น เพราะ
 ลดค่า error ในการกาหนดค่า K
 ลดค่า error สาหรับการให้ค่าน้าหนักสาหรับการหา distance
36

 Local linear function:
f^(x)=β0+ β1a1(x)+…+βnan(x)
 Error criterions:



qxofnbrsnearestkx
q xfxfxE
____
2
1 ))()((
2
1
)(
)),(())()((
2
1
)( 2
2 xxdKxfxfxE q
Dx
q 


37

f1 (simple regression)
ข้อมูลสอน (Trainingdata)
ใช้ทานายโดยใช้สมการเชิงเส้นแบบแบ่งส่วน( Predictedvalue using locally weighted (piece-wise)regression)
ใช้ทานายโดยใช้สมการเชิงเส้นอย่างง่าย(Predictedvalue using simple regression)
Locally-weighted regression (f2)
Locally-weighted regression (f4)
38

HW#6
39
 What is Bayesian Classification?
 What is Naïve Bayesian Learning?
 What is Instance-Based Classification?
 Please explain Lazy & Eager Learning?

HW#6
40
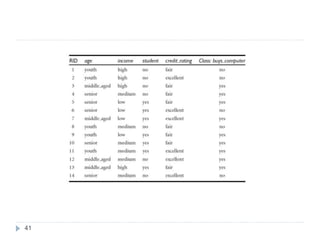
 Predicting a class label using naïve Bayesian
classification. We wish to predict the class label of a tuple
using naïve Bayesian classification, given the training
data as in the table below. The data tuples are described
by the attributes age, income, student and credit_rating.
The class label attribute, buy_computer, has two distinct
values (namely, {yes, no}). Let C1 correspond to the
class buys_computer = yes and C2 correspond to
buys_computer = no. The tuple we wish to classify is
 X = (age=youth, income=medium, student=yes,
credit_rating = fair)
 We need to maximize P(X|Ci)P(Ci), for i=1,2. P(Ci), the
probability of each class, can be computed based on the
training tuples.

LAB 6
42
 Use weka program to construct a baysian network
classification and instance base classification from
the given file.
 Labor.arff

06 classification 2 bayesian and instance based classification

More Related Content

What's hot

Similar to 06 classification 2 bayesian and instance based classification

More from นนทวัฒน์ บุญบา

06 classification 2 bayesian and instance based classification