Downloaded 286 times
04 การเคลื่อนที่แบบต่างๆ
- 1. อาจารย์วิริยะ โกษิต โรงเรียนวัดป่าประดู่ จังหวัดระยอง บทที่4 การเคลื่อนที่แบบต่างๆ
- 2. Outline o การเคลื่อนที่แบบโพรเจกไทล์ o การเคลื่อนที่แบบวงกลมด้วยความเร็วคงที่ oการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
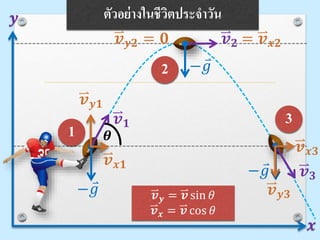
- 3. การเคลื่อนที่แบบโพรเจคไตล์ คือ การเคลื่อนที่ในแนวโค้งพาราโบลาซึ่งเกิด จากวัตถุได้รับความเร็วใน 2 แนวพร้อมกัน คือ ความเร็วในแนวราบและ ความเร็วในแนวดิ่ง ตัวอย่างของการเคลื่อนที่แบบโพรเจกไทล์ ได้แก่ ดอกไม้ ไฟ น้าพุ การเคลื่อนที่ของลูกบอลที่ถูกเตะขึ้นจากพื้น การเคลื่อนที่ของนัก กระโดดไกล การเคลื่อนที่แบบโพรเจคไตล์
- 4. ตัวอย่างในชีวิตประจาวัน 𝒗 𝟐 𝒗 𝟑 𝒗𝟏 − 𝑔 − 𝑔 − 𝑔 1 2 3
- 5. ตัวอย่างในชีวิตประจาวัน𝒚 𝒙 𝒗 𝟐 𝒗 𝟑 𝒗𝟏 − 𝑔 − 𝑔 − 𝑔 𝒗 𝒙𝟏 𝒗 𝒚𝟏 𝒗 𝒚𝟐 = 𝟎 1 2 3 = 𝒗 𝒙𝟐 𝒗 𝒙𝟑 𝒗 𝒚𝟑 𝜽 𝒗 𝒚 = 𝒗 sin 𝜃 𝒗 𝒙 = 𝒗 cos 𝜃
- 6. 𝒗 𝟏 − 𝑔 𝒗𝒙𝟏 𝒗 𝒚𝟏 การเคลื่อนที่แบบโพรเจคไตล์ o ในแนวราบ (แนวแกนX) วัตถุจะเคลื่อนที่ด้วยความเร็วคงตัว (ไม่มีแรงกระทา) และความเร่งในแนวราบเป็นศูนย์ o ในแนวดิ่ง (แนวแกนY) วัตถุจะเคลื่อนที่อย่างเสรีภายใต้แรงโน้มถ่วงคงตัว และความเร่งในแนวดิ่งคือความเร่งโน้มถ่วงของโลก o จึงทาให้แนวทางการเคลื่อนที่เป็นแนว โค้งพาราโบลา เช่น การเคลื่อนที่ของ ก้อนหินเมื่อถูกขว้างออกไปแนวระดับ การเคลื่อนที่ของลูกฟุตบอลที่ถูกเตะ การเคลื่อนที่ของลูกปืนใหญ่ที่ถูกยิง เป็นต้น 𝒚 𝒙 𝜽
- 7. การทดลองการเคลื่อนที่แบบโพรเจคไตล์ − 𝑔 𝒕 𝟎 𝒕𝟏 𝒕 𝟐 𝒕 𝟑 𝒕 𝟎 𝒕 𝟏 𝒕 𝟐 𝒕 𝟑 −𝒚 𝒙
- 8. 𝒗 − 𝑔 𝒗 𝒙𝟏 𝒗𝒚 รูปแบบของการเคลื่อนที่แบบโพรเจคไตล์ 1. ความเร็วต้นตามแนวระดับ 𝒚 𝒙 𝜽 𝒗 2. ความเร็วต้นทามุมกับแนวระดับ − 𝑔
- 9. 1. ความเร็วต้นตามแนวระดับ a) หาความเร็วณ จุดใดๆ (มีทิศ สัมผัสกับเส้นทางเดิน ณ จุดนั้น) 𝒗 𝒗 𝒗 𝒙 𝒗 𝒚 𝜽 𝒗 𝟐 = 𝒗 𝒙 𝟐 + 𝒗 𝒚 𝟐 𝜽 = 𝐭𝐚𝐧−𝟏 𝒗 𝒚 𝒗 𝒙 b) หาการกระจัด ณ จุดใดๆ 𝒔 𝒙 𝒔 𝒚 𝑠2 = 𝑠 𝑥 2 + 𝑠 𝑦 2 − 𝑔
- 10. 1. ความเร็วต้นตามแนวระดับ𝒗 𝒗𝒗 𝒙 𝒗𝒚𝜽 หลักการคานวณ • ตั้งแกน X ให้อยู่ในแนวระดับ และ แกน Y อยู่ใน แนวดิ่ง โดยจุดกาเนิด(origin) ต้องอยู่ที่จุดเริ่มต้น • แตกเวกเตอร์ทุกค่าคือ ความเร็ว ระยะทาง ให้อยู่ใน แนวแกน X และ Y • ax = 0 และ ay = -g − 𝑔
- 11. 2. ความเร็วต้นทามุมกับแนวระดับ𝒚 𝒙 𝒗 𝟐𝒗𝒚𝟐 = 𝟎 2 3 = 𝒗 𝒙𝟐 𝑣 = 𝑣 𝑥 𝑖 + 𝑣 𝑦 𝑗 𝑣 𝑦 = 𝑣 𝑠𝑖𝑛 𝜃 และ 𝑣 𝑥 = 𝑣 cos 𝜃 𝒗 𝟑 𝒗 𝒙𝟑 𝒗 𝒚𝟑 𝒗 𝟏 𝒗 𝒙𝟏 𝒗 𝒚𝟏 1 𝜽 𝒔 𝒚 𝒔 𝒙 − 𝑔
- 12. สูตรการคานวณการเคลื่อนที่แบบโพรเจกไตล์ ในแนวดิ่งในแนวราบ ความเร็วในแนวราบคงที่ ax =0 ความเร็วในแนวดิ่งไม่คงที่ ay = -g 𝒔 𝒙 = 𝒖 𝒙 𝒕 𝒗 𝒙 = 𝒖 𝒙 𝒗 𝒙 𝟐 = 𝒖 𝒙 𝟐 𝒔 𝒚 = 𝒖 𝒚 𝒕 − 𝟏 𝟐 𝒈𝒕 𝟐 𝒗 𝒚 = 𝒖 𝒚 − 𝒈𝒕 𝒗 𝒚 𝟐 = 𝒖 𝒚 𝟐 − 𝟐𝒈 ∙ 𝒔 𝒚
- 13. สูตรการคานวณการเคลื่อนที่แบบโพรเจกไตล์ การเวลาที่วัตถุอยู่ที่จุดสูงสุด• จาก 𝒗𝒚 = 𝒖 𝒚 − 𝒈𝒕 • ที่จุดสูงสุด ความเร็วในแนวดิ่ง 𝒗 𝒚 = 𝟎 𝟎 = 𝒖 𝒚 − 𝒈𝒕 • เวลาที่วัตถุอยู่ที่จุดสูงสุด 𝒕 = 𝒖 𝒚 𝒈 • เวลาที่วัตถุอยู่ที่จุดสูงสุดจนตกถึงพื้น • 𝑻 = 𝟐𝒕 = 𝟐𝒖 𝒚 𝒈 𝒗 𝒚 = 𝟎 𝒗 𝒙 𝒖 𝒙 𝒖 𝒚 𝒔 𝒚 − 𝑔
- 14. สูตรการคานวณการเคลื่อนที่แบบโพรเจกไตล์ การกระจัดที่วัตถุอยู่ที่จุดสูงสุด• จาก 𝒗𝒚 𝟐 = 𝒖 𝒚 𝟐 − 𝟐𝒈 𝒔 𝒚 • ที่จุดสูงสุด ความเร็วในแนวดิ่ง 𝒗 𝒚 = 𝟎 𝟎 = 𝒖 𝒚 𝟐 − 𝟐𝒈 𝒔 𝒚 • การกระจัดที่วัตถุอยู่ที่จุดสูงสุด 𝒔 𝒚 = 𝒖 𝒚 𝟐 𝟐𝒈 𝒗 𝒚 = 𝟎 𝒗 𝒙 𝒖 𝒙 𝒖 𝒚 𝒔 𝒚 − 𝑔
- 15. สูตรการคานวณการเคลื่อนที่แบบโพรเจกไตล์ วัตถุจะตกถึงพื้นได้ไกลที่สุดจากจุดยิง • การกระจัดที่วัตถุตกถึงพื้นจากจุดยิง 𝒔𝒙 = 𝒖 𝒙 𝑻 𝒔 𝒙 = 𝟐𝒖 𝒙 𝒖 𝒚 𝒈 = 𝟐𝒖 cos 𝜽 𝒖 sin 𝜽 𝒈 = 𝟐𝒖 𝟐 cos 𝜽 sin 𝜽 𝒈 • เมื่อ 2 cos 𝜽 sin 𝜽 = sin 2𝜽 𝒔 𝒙 = 𝒖 𝟐 sin 2𝜽 𝒈 • วัตถุจะตกถึงพื้นได้ไกลที่สุดจากจุดยิง(เตะ) 𝒖 𝒖 𝒙 𝒖 𝒚 𝜽 =? ? ?
- 16. สูตรการคานวณการเคลื่อนที่แบบโพรเจกไตล์ วัตถุจะตกถึงพื้นได้ไกลที่สุดจากจุดยิง • วัตถุจะตกถึงพื้นได้ไกลที่สุดจากจุดยิง(เตะ) ทามุม𝜽 = 45° 𝒔 𝒙 = 𝒖 𝟐 sin 2𝜽 𝒈 𝒔 𝒙 = 𝒖 𝟐 sin 2 𝟒𝟓° 𝒈 𝒔 𝒙 = 𝒖 𝟐 sin 𝟗𝟎° 𝒈 • เมื่อ sin 𝟗𝟎° = 𝟏 ดังนั้น 𝒔 𝒙 = 𝒖 𝟐 𝒈 𝒖 𝒖 𝒙 𝒖 𝒚 𝜽 𝒔 𝒙 − 𝑔
- 17. นักอเมริกันฟุตบอลคนหนึ่งเตะลูกบอลทามุม 30o กับแนวระดับด้วย ความเร็วต้น80 เมตร/วินาที จงหาว่าเมื่อลูกบอลเคลื่อนที่ไปได้ 3 วินาที จะมีความเร็วเท่าไร และใช้เวลานานเท่าไรลูกบอลนั้นจึงตกถึงพื้น ตัวอย่าง 14 30o ระดับอ้างอิง
- 18. ชายคนหนึ่งยืนอยู่บนตึกสูง 45 เมตรขว้างลูกเทนนิสออกไปใน แนวราบด้วยความเร็ว 12 เมตร/วินาที กระทบกับกาแพงแล้ว กระดอนกลับ จงหาว่าลูกเทนนิสจะตกกระทบพื้นที่จุดห่างจากฐาน ตึกเท่าไร ถ้าให้หน้าตึกห่างจากกาแพง 20 เมตร ตัวอย่าง 1545m 𝑢 𝑥 = 12 𝑚/𝑠 ระดับอ้างอิง
- 19. ชายคนหนึ่งเตะลูกบอลด้วยความเร็ว 25 เมตร/วินาทีในทิศทามุมเงย 53o จงหาว่าลูกบอลนี้ขึ้นได้สูงสุดเท่าไร และ ใช้เวลานานเท่าไรลูก บอลจึงตกถึงพื้น (เมื่อ g = 10 เมตร/วินาที2) ตัวอย่าง 16 53o ระดับอ้างอิง
- 20. ยิงลูกกระสุนออกไปในแนวระดับด้วยความเร็ว 400 เมตร/วินาทีเมื่อ เวลาผ่านไป 3 วินาที จงหา (เมื่อ g = 10 เมตร/วินาที2) ก) ความเร็วและทิศทางของกระสุน ข) ระยะกระจัดของลูกกระสุน ตัวอย่าง 17 𝑢 𝑥 = 400 𝑚/𝑠 ระดับอ้างอิง
- 21. ยิงปืนทามุมเงย 37 องศากับแนวราบด้วยความเร็ว 500 เมตร/วินาที จง คานวณหา (เมื่อ g = 10 เมตร/วินาที2) ก) ความเร็วของลูกกระสุน เมื่อเวลาผ่านไป 1 วินาที ข) เวลาที่ลูกกระสุนอยู่ที่ตาแหน่งสูงสุด ค) การกระจัดของลูกกระสุน เมื่อตกถึงพื้น ตัวอย่าง 18 37o ระดับอ้างอิง
- 22. การเคลื่อนที่แบบวงกลม (Circular Motion) การเคลื่อนที่ในแนววงกลม หมายถึงการเคลื่อนที่ของวัตถุ ที่มีการ เปลี่ยนแปลงความเร็วตามทิศทางการเคลื่อนที่ตลอดเวลา ใน การศึกษาเราส่วยใหญ่จะให้อัตราเร็วของวัตถุจะคงที่ เช่น การโคจร ของดวงจันทร์รอบโลก เป็นต้น
- 23. องค์ประกอบการเคลื่อนที่แบบวงกลม การเคลื่อนที่แบบวงกลมประกอบไปด้วย • แรงกระทาจากภายนอก • การเปลี่ยนแปลงความเร็วตาม ทิศทาง •ความเร่งมีทิศเข้าสู่ศูนย์กลาง • เกิดแรงสู่ศูนย์กลาง • อัตราเร็วตามแนวสัมผัสคงที่𝑭 𝒄 𝒗 𝑭 𝒄 𝒗 𝑭 𝒄 𝑭 𝒄 𝑭 𝒄 𝑭 𝒄 𝒗 𝒗 𝒗 𝒗 𝜽 𝑹 𝒂 𝒄
- 24. การเคลื่อนที่แบบวงกลม และ การเคลื่อนเชิงเส้น 𝒗 𝒗 𝜽 𝑹 𝑹 𝑠 𝜽𝟎 𝜽 𝟏 • ระยะทาง (s) คือ ระยะทางตาม เส้นทางของการเคลื่อนที่ หน่วยเป็น เมตร(m) • มุม (q) คือ มุมที่วัตถุกวดไป ได้หน่วยเป็นเรเดียน (rad) 𝒔 𝟎, 𝒕 𝟎 𝒔 𝟏, 𝒕 𝟏
- 25. สัญลักษณ์ในการคานวณ การเคลื่อนที่แบบวงกลม • คาบ (T)คือ เวลาที่ใช้ในการ เคลื่อนที่ครบ 1 รอบ หรือ วินาทีต่อรอบ (s) • ความถี่ (f) คือ จานวนรอบที่ เคลื่อนที่ได้ในหนึ่งหน่วยเวลา หรือ รอบต่อวินาที (Hz) 𝑭 𝒄 𝒗 𝑭 𝒄 𝒗 𝑭 𝒄 𝑭 𝒄 𝑭 𝒄 𝑭 𝒄 𝒗 𝒗 𝒗 𝒗 𝒇 = 𝟏 𝑻 , 𝑻 = 𝟏 𝒇 𝜽 𝑹 𝒂 𝒄
- 26. การเคลื่อนที่แบบวงกลม และ การเคลื่อนเชิงเส้น 𝒗 𝒗 𝜽 𝑹 𝑹 Δ𝑠 𝒔𝟎, 𝒕 𝟎 𝒔 𝟏, 𝒕 𝟏 𝜽 𝟎 𝜽 𝟏 • อัตราเร็วเชิงเส้น (v) คือ ระยะทางตาม แนวเส้นรอบวงของวงกลมที่วัตถุ เคลื่อนที่ได้ในหนึ่งหน่วยเวลา ( m/s) 𝒗 = 𝚫𝒔 𝚫𝒕 == 𝒔 𝟏 − 𝒔 𝟎 𝒕 𝟏 − 𝒕 𝟎 • อัตราเร็วเชิงมุม ( w) คือ คือ มุมที่ จุดศูนย์กลางของวงกลมที่รัศมี กวาดไปได้ในหนึ่งหน่วยเวลา (เรเดียน/วินาที หรือ rad/s) 𝝎 = 𝚫𝜽 𝚫𝒕 = 𝜽 𝟏 − 𝜽 𝟎 𝒕 𝟏 − 𝒕 𝟎
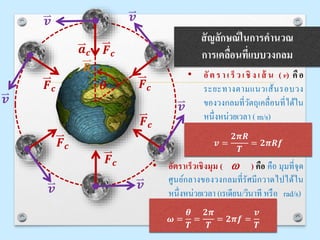
- 27. สัญลักษณ์ในการคานวณ การเคลื่อนที่แบบวงกลม • อัตราเร็ วเชิง เส้ น (v) คือ ระยะทางตามแนวเส้นรอบวง ของวงกลมที่วัตถุเคลื่อนที่ได้ใน หนึ่งหน่วยเวลา ( m/s) 𝑭 𝒄 𝒗 𝑭 𝒄 𝒗 𝑭 𝒄 𝑭 𝒄 𝑭 𝒄 𝑭 𝒄 𝒗 𝒗 𝒗 𝒗 𝒗 = 𝟐𝝅𝑹 𝑻 = 𝟐𝝅𝑹𝒇 • อัตราเร็วเชิงมุม ( w ) คือ คือ มุมที่จุด ศูนย์กลางของวงกลมที่รัศมีกวาดไปได้ใน หนึ่งหน่วยเวลา (เรเดียน/วินาที หรือ rad/s) 𝝎 = 𝜽 𝑻 = 𝟐𝝅 𝑻 = 𝟐𝝅𝒇 = 𝒗 𝑻 𝜽 𝑹 𝒂 𝒄
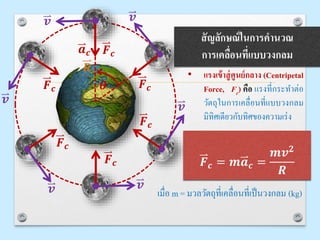
- 28. สัญลักษณ์ในการคานวณ การเคลื่อนที่แบบวงกลม • ความเร่ งเข้าสู่ ศู นย์ กลาง (Centripetal Acceleration, ac) ac คือ ความเร่งเนื่องจากการ เคลื่อนที่แบบวงกลมมีขนาดคงที่ และมีทิศเข้าสู่ศูนย์กลางเสมอ 𝑭 𝒄 𝒗 𝑭 𝒄 𝒗 𝑭 𝒄 𝑭 𝒄 𝑭 𝒄 𝑭 𝒄 𝒗 𝒗 𝒗 𝒗 𝒂 𝒄 = 𝒗 𝟐 𝑹 𝜽 𝑹 𝒂 𝒄 เมื่อ R= รัศมีการเคลื่อนที่ในแนววงกลม (m)
- 29. สัญลักษณ์ในการคานวณ การเคลื่อนที่แบบวงกลม • แรงเข้าสู่ศูนย์กลาง (Centripetal Force,Fc) คือ แรงที่กระทาต่อ วัตถุในการเคลื่อนที่แบบวงกลม มิทิศเดียวกับทิศของความเร่ง 𝑭 𝒄 𝒗 𝑭 𝒄 𝒗 𝑭 𝒄 𝑭 𝒄 𝑭 𝒄 𝑭 𝒄 𝒗 𝒗 𝒗 𝒗 𝑭 𝒄 = 𝒎𝒂 𝒄 = 𝒎𝒗 𝟐 𝑹 𝜽 𝑹 𝒂 𝒄 เมื่อ m = มวลวัตถุที่เคลื่อนที่เป็นวงกลม (kg)
- 30. กฎแรงดึงดูดระหว่างมวลนิวตัน กฎแรงดึงดูดระหว่างมวลนิวตัน กล่าวว่า “วัตถุทั้งหลายในเอกภพจะออก แรงดึงดูดซึ่งกันและกันโดยขนาดของแรงดึงดูดระหว่างวัตถุคู่หนึ่งๆ จะแปร ผันตรงกับผลคูณระหว่างมวลวัตถุทั้งสองและจะแปรผกผันกับกาลังสอง ระยะทางระหว่างวัตถุทั้งสองนั้น” 𝑭 = 𝑮𝒎𝑴 𝑹 𝟐 เมื่อ 𝑭 𝒎 = 𝑭 𝑬 G คือ ค่านิจความโน้มถ่วงสากล มีค่า 6.672 x 10-11 Nm2/kg2 𝑭 𝑬 𝑭 𝒎 𝑴 𝒎 𝑹
- 31. หลักการคานวณเรื่องการเคลื่อนที่แบบวงกลมแบบต่าง ๆ 1. เขียนระนาบกลมขณะที่วัตถุกาลังหมุน 2.เขียนแรงที่กระทาต่อวัตถุ แล้วแตกแรงทั้งหมดให้อยู่ในแนวสู่ ศูนย์กลางวงกลม และแนวตั้งฉากกับแนวสู่ศูนย์กลาง 3. ในแนวสู่ศูนย์กลาง หาแรงลัพธ์ที่ทีทิศทางพุ่งเข้าสู่ศูนย์กลาง แรง นี้จะทาหน้าที่เป็นแรงสู่ศูนย์กลาง • ในแนวตั้งฉากกับระนาบวงกลมนี้ ถือว่า สมดุล ∴ 𝑭 ในแนวนี้เท่ากับศูนย์ 𝑭 = 𝟎
- 32. การเคลื่อนที่วงกลมตามแนวระดับ o เมื่อระบบของวงกลมวางอยู่ในแนว ระดับวัตถุผูกเชือก แกว่งเป็น วงกลมบนโต๊ะระดับผิวเกลี้ยง •หาความเร็วเชิงมุมได้จาก 𝝎 = 𝜽 𝑻 = 𝟐𝝅 𝑻 = 𝟐𝝅𝒇 = 𝒗 𝑻 • หาความเร่งสู่ศูนย์กลางได้จาก 𝒂 𝒄 = 𝒗 𝟐 𝑹 = 𝝎 𝟐 𝑹 • หาแรงสู่ศูนย์กลางได้จาก 𝒗 𝑭 𝒄 = 𝒎𝒂 𝒄 = 𝒎𝒗 𝟐 𝑹 = 𝒎𝝎 𝟐 𝑹
- 33. การเคลื่อนที่เป็นวงกลมในแนวดิ่ง การเคลื่อนที่ของวงกลมในแนวดิ่ง แตกต่างจากแนวระดับ คือมีค่า g • แรงตามแนวรัศมี 𝑭 𝒄 = 𝑻 − 𝒎𝒈 cos 𝜽 • แรงตามแนวสัมผัส 𝑭 𝑻 = 𝒎𝒈 sin 𝜽 • จาก 𝑭 𝒄 = 𝒎𝒂 𝒄 ได้ว่า 𝒂 𝒄 = 𝑭 𝒄 𝒎 = 𝑻−𝒎𝒈 cos 𝜽 𝒎 • เมื่อ 𝒂 𝒄 = 𝒗 𝟐 𝑹 ได้ว่า 𝒗 𝟐 𝑹 = 𝑻−𝒎𝒈 cos 𝜽 𝒎 • ดังนั้น ความตึกเชือกคือ q 𝑚𝑔 𝑇 𝑻 = 𝒎𝒗 𝟐 𝑹 + 𝒎𝒈 cos 𝜽 𝑹
- 34. การเคลื่อนที่บนทางโค้งในแนวราบ การที่วัตถุหรือรถจะเลี้ยวโค้งต้องมีแรงสู่ศูนย์กลางเสมอ ในขณะที่รถเลี้ยวโค้งแรง สู่ศูนย์กลางที่กระทาต่อรถก็คือ แรงเสียดทานนั่นเองโดยแรงเสียดทานมีทิศเข้าสู่ศูนย์กลางใน ขณะที่รถเลี้ยวโค้งการหาความเร็วที่พอดีทาให้รถเลี้ยวโค้งได้ รถจะเลี้ยวโค้งได้ด้วยความเร็วมากหรือน้อยขึ้นอยู่กับรัศมี (R) วงกลมของทางโค้ง และมุม q ที่รถเอียงจากแนวดิ่ง ถ้า R และ q มีค่ามาก รถจะเลี้ยวโค้งได้ด้วยความเร็วสูง q 𝑓 𝑘 = 𝜇𝑁 𝑁=𝑚𝑔 • 𝜇 = ส.ป.ส. ของแรงเสียดทานระหว่างล้อกับถนน o เมื่อ 𝐹 𝑐 = 𝑓 𝑘 = 𝑚𝑣2 𝑅 o ดังนั้น 𝑡𝑎𝑛 𝜃 = 𝑓 𝑘 𝑁 = 𝜇 = 𝑚𝑣2 𝑅 𝑚𝑔 o ได้ว่า 𝒕𝒂𝒏 𝜽 = 𝝁 = 𝒗 𝟐 𝑹𝒈 𝒗 = 𝒕𝒂𝒏 𝜽 𝑹𝒈 = 𝝁𝑹𝒈
- 35. การเคลื่อนที่เป็นทางโค้งบนถนนลื่นเอียงทามุม q กับแนวระดับ ในกรณีทางโค้งนิยมยกขอบด้านนอกให้สูงกว่าด้านในเพื่อช่วยทาให้เกิดแรงสู่ ศูนย์กลางโดยไม่ต้องอาศัยแรงเสียดทาน q 𝑵𝐜𝐨𝐬𝜽 𝑵 𝐬𝐢𝐧 𝜽 𝒎𝒈 อัตราเร็วพอดีกับมุมที่ยกขึ้น หาได้ดังนี้ o เมื่อ 𝐹 𝑐 = 𝑁 sin 𝜃 = 𝑚𝑣2 𝑅 o และ 𝑁 cos 𝜃 = 𝑚𝑔 o ได้ว่า 𝒕𝒂𝒏 𝜽 = 𝒗 𝟐 𝑹𝒈 o อัตราเร็วพอดีกับมุมที่ยกขึ้น คือ q q = มุมที่ผิวถนนกระทาต่อพื้นราบ v = อัตราเร็วที่พอดีกับมุมที่ยกผิวถนน R = เป็นรัศมีความโค้ง g = ความเร่งเนื่องจากความโน้มถ่วง 𝒗 = 𝒕𝒂𝒏 𝜽 𝑹𝒈
- 36. การเคลื่อนที่วงกลมของดาวเทียม • แรงสู่ศูนย์กลาง 𝑭𝒄 = 𝒎𝒈 𝒉ดังนั้น 𝒎𝒈 𝒉 = 𝒎𝒗 𝟐 𝑹 หรือ 𝒎𝒈 𝒉 = 𝑮𝒎𝑴 𝑹 𝟐 • ค่าแรงโน้มถ่วงกระทากับดาวเทียม 𝒈 𝒉 = 𝑮𝑴 𝑹 𝟐 เมื่อ 𝑹 = 𝑹 𝑬 + 𝒉 • ความเร็วของดาวเทียม 𝒈 𝒉 = 𝒗 𝟐 𝑹 𝒗 𝑹 น้าหนักดาวเทียมลงสู่โลก เป็นแรงสู่ศูนย์กลาง 𝒎𝒈 𝒉 𝒎 𝑴 𝑹 𝑬 • G คือ ค่านิจความโน้มถ่วงสากล มีค่า 6.672 x 10-11 Nm2/kg2𝒗 = 𝒈 𝒉 𝑹 = 𝒈 𝒉 𝑹 𝑬 + 𝒉 = 𝑮𝑴 𝑹 𝑬 + 𝒉
- 37. จงหาความเร่งเข้าสู่ศูนย์กลางของวัตถุที่เคลื่อนที่เป็นรูปวงกลมรัศมี 8 เมตร ด้วยอัตราเร็ว20 เมตร/วินาที และหากมวลที่เคลื่อนที่มีขนาด 5 กิโลกรัม จงหาแรงเข้าสู่ศูนย์กลาง ตัวอย่าง 19 𝑣 = 20 𝑚/𝑠 𝑅 = 8 𝑚
- 38. วัตถุมวล 2 กิโลกรัมผูกเชือกยาว 1 เมตร แล้วแกว่งให้เคลื่อนที่เป็น วงกลมตามแนวระดับด้วยความถี่คงที่ 2 รอบต่อวินาที จงหา ก) ความเร่งสู่ศูนย์กลาง ข) แรงตึงในเส้นเชือก ตัวอย่าง 20
- 39. โลกหมุนรอบตัวเองครบ 1 รอบใช้เวลา 24 ชั่วโมง และรัศมีของโลก เท่ากับ 6.37x106 เมตร จงคานวณหา ก) อัตราเร็วเชิงมุมของวัตถุบนผิวโลก ข) อัตราเร็วเชิงเส้น และขนาดของความเร่งสู่ศูนย์กลางของวัตถุ ที่อยู่บนเส้นศูนย์สูตรของโลก ตัวอย่าง 21
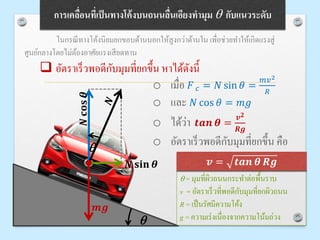
- 40. เส้นเชือกเบายาว 1 เมตรปลายข้างหนึ่งติดวัตถุมวล 0.5 กิโลกรัม อีก ปลายหนึ่งตรึงแน่นแกว่งให้วัตถุเคลื่อนที่เป็นวงกลมในแนวราบรัศมี 30 เซนติเมตร และ เส้นเชือกทามุม 37o กับแนวดิ่ง จงคานวณหา ก) อัตราเร็วเชิงเส้น และ อัตราเร็วเชิงมุม ข) แรงตึงในเส้นเชือก ค) คาบของการแกว่ง ตัวอย่าง 22 0.5 kg 37o 30 cm
- 41. การเคลื่อนที่แบบซิมเปิลฮาร์โมนิก (Simple Harmonic Motion,SHM) การเคลื่อนที่แบบซิมเปิลฮาร์โมนิก หมายถึง การที่ วัตถุเคลื่อนที่กลับไปมาซ้ารอยเดิม มักจะใช้ สัญญลักษณ์ว่า SHM. ตัวอย่างของการเคลื่อนที่แบบ นี้ได้แก่ การเคลื่อนที่ของวัตถุที่ถูกผูกติดไว้กับสปริง ในแนวราบ การแกว่งของชิงช้า การแกว่งของลูกตุ้ม นาฬิกา เป็นต้น
- 42. สมการของการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก จากภาพจะเห็นว่าเมื่อวัตถุสีเหลืองเคลื่อนที่เป็นวงกลม เงาของวัตถุบนฉากจะ เคลื่อนที่เป็นเส้นตรงกลับไปกลับมา เรียกการเคลื่อนที่แบบซ้ารอยเดิมนี้ว่าการ เคลื่อนที่แบบซิมเปิลฮาร์โมนิค (Simple Harmonic Motion) หรือการเคลื่อนที่ แบบ S.H.M q ฉาก เงาของบอล 𝑹 𝒀
- 43.
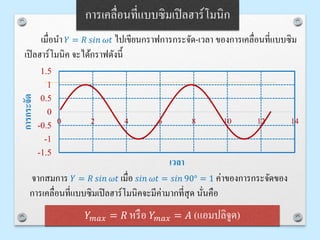
- 44. การเคลื่อนที่แบบซิมเปิลฮาร์โมนิก 𝑌 𝑚𝑎𝑥 =𝑅 หรือ 𝑌 𝑚𝑎𝑥 = 𝐴 (แอมปลิจูด) เมื่อนา 𝑌 = 𝑅 𝑠𝑖𝑛 𝜔𝑡 ไปเขียนกราฟการกระจัด-เวลา ของการเคลื่อนที่แบบซิม เปิลฮาร์โมนิค จะได้กราฟดังนี้ จากสมการ 𝑌 = 𝑅 𝑠𝑖𝑛 𝜔𝑡 เมื่อ 𝑠𝑖𝑛 𝜔𝑡 = 𝑠𝑖𝑛 90° = 1 ค่าของการกระจัดของ การเคลื่อนที่แบบซิมเปิลฮาร์โมนิคจะมีค่ามากที่สุด นั่นคือ -1.5 -1 -0.5 0 0.5 1 1.5 0 2 4 6 8 10 12 14 การกระจัด เวลา
- 45.
- 46. 2 2 2 2 F ma kx mx k m T m T k w v v 2 k T m w ซิมเปิลฮาร์โมนิคในสปริง ตาแหน่งสมดุล −𝒙 +𝒙
- 47. สปริงเบาตัวหนึ่งมีค่านิจ 100 นิวตัน/เมตรผูกติดกับมวล 1 กิโลกรัม ซึ่งวางอยู่บนพื้น ราบเกลี้ยง เมื่อดึงสปริงออกไป 30 เซนติเมตร แล้ว ปล่อยมือ มวลก้อนนี้จะมีอัตราเร่งสูงสุดเท่าใด ตัวอย่าง 23
- 48. รถทดลองมวล 500 กรัมติดอยู่กับปลายสปริงดังรูป เมื่อดึงด้วยแรง 5 นิวตัน ในทิศขนานกับพื้น จะทาให้สปริงยืดออก 10 เซนติเมตร เมื่อ ปล่อยรถจะเคลื่อนที่กลับไปกลับมาบนพื้นเกลี้ยงแบบซิมเปิลฮาร์โมนิก ด้วยคาบเท่าไร(ค่าคงที่สปริงเท่ากับ 10 N/m) ตัวอย่าง 24
- 49. แขวนมวล 2 กิโลกรัมกับสปริง แล้วปล่อยให้สั่นขึ้นลง วัดคาบของ การสั่นได้1 วินาที ถ้าเอามวล 2 กิโลกรัม ออกสปริงจะสั้นกว่าตอนที่ แขวนมวลนี้อยู่กี่เมตร ตัวอย่าง 25
- 50. การเคลื่อนที่แบบลูกตุ้มนาฬิกา จากรูป เป็นการเคลื่อนที่แบบลูกตุ้มนาฬิกา (simple pendulum)ซึ่งเป็นการเคลื่อนที่แบบซิมเปิลฮาร์มอนิ กอย่างง่าย อีกลักษณะหนึ่งโดยการนาวัตถุมวล m ผูกเชือกยาว l เมื่อวัตถุแกว่งเป็นมุมแคบๆ (q มีค่า น้อย ๆ) ซึ่งถือได้ว่าแรงลัพธ์ที่ทาให้วัตถุเคลื่อนที่มี ทิศขนานกับเส้นทางการเคลื่อนที่ของวัตถุ และส่วน โค้งของวงกลมจากตาแหน่งสมดุลถึงตาแหน่งต่างๆ ของวัตถุเป็นเส้นตรง q 𝑚𝑔 𝑇 𝒍 𝒙
- 51. การเคลื่อนที่แบบลูกตุ้มนาฬิกา o จากกฎข้อสองของนิวตัน 𝑭= 𝒎𝒂 𝑚𝑎 = −𝑚𝑔 sin 𝜃 𝑎 = −𝑔 sin 𝜃 o เมื่อ q มีค่าน้อย ๆ 𝜽 = 𝒙 𝒍 ดังนั้น 𝑎 = −𝑔 𝒙 𝒍 o จาก 𝑎 = −ω2 𝑥 ได้ว่า ω2 𝑥 = 𝑔 𝒙 𝒍 ω2 = 𝒈 𝒍 q 𝑚𝑔 𝑇 𝒍 𝒙 ∴ 𝜔 = 𝒈 𝒍 , 𝑇 = 2𝜋 𝒍 𝒈 และ 𝑓 = 1 2𝜋 𝒈 𝒍
- 52. ลูกตุ้มแขวนด้วยเชือกยาว 0.4 เมตรแกว่งไปมาด้วยแอมพลิจูด 0.1 เมตร จงหา ความเร็วขณะเคลื่อนผ่านจุดสมดุล ตัวอย่าง 26 q 𝑥 = 0.1 𝑚
- 53. ลูกตุ้มแขวนด้วยเชือกยาว 100 เซนติเมตรเมื่อจับลูกตุ้มให้เบนออกมา จากตาแหน่ง สมดุลเป็นระยะ 5 เซนติเมตร แล้วปล่อยให้แกว่งอย่าง อิสระความเร็วสูงสุดในการแกว่ง จะมีค่าเท่ากับกี่ เซนติเมตร / วินาที ตัวอย่าง 27