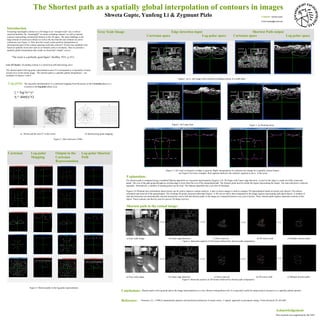
The document discusses using the shortest path algorithm in a log-polar representation to interpolate and extract meaningful contours from 2D images in an unsupervised manner. It presents computing the shortest path in a log-polar space as a spatially global interpolation method that results in closed, simple curves. Figures are provided to illustrate examples of shortest paths captured in both the log-polar and image representations, which effectively interpolate contours.

1. Introduction
Extracting meaningful contours in a 2D image in an “unsupervised” way is still an
unsolved problem. By “meaningful” we mean occluding contours, as well as internal
contours representing symmetrical features in the 3D space. The main challenge is the
large amount of irrelevant contours as well as the fact that the real contours are never
continuous (see Figure 1). How does the visual system perform interpolation of
disconnected parts of the contour ignoring irrelevant contours? All previous methods were
based on spatially local rules such as co-linearity and co-circularity. Here we present a
spatially global interpolation that results in closed and “simple” curves.
The Shortest path as a spatially global interpolation of contours in images
Shweta Gupte, Yunfeng Li & Zygmunt Pizlo
Conclusions:
Acknowledgement
Contact: Shweta Gupte
Email:svaidya@purdue.edu
This research was supported by the NSF.
Reference:
Gray Scale Image Edge detection input
Cartesian space Log-polar space
Shortest Path output
Cartesian space Log-polar space
Log-polar: The log-polar transformation is a conformal mapping from the points on the Cartesian plane (x,y)
to points in the log-polar plane (ξ,η):
Cartesian Log-polar
Mapping
Output in the
Cartesian
Representation
Log-polar Shortest
Path
a) Retina and the area V1 in the cortex b) Idealized log-polar mapping
Figure 2. After Schwartz (1980).
Figure1. (a) A real image with extracted occluding contour of a small chair.
“The circle is a perfectly good figure” (Koffka, 1935, p.151)
Explanation:
The shortest path is computed using a modified Dijkstra algorithm in a log-polar representation (Figures 2-4). We begin with Canny edge detection. A pixel on the edge is a node of a fully connected
graph. The cost of the path going through an existing edge is lower than the cost of the interpolated path. The fixation point must be inside the region representing the object. The start-end point is selected
manually. Alternatively, a number of starting points can be tried. The Dijkstra algorithm has a run time of O(nlogn).
Figures 5-6 illustrate how information about texture can be used to improve contour analysis. A pair of stereo-images is used to compute 3D representation based on texture (not shown). This allows
estimation and removal of the ground plane. The resulting 3D points represent individual objects. A 2D convex hull is then computed for the image regions representing individual objects. A number of
start and end points are automatically selected around the convex hull and shortest paths in the image are computed between every pair of points. These shortest paths capture important contours of the
object. These contours can then be used for precise 3D shape recovery.
ξ = log√x2
+y2
η = atan(y/x)
Figure1. (b) Large chair. Figure 1. (c) Rocking horse.
Figure 4. Shortest paths in the log-polar representation
Figure 3. Left: local co-linearity of edges is ignored. Right: interpretation of a junction can change by a spatially remote feature –
see Figure 4 for more examples. Red segment marked is the selected segment to move in the scene.
Shortest path in the log-polar and in the image representations is a very effective interpolation tool. It is especially useful for shape analysis because it is a spatially global operator.
Law of Closure: Occluding contour is a closed non-self-intersecting curve.
The shortest path in the log-polar representation (area V1) corresponds to a maximally circular,
closed curve in the retinal image. The shortest path is a spatially global interpolation – see
examples in Figures 3 and 4.
Shortest path in the retinal image:
a) Gray scale image b) Canny edge detection c) Floor removed d) 2D convex hull e) Multiple shortest paths
Figure 5. Binocular analysis of 3D texture followed by shortest path computation.
a) Gray scale image b) Canny edge detection c) Floor removed d) 2D convex hull e) Multiple shortest paths
Figure 6. Binocular analysis of 3D texture followed by shortest path computation.
Schwartz, E.L. (1980) Computational anatomy and functional architecture of striate cortex: A spatial approach to perceptual coding. Vision Research 20, 645-669.