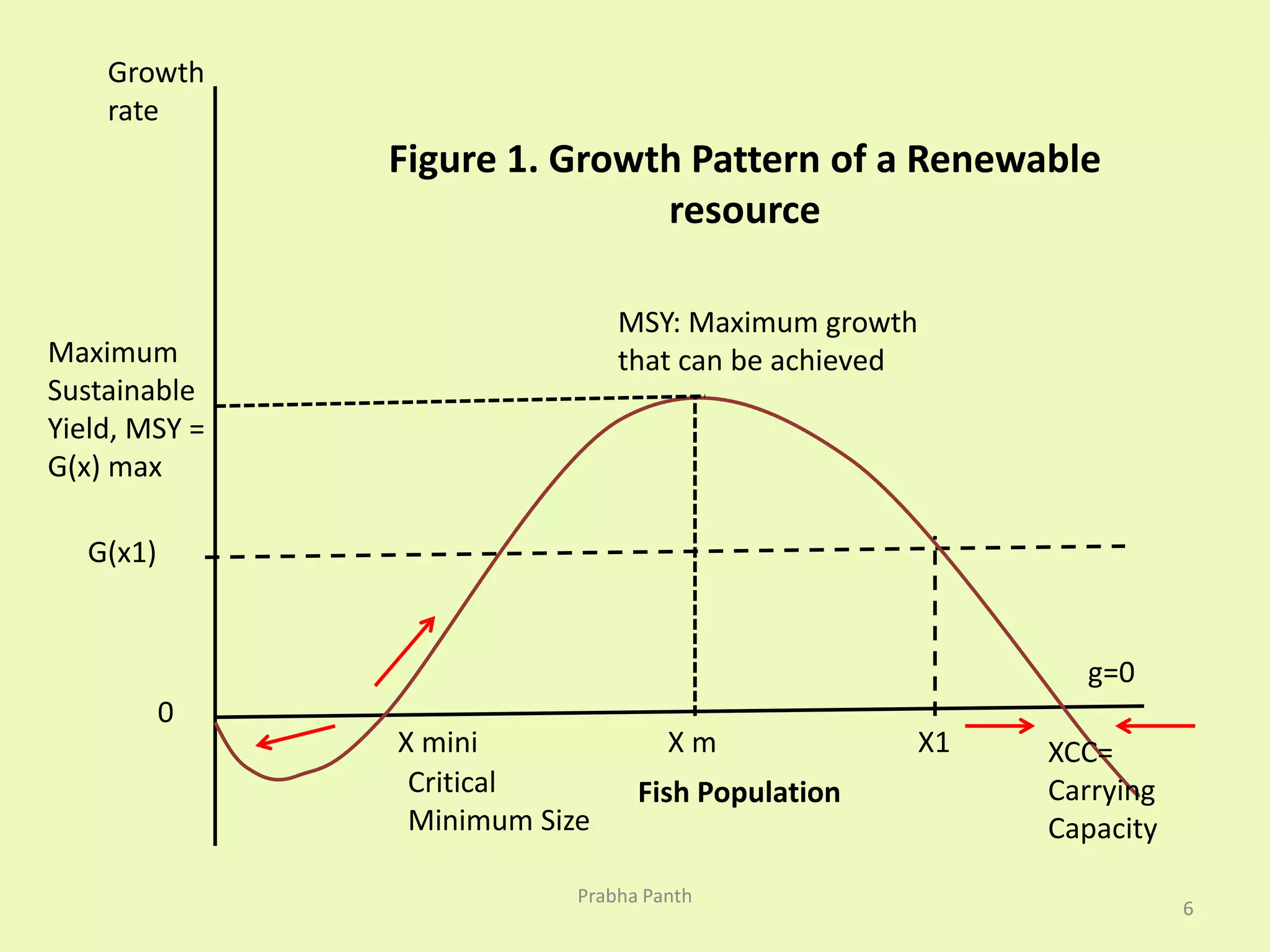
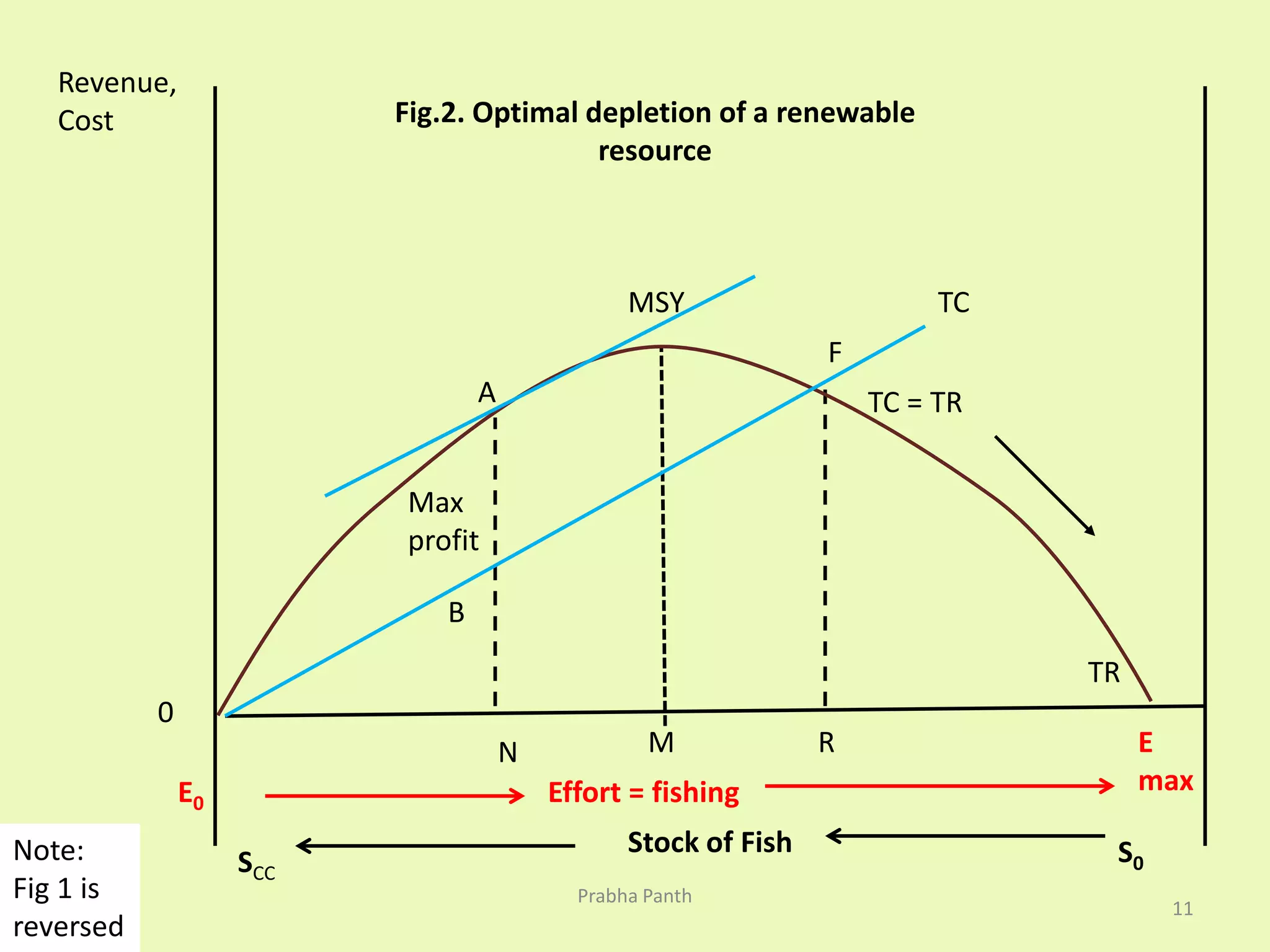
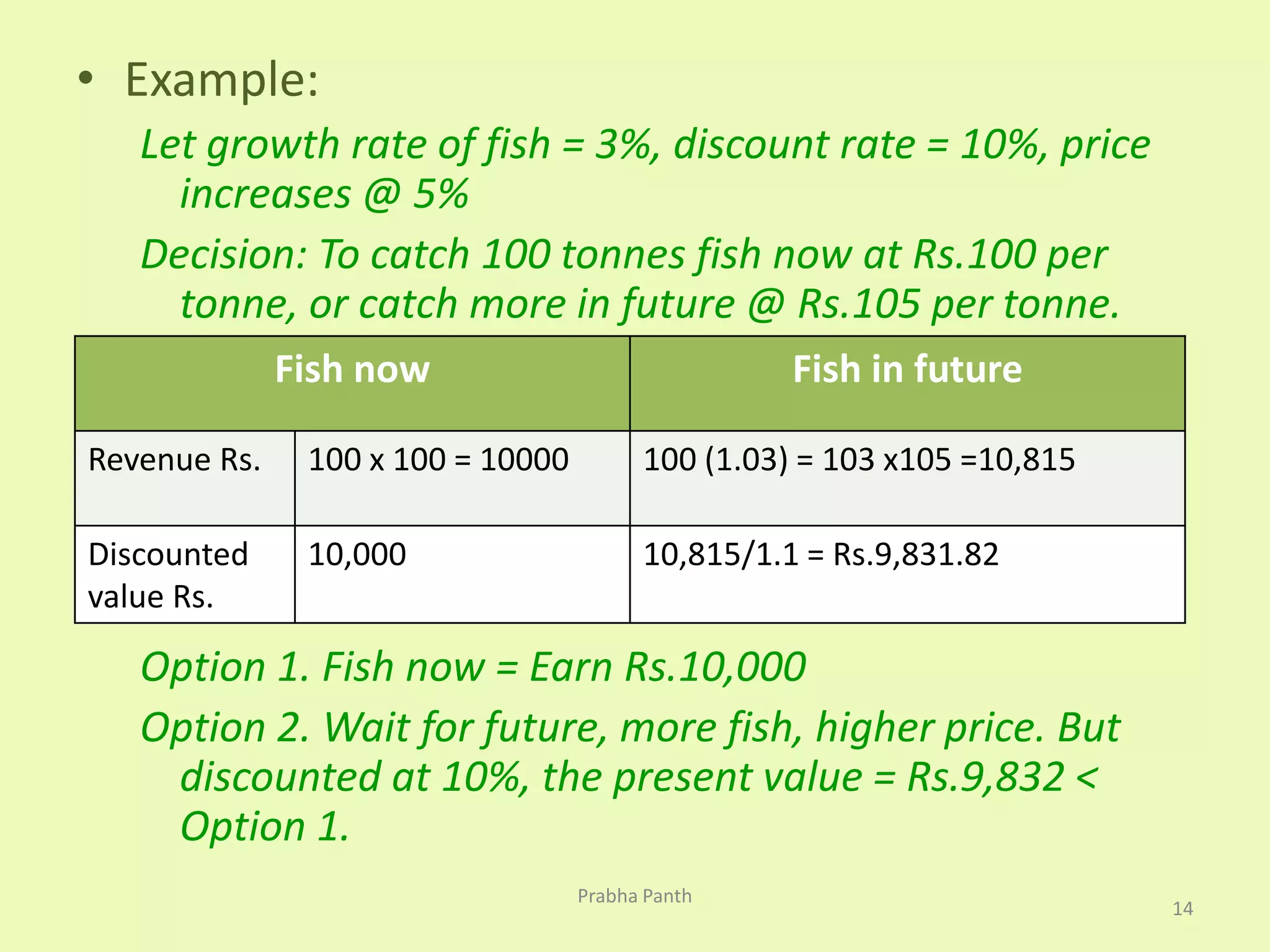
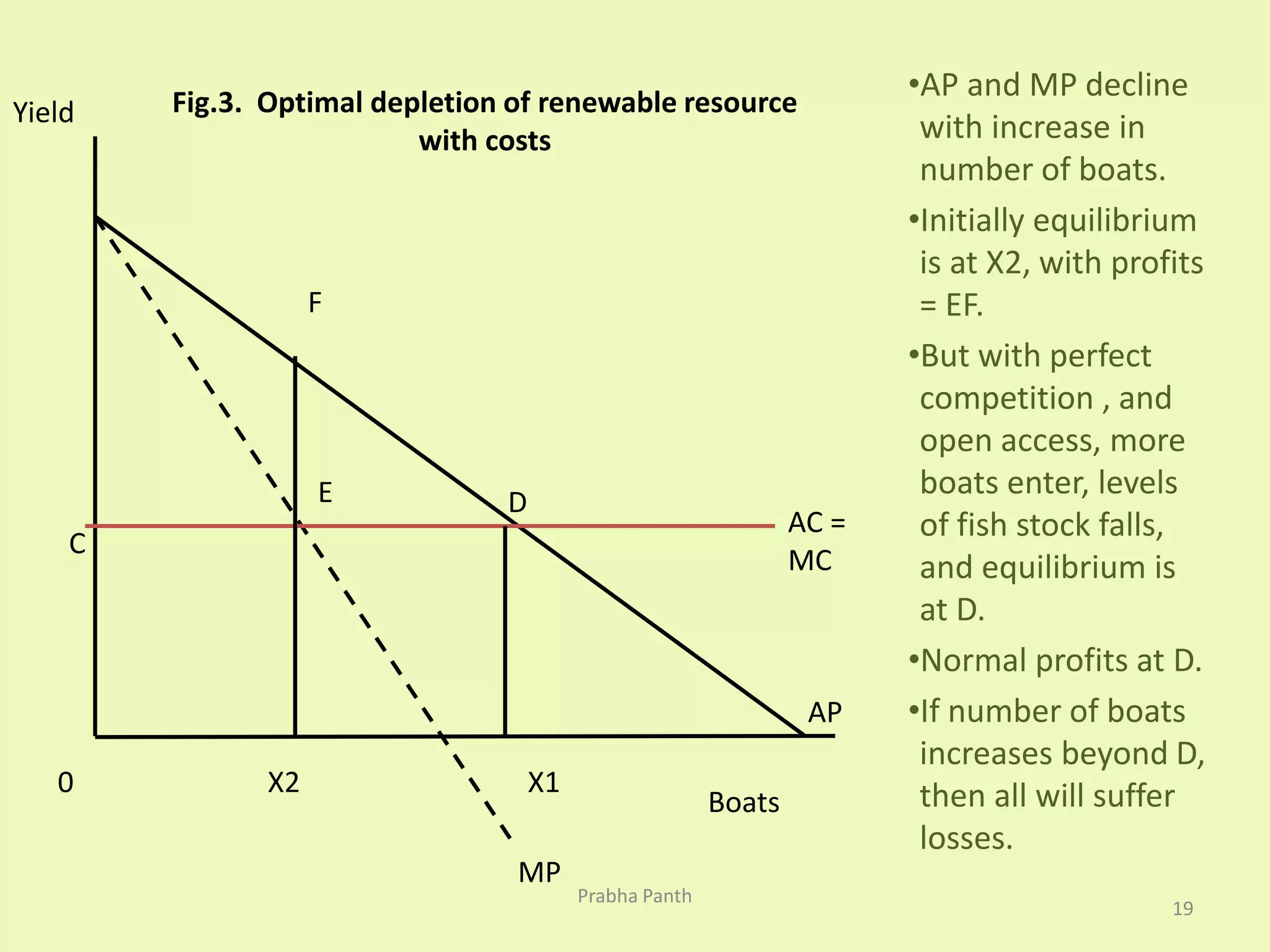
The document discusses the optimal depletion of renewable resources, emphasizing the importance of balancing the rate of exploitation with the rate of regeneration to avoid depletion. It uses the example of fish in a lake to illustrate sustainable yield and the critical minimum size, below which renewal becomes unviable. Additionally, it examines the economic implications of discount rates in resource harvesting decisions and the conflict between ecological sustainability and economic growth.

1. OPTIMAL DEPLETION OF
RENEWABLE RESOURCES
Prof. Prabha Panth
Osmania University,
Hyderabad

2. Renewable resources
• Renewable resources can reproduce themselves.
• E.g. forests, animals, birds, etc.
• But they are also prone to be depleted if the
rate of economic exploitation > the rate of
reproduction.
• Once depleted it is extremely difficult to bring
them back to their original level.
• Optimal rate of exploitation = rate of
regeneration (reproduction).
Prabha Panth 2

3. Optimal rate of depletion of
renewable resources
• Example: There is a lake with 1000 fishes, initial
stock.
• Maximum possible rate of growth of fish = 10%
p.a. Cet. Par.
• End of the year, 1000 + 100 = 1100 fishes are
available in the lake.
• Rate of depletion (catch) = 100 fish, then
remaining 1000 fishes are still available for future
growth.
• This is called Sustainable Yield.
Prabha Panth 3

4. • If 200 fishes are caught, then only 900 remain in the
lake, (1100 – 200), and addition to stock at the end of
the year @ of 10% growth = 90 fishes.
• Next year if 250 fishes are caught, then at the end of
the year, the stock will be 740, (990 – 250).
• Economists want output to grow every year,  leads to
progressive depletion of the renewable resource.
• Also growth of the resource based on various other
factors, such as age and health of the fish, water and
climatic conditions, etc.
• If the stock becomes too small: biological limits: then
this rate of reproduction cannot be maintained.
• The point where the population growth becomes
unviable is called “Critical Minimum Size”.
• If population falls below this level, stocks will die out.
4
Prabha Panth

5. • If the rate of harvesting of the renewable resources >
rate of its growth, there will be progressive depletion.
• When the renewable resource size or population falls
to a very low level, it cannot regenerate itself.
• This is the biological limit, for instance if there are only
5-6 fishes remaining, then gth cannot be sustained at
10%.
• This point where the population becomes unviable is
called “The Critical Minimum Size”.
• Below this level, the population cannot survive, and
dies out.
• Left to itself, the resource will not grow forever.
• There are natural checks which will regulate the
population and keep it within the ecological limits.
5
Prabha Panth

6. Growth
rate
Maximum
Sustainable
Yield, MSY =
G(x) max
0
Figure 1. Growth Pattern of a Renewable
resource
MSY: Maximum growth
that can be achieved
G(x1)
g=0
X mini X m X1 XCC=
Carrying
Capacity
Critical
Minimum Size
Fish Population
6
Prabha Panth

7. Growth pattern of a Renewable
resource
• Figure 1 shows the growth and decline of a
renewable resource – fish.
• Xmin is the point below which fish stock dies, and
becomes zero.
• After this point, there is growth of the fish
population.
• The fish population grows till it reaches Xm.
• Xm shows the highest rate of growth of fish, also
called MSY = Maximum Sustainable Yield.
7
Prabha Panth

8. Growth pattern of a Renewable
resource
• After this point, rate of growth of fish starts declining,
till it falls to XCC
• At this point, growth rate of fish = 0.
• XCC is a Stable Equilibrium, if fish stock increases
beyond it, then death rate increases, bringing it back to
XCC,
• If it is less, say at X1, then the population increases till it
reaches XCC,
• XCC is known as the “Carrying Capacity” of the
Ecosystem.
• It is the maximum amount of the renewable resource
that can be supported by the ecosystem.
8
Prabha Panth

9. • Economists assume that renewable resources can grow
indefinitely.
• But this is not true, as the resource growth is
constrained by biological and ecological limits.
• Economists feel that increasing the rate of harvesting
of the renewable resource, will not affect its growth.
• But, if the resource is exploited up to the point of its
Critical Minimum Size, then the resource will die out or
even become extinct.
• It is difficult to revive the species once it reaches the
critical minimum size.
• E.g. rhinos, tigers, pandas, lions, etc. are all in danger
of reaching this critical level, due to over kill.
9
Prabha Panth

10. Model of Optimal Level of Depletion
of a Renewable resource
• How much of the resource should be
harvested ?
• Conflict between ecologists and economists.
Assumptions:
1. Micro unit,
2. Price of the resource (fish) is constant (P.C.).
3. No discounting,
4. MC of fishing is constant.
10
Prabha Panth

11. Revenue,
Cost
0
Fig.2. Optimal depletion of a renewable
resource
MSY
Max
profit
B
F
R
A
M
TC
TR
TC = TR
E max 0
Stock of Fish
N
Effort = fishing
E
S S0 CC
Note:
Fig 1 is
reversed
11
Prabha Panth

12. • TR = p.Q, TC = ΣMC, Profit maximising condition =
MC = MR, MC
• When Effort (fishing) = 0, then there is maximum
carrying capacity, Scc.
• When Effort is maximum, fish stock is zero, So, E
max.
• As effort increases TC increases, yield increases, and
TR increases.
• Max profit = MC=MR, MC, at N. Max profit = AB.
• But this is less than Max Sust Yield (MSY) at M.
• If there is perfect competition, long run equilibrium is
at F, where TR=TC,
• But now this is the declining part of fish growth, and
stocks will start depleting, and fall to So.
• Open access with unrestricted entry, leads to over
exploitation, and the renewable resource is driven to
extinction.
12
Prabha Panth

13. Discounting
• The above model is a static analysis.
• Taking ‘time’ into consideration we get:
– A) Time preference
– B) Growth in capital value (interest). Leads to positive discount
rate.
• If the fish is caught now, profits earned now (time
preference).
• If left in pond, will reproduce in future. Also prices in future
may rise. More profits in future.
• But the fisherman has to wait.
• So harvesting the renewable resource now depends on:
Discount rate > = < Biological rate of growth + Growth in
capital value (expected price).
13
Prabha Panth

14. • Example:
Let growth rate of fish = 3%, discount rate = 10%, price
increases @ 5%
Decision: To catch 100 tonnes fish now at Rs.100 per
tonne, or catch more in future @ Rs.105 per tonne.
Fish now Fish in future
Revenue Rs. 100 x 100 = 10000 100 (1.03) = 103 x105 =10,815
Discounted
value Rs.
10,000 10,815/1.1 = Rs.9,831.82
Option 1. Fish now = Earn Rs.10,000
Option 2. Wait for future, more fish, higher price. But
discounted at 10%, the present value = Rs.9,832 <
Option 1.
14
Prabha Panth

15. • If Discount rate > Biological rate of growth +
capital appreciation = Harvest now.
• E.g. 10% > 3% + 5% in our former example.
• If Discount rate < Biological rate of growth +
capital appreciation = Harvest later.
• E.g. Discount rate 10% < Biological rate of
growth 4% + capital appreciation 8%
• If both are equal, then the fisherman is
indifferent between present and future.
15
Prabha Panth

16. • Therefore:
o If discounted value of future P < Present price,
present is preferred. (Rs.9832 < Rs.10,000)
o Otherwise wait for the future.
• In other words:
P0(1+r) = P1(1+g), or P0/P1 = (1+g)/(1+r)
1) If r = g, P1 = P0 , indifferent
2) If r < g, P0 < P1, conserve for future,
3) If r > g, P0 > P1, exploit now.
16
Prabha Panth

17. Dasgupta and Heal Model
Former models assume fishing is free, i.e. there are no
costs of fishing.
Assumptions:
1. Open access, e.g. sea fishing.
2. Identical fishing firms, n,
3. X = total number of fishing vessels, xi = composite
input: labour, fishing equipment (variables).
4. S = size of fishing area,
5. Y = fish catch or output, YH(X,S)
6. H = production function, CRS. H=f(X,S), since S is
fixed, H = F(X)
7. Diminishing returns to X, i.e. As fishing boats
increase, congestion leads to loss of output.
17
Prabha Panth

18. • Let the firm own xi vessels, then its catch will
be xi.(F(X)/X) = xi.A(X)
• Rental cost of each boat = r, (constant)
• As number of boats increases, TC increases,
but AC = MC = r.
• Over crowding with too many boats.
• Leads to low catch, low profits.
• Perfect competition, P = MC at D, leads to over
crowding and over exploitation.
18
Prabha Panth

19. •AP and MP decline
with increase in
number of boats.
•Initially equilibrium
is at X2, with profits
= EF.
•But with perfect
competition , and
open access, more
boats enter, levels
of fish stock falls,
and equilibrium is
at D.
•Normal profits at D.
•If number of boats
increases beyond D,
then all will suffer
losses.
Yield
Fig.3. Optimal depletion of renewable resource
Boats
0
F
AC =
MC
with costs
X2 X1
C
E D
AP
MP
19
Prabha Panth