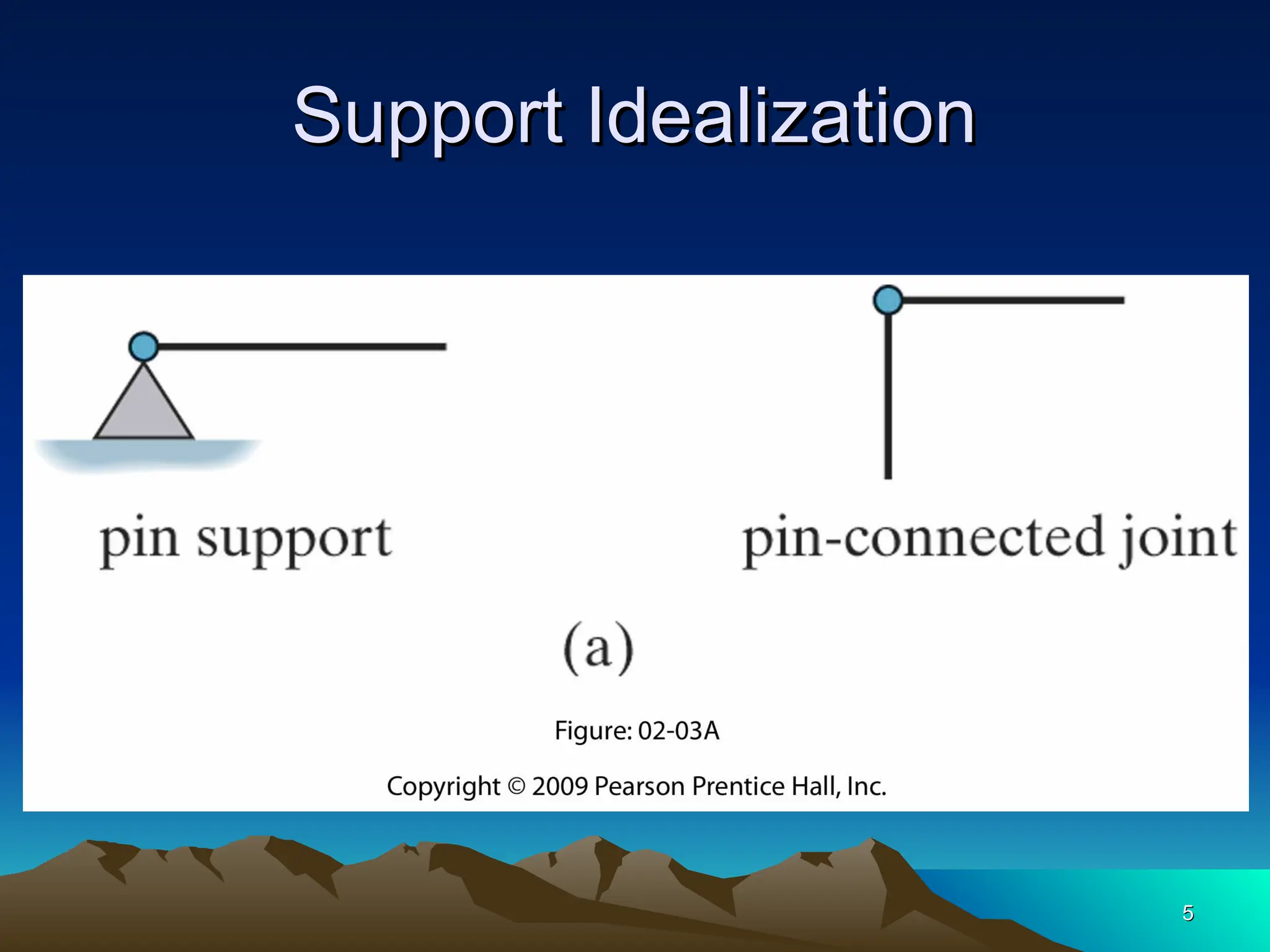
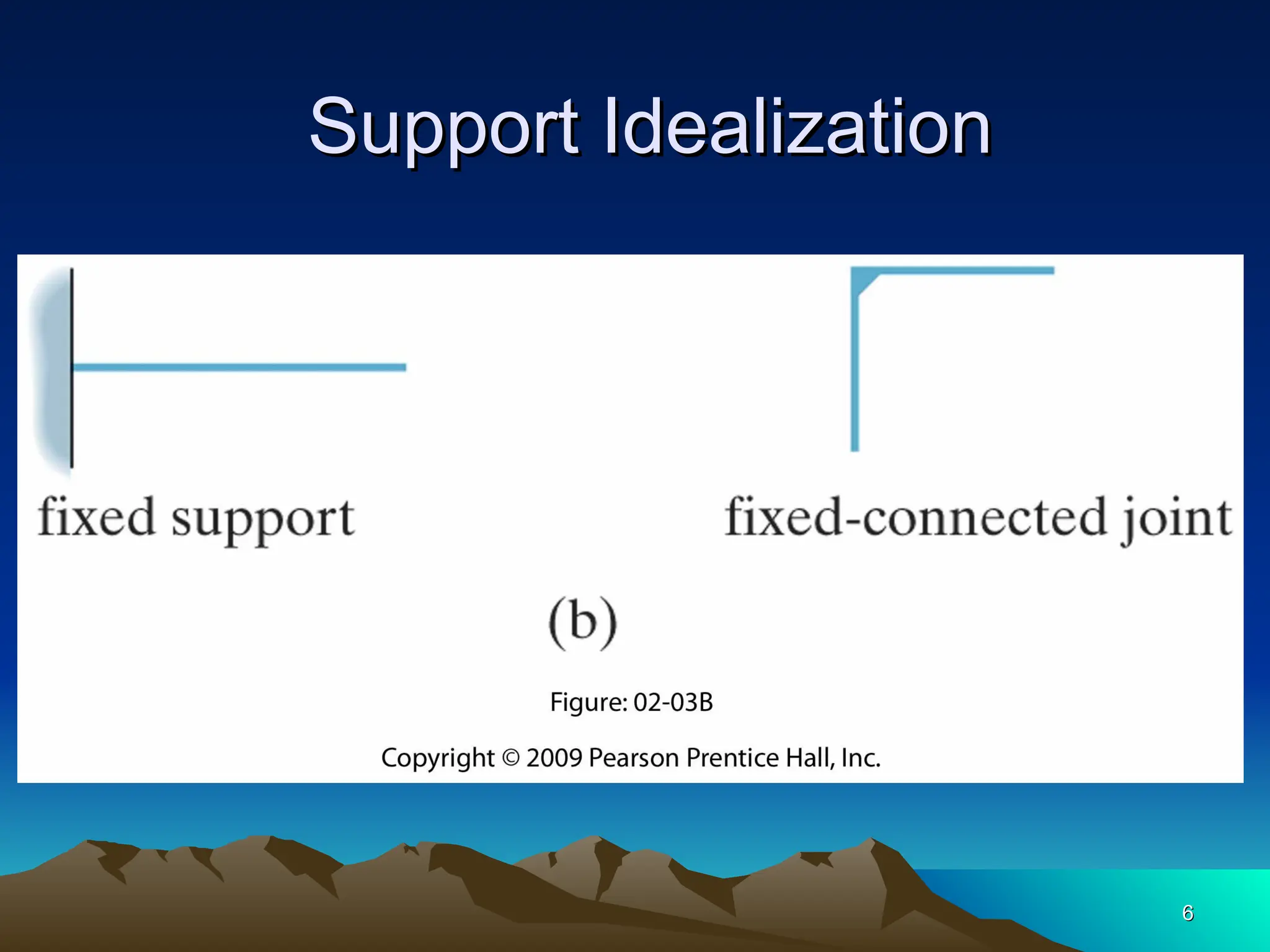
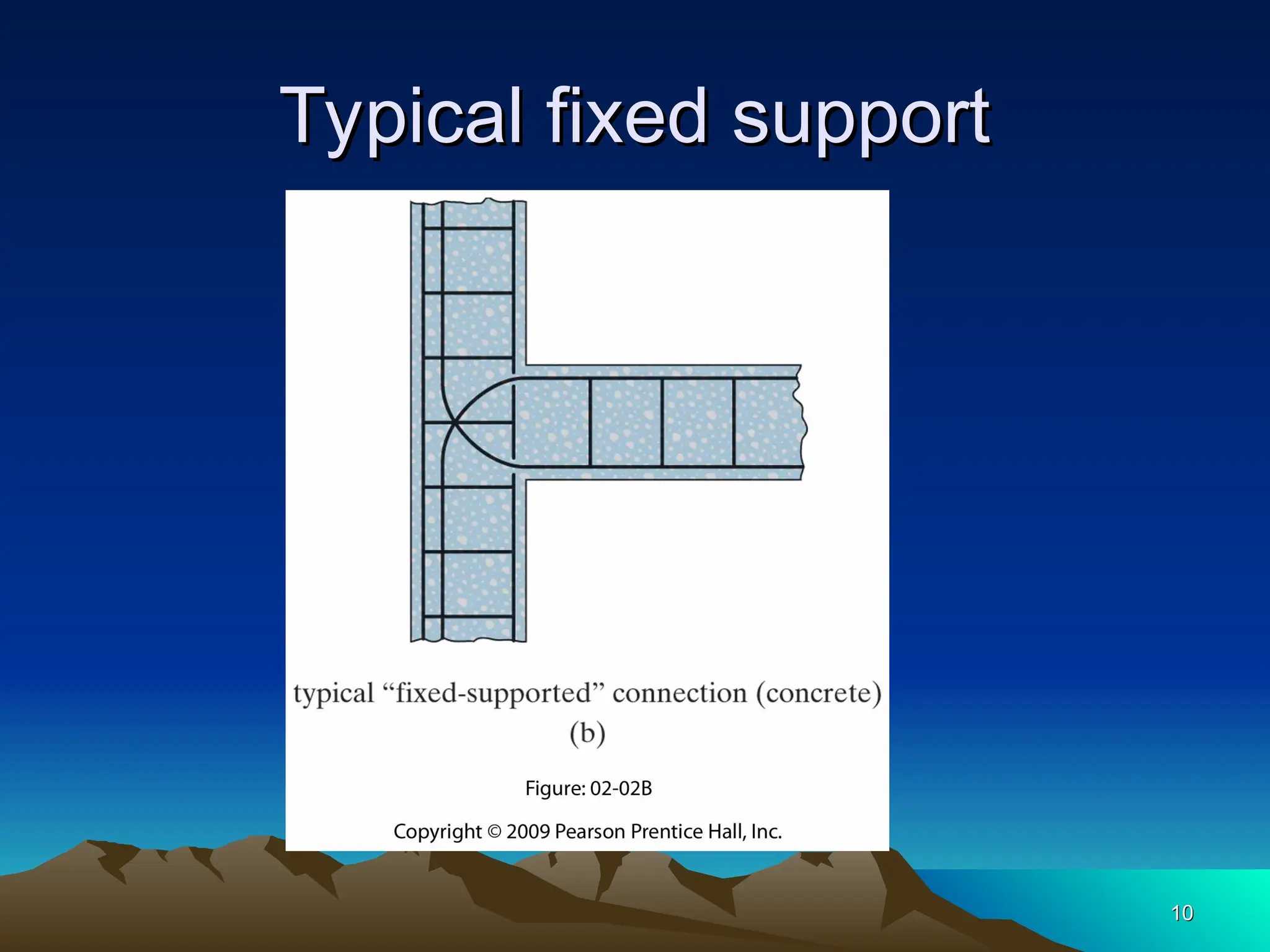
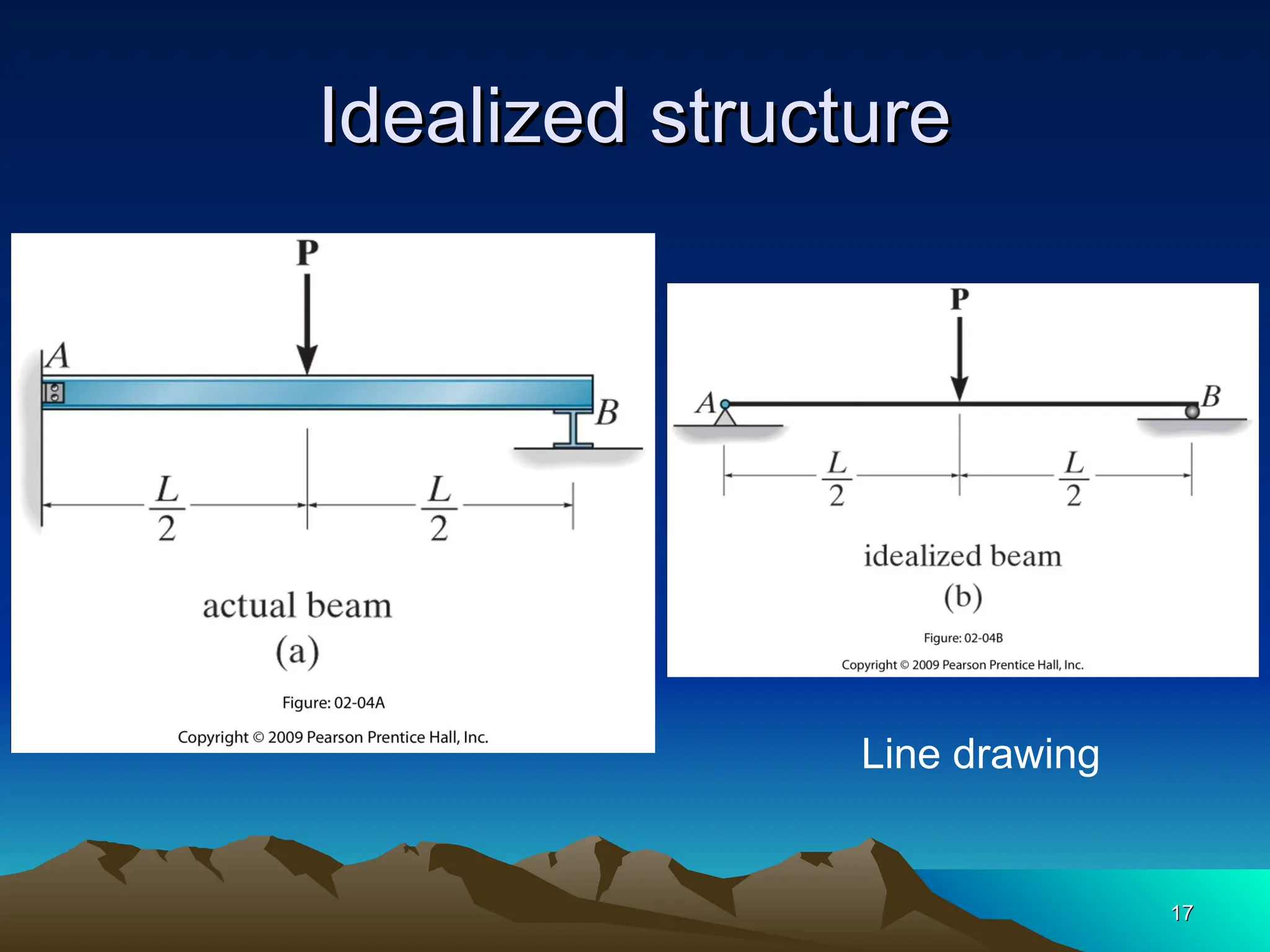
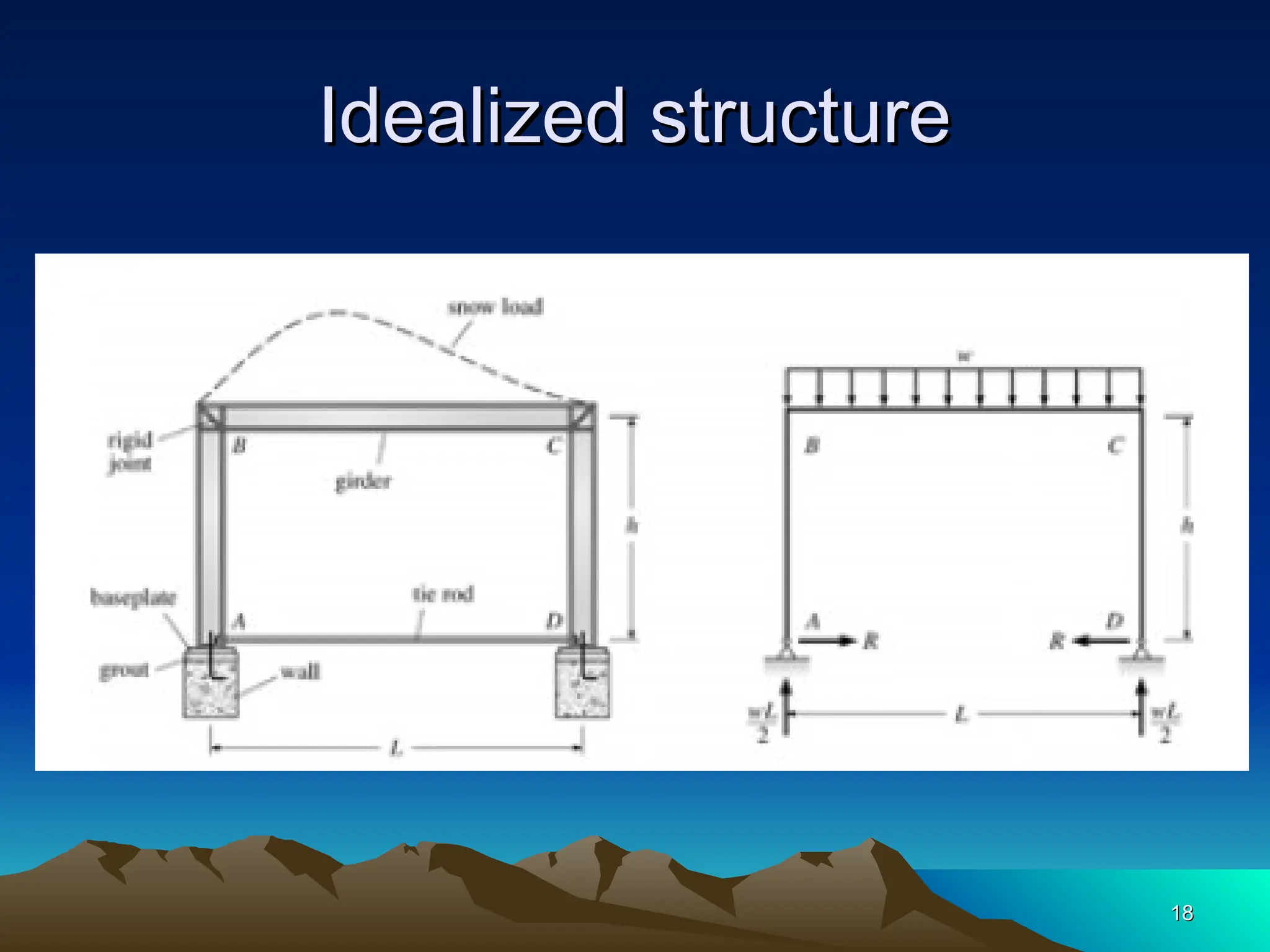
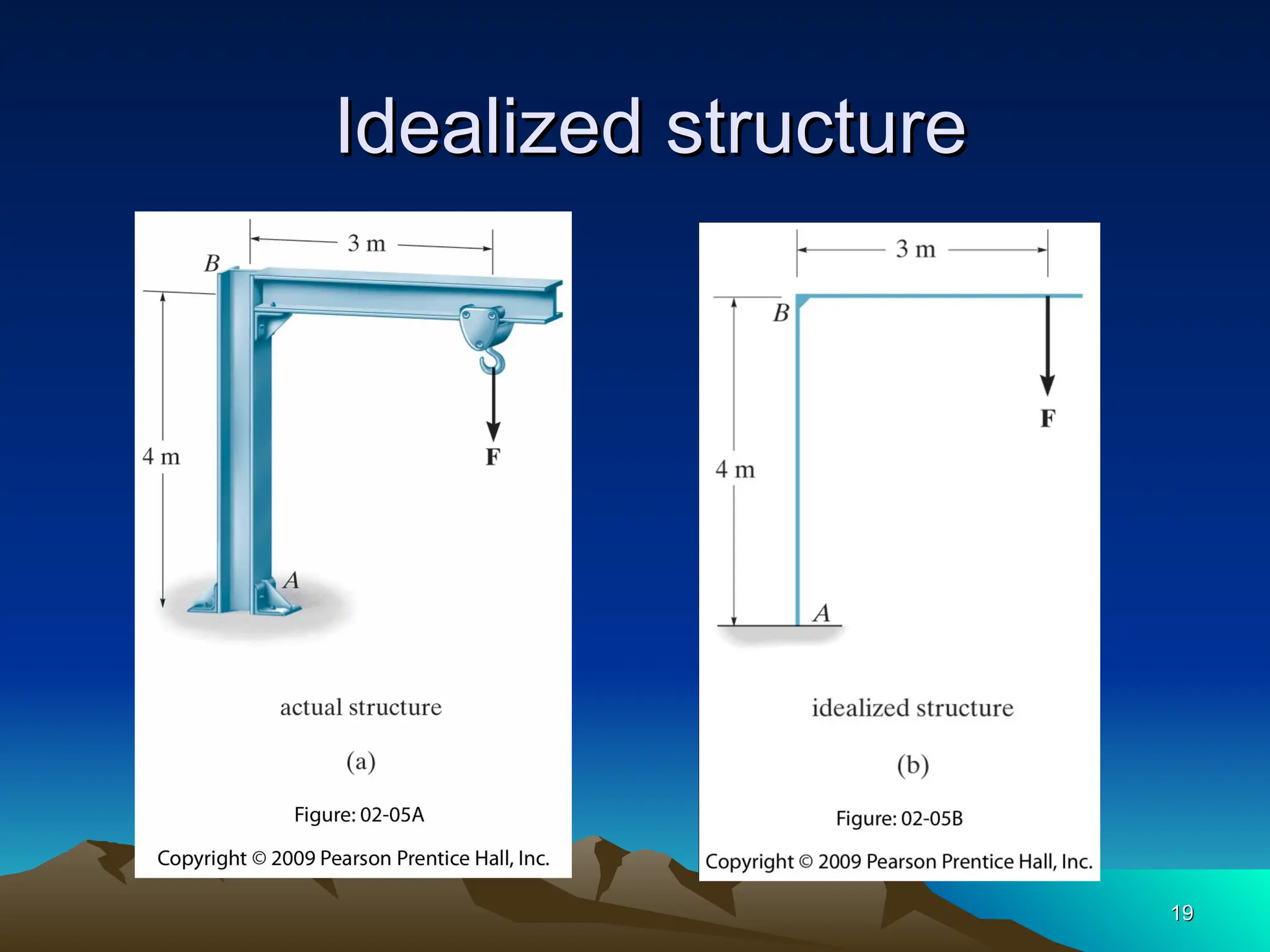
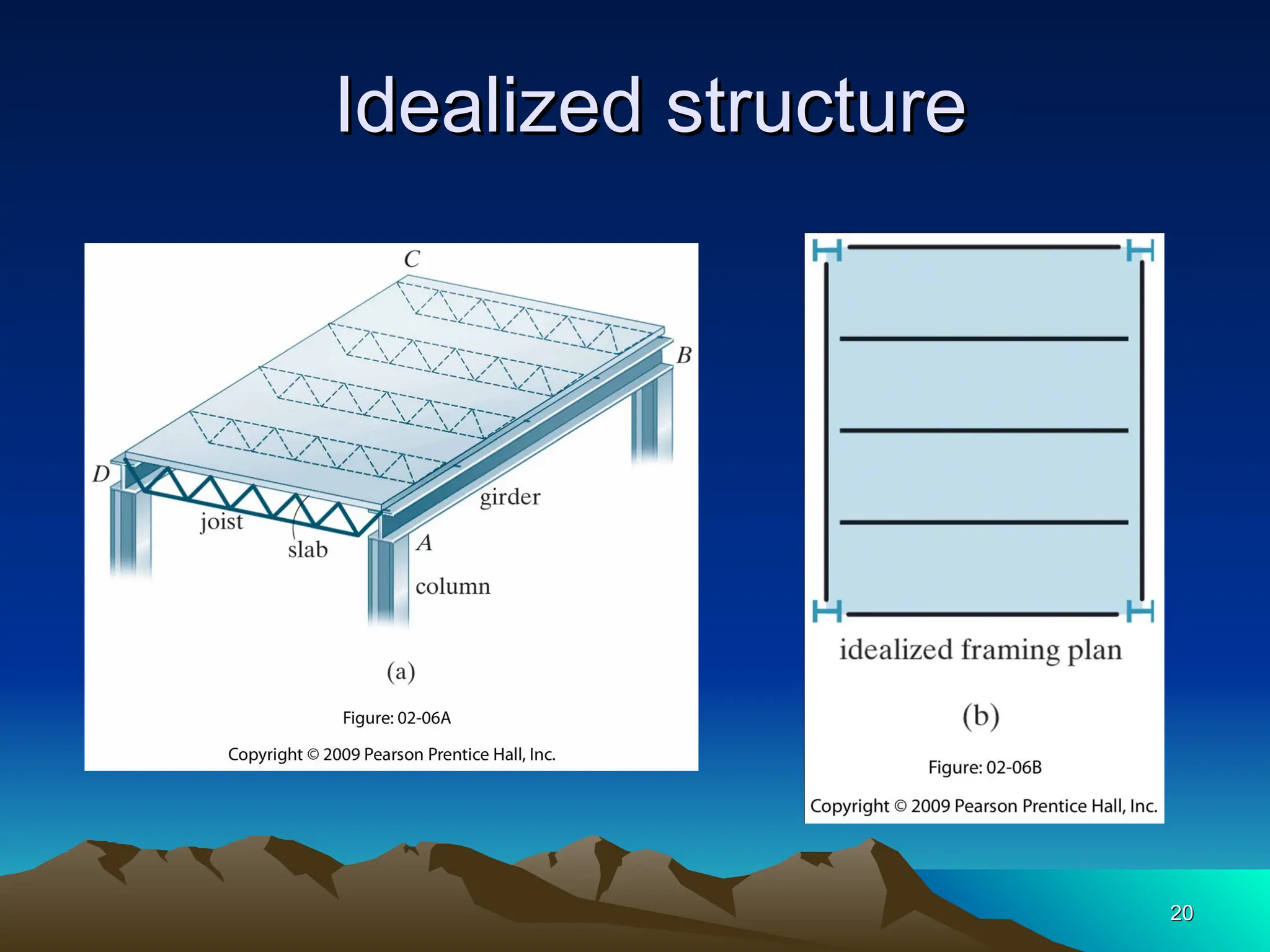
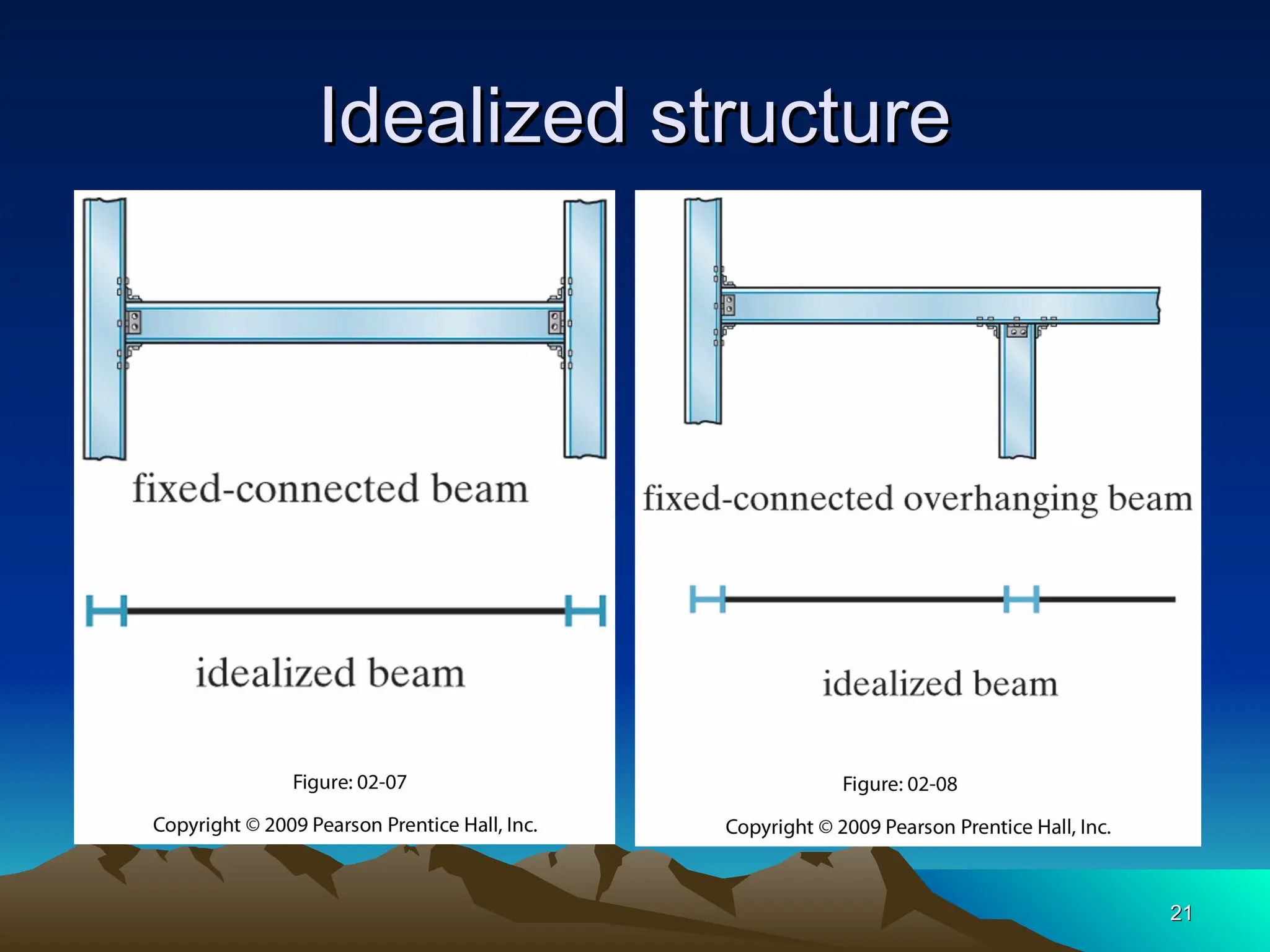
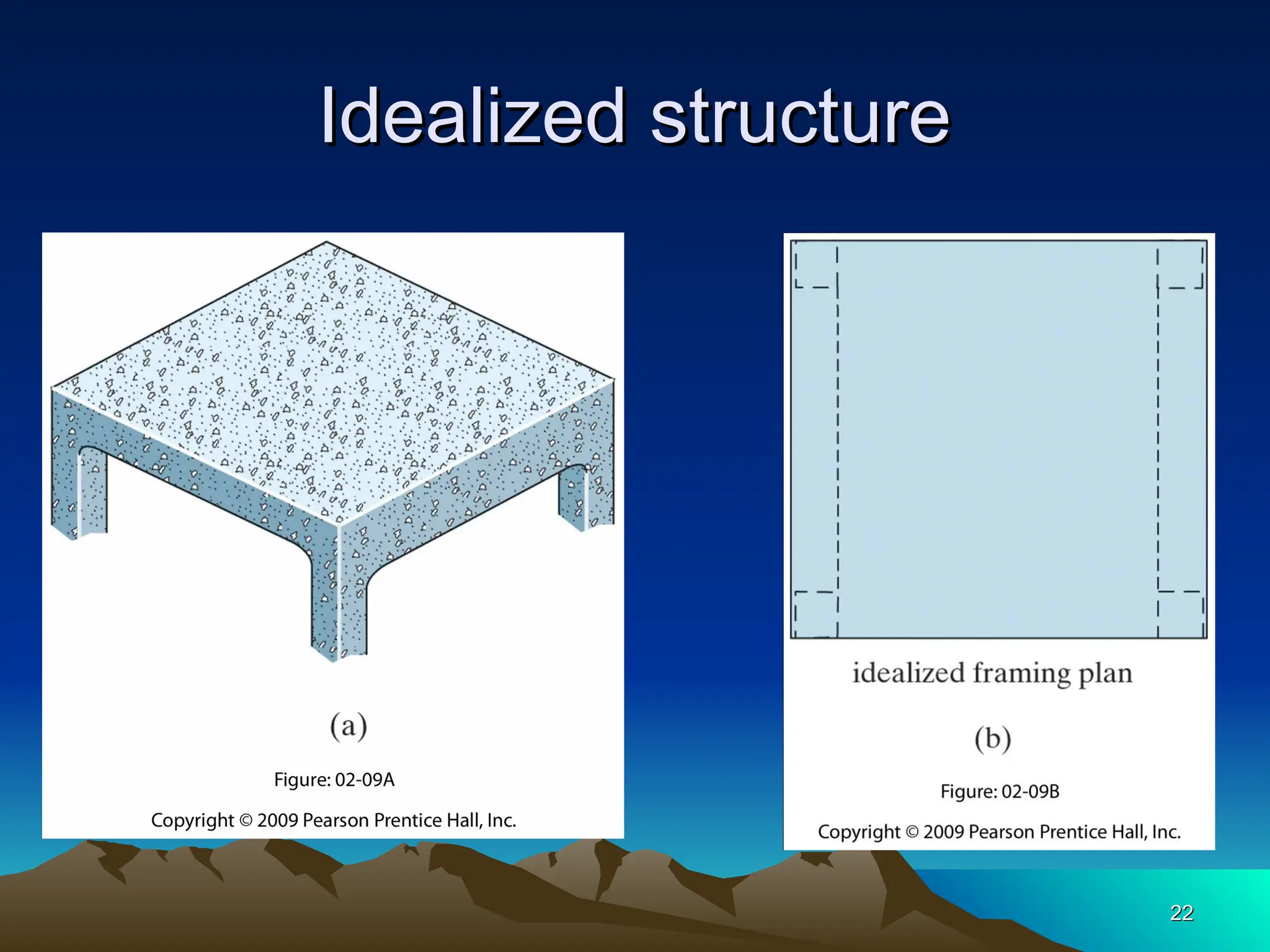
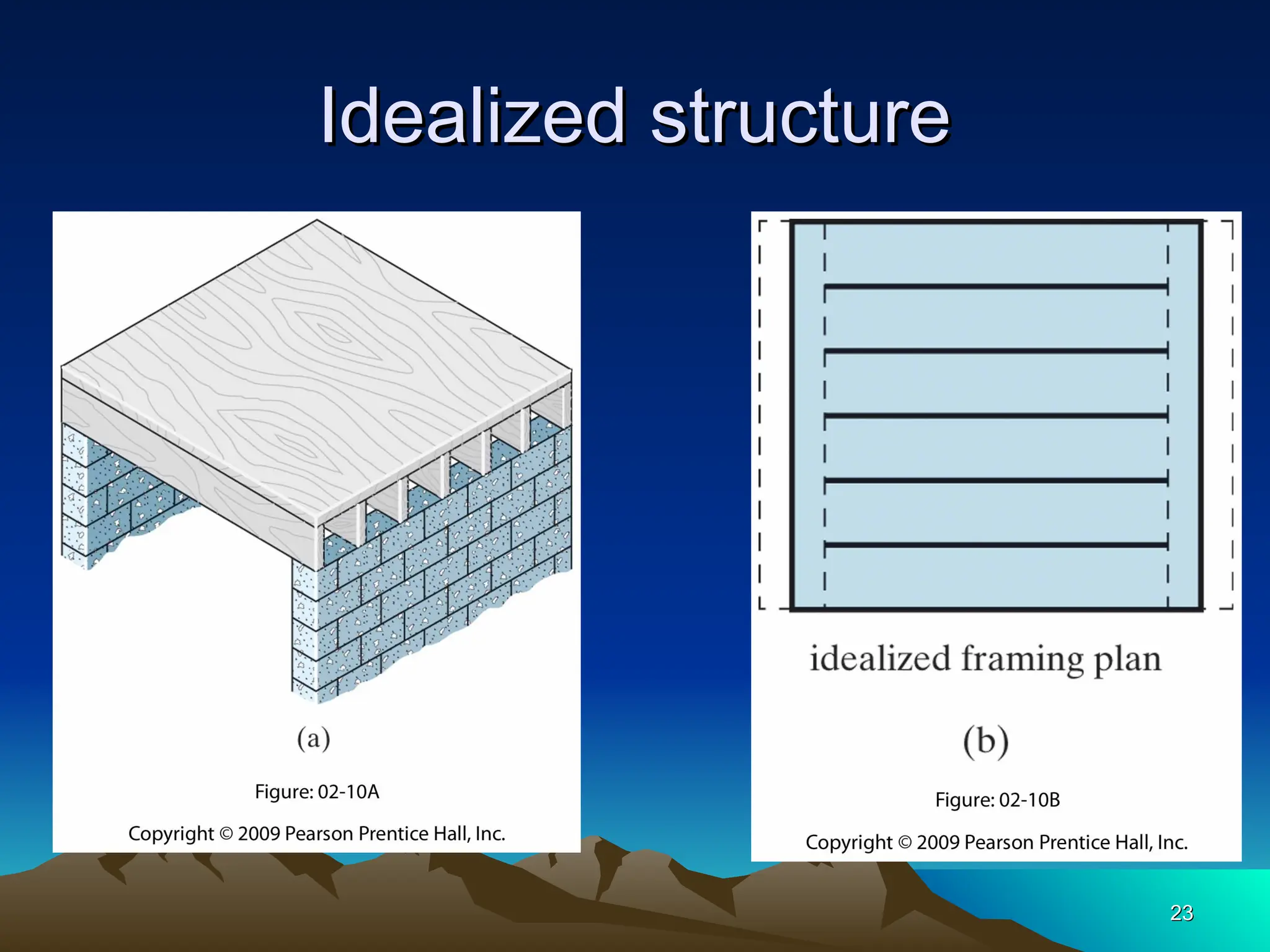
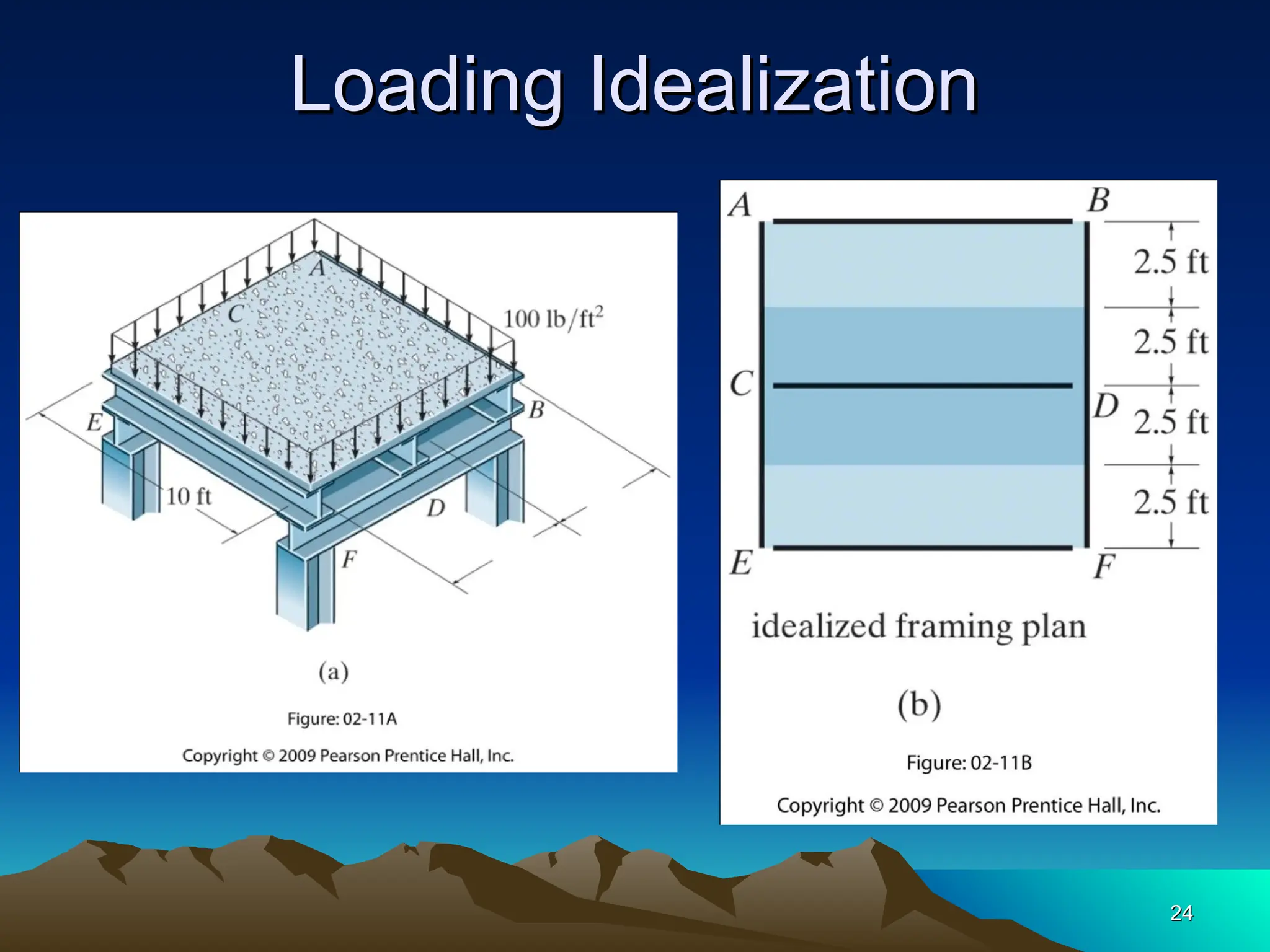
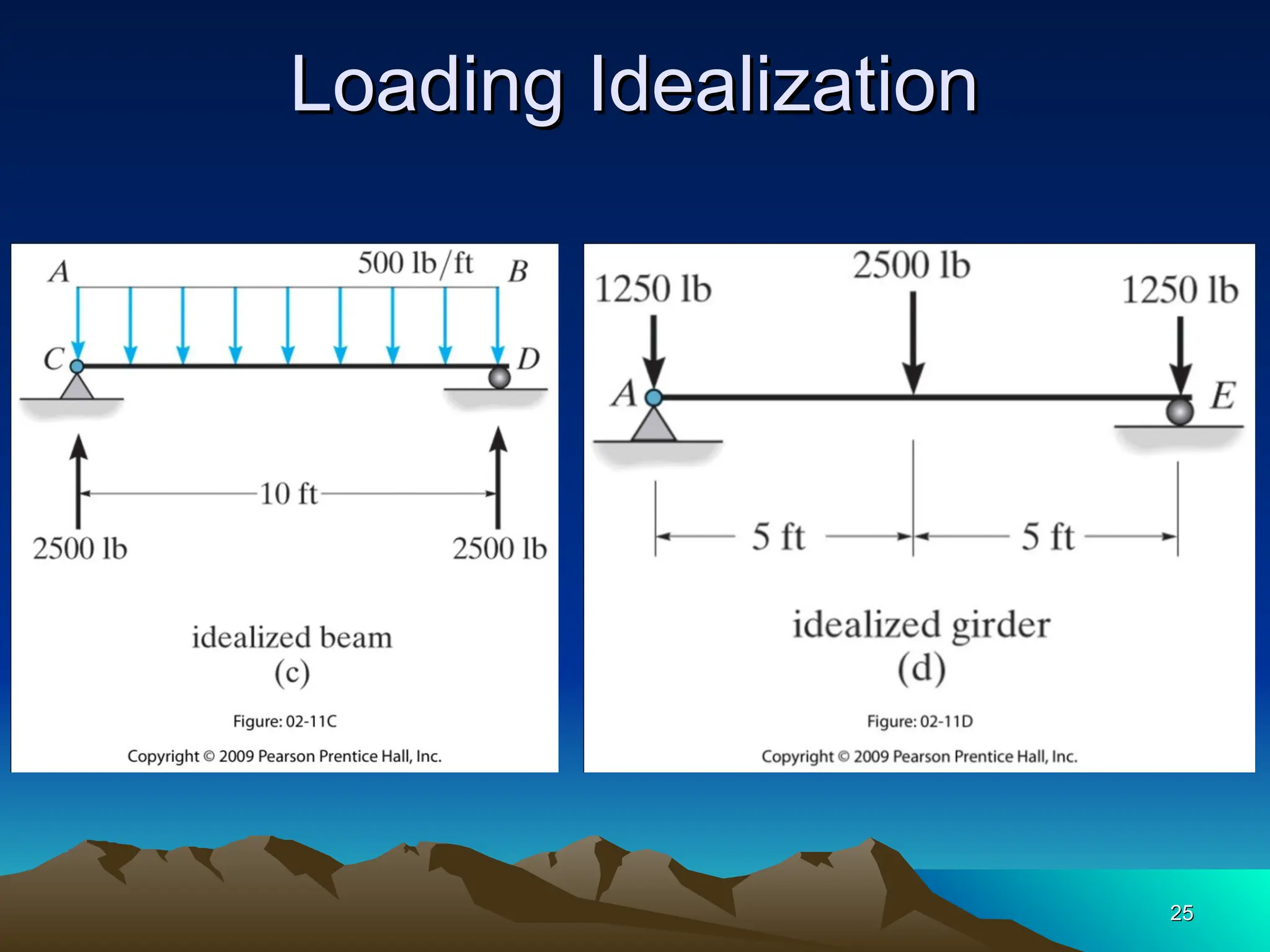
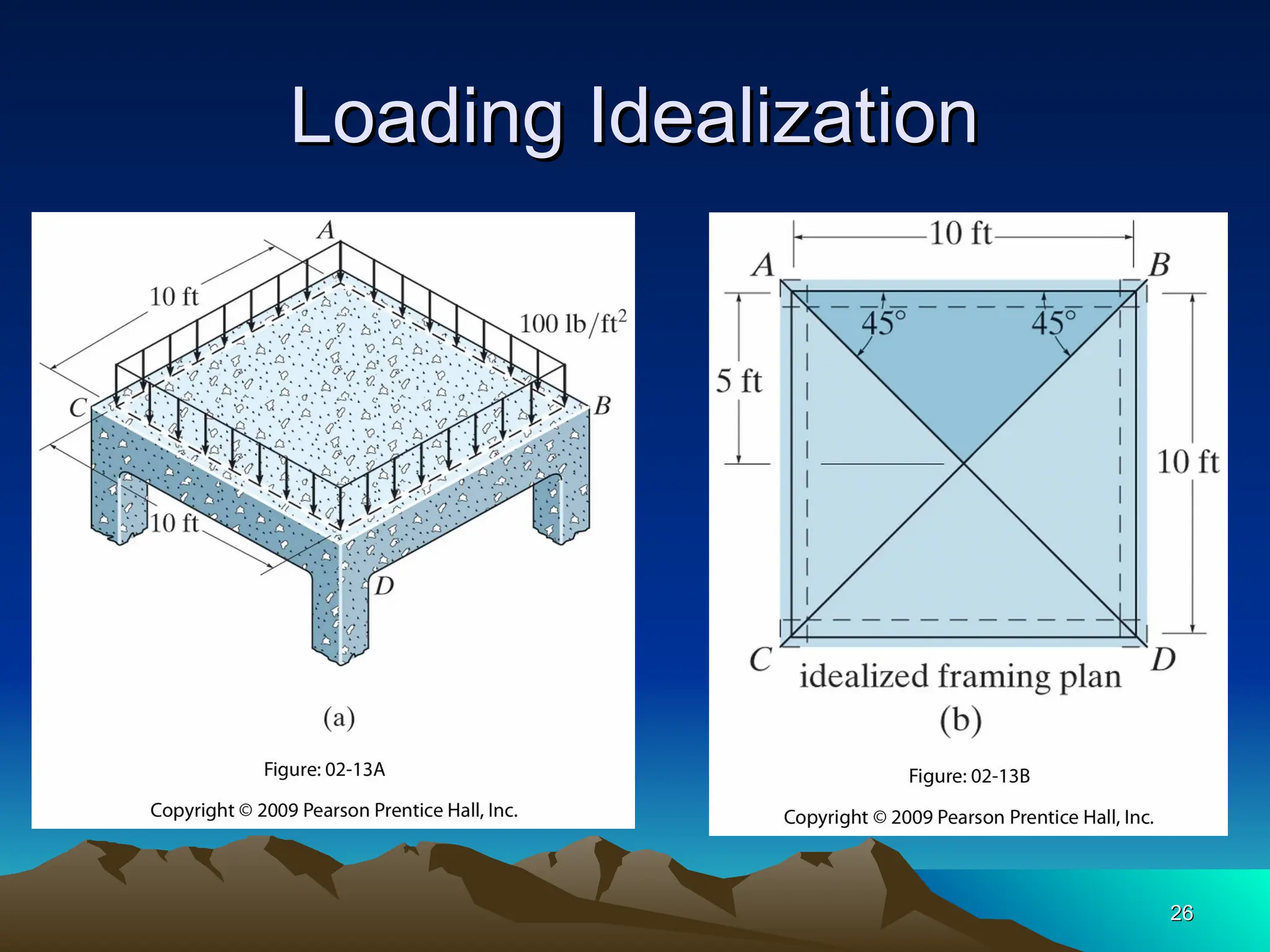
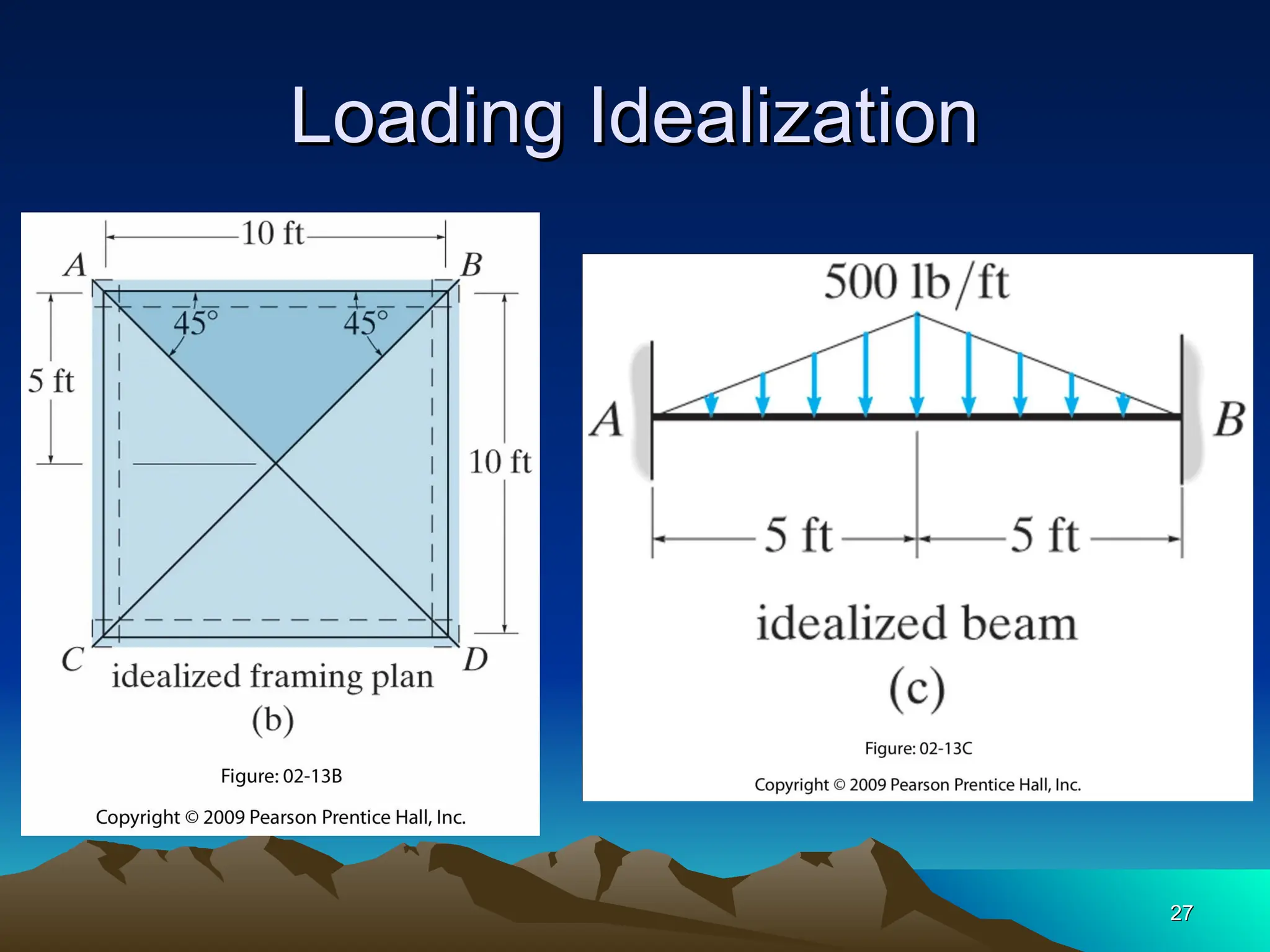
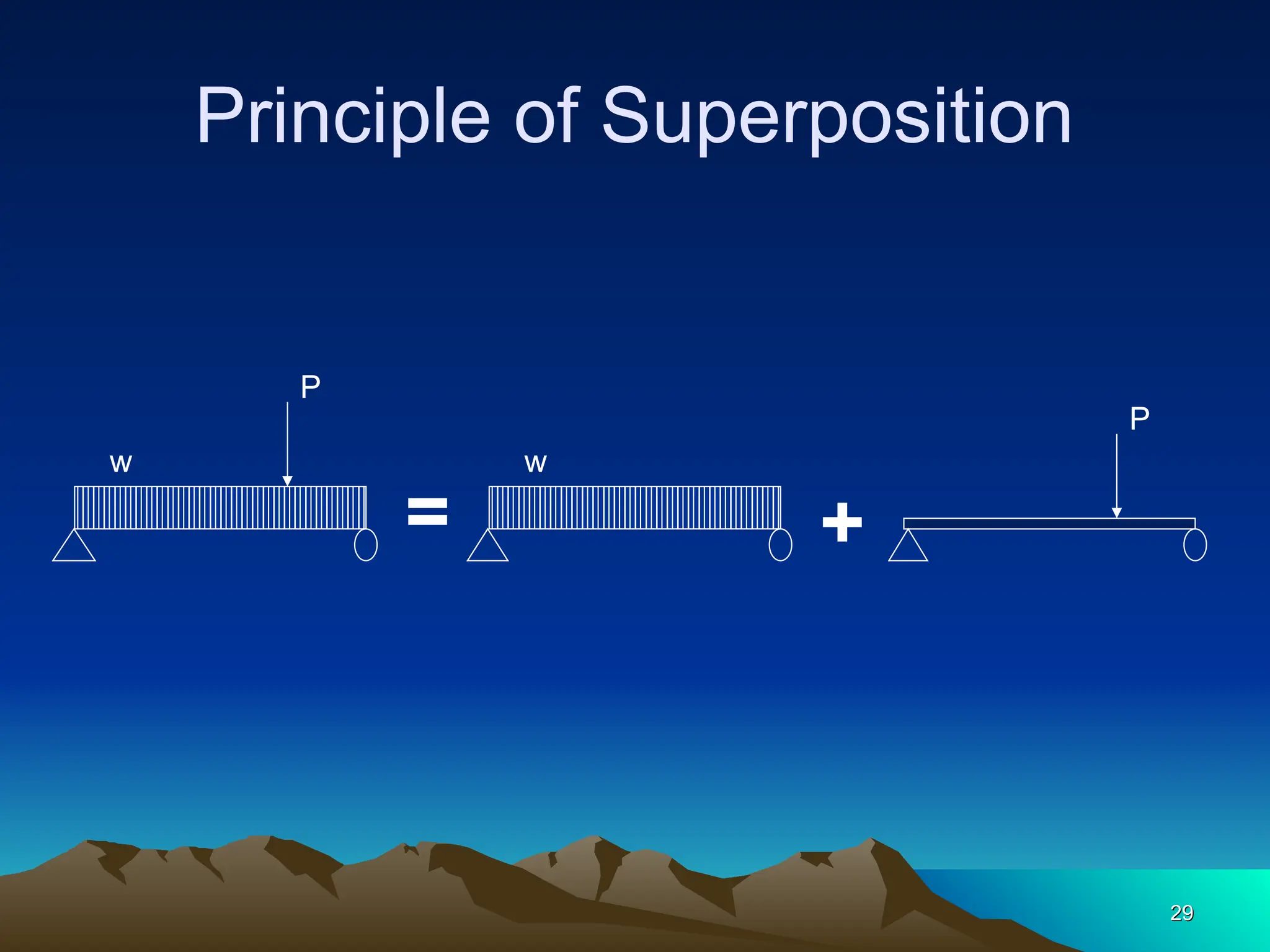
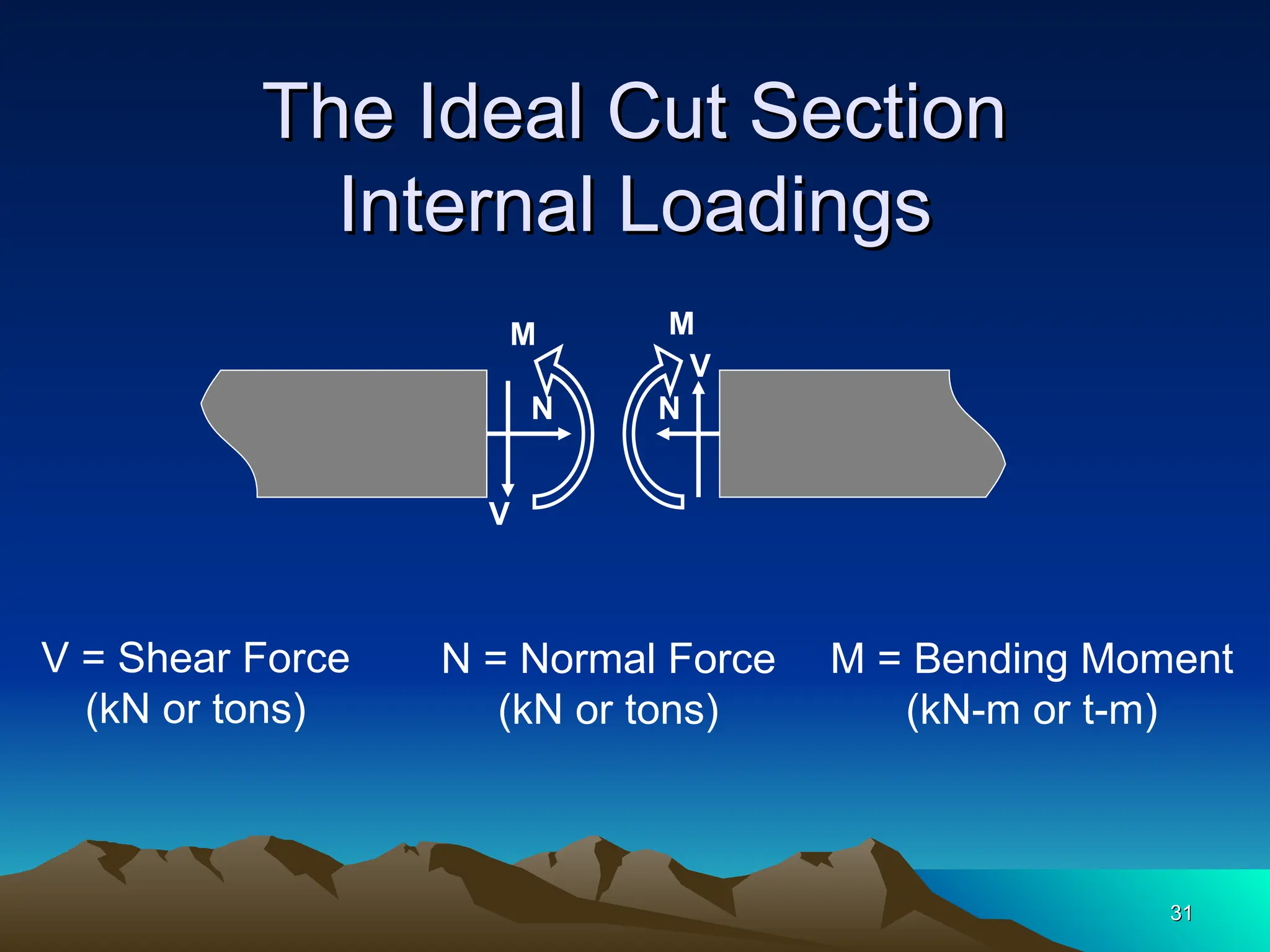
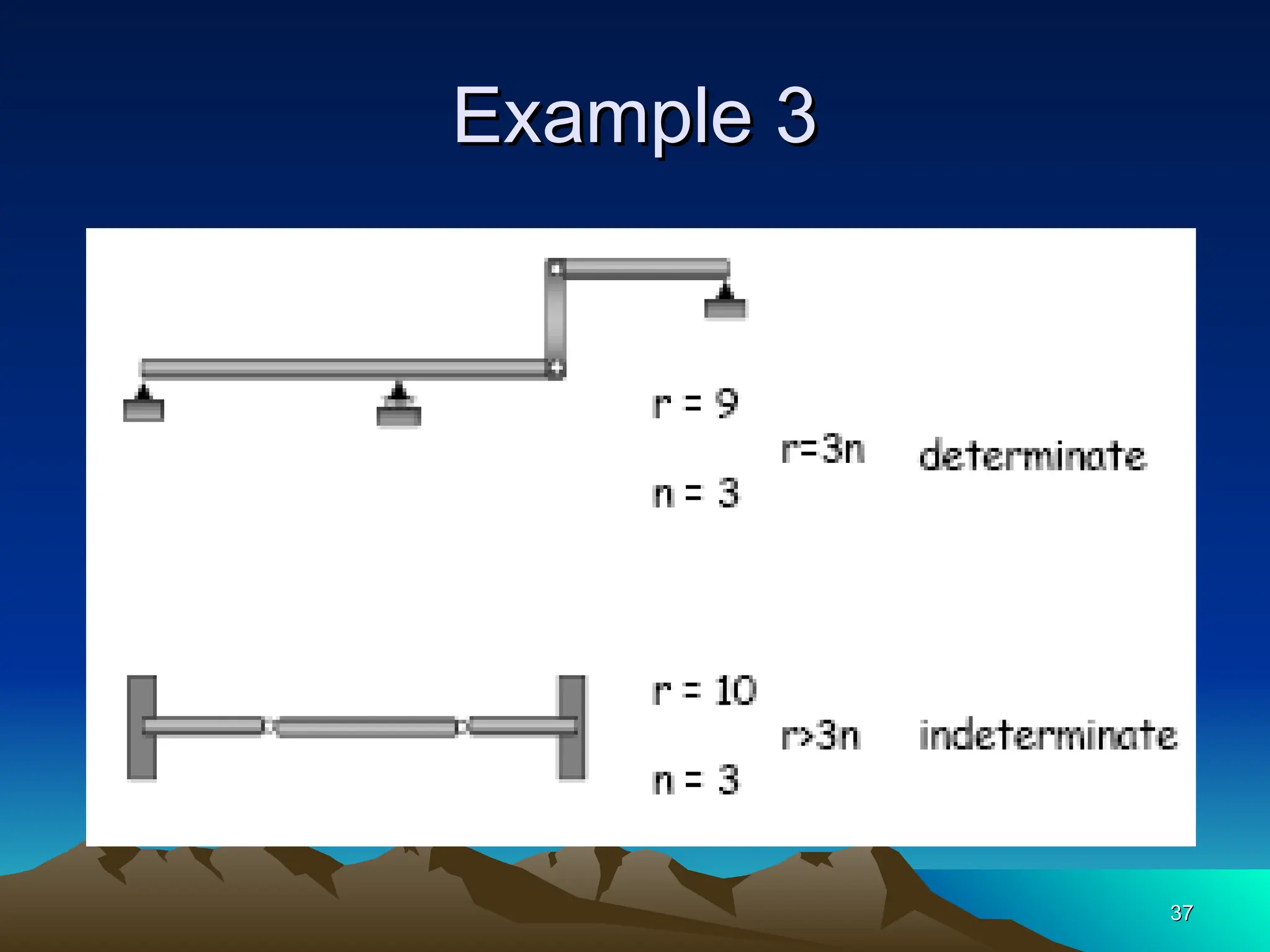
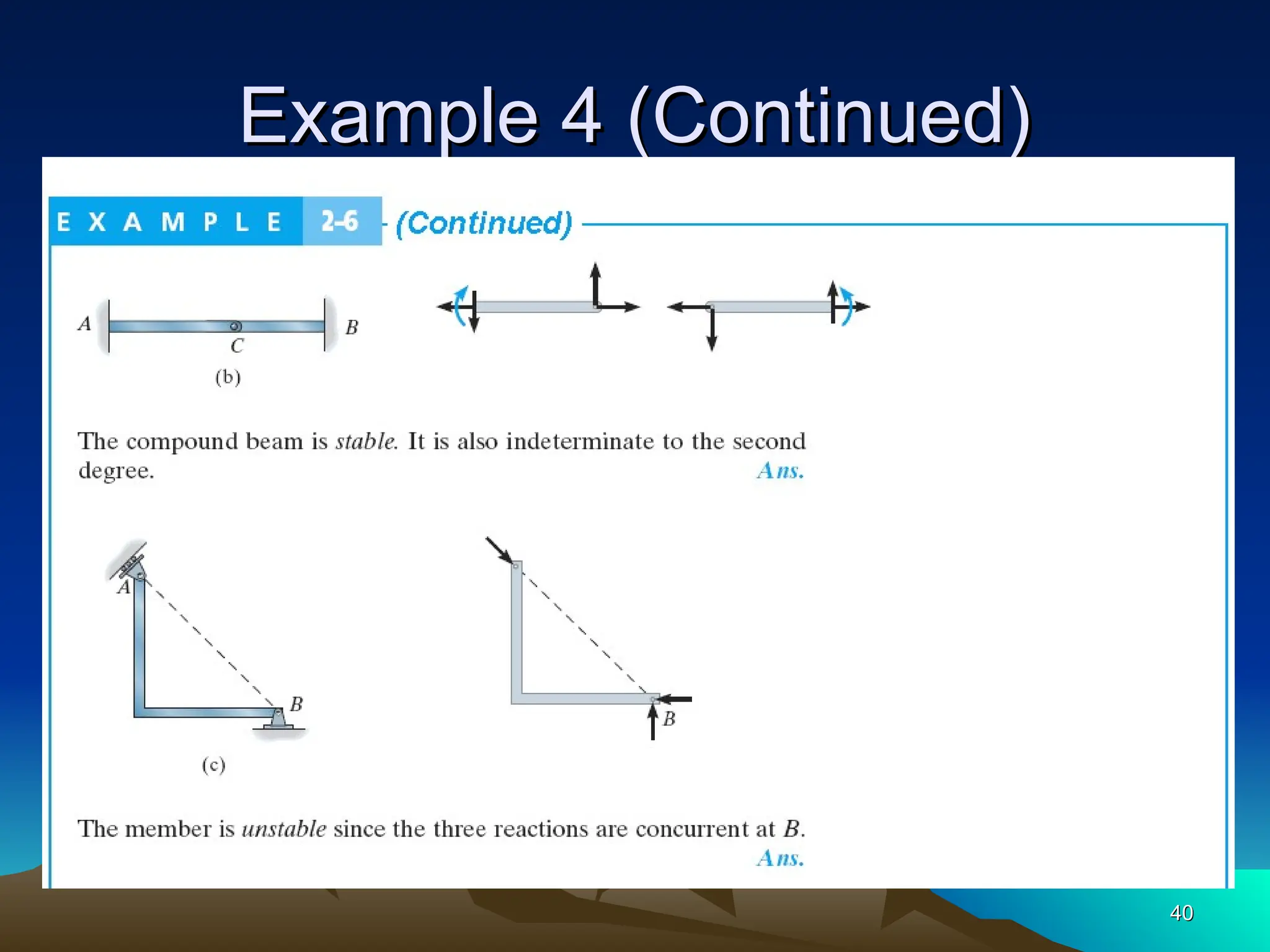
The document discusses the analysis of statically determinate structures, emphasizing the common types of supports such as hinge, fixed, and roller supports. It explains the concept of idealizing structures and loading, as well as the principle of superposition in linear elastic structural analysis. Additionally, it covers determinacy and stability conditions required for structures to maintain equilibrium.

1. Copyright September, 2010
Copyright September, 2010 1
1
Analysis of Statically
Analysis of Statically
Determinate Structures
Determinate Structures
Prof. Basuony El-Garhy
Civil Engineering Department
Faculty of Engineering

2. 2
2
Analysis of SD Structures
Analysis of SD Structures
 The most common type of structure an engineer will
analyze lies in a plane subject to a force system in the
same plane.
 In general, it is not possible to perform an exact analyze
of a structure.
 Approximations for structure geometry, material
parameters, and loading type and magnitude must be
made.

3. 3
3
Types of Supports
Types of Supports
 Hinge or pin support prevents horizontal and vertical
displacements; allows rotation. However, in reality, a pin
connection has some resistance against rotation due to friction
 A fixed connection prevents vertical and horizontal
displacements and rotation
 The most common types of supports are hinge or pin
support, roller support and fixed support.
 Roller support prevents vertical displacements and allows
horizontal displacement and rotation

4. Support Idealization
Support Idealization
 Hinge or pin support
4
4
 Fixed support
 Roller support

5. Support Idealization
Support Idealization
5
5

6. 6
6
Support Idealization
Support Idealization

7. 7
7
Typical hinge (pin) support
Typical hinge (pin) support

8. Typical fixed support
Typical fixed support
8
8

9. Typical roller support
Typical roller support
9
9

10. Typical fixed support
Typical fixed support
10
10

11. Actual beams pin connected
Actual beams pin connected
to column
to column
11
11

12. 12
12
Roller support
Roller support

13. 13
13
Roller support
Roller support

14. 14
14
Typical pin support
Typical pin support

15. Typical fixed support
Typical fixed support
15
15

16. Idealized structure
Idealized structure
16
16
 A structure may be idealized as
a line drawing where orientation
of members and type of
connections are assumed.
 The elements of a structure, like
the beams and girders of this
building frame, are connected
together in a manner where the
analysis can be considered
statically determinate.

17. Idealized structure
Idealized structure
17
17
Line drawing

18. Idealized structure
Idealized structure
18
18

19. 19
19
Idealized structure
Idealized structure

20. 20
20
Idealized structure
Idealized structure

21. Idealized structure
Idealized structure
21
21

22. Idealized structure
Idealized structure
22
22

23. Idealized structure
Idealized structure
23
23

24. Loading Idealization
Loading Idealization
24
24

25. Loading Idealization
Loading Idealization
25
25

26. Loading Idealization
Loading Idealization
26
26

27. Loading Idealization
Loading Idealization
27
27

28. Principle of Superposition
28
28
 Basics for the theory of linear elastic structural analysis:
The total displacement or stresses at a point in a
structure subjected to several loadings can be
determined by adding together the displacements or
stresses caused by each load acting separately.
 There are two exceptions to these rule:
1. If the material behaves in a nonlinear
2. If the geometry of the structure changes significantly under loading
(example: a column subjected to a bucking load)

29. Principle of Superposition
29
29
= +
w w
P
P

30. Equations of Equilibrium
30
30
 From statics the equations of equilibrium in plane are:
 Requires that a free body diagram be constructed of the
structure or its members.
 All forces and couple moments must be shown that act on the
member
 Method of sections will be used to determine the internal
loadings at a specific point with a cut perpendicular to the axis
of the member at that point.

31. The Ideal Cut Section
The Ideal Cut Section
Internal Loadings
Internal Loadings
M
M
V
V
N N
V = Shear Force
(kN or tons)
M = Bending Moment
(kN-m or t-m)
N = Normal Force
(kN or tons)
31
31

32. Determinacy and Stability
Determinacy and Stability
32
32
 Determinacy: provide both necessary and sufficient
conditions for equilibrium.
 When all the forces in structure can be determined
from the equations of equilibrium then the structure
is considered statically determinate
 If there are more unknowns than equations of
equilibrium, the structure is statically indeterminate.

33. Determinacy
Determinacy
33
33
 For plane structures, there are three equations of
equilibrium for each Free Body Diagram (FBD), so that
for n members and r reactions:
r = 3n statically determinate structure
r > 3n statically indeterminate structure
Degree of determinacy = 3n - r
r = number of reactions
n = number of members
Where:

34. Example 1
Example 1
34
34

35. Example 1 (Continued)
Example 1 (Continued)
35
35

36. 36
36
Example 2
Example 2

37. 37
37
Example 3
Example 3

38. Stability
Stability
 Stability: Structures must be properly held or
constrained by their supports.
38
38
 Cases in which the structures is considered
unstable
2. When all the reactions are parallel
1. If r < 3n Unstable structure
3. When all the reactions are concurrent at a point

39. Example 4
Example 4
39
39

40. Example 4 (Continued)
Example 4 (Continued)
40
40

41. Example 4 (Continued)
Example 4 (Continued)
41
41