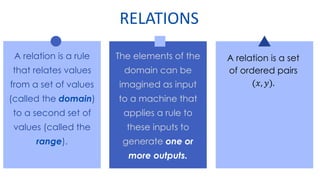
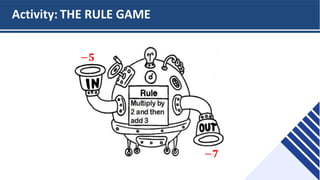
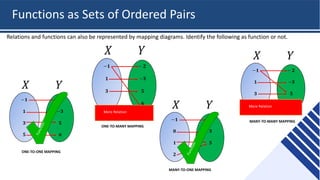
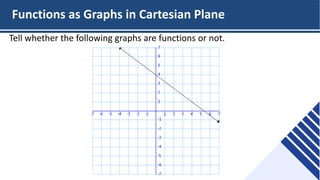
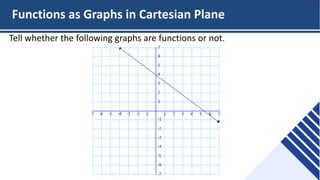
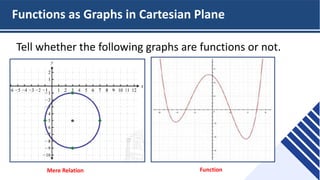
This document provides an overview of functions and their representations. It defines relations and functions, and notes that a function is a relation where each input maps to a unique output. It then discusses several ways to represent functions: as machines that take inputs and produce outputs according to a rule; as sets of ordered pairs; as mapping diagrams; and as graphs in the Cartesian plane. Examples are provided to illustrate functions versus relations for each representation. The overall purpose is to recall key concepts about functions and their graphical and symbolic representations.

1. GENERAL
MATHEMATICS
AGUSAN NATIONAL HIGH SCHOOL
SCIENCE, TECHNOLOGY, ENGINEERING AND MATHEMATICS

2. FUNCTIONS AND THEIR
GRAPHS
FUNCTIONS AS MODELS

3. At the end of the lesson, the learners are able to:
1. RECALL THE FOLLOWING
• Definition of relations and Functions
• Identifying Functions as a machine, set of
ordered pairs, mapping diagrams and
graphs in cartesian plane
• Identify Domain and Range of a Function
INTENDED LEARNING OUTCOME:
Expectations and outcomes

4. RECALL!

5. RELATIONS
A relation is a rule
that relates values
from a set of values
(called the domain)
to a second set of
values (called the
range).
The elements of the
domain can be
imagined as input
to a machine that
applies a rule to
these inputs to
generate one or
more outputs.
A relation is a set
of ordered pairs
(𝑥, 𝑦).

6. FUNCTIONS
A function is a
relation where each
element in the
domain is related to
only one value in the
range by some rule
The elements of the
domain can be
imagined as input
to a machine that
applies a rule so
that each input
corresponds to only
one output.
A function is a set
of ordered pairs
(𝑥, 𝑦) such that no
two ordered pairs
have the same 𝑥
value.

7. Relations vs. Functions
Relation
A relation 𝑅 between
two sets 𝑋 and 𝑌 is simply a
subset of the Cartesian
product 𝑋 × 𝑌 , i.e., a
collection of ordered pairs
(𝑥, 𝑦) where 𝑥 ∈ 𝑋 and 𝑦 ∈ 𝑌.
Function
Let 𝑋 and 𝑌 be sets. Then a
function from 𝑋 to 𝑌, denoted by
𝑓: 𝑋 → 𝑌, is a set f of ordered pairs in
𝑋 × 𝑌 such that for each 𝑥 ∈ 𝑋 there
exists a unique 𝑦 ∈ 𝑌 with (𝑥, 𝑦) ∈ 𝑓.
In other words, if (𝑥, 𝑦) ∈ 𝑓 and
(𝑥, 𝑦′ ) ∈ 𝑓, then 𝑦 = 𝑦′.

8. Function Notation
Function Notation: 𝒇(𝒙)
It is read as "𝑓 of 𝑥" or “function of
𝑥“ where 𝑥 is independent variable
and 𝑓(𝑥) = 𝑦 is the dependent
variable.

9. WAYS TO
REPRESENT
FUNCTIONS
FUNCTIONS AS MACHINE
FUNCTIONS AS SETS OF ORDERED PAIRS
FUNCTIONS AS MAPPING DIAGRAMS
FUNCTIONS AS GRAPHS IN CARTESIAN PLANE

10. FUNCTIONS
AS MACHINE
• A function can be illustrated as a machine
where there is the input and the output.
• When you put an object (input) into a
machine, you expect a product as output
after the process being done by the
machine.
• Functions can be represented as machines
with an input and an output in which the
output is related to the input by some rule.

11. ILLUSTRATION

12. Direction:
I will input a photo and using the rule you will
give the output.
Activity: THE RULE GAME

13. Click here to customize your own
Typeform!
Activity: THE RULE GAME
RULE:
Spit out the title of
the TV series
OUTPUT:
Stranger Things

14. Click here to customize your own
Typeform!
Activity: THE RULE GAME
RULE:
Spit out the name of
this mobile game
OUTPUT:
Mobile Legends

15. Activity: THE RULE GAME
RULE:
𝒇 𝒙 = 𝟐𝒙𝟐
− 𝟕𝒙 + 𝟓
OUTPUT:
−𝟏
INPUT:
𝒙 = 𝟐

16. Activity: THE RULE GAME
−𝟓
−𝟕

17. Functions as Sets of Ordered Pairs
Let’s Practice. Determine whether the
following relations are functions or not.
1. 𝑓 = 5,1 , 6,0 , 7,1 , 8,0 , 9,0
2. ℎ = 1,23 , 2,17 , 7,11 , 8,11 , 2,13
3. 𝑗 = 1,3 , 2,6 , 3,9 , … , 𝑛, 3𝑛
Function
Not a Function
Function

18. Functions as Sets of Ordered Pairs
Relations and functions can also be represented by mapping diagrams. Identify the following as function or not.
Mere Relation
ONE-TO-ONE MAPPING
ONE-TO-MANY MAPPING
MANY-TO-ONE MAPPING
Mere Relation
MANY-TO-MANY MAPPING

19. Functions as Graphs in Cartesian Plane
Tell whether the following graphs are functions or not.

20. Functions as Graphs in Cartesian Plane
The Vertical Line Test
A graph represents a function if and only if
each vertical line intersects the graph at most
once.

21. Functions as Graphs in Cartesian Plane
Tell whether the following graphs are functions or not.

22. Functions as Graphs in Cartesian Plane
Tell whether the following graphs are functions or not.
Mere Relation Function

23. Functions as Graphs in Cartesian Plane
Example:
Which of the following represents a
function?
1.𝑦 = 𝑥2
− 2𝑥 + 2
2. 𝑥2
+ 𝑦2
= 1
3. 𝑦 = 𝑥 + 1
Go to https://www.desmos.com/calculator to graph
the relations above.