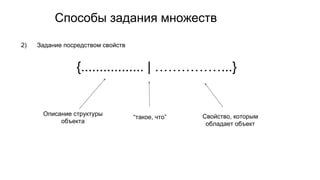
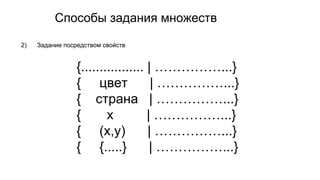
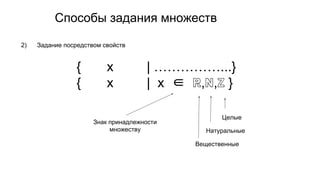
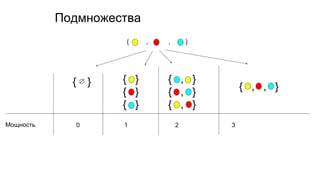
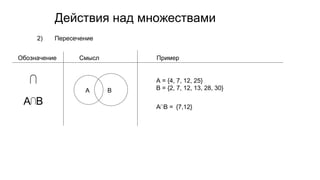
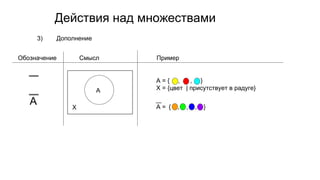
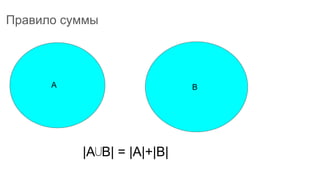
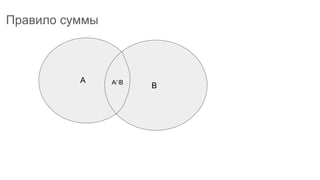
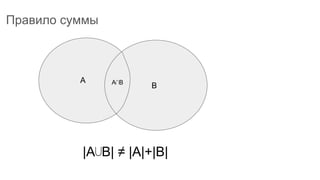
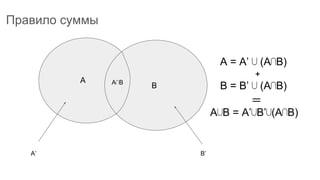
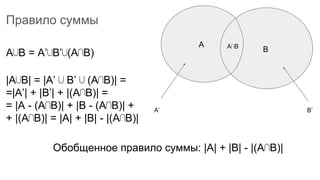
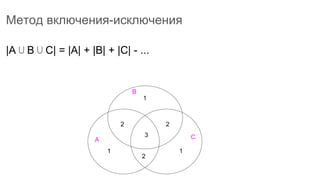
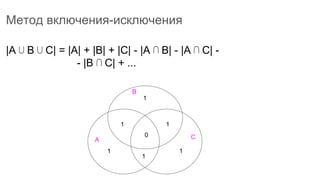
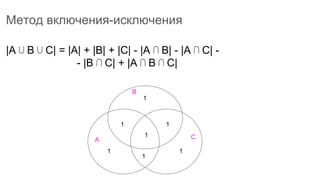
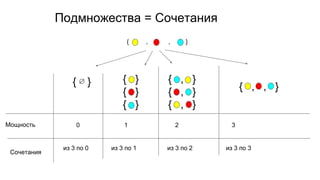
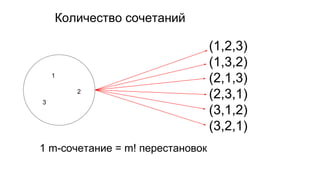
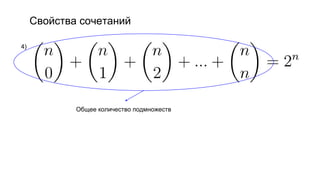
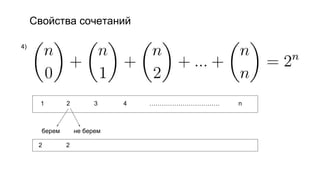
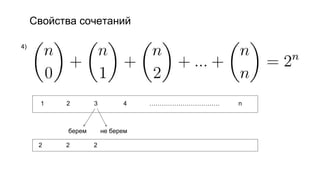
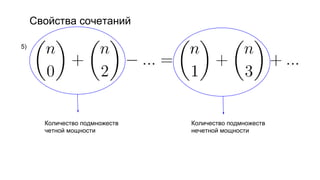
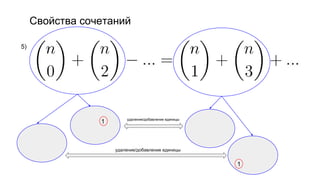
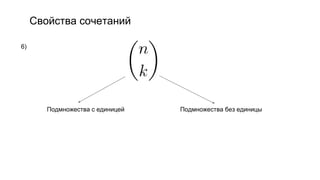
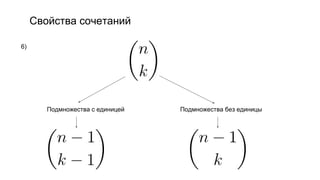
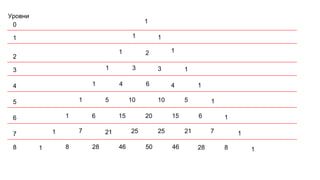
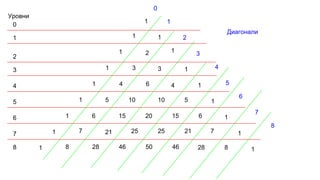
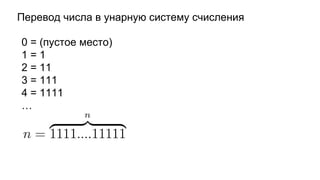
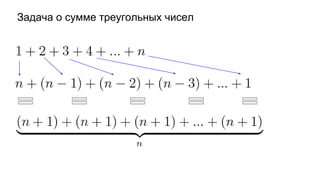
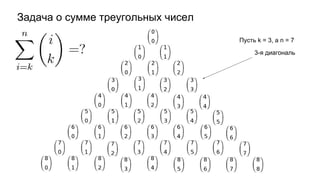
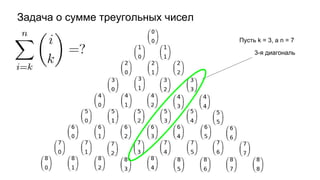
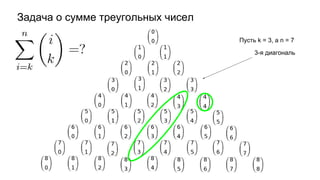
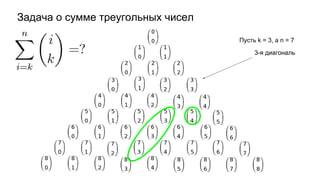
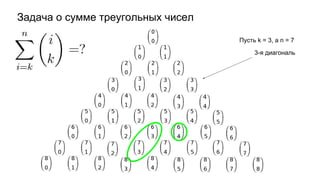
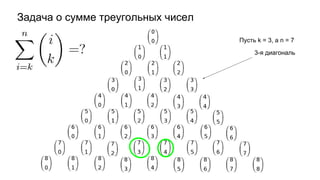
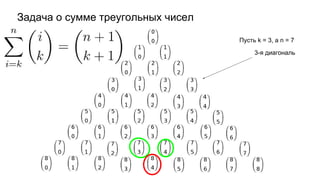
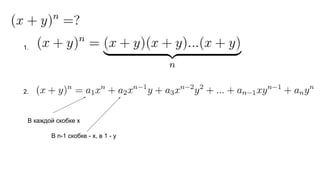
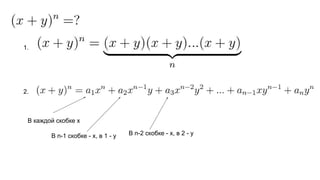
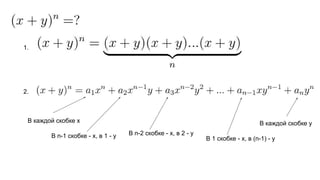
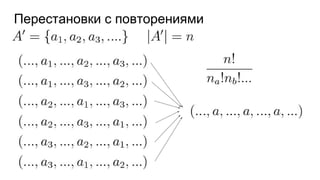
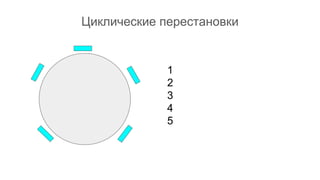
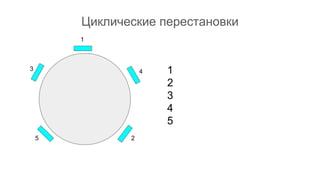
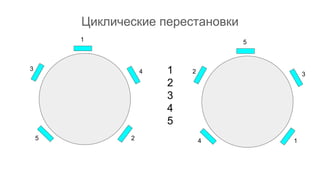
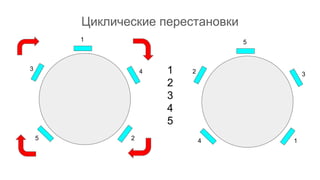
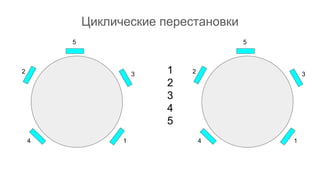
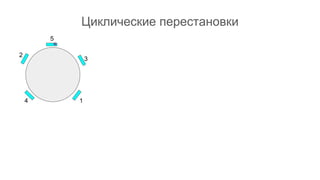
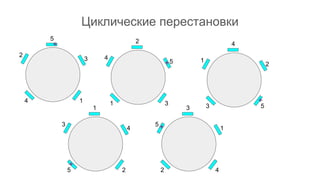
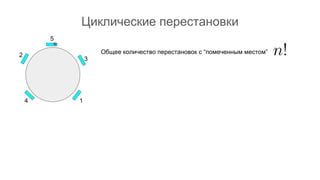
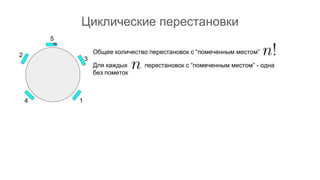
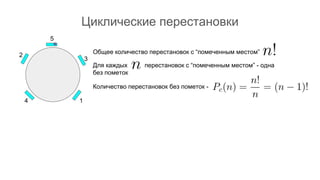
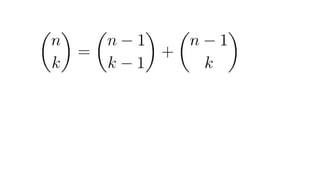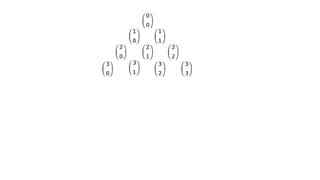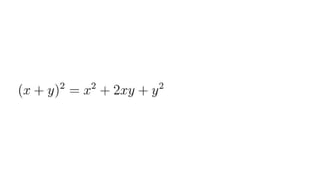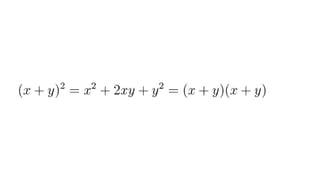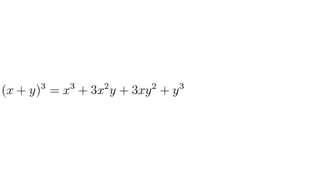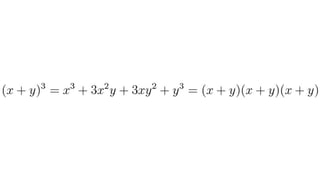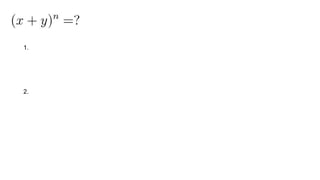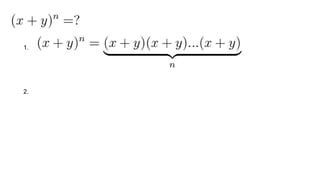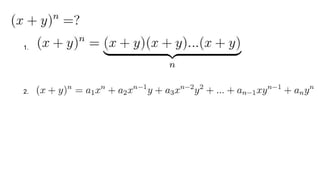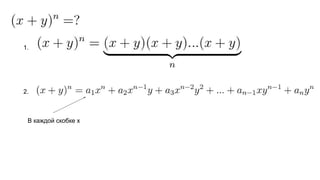Документ описывает основы теории множеств, включая определения, способы задания и действия над множествами, такие как объединение, пересечение и дополнение. Также рассматриваются комбинации и подмножества, а также метод включения-исключения для вычисления мощностей множеств. Включает примеры, иллюстрации и концепции, связанные с комбинаторикой.