Документ представляет собой учебный материал по математике для 4 класса, содержащий теоретические и практические задачи на основе учебного плана ФГОС. В нем рассматриваются основы арифметики, деление с остатком, свойства чисел и размерностей, а также различные способы решения задач, включая применение алгоритмов. Также приведены рекомендации по использованию учебника в сочетании с тетрадями и различными заданиями для проверки знаний.

1. МКНИГЛ/УЧГ нпик
|11090 I

2. МИЛЛИОН (1000000)
1 миллион (1 млн.) = 1000 тысяч (1000 тыс.) =
= 100 десятков тысяч (100 дес. тыс.)
= 10 сотен тысяч (10 сот. тыс.)
1000000 = 1000•1000 = 100000•100 = 100000 • 10
1000000 = 100- 100- 100
МИЛЛИАРД (1000000000)
миллиард (1 млрд.) = 1000 миллионов (1000 млн.)
= 1000000 тысяч (1000000 тыс.)
1000000000 = 1000000 • 1000 = 1000 • 1000000
1000000000 = 1000 ■1000 ■1000
ДЕЛЕНИЕ С ОСТАТКОМ
37 : 5 = 7 (ост. 2)
а : Ь —с (ост. б)
а - делимое
Ь - делитель
с - неполное частное
с! - остаток
Остаток должен быть больше или равен 0,
но меньше делителя:
0 < б < Ь
I ели делитель умножить на неполное частное
и н полученному результату прибавить остаток,
то в итоге получится делимое:
Ь•с + б = а
ЗАПИСЬ ДЕЛЕНИЯ С ОСТАТКОМ СТОЛБИКОМ
25 : 8 = 3 (ост. 1)
25
'24
8
3
1 — ост.
ЧЁТНЫЕ И НЕЧЁТНЫЕ ЧИСЛА
Чётные числа (которые при делении на 2 дают в остатке 0
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22 и т. д.
Нечётные числа (которые при делении на 2 дают в остатке '
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и т. д.
СТОИМОСТЬ И ЦЕНА
Единицы стоимости:
1 рубль (1 руб.) = 100 копеек (100 коп.)
1 евро (1 €) = 100 евроцентов
Цена - стоимость единицы количества товара или услуж
Единицы цены:
1 рубль за килограмм (1 руб./кг) =
= 100 копеек за килограмм (100 коп./кг)
1 рубль за метр (1 руб./м) = 100 копеек за метр
(100 коп./м) = 1 копейка за сантиметр (1 коп./см)
1 рубль за минуту (1 руб./мин.) =
= 60 рублей за час (60 руб./ч)
1 евро за квадратный деци-метр (1 €/дм2) =
= 100 евро за квадратный метр (100 €/м2)

3. Лауреат
Главной Премии
за лучшую работу
в области науки,
технологий
и образования
А.Л. ПЕКИН
МАТЕМАТИКА
4кл а с с
Учебник
В двух частях
Часть 1
2-е издание
Под редакцией Р. Г. Чураковой
Учебник прошел экспертизу
в РАН (протокол 10106-5215/493 от 01.11.2010)
и РАО (протокол 01-5/7д-290 от 20.10.2010)
на соответствие требованиям ФГОС НОО
Рекомендовано Министерством образования
и науки Российской Федерации
Москва
АКАДЕМКНИГА/УЧЕБНИК
2012

4. УДК 51(075.2)
ББК 22.1я71
4-37
Чекин А.Л.
4-37 Математика [Текст] : 4 кл. Учебник В 2 ч./
А.Л. Чекин; под ред. Р.Г Чураковой. — 2-е изд. — М.
Академкнига/Учебник, 2012. — 4.1 : 128 с. : ил.
15ВЫ 978-5-49400-089-7 (общ.)
13ВЫ 978-5-49400-090-3 (ч. 1)
Учебник разработан в соответствии с требованиями федерального
государственного образовательного стандарта начального общего обра­
зования и концепцией комплекта «Перспективная начальная школа».
Учебник состоит из двух частей, каждая из которых рассчитана на учеб­
ное полугодие.
Учебник рекомендуется использовать в комплекте с тетрадями № 1,
№ 2 и № 3.
В первую часть включены вопросы, связанные с изучением нумера­
ции, зависимости между величинами, алгоритмов умножения и деления
столбиком, вместимости и объёма, свойств многоугольников. Большое
внимание уделяется решению сюжетных арифметических задач на все
действия и на работу с данными.
УДК 51(075.2)
ББК 22.1я71
13ВМ 978-5-49400-089-7 (общ.)
15ВЫ 978-5-49400-090-3 (ч. 1)
© Чекин А. Л., 2011
© Оформление. ООО «Издательство
«Академкнига/Учебник», 2012
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Работа в парах
Не торопись с ответом,
подумай
Выскажи предположение
Проверь правильность
выполнения задания
Работа в группе
15. Трудное задание
Загляни в словарь* (с. 115)
ЗАПОМНИ СЛОВО
Правило
ЕЯ Смотри Тетрадь для самостоятель
|8 | ной работы № 1, страница 8

5. Содержание
Сначала займёмся повторением.........................................7
Когда известен результат разностного
сравнения............................. 12
Когда известен результат кратного
сравнения................................................................ 16
Учимся решать задачи........................................................ 19
Алгоритм умножения столбиком.......................................22
Поупражняемся в вычислениях столбиком............. 25
Тысяча тысяч, или миллион.............................................. 26
Разряд единиц миллионов и класс миллионов 28
Когда трёх классов для записи числа
недостаточно..........................................................................30
Поупражняемся в сравнении чисел
и повторим пройденное.................................................... 31
Может ли величина изменяться?.....................................33
Всегда ли математическое выражение
является числовым?............................................................ 36
Зависимость между величинами.......................................39
Поупражняемся в нахождении значений
зависимой величины............................................................42
Стоимость единицы товара, или цена...........................44
Когда цена постоянна........................................................ 47
Учимся решать задачи........................................................ 49
4
Дплоние с остатком и деление нацело........
Неполное частное и остаток...........................
Осинок и делитель...........................................
Когда остаток равен 0 ...................................
Ко(да делимое меньше делителя...................
Деление с остатком и вычитание..................
Какой остаток может получиться
при делении на 2?............................................
Поупражняемся в вычислениях
и повторим пройденное...................................
Запись деления с остатком столбиком........
Способ поразрядного нахождения
результата деления.............................................
Поупражняемся в делении столбиком..........
Вычисления с помощью калькулятора..........
Час, минута и секунда.....................................
Кто или что движется быстрее?....................
Длина пути в единицу времени,
или скорость.........................................................
Учимся решать задачи.......................................
Какой сосуд вмещает больше?.......................
Литр. Сколько литров?.....................................
Вместимость и объём.......................................
Кубический сантиметр и измерение объёма

6. Кубический дециметр
и кубический сантиметр.................................................... 94
Кубический дециметр и л и тр .......................................... 96
Литр и килограмм ...................................................... 97
Разные задачи......................................................................98
Поупражняемся в измерении объёма...........................100
Кто выполнил большую работу.......................................102
Производительность —
это скорость выполнения работы.................................103
Учимся решать задачи...................................................... 105
Отрезки, соединяющие вершины
многоугольника............... 107
Разбиение многоугольника на треугольники............... 108
Записываем числовые последовательности................. 110
Работа с данными .................................................112
Словарь............................. 115
Приложение 1...................................................................... 119
Площадь прямоугольного треугольника....................... 119
Вычисление площади треугольника...............................121
Поупражняемся в вычислении площади..................... 123
Приложение 2...................................................................... 125
Геометрические фигуры
и геометрические величины.............................................125
6
Сначала займ ём ся повторением
| ||с. Проверь себя: всё ли ты помнишь из того, чн>
П швы изучали в 3-м классе?
1. Запиши шестизначное число, каждая цифра
записи которого совпадает с номером разряда, ело
дующего за разрядом, в котором она находится.
2. Запиши самое большое шестизначное число,
в записи которого три раза встречается цифра 1.
3. Составь и запиши пары чисел, каждая из кою
рых состоит из шестизначного числа и пятизначною
числа, а результат разностного сравнения между чи<
лами в паре равен 5. Сколько таких пар получилось'’
4. Выполни кратное сравнение между следуклци
ми разрядными единицами: 1000 и 10. Состань и
запиши ещё четыре пары разрядных единиц с ыким
же результатом кратного сравнения.
5. Устно вычисли значение следующего выражения
(45863 + 75981) : (75981 + 45863) •(982564 - 982560)
6. Сравни устно значения двух выражений. Со
ставь из них верное равенство или неравенство и
запиши его.
983657 - (983657 - 144) и 14400:100 • (569873 - 569872)
7

7. 7. Выполни умножение столбиком многозначного
числа на однозначное число и на двузначное число.
20863 20863
х _____ 2 х 22
8. Длина прямоугольника 5 см 5 мм, а ширина
3 см. Вычисли периметр и площадь прямоугольника.
9. Начерти два прямоугольника по данным из
следующей таблицы.
Номер
прямоугольника Длина Ширина Периметр Площадь
1 4 см 3 см ? ?
2 6 см 2 см ? ?
Заверши заполнение таблицы в тетради. Сравни
периметры этих прямоугольников. Сравни площади
этих прямоугольников. Используя данные из заполнен­
ной таблицы, установи, могут ли прямоугольники
иметь равные площади, но разные периметры?
10. Начерти два прямоугольника по данным из
следующей таблицы.
Номер
прямоугольника
Длина Ширина Периметр Площадь
1 8 см 2 см ? ?
2 6 см 4 см ? ?
8
Заверши заполнение таблицы в тетради. Сранни
периметры этих прямоугольников. Сравни площади
агих прямоугольников. Используя данные из заполнен
мой таблицы, установи, могут ли прямоугольники
иметь равные периметры, но разные площади?
11. Периметр квадрата равен 32 дм. На сколько
квадратных дециметров увеличится площадь квадрат,
если его периметр увеличить на 12 дм?
12. Измерь с помощью палетки площадь данною
прямоугольника.
13. На сколько минутных делений должна повор
нуться минутная стрелка, чтобы получился поворот на
прямой угол? Какую часть прямого угла составляет утл,
на который поворачивается минутная стрелка за 5 мин'1
14. Начерти квадрат со стороной 4 см. Разбои
этот квадрат на два прямоугольных треугольника. Со
ставь из этих треугольников равнобедренный треуголь
ник с основанием 8 см. Покажи на чертеже, как о т
сделать.
15. Методом подбора определи, какими могут бын.
длина и ширина прямоугольника, если его площадь раина
20 кв. см. Построй треугольник с площадью 10 кв. см

8. 16. Рассмотри краткую запись задачи.
Света Ира Марина
Возраст
14 лет,
на 3 года
старше
?
?, на
1 год
моложе
Сформулируй задачу по краткой записи.
Реши эту задачу. Вычисли и запиши ответ.
17. Сделай краткую запись к следующей задаче.
Серёже 10 лет. Он на 4 года моложе Андрея, а
Борис в 2 раза моложе Андрея. Сколько лет Борису?
Реши задачу. Вычисли и запиши ответ.
18. Сформулируй задачу, решением которой
ь1будет выражение 12 • 10 + 15*8.
Вычисли и запиши ответ этой задачи. Запиши
решение задачи и вычисление ответа по действиям.
19. Сформулируй задачу на кратное сравнение,
4 *^ взяв необходимые числовые данные из этой диа­
граммы.
I шиш—' ' I
I— I— I— I— I— I— I— I— I— I— I— I— I— I— I— I— I— I— I— I— I— I— I— ►
0 10 20 30 40 50 60 70 80 90 100 110
Реши эту задачу. Для нахождения ответа выполни
устно деление двузначного числа на двузначное число.
10
т
20. Реши задачу. Вычисли и запиши ответ.
На складе хранилось 40 упаковок с яблочным
соком и 35 упаковок с апельсиновым. Со склада
вывезли 18 упаковок с яблочным соком, а с апель
синовым — на 3 больше. На сколько больше ос:(а
лось на складе упаковок с яблочным соком, чем <
апельсиновым?
Попробуй найти рациональный путь решения дан
ной задачи, который приведёт к получению ответа аа
два действия.
'Х. ■
21. Сформулируй задачу на разностное сравно
Жк] ние, в условии которой одно из данных являема!
результатом кратного сравнения.
Для формулирования условия воспользуйся следу
ющей диаграммой.
I 1 1 1 1 ( 1 1 1 1 1 1 1 1 1 1 1 1 1 1---------- ------
I
Реши эту задачу. Вычисли и запиши ответ.
22. Сформулируй задачу на кратное сравнен
ж к в условии которой одно из данных являема!
результатом разностного сравнения.
Подбери числовые данные так, чтобы у тебя
была возможность вычислить ответ.
Реши эту задачу. Вычисли и запиши ответ.
11

9. Когда известен результат разностного сравнения
23. Полоска длиной 10 см разделена на две
части. При этом синяя часть полоски на 2 см длин­
нее белой её части. Рассмотри рисунок и установи,
с помощью какого из двух данных выражений: 1 0 - 2
или 10 + 2 можно вычислить удвоенную длину мень­
шей части полоски.
10 см
2 см 2 см
Вычисли удвоенную длину меньшей части поло­
ски. После этого с помощью деления вычисли длину
меньшей части полоски.
Как теперь можно вычислить длину большей части
полоски? Проведи вычисления двумя способами:
с помощью сложения и с помощью вычитания.
24. Маша разрезает ленточку на две части.
12
Маше нужно разрезать ленточку длиной 1 м на
две части так, чтобы одна часть была на 20 см длин
нее другой. Для этого она сначала отогнула с одного
конца часть ленточки длиной 20 см. После чего она
сложила пополам оставшуюся часть и разрезала лом
точку в месте только что получившегося сгиба.
Переведи на язык математических действий йен
манипуляции, которые Маша производила с ленточкой
Запиши вычисления, с помощью которых можно
узнать длину каждой части ленточки. На сколько сан
тиметров одна часть ленточки, получившаяся поело
разрезания, длиннее, чем другая? За счёт какого при
ёма Маше удалось этого добиться?
25. Кусок масла в 1 кг нужно разделить на дно
части так, чтобы в одной части было на 2001
больше, чем в другой. Сколько граммов должно бы п.
в каждой части? Какой из следующих варианта
решения является решением данной задачи?
1-й вариант 2-й вариант
1) 1 кг : 2 = 1000 г : 2 = 1)1 кг-200г= 1000 г - 200 I
= 500 г = 800 г
2) 500 г + 200 г = 700 г2) 800 г : 2 = 400
3) 500 г - 200 г = 300 г3) 400 г + 200 г =
_________ 1000 г_________ __
I, в » г ягяшюяшттш. I
200 г
Выполни проверку выбранного варианта решении,
сопоставив его с условием. Перепиши это решение; <
вычислением ответа в тетрадь. Запиши ответ.
13

10. 26. Реши задачу. Вычисли и запиши ответ.
Всего в двух классах 52 ученика. В одном клас­
се на 2 ученика меньше, чем в другом. Сколько уче­
ников в каждом классе?
27. По данной краткой записи сформулируй задачу.
В 1-й
бригаде
Во 2-й
бригаде
В двух
бригадах
Число
рабочих
? ?, на
7 больше
47
Реши эту задачу. Вычисли и запиши ответ.
28. Из каких двух слагаемых должна состоять
сумма, чтобы её значение равнялось числу 550, а
одно слагаемое было больше другого на 70.
29. Найди два числа, при сложении которых
получается число 235, а при вычитании — число 135.
I ^ 30. Сформулируй задачу, в которой требуется
-•УЯШ! найти два числа, если известно значение суммы
и значение разности этих чисел. Предложи соседу по
парте решить сформулированную тобой задачу.
31. Реши задачи. Вычисли и запиши ответы.
За тетрадь и альбом заплатили 52 руб. Альбом
дороже тетради на 4 руб. Сколько стоит альбом?
Сколько стоит тетрадь? Сколько нужно заплатить за 3
таких альбома? За 10 таких тетрадей?
14
32. Миша и Маша собирали малину. Миша
брал 2 одинаковых лукошка, а Маша — 3 таких лу
кошка. Когда мама взвесила собранную малину, го
оказалось, что Маша собрала на 900 г больше, чом
собрал Миша.
К данному условию сформулируй требование, на
которое можно ответить с помощью следующем <»
решения с вычисленным ответом.
1) 3 - 2 = 1 (л.)
2) 900 : 1 = 900 (г)
Запиши действия, которые ещё нужно выполни п.
для того, чтобы получить ответ для каждого из еле
дующих требований к данному условию.
Сколько граммов малины собрал Миша? А сколь
ко Маша?
33. Изобрази в тетради с помощью двухцвет
полоски карандаш, о котором имеется следующая
информация.
Двухцветный красно-синий карандаш имеет длину
15см. Красная часть карандаша использовалась мень
ше, поэтому её длина на 3 см больше, чем длина
синей части.
Какой длины был бы карандаш, если бы синяя
часть имела такую же длину, какую имеет сейчас
красная часть?
Запиши выражение, с помощью которого можно
найти удвоенную длину большей (красной) чага и
Вычисли эту удвоенную длину. После этого вычисли
длину большей (красной) части, а затем — длину
меньшей (синей) части.
15

11. Когда известен результат кратного сравнения
34. Рассмотри рисунок и скажи, на сколько рав­
ных частей разрезан торт. Какая часть торта
лежит на лопатке?
Во сколько раз одна часть торта меньше, чем
все оставшиеся части? Сколько граммов будет в
одной части, если весь торт имеет массу 800 г?
Запиши соответствующие вычисления.
Сколько граммов будет во всех оставшихся частях,
кроме одной? Запиши соответствующие вычисления.
35. Верёвку длиной 30 м нужно разрезать на две
части так, чтобы одна часть была в 5 раз длиннее, чем
другая. Сколько метров должно быть в каждой части?
30 м
Рассмотри схему к этой задаче и установи, ка
кой из следующих вариантов решения является ремпо
нием данной задачи?
1-й вариант
1) 5 + 1 =6(ч.)
2) 30 м : 6 = 5 м
3) 30 м - 5 м = 25 м
Перепиши выбранное решение с пояснением дой
ствий в тетрадь. Запиши ответ задачи.
36. Реши задачу. Вычисли и запиши ответ.
Всего в двух кружках занимается 45 учеников И
одном кружке занимается в 4 раза больше учеников,
чем в другом. Сколько учеников занимается в каждом
кружке?
I I «и
1 ч. 4 ч.!
37. По данной краткой записи сформулируй задачу
В 1-й Во 2-й бри­ В двух бри
бригаде гаде гадах
Число
рабочих
?
-----
?, в 3 раза
больше
____ ------------------
48
2-й вариант
Ч 1) 30 м : 5 = 6 м
2) 30 м - 6 м = 24 м
Реши эту задачу. Вычисли и запиши ответ.
17

12. 38. Из каких двух слагаемых должна состоять
сумма, чтобы одно слагаемое было больше другого в
9 раз, а её значение равнялось числу 350?
__ _ 1 ____ т т--------------------------------------------------------------------------------------------------►
Ш
39. Выбери два двузначных числа так, чтобы
можно было найти значение их частного. Вычисли
значение суммы этих чисел и значение их частного.
Используя эти значения, сформулируй задачу, в кото­
рой требуется найти два числа, если известно значе­
ние суммы и значение частного этих чисел.
Предложи соседу по парте решить сформулиро­
ванную тобой задачу.
40. Найди два числа, при сложении которых
получается число 180, а при делении одного числа
на другое — число 8.
41. Реши задачу. Вычисли и запиши ответ.
За ручку и набор фломастеров заплатили 48 руб.
Набор фломастеров в 5 раз дороже ручки. Сколько
стоит ручка? Сколько стоит набор фломастеров?
Сколько нужно заплатить за 10 таких ручек? За 3
таких набора фломастеров?
На какое требование задачи можно ответить с
помощью следующего выражения:
48 : (5 + 1) •5?
18
Учимся решать задачи
42. Составь краткую запись следующей задачи,
заполнив данную таблицу в тетради.
В двух автобусах разместилось 85 экскурсанта
В первом автобусе разместилось на 7 человек мень
ше, чем во втором. Сколько экскурсантов находилось
в каждом автобусе?
В 1-м Во 2-м В двух
автобусе автобусе автобусах
Число
экскурсантов — ------------------ --------------------------
Реши задачу. Вычисли и запиши ответ.
43. Найди два числа, при сложении которых
получается число 240, а при вычитании — число и 2
раза меньше, чем при сложении.
44. Реши задачу. Вычисли и запиши ответ.
За линейку и ручку заплатили 45 руб. 50 коп
Ручка дороже линейки на 5 руб. 50 коп. Сколько стот
ручка? Сколько стоят 5 линеек?
45 оуб. 50 коп
5 руб. 50 коп.
Покажи на схеме, какая часть полоски изображу
ет стоимость двух линеек?
19

13. 45. Составь краткую запись следующей задачи,
заполнив данную таблицу в тетради.
В двух спортивных секциях занимаются 80 уча­
щихся. В первой секции занимается в 3 раза меньше
учащихся, чем во второй. Сколько учащихся занимает­
ся в каждой секции?
В 1-й
секции
Во 2-й
секции
В двух
секциях
Число
учащихся
•
Сделай чертёж к составленной задаче и реши
её. Вычисли и запиши ответ.
46. Одна сторона прямоугольника имеет длину
на 2 см больше, чем другая. Общая длина этих двух
сторон 12 см. Найди длину каждой стороны этого
прямоугольника.
47. Периметр прямоугольника 24 см. Одна сто­
рона этого прямоугольника имеет длину на 2 см
больше, чем другая. Найди длину каждой стороны
этого прямоугольника.
Можно ли решение предыдущей задачи использо-
вать как часть решения данной задачи?
48. Одна сторона прямоугольника имеет длину в
2 раза больше, чем другая. Общая длина этих двух
сторон 12 см. Найди длину каждой стороны этого
прямоугольника.
20
49. Периметр прямоугольника 24 см. Одна сю
рона этого прямоугольника имеет длину в 2 раза
больше, чем другая. Найди длину каждой стороны
этого прямоугольника.
Можно ли решение предыдущей задачи использо
вать как часть решения данной задачи?
50. Реши задачу. Вычисли и запиши ответ.
За 10 одинаковых тетрадей нужно заплатить на
75 руб. больше, чем за 7 таких же тетрадей. Сколько
стоят 5 таких тетрадей?
51. По данной схеме сформулируй задачу.
5 меш. __ 3 меш.
ш м тш ш т:I^ ' I и н м ш м
50 кг
Реши сформулированную задачу. Вычисли и запи
ши ответ.
52. Определи площадь каждой фигуры, если они
составлены из одинаковых квадратов и площадь пор
вой фигуры на 3 кв. см больше площади второй.
2 1

14. Алгоритм умножения столбиком
53. Выполни умножение столбиком многозначного
числа на однозначное число и ответь на следую­
щие вопросы. 2052
х 3
С какого разряда первого множителя нужно начи­
нать умножение на однозначное число столбиком и к
какому разряду следует переходить далее?
Какое число нужно записывать в соответствующий
разряд результата, если при умножении в этом раз­
ряде получается однозначное число, и какое — если
двузначное?
Какое число при умножении в данном разряде
должно получиться, чтобы не было перехода через
разряд?
В каких случаях имеет место переход через раз­
ряд и как его нужно учитывать при дальнейших
вычислениях?
54. Рассмотри, как выполнено умножение стол­
биком многозначного числа на двузначное число,
и ответь на следующие вопросы.
2052
х 23
6156
+41040
47196
На какое разрядное слагаемое второго множителя
сначала умножаем первый множитель? На какое число
22
нужно умножать далее? Чем отличается расположена» -
записи результата умножения числа 2052 на 3 единицы
от результата умножения этого же числа на 2 десятка?
С какого разряда начинаем записывать резульпп
умножения числа 2052 на 2 десятка? Какая цифра
стоит в этом случае в разряде единиц этого резулн
тата? Обязательно ли её записывать или можно осаа
вить это место свободным?
Какое действие нужно выполнить над двумя полу
ченными результатами умножения? Можно ли для
выполнения этого действия применить алгоритм сло­
жения столбиком? Можно ли использовать для сложо
ния столбиком уже имеющуюся запись полученных
чисел или нужно делать отдельную запись?
55. Сформулируй алгоритм умножения стол
а ком*, ответив на следующие вопросы и истин,
зуя данный пример. Способ умножения столбиком на
однозначное число подробно описывать не нужно.
2052
х 123
6156
+ 41040
205200
252396
Как нужно записывать множители?
На какое разрядное слагаемое второго множим-
ля нужно сначала умножить первый множитель?
На какое разрядное слагаемое второго множиммт
нужно умножать далее? Как нужно действовать, если
23

15. какое-то разрядное слагаемое равно 0? Когда нужно
заканчивать умножение на разрядные слагаемые второ­
го множителя?
После того как первый множитель умножили от­
дельно на каждое разрядное слагаемое второго множи­
теля, что нужно делать с полученными результатами?
Когда будет получен окончательный результат
умножения данных многозначных1чисел?
56. Устно сделай прикидку, сколько цифр будет
в записи результата умножения чисел 2365 и 43.
Проверь предположение с помощью алгоритма умно­
жения столбиком.
57. В первой строке записаны задания на умно­
жение столбиком, а во второй — выполнение этих
заданий, но порядок выполнения заданий не соответ­
ствует порядку их предъявления.
467 467 ч > 467
х 504 - х 54 х 540
1868 1868 18680
Ь23350 +233500 +233500
25218 235368 252180
Установи соответствие между записями из первой
и второй групп и запиши в тетрадь полные запи­
си выполнения умножения столбиком для данных чисел.
Можно ли восстановить записи без проведения
вычислений, если считать, что все вычисления выпол­
нены верно. Как это сделать? Объясни.
24
Поупражняемся в вычислениях столбиком
58. Выполни сложение столбиком.
23568 3072 6156 6156
+ 4365 + 86532 + 4104 +41040
568 365645 8208 820800
' 'К Ц .'V.
-V * >. у . • . >
59. Проверь,/правильно ли выполнено умножении
ш столбиком.
2052
х 423
6156
+ 4104
8208
867996
Что необычного в данной записи? Объясни, почо
му можно не записывать нули в конце записи чисел,
которые получаются в результате умножения первою
мнбжителя на 2 десятка и на 4 сотни.
60. Выполни умножение столбиком.
2935 2935 293!»
х _ 4 * " х 34 х 234
.' . , -I. '
61. Найди значения данных выражений, применим
вычисления столбиком.
(3561 + 2568)•(789365 - 789331)
(1728 + 8327)•(87524 - 87321)
25

16. Тысяча тысяч, или миллион
62. Из какого числа маленьких кубиков состоит
кубик, изображённый на рисунке?
у р ^ > ; о '^ 2^ 2^21
2:
И
>1
И
И
И
иУ
Если взять 1000 таких кубиков, как на рисунке, и
составить из них один большой куб, то как с помо­
щью произведения записать число маленьких кубиков,
из которых состоит построенный большой куб?
Вычисли значение этого произведения, используя
правило умножения на число 1000. Объясни, почему
справедливо данное равенство.
1000 • 1000 = 1000000
Как называется число, которое получается в
^з.| результате увеличения числа 1000 в 1000 раз?
Сколько раз нужно сложить число 1000 с самим
собой, чтобы получилось число МИЛЛИОН?
26
63. Во *сколько раз нужно увеличить 'чис
1а 10000, чтобы получить миллион? Запиши в тимрл
ди соответствующее равенство.
64. Во сколько раз нужно увеличить число
100000, чтобы получить миллион? Записи н
тетради соответствующее равенство.
д
65. Запиши натуральное число, которое непо­
средственно предшествует числу 1000000. Вьнполни
разностное сравнение этих чисел.
66. Запиши натуральное число, которое следую
сразу за числом 1000000.
Выполни разностное сравнение этих чисел.
67. Во сколько раз 1000000 больше 10? Выполни
кратное сравнение этих чисел.
68. Запиши решение данной задачи с помощь
произведения.
В типографии были отпечатаны избирательный
бюллетени. Их упаковали в пачки по 1000 бюллеипюи
в каждой, и получилось 1000 пачек.
Сколько всего бюллетеней было отпечатано?
Вычисли и запиши ответ данной задачи.
69. Сформулируй задачу, при вычислении от пс
которой получалось бы число 1000000.
Реши сформулированную задачу. Вычисли и знни
ши ответ.
27

17. Разряд единиц миллионов и класс миллионов
70. Сколько разрядов содержит таблица, которая
с^а_1 состоит из двух классов: класса единиц и класса
тысяч? Какое минимальное число разрядов должно
быть в таблице, чтобы в ней можно было записать
число 1000000?
Рассмотри данную таблицу и скажи, какой по
счёту справа разряд называется РАЗРЯДОМ ЕДИНИЦ
миллионов.
Разряд
единиц
милли­
онов
Разряд
сотен
тысяч
Разряд
десят­
ков
тысяч
Разряд
единиц
тысяч
Разряд
сотен
Разряд
десят­
ков
Разряд
единиц
1 0 0 0 0 0 0
71. Запиши число 1111111 в таблицу разрядов в
тетради. Представь это число в виде суммы разряд­
ных слагаемых. Заключи в скобки слагаемые, которые
относятся к классу единиц. Заключи в скобки слагае­
мые, которые относятся к классу тысяч. Назови сла­
гаемое, которое не входит в первые два класса. Это
слагаемое относится к третьему классу — КЛАССУ
МИЛЛИОНОВ. Сколько разрядов должно быть в каж­
дом классе? Назови разряды класса миллионов.
72. Запиши в порядке возрастания все разряд­
ные слагаемые, которые относятся к разряду единиц
миллионов.
28
73. Перечерти в тетрадь данную таблицу разрядо
и классов. Запиши в этой таблице число 257689245.
Класс
миллионов
Класс тысяч Класс единиц
Раз­ Раз­ Раз­ Раз­ Раз­ Раз­ Раз­ Раз­ Раз­
ряд ряд ряд ряд ряд ряд ряд ряд ряд
сотен де­ еди­ сотен де­ еди­ сотен де­ еди­
сят­ ниц сят­ ниц сят­ ниц
ков ков ков
г
л
ъ 1 1
V
Ш
74. Разбей' запись числа 257689245 на классы с
помощью знака Представь это же число в виде
слагаемых по классам. Назови каждое из слагаемых,
начиная с класса миллионов. У тебя получилось назил
ние данного числа — двести пятьдесят семь миллионом
шестьсот восемьдесят девять тысяч двести сорок пять.
75. Запиши в таблицу разрядов и классов ело
дующие числа:
а) один миллион триста шестьдесят две тысячи
двести восемьдесят семь;
б) один миллион девяносто четыре тысячи
девятьсот восемь;
в) два миллиона восемь тысяч пятьсот;
г) двадцать миллионов двадцать тысяч двадцать;
д) девятьсот девяносто девять миллионов д<‘
вятьсот девяносто девять тысяч девятьсот девяност
девять.
29

18. Когда трёх классов для записи числа недостаточно
76. Запиши самое маленькое десятизначное
число. Можно ли это число записать в таблицу раз­
рядов и классов, которая состоит из трёх классов?.
Для записи в таблицу числа 1'ООО'ООО'ООО требуется
дополнить уже имеющуюся таблицу четвёртым клас­
сом — КЛАССОМ МИЛЛИАРДОВ*.
Как называется число 1000000000, если его
:^Ё_1 название применяется для названия четвёртого
класса?
77. Из перечисленных примеров выбери те, при
описании которых используются числа класса милли­
ардов:
а) число жителей России,
б) число жителей Земли,
в) состояния самых богатых людей в мире,
г) расстояние* от Земли до Солнца (км),
д) расстояние от Земли до Солнца (м).
78. Запиши цифрами следующие числа:
а) три миллиарда сто двадцать пять миллионов
двести тысяч восемь;
б) десять миллиардов десять миллионов десять
тысяч десять;
в) один миллиард один миллион одна тысяча один;
г) сто миллиардов.
79. Прочитай следующие числа, выделив предва­
рительно каждый класс в записи с помощью знака '.
1256894735 7000635000 123456789000
30
Поупражняемся в сравнении чисел
и повторим пройденное
80. Запиши следующие числа в порядке возрл
стания.
256358975 г 35698712 9699697 256358969
3569872 9699997 25638969 6996979
81. Запиши следующие числа в порядке убывания
5264837 62348927 217396 4587369
98632475 2138657 458231 69371452
82. Вычисли значение следующего выражения.
л л
(6548 + 1458)•(786965 - 786938)
' 83. Раздели ленту длиной 587 см на две части шк.
чтобы одна часть была на 37 см больше, чем другая.
84. Раздели массу 1 ц 80 кг на две части ын.
чтобы одна часть была в 5 раз больше, чем другая
85. Выполни умножение столбиком.
2354 3187 4823
х 47 (х 32 х 26
Расположи полученные результаты умножения и
порядке возрастания.
г&•». „ «

19. 86. Запиши самое большое семизначное число,
в запись которого входит три раза цифра 0 и четыре
раза цифра 1. ДД1ДО О0
87. Запиши самое маленькое восьмизначное
число, в запись которого входит четыре раза цифра
О и четыре раза цифра 1. Л О ^ о ф / %
88. Реши задачу. Вычисли и запиши ответ.
За 8 одинаковых пакетов молока нужно заплатить
на 45 руб. больше, чем за 5 таких же пакетов.
Сколько стоят 4 таких пакета молока? -
89. Для каждого из данных выражений сформули­
руй задачу, решением которой и будет это выражение:
а) (24 - 4) : 2,
б) 72 : (5 + 1)*5.
Вычисли и запиши ответ каждой сформулирован­
ной задачи.
90. Реши две задачи. Сравни решения и ответы
этих задач.
а. Площадь участка 1000 кв. м. Этот участок
нужно разбить на две части так, чтобы одна была в
4 раза больше, чем другая. Какую площадь должна
иметь меньшая из двух частей?
б. Площадь участка 1000 кв. м. Этот участок
нужно разбить на две части так, чтобы одна была на
600 кв. м больше, чем другая. Какую площадь долж­
на иметь меньшая из двух частей?
1 ч. 4 ч.
32
Может ли величина изменяться?
91. Заверши в тетради заполнение данной табл
цы, в которой должны быть представлены длина и
ширина каждого из четырёх изображённых прямоуголь
ников. Длина обозначена буквой а, ширина — буквой //.
©
©
Номер прямоугольника 1 2 3
/ а (см) ? ? ?
Ъ (см) 2 2 2
4
?
2
Какая величина не изменяется при переходе 01
одного из данных прямоугольников к другому?
Такую величину называют ПОСТОЯННОЙ.
Какая величина изменяется при переходе <и
одного из данных прямоугольников к другому? Такая
величина называется ПЕРЕМЕННОЙ.
Что мржно сказать о площади этих прямоуклн.
ников? Будет ли эта величина постоянной или мере
менной при переходе от одного из данных прямо­
угольников к другому?
33

20. Будет ли площадь постоянной или переменной
при изменении только одной из сторон’ прямо­
угольника?
Будет ли площадь одной и той же данной фигу­
ры всегда величиной постоянной, или она может
изменяться в зависимости от положения фигуры?
92. Среди перечисленных величин укажи те,
которые являются переменными:
а) рост человека в течение жизни, у
б) масса человека в течение жизни, Г
в) площадь классной комнаты, в которой ты учишься,
г) высота стакана по мере наполнения его водой,ЖУх4
д) масса стакана с водой по мере наполнения его
этой водой,
е) число учащихся твоего класса за все годы обучения. |
93. Учительница Мария Евдокимовна поручила
Маше фиксировать посещаемость занятий учащимися
класса в течение двух недель.
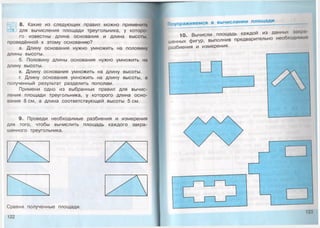
Маша составила следующую таблицу.
Поне­
дель­
ник
Втор­
ник
Среда Четверг
Пят­
ница
Суб­
бота
1-я
неделя
21 21
1?]ь'Ы
21 21 21 21
2-я
неделя
22 20 20 18 19 19
В течение какой недели число учащихся, присут­
ствующих на занятиях, было постоянным, а в
течение какой — переменным?
34
94. Приведи по три примера постоянных и пе
минных величин из окружающей действительности
95. Проведи необходимые вычисления и продол
+н шполнейие данной таблицы в тетради.
Номер прямоугольника 1 2 3 4
Длина (см) 24 12 8 6
Ширина (см) 1 2 3 4
Периметр (см) ? ? ? ?
Площадь (кв. см) ? ? ? ?
Какая из перечисленных в таблице величин н<
изменяется при переходе от одного прямоугольник! I
другому, а какие — изменяются?
96. Начерти три ломаных линии, длинакоторых
при переходе от одной к другой остаётся постоянной,
а число звеньев уменьшается.
97. Начерти три окружности, радиусы которых
при переходе по порядку от одной окружности к дру
гой увеличиваются.
98. Начерти три ломаных линии, длинакоторых
при переходе по порядку от одной к другой умпнп
шается, а( число звеньев остаётся постоянным.
Может ли одновременно число звеньев ломаной
линии увеличиваться, а длина уменьшаться?
35

21. 25
Всегда ли м атематическое выражение
является числовым?
99. Чем похожи и чем отличаются следующие
суммы?
256+ 15 и а +15
Какое число может стоять на месте первого сла­
гаемого во второй сумме? Какое слагаемое в этой
сумме является переменным, а какое — постоянным?
Сумма с переменным слагаемым и постоянным
слагаемым 15 представлена выражением, содержащим
букву, или БУКВЕННЫМ ВЫРАЖЕНИЕМ*.
Вычисли значения буквенного выражения а +15
при значениях переменной а, которые представлены в
данной таблице. Запиши полученные значения в
таблицу в тетради.
а 256 43 78659 243687
о +15 ? ? ? ?
1 100. Запиши буквенное выражение, с помощью
ь1которого можно вычислить периметр квадрата.
Длину стороны квадрата обозначь буквой а.
Вычисли значение этого выражения, если
а =25 см.
101. Запиши буквенное выражение, с помощью
которого можно вычислить площадь квадрата. Длину
стороны квадрата обозначь буквой а.
Вычисли значение этого выражения, если
а = 25 см.
*
36
102. Запиши буквенное выражение, с помощью
которого можно вычислить периметр прямоугольники
Длины сторон прямоугольника обозначь буквами о и 6
Вычисли значение выражения, если а = 215 мм и
Ь 35 мм.
103. Вычисли значение буквенного выражении
а • 6 , если а =756 и 6 = 895.
Нужно ли проводить какие-либо дополнительные'
иычисления для того, чтобы найти значение буквонно
Iо выражения 6 + апри тех же значе
Почему? Какое свойство сложения выражает следую
щее равенство?
а + Ь = Ь + а
104. Выполняя предыдущее задание, мы ужн
научились записывать с помощью буквенных выражо
ний переместительное свойство сложения.
Запиши, используя буквенные выражения, ранни
/С1во, в котором выражено переместительное своиспю
умножения.
Проверь справедливость полученного равенств
Ий при а =236, 6 = 165, выполнив вычисления
столбиком.
Ж
105. В каком из следующих равенств выражено
сочетательное свойство сложения (правило при
бавления суммы к числу)?
а + (6 + с) = (а + 6) + с
/ а + (6 - с) = (а + 6) - с
а - (6 + с) = (а - 6) - с
Запиши это равенство в тетради.
37

22. 106. Запиши, используя буквенные выражения с
буквами а, Ь, с, равенство, в котором выражено соче­
тательное свойство умножения (правило умножения
числа на произведение).
5 5 ) Проверь справедливость данного равенства при
а= 231, Ь= 4, с= 12.
107. Вычисли значения выражений (8 + 9) • 9 и
(20 - 7) • 8, применяя соответственно правила умноже­
ния суммы на число и разности на число.,
Используя буквенные выражения, заверши в
тетради составление равенств, в первом из которых
выражено правило умножения суммы на число, а во
втором — правило умножения разности на число.
(а+ Ъ)• с=...
...= а • с - Ъ • с
108. Какое правило выражает следующее равен­
ство, если оба деления в правой части выполнимы?
(а + Ъ) : с = а : с + Ь : с
Проверь справедливость данного равенства при
а = 48, Ъ =24, с-6, выполнив вычисления устно.
Запиши аналогичное равенство для правила деле­
ния разности на число.
Проверь его справедливость при тех же значени­
ях букв а, Ь, с.
109. Запиши, используя буквенные выражения,
равенства, в которых выражено соответственно прави­
ло умножения числа на сумму и правило умножения
числа на разность.
38
Зависимость м еж ду величинами
110. Обозначим длину стороны квадрата буквой
Периметр квадрата обозначим буквой Заполни дан
ную таблицу и установи, изменяется ли периметр квад
рата в зависимости от изменения длины его стороны
а (см) 8 11
/' (см) ? ?
<уЩ| Может ли периметр квадрата не измени!вся,
если длина стороны квадрата изменилась?
Могут ли получиться разные значения перимезгра
квадрата при одном и том же значении длины ого
стороны?
Объясни смысл фразы: периметр квадрата одно­
значно ЗАВИСИТ от длины его стороны.
1 Что происходит с периметром квадрата, еспи
длина стороны этого квадрата увеличивается?
Что происходит с периметром квадрата, если
длина стороны этого квадрата уменьшается?
^^1 111. Среди перечисленных пар величин укажи
те, в которых одна величина зависит от другой
а) площадь квадрата и длина его стороны,
б) рост человека и его возраст,
(§) число квартир и число номеров этих квартир,
(0 масса купленных яблок и стоимость этой покупки
В каких из перечисленных выше случаях зависи
мость является однозначной?

23. 112. Приведи пример двух величин, которые нахо­
дятся в некоторой зависимости одна от другой, а
также двух величин, которые не зависят друг от друга.
113. Заполни в тетради данную таблицу, если
27 известно, что длина а на 3 см больше, чем длина Ъ.
а(см) 12 65 50 187 4568
Ь(см) ? 9 ? ? ?
Будет ли в данном случае величина Ъ однозначно
зависеть от величины а?
114. Если известен периметр квадрата, то можно
ли однозначно установить его площадь? Сделай
это для квадрата, периметр которого равен 20 см.
Объясни,4 почему площадь квадрата однозначно
зависит от его периметра.
115. Начерти два прямоугольника, у одного из
которых стороны имеют длину 6 см и 4 см, а у дру­
гого соответственно - 8 см и 2 см. Вычисли пери­
метр и площадь каждого из этих прямоугольников.
Сравни получившиеся периметры между собой и
получившиеся площади между собой.
Если известен периметр прямоугольника, то
м о ж н о ли однозначно установить его площадь?
Объясни, почему площадь прямоугольника не
будет однозначно зависеть от его периметра. А что
можно сказать о зависимости площади квадрата от
его периметра? Проиллюстрируй это на примере.
40 41
1118. В сумме а + Ь второе слагаемое отличаоюи
Ыот первого в 2 раза. Каким в этом случае можт
быть второе слагаемое, если первое равно !»()'
Можно ли д^ть однозначный ответ? Как нужно измп
нить условие для того, чтобы второе слагаемое одно
значно зависело от первого?
Номер окружности 1
Радиус (мм)
Диаметр (см)
БйЯ 116. Будет ли периметр равностороннего ц>н
угольника однозначно зависеть от длины его о т
роны? Будет ли площадь равностороннего треугольни
им однозначно зависеть от длины его стороны?
117. Будет ли диаметр окружности однозначно
швисеть от радиуса этой окружности? Проведи
намерение радиусов и вычисление диаметров дан
ных окружностей и заполни в тетради приведённую
ниже таблицу.

24. Поупражняемся в нахождении значений
зависим ой величины
119. Какие из следующих равенств показывают,
что получающееся значение величины Ъ всегда в 2
раза больше любого возможного значения величины а?
Ь = а +2 Ъ —а• 2 Ъ = а + а = •
Запиши эти равенства и вычисли значение вели­
чины Ъ, если а= 325 кг. ,
120. Запиши формулу, которая позволяет по зна­
чению длины стороны квадрата (обозначается бук­
вой а) однозначно вычислить периметр этого квадрата
(обозначается буквой Р).
Заверши в тетради заполнение данной таблицы.
а (см) 2
с
3 5 8 10 50
Р (см) ? ? ? ? ? ?
121. Запиши формулу, которая позволяет по зна­
чению длины стороны квадрата (обозначается бук­
вой а) однозначно вычислить площадь этого квадрата
(обозначается буквой 8).
Заверши в тетради заполнение данной таблицы.
а (см) 2 3 5 8 10 50
Л" (кв. см) ? ? ? 9 ? ?
42
122. Вычисли и запиши в таблицу в тетради
шачения указанных величин по следующим значениям
меличины а.
а 25 50 65 90 100
а + 25 ? ? ? ? ?
г/ • 15 ? ? ? ? ?
а - 23 ? ? ? ? ?
а : 5 ? ? ? ? ?
123. Вычисли значение величины с, если
с- 8 • а+ 45 *Ъпри а = 42,6=
124. В одной коробке находится 12 карандашей
Вычисли число карандашей в нескольких таких корон
ках, записав результат в соответствующую графу п»б
лицы в тетради.
Число коробок 2 5 10 50
Число карандашей ? ? ? ?
125. Вычисли периметр равностороннего г
угольника, если длина его стороны равна 25 мм.
Во сколько раз увеличится периметр треугольно
ка, если длину его стороны увеличить в 3 раза?

25. Стоимость единицы товара, или цена
126. Для каждой из названных единиц приведи
5ЭЦ пример товара, который исчисляется в этих еди­
ницах: а) штука, б) пакет, в) коробка, г) упаковка,
д) метр, е) килограмм, ж) квадратный метр.
127. Сколько стоит 1 пакет молока, если 3, таких
пакета стоят 36 руб.?
Запиши вычисленную цену пакета молока в
таблицу, где уже указано соответствующее наименова­
ние цены. Например, 12 руб./пак., которое нужно
читать так: 12 рублей за пакет.
Вычисли цену других товаров из данной таблицы
и запиши полученные результаты.
Прочитай и объясни смысл каждого из наимено-
I ваний цены.
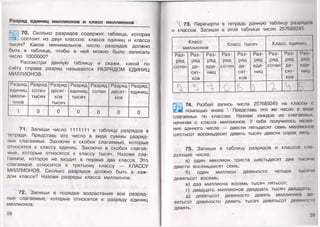
Вид товара Цена Количество Стоимость
Молоко ? руб./пак. 3 пак. 36 руб.
Хлеб ? руб./бат. 2 бат. 18 руб.
Макароны ? руб./кг 4 кг 60 руб.
Лента ? руб./м 5 м 55 руб.
Ковровое
покрытие
? руб./кв. м 1 кв. м 310 руб.
Конверты ? руб./шт. 10 шт. 85 руб.
44
128. Реши задачу. Вычисли и запиши ответ
Стоимость 1 билета в театр — 90 руб. Запиши
цену билета. Сколько нужно заплатить за 2 ыких
билета? За 10 таких билетов?
129. По
4 Ш задачу.
следующей краткой записи сформулируй
Вид товара Цена Количество Стоимость
Яблоки на 10 руб./кг>
меньше
3 кг 60 руб.
Груши ? >
) 2 кг ?
Реши задачу. Вычисли и запиши ответ.
130. Прочитай задачу.
За тетрадь и альбом заплатили 60 руб. Альбом
дороже тетради на 12 руб. Сколько стоит тетрадь и
сколько стоит альбом?
«ЗЩ] Ответь на следующие вопросы.
е а ! На сколько рублей должен подешеветь альбом,
чтобы его цена сравнялась с ценой тетради?
Сколько стоила бы эта покупка, если бы цони
альбома стала равна цене тетради?
Какова цена тетради?
Какова действительная цена альбома?
Реши задачу. Вычисли и запиши ответ.
Стоимость какой покупки можно вычислить с по
мощью выражения 60 + 12?
4!

26. 131. За блокнот и книгу заплатили 120 руб.
Книга дороже блокнота в 5 раз. Сколько стоит каж­
дая из покупок? Сделай краткую запись задачи,
дополнив следующую таблицу в тетради.
Вид товара Цена Количество Стоимость
Блокнот ? 1 шт.
120 руб.
Книга ? 1 шт.
Сколько блокнотов можно купить за те же день­
ги, что потрачены на покупку 1 книги? Сколько всего
блокнотов можно купить за 120 руб.? Какова цена
блокнота? Реши задачи. Вычисли и запиши ответы.
132. Сформулируй задачу на кратное сравнение
^ стоимостей, решением которой являлось бы сле­
дующее выражение.
(16 • 6) : (8 -4)
133. Реши задачу. Вычисли и запиши ответ.
Стоимость 1 кг помидоров в 3 раза или на
30 руб. больше, чем 1 кг картофеля. Какова цена
картофеля и цена помидоров?
Покажи на схеме, какая часть полоски изобра­
жает 30 рублей.
1ч. Зч.
46
Когда цена постоянна
134. Реши задачу. Вычисли и запиши ответ.
Месяц назад Маша при покупке двух тетрадой
заплатила 24 руб. Сегодня она купила три такие жо
тетради за 36 руб. Изменилась ли цена этих тетра
дей за прошедший месяц?
135. За 3 кг картофеля было заплачено 27 р
СМ_] Во сколько раз больше нужно заплатить за 12 и
картофеля по той же цене?
Рассмотри и объясни каждый из двух вариантом
решения этой задачи.
1-й вариант 2-й вариант
1) 27 руб. : 3 кг = 9 руб./кг 1) 12 кг : 3 кг = 4 (раза)
2) 9 руб./кг • 12 кг = 108 руб.
3) 108 руб. : 27 руб. =
= 4 (раза)
«'уЩ] 136. Два покупателя купили ткань по одинаковой
;Ж цене. Только первый купил в 2 раза больше, чем
второй. Во сколько раз больше заплатил первый
покупатель, чем второй?
137. Во сколько раз больше нужно заплатим, ш
9 м ткани, чем за 3 м такой же ткани?
138. Покупатель заплатил за 4 м ткани 840 руп
Сколько нужно заплатить за 12 м такой же ткани''’

27. Количество Стоимость
1-й
покупатель
Одинаковая
покупатель
Реши сформулированную задачу. Вычисли и запи­
ши ответ.
Как можно было бы рациональнее решить соот-
* д ] ветствующую задачу, если бы в графе
«Количество» вместо 20 шт. стояло 27 шт.?
140. Заполни в тетради данную таблицу, если
цена тетрадей не меняется и равняется 20 руб./тет.
Количество (шт.)
Стоимость (руб.)
141. Заполни в тетради данную таблицу, если
цена ручек не меняется и равняется 10 руб./руч.
Количество (шт.)
Стоимость (руб.)
139. Сформулируй задачу по следующей краткой
записи, представленной в виде таблицы.
48
Учимся решать задачи
142. Реши задачу, не вычисляя цены электропро
вода. Вычисли и запиши ответ.
За 20 м электропровода покупатель заплатил
160 руб. Сколько нужно заплатить за 100 м такою
же провода?
143. Реши задачу двумя способами: вычисляя и
у не вычисляя цены сахарного песка.
За 3 кг сахарного песка заплатили 75 руб
Сколько нужно заплатить за 12 кг сахарного .......
той же цене?
По каждому варианту решения вычисли и запиши
ответ задачи.
144. Сформулируй задачу по следующей кршк
Ш записи.
Цена Количество Стоимость
Одинаковая
5 кг 60 руб.
? 120 руб.
Реши сформулированную задачу двумя способа
ми: вычисляя и не вычисляя цены товара.
Вычисли и запиши ответ.
Какой из этих двух способов ты не сможешь при
менить, если стоимость 120 руб. заменить на 96 руб ?
4‘)

28. I 145. На диаграмме представлена цена трёх
^ Ль» видов товара.
I—I—|—I—|—I—|—I—|—I—|—I—|—I—|—I—|—I—|—I—|--------- ►
О 20 40 60 80 100 120 140 160 180 200 (руб./шт.)
Выполни по этой диаграмме попарное разностное
и кратное сравнения данных цен. Сформулируй задачу
на нахождение стоимости товара с использованием
данных цен. Реши задачу. Вычисли и запиши ответ.
146. Условия и требования трёх задач заданы в
табличной форме.
Реши задачи. Вычисли и запиши ответы.
Вид
продукции
Расход
(нормативный) Количество
Общий
расход
Костюмы 3 м/шт. ? шт. 75 м
Юбки ? м/шт. 30 шт. 30 м
Брюки 130 см/шт. 20 шт. ? см
147. Реши задачу. Вычисли и запиши ответ.
В плацкартном вагоне пассажирских мест на 18
больше, чем в купейном. Всего в этих двух вагонах
90 пассажирских мест. Сколько пассажирских мест в
плацкартном вагоне? В купейном вагоне?
50
Деление с остатком и деление нацело
148. Маша и Миша ждут в гости четырёх друзо
Мама сказала, чтобы они угостили их конфемми
Миша решил заранее разделить конфеты между
6 детьми поровну. В вазе было 12 «Васильков», !!>
«Ромашек» и 18 «Юбилейных». Миша сразу сказал, что
он легко разделит поровну «Васильки» и «Юбилейш....
и записал на листочке соответствующие действия:
12 : 6 = 2 (к.) и 18 : 6 = 3 (к.).
«Всем поровну получилось. Ни одной лишней III
ОСТАЛОСЬ, — сказал Миша. — А вот подели п.
“Ромашки” мне не удаётся. Если я кладу каждому по
3, то мне конфет не хватает. Если по 2 — ещё осы
ётся! Смотри сама».
Сначала Миша разложил на столе 6 конфет по
одной каждому. Потом положил ещё по одной конфет
«Каждый получит по 2 “Ромашки”», — сказал Миша.
«А эти ОСТАВШИЕСЯ 3 конфеты мы вернем
маме, — сказала Маша. — Это и есть ОСТАТОК*. Мы
выполнили ДЕЙСТВИЕ ДЕЛЕНИЯ С ОСТАТКОМ!»
Посмотри на запись того, что сделали ребята:
15 : 6 = 2 (ост. 3).
Объясни, что обозначает каждое число в записи
деления с остатком.
«Значит, “Васильки” и “Юбилейные” мы разделит)
без остатка?» — спросил Миша.
«Без остатка», — подтвердила Маша.
ДЕЙСТВИЕ лДЕЛЕНИЯ БЕЗ ОСТАТКА называю!
ДЕЛЕНИЕМ НАЦЕЛО.______________________

29. 149. После того как мама положила на каждую
из четырёх тарелок по 3 сосиски, в кастрюле оста­
лось 2 сосиски. Сколько всего сосисок сварила мама?
Запиши решение этой задачи в виде одного
выражения. Раздели с остатком число 14 на число 4.
150. Выполни деление с остатком, используя для
этого соответствующие табличные случаи деления.
24 : 6 = 27: 3 = 32 : 8 = 8 1 : 9 =
27 : 6 = 29: 3 = 39 : 8 = 85 : 9 =
Рассмотри действия деления в первом столбике.
*Й_| Какое из них является табличным случаем деле­
ния? На сколько одно делимое отличается от друго­
го? Будет ли это число совпадать с остатком?
Вычисли, на сколько отличаются делимые в
остальных столбиках. Проверь,, совпадает ли каждое
из этих чисел с соответствующим ему остатком.
151. Объясни, почему с помощью табличного
случая деления 42:7 = 6 можно разделить с
остатком число 45 на число 7. Выполни и запиши
деление с остатком числа 45 на число 7.
Почему выбранный табличный случай деления
можно получить, выполнив действие в скобках в сле­
дующем выражении: (45 - 3):7?
Вычисли значение этого выражения. В полученном
равенстве подчеркни соответственно одной и двумя чер­
тами числа, которые получаются в результате деления
с остатком числа 45 на число 7. Всегда ли аналогич­
ным образом можно получить по результатам деления
с остатком соответствующий случай деления нацело?
52
152. Для того чтобы разделить с остатком чис
67 на число 9, выбери сначала из следующей поело
довательности разностей ту, значение которой можно
разделить на 9 нацело.
67 - 1 6 7 - 2 6 7 - 3 67
6 7 - 5 6 7 - 6 6 7 - 7 67 8
Вычисли значение выражения (67 - 4) : 9 и зами
ши соответствующее равенство. Назови числа, кою
рые получаются при делении числа 67 на число 9.
Какая из следующих записей будет являться записью
деления с остатком числа 67 на число 9?
67 : 9 = 7 (ост. 4) 67 : 7 = 9 (ост. 4)
153. Можно ли разделить число 76 на число 9
еэц нацело?
Перебирая числа в порядке убывания, начиная <
числа 75, найди первое число, которое можно ра:щ<‘
лить на 9 без остатка. Выполни это деление.
Какие числа получатся в результате деления с
остатком числа 76 на число 9? Сделай полную запись
деления с остатком числа 76 на число 9.
154. Выполни устно деление состатком
Полученные результаты запиши.
76 : 8 = 59 : 6 = 67 : 9 = 50 : 7 = 44 : 5
155. Среди чисел 62, 61, 60, 59, 58, 57, 56, !>!>.
54, 53, 52, 51, 50 выбери то, которое делится нацо
ло на 7. Выпблни это деление. С помощью получен
ного результата раздели с остатком на 7 каждое и I
следующих чисел: 62, 61, 60, 59, 58, 57.

30. Неполное частное и остаток
156. «Маша, а числа при делении с остатком
тоже имеют свои названия?» — спросил Миша.
«Да. Они называются делимое, делитель, НЕПОЛ­
НОЕ ЧАСТНОЕ* и остаток», — ответила Маша.
Используя следующую запись деления с остатком
и объяснение Маши, дай названия всем участвующим
в этом делении числам.
58 : 8 = 7 (ост. 2)
Какие названия тебе уже хорошо знакомы? Какие
названия являются новыми?
Попробуй объяснить смысл термина «неполное
частное».
157. Выполни деление нацело и деление с
остатком.
6 0 : 1 0 = и 63:10 =
Как получить делимое 60, используя значение
частного и делитель? Запиши соответствующее выра­
жение и его значение.
Как получить делимое 63, используя неполное
частное, делитель и остаток? Запиши соответствую­
щее выражение и его значение.
158. Выполни деление с остатком.
5 5 : 7 = 6 3 : 8 = 8 0 : 9 = 9 5 : 1 0 = 46:15 =
Убедись, что во всех приведённых выше случаях
выполняется правило.
54
Если делитель умножить на неполное частное и
к полученному результату прибавить остаток, го и
итоге получится делимое.
Может ли это правило нарушиться при правиле
ном выполнении деления с остатком?
Запиши данное правило в виде равенства бук
венных выражений, обозначив буквой а — делимо»>,
буквой Ь — делитель, буквой с — неполное частное,
буквой а— остаток.
Щ&З 159. Проверь выполнимость правила из предыду
щего задания для следующих двух записей:
69 : 4 = 17 (ост. 1) и 99 : 4 = 24 (ост. 3).
160. Из данных четырёх чисел: 12, 131, II,
10 составь верную запись деления с остатком.
Можно ли в качестве делителя взять число 10?
Почему?
161. Проверь справедливость следующего ранен
ш ства.
224 = 15*14 + 14
Используя это равенство, составь верную заиим.
деления с остатком для тех же чисел.
I
162. Составь и запиши три случая деления е
остатком, в каждом из которых делитель равен числу
7, а остаток — числу 5.

31. Остаток и делитель
163. «Маша! Помнишь, мы делили конфеты
“Ромашка”? — спросил Миша. — Дали всем по 2
конфеты и получили 3конфеты в остатке? Но ведь
мы могли поделить и по-другому! Мы могли дать
каждому только по 1 конфете, итогда унас был бы
другой остаток: не 3, а9!»
«Это называется жадностью, а не делением с
остатком!» — сказала Маша.
Маша объяснила, что для правильного деления с
остатком должно обязательно выполняться условие:
Остаток должен быть меньше делителя.
Раздели с остатком число 52 на число 7 и про­
верь выполнимость условия, о котором сказала Маша.
164. Верно ли следующее равенство?
76 = 9 • 8 + 4
Используя это равенство, выполни деление с ос­
татком числа 76 на число 9. Сделай соответствующую
запись. Проверь выполнимость условия из задания 163.
165. Из следующих равенств выбери те, которые
можно преобразовать в соответствующие случаи деле­
ния с остатком. Для каждого выбранного равенства
запиши соответствующий случай деления с остатком.
57 = 9*6 + 3 82 = 9 *9 + 1
69 = 8 * 7 + 13 95 = 10 * 9 + 5
Почему равенство 69 = 8 • 7 + 13 нельзя использо-
г вать для нахождения неполного частного и остатка?
$
56
166. Можно ли с помощью равенст
58 = 10*5 + 8 разделить с остатком число 58 на
число 10? Сделай соответствующую запись.
Можно ли с помощью равенства 58 = 5* 10 »8
разделить с остатком число 58 на число 5? Почему?
Какое правило будет тогда нарушено?
Выполни и запиши деление с остатком числа 58
на число 5.
Ш
167. Составь равенство, с помощью которою
можно выполнить только один случай деления с
остатком. Предложи соседу по парте записать его.
168. Может ли при делении на 9 в остатке
получиться число 10? Почему?
Выпиши все остатки, которые могут получаться
при делении на 9.
Какое из следующих двух равенств можно преоб­
разовать в запись деления с остатком?
93 = 9*10 + 3 93 = 9*9+ 12
169. Прочитай правило.
Остаток должен быть больше нуля или ранен
нулю, но меньше делителя.
На основании этого правила выпиши все остами,
которые могут получиться при делении на 2.
Какой остаток может получиться при делении на 1?
При делении на какое число могут получиться
ровно семь различных остатков?

32. Когда остаток равен О
170. Используя следующее равенство, запиши
соответствующий случай деления с остатком.
63 = 9 • 7 + О
Чему равен остаток в этом случае? Будет ли он
меньше делителя?
Когда остаток равен нулю, то принято считать,
что одно число делится на другое без остатка, или
делится нацело.
Приведи пример двух чисел, которые делятся
друг на друга без остатка. Могут ли эти числа
быть разными?
171. Выполни деление с остатком для пар чисел:
59 на 10, 72 на 9, 45 на 15, 99 на 98, 37 на 1.
Подчеркни те случаи, в которых остаток равен 0.
Какое другое название можно использовать для
неполного частного, если остаток равен 0?
172. Проверь правильность выполнения деления
с остатком.
123 : 8 = 15 (ост. 3)
Учитывая полученный остаток, определи, какое бли­
жайшее к числу 123 число делится на 8 без остатка.
Запиши следующее за числом 120 число, которое
делится на 8 без остатка.
58
173. Запиши первые пять натуральных чисел,
которые делятся на 2 без остатка.
174. В столовой испекли 93 блина. В каждой
порции должно быть по 5 блинов. Какое самое ма
ленькое число блинов может съесть сам повар, чтобы
из всех оставшихся блинов можно было составим,
полные порции?
175. Запиши по порядку первые пять натураль
ных чисел, которые делятся на 7 без остатка.
На какое число отличаются друг от друга сосед
ние из полученных чисел?
176. Запиши по порядку первые шесть натуральных
чисел, которые при делении на 7 дают в остатке 1.
Сравни их с числами из предыдущего задания.
177. Реши задачу. Вычисли и запиши ответ.
В вазе лежит 25 одинаковых конфет. Какое самое
большое число конфет Маша может взять из ва мы
для того, чтобы поровну угостить ими семерых одно
классников, которые к ней пришли в гости? Сколько
ещё в этом случае конфет останется в вазе?
178. Выпиши все числа, на которые число 24
делится без остатка.
179. Какое наименьшее число нужно прибавить и
числу 75, чтобы полученное в результате число дели
лось на число 9 без остатка? Как это число связано
с остатком от деления числа 75 на число 9?
59

33. Когда делим ое меньш е делителя
Ж Э 180. Проверь, правильно ли для данного равен-
шства приведён соответствующий случай деления
с остатком.
58 = 8- 7 + 2 5 8 : 8 = 7 (ост. 2)
Для следующего равенства аналогично составь и
запиши соответствующий случай деления с остатком.
1 2 = 1 5 - 0 + 12
181. Раздели с остатком на 10 последовательно
следующие числа: 48, 38, 28, 18. Что общего во всех
этих случаях деления и чем они отличаются?
Во всех случаях сравни остаток с числом в раз­
ряде единиц делимого, а неполное частное — с чис­
лом в разряде десятков делимого.
Какой должен быть остаток при делении числа 8
на число 10? Какое неполное частное должно полу­
читься в этом случае деления с остатком?
Проверь, правильно ли выполнено деление
с остатком 8 : 10 = 0 (ост. 8).
*'уЩ| 182. Какому условию должны удовлетворять дели-
Е&.. мое и делитель для того, чтобы в результате де­
ления с остатком неполное частное равнялось 0? При­
веди три примера таких случаев деления с остатком.
Как в рассмотренных случаях остаток связан
с делимым?
183. Составь и запиши три случая деления с ос­
татком, в каждом из которых делимое равно остатку.
60
184. Выполни деление с остатком в каждом и;»
данных случаев.
9 : 1 0 = 1 2 : 2 4= 1 : 1 0 0= 364:387
1000 : 10000 =
Проверь правильность выполнения деления с
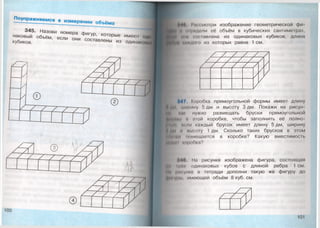
помощью следующего правила.
Если при делении с остатком делимое меньше
делителя, то неполное частное равно 0, а остаток
равен делимому.
185. Приведи пример двух чисел, которые мри
делении на 56897 дают в остатке число 1.
«*<•<г
186. Приведи пример числа, которое при делении
на 5, на 6, на 7, на 8, на 9 и на 10 даёт в остатке Л
187. Найди число, которое при делении на
любое двузначное число даёт в остатке 9.
188. Существует ли число, которое при делении
на все натуральные числа, кроме числа 1, даё1 и
остатке число 1?
189. Какими могут быть делимое и делитель,
если неполное частное равно 0, а остаток равен 5?
] 190. Выпиши все натуральные числа, при деле
у нии каждого из которых на число 10 в неполном
частном получается число 0. Чему равен остаток и
каждом таком случае?
61

34. Деление с остатком и вычитание
191. Сравни между собой записи из одного
столбика.
41 : 19 = 2 (ост. 3) 56 : 17 = 3 (ост. 5)
41 - 1 9 - 19 = 3 5 6 - 1 7 - 1 7 - 17 = 5
Как с помощью вычитания найти остаток от
ь1 деления одного числа на другое?
Обрати внимание на то, сколько раз делитель
вычитали из делимого. В каждом из рассмотренных
случаев сравни это число с неполным частным.
192. Вычисли значение разности: 5 3 - 7 * 7 .
Используя полученное равенство, запиши резуль­
тат деления с остатком числа 53 на число 7.
193. Представь разность 6 9 - 6 в виде произведе­
ния двух множителей, один из которых равен 9.
Используя полученное равенство, запиши результат
деления с остатком числа 69 на число 9 и на число 7.
194. На овощной базе 1 ц 50 кг картофеля упако­
вали в мешки по 35 кг в каждом. Сколько полных
мешков получилось и сколько килограммов картофеля
при этом ещё осталось?
Запиши решение задачи с помощью деления с
остатком. Вычисли ответ задачи с помощью вычитания.
195. Выполни деление с остатком для следую­
щих пар чисел с помощью вычитания.
387 : 350 = 927 : 291 = 1003 : 250 =
62
Какой остаток может получиться при делении на 2?
иЖ1 196. Некоторое натуральное число разделили
Ш М ня 2 с остатком. Какой остаток мог получиться?
Приведите в качестве примера пять чисел, которни1
при делении на 2 дают в остатке число 1. За
помните: такие числа называются НЕЧЁТНЫМИ*.
Приведите в качестве примера пять чисел, кото
рые делятся на 2 нацело. Запомните: такие числа
называются ЧЁТНЫМИ*.
Могут ли при делении с остатком на 2 получи па л
в остатке другие числа, кроме чисел 0 и 1? Почему':'
Может ли натуральное число не быть чётным и
не быть нечётным?
197. Запиши по порядку первые двадцать нату­
ральных чисел. Подчеркни одной чертой нечётные
числа. Какие числа остались неподчёркнутыми? Как
располагаются в натуральном ряду чётные и нечёпи.ю
числа? Запиши двадцатое по порядку нечётное число
198. Назови самое маленькое нечётное натураль
ное число. Существует ли самое большое нечётное
натуральное число?
199. Какой остаток получится при делении
числа 0 на 2? Выполни соответствующую запись.
Число 0 относят к чётным числам.
Назови самое маленькое чётное натуральное число
Существует ли самое большое чётное число?
Почему?

35. 200. Человек стоит в начале улицы и видит: по
левой её стороне расположены дома с нечётными
номерами, а по правой — с чётными. По какой сто
роне улицы он пойдёт, чтобы прийти к дому № 19, и
каким по счёту будет этот дом среди домов этой
стороны улицы?
Каким по счёту среди домов правой стороны
улицы будет дом № 16?
201. Какое число получится: чётное или нечёт­
ное, если складывать чётные числа? Приведи
несколько примеров, подтверждающих твоё предпо
ложение.
202. Какое число получится: чётное или нечёт­
ное, если складывать нечётные числа? Приведи
несколько примеров, подтверждающих твоё предполо­
жение.
203. Какое число получится: чётное или нечётной,
если складывать чётное число с нечётным? При­
веди несколько примеров, подтверждающих твоё пред
положение.
Изменится ли ответ, если складывать нечётной
число с чётным? Почему?
204. Какое число получится: чётное или нечёт
ное, если умножать чётные числа? Приведи
несколько примеров, подтверждающих твоё предполо
жение.
205. Какое число получится: чётное или нечётное,
если умножать нечётные числа? Приведи несколь
ко примеров, подтверждающих твоё предположение.
64
206. Какое число получится: чётное или нечёы
ное, если умножать чётное число на нечётное?
Приведи несколько примеров, подтверждающих твоё
предположение.
Изменится ли ответ, если нечётное число умно-
(.т . на чётное? Почему?
! 207. Какое число получится: чётное или неч<м
■** мое, если из чётного числа вычитать чётное
ип мо? Приведи несколько примеров, подтверждающих
11кк* предположение.
208. Какое число получится: чётное или нечё!
ное, если из нечётного числа вычитать нечётное
число? Приведи несколько примеров, подтверждающих
I|нк ')предположение.
I* ) 209. Какое число получится: чётное или нечёт
!■■*« ное, если из чётного числа вычитать нечётное
ик мо? Приведи несколько примеров, подтверждающих
(неё предположение.
210. Какое число получится: чётное или нечё!
ное, если из нечётного числа вычитать чётное
ик ло? Приведи несколько примеров, подтверждающих
пюе предположение:
Г#♦я
211. Какое число получится: чётное или нечёт
ное, если чётное число делить на чётное число
при условии, что выполнено деление нацело? Приведи
•и сколько примеров, подтверждающих твоё предполо
мшие. Выполни деление числа 24 на 2, 4 и 8.

36. 212. Какое число получится: чётное или нечётное,
если нечётное число делить на нечётное число
при условии, что выполнено деление нацело? Приведи
три примера, подтверждающих твоё предположение.
|Щ З 213. Какое число получится: чётное или нечё1-
ное, если чётное число делить на нечётное число
при условии, что выполнено деление нацело? Приведи
несколько примеров, подтверждающих твоё предполо­
жение. Обсуди результат с соседом по парте.
214. Можешь ли ты привести пример такого слу­
чая деления, когда нечётное число делится нацело на
чётное число? Почему? Вспомни, как можно получить
делимое из делителя и значения частного.
215. Представь число 2873 в виде суммы круг
лых десятков и однозначного числа. Чётным или
нечётным числом является каждое из слагаемых?
Чётным или нечётным числом будет значение их
суммы? На какую цифру может оканчиваться запись
чётного числа? А нечётного?
216. Выпиши чётные числа в один столбик, а
нечётные — в другой.
57893 2844 67586 9231 10050 9929
217. Сколько существует чётных двузначных нату
ральных чисел? А сколько таких же нечётных чисел?
218. Запиши самое большое чётное шестизнач
ное число.
66
НйМ|1йи(мяемся в вычислениях
ц мниырим пройденное ____
10. Продолжи в тетради заполнение следую
•в*>мнцы значениями выражений 2 и 1 при раз
•Мчим» течениях переменной п.
II 2п 2« + 1
0 0 1
1 2 3
2 ? ?
3
? 9
4 ? ?
5 ? ?
Какими числами будут выражены значения фор
4 > мулы 2л?
Какими числами будут выражены значения фор
мулы 2 п+ 1?
220. В доме на каждом этаже по 4 квартиры
• помощью какого действия можно узнать, на каком
•ншп расположена квартира №29? Сделай эго,
лыиолнив деление с остатком.
Как связано искомое число с полученным непол
иым частным?
Проведи такие же вычисления для квартиры № X'

37. 221. Реши задачу. Вычисли и запиши ответ.
Книга дороже тетради в 5 раз. За книгу и
тетрадь заплатили 120 руб. Сколько всего нужно
заплатить за 4 такие тетради и 2 такие книги?
222. Реши задачу. Вычисли и запиши ответ.
Книга дороже тетради на 80 руб. За книгу и
тетрадь заплатили 120 руб. Сколько нужно заплатить
за 5 таких тетрадей и 3 такие книги?
223. Реши задачу. Вычисли и запиши ответ.
Книга дороже тетради в 5 раз. За книгу заплати­
ли на 80 руб. больше, чем за тетрадь. Сколько нужно
заплатить за 3 такие тетради и 2 такие книги вместе?
1 ч. 5 ч.
80 руб.
224. Не вычисляя значений следующих выраже­
ний, выпиши те выражения, значения которых при
делении на 2 дают в остатке 1.
2573 + 48686 6549 - 35.82 1237 •468
1735 + 6319 4327 - 1633 ^357•98&
89232 + 436 1968 - 246 342-518
225. Запиши самое маленькое нечётное шестиз­
начное число.
68
Эйпипь деления с остатком столбиком
УУ(.Маша, я умею записывать столбиком ело
♦пит», иычитание и умножение. А можно деление
ьн1и< »и. столбиком?» — спросил Миша.
•Мммю», — ответила Маша и показала Мише дна
мири 1лписи для одного случая деления с остатком.
■.Щ В = 3 (ост. 1) “ 24 1 т-
1 — ост.
(•акой знак обозначает деление при записи н
1ц <мжбик?
( )гн.исни, где записываются делимое, делитель и
пополнен частное при записи столбиком.
Иш- получилось число 24 и где оно записано?
При ми1иси каких чисел важно соблюдать основной
принцип записи столбиком, когда разряд записывается
под ..... разрядом?
( помощью какого действия вычислили остаток?
УУ/.Запиши следующие случаи деления с ост.н
ком, и< пользуя запись столбиком.
47 :8 !>(ост. 7) 86 : 9 = 9 (ост. 5) 97 : 6 = 16 (ост. I )
22В. Запиши следующие случаи деления с ост;п
ком, и< пользуя запись в строчку.
39
#
( 73 9 65 10 99
и 72 8 60 6 96
ост. ост. ост.
16
69

38. Способ поразрядного нахождения
результата деления
229. Мама купила 46 куриных яиц (4 десятка и
ещё 6 штук). Половину она решила отнести бабушке.
Для этого она сначала отложила по 2 десятка себе
и бабушке. Затем оставшиеся 6 яиц она разделила
пополам. В итоге в каждой из двух равных частей
получилось по 2 десятка яиц и ещё по 3 штуки, то
есть по 23 штуки.
Для решения этой задачи маме пришлось выпол­
нить следующие действия.
1) 4 дес. : 2 = 2 (дес.)
2) 6 : 2 = 3 (шт.)
3) 2 дес. + 3 = 23 (шт.)
230. Используя решение предыдущей задачи,
выполни деление числа 96 на число 3 по действиям.
Для этого разложи делимое на разрядные слагае­
мые. Затем раздели число десятков делимого на
число 3 нацело. Потом раздели количество единиц
делимого на число 3. Полученные значения частных
сложи.
231. Мама купила 56 куриных яиц (5 десятков
и ещё 6 штук). Половину она решила отнести
бабушке. Для этого она сначала отложила по 2
десятка себе и бабушке. Затем оставшийся 1 деся­
ток и ещё 6 яиц, то есть 16 яиц, разделила попо­
лам. В итоге в каждой из двух равных частей полу­
чилось по 2 десятка яиц и ещё по 8 штук, то есть
по 28 штук.
70
Для решения этой задачи маме пришлось вымол
пип. следующие действия.
1) 5 дес. : 2 = 2 (ост. 1 дес.)
2) 1 дес. + 6 = 16 (шт.)
3) 16 : 2 = 8 (шт.)
4) 2 дес. + 8 = 28 (шт.)
232. Используя решение предыдущей задачи,
иымолни деление числа 86 на число 3 по действиям
Ц|' забудь сложить остаток от деления десятков с
числом единиц делимого.
233. Сравни решение задач 230 и 232. С каким
разрядом делимого выполнялось первое действие;
с разрядом десятков или с разрядом единиц?
И какой из задач в первом действии получился осы
юк? В решении какой задачи получилось больше
действий? Почему?
Способ деления, при котором делимое раскла­
дывают на разрядные слагаемые, — это СПОСОБ
ПОРАЗРЯДНОГО НАХОЖДЕНИЯ результата.
234. Используя способ поразрядного нахождения
результата деления, определи в частном цифру в раз
ряде десятков.
70 : 2 92 : 3 70 : 5 82: 4 101 : 2
235. Используя записанные ниже случаи деления,
найди значение частного 96 : 4.
9 :4 = 2 (ост. 1) и 16 : 4 = 4.
Вычисли значение частного 96 : 4 по действиям.
71

39. 236. Для данных пар чисел выполни деление с
остатком способом поразрядного нахождения резуль­
тата деления. Запиши решение по действиям.
84 и 7 46 и 5 62 и 2 75 и 3 100 и 7
Теперь перепиши эти же случаи деления, исполь­
зуя запись столбиком.
Обведи те записи, где при делении числа десят­
ков делимого получился остаток.
237. Для каждой записи деления столбиком
выполни запись деления в строчку по действиям.
81 М3_
6_ [27
21
21
0
238. Выполни деление с остатком чисел 77, 66,
55, 44 на число 6 по действиям. Затем для каждого
случая деления выполни запись столбиком. Подчеркни
случай деления нацело. Какой остаток получается в
этом случае?
239. По данной записи деления с остатком стол­
биком назови делимое, делитель, неполное частное и
остаток.
75 5 72 4
5_ 15 4_ 18
25 32
25 32
0 0
Поупражняемся в делении столбиком
240. Выполни деление столбиком для следующих
мир чисел.
г : на 6 85 на 5 58 на 2 92 на Л
241. Сколько получится пучков моркови, если
(»') морковок связать в пучки по 5 штук?
Реши задачу. При вычислении ответа выполни
деление столбиком.
242. Восстанови в записи деления столбиком про
пущенные цифры, которые обозначены знаком
_74
6_
1*
* *
~0
243. Запиширешение данной задачи в виде
одного выражения. При вычислении ответа задачи
деление выполни столбиком.
Муку из двух мешков, в каждом из которых было
по 45 кг,расфасовали в пакеты по 2 кг.Сколько
пакетов с мукой получилось?
244. Выполни деление столбиком числа 117 на
число 9, используя данные случаи деления с оста жом
11 : 9 = 1 (ост. 2) 27 : 9 = 3 (ост. 0)
73

40. 245. Сравни данные записи деления столбиком и
умножения столбиком.
76 4 4
4_ 19 х19
36 36
36 4_
0 76
Можно ли было до выполнения умножения утверж­
дать, что в результате получится число 76? Почему?
Щ Б Есть ли в записи деления числа, которые соот-
я ветственно являются результатом умножения числа
4 на 1 десяток и числа 4 на 9 единиц? Укажи их.
246. Используя следующие случаи деления с
остатком, выполни деление числа 858 на число 3.
8 :3 = 2 (ост. 2) 25 : 3 = 8 (ост. 1) 1 8:3 = 6 (ост. 0)
Можно ли из полученных результатов деления с
остатком получить неполное частное при делении
числа 858 на число 3? Покажи, как это сделать.
Щ З Сравни данные записи деления с остатком
«в в строчку со следующей записью деления стол­
биком.
858 3
6_ 286
25
24
18
18
0
74
вычисления с пом ощ ью калькулятора
247. Вычисли значение следующего выражения,
ыниоивая в тетради промежуточные результаты поело
им-дого выполнения сложения.
23 + 23 + 23 + 23 + 23
Л теперь выполни на калькуляторе следующую
п. н ледовательность нажатий клавиш и запиши резуль
п т .1, которые получаются после каждого нажатия кла
т т ш ш т в в в в
;|. Сравни полученные результаты в первом и во
!* «и втором случаях. Можно ли утверждать, что во
тором случае мы также вычислили значение выраже
нии 23 + 23 + 23 + 23 + 23? Этот способ вычислении
мы будем называть сокращённым.
248. Вычисли значение следующего выражении
мписывая в тетради промежуточные результаты поело
тждого выполнения умножения.
5 • 5 • 5 • 5 • 5 • 5
А теперь выполни на калькуляторе следующую
последовательность нажатий клавиш и запиши резуль
гаты, которые получаются после каждого нажатия кла
виши =- г а г а г а г а г а и в
Сравни полученные результаты в первом и во
- _ втором случаях. Можно ли утверждать, что во
втором случае мы также вычислили значение выражо
ния 5 • 5 • 5 • 5 • 5 • 5? Этот способ вычисления мы
будем называть сокращённым.

41. 249. Вычисли сокращённым способом значения
следующих выражений.
47 + 47 + 47 + 47 + 47 + 47 д . д . д . д . д
^53 Проверь правильность выполненных вычислений в
| « первом случае с помощью умножения, а во вто­
ром — с помощью деления.
250. Восстанови пропущенные цифры, обозначен­
ные знаком *.
867
х _16
* * * *
+3468
★* * * *
251. Вычисли значения следующих выражений,
используя возможность запоминания промежуточного
результата с помощью клавиши М+ и воспроизведе­
ния этого результата с помощью клавиши МП.
а) (26154 + 45927) : (869753 - 869744),
б) (6783+ 2719)-(987654-987637),
в) (539671 - 539328) • (42763 - 42725),
г) (35352 + 27927) : (98754 - 98745),
д) (4123 + 5813) : (76935 - 76917).
252. Запиши выражение, значение которого будет
вычислено в результате нажатия на калькуляторе кла­
виш в следующей последовательности.
Час, минута и секунда
253. «Маша, я обратил внимание, что на неко
Iорых часах кроме часовой и минутной стрелок осп.
ощё одна стрелка. Для чего она нужна?» — спросил
Миша.
«Это стрелка отсчитывает СЕКУНДЫ. Поэтому ома
называется секундной. Когда секундная стрелка дела
<ч полный оборот, проходя все 60 делений, минутная
стрелка сдвигается только на 1 деление», — ответила
Маша.
Как связаны минуты и секунды? Объясни следую
4 щее соотношение.
1 мин = 60 с
254. Вырази в секундах.
2 мин 5 мин 10 мин 30 мин 60 мин
255. Сколько минут в 1 ч? Сколько секунд в 1мин?
Сколько секунд в 60 мин? Сколько секунд в 1 ч?
Объясни следующее соотношение.
1 ч = 3600 с
256. Вырази в секундах:
2 ч 10 ч 1 ч 1 мин 1 ч 10 мин 10 ч 10 мин
257. Урок длится 45 мин, а перемена 15 мин
Сколько секунд длится урок вместе с переменой?
77

42. 258. Расположи в порядке возрастания следую
щие временные промежутки.
1 ч 1 мин 1 с 59 мин 59 с 1 ч 10 с
62 мин 1 ч 1 мин 60 мин 60 с
259. Сколько секунд длится мультфильм, если
его продолжительность 9 мин 20 с?
260. Определи по таблице результатов соревно
ваний по бегу номер спортсмена, который стал побо
дителем этих соревнований.
Номер спортсмена 1 2 3 4
Результат 5 мин 3 с 300 с 4 мин 59 с 298 с
261. Продолжительность телепередачи 1 ч 10 мин
Реклама в ней занимает 360 с. Сколько времени
занимает сам сюжет данной телепередачи?
262. Вычисли стоимость каждого телефонного
разговора, тариф (цена) и продолжительность которо
го указаны в следующей таблице.
Номер Тариф Продолжительность Стоимости
1 3 руб./мин 300 с ?
2 4 руб./мин 240 с ?
3 2 руб. 50 коп./мин 600 с 9
78
Им» или что движется быстрее?
7(13. Спортсмен под каким номером пробежал
Iлнцию быстрее всех остальных участников?
, г . 1ким образом судьи соревнований решаю!
|г* 1момрос о том, кто какое место должен занять?
764. За первый час пути туристы прошли 5 км,
• «н агорой час пути — 4 км. Когда туристы шли
|ц н 1|)н(! в течение первого часа или второго?
265. На автомобиле за одну минуту можно про-
|К#||. км, а на поезде за одну минуту — 1500 м
ч«н л аюм случае движется медленнее?
266. При самой быстрой ходьбе Миша может ма
мним час преодолеть расстояние 3 км. Сможет ли
Мииш «а 1 ч 30 мин пройти 5 км?
I 267. Какое из известных тебе средств передай
нм(ия может двигаться быстрее всех остальных?
Расположи следующие средства передвижения по
амрндку от самого быстрого к самому медленному
||«!имобиль, самолёт, вертолёт, ракета, велосипед,
|Шдка без мотора.

43. 270. Автомобиль, двигаясь равномерно, преодо
левает 80 км за 1 ч. Сколько километров он преодо
леет за 120 мин? За 30 мин? За 15 мин?
•^Щ| На каком транспортном средстве можно за 1ч
е э _ преодолеть расстояние в 1000 км?
268. Приведи примеры животных, которые мо1у»
очень быстро передвигаться по земле. Кто и|
зверей считается самым быстрым?
ил «/»
I
269. Какие животные передвигаются по земли
очень медленно? Приведи примеры таких животных,
80
ими пути в единицу времени, или скорость
771. За 1ч на автомобиле был проделан пун.
ннимии 90 км. Длина пути, пройденного в единицу про
м..ни называется СКОРОСТЬЮ* (средней). Записать ско
и»,, и. мигомобиля в данном случае можно следующим
••Чипом: 90 км/ч (читается: 90 километров в час).
1м 20 мин на другом автомобиле был проделан
нуп. длиной 25 км. Сколько километров можно проо
•и. на этом автомобиле за 1 ч, если двигаться точно
ни +о, как и в указанные 20 мин? Запиши скорость
й1о|ш1о автомобиля.
272. Самолёт летел 2 ч с постоянной скоростью
и пролетел за это время 1800 км. С какой скоростью
мшил самолёт?
273. Спортсмен пробегает дистанцию 100 м за
ни Какое расстояние он пробегает за 1с, если
аридноложить, что всю дистанцию он двигается
» одинаковой скоростью? Какое расстояние он смш
бы пробежать за 1 мин, если всё это время бежал
бы ( шкой же скоростью, что и первые 10 с?
К/ 274. Объясни, почему справедливы данные С001
ношения.
I м/с 60 м/мин 1 м/мин = 60 м/ч 1 м/с = 3600 м/ч
775. Вырази данные скорости в км/ч.
г'<I м/с 5 м/с 30 м/с 15 м/с
81

44. 276. Вырази данные скорости в м/с.
120 м /м инр*^ 240 м/мин ^600 м/мин | ^ 300 м/м
277. В таблице приведены возможные скорое Iи
Название
объекта,
явления
Авто­
мобиль
Самолёт Ветер Пловец
Скорость 90 км/ч 900 км/ч 10 м/с 100 м/мин
Расположи данные скорости в порядке возрастания
Сформулируй задачу на кратное сравнение, ис
пользуя данные из таблицы. Реши сформулиро
ванную задачу. Ответ можно не вычислять.
278. Во время урагана скорость ветра можем
достигать 30 м/с. Вырази эту скорость сначала в м/ч.
а потом в км/ч. Объясни, почему имеет место данное
соотношение.
10 м/с = 36 км/ч
279. Велосипедист едет по прямому шоссе с
собственной скоростью 18 км/ч. С какой скоростью
будет ехать велосипедист, если ему в спину будем
дуть ветер со скоростью 5 м/с? А если ветер будем
дуть в лицо, какой будет скорость велосипедиста?
280. Расстояние между двумя населёнными пун
ктами 180 км. На каком транспортном средство
можно преодолеть это расстояние за 3 ч?
82
иать задачи
2Н1. Чем похожи и чем отличаются формулиров
Ш ' М1 двух данных задач?
Г й Мотоциклист двигался спостоянной скоростью
|0»м'| в течение 3 ч. Какое расстояние преодолел
■пщиклист за это время?
г» Цена проката водного велосипеда 80 руб./ч.
Шмп.н) нужно заплатить за 3 ч катания на этом
Цнмн нннде?
1'ишите задачи. Вычислите и запишите ответы.
Чнм похожи и чем отличаются решения и ответы
|1Ии чндач?
| Можно ли утверждать, что эти задачи аналогич
* мм, только в них речь идёт о разных процессах
И ««личинах?
Кикая величина аналогична величине «скорость» в
.»<♦«>т . описанном во второй задаче?
21)2. Для данной задачи на движение сформули-
§уи аналогичную задачу на процесс купли-продажи.
Эн Зч автомобиль преодолел расстояние в 270 км.
0 мн ой средней скоростью двигался автомобиль?
1'пши данную и сформулированную задачи.
Мм нп пи и запиши ответы.
703. За 4 ч поезд преодолел расстояние в
1НМкм Во сколько раз большее расстояние преодо-
И«мм >н)| поезд за 12 ч, если будет двигаться с той
|Н «родней скоростью?
I‘посмотри и объясни каждый из двух вариантов
(« ни мня этой задачи.
^ 83

45. 1-й вариант
1) 360 км : 4 ч = 90 км/ч
2) 90 км/ч • 12 ч = 1080 км
3) 1080 км : 360 км =
= 3 (раза)
2-й вариант
1) 12 ч : 4 ч = 3 (раза)
284. Сформулируй задачу по следующей краткой
записи, представленной в виде таблицы. |
Скорость Время Пройденный пуп
1-я группа
туристов
Одинаковая
2ч 12 км
2-я группа
Зч о
туристов
г
Реши сформулированную задачу. Вычисли и зами
ши ответ.
Как можно было бы рациональнее решить сос>1
ветствующую задачу, если бы в графе «Время» вмо
сто 3 ч стояло 4 ч?
285. Как изменится пройденный путь, если см>
рость увеличится в 3 раза, а время движении
останется тем же самым?
Подтверди свой вывод несколькими примерами.
286. Как изменится стоимость товара, если цена
уменьшится в 2 раза, а количество купленною
товара останется тем же самым?
Подтверди свой вывод несколькими примерами.
84
207. Скорость велосипедиста 15 км/ч. Какое рас
• 1ИНИИО преодолеет велосипедист за Г часов, если
Нуди! двигаться с этой же скоростью?
Запиши решение задачи в виде буквенного выра
фммии Вычисли значение этого выражения при I 2 ч.
мри / : 3 ч.
288. Реши задачу. Вычисли и запиши ответ.
За 3 ч, которые был в пути скорый поезд, он
и|1пидолел расстояние в 240 км. Сколько километром
н| долеет этот поезд за 5 ч, если будет двигаться с
••■и со средней скоростью?
•# 289. На чертеже с помощью отрезка показано
4^1 расстояние между двумя населёнными пунктами А
И II, а с помощью направленного отрезка (стрелки)
мни! »ано направление движения и расстояние, кою
|мю преодолевает автобус за 1 ч. Проведя необходи
мып намерения и вычисления, установи, сколько часом
• нраIиг автобус на весь путь от А до В.
у----------->|
290. Автомобиль движется с постоянной скоро
гп.и! МОкм/ч. Сколько километров он преодолеет ал
I '<) мин? За 30 мин? За 15 мин?
<:может ли этот автомобиль преодолеть 20 м за
I в? С какой наименьшей скоростью должен двигать
• и данный автомобиль, чтобы выполнить указанное
•рипомание?
85

46. Какой сосуд вмещ ает больше?
иЕЯ 291. Бабушка налила молоко из пакета Мише и
Щ й стакан, Маше — в чашку, а кошке — в блюдце
Всем — до краёв. Миша заинтересовался, кому
бабушка налила молока больше. Он решил, что ему,
так как стакан выше чашки и уж тем более выше
блюдца. Маша с этим не согласилась. Кто из них
прав? Как сравнить ВМЕСТИМОСТЬ* стакана, чашки и
блюдца? Предложите свой способ сравнения.
Можно ли утверждать, что вместимость молочно
го пакета больше вместимости стакане'’
Вместимости чашки? Вместимости блюдца"
Вместимости стакана и чашки вместе? Почему?
292. Мама варила варенье в большом тазу, а
потом разлила его в три банки, наполнив их всклинь,
до краёв. Вместимость чего больше: таза или одной
банки?
293. Чтобы заполнить бочку водой, нужно налип.
в неё 20 вёдер воды. Для заполнения ванны нужно
15 таких вёдер воды. Вместимость чего меньше
бочки или ванны?
86
794. Сколько полных вёдер воды ВМЕЩАЕТ дсп
§|рн о.ксейн, если для его заполнения потребовалось
М|"....сIи 32 одинаковых бидона с водой, а дли
Ми*'.ниюиия водой ведра нужно 3 таких бидона?
Получи ответ на поставленный вопрос с помощью
цил'мнш с остатком.
795. Сравни вместимости двух бассейнов прямо-
уюльной формы. Первый имеет длину 10 м,
щирицу 4 м, а глубину 2 м. Второй имеет длину 10 м,
Ширину 4 м, а глубину 1 м. Объясни свой ответ.
.‘06.. В двух одинаковых чашках помещаемся
Мньм> же воды, сколько в трёх одинаковых стаканах
й пдмой кастрюле помещается 12 таких чашек, а и
||>у|**и 20 таких стаканов. Какая кастрюля имош
Млыную вместимость?
797. Для того чтобы наполнить бак водой, нужно
И"и нс н него либо 12 вёдер, либо 20 бидонов воды
I Олк налили 6 вёдер воды. Сколько ещё бидоном
щцы нужно налить в бак, чтобы его наполнить?
298. Реши задачу. Вычисли и запиши ответ.
Клсфюля вмещает 15 стаканов воды. Сколько
Пшик в о д ы вмещает эта кастрюля, если 4 чашки по
Мйныимости равны 5 таким стаканам?
799. Аквариум имеет форму куба с длиной
Июра 60 см. До какой высоты нужно наполнить акин
|*ум нодой, чтобы заполнить его наполовину? На
I" чI.' На четверть?
87

47. Литр. Сколько литров?
300. «Маша, на пакете с молоком написано
1 ЛИТР*. А что это значит?» — спросил Миша. .Я
«Это означает, что на молокозаводе в такие пако
ты автомат наливает одно и то же количество молока,
которое измеряется 1 литром. Вот в такой банка
помещается ровно 1 литр жидкости», — поясница
Маша и показала Мише литровую стеклянную банку.
Ммоко
Где ещё в жизни тебе приходилось иметь дело о
такой единицей вместимости, как литр?
301. Сколько литров сока привезли в школы |ую
столовую, если литровых пакетов было 3 упаковки по
12 штук, а двухлитровых — 2 упаковки по 8 штук?
302. Сколько литров молока в пакетах можно купип.
на 100 руб., если литровый пакет молока стоит 15 руб.?
303. Сколько литров питьевой воды израсходова­
ли туристы к концу похода, если они взяли с собой
6 пятилитровых канистр, а осталось у них 2 л а
одной канистре и 1 л в другой канистре?
Реши задачу. Вычисли и запиши ответ.
88
Цм«*< 'имость и объём
304. Когда Миша взял стакан, заполненный
ом, и перелил всё молоко в чашку, то она
ни*-и* оказалась заполненной до краёв. Таким обра
|пм, вместимость стакана оказалась равна вместимо
•Ии чашки. В этом случае говорят, что жидкость,
жиомниющая стакан, имеет такой же ОБЪЁМ, как и
ЖИДмнпь, заполняющая чашку.
Как можно сравнить объёмы 1 кг муки и 1 кг
ч ••'«мппа?
305. В стеклянную бутылку налили воду и поста
мили на мороз. Ты уже знаешь, что, когда вода
ммпцанет, бутылка лопнет. Попробуй дать объяснение;
ним) факта на основе сравнения объёмов воды и
Лкаа, получившегося из этой воды.
306. Круглое бревно, толщина которого по всей
-* длине одинакова, распилили пополам по длине.
• рпвни объёмы получившихся частей.
11(менится ли ответ, если бревно от одного
конца к другому утолщается?
89

48. 307. Для построения следующих фигур использо^
вались одинаковые кубики. Назови номер фигуры,
которая имеет наименьший объём, и номер фигуры,
которая имеет наибольший объём.
308. В большую кастрюлю, стоящую в тазу, до
самого края налили воду, а потом опустили и
неё кирпич. В результате часть воды вытекла в таз,
Что ты можешь сказать об объёме кирпича и объёме)
вытесненной им воды?
309. Опишите по рисунку практическую раб()|у,
по результатам которой можно сравнить вмесщ-
мость стакана и его объём (как реального предмет.!)
НО. Какие из изображённых на рисунке геомо
•и ми кик фигур имеют объём? Знаешь ли ты, как
1НИ на пинаются?
311. При выполнении какого условия объёмы
кубов равны?
Но сколько раз объём куба с ребром 1 см отли
чается от объёма куба с ребром 2 см? Выполни
иное сравнение объёмов с помощью рисунка.

49. Кубический сантиметр и изм ерение объёма
312. Чему равна площадь квадрата со стороной
1 см? Чему равен объём куба с ребром 1 см?
Как можно назвать эту единицу объёма? Объясни
смысл названия КУБИЧЕСКИЙ САНТИМЕТР*.
Чему равен объём куба с ребром 2 см? Вырази
этот объём в кубических сантиметрах, используя со
кращённую запись: куб. см.
313. Каждое деление мерного сосуда соотвоы
ствует 10 куб. см. Определи объём жидкости в сосу
де на каждом рисунке.
314. Сколько кубиков с ребром 1 см можно
поместить в прямоугольную коробку, длина которой
10 см, ширина 5 см, а высота 4 см. Чему равна ВМ1
СТИМОСТЬ этой коробки в кубических сантиметрах?
92
1Г» Опишите по рисунку практическую рабо1у
|*1 но измерению объёма металлического шарика с
.......... юнанием следующего оборудования: мерный
1*1н уд ( делениями по 1 куб. см, который заполнен
Инд* и до отметки 10 куб. см, и металлический шарик
Д1мм* 11ром 2 см.
Л
*50
140
{30
Т 20
ИЧкИм
10
316. Определи объём в кубических сантиметрах
ИтПражонной на рисунке фигуры, если она составле
• « и * кубов с ребром 1 см.
Запиши в виде произведения число кубов, из
|ннпр|,|х составлена данная фигура.

50. Кубический дециметр и кубический сантиметр
317. Чему равен объём куба с ребром I о
Как можно назвать единицу объёма, представл
ную кубом с ребром 1 дм? Сколько сантиметров
1 дециметре? Сколько квадратных сантиметроЕ!
1 квадратном дециметре? Сколько кубических сантим»
тров в 1 КУБИЧЕСКОМ ДЕЦИМЕТРЕ*? Докажи спр
ведпивость данного равенства.
1 куб. дм = 1000 куб. см
318. Обувная коробка имеет длину Здм, ширину
2 дм и высоту 1 дм. Какое наибольшее число кубикон О
ребром 1 дм можно разместить в этой коробке? Вырази
вместимость этой коробки в кубических дециметрах.
319. Во сколько раз нужно увеличить отрезок
длиной 1 см, чтобы получить отрезок длиной 1 дм?
Во сколько раз 1 кв. см меньше 1 кв. дм? Во сколько
раз 1 куб. см меньше 1 куб. дм?
320. Вырази в кубических сантиметрах и выпол­
ни сложение.
куб. дм + 500 куб. см =
куб. дм + 10 куб. см =
3 куб. дм + 3 куб. см
10 куб. дм + 1 куб. см
321. Выполни столбиком указанные действия.
326532 куб. дм + 867543 куб. дм =
1785634 куб. дм - 1423156 куб. дм =
94
»2.' Пырази в кубических сантиметрах.
пул дм !>00 куб. см 5 куб. дм 5 куб. см
*»п мп 10 куб. см 10 куб. дм 10 куб. см
|| 323. Вместимость чашки 250 куб. см. Сколько
нужно взять таких чашек воды для того, чтобы
III ■ !ИМ. I куб. ДМ ВОДЫ?
мр<’+де чем отвечать на этот вопрос, заполни
л* м,м.щую таблицу.
5
?
Аквариум прямоугольной формы имео!
«|1»нму I. дм, ширину 5 дм и высоту 4 дм. Этот акна
||Ну'1 юполнен водой наполовину. Каких размером
...... быть аквариум, чтобы этим количеством моды
91и можно было бы заполнить полностью?
325. Расположи в порядке возрастания следую
Шип обьёмы.
10500 куб. см 10 куб. дм 50 куб. см
К) куб. дм 5 куб. см 15000 куб. см
К)!>50 куб. см 10 куб. дм 555 куб. см
326. Выполни кратное сравнение двух данных
мПьММОВ.
10 куб. дм и 100 куб. см
■
95 I
1|ц< но чашек
рмтиимость (куб. см) 250

51. Кубический дециметр и литр
327. «Маша, почему на мерной кружке около
одного и того же деления с одной стороны написано
1 л, а с другой 1 куб. дм?» — спросил Миша.
Ответ Маши был таким: «Литр и кубический
дециметр — это единицы объёма. А написаны они
около одного и того же деления потому, что...»
Продолжи ответ Маши, опираясь на следующие
соотношение.
1 л = 1 куб. дм
328. Сколько литров жидкости помещается в г>н*
с прямоугольным дном площадью 6 кв. дм и высотй
1 дм? Какие размеры по длине и ширине можт
иметь дно этого бака?
329. Металлический бак имеет форму купа
Длина его ребра 2 дм. Сколько литров воды помеща
ется в этом баке?
330. Вместимость кастрюли 5500 куб. см. Можно
ли в эту кастрюлю налить 5 л воды?
331. В двух одинаковых кастрюлях помещаем:*!
5 л воды. Определи вместимость одной такой кастрк»
ли в кубических сантиметрах.
332. Банка имеет вместимость 3 л. В неё налили
2300 куб. см молока. Сколько ещё кубических санш
метров молока нужно долить, чтобы наполнить банку'1
96
||н 1|| и килограмм
993. В банку налили 1 л воды и поставили на
щдму чашу рычажных весов. На другую чашу поставили
пустую банку и гирю 1 кг. Весы оказались и
РКНпнмии равновесия. Что это означает?
«:14. Сколько граммов в 1 кг? Если масса I л
нЦлы I оыавляет 1 кг, то какую часть литра составляв
I I ЙОДЫ?
335. Если бензин налить в воду, то этот бензин
Лудш плавать сверху. Что легче: 1 л воды или 1 л
Лин!ина?
336. На комбинате расфасовали 100 кг морожо
н о т и коробочки вместимостью 1л. Для этого потре
Ломалось 120 коробочек. Что тяжелее: 1 л этого моро
тиною или 1 л воды?
|| 337. Если растительное масло плавает на
1поверхности пресной воды, где масла будо!
Пплмно: в 1 л или в 1 кг? Почему?

52. Разные задачи
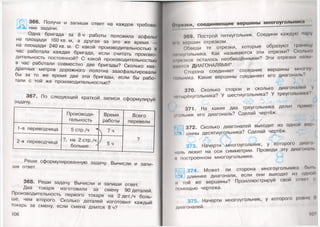
338. Имеются банки вместимостью 2 л
5 л. Как с помощью этих банок налить в кастрмиЦ
1 л воды из водопроводного крана?
^ 339. На почте продаётся 4 вида поздрави ичи,«
Жк, ных открыток и 3 вида конвертов к ним. М.ним
нужно выбрать открытку и конверт и послать поздр.н»
ление подруге. I
Из скольких вариантов ей придётся делать выбор!
Запиши каждый вариант с помощью шифра, состоящего
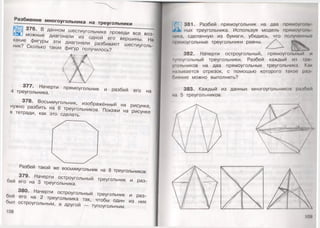
из цифры и буквы. Цифрами 1, 2, 3, 4 обозначь номер
открытки, а буквами А, Б, В — каждый вид конверта.
340. Имеются банки вместимостью 2л и Мм
■т ] Как с помощью этих банок налить в бак I / м
воды из водопроводного крана?
Запиши решение этой задачи в виде суммы
нескольких слагаемых, где в качестве слагаемым
используются только числа 2 и 3, а значение суммы
равно числу 17. Предложи три варианта решения.
341. В трёх ящиках лежат детали, изготовленные
соответственно тремя рабочими. Один из рабочих изн>
товил детали, каждая из которых на 10 г тяжелее, чем
должна быть по утверждённой норме. Два других рабо
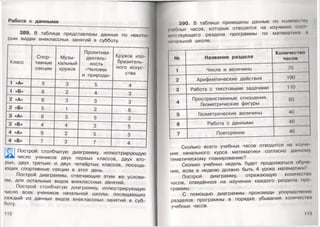
чих изготовили стандартные детали с массой 9001
каждая. Из первого ящика взяли для контроля одну
деталь, из второго — две, а из третьего — три. Э т
шесть деталей взвесили на весах и получили 54201
Определи, в каком ящике лежат бракованные детали.
98
На четырёх автоматических линиях расфасо-
» ...... ижфеты в упаковки по 300 г. На одной
•|| й|н1и.н)Шол сбой, и упаковки стали получииюн
§40 Как с помощью одного взвешивания опредо-
н нн какой линии произошёл сбой?
!§§•, На следующей схеме изображены тропинки,
1м*1 ниорым можно пройти от дома к берегу
С Си ап,ко всего имеется различных вариантом
_&§|у'а "I дома до реки, если не проходить еще
| Мн у*1’ пройденному маршруту.
М 1 Изобразите в тетради в виде схемы, состо-
I нщмй из точек и отрезков, их соединяющих,
§В§|*ни1п, югорая описана в формулировке задачи.
Сими,ко карандашей в 2-х упаковках, если в каж
Мин умакпике находится по 3 коробки, а в каждой
»§|)Н1'м* лежит по 6 карандашей?
1«ни|пите решение задачи в виде одного выра-
пиь ** Мычислите ответ задачи и сравните его с тем
которое можно получить с помощью схемы.
99

53. П оупражняем ся в измерении объёма
345. Назови номера фигур, которые
наковый объём, если они составлены из
кубиков.
имеют одн
одинакопы.
•МП I'посмотри изображение геометрической фи-
I И "Продели её объём в кубических сантиметрах,
Яшм (.(кнавлена из одинаковых кубиков, длина
Р§ ийфдого из которых равна 1 см.
* 4 / I оробка прямоугольной формы имеет длину
■4, ширину 5 дм и высоту Здм. Покажи на рисун-
нужно размещать бруски прямоугольной
» «рМН и пой коробке, чтобы заполнить её полно
!||Й1 •" ми каждый брусок имеет длину 5 дм, ширину
1^1 и мысоту 1 дм. Сколько таких брусков в этом
Ручям (и>м<мцается в коробке? Какую вместимосп.
ПМИН' »•пробка?
МП На рисунке изображена фигура, состоящая
Пв 1|»Пм одинаковых кубов с длиной ребра 1 см.
Нм р и ! ум н о в тетради дополни такую же фигуру до
•}|ИУ||| |, имеющей объём 8 куб. см.
/
/ / /
/
101

54. Кто выполнил больш ую работу
349. Первый токарь за каждый час работы обра­
батывает 5 деталей, а второй — за смену 42
детали. Кто из них выполняет большую работу за
смену, если смена длится 8 ч? Сколько деталей
обрабатывает первый токарь за смену?
Выполни разностное сравнение числа деталей,
обработанных первым и вторым токарями за смену.
350. Миша прополол до обеда 6 грядок, а после
обеда на 2 грядки больше. Маша прополола до обеда
5 грядок, а после обеда в 2 раза больше. Кто из
детей за весь день выполнил большую работу, если
считать все грядки одинаковыми?
351. Одна бригада собрала клубнику с участка
площадью 85 соток, а другая за это же время — с
участка площадью 1 га. Какая бригада выполнила
больший объём работы за отведённое время?
352. На старом оборудовании за смену изготавли­
вают 45 деталей, а на новом — 90 деталей. Во сколько
раз больше объём работы, выполняемой за смену
на новом оборудовании, чем на старом? На сколько
больше деталей можно изготовить на новом оборудова­
нии, чем на старом, за 2 смены? За 3 смены?
353. Одна бригада разгрузила 3 т 500 кг удо­
брений, а другая — 35 ц таких же удобрений. Сравни
между собой работу, выполненную этими бригадами.
102
Производительность — это скорость выполнения
(шОоты_________________________________________________
354. За 6 ч рабочий изготовил 72 детали. С ка
и щ ПРОИЗВОДИТЕЛЬНОСТЬЮ в час работает окн
||§п<с1ий, если число изготовленных деталей в час но
И 1М1Ч1ИОТСЯ?
, Какова производительность этого рабочего аа
ф1 . смену, если смена длится 8 ч, а производителе
с и час остаётся постоянной?
355. Сформулируй задачу по данной краткой записи
Производи­ Время Всего
тельность работы изготовили
1 и токарь 8 дет./ч 8ч
?
• и гокарь 7 дет./ч 6 ч
Реши составленную задачу. Вычисли и запиши
ответ.
356. Составь краткую запись в виде таблицы к
• »мдующей задаче.
Первый контролёр за 1 ч проверяет 240 деталей
Производительность второго контролёра на 20 дет./ч
Польше. Сколько деталей может проверить каждый
и ролёр за 8 ч работы, если производительное о.
н 1ждого будет постоянной? С какой совместной про
и июдительностью работают эти контролёры?
Реши задачу. Вычисли и запиши ответ.
103

55. 357. Реши задачу. Вычисли и запиши ответ.
На ткацкой фабрике за шестидневную рабочую
неделю изготовили 48000 м ткани. Сколько ткани
изготовят на этой фабрике за месяц, если в месяце
26 рабочих дней, а ежедневная производительность
фабрики остаётся постоянной.
358. Как изменится объём выполненной работы,
если при том же рабочем времени производи­
тельность увеличится в 2 раза? Уменьшится в 3 раза?
Приведи по одному подтверждающему примеру.
1 359. Производительность печатающего устройства
у 60 стр./мин. Вырази эту же производительность
в стр./с и стр./ч.
360. Какая копировальная машина работает с
большей скоростью: машина с производительностью
2 стр./с или с производительностью 7000 стр./ч?
361. Реши задачу. Вычисли и запиши ответ.
Два контролёра готовой продукции совместно
за 1 ч работы проверяют 500 деталей. С какой
производительностью работает каждый контролёр,
если производительность первого на 20 дет./ч мень­
ше, чем второго?
362. Реши задачу. Вычисли и запиши ответ.
Токарь и его ученик вместе за 1 ч производят
60 деталей. С какой производительностью в час рабо­
тает каждый из них, если производительность токаря
в 3 раза больше, чем производительность ученика.
104
Учимся решать задачи
363. Чем похожи и чем отличаются формулирои
** ки следующих задач?
а. Стоимость 3 ч аренды спортивного зала
миаавляет 360 руб. Какова цена аренды в час, если
она постоянная?
б. Скорый поезд за 3 ч преодолел расстояние
|(»()км. С какой скоростью двигался поезд, если она
пыла постоянной?
в. Бригада дорожных рабочих за 3 ч работы рас
чистила 360 кв.м дорожного полотна. С какой проиа
модительностью в час работала бригада, если её про
итодительность постоянная?
Реши данные задачи. Вычисли и запиши ответы.
Чем похожи и чем отличаются между собой полу
чанные решения?
Чем похожи и чем отличаются между собой полу
ченные ответы?
|<Г-П 364. Сформулируй задачи: одну на нахождение
. к! скорости, другую на нахождение производитель
пости и ещё одну на нахождение расхода материале,
решение которых может быть записано в виде вырн
жения 450 : 5. Для каждой из сформулированных
задач вычисли и запиши ответы.
365. Реши задачу. Вычисли и запиши ответ.
Сколько дней потребуется Маше для того, чтобы
прочитать две книги, в одной из которых 240 стра
ниц, а в другой — 210, если она будет читать со
скоростью 50 страниц в день (стр./д.)?

56. 366. Получи и запиши ответ на каждое требова­
ние задачи. 11
Одна бригада за 8 ч работы положила асфальт
на площади 160 кв.м, а другая за это же время —
на площади 240 кв. м. С какой производительностью в
час работала каждая бригада, если считать произво­
дительность постоянной? С какой производительностью
в час работали совместно две бригады? Сколько ква­
дратных метров дорожного полотна заасфальтировали
бы за то же время две эти бригады, если бы рабо­
тали с той же производительностью?
367. По следующей краткой записи сформулируй
задачу.
Производи­
тельность
Время
работы
Всего
перевели
1-я переводчица 5 стр./ч ^ Ч 7ч
?
2-я переводчица ?, на 2 стр./ч
больше ' ' 5ч
Реши сформулированную задачу. Вычисли и запи­
ши ответ.
368. Реши задачу. Вычисли и запиши ответ.
Два токаря изготовили за смену 90 деталей.
Производительность первого токаря на 2 дет./ч боль­
ше, чем второго. Сколько деталей изготовил каждый
токарь за смену, если смена длится 8 ч?
106
<**|и•чки, соединяю щ ие верш ины м ногоугольника
369. Построй пятиугольник. Соедини каждую пару
що вершин отрезком.
Обведи те отрезки, которые образуют границу
пыиугольника. Как называются эти отрезки? Сколько
•презков осталось необведёнными? Эти отрезки назы
маются ДИАГОНАЛЯМИ*.
Сторона соединяет соседние вершины многоу-
тльника. Какие вершины соединяет его диагональ?
Г
370. Сколько сторон и сколько диагоналей у
•нпырёхугольника? У шестиугольника? У треугольника?
371. На какие два треугольника делит прямо
утл ьн ик его диагональ? Сделай чертёж.
372. Сколько диагоналей выходит из одной пор-
цЯ- шины десятиугольника? Сделай чертёж.
3 7 3 . Начерти многоугольник, у которого диаго­
наль лежит на оси симметрии. Проведи эту диагональ
и построенном многоугольнике.
куЩ 374. Может ли сторона многоугольника бы п.
длиннее диагонали, если они выходят из одной
и той же вершины? Проиллюстрируй свой отве! <
помощью чертежа.
3 7 5 . Начерти многоугольник, у которого ровно
диагоналей.
107

57. Разбиение м ногоугольника на треугольники
376. В данном шестиугольнике проведи все воз-
. можные диагонали из одной его вершины. На
какие фигуры эти диагонали разбивают шестиуголь­
ник? Сколько таких фигур получилось?
377. Начерти прямоугольник и разбей его на
4 треугольника.
378. Восьмиугольник, изображённый на рисунке,
нужно разбить на 6 треугольников. Покажи на рисунке
в тетради, как это сделать.
Разбей такой же восьмиугольник на 8 треугольников.
379. Начерти остроугольный треугольник и раз­
бей его на 3 треугольника.
380. Начерти остроугольный треугольник и раз­
бей его на 2 треугольника так, чтобы один из них
был остроугольным, а другой — тупоугольным.
108
381. Разбей прямоугольник на два прямоуголь
и<к) ных треугольника. Используя модель прямоу!о/н.
ника, сделанную из бумаги, убедись, что полученный
прямоугольные треугольники равны.
382. Начерти остроугольный, прямоугольный и
|уноугольный треугольники. Разбей каждый из гре
ушльников на два прямоугольных треугольника. Как
называется отрезок, с помощью которого такое рам
оиение можно выполнить?
383. Каждый из данных многоугольников разбо
на 5 треугольников.

58. Записы ваем числовые последовательности
384. Последовательность начинается с числа 2,
а каждое следующее число получается из предыдуще­
го в два этапа: сначала предыдущее число нужно
увеличить в 2 раза, а потом получившееся число
нужно увеличить на 2.
Одна из трёх данных последовательностей состав­
лена по этому правилу:
а) 2, 6, 18, ... б) 2, 6, 10, ... в) 2, 6, 14, ...
Установи, какая это последовательность, и пере­
пиши её в тетрадь. Напиши первые четыре числа
этой последовательности.
385. Угадай, каким образом числа 1, 4, 9,
16 связаны с изображёнными на рисунке геометриче­
скими фигурами.
Как должна выглядеть пятая геометрическая фигу­
ра в этом ряду? Изобрази её.
Каким должно быть пятое число в последователь­
ности, которая составлена с учётом установленной
зависимости?
Запиши установленную числовую последователь­
ность, указав первые шесть чисел этой последова­
тельности.
110
386. Угадай, каким образом числа 1, 8, 27 сия
юны с изображёнными на рисунке геометрическими
Каким должно быть четвёртое число в последом. I
1ельности, которая составлена с учётом установленной
зависимости? Запиши эту последовательность, указан
первые четыре числа этой последовательности.
387. Последовательность начинается с числа
а каждое следующее число получается из предыдум*е
го в два этапа: сначала предыдущее число нужно
увеличить в 3 раза, а потом получившееся число
нужно увеличить на 3.
ШЗапиши первые пять чисел этой последователе
ности. Сравни свою последовательность с после
довательностью, полученной соседом по парте.
388. Последовательность начинается с числа
а каждое следующее число получается из предыдущг
го в два этапа: сначала предыдущее число нужно
увеличить в 2 раза, а потом получившееся число
нужно уменьшить на 2.
ШЗапиши первые три числа этой последовавелннп
сти. Сравни свою последовательность с последе
вательностью, полученной соседом по парте.
111

59. Работа с данны ми
389. В таблице представлены данные по некото­
рым видам внеклассных занятий в субботу.
Класс
Спор­
тивные
секции
Музы­
кальный
кружок
Проектная
деятель­
ность
«Человек
и природа»
Кружок изо­
бразитель­
ного искус­
ства
1 «А» 5 3 5 4
1 «Б» 6 2 4 3
2 «А» 6 3 3 3
2 «Б» 5 1 2 6
3 «А» 8 3 5 3
3 «Б» 4 4 3 5
4 «А» 9 2 5 3
4 «Б» 7 3 7 4
^ I Построй столбчатую диаграмму, иллюстрирующую
число учеников двух первых классов, двух вто­
рых, двух третьих и двух четвёртых классов, посеща­
ющих спортивные секции в этот день.
Построй диаграммы, отвечающие этим же услови­
ям, для остальных видов внеклассных занятий.
Построй столбчатую диаграмму, иллюстрирующую
число всех учеников начальной школы, посещающих
каждый из данных видов внеклассных занятий в суб­
боту.
112
390. В таблице приведены данные по количесту
учебных часов, которые отводятся на изучение С001
шествующего раздела программы по математике и
печальной школе.
№ Название раздела
Количество
часов
1 Числа и величины 70
2 Арифметические действия 190
3 Работа с текстовыми задачами 110
4
Пространственные отношения.
Геометрические фигуры
50
5 Геометрические величины 40
6 Работа с данными 40
7 Повторение 40
Сколько всего учебных часов отводится на изуче
ние начального курса математики согласно данному
тематическому планированию?
Сколько учебных недель будет продолжаться обучо
ние, если в неделю должно быть 4 урока математики':
Построй диаграмму, отражающую количесшо
часов, отведённое на изучение каждого раздела про­
граммы.
С помощью диаграммы произведи упорядочение
разделов программы в порядке убывания количества
учебных часов.

60. Л 391. В таблице 1 представлены результаты высту­
пления мальчиков 4-го отряда по некоторым видам
спартакиады летнего оздоровительного лагеря «Дружба».
№ Участник
Бег
на
200 м
Прыжки
в длину
Прыжки
в высоту
М етание
мяча
1 Виктор Б. 50 с 3 м 45 см 1м 10 см 38 м
2 Сергей Д. 51 с 3 м 40 см 1м 13 см 35 м
3 Андрей 3. 48 с 3 м 55 см 1м 16 см 40 м
4 Борис К. 49 с 3 м 30 см 1 м 7 см 34 м
5 Руслан Т. 46 с 3 м 60 см 1м 22 см 39 м
6 Сергей Ф. 47 с 3 м 75 см 1м 25 см 43 м
/ Максим Ш. 45 с 3 м 70 см 1м 28 см 41 м
В таблице 2 показано число очков, которые
начисляются за то или другое место по каждому виду
спортивных состязаний.
М есто 1 2 3 4 5 6 7
Число очков 7 6 5 4 3 2 1
Составь таблицу 3, в которой будет показано,
сколько очков в каждом виде спорта набрал каждый
участник.
Составь столбчатую диаграмму, на которой будет
видно, сколько очков в сумме набрал каждый участ­
ник за все четыре вида спортивных состязаний.
С помощью составленной диаграммы определи
победителя и расставь остальных участников много­
борья по занятым местам. Можешь составить соот­
ветствующую таблицу.
114
Словарь
АЛГОРИТМ УМНОЖЕНИЯ СТОЛБИКОМ
I Множители записывают друг под другом столбик >м
I. »к, чтобы разряд находился под соответствующим
разрядом. После этого снизу проводят черту, а сиена
записывают знак умножения «х». 2. Умножение первою
множителя на разрядные слагаемые второго множив1
ля выполняют по порядку, начиная с разряда единиц
второго множителя. 3. Умножение первого множителя
на данное разрядное слагаемое второго множителя
1акже выполняют поразрядно, используя способ умно­
жения многозначного числа на однозначное столбиком.
Полученные промежуточные результаты умножения пор
вого множителя на каждое разрядное слагаемое вто­
рого множителя записывают столбиком так, чтобы
соответствующие разряды располагались друг под
другом. При этом запись второго промежуточною
результата можно начинать с разряда десятков, не
записывая 0 в разряде единиц, запись третьего про
межуточного результата можно начинать с разряда
сотен, не записывая 0 ни в разряде единиц, ни в
разряде десятков, и т.д. После записи последнею
промежуточного результата снизу проводят черту, а
слева записывают знак «+». 4. Сложение всех полу
ченных ранее промежуточных результатов умножения
выполняют столбиком, используя, если это требуется,
способ сложения столбиком для трёх и более чисел
БУКВЕННОЕ ВЫРАЖЕНИЕ — запись, в сосни,
которой входят цифры, знаки действий и буквы
(например, а +15) или только буквы и знаки дейсжии
(например, (а+ Ъ): с).

61. ВМЕСТИМОСТЬ — это объём жидкости, которая
заполняет данный сосуд. Измеряется вместимость, как
правило, в литрах (л) или миллилитрах (мл).
ДИАГОНАЛЬ МНОГОУГОЛЬНИКА — отрезок, соеди­
няющий две вершины этого многоугольника, не при­
надлежащие одной его стороне.
КЛАСС МИЛЛИАРДОВ — четвёртый класс таблицы
разрядов и классов. В него входят разряды с 10-го
по 12-й, которые называются соответственно единица­
ми миллиардов, десятками миллиардов, сотнями мил­
лиардов. Вместо термина «миллиард» иногда исполь­
зуют другой термин — «биллион».
КУБИЧЕСКИЙ ДЕЦИМЕТР — единица объёма,
которая равна 1000 куб. см. Сокращённо записывается
куб. дм или дм3. Объём куба со стороной 1 дм равен
1 куб. дм.
КУБИЧЕСКИЙ МЕТР — единица объёма, которая
равна 1000000 куб. см или 1000 куб. дм. Сокращённо
записывается куб. м или м3. Объём куба со стороной
1 м равен 1 куб. м.
КУБИЧЕСКИЙ САНТИМЕТР — единица объёма,
которая равна 1000 куб. мм. Сокращённо записывается
куб. см или см3. Объём куба со стороной 1 см равен
1 куб. см.
КУБОМЕТР — используемое в повседневной прак­
тике название кубического метра.
ЛИТР — единица вместимости (объёма), которая
равна 1 куб. дм или 1000 куб. см. Сокращённо записы­
вается л. В литрах обычно измеряют вместимость
различных ёмкостей (банок, кастрюль, баков, канистр
и т. д.) и объёмы жидких тел (молока, воды, кваса,
бензина и т. д.).
116
МИЛЛИАРД — самое маленькое десятизначное
число. Оно записывается как 1000000000. Миллиард
может быть получен увеличением числа 1000000 (мил
лион) в 1000 раз. Название числа используется для
названия класса, следующего за классом миллионом
(IV класс — класс миллиардов).
МИЛЛИЛИТР — единица вместимости (объёма),
которая составляет тысячную часть литра
(1000 мл = 1 л). Сокращённо записывается мл. Объём
куба со стороной 1 см равен 1 мл (1 мл = 1 куб. см).
НЕПОЛНОЕ ЧАСТНОЕ — результат деления <
остатком, который показывает, какое максимальном
число раз делитель содержится в делимом. Если
остаток равен 0, то деление выполнено нацело и
неполное частное становится просто значением час I-
ного. Смысл использования слова «неполное» в дан
ном термине заключается в том, что при умножении
неполного частного на делитель мы ещё не получаем
полностью делимого (как это имеет место при умн<»
жении значения частного на делитель), а получаем
число, которое меньше делимого на величину остаIка
НЕЧЁТНЫЕ ЧИСЛА — числа, которые при делении
на 2 дают в остатке 1. Ряд нечётных натуральны»
чисел выглядит так: 1, 3, 5, 7, 9, 11 и т.д. Запись
любого нечётного числа оканчивается на нечётную
цифру (1, 3, 5, 7, 9). Например, число 468249 ноч<ч
ное.
ОСТАТОК — число, которое получается в реауль
тате деления с остатком и которое показывает, каком
минимальное число нужно вычесть из делимого, чтобы
полученное число делилось нацело на данный дели
тель. Остаток всегда больше или равен 0, но меньше

62. делителя. Если остаток равен 0, то деление выполне­
но нацело. Остаток показывает, на сколько делимое
больше того ближайшего к нему числа, которое
делится на делитель нацело.
РАССТОЯНИЕ между двумя точками — длина
отрезка, соединяющего эти точки (на чертеже или на
местности). Так, расстояние от Земли до Солнца при­
близительно равно 150000000 км. Термин «расстоя­
ние» используется и в качестве замены для термина
«длина пройденного пути».
СКОРОСТЬ (средняя) — длина пути, пройденного
в единицу времени. Например, если за 1 ч был прой­
ден путь длиной 70 км, то движение осуществлялось
со средней скоростью 70 км/ч (читается: 70 киломе­
тров в час). Другой часто употребляемой единицей
скорости является м/с (метр в секунду), читается:
метров в секунду. Например, при скорости ветра
20 м/с объявляется штормовое предупреждение.
ЧЁТНЫЕ ЧИСЛА — числа, которые делятся на
2 нацело. Ряд чётных натуральных чисел выглядит так:
2, 4, 6, 8, 10, 12 и т. д. Число 0 относится к чётным
числам. Запись любого чётного числа заканчивается
чётной цифрой (0, 2, 4, 6, 8). Например, число
3567918 чётное.
Приложение 1
Площадь прямоугольного треугольника
1. Можно ли из двух одинаковых прямоугольных
треугольников составить прямоугольник? Покажи
на чертеже, как это сделать.
Во сколько раз площадь составленного прямо
угольника больше площади каждого из исходных пря
моугольных треугольников?
2. Начерти прямоугольный треугольник, стороны
которого, образующие прямой угол, то есть катюы,
имеют длину 3 см и 4 см.
Начерти прямоугольник, который можно составип.
из двух таких треугольников. Какую длину имеют сю
роны этого прямоугольника? Вычисли площадь этою
прямоугольника.
Вычисли площадь прямоугольного треугольника, ко
торый был использован при составлении прямоугольники
Л',/Щ 3. Какие из следующих правил позволяют вычис
лить площадь прямоугольного треугольника?
а. Длину одного катета нужно умножить на поло
вину длины другого.
б. Длину одного катета нужно умножить на длину
другого, а полученный результат разделить пополам
в. Длину одного катета нужно умножить на длину
другого.
г. Половину длины одного катета нужно умножип.
на половину длины другого.
Примени одно из выбранных правил для вычи<
ления площади прямоугольного треугольника, канны
которого имеют длину 5 см и 6 см.

63. 5. Проведи необходимые
площадь каждого закрашенного
измерения и вычисли
треугольника.
4. Как нужно разрезать на две части прямоу­
гольный треугольник, изображённый на рисунке,
чтобы из них можно было составить прямоугольник,
изображённый на этом же рисунке? Покажи на черте­
же в тетради такое разбиение.
120
Вычисление площ ади треугольника
6. Начерти равнобедренный треугольник с осно
манием 6 см и высотой 4 см. Разбей этот треуго/и.
ник на два прямоугольных треугольника. Будут ли пи
треугольники равны? Какую длину имеют катеты Э1их
Iреугольников? Вычисли площадь такого прямоугольно
го треугольника и площадь исходного равнобедренно
го треугольника. Сравни вычисленную площадь равно
бедренного треугольника с площадью прямоугольника
со сторонами 6 см и 4 см.
7. На чертеже изображён прямоугольник, который
разбит на два прямоугольника. На таком же чертеже н
тетради проведи в каждом из этих двух прямоугольни
ков диагонали так, чтобы они имели общую вершину
Сравни площади исходного прямоугольника и гре
угольника, сторонами которого являются эти диагонали
Проведи необходимые измерения и вычисли мае
щадь данного прямоугольника. Вычисли площадь ка*
дого из построенных прямоугольных треугольников и
треугольника, составленного из них.

64. 8. Какие из следующих правил можно применит
для вычисления площади треугольника, у которо­
го известны длина основания и длина высоты,
проведённой к этому основанию?
а. Длину основания нужно умножить на половину
длины высоты.
б. Половину длины основания нужно умножить на
длину высоты.
в. Длину основания умножить на длину высоты.
г. Длину основания умножить на длину высоты, а
полученный результат разделить пополам.
Примени одно из выбранных правил для вычис­
ления площади треугольника, у которого длина осно­
вания 8 см, а длина соответствующей высоты 5 см.
9. Проведи необходимые разбиения и измерения
для того, чтобы вычислить площадь каждого закра­
шенного треугольника.
Сравни полученные площади.
122
Поупражняемся в вычислении площ ади
10. Вычисли площадь каждой из данных закра­
шенных фигур, выполнив предварительно необходимые
разбиения и измерения.
123

65. 11. Вычисли жилую площадь трёхкомнатной квар­
тиры, если каждая из комнат имеет прямоугольную
форму, а размеры комнат можно узнать из следую­
щей таблицы.
Длина Ширина Площадь
комнат
Жилая
площадь
1-я комната 6 м 4 м ?
?2-я комната 5 м 3 м ?
3-я комната 4 м 3 м ?
12. У Миши есть лист цветной бумаги квадрат­
ной формы с длиной стороны 7 см. Можно ли из
этого листа вырезать 50 квадратиков с длиной сторо­
ны 1 см? Почему?
Какое максимальное число квадратиков с длиной
стороны 2 см можно вырезать из этого листа бумаги?
Покажи в тетради, как это сделать.
Сколько ещё квадратиков с длиной стороны 2 см
можно было бы составить из оставшихся полосок —
обрезков этого листа бумаги?
13. Реши задачу. Вычисли и запиши ответ.
У Маши есть лист цветной бумаги прямоугольной
формы с длинами сторон 10 см и 20 см. Маша выреза­
ла из него деталь для аппликации в форме прямоуголь­
ного треугольника, стороны которого имеют длину 9 см,
12 см и 15 см. Вычисли площадь оставшихся обрезков.
124
Приложение 2
Геометрические ф игуры
и геом етрические величины
1. Аквариум в форме куба с длиной ребра I дм
вмещает 1 л воды. Сколько литров воды вмещшн
аквариум в форме куба с длиной ребра 1 м?
2. Аквариум в форме куба с длиной ребра I дм
вмещает 1 л воды. Какой длины должно быть ребро
аквариума в форме куба, чтобы его вместимость была
равна 125л? Прежде чем ответить на вопрос задания,
изобрази модель куба, составленную из 125 кубикон
3. Рассмотри фигуру, состоящую из 12 одинако
вых квадратов.
Раздели эту фигуру на две части так, чтобы каж
дая часть являлась развёрткой куба. Закрась каждую
развёртку своим цветом.

66. 4. Коробку в форме куба с длиной ребра 2 дм
нужно полностью обернуть листом обёрточной бумаги.
Из двух листов обёрточной бумаги прямоугольной
формы выбери тот, которым можно полностью обер­
нуть коробку. Один лист имеет длину 8 дм, а ширину
4 дм. Другой лист имеет длину 7 дм, а ширину 5 дм.
Изобрази выбранный тобой лист в тетради
в виде прямоугольника с длиной сторон, выраженной
теми же числами, но в сантиметрах. Место, куда
нужно поставить коробку в начале обёртывания, изо­
брази на этом листе квадратом с длиной стороны,
выраженной тем же числом, но в сантиметрах.
Проверь правильность решения: «оберни» модель
коробки листом обёрточной бумаги. Размеры модели
коробки и листа обёрточной бумаги вырази в санти­
метрах.
5. Коробку в форме куба с ребром 30 см пере­
вязали цветной лентой, как это показано
на рисунке.
Какой длины потребовалась для этого лента, если
на завязывание банта с одного и другого конца пона­
добилось по 40 см ленты?
126
| ■ в. Земельный участок, имеющий форму прямо-
ника с длиной 90 м и шириной 80 м, решили
и11> (размежевать) на одинаковые садовые участки
I форме прямоугольников с длиной 30 м и шириной
р )м Предложи свой план разбивки и изобрази его
(• ом.нически в тетради. Для этого исходный земель
Ими участок изобрази в виде прямоугольника с дли
Нои ') см и шириной 8 см.
Какую площадь будет иметь каждый из получил
И)их< VI садовых участков?
Сколько садовых участков получится в результате
|Н1 Юивки?
Какой длины потребуется ограждение, чтобы каж-
дыи садовый участок огородить со всех сторон? При
ним следует учесть, что соседние участки по обпщи
ч'лнице должны иметь общее ограждение.
7. Пол в кухне имеет форму квадрата с длиной
троны 3 м. В магазине был выбран линолеум, кого
Iннм нужно застелить пол в кухне. Ширина этого лине
иоума 2 м, а длина выбирается покупателем. Какой
наименьшей длины нужно купить кусок этого линолну
ма, чтобы его хватило для настила пола в кухне?
При этом следует учесть, что на линолеуме жм
определённого узора, что позволяет составлять (сое
динять) любые части куска. Покажи схематически, как
нужно раскроить купленный кусок линолеума на час1и
и как эти части должны располагаться на полу
и кухне.
Сколько нужно заплатить за покупку, если каждый
метр длины (погонный метр) линолеума стот
2000 рублей?
127

67. Учебное издание
Чекин Александр Леонидович
МАТЕМАТИКА
4 класс
Учебник
В двух частях
Часть 1
Подписано в печать 26.06.2012. Формат 70x90/16.
Гарнитура Ргадтайса С. Печать офсетная. Бумага офсетная
Печ. л. 8,0. Доп. тираж 10 000 экз. Тип. зак. № 33047.
Издател ьство «Академкнига/Учебн ик»
117997, Москва, ул. Профсоюзная, д. 90, офис 602
Тел.: (495)334-76-21, факс: (499)234-63-58.
Е-плаЛ: а са б е ти сН @ та 1к.ги лл/лл/.акас1етктда.ги
Отпечатано в соответствии с качеством
предоставленных издательством электронных носителей
в ОАО «Саратовский полиграфкомбинат».
410004, г. Саратов, ул. Чернышевского, 59. ллллл/.5агрк.ги

68. ВРЕМЯ
Единицы времени:
1 минута (1 мин) = 60 секунд (60 с)
1 час (1 ч) = 60 минут (60 мин) = 3600 секунд (3600(3600 <||
СКОРОСТЬ
Скорость (средняя) - длина пройденного пути уж
за единицу времени.
Единицы скорости:
1 километр в минуту (1 км/мин) =
= 60 километров в час (60 км/ч)
1 метр в секунду (1 м/с) = 60 метров в минуту уту
(60 м/мин) = 3600 метров в час (3600 м/ч) )
ПРОИЗВОДИТЕЛЬНОСТЬ
изводительность (средняя) - объём выполненной рлГЙ рпбни4
единицу времени (или скорость выполнения рабоп.йбон.О
Единицы производительности:
страница в секунду (1 стр./с) = 60 страниц в минуту|ину|у
(60 стр./мин) = 3600 страниц в час (3600 стр./ч) ^ч)
1 деталь в минуту (1 дет./мин) =
= 60 деталей в час (60 дет./ч)
1 кв. метр в минуту (1 кв.м/мин) =
100 кв. дециметров в минуту (100 кв. дм/мин) 1н)
и» М1МИ ОУ1ОЛЬНИКА НА ТР1 [УГОЛЬНИКИ
Н1ИНИЦМ НМ1СТИМОСТИ И ОБЪЁМА
I ►уПн'ин ний гш и и м ш р ( I куб. см) -
мП| НМ »■уГм и ДЛИНОЙ стороны I см
I »уОИЧ»М>ИЙ дециметр ( I куб. д м ) -
нСи иМ •■убн О д ли н о й стороны 1 дм
I ►уЛичжжий метр (1 куб. м) -
об»,ММ И уГи| о д ли н о й стороны 1 м
и |1 д м ') 1000 куб. см (1 0 0 0 см*) * I литр (1 л)
|Ц М (I м '| 1000 куб, дм (1 0 0 0 д м ') ■ 1 0 0 0 литроп
(1 0 0 0 л) - 1 0 0 0 0 0 0 куб, см (1 0 0 0 0 0 0 см3)
МММЩАДЬ 111Ч«МОУГОЛЬНОГО ТРЕУГОЛЬНИКА
ни и 11,1 прямоугольного треугольника
5 - площадь
3 * (а •Ь) : 2