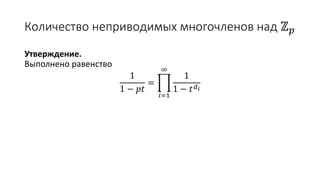
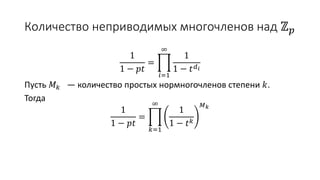
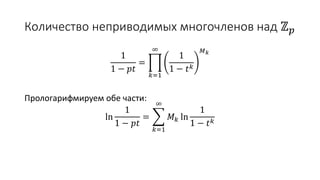
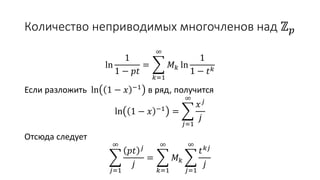
Документ описывает формальные степенные ряды и операции над ними, включая сумму, разность, произведение и частное рядов. Он также рассматривает производящие функции и радиус сходимости, а также предоставляет вывод обобщенной формулы бинома и чисел Каталана с использованием производящих функций. В конце документа приводятся теоремы о разбиениях чисел и их производящих функциях.

1. Дискретные структуры
МФТИ, весна 2014
Александр Дайняк
www.dainiak.com

2. Формальные степенные ряды
Формальный степенной ряд — это запись вида
𝑎0 + 𝑎1 𝑥 + 𝑎2 𝑥2 + ⋯ + 𝑎 𝑘 𝑥 𝑘 + ⋯
Числа 𝑎0, 𝑎1, … называются коэффициентами ряда.

3. Операции над рядами
Обозначим
𝐴 𝑥 ≔ 𝑎0 + 𝑎1 𝑥 + 𝑎2 𝑥2 + ⋯ + 𝑎 𝑘 𝑥 𝑘 + ⋯
𝐵 𝑥 ≔ 𝑏0 + 𝑏1 𝑥 + 𝑏2 𝑥2
+ ⋯ + 𝑏 𝑘 𝑥 𝑘
+ ⋯
• Сумма рядов 𝐴 и 𝐵 — это ряд
𝑐0 + 𝑐1 𝑥 + 𝑐2 𝑥2
+ ⋯ + 𝑐 𝑘 𝑥 𝑘
+ ⋯
с коэффициентами 𝑐 𝑘 = 𝑎 𝑘 + 𝑏 𝑘
• Разность рядов 𝐴 и 𝐵 — это ряд с коэффициентами 𝑐 𝑘 = 𝑎 𝑘 − 𝑏 𝑘

4. Операции над рядами
Обозначим
𝐴 𝑥 ≔ 𝑎0 + 𝑎1 𝑥 + 𝑎2 𝑥2 + ⋯ + 𝑎 𝑘 𝑥 𝑘 + ⋯
𝐵 𝑥 ≔ 𝑏0 + 𝑏1 𝑥 + 𝑏2 𝑥2
+ ⋯ + 𝑏 𝑘 𝑥 𝑘
+ ⋯
• Произведение рядов 𝐴 и 𝐵 — это ряд
𝑐0 + 𝑐1 𝑥 + 𝑐2 𝑥2
+ ⋯ + 𝑐 𝑘 𝑥 𝑘
+ ⋯
с коэффициентами
𝑐 𝑘 =
𝑖=0
𝑘
𝑎𝑖 𝑏 𝑘−𝑖

5. Операции над рядами
Обозначим
𝐴 𝑥 ≔ 𝑎0 + 𝑎1 𝑥 + 𝑎2 𝑥2 + ⋯ + 𝑎 𝑘 𝑥 𝑘 + ⋯
𝐵 𝑥 ≔ 𝑏0 + 𝑏1 𝑥 + 𝑏2 𝑥2
+ ⋯ + 𝑏 𝑘 𝑥 𝑘
+ ⋯
Пусть 𝑏0 ≠ 0.
• Частное рядов 𝐴 и 𝐵 — это ряд
𝑐0 + 𝑐1 𝑥 + 𝑐2 𝑥2
+ ⋯ + 𝑐 𝑘 𝑥 𝑘
+ ⋯
коэффициенты которого определяются последовательно из
соотношений:
𝑐0 ≔
𝑎0
𝑏0
, 𝑐1 ≔
𝑎1−𝑏1 𝑐0
𝑏0
, 𝑐2 ≔
𝑎2−𝑏2 𝑐0−𝑏1 𝑐1
𝑏0
, …

6. Операции над рядами
Производная ряда
𝑎0 + 𝑎1 𝑥 + 𝑎2 𝑥2 + ⋯ + 𝑎 𝑘 𝑥 𝑘 + ⋯
— это ряд
𝑐0 + 𝑐1 𝑥 + 𝑐2 𝑥2 + ⋯ + 𝑐 𝑘 𝑥 𝑘 + ⋯
с коэффициентами
𝑐 𝑘 ≔ 𝑘 + 1 𝑎 𝑘+1

7. Производящие функции
Производящая функция числовой последовательности 𝑎0, 𝑎1, … — это
сумма ряда
𝑎0 + 𝑎1 𝑥 + 𝑎2 𝑥2 + ⋯ + 𝑎 𝑘 𝑥 𝑘 + ⋯
(при условии, что в окрестности нуля ряд сходится)
Например, производящая функция последовательности 𝑛
0
, 𝑛
1
, 𝑛
2
…
— это ряд
𝑛
0
+
𝑛
1
𝑥 +
𝑛
2
𝑥2
+ ⋯ +
𝑛
𝑛
𝑥 𝑛
+ ⋯
Мы знаем, что этот ряд можно «свернуть»:
1 + 𝑥 𝑛

8. Производящие функции
Основное правило применения производящих функций:
Любая функция может быть производящей функцией не более чем
одной последовательности.
А это значит, что если мы взяли две последовательности,
на первый взгляд «разные», и доказали, что их производящие
функции равны в окрестности нуля, то и сами последовательности
совпадают.

9. Радиус сходимости
Для применимости метода нужно проверять, что ряды сходятся в
окрестности нуля.
Радиус сходимости ряда ∑𝑎 𝑘 𝑥 𝑘 — это такое 𝑟, что ряд сходится
при всех 𝑥, таких, что 𝑥 < 𝑟. (𝑥 в общем случае комплексное)
Радиус сходимости помогает найти Теорема Коши:
𝑟 = lim
𝑘→∞
𝑘
𝑎 𝑘
−1

10. Рациональные производящие функции
Утверждение.
Если последовательность 𝑎 𝑘 удовлетворяет л.р.с. с п.к.,
то производящая функция 𝑓 для 𝑎 𝑘 представима в виде
𝑓 𝑥 =
𝑃 𝑥
𝑄 𝑥
,
где 𝑃, 𝑄 ∈ ℝ 𝑥 .

11. Доказательство утверждения
Пусть п-ть 𝑎 𝑘 удовлетворяет соотношению 𝑐 𝑟 𝑎 𝑘+𝑟 + ⋯ + 𝑐0 𝑎 𝑘 = 0, или, что то же самое,
𝑐 𝑟 𝑎 𝑘 + 𝑐 𝑟−1 𝑎 𝑘−1 … + 𝑐1 𝑎 𝑘−𝑟+1 + 𝑐0 𝑎 𝑘−𝑟 = 0.
Пусть 𝑓 𝑥 ≔ ∑𝑎 𝑘 𝑥 𝑘
. Имеем
𝑐0 𝑥 𝑟
⋅ 𝑓 𝑥 =
𝑘=𝑟
∞
𝑐0 𝑎 𝑘−𝑟 𝑥 𝑘
𝑐1 𝑥 𝑟−1 ⋅ 𝑓 𝑥 =
𝑘=𝑟−1
∞
𝑐1 𝑎 𝑘−𝑟+1 𝑥 𝑘
⋮
𝑐 𝑟 ⋅ 𝑓 𝑥 =
𝑘=0
∞
𝑐 𝑟 𝑎 𝑘 𝑥 𝑘
Отсюда 𝑐0 𝑥 𝑟
+ 𝑐1 𝑥 𝑟−1
+ ⋯ + 𝑐 𝑟 ⋅ 𝑓 𝑥 = 𝑃 𝑥 + ∑ 𝑘=𝑟
∞
𝑐 𝑟 𝑎 𝑘 + 𝑐 𝑟−1 𝑎 𝑘−1 … + 𝑐1 𝑎 𝑘−𝑟+1 + 𝑐0 𝑎 𝑘−𝑟
=0
𝑥 𝑘
,
где 𝑃 — многочлен степени не выше 𝑟 − 1 .

12. Применение производящих функций
Пусть надо вычислить сумму
𝑘=0
𝑛
𝑘2
𝑛
𝑘
1
2 𝑘
Заметим, что она равняется 𝑔 1 2 , где 𝑔 𝑥 — производящая
функция для последовательности
𝑎 𝑘 = 𝑘2
𝑛
𝑘
то есть
𝑔 𝑥 ≔
𝑘=0
∞
𝑘2
𝑛
𝑘
𝑥 𝑘

13. Применение производящих функций
Имеем 𝑔 𝑥 = ∑ 𝑘=0
∞
𝑘2 𝑛
𝑘
𝑥 𝑘
Пусть 𝑓 𝑥 ≔ ∑ 𝑘=0
∞ 𝑛
𝑘
𝑥 𝑘
= 1 + 𝑥 𝑛
.
Заметим, что 𝑔 𝑥 = 𝑥 𝑥𝑓′ 𝑥
′
, а значит
𝑔 𝑥 = 𝑥 𝑥 1 + 𝑥 𝑛 ′ ′
= 𝑥 𝑥𝑛 1 + 𝑥 𝑛−1 ′ =
= 𝑥𝑛 1 + 𝑥 𝑛−1 + 𝑥 𝑛 − 1 1 + 𝑥 𝑛−2
И теперь легко вычислить
𝑔 1/2 =
𝑛
2
3
2
𝑛−1
+ 1
2 𝑛 𝑛 − 1 ⋅ 3
2
𝑛−2

14. Обобщённая формула бинома
«Обычная» формула бинома для 𝑛 ∈ ℕ:
1 + 𝑥 𝑛 = 1 +
𝑛
1
𝑥 +
𝑛
2
𝑥2 + ⋯ +
𝑛
𝑛
𝑥 𝑛
Обобщённая формула бинома для 𝛼 ∈ ℝ:
1 + 𝑥 𝛼 = 1 +
𝛼
1
𝑥 +
𝛼
2
𝑥2 + ⋯ +
𝛼
𝑘
𝑥 𝑘 + ⋯
Здесь 𝛼
𝑘
— обобщённые биномиальные коэффициенты:
𝛼
𝑘
=
𝛼 𝛼 − 1 𝛼 − 2 ⋅ … ⋅ 𝛼 − 𝑘 − 1
𝑘!

15. Обобщённая формула бинома
1 + 𝑥 𝛼
= 1 + 𝛼
1
𝑥 + 𝛼
2
𝑥2
+ ⋯, где 𝛼
𝑘
=
𝛼 𝛼−1 𝛼−2 ⋅…⋅ 𝛼− 𝑘−1
𝑘!
Пример применения:
1 + 𝑥 1/2 = 1 +
1
2
𝑥 +
1
2
1
2 − 1
2!
𝑥2 +
1
2
1
2 − 1 1
2 − 2
3!
𝑥3 + ⋯ =
= 1 +
1
2
𝑥 +
1 − 2
2! ⋅ 22
𝑥2
+
1 − 2 1 − 4
3! ⋅ 23
𝑥3
+ ⋯
= 1 +
1
2
𝑥 −
1
2! ⋅ 22
𝑥2
+
1 ⋅ 3
3! ⋅ 23
𝑥3
−
1 ⋅ 3 ⋅ 5
4! ⋅ 24
+ ⋯
= 1 + 𝑥
𝑘=0
∞
−1 𝑘
1 ⋅ 3 ⋅ 5 ⋅ … ⋅ 2𝑘 − 1
𝑘 + 1 ! 2 𝑘+1
𝑥 𝑘

16. Обобщённая формула бинома
Ещё немного преобразуем:
1 + 𝑥 1/2 = 1 + 𝑥
𝑘=0
∞
−1 𝑘
1 ⋅ 3 ⋅ 5 ⋅ … ⋅ 2𝑘 − 1
𝑘 + 1 ! 2 𝑘+1
𝑥 𝑘
= 1 + 𝑥
𝑘=0
∞
−1 𝑘
1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ … ⋅ 2𝑘 − 2 2𝑘 − 1
2 ⋅ 4 ⋅ 6 ⋅ … ⋅ 2𝑘 − 2 ⋅ 𝑘 + 1 ! 2 𝑘+1
𝑥 𝑘
= 1 + 𝑥
𝑘=0
∞
−1 𝑘
2𝑘 − 1 !
2 𝑘−1 𝑘 − 1 ! ⋅ 𝑘 + 1 ! 2 𝑘+1
𝑥 𝑘
= 1 + 𝑥
𝑘=0
∞
2𝑘 − 1 !
𝑘 − 1 ! ⋅ 𝑘 + 1 !
−1
4
𝑥
𝑘

17. Числа Каталана
Одно из многочисленных определений:
Число Каталана 𝑎 𝑛 — это количество правильных скобочных
последовательностей из 𝑛 пар скобок
Пример, при 𝑛 = 3 имеем 𝑎3 = 5:
, , , ,

18. Числа Каталана: рекуррентное соотношение
Рекуррентное соотношение для чисел Каталана:
𝑎 𝑛+1 =
𝑘=0
𝑛
𝑎 𝑘 𝑎 𝑛−𝑘
Обоснование:
прав. ск. посл.
внутри 𝑘 пар скобок
прав. ск. посл.
𝑛−𝑘 пар скобок
Начальные условия: 𝑎0 = 𝑎1 = 1

19. Числа Каталана: производящая функция
Рассмотрим производящую функцию для последовательности
чисел Каталана:
𝐴 𝑥 = 𝑎0 + 𝑎1 𝑥 + 𝑎2 𝑥2
+ 𝑎3 𝑥3
+ ⋯
Заметим, что соотношение 𝑎 𝑛+1 = ∑ 𝑘=0
𝑛
𝑎 𝑘 𝑎 𝑛−𝑘 похоже по форме
на то, что возникает при произведении рядов. Рассмотрим
𝐴 𝑥 ⋅ 𝐴 𝑥 =
= 𝑎0
2
+ 𝑎0 𝑎1 + 𝑎1 𝑎0 𝑥 + 𝑎0 𝑎2 + 𝑎1 𝑎1 + 𝑎2 𝑎0 𝑥2
+ 𝑎0 𝑎3 + 𝑎1 𝑎2 + 𝑎2 𝑎1 + 𝑎3 𝑎0 𝑥3 + ⋯ =
= 𝑎1 + 𝑎2 𝑥 + 𝑎3 𝑥2
+ 𝑎4 𝑥3
+ ⋯

20. Числа Каталана: производящая функция
Итак,
𝐴 𝑥
2
= 𝑎1 + 𝑎2 𝑥 + 𝑎3 𝑥2 + 𝑎4 𝑥3 + ⋯
Отсюда
𝑎0 + 𝑥 𝐴 𝑥
2
= 𝑎0 + 𝑎1 𝑥 + 𝑎2 𝑥2 + ⋯ = 𝐴 𝑥
Получаем уравнение для производящей функции 𝐴:
𝑎0 + 𝑥 𝐴 𝑥
2
= 𝐴 𝑥

21. Числа Каталана: производящая функция
Уравнение для производящей функции:
𝑥 𝐴 𝑥
2
− 𝐴 𝑥 + 1 = 0
Отсюда
𝐴 𝑥 =
1 ± 1 − 4𝑥
2𝑥
Теперь воспользуемся обобщённой формулой бинома, чтобы
записать 𝐴 𝑥 в виде ряда:
𝐴 𝑥 =
1 ± 1 + (−4𝑥) 1 2
2𝑥

22. Числа Каталана: вывод формулы
𝐴 𝑥 =
1 ± 1 + (−4𝑥) 1 2
2𝑥
где по формуле обобщённого бинома
1 + (−4𝑥) 1 2
=
= 1 +
1
2
−4𝑥 +
1
2
1
2 − 1
2!
−4𝑥 2 +
1
2
1
2 − 1 1
2 − 2
3!
−4𝑥 3 + ⋯
Отсюда уже видно, что на самом деле
𝐴 𝑥 =
1 − 1 + (−4𝑥) 1 2
2𝑥

23. Числа Каталана: вывод формулы
Подставим в выражение для 𝐴 𝑥 ряд для 1 + (−4𝑥) 1 2
:
𝐴 𝑥 =
1 − 1 + (−4𝑥) ∑ 𝑘=0
∞ 2𝑘−1 !
𝑘−1 !⋅ 𝑘+1 !
𝑥 𝑘
2𝑥
Отсюда
𝐴 𝑥 = 2
𝑘=0
∞
2𝑘 − 1 !
𝑘 − 1 ! ⋅ 𝑘 + 1 !
𝑥 𝑘
В итоге
𝑎 𝑘 = 2
2𝑘 − 1 !
𝑘 − 1 ! ⋅ 𝑘 + 1 !
=
2𝑘 − 1 ! ⋅ 2𝑘
𝑘 − 1 ! ⋅ 𝑘 ⋅ 𝑘 + 1 !
=
2𝑘 !
𝑘! ⋅ 𝑘 + 1 !
=
2𝑘
𝑘
𝑘 + 1

24. Числа Каталана
Итак,
𝑎 𝑘 =
2𝑘
𝑘
𝑘 + 1
Асимптотика:
𝑎 𝑘 ∼
4 𝑘
𝜋 ⋅ 𝑘3 2

25. Теорема Эйлера
Обозначим 𝑝чёт(𝑁) и 𝑝неч 𝑁 количества разбиений 𝑁
соответственно на чётное и нечётное число различных слагаемых.
Теорема.
𝑝чёт 𝑁 − 𝑝неч 𝑁 =
−1 𝑘, если 𝑁 = 3𝑘2±𝑘
2
0, иначе

26. Производящая функция для числа
неупорядоченных разбиений
Утверждение.
Если 𝑝 𝑁 — количество неупорядоченных разбиений числа 𝑁,
то для производящей функции последовательности 𝑝 0 , 𝑝 1 , …
справедлива формула
𝑛=0
∞
𝑝 𝑛 ⋅ 𝑥 𝑛 =
𝑘=1
∞
1
1 − 𝑥 𝑘

27. Производящая функция для числа
неупорядоченных разбиений
Т.к. 1 − 𝑡 −1 = 1 + 𝑡 + 𝑡2 + ⋯, то
𝑘=1
∞
1 − 𝑥 𝑘 −1
=
𝑖1
𝑥 𝑖1
𝑖2
𝑥2𝑖2
𝑖3
𝑥3𝑖3 ⋅ … =
𝑛=0
∞
𝑎 𝑛 𝑥 𝑛
где 𝑎 𝑛 — количество наборов 𝑖1, 𝑖2, 𝑖3, … таких, что
𝑛 = 𝑖1 + 2𝑖2 + 3𝑖3 + ⋯

28. Производящая функция для числа
неупорядоченных разбиений
𝑘=1
∞
1 − 𝑥 𝑘 −1
=
𝑛=0
∞
𝑎 𝑛 𝑥 𝑛
где 𝑎 𝑛 — количество наборов 𝑖1, 𝑖2, 𝑖3, … таких, что
𝑛 = 𝑖1 + 2𝑖2 + 3𝑖3 + ⋯
Любой такой набор 𝑖1, 𝑖2, 𝑖3, … однозначно соответствует
разбиению числа 𝑛, в котором 𝑖1 слагаемых равны 1,
𝑖2 слагаемых равны 2, и т.д.
Отсюда следует, что 𝑎 𝑛 = 𝑝 𝑛 .

29. Вывод рекуррентного соотношения
для числа неупорядоченных разбиений
Итак,
𝑘=1
∞
1
1 − 𝑥 𝑘
=
𝑛=0
∞
𝑝 𝑛 𝑥 𝑛
Отсюда
𝑛=0
∞
𝑝 𝑛 𝑥 𝑛 ⋅
𝑘=1
∞
1 − 𝑥 𝑘 = 1

30. Вывод рекуррентного соотношения
для числа неупорядоченных разбиений
𝑛=0
∞
𝑝 𝑛 𝑥 𝑛 ⋅
𝑘=1
∞
1 − 𝑥 𝑘 = 1
Разложим в ряд произведение 𝑘=1
∞
1 − 𝑥 𝑘 :
1 − 𝑥 1 − 𝑥2
1 − 𝑥3
⋅ … =
𝑚=0
∞
𝑏 𝑚 𝑥 𝑚
где 𝑏 𝑚 = 𝑝чёт 𝑚 − 𝑝неч 𝑚 .

31. Вывод рекуррентного соотношения
для числа неупорядоченных разбиений
𝑛=0
∞
𝑝 𝑛 𝑥 𝑛 ⋅
𝑚=0
∞
𝑏 𝑚 𝑥 𝑚 = 1
где
𝑏 𝑚 =
−1 𝑘, если ∃𝑘: 𝑚 = 3𝑘2±𝑘
2
0, иначе
Итак,
𝑛=0
∞
𝑝 𝑛 𝑥 𝑛 ⋅ 1 +
𝑘=1
∞
−1 𝑘 𝑥 3𝑘2−𝑘 2 + 𝑥 3𝑘2+𝑘 2 = 1

32. Вывод рекуррентного соотношения
для числа неупорядоченных разбиений
𝑗=0
∞
𝑝 𝑗 𝑥 𝑗 ⋅ 1 +
𝑘=1
∞
−1 𝑘 𝑥 3𝑘2−𝑘 2 + 𝑥 3𝑘2+𝑘 2 = 1
При раскрытии скобок и приведении подобных слагаемых
коэффициенты при всех положительных степенях 𝑥 должны быть
нулевыми, отсюда для любого 𝑚 > 0 выполнено
𝑝 𝑚 +
𝑘>0
−1 𝑘 𝑝 𝑚 − 3𝑘2−𝑘
2
+ 𝑝 𝑚 − 3𝑘2+𝑘
2
= 0
(считаем формально, что 𝑝 𝑁 = 0 при любом 𝑁 < 0)

33. Рекуррентное соотношение для числа
неупорядоченных разбиений
Теорема.
Для любого 𝑚 > 0 выполнено равенство
𝑝 𝑚 =
𝑘>0
−1 𝑘+1 𝑝 𝑚 − 3𝑘2−𝑘
2
+ 𝑝 𝑚 − 3𝑘2+𝑘
2
Несколько первых слагаемых ряда:
𝑝 𝑚 =
= 𝑝 𝑚 − 1 + 𝑝 𝑚 − 2 − 𝑝 𝑚 − 5 − 𝑝 𝑚 − 7 + 𝑝 𝑚 − 12
+ 𝑝 𝑚 − 15 − ⋯

34. Количество неприводимых многочленов над ℤ 𝑝
Пусть 𝑓1, 𝑓2, … — последовательность всех простых
нормногочленов над ℤ 𝑝, в порядке неубывания их степеней.
Обозначим 𝑑𝑖 ≔ deg 𝑓𝑖.
Любой нормногочлен 𝑓 представляется единственным образом в
виде
𝑓 = 𝑓𝑖1
𝛼 𝑖1
⋅ … ⋅ 𝑓𝑖 𝑠
𝛼 𝑖 𝑠
где 𝑖1 < 𝑖2 < ⋯ < 𝑖 𝑠 и 𝛼𝑖1
, … , 𝛼𝑖 𝑠
> 0. При этом
deg 𝑓 = 𝑑𝑖1
𝛼𝑖1
+ ⋯ + 𝑑𝑖 𝑠
𝛼𝑖 𝑠

35. Количество неприводимых многочленов над ℤ 𝑝
Любой нормногочлен 𝑓 представляется единственным образом
в виде
𝑓 = 𝑓𝑖1
𝛼 𝑖1
⋅ … ⋅ 𝑓𝑖 𝑠
𝛼 𝑖 𝑠
где 𝑖1 < 𝑖2 < ⋯ < 𝑖 𝑠 и 𝛼𝑖1
, … , 𝛼𝑖 𝑠
> 0.
Поэтому для любого 𝑛 число наборов 𝛼1, 𝛼2, 𝛼3, … ,
удовлетворяющих уравнению
𝑛 = 𝑑1 𝛼1 + 𝑑2 𝛼2 + 𝑑3 𝛼3 + ⋯
равно 𝑝 𝑛 (т.к. каждому такому набору 𝛼1, 𝛼2, 𝛼3, … можно
взаимно однозначно сопоставить многочлен степени 𝑛).

36. Количество неприводимых многочленов над ℤ 𝑝
Утверждение.
Выполнено равенство
1
1 − 𝑝𝑡
=
𝑖=1
∞
1
1 − 𝑡 𝑑 𝑖

37. Количество неприводимых многочленов над ℤ 𝑝
Доказательство:
Т.к. 1 − 𝑡 𝑑 𝑖
−1
= 1 + 𝑡 𝑑 𝑖 + 𝑡2𝑑 𝑖 + 𝑡3𝑑 𝑖 + ⋯, то
𝑖=1
∞
1 − 𝑡 𝑑 𝑖
−1
=
𝑗1=0
∞
𝑡 𝑑1 𝑗1
𝑗2=0
∞
𝑡 𝑑2 𝑗2
𝑗3=0
∞
𝑡 𝑑3 𝑗3 … =
𝑘=0
∞
𝑎 𝑘 𝑡 𝑘
где 𝑎 𝑘 — количество наборов (𝑗1, 𝑗2, 𝑗3, … ), удовлетворяющих
соотношению 𝑘 = 𝑑1 𝑗1 + 𝑑2 𝑗2 + ⋯. Значит, 𝑎 𝑘 = 𝑝 𝑘
, и отсюда
𝑖=1
∞
1 − 𝑡 𝑑 𝑖
−1
=
𝑘=0
∞
𝑝 𝑘
𝑡 𝑘
=
𝑘=0
∞
𝑝𝑡 𝑘
=
1
1 − 𝑝𝑡

38. Количество неприводимых многочленов над ℤ 𝑝
1
1 − 𝑝𝑡
=
𝑖=1
∞
1
1 − 𝑡 𝑑 𝑖
Пусть 𝑀 𝑘 — количество простых нормногочленов степени 𝑘.
Тогда
1
1 − 𝑝𝑡
=
𝑘=1
∞
1
1 − 𝑡 𝑘
𝑀 𝑘

39. Количество неприводимых многочленов над ℤ 𝑝
1
1 − 𝑝𝑡
=
𝑘=1
∞
1
1 − 𝑡 𝑘
𝑀 𝑘
Прологарифмируем обе части:
ln
1
1 − 𝑝𝑡
=
𝑘=1
∞
𝑀 𝑘 ln
1
1 − 𝑡 𝑘

40. Количество неприводимых многочленов над ℤ 𝑝
ln
1
1 − 𝑝𝑡
=
𝑘=1
∞
𝑀 𝑘 ln
1
1 − 𝑡 𝑘
Если разложить ln 1 − 𝑥 −1
в ряд, получится
ln 1 − 𝑥 −1 =
𝑗=1
∞
𝑥 𝑗
𝑗
Отсюда следует
𝑗=1
∞
𝑝𝑡 𝑗
𝑗
=
𝑘=1
∞
𝑀 𝑘
𝑗=1
∞
𝑡 𝑘𝑗
𝑗

41. Количество неприводимых многочленов над ℤ 𝑝
𝑗=1
∞
𝑝𝑡 𝑗
𝑗
=
𝑘=1
∞
𝑀 𝑘
𝑗=1
∞
𝑡 𝑘𝑗
𝑗
Коэффициенты при 𝑡 𝑛
для каждого 𝑛 должны совпадать в левой
и правой частях равенства.
Поэтому
𝑝 𝑛
𝑛
=
𝑘|𝑛
𝑀 𝑘
𝑛 𝑘
Окончательно,
𝑝 𝑛
=
𝑘|𝑛
𝑘𝑀 𝑘

42. Количество неприводимых многочленов над ℤ 𝑝
𝑝 𝑛 =
𝑘|𝑛
𝑘𝑀 𝑘
Применяя обращение Мёбиуса, получаем следующую теорему.
Теорема.
Число нормногочленов степени 𝑛, неприводимых над ℤ 𝑝, равно
1
𝑛
𝑘|𝑛
𝑝 𝑘
𝜇 𝑛 𝑘
где 𝜇 — функция Мёбиуса.

43. Количество неприводимых многочленов над ℤ 𝑝
Следствие 1.
При каждом 𝑝 и при каждом 𝑛 ≥ 2 существует хотя бы один
неприводимый над ℤ 𝑝 нормногочлен степени 𝑛.
Следствие 2.
Число нормногочленов степени 𝑛, неприводимых над ℤ 𝑝,
при 𝑛 → ∞ асимптотически равно
𝑝 𝑛
𝑛
(См. доказательство асимптотики для числа циклических слов)