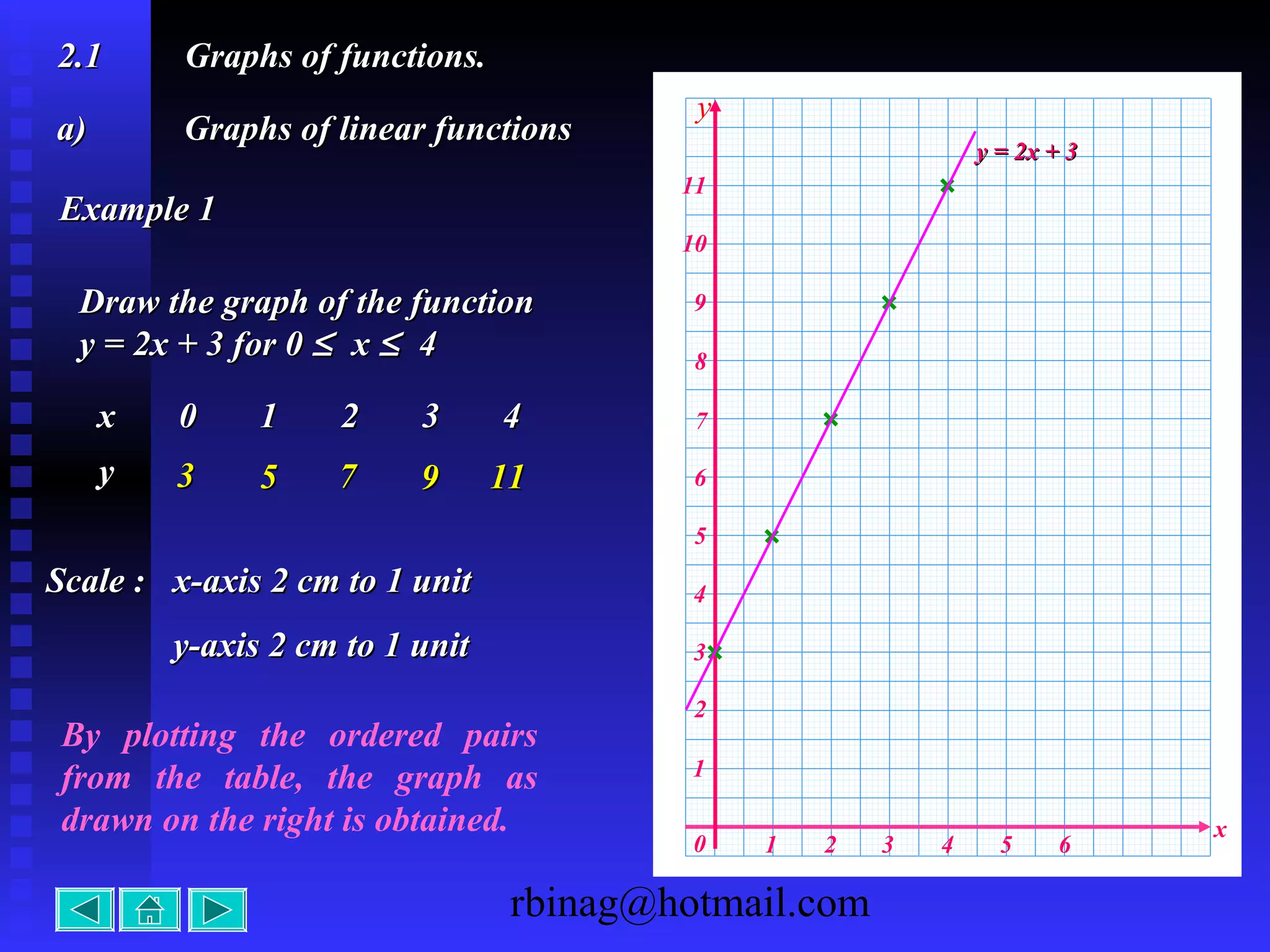
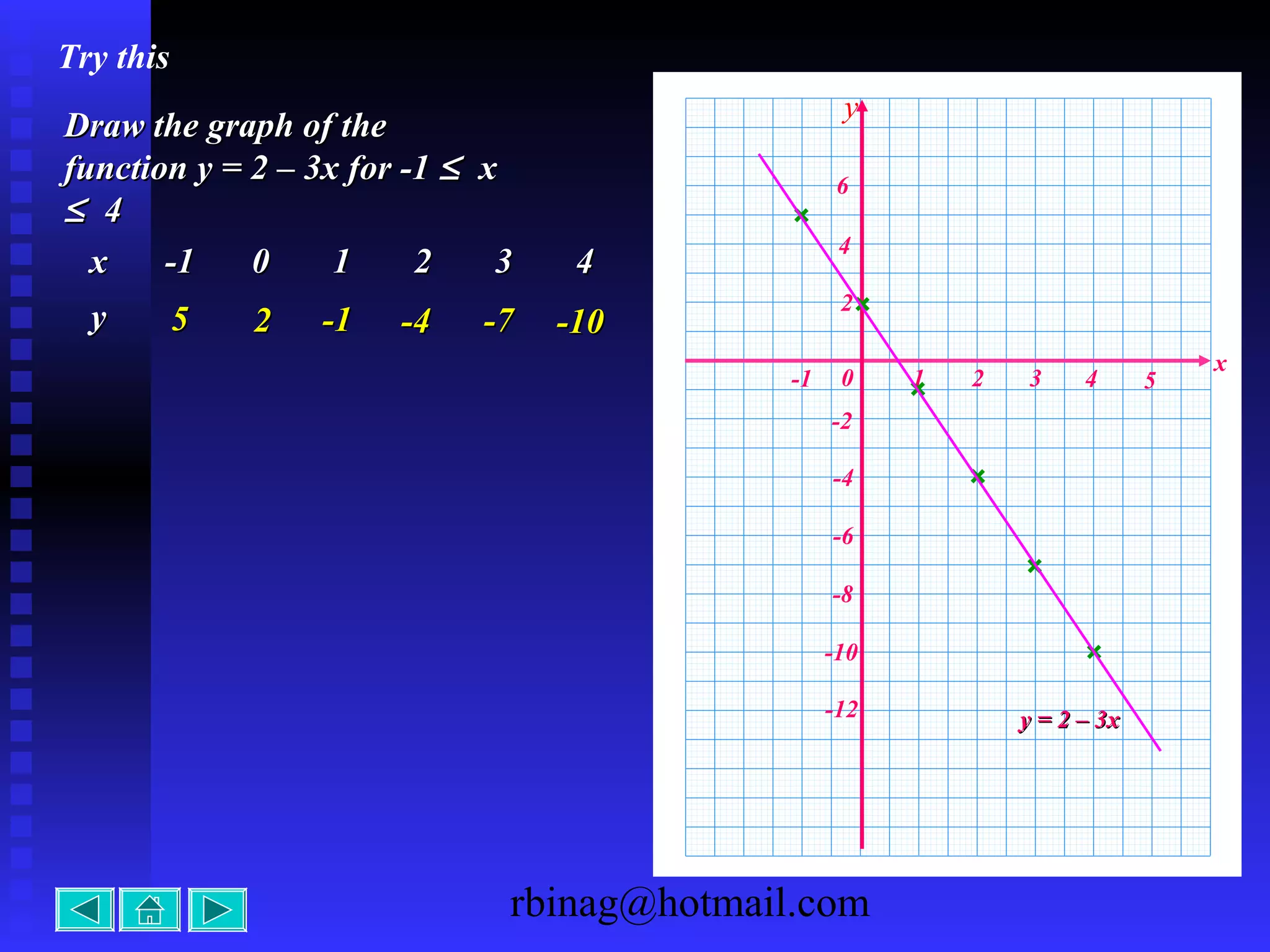
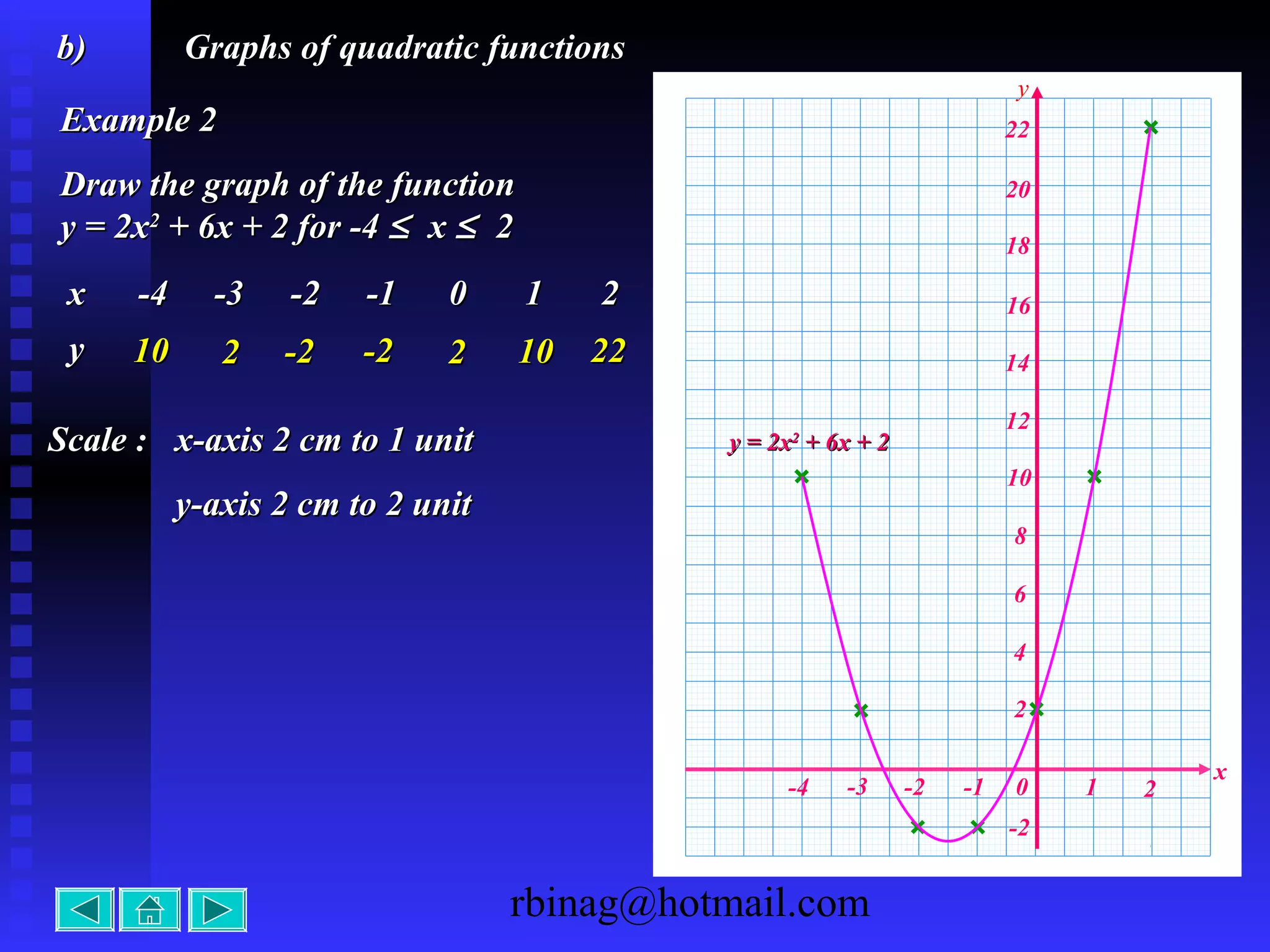
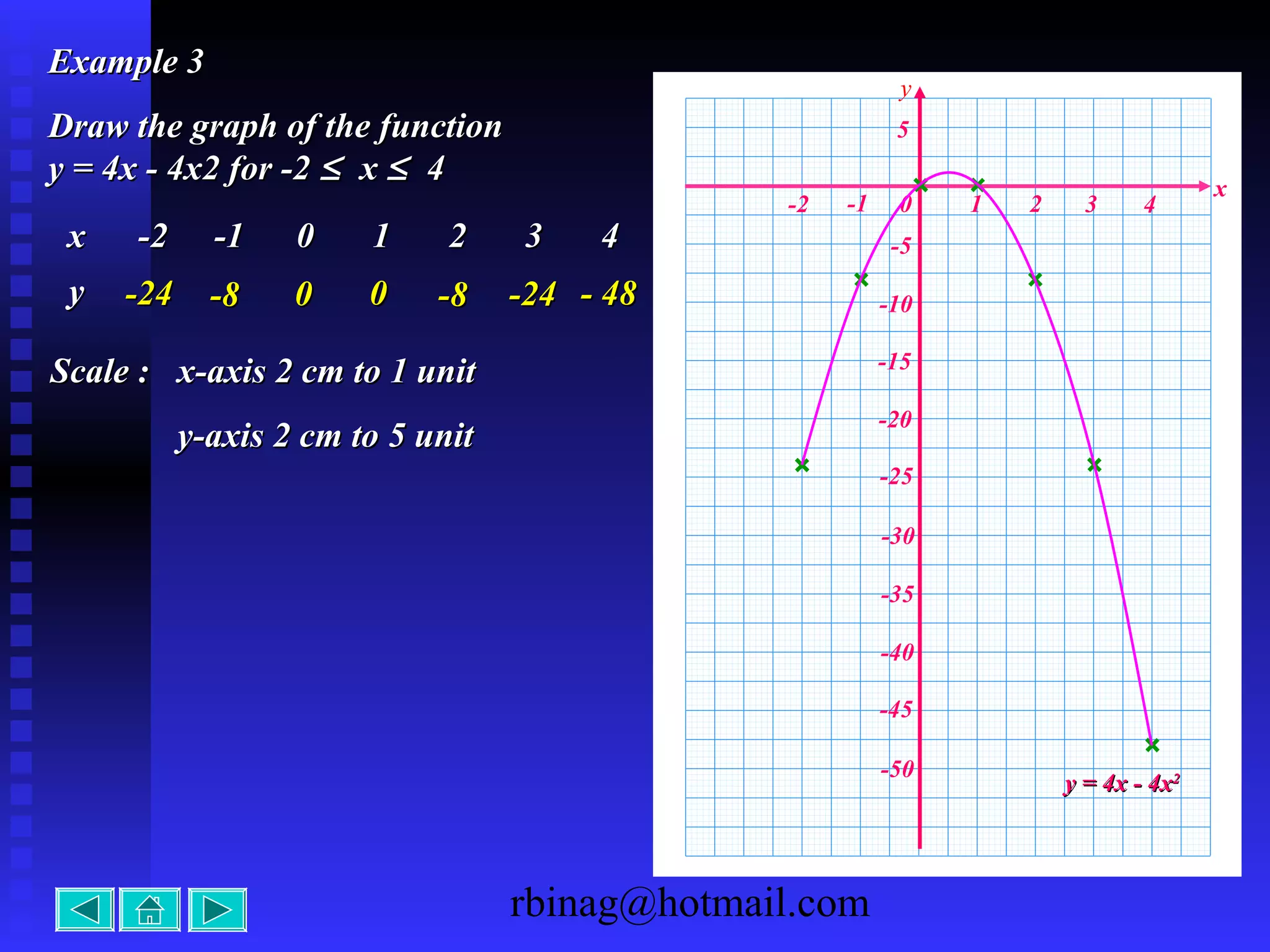
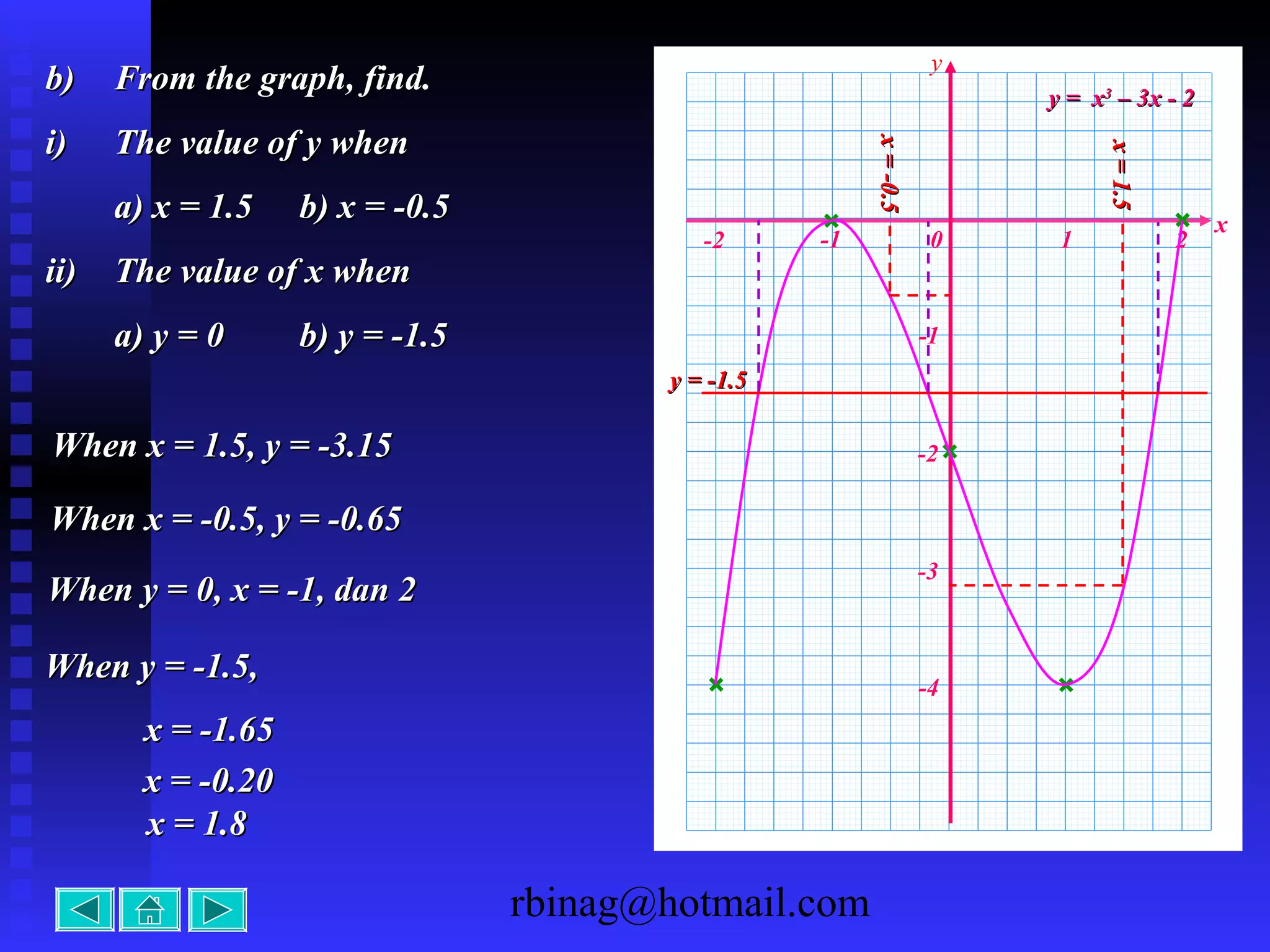
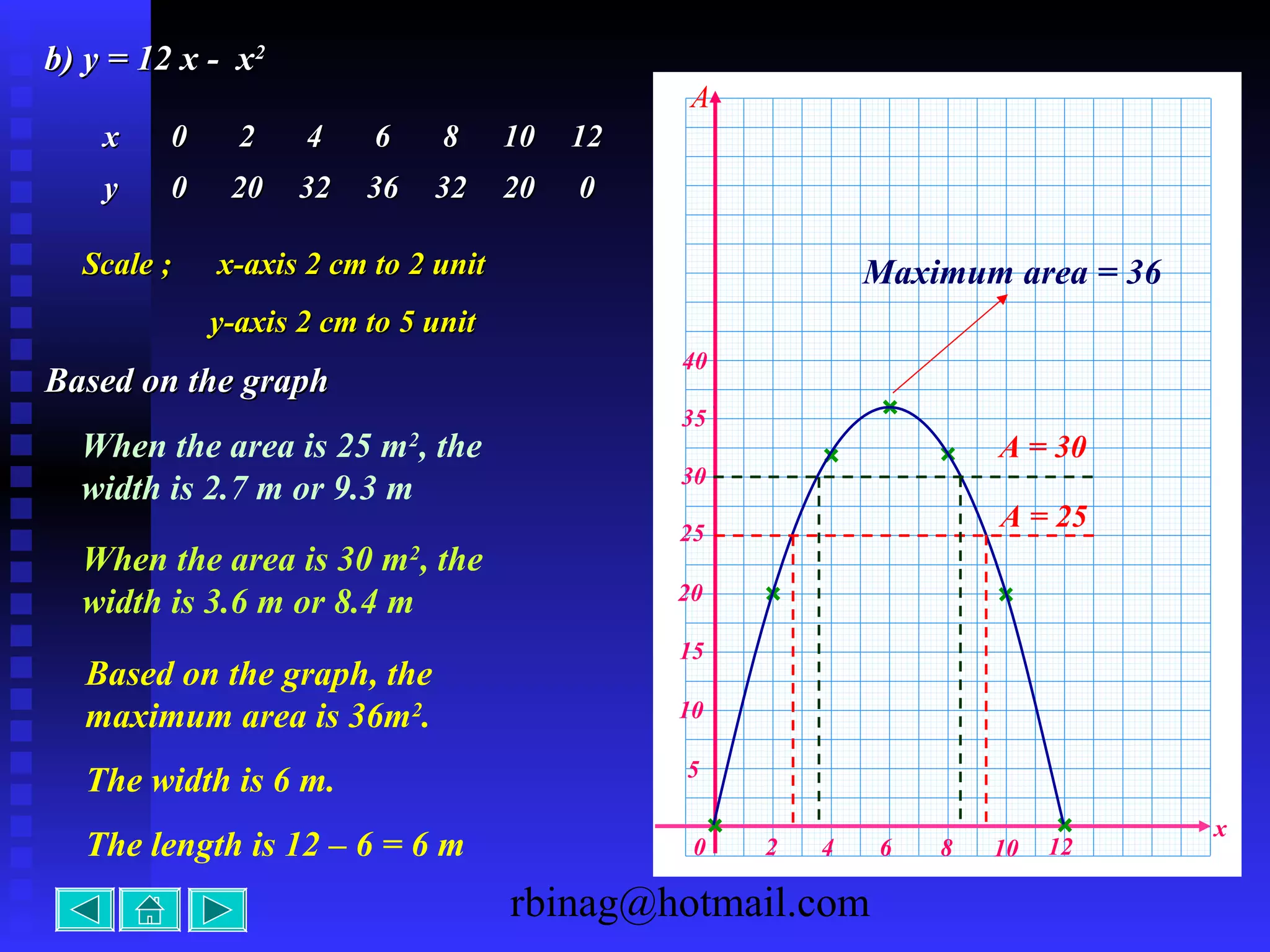
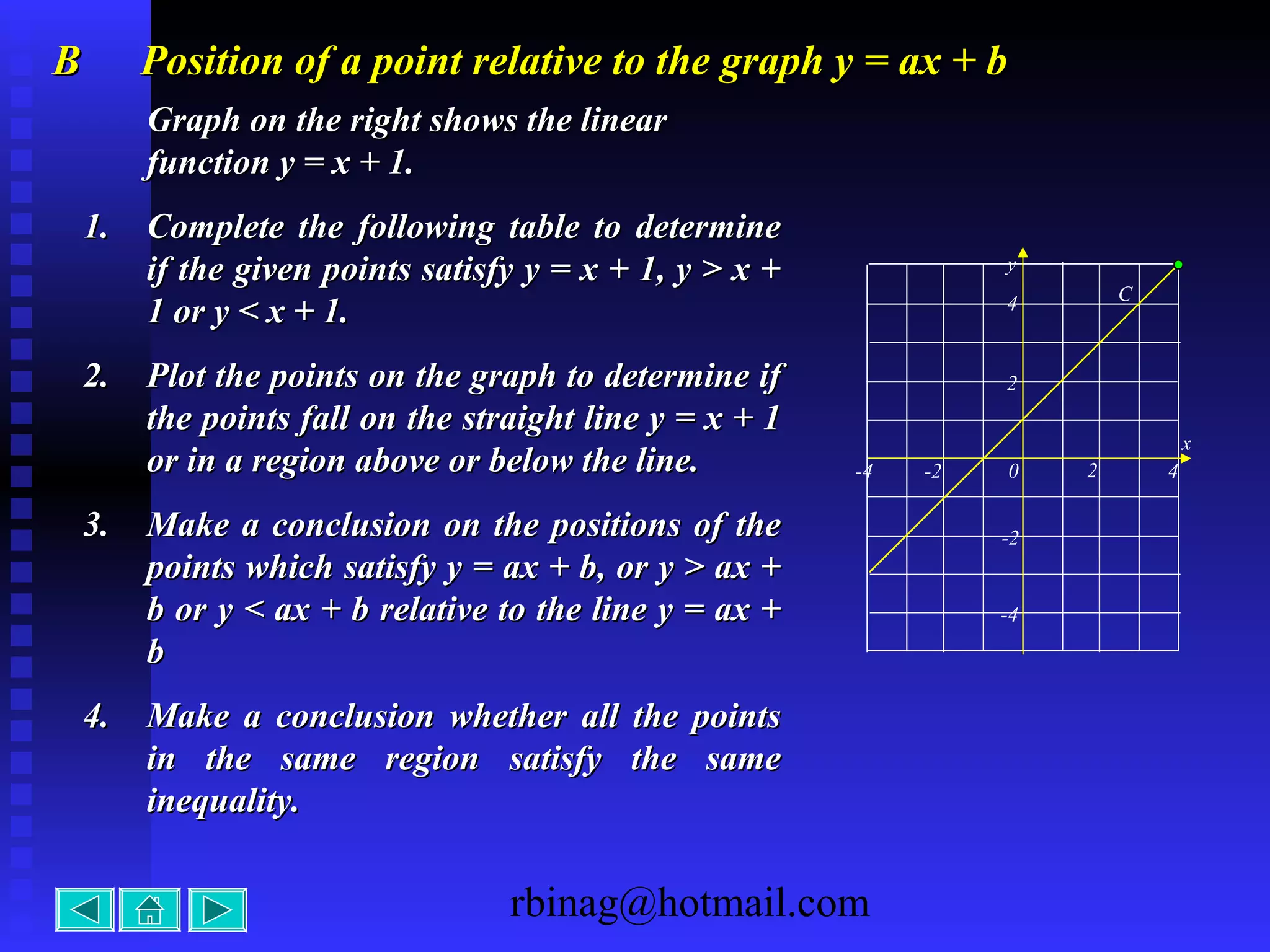
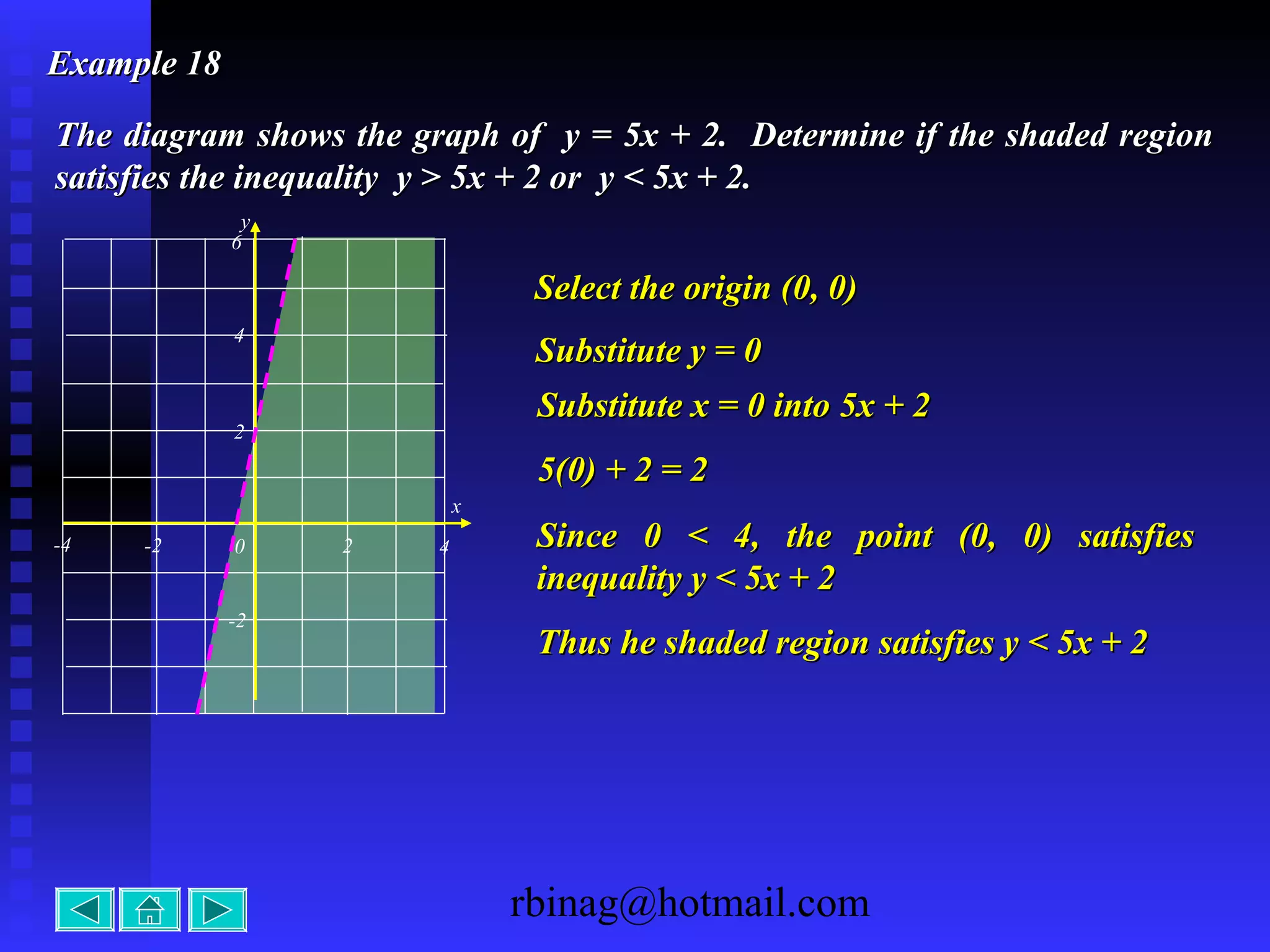
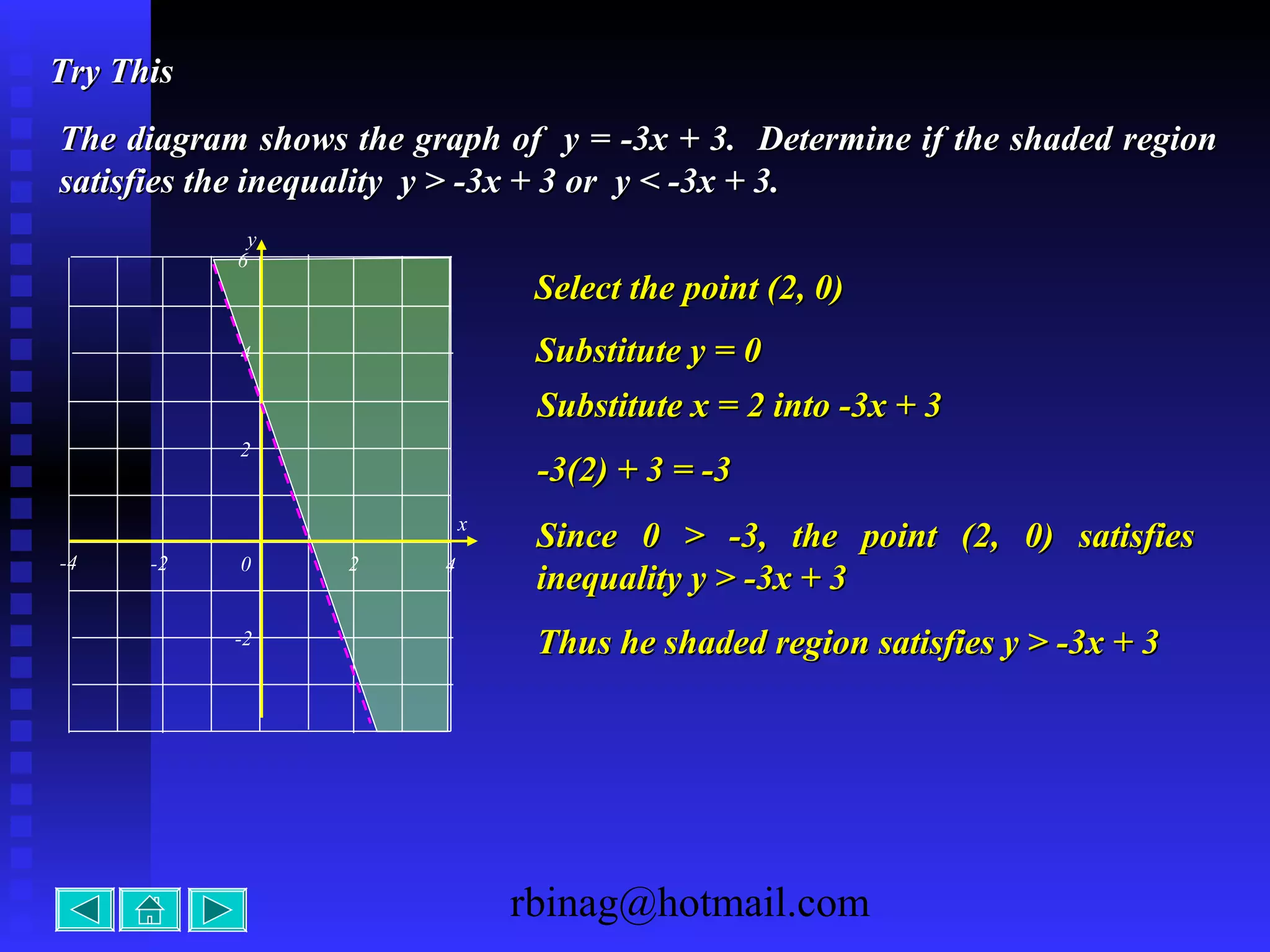
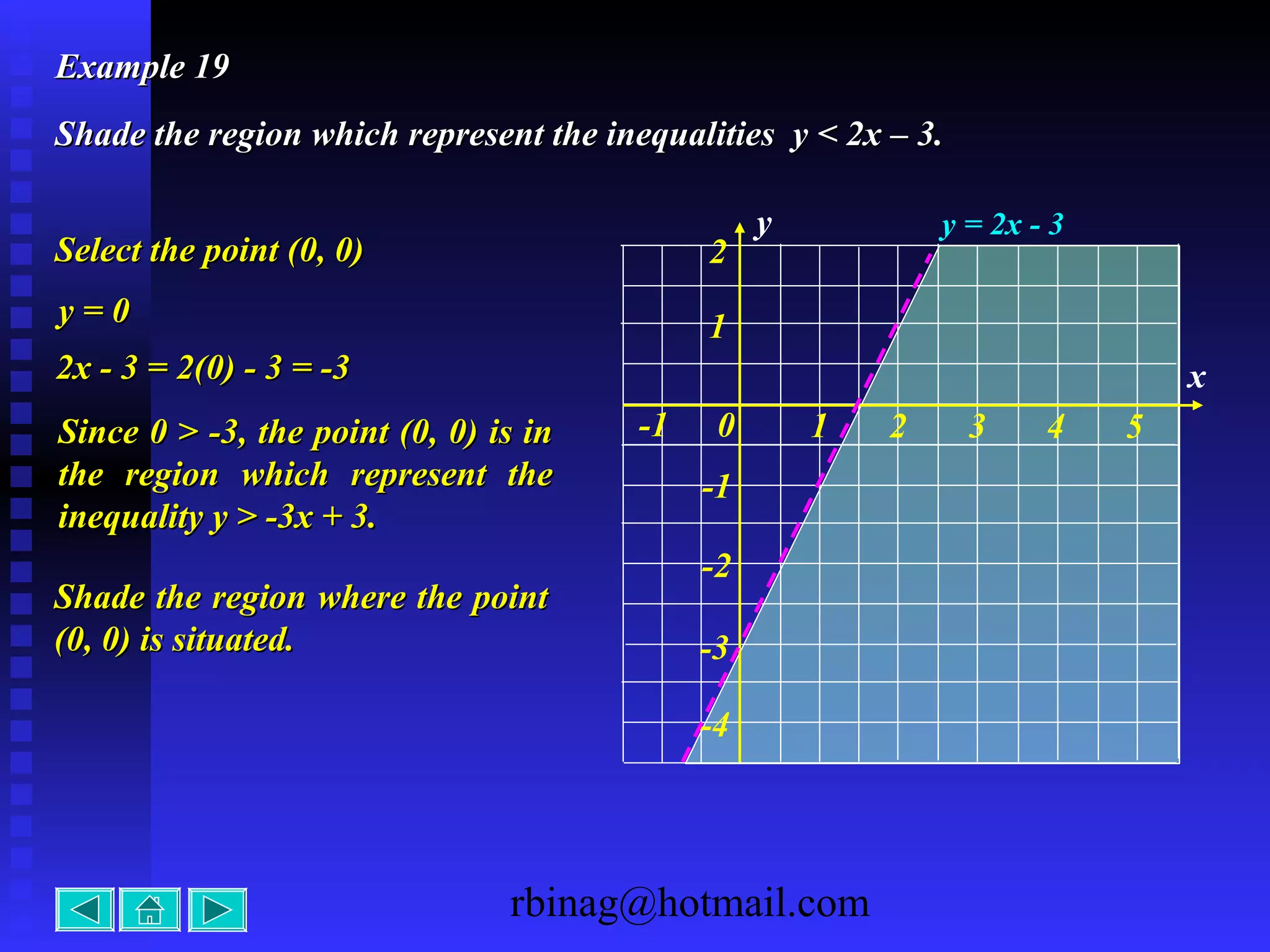
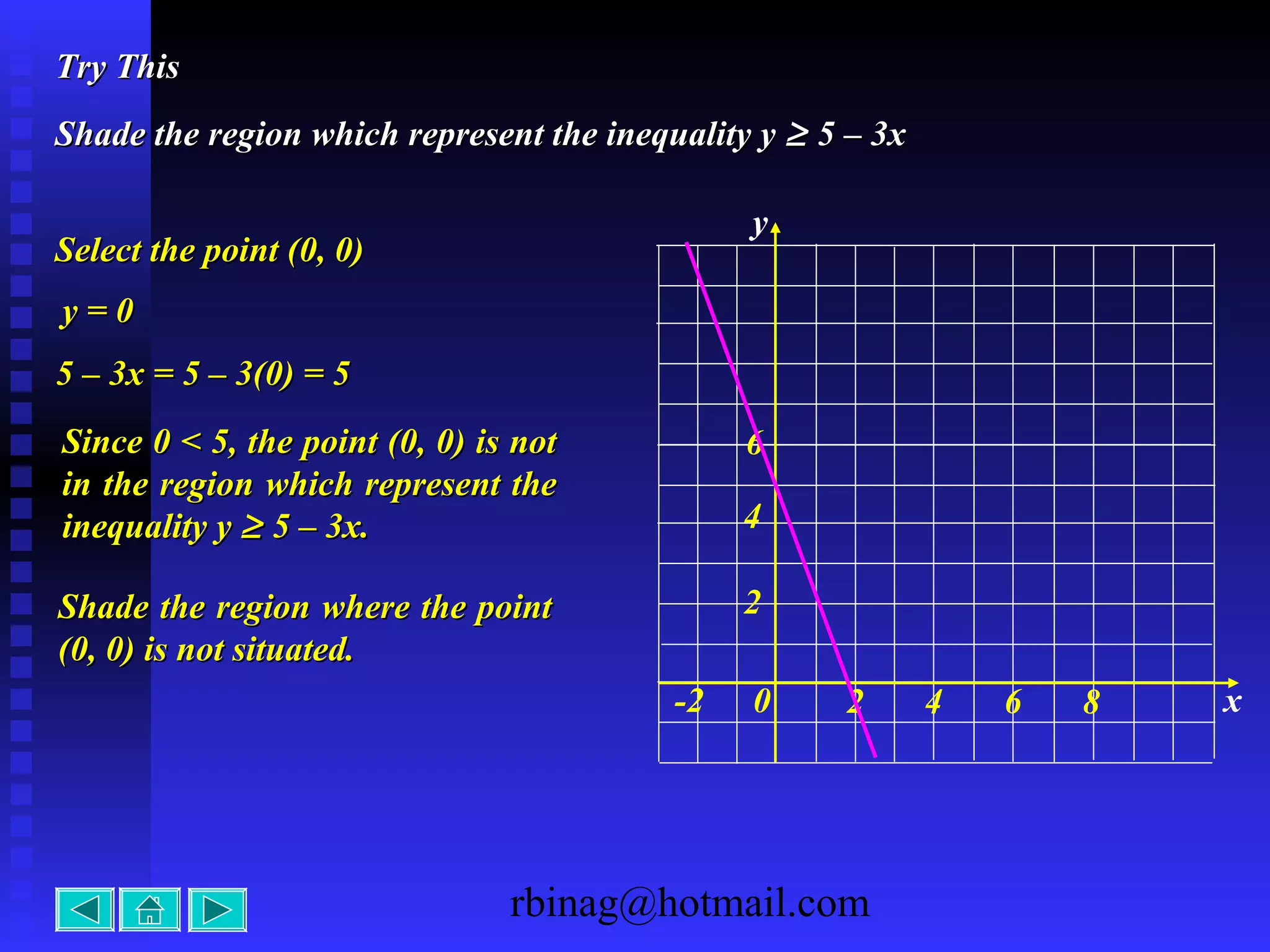
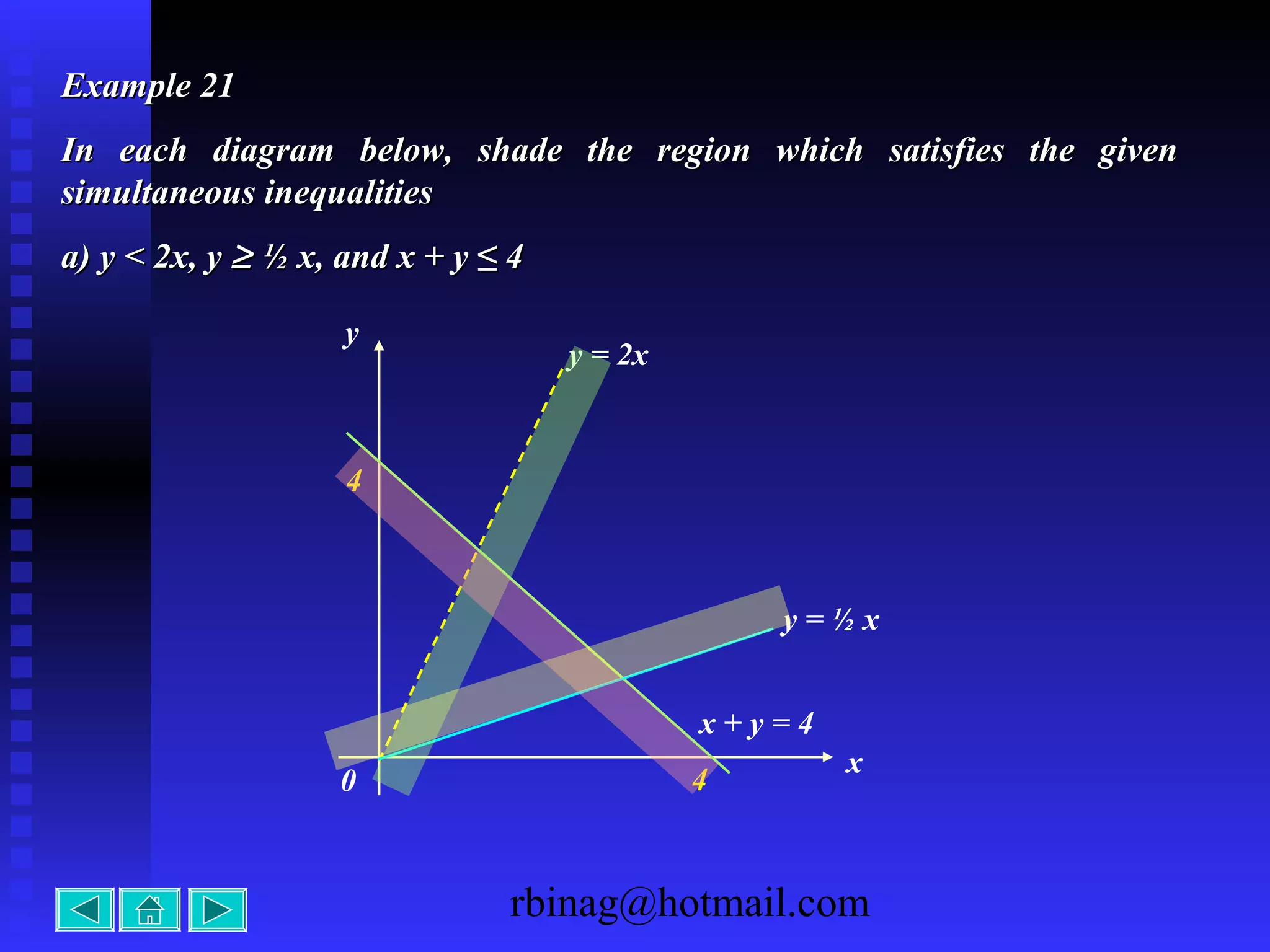
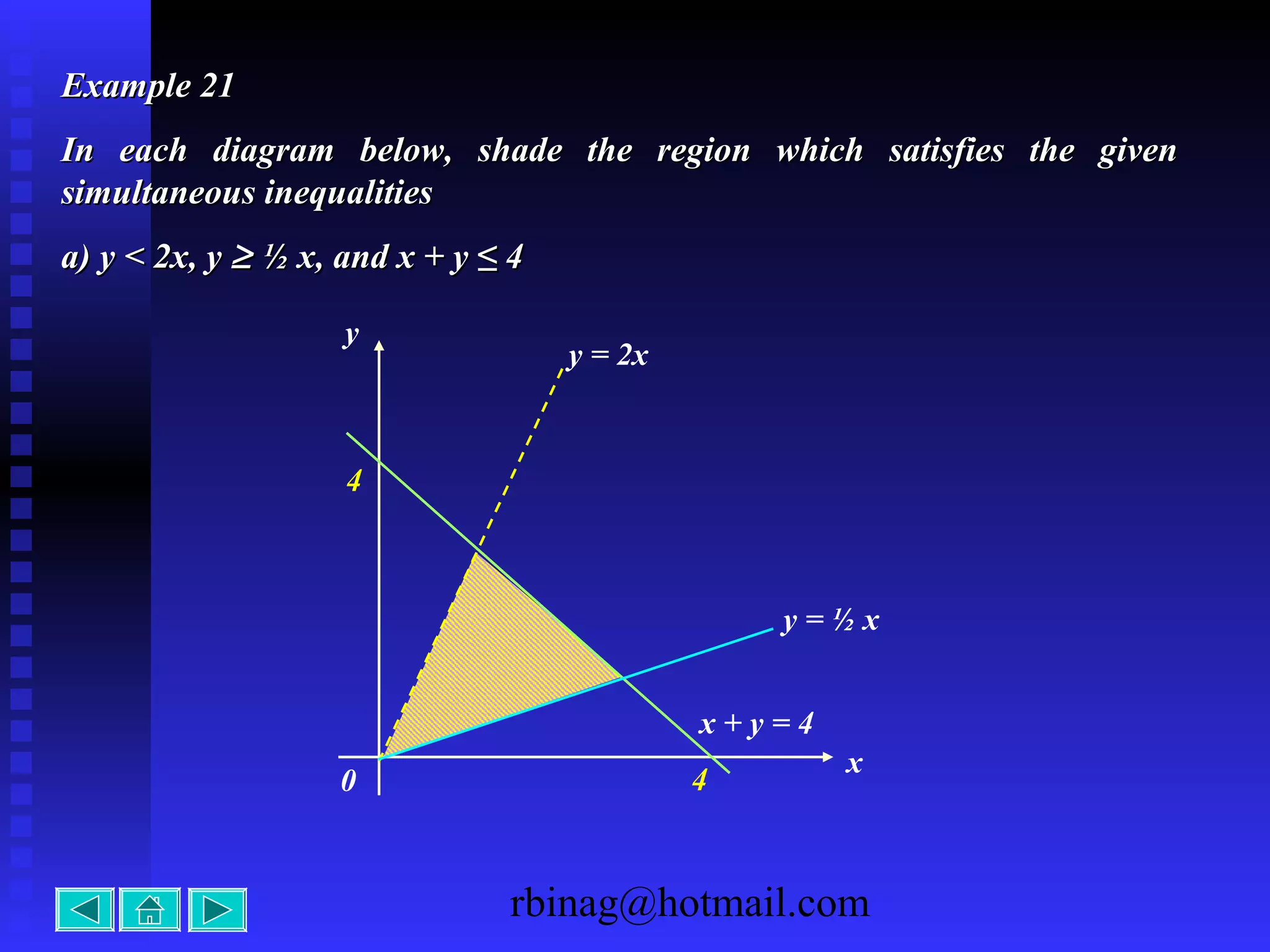
The document provides examples and explanations for sketching the graphs of various types of functions, including:
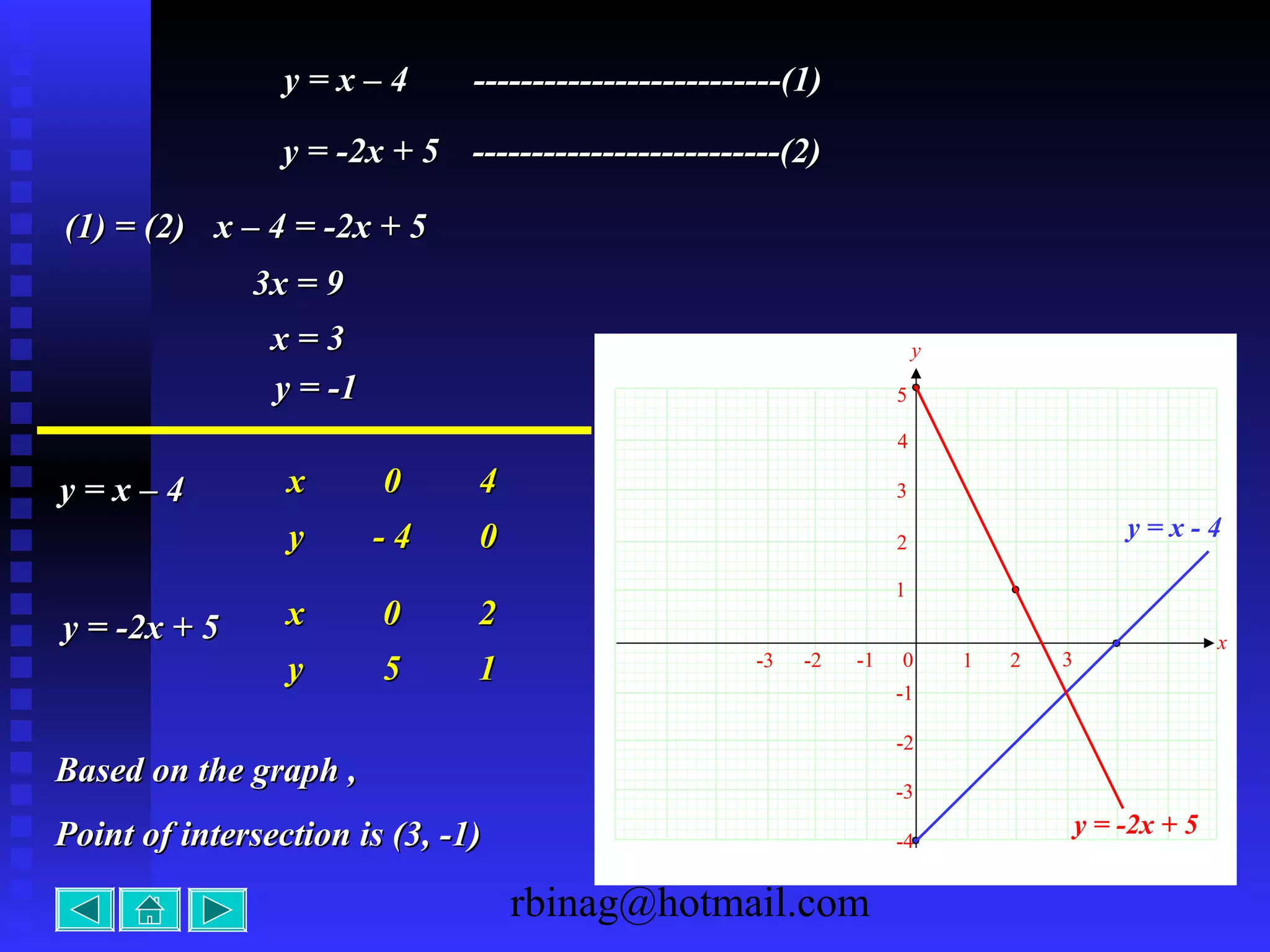
1) Linear functions, which produce straight lines. The slope and y-intercept determine the graph.
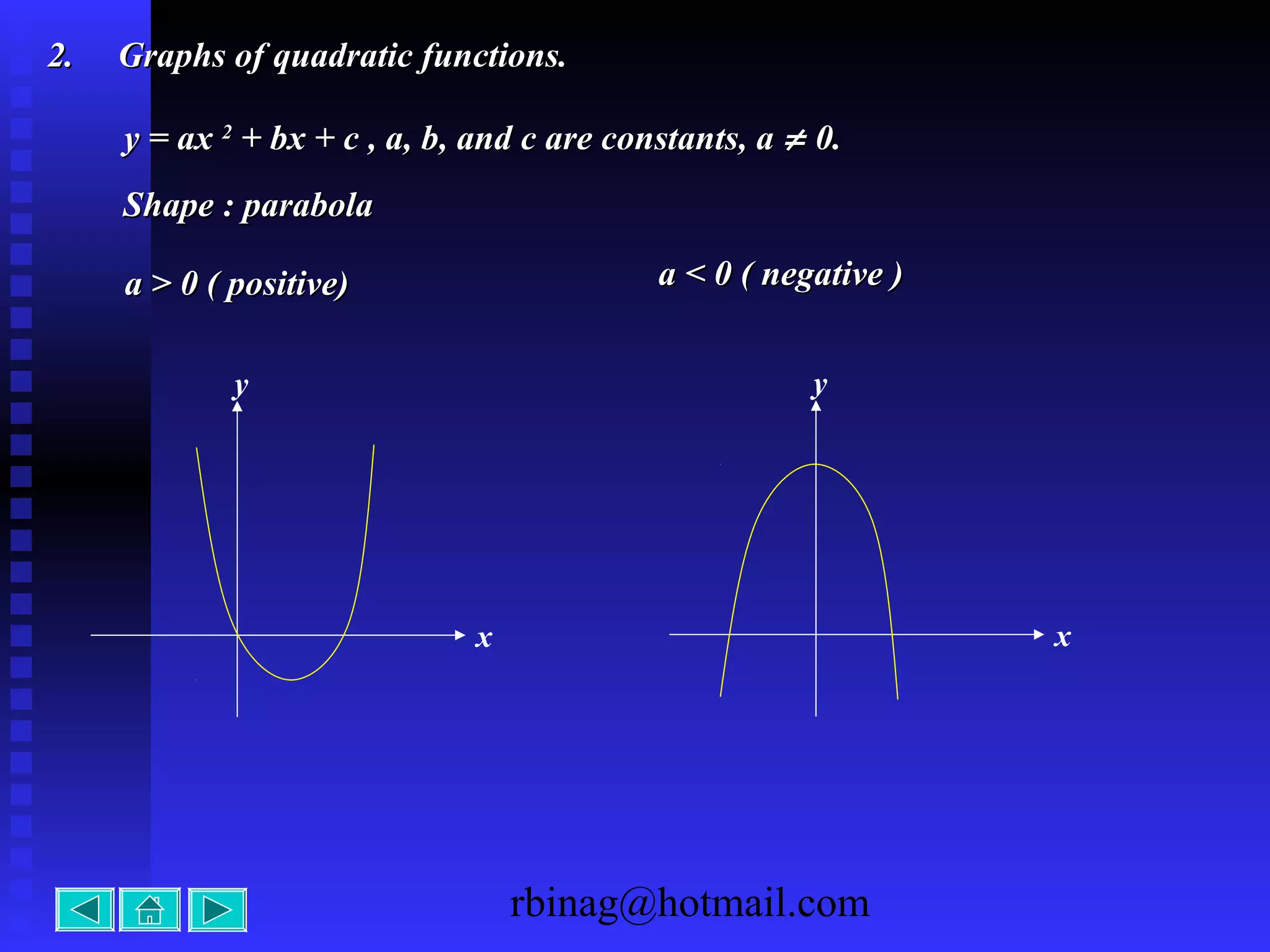
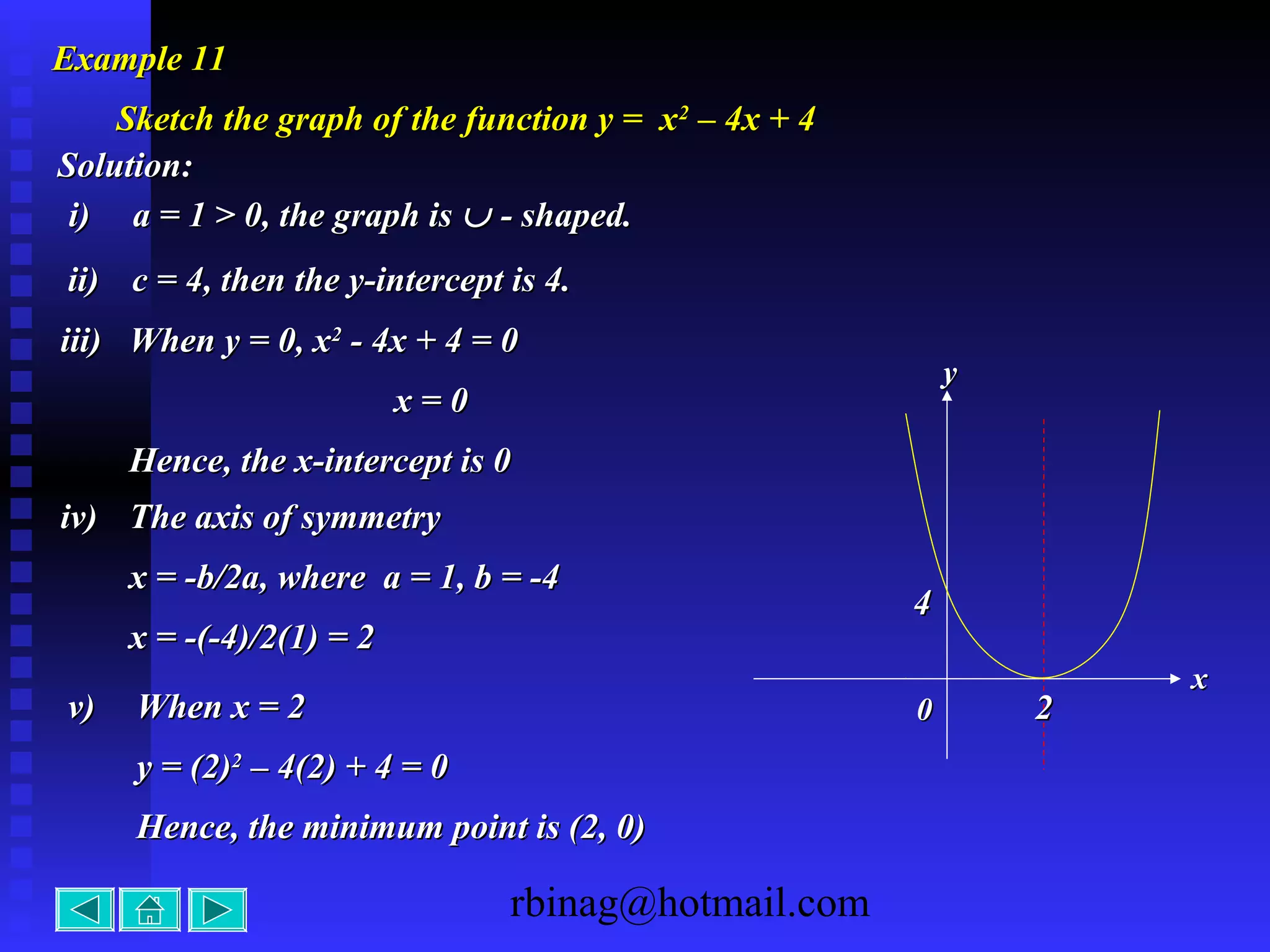
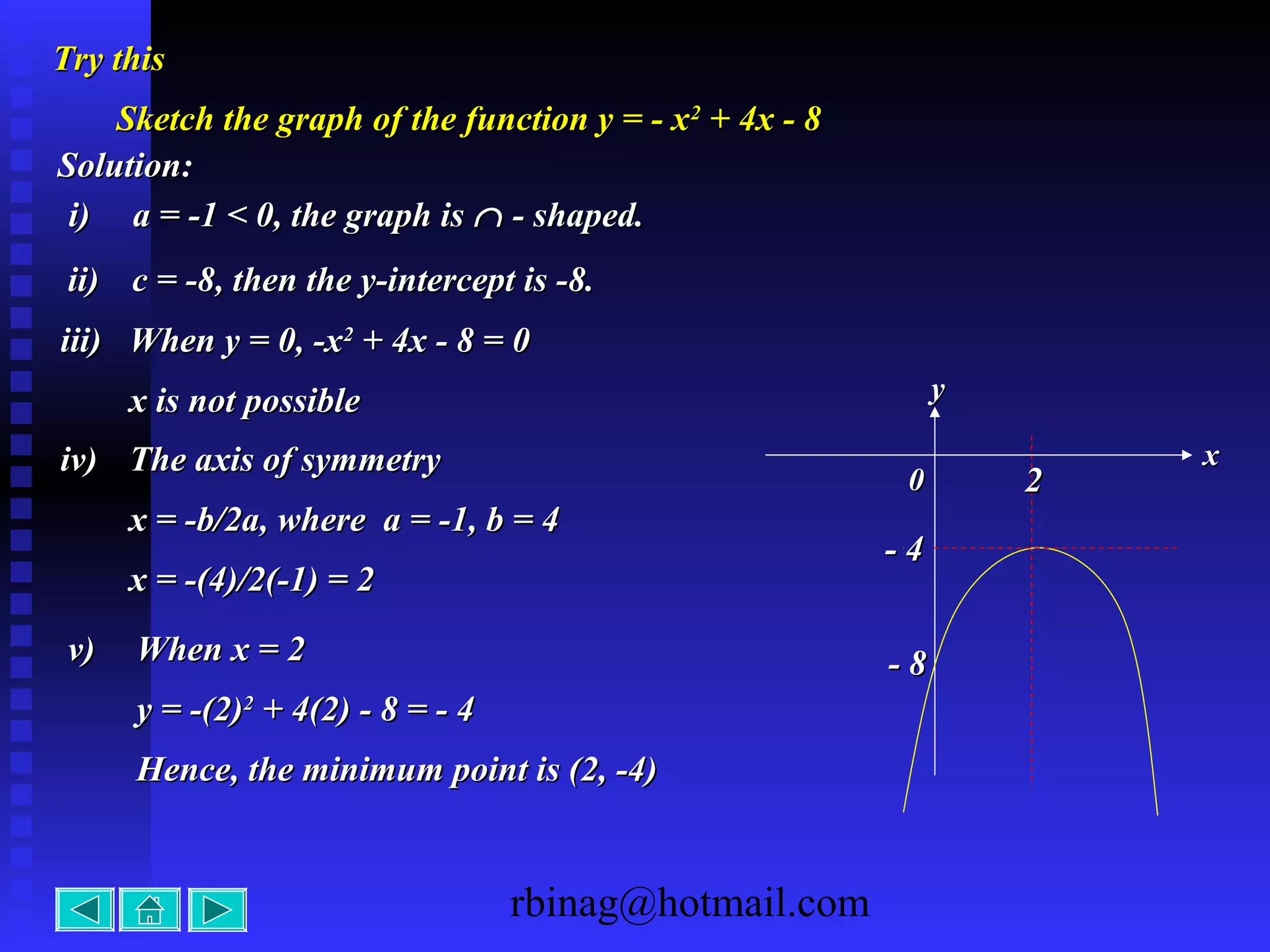
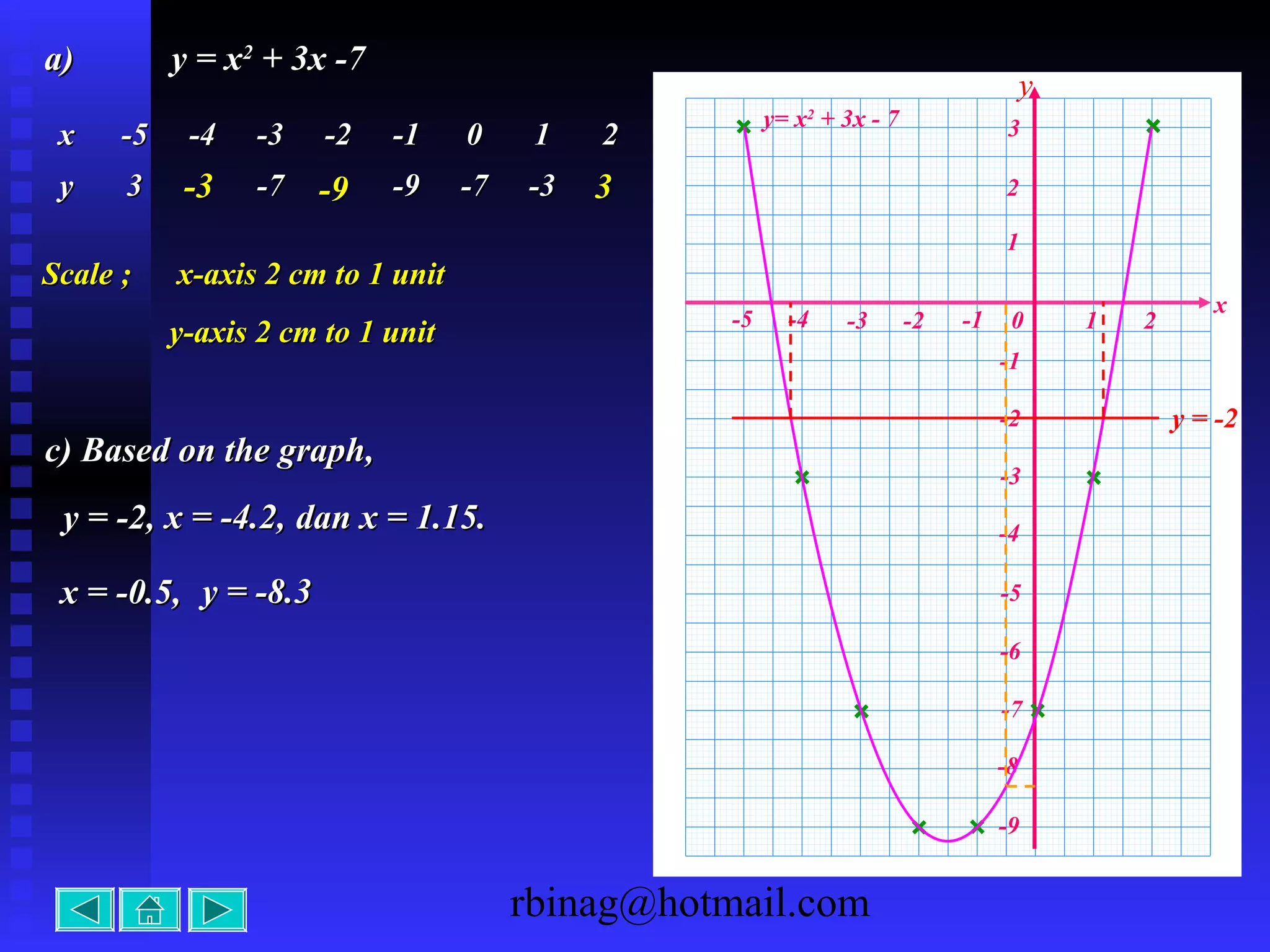
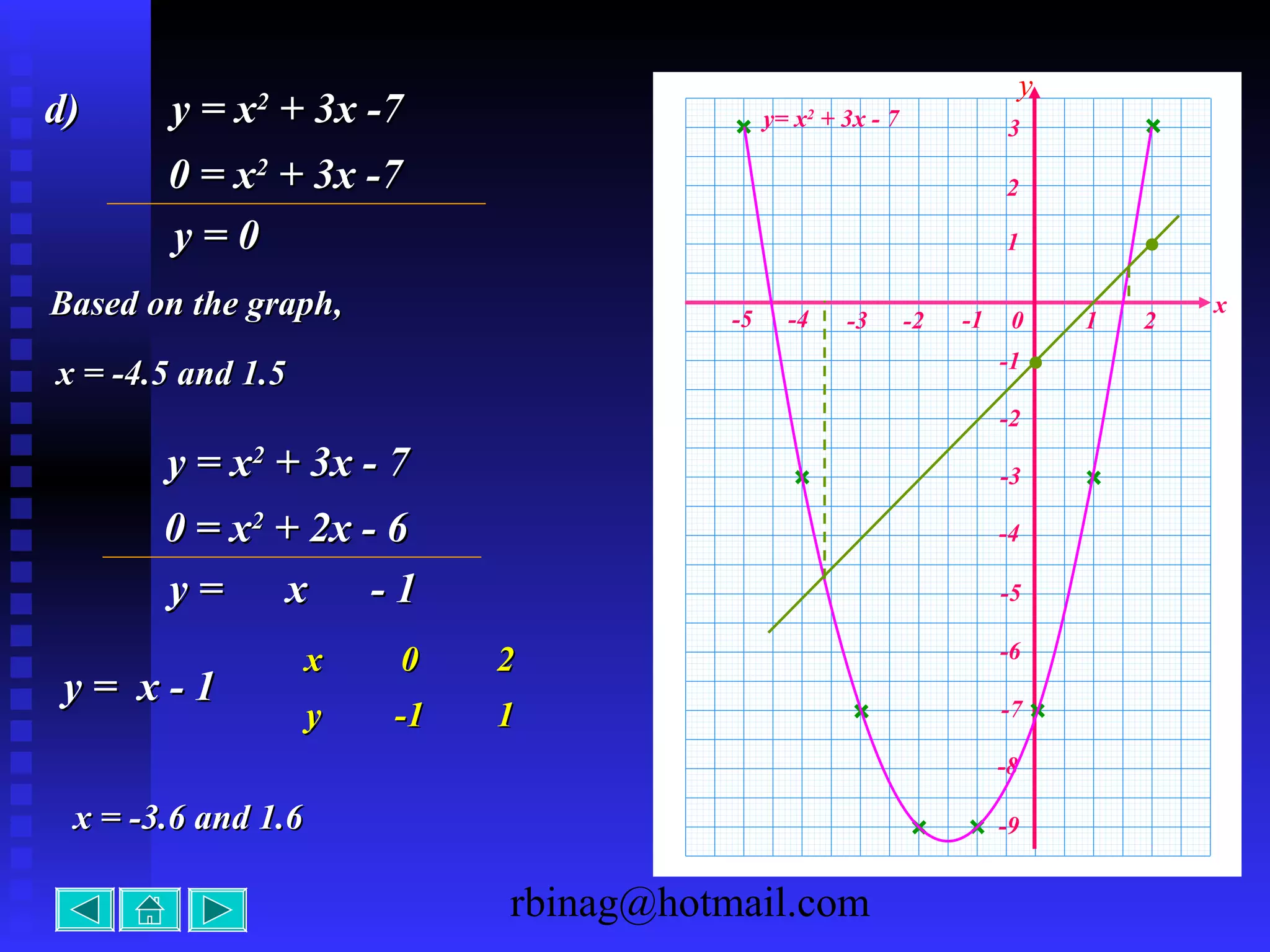
2) Quadratic functions, which produce parabolas. The direction of opening and intercepts are used to sketch the graph.
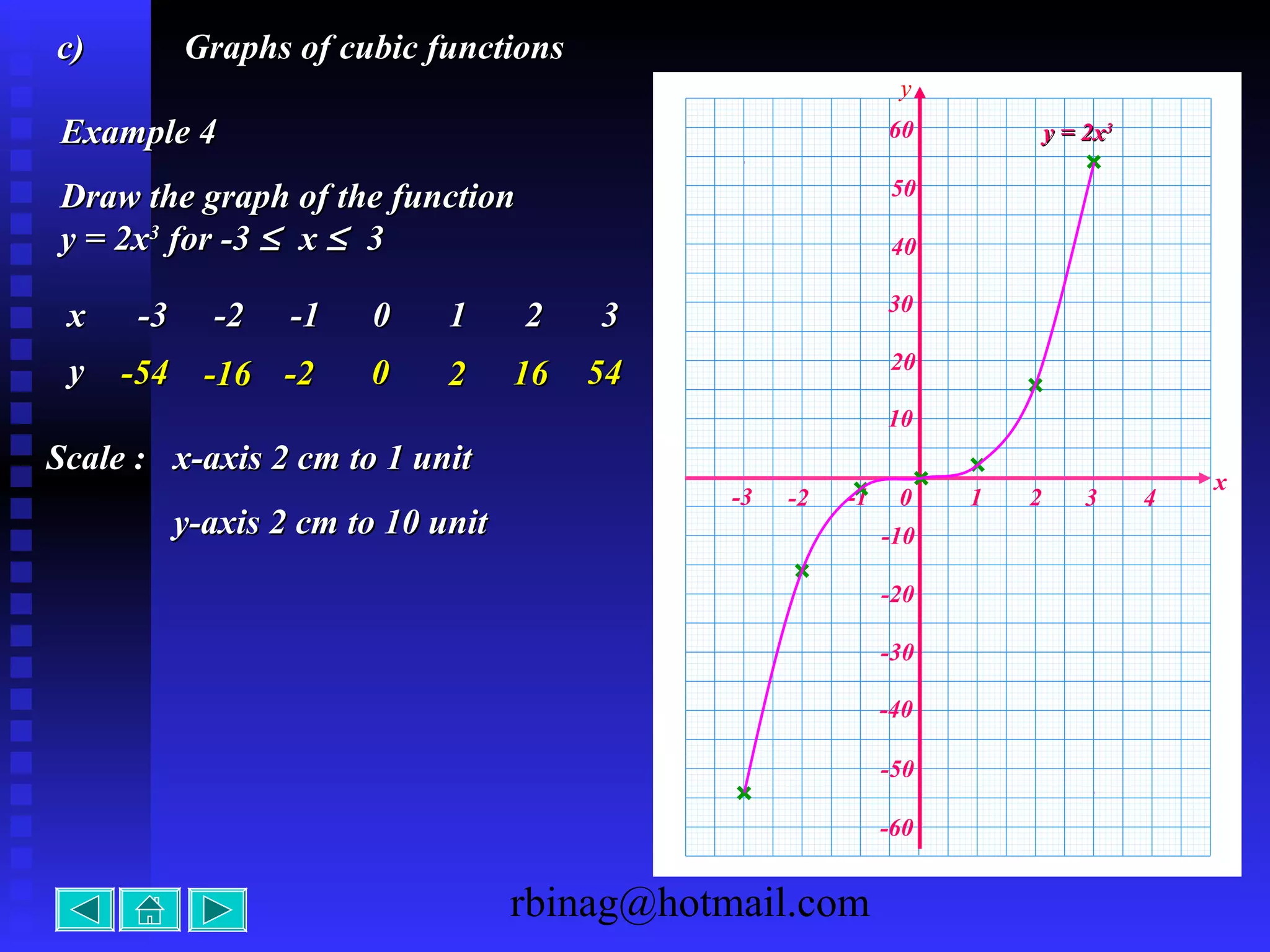
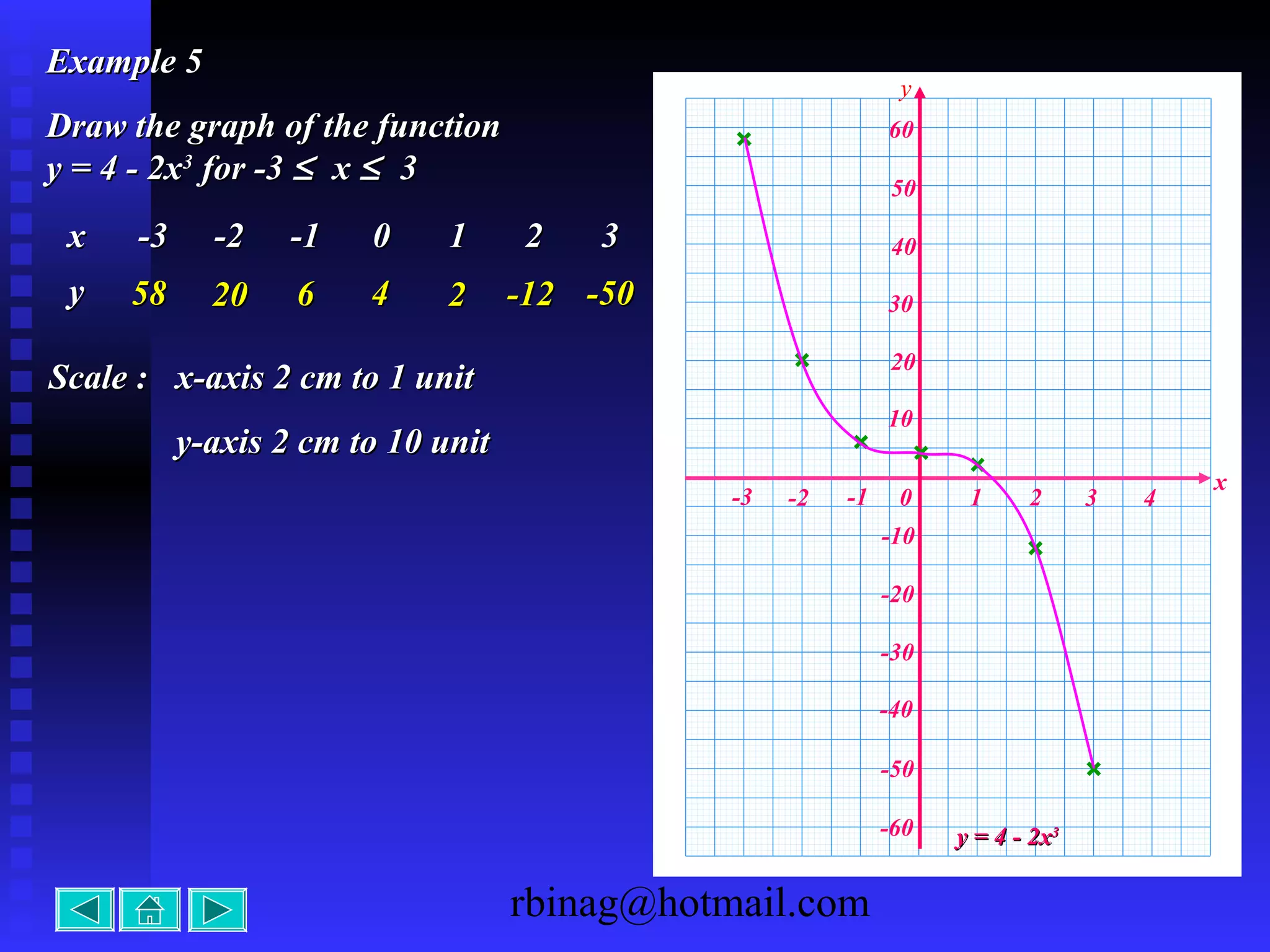
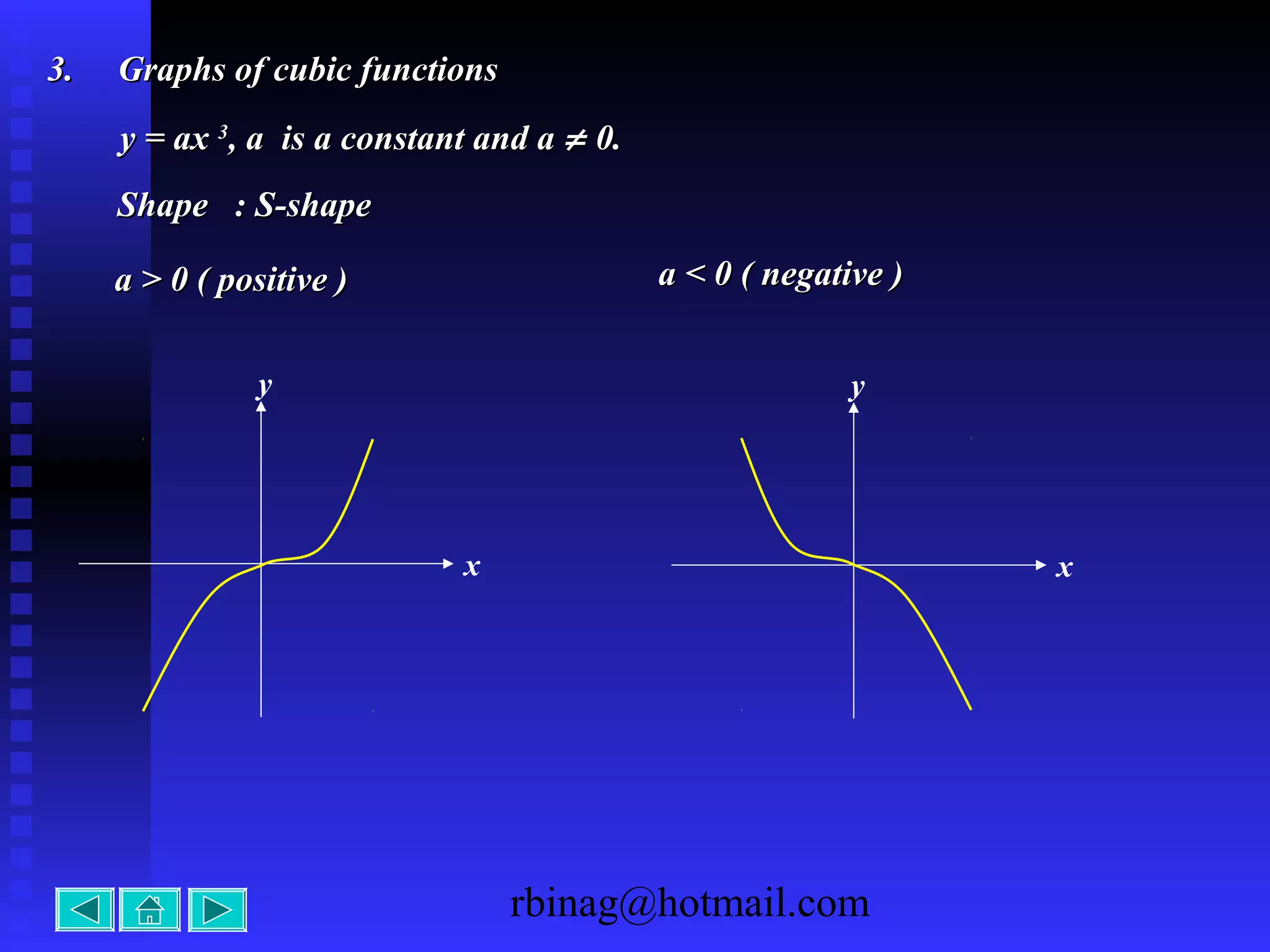
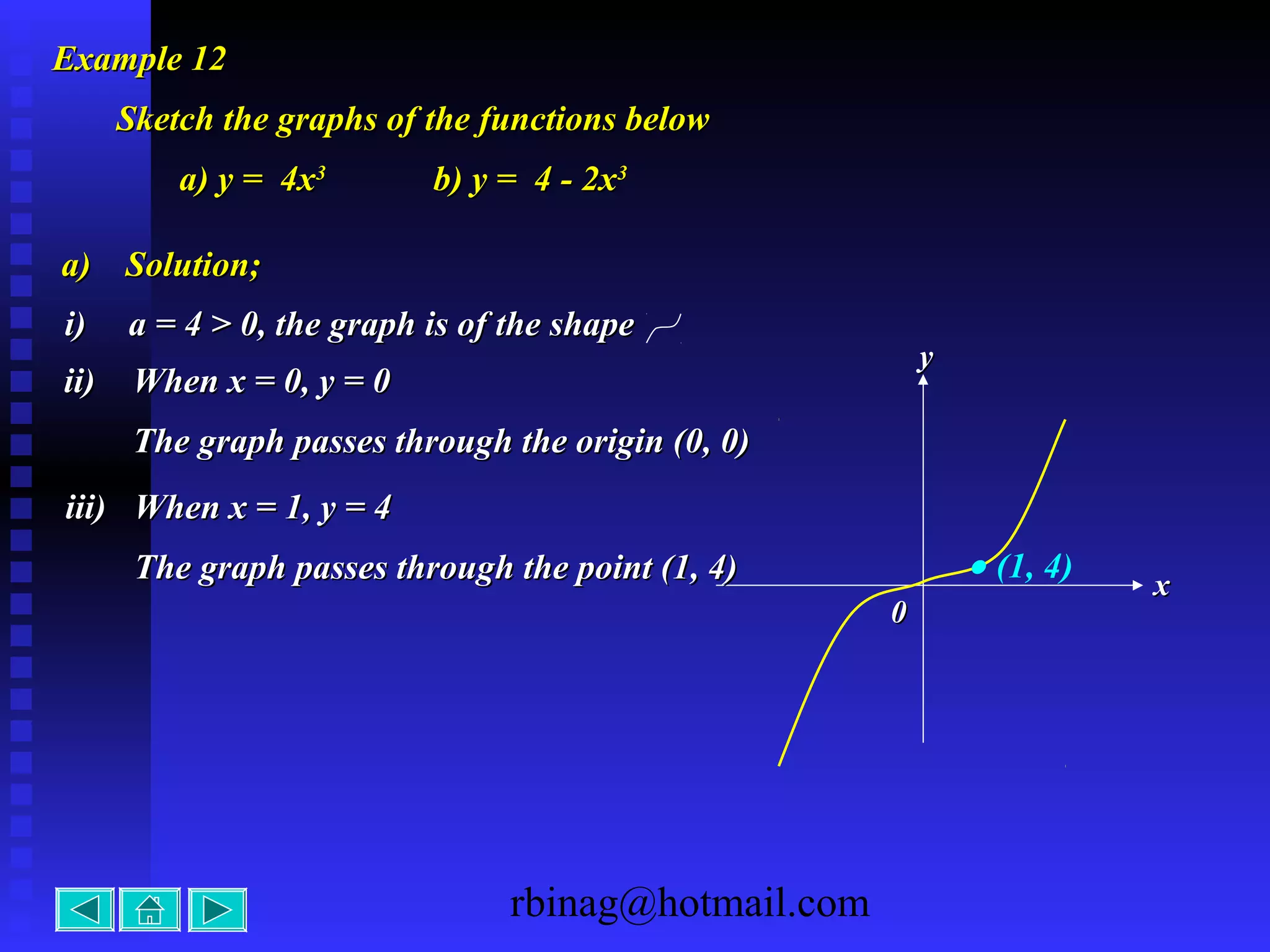
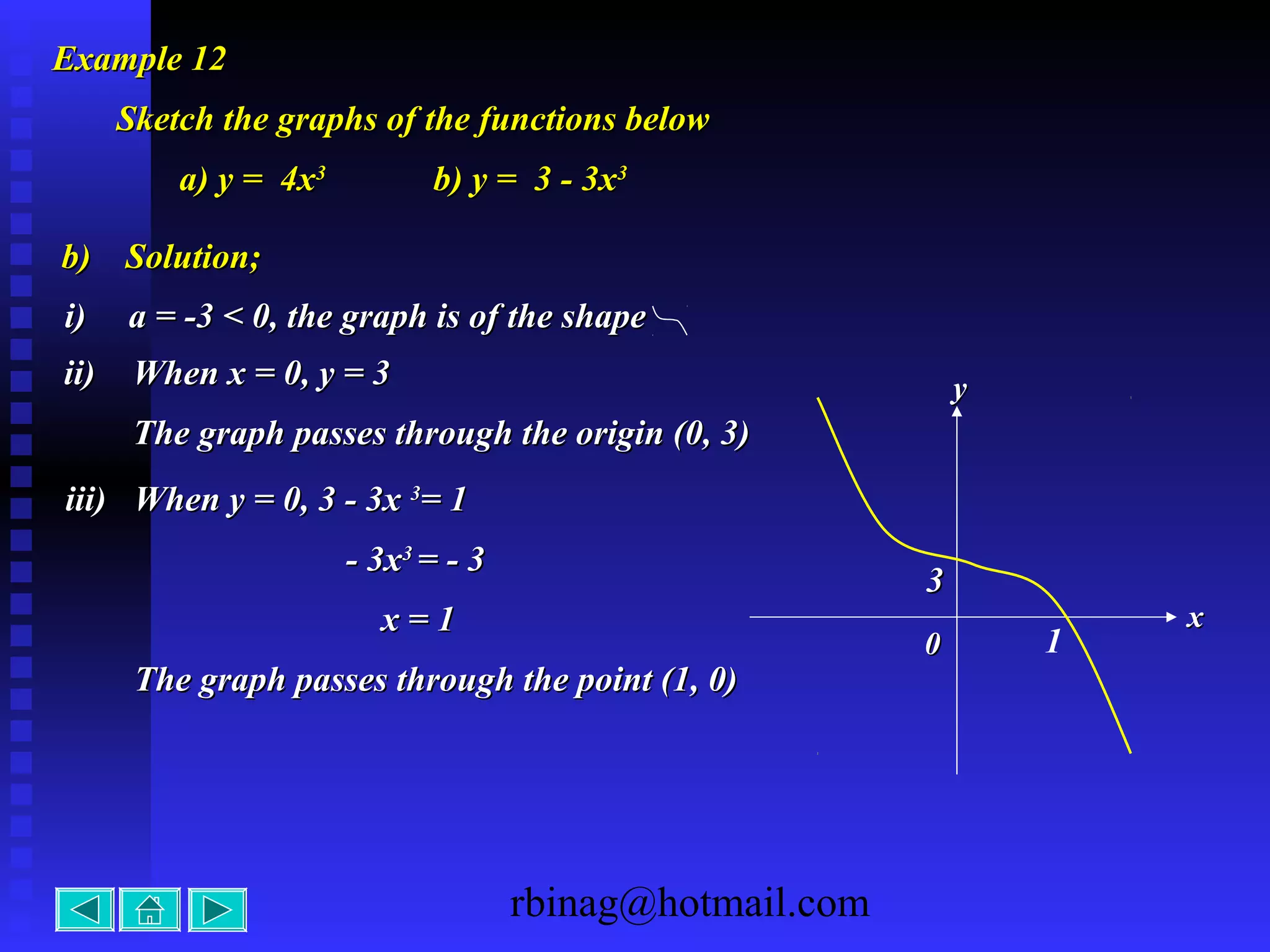
3) Cubic functions, which produce S-shaped curves. The direction of turning and intercepts are considered.
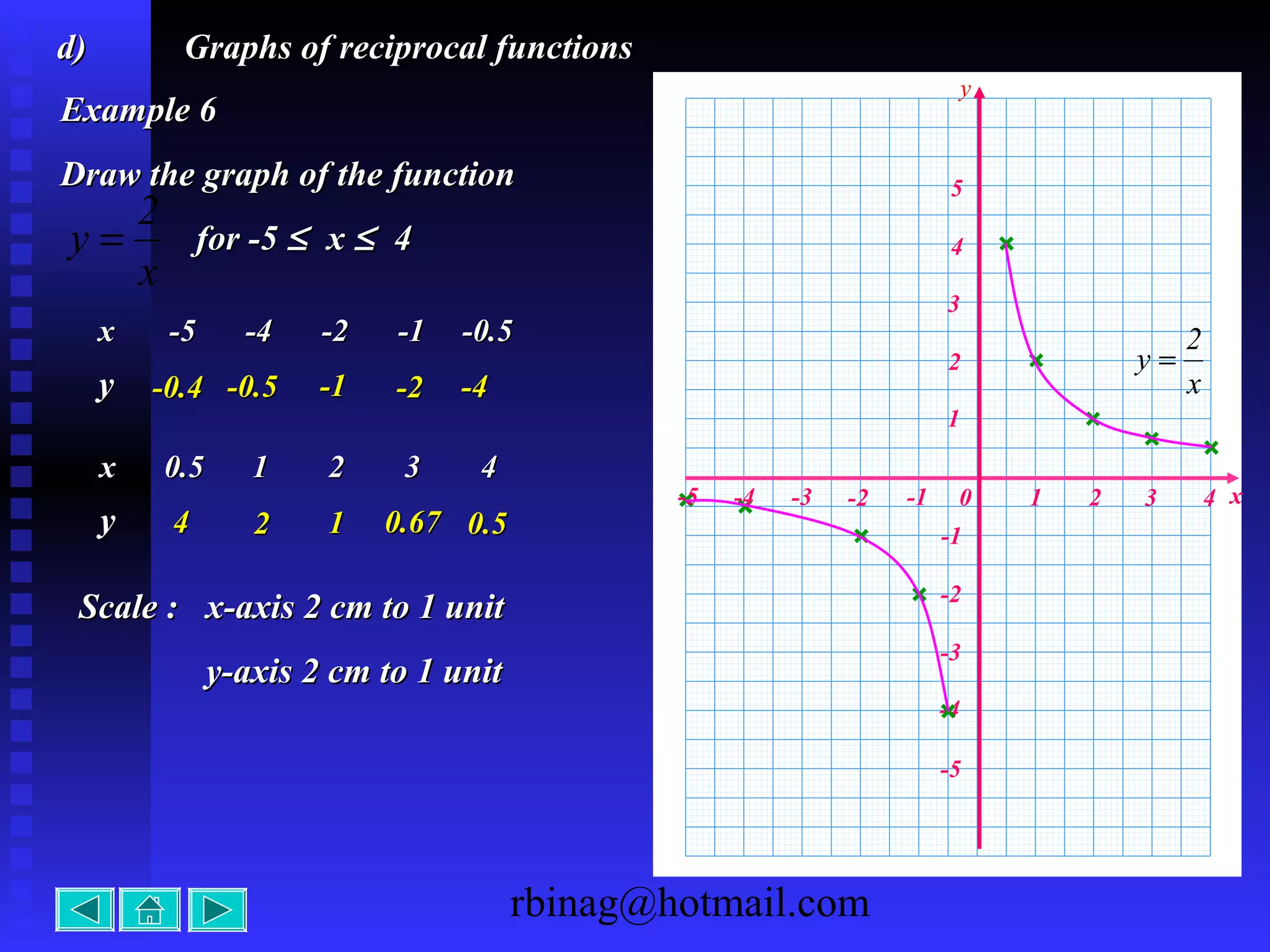
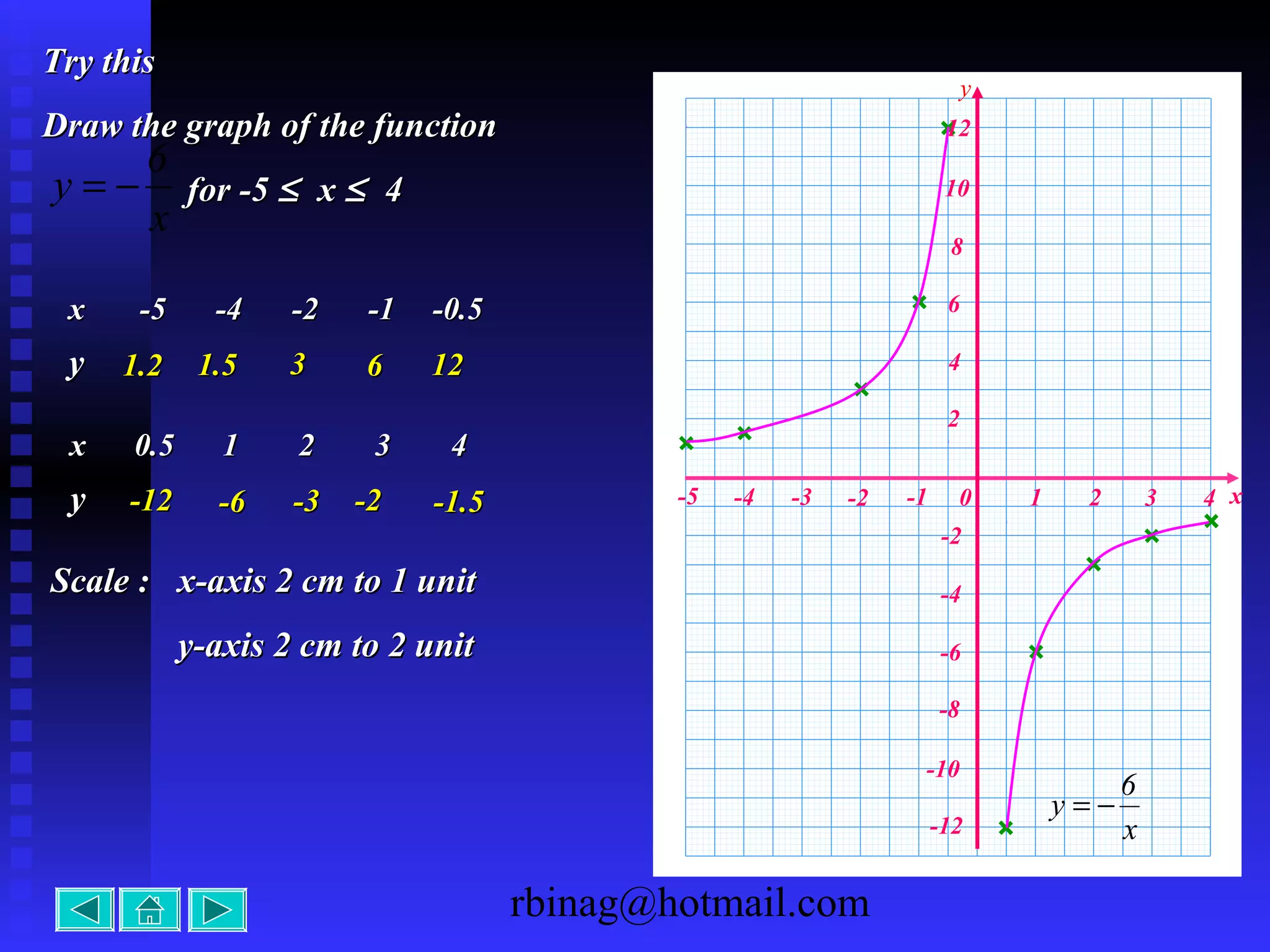
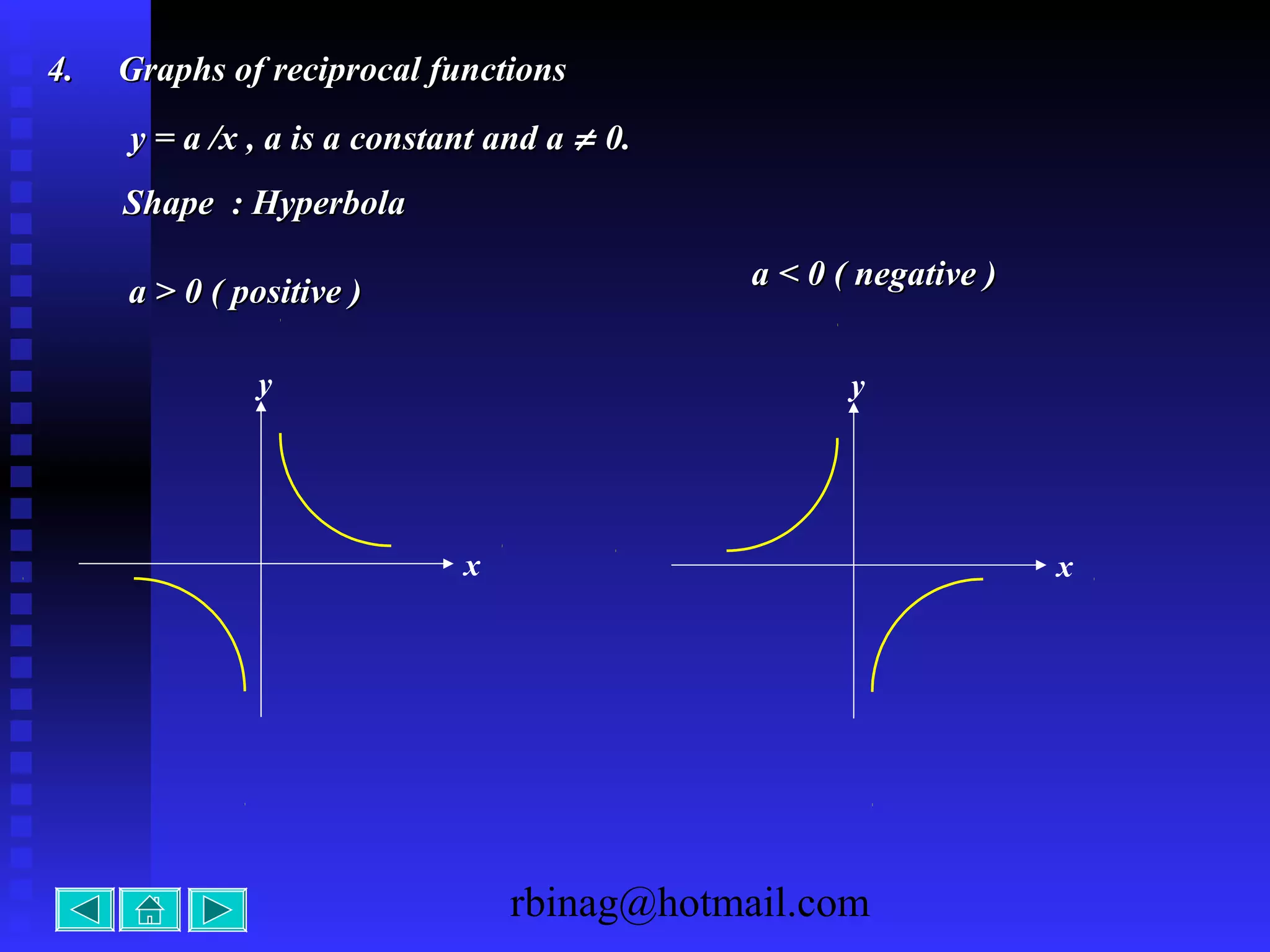
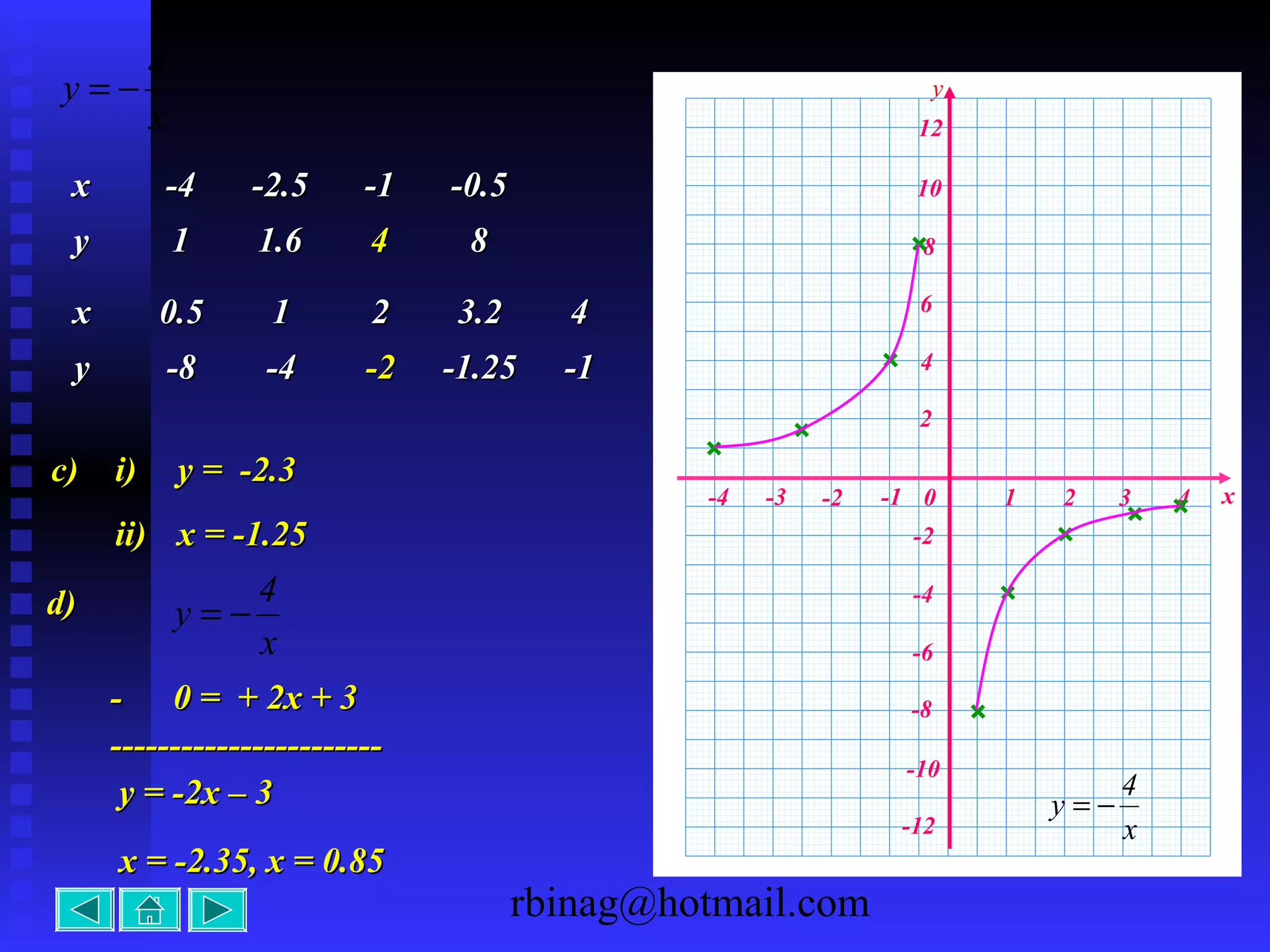
4) Reciprocal functions, which produce hyperbolas. The direction and intercepts are the key factors for the graph.
Step-by-step methods are outlined for accurately sketching graphs of each function type based on their defining characteristics.