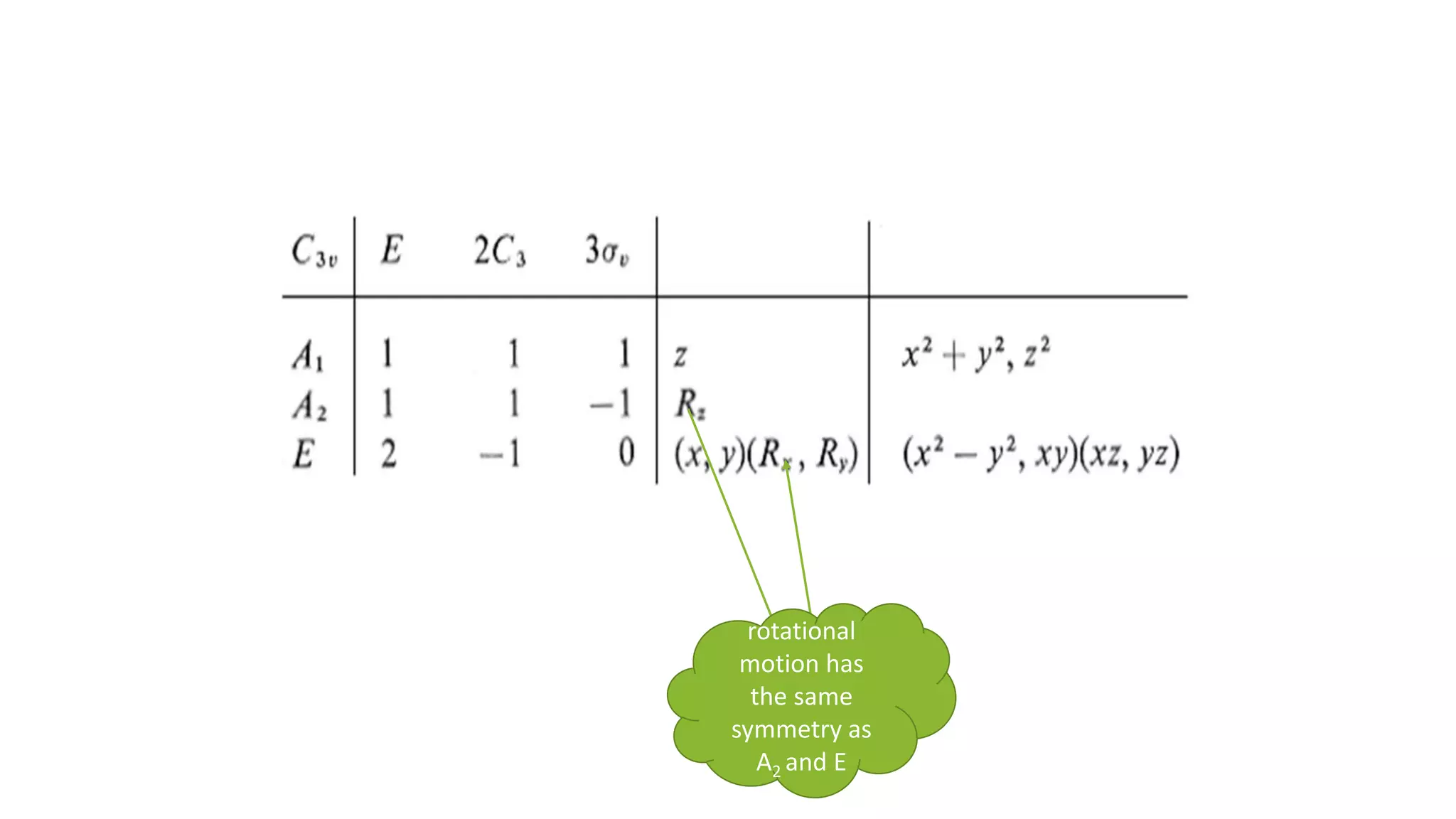
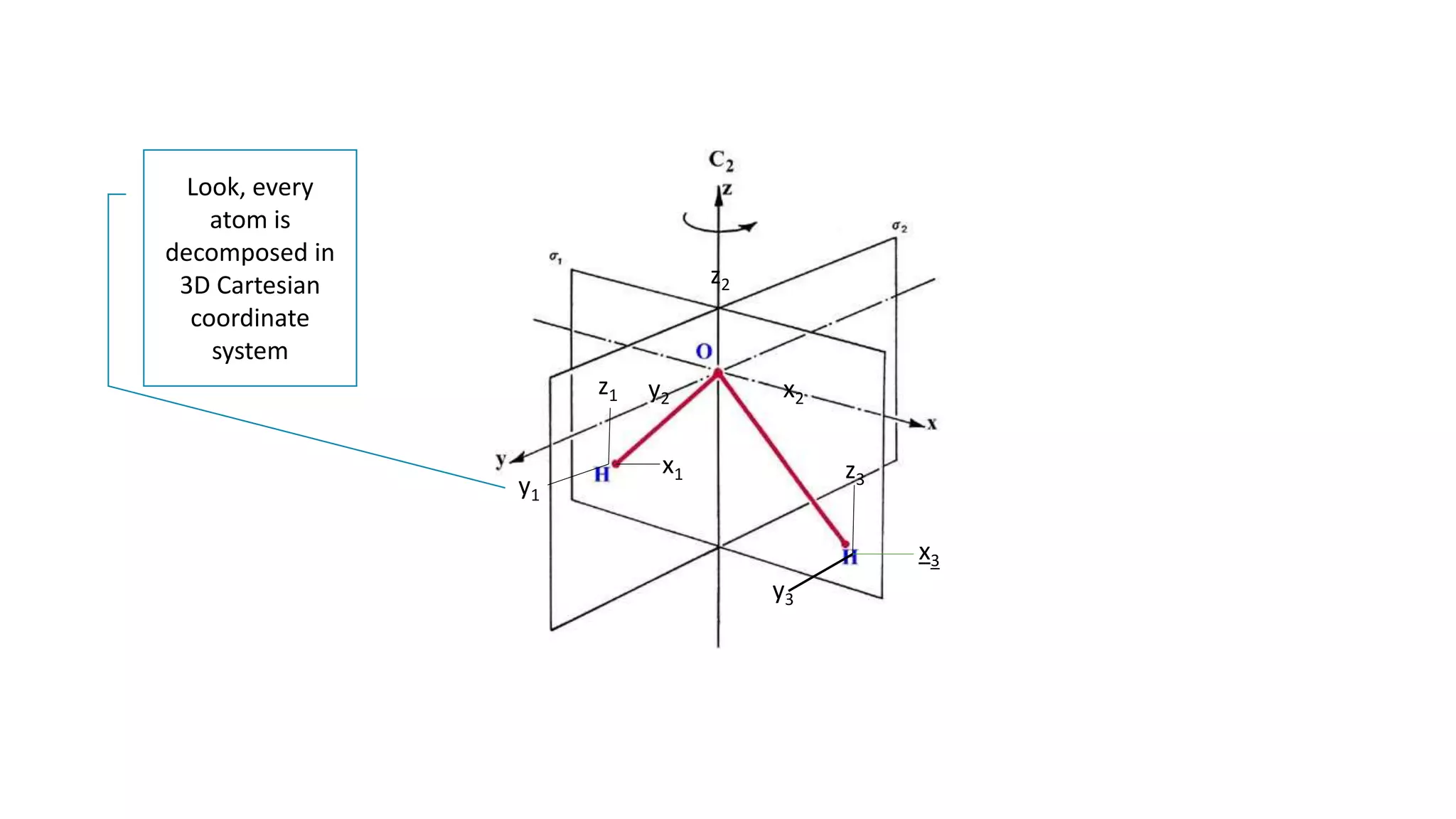
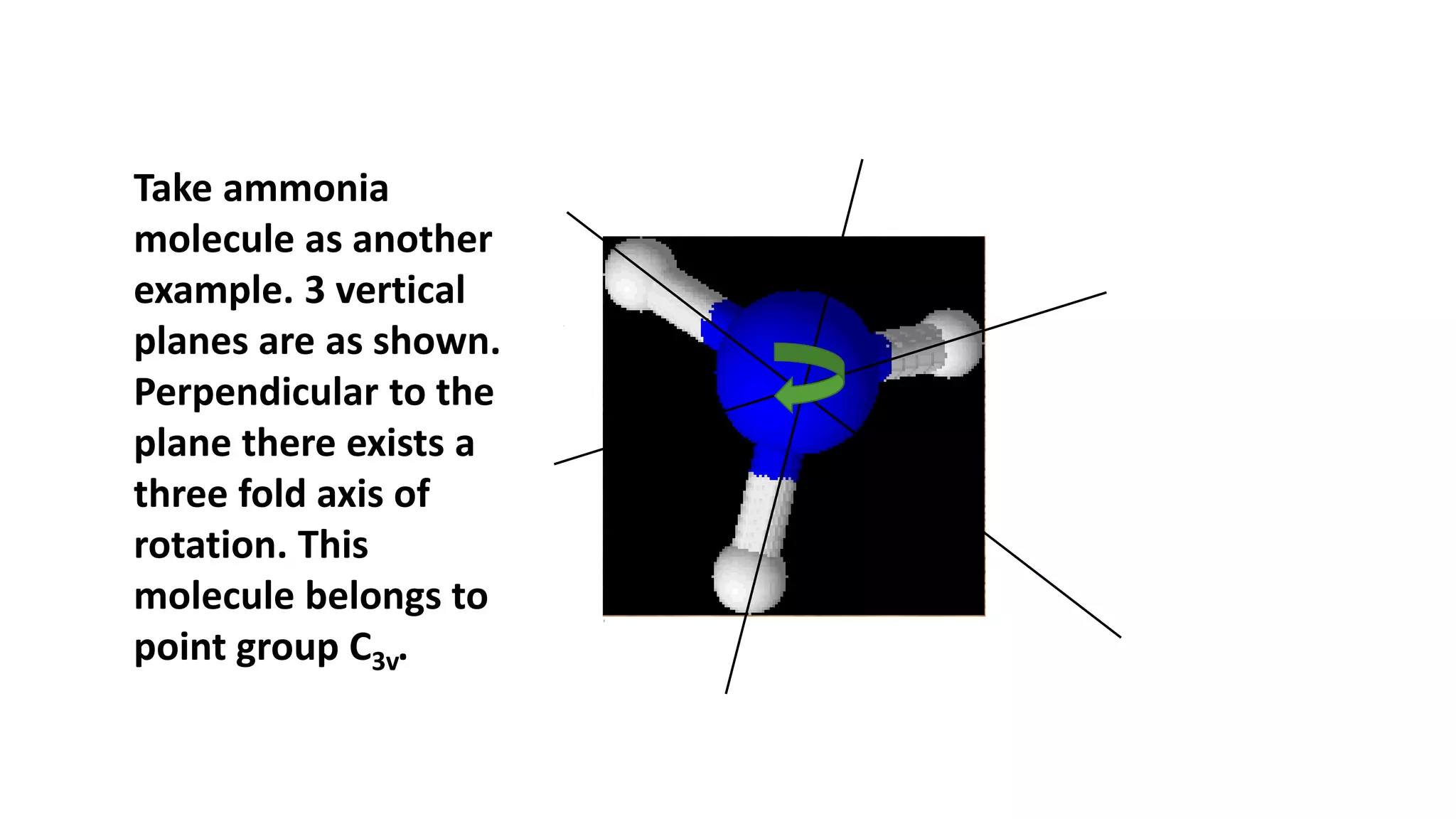
The document outlines how to read a character table in vibrational spectroscopy, detailing the process of utilizing group theory to analyze molecular vibrations and their associated infrared (IR) and Raman activities. It explains the steps needed to identify a molecule's point group and decomposes the reducible representations into irreducible ones using a character table, with specific examples provided using the water molecule. The document also addresses the predictions of IR and Raman active vibrations based on changes in dipole moment and polarizability.

1. How to read a character
table!...............Part 3
character table In vibrational
spectroscopy
DR. SOURABH MUKTIBODH
PROFESSOR OF CHEMISTRY
DEPARTMENT OF HIGHER EDUCATION
GOVT. OF MADHYA PRADESH
INDIA

2. IR spectral data are the blue-print of molecular
vibrations. Group theory provides an inner vision
for analysis of such vibrations and concrete
theoretical base.

3. Vibrational spectroscopy
1. We know that the molecules vibrate with characteristic frequencies.
2. These frequencies match to the IR region of electromagnetic
radiation.
3. Molecular vibrations are nothing but the relative motions of atoms
with respect to each other.
4. Thus molecular vibrations actually define the energy states of the
molecules, which are of-course quantized.
5. Group theory can help us to identify which molecular vibrations can
really exist.

4. How can this be done
1. Identify the point group of the molecule.
2. Generate reducible representations by considering every
atom of the molecule in a 3D Cartesian coordinate.
3. Refer to thee character table of the molecule concerned.
4. Decompose the reducible representations as the sum of
irreducible representation, using standard reduction
formula.
5. Subtract rotational and translational representations from
this, taking help of character table.
6. Remaining representations are corresponding vibrational
symmetries.
7. Again taking help from character table, predict IR and
Raman activity of molecular vibrations.

5. Let us start with a simple molecule of point
group C2v –Water molecule
Z axis,
C2, v
v’

6. And the character table for water molecule is-
C2v E C2 v v’
A1 1 1 1 1 Z X2 y2 z2
A2 1 1 -1 -1 Rz xy
B1 1 -1 1 -1 X, Rx xz
B2 1 -1 --1 1 Y, Ry yz

7. x1 z3
x3
z2
x2y2
z1
y1
y3
Look, every
atom is
decomposed in
3D Cartesian
coordinate
system

8. 1. As every atom has been assigned Cartesian coordinates, obviously
we need to construct a 9× 9 order matrix. It will be such that all
diagonal elements will be 1 and off- diagonal elements zero, for
identity.
2. Of-course, character of such a matrix will be 9.
3. This way we are able to observe symmetry transformations for
every atom in a molecule, and thus useful inferences can be drawn
concerning IR and Raman spectroscopy.

9. Transformation of coordinates during symmetry
operation
1. Identity
𝑥1
𝑦1
𝑧1
𝑥2
𝑦2
𝑧2
𝑥3
𝑦3
𝑧3
1 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0
0 0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1 0
1 0 0 0 0 0 0 0 1
=
𝑥1′ 𝑦1′ 𝑧1′ 𝑥2′ 𝑦2′ 𝑧2′ 𝑥3′ 𝑦3′ 𝑧3′
E× E= 9

10. Two fold axis of rotation- C2 symmetry
1. During this operation hydrogen 1 is replaced by hydrogen 3 and
oxygen atom labelled as 2, remains un-shifted.
2. We also notice that as the rotation is carried out along z axis, there
will be no change in its coordinates of isolated atoms, however,
there is a complete reversal of x and y axis. The character of 1, in
such a case transforms to -1.
3. C2=
−1 0 0
0 −1 0
0 0 1
x goes to –x
y goes to –y
z remains un
changed.

11. Transformation of coordinates during symmetry
operation
2. rotation by 1800 (C2)
𝑥1
𝑦1
𝑧1
𝑥2
𝑦2
𝑧2
𝑥3
𝑦3
𝑧3
0 0 0 0 0 0 −1 0 0
0 0 0 0 0 0 0 −1 0
0 0 0 0 0 0 0 0 1
0 0 0 −1 0 0 0 0 0
0 0 0 0 −1 0 0 0 0
0 0 0 0 0 1 0 0 0
−1 0 0 0 0 0 0 0 0
0 −1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0
=
𝑥1′ 𝑦1′ 𝑧1′ 𝑥2′ 𝑦2′ 𝑧2′ 𝑥3′ 𝑦3′ 𝑧3′
C2 ×
(C2)= -1

12. Plane of reflaction (yz)
A plane of reflection bisects the molecule into equal halves. The
coordinates of plane remain unchanged. However, the coordinates,
which are not present in the plane gets reflected. The character of1
goes to -1.
In this case, characters of coordinates y and z are unchanged(i.e. 1),
while that of x goes to -1.
Please note that atom 1 is replaced by atom 3, while atom 2 remains
un-shifted. yz =
−1 0 0
0 1 0
0 0 1

13. Transformation of coordinates during symmetry
operation
1.Reflaction through yz plane (yz )
𝑥1
𝑦1
𝑧1
𝑥2
𝑦2
𝑧2
𝑥3
𝑦3
𝑧3
0 0 0 0 0 0 −1 0 0
0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 1
0 0 0 −1 0 0 0 0 0
0 0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0 0
−1 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0
=
𝑥1′ 𝑦1′ 𝑧1′ 𝑥2′ 𝑦2′ 𝑧2′ 𝑥3′ 𝑦3′ 𝑧3′
yz ×
(yz)= 1

14. Plane of reflection-(xz)
This is also a vertical plane which bisects every atom of water molecule
Into equal halves, but non of the atoms leave their position.
For isolated atoms, characters of x and z are unchanged, but those of y
are reversed. (goes to -1 from +1)
xz=
1 0 0
0 −1 0
0 0 1

15. Transformation of coordinates during symmetry
operation
1.Reflaction through xz plane (xz)
𝑥1
𝑦1
𝑧1
𝑥2
𝑦2
𝑧2
𝑥3
𝑦3
𝑧3
1 0 0 0 0 0 0 0 0
0 −1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0
0 0 0 0 −1 0 0 0 0
0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 −1 0
1 0 0 0 0 0 0 0 1
=
𝑥1′ 𝑦1′ 𝑧1′ 𝑥2′ 𝑦2′ 𝑧2′ 𝑥3′ 𝑦3′ 𝑧3′
xz ×
(xz)= +3

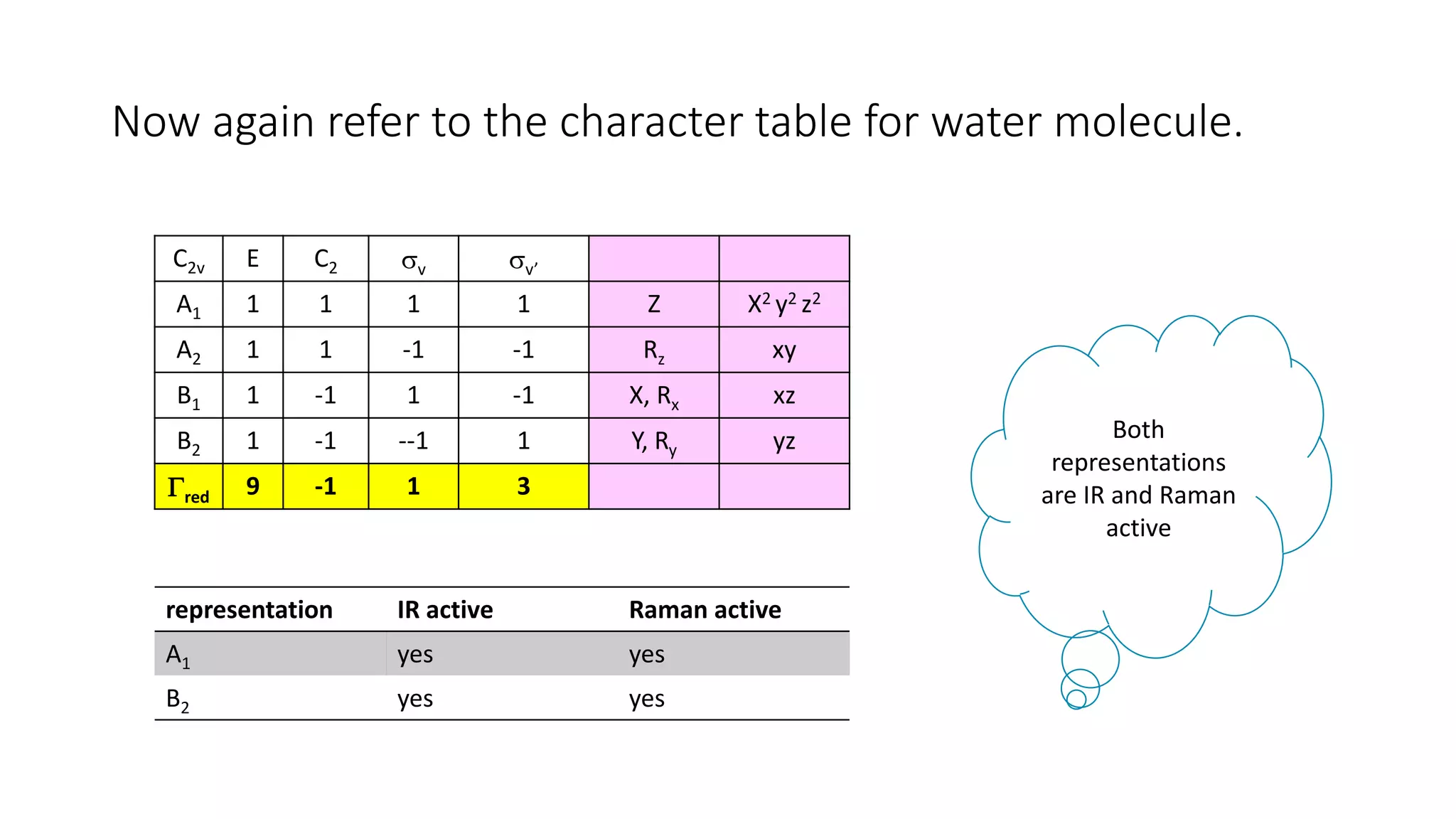
16. This way, the characters obtained for water molecule belongs to
a reducible representation, if every atom is given a 3D basis.
C2v E C2 v v’
A1 1 1 1 1
A2 1 1 -1 -1
B1 1 -1 1 -1
B2 1 -1 --1 1
red 9 -1 1 3
ai= i/h [  I (R)*j(R) ]
Use standard reduction formula
a1= ¼[ 9*1*1+(-1)*1*1+1*1*1+3*1*1]=1/4[9-1+1+3]=1/4*12=3
a2= ¼[ 9*1*1+(-1)*1*1+1*-1*1+3*-1*1]=1/4[9-1-1-3]=1/4*4=1
b1= ¼[ 9*1*1+(-1)*1*1+1*-1*1+3*1*1]=1/4[9+1+1-3]=1/4*8=2
b2= ¼[ 9*1*1+(-1)*-1*1+1*-1*1+3*-1*1]=1/4[9+1-1+3]=1/4*12=3
Clearly
red = 3A1 +A2 +2B1 + 3B2

17. Now again refer to the character table for water molecule.
C2v E C2 v v’
A1 1 1 1 1 Z X2 y2 z2
A2 1 1 -1 -1 Rz xy
B1 1 -1 1 -1 X, Rx xz
B2 1 -1 --1 1 Y, Ry yz
red 9 -1 1 3
Our results are
red = 3A1 +A2 +2B1 + 3B2
We know that a molecule shows 3N type of motions (which include rotational
vibrational and translational). If we are interested in fundamental modes of vibrations,
than 3 for rotation and 3 for vibration (along x,y,z, coordinates). Finally total
fundamental modes of vibrations left are
3N-6

18. Now again refer to the character table for water molecule.
C2v E C2 v v’
A1 1 1 1 1 Z X2 y2 z2
A2 1 1 -1 -1 Rz xy
B1 1 -1 1 -1 X, Rx xz
B2 1 -1 --1 1 Y, Ry yz
red 9 -1 1 3
Our results are
red = 3A1 +A2 +2B1 + 3B2
Our solution include total modes of motions, therefore we can state that-
reducible =vibrational +rotational +translational= 3A1 +A2 +2B1 + 3B2
vibrational =3A1 +A2 +2B1 + 3B2 -rotational -translational

19. Now again refer to the character table for water molecule.
C2v E C2 v v’
A1 1 1 1 1 Z X2 y2 z2
A2 1 1 -1 -1 Rz xy
B1 1 -1 1 -1 X, Rx xz
B2 1 -1 --1 1 Y, Ry yz
red 9 -1 1 3
Rotational and translational
representations can be directly
obtained from character table
Rotational representations,
A2, B1 and B2

20. Now again refer to the character table for water molecule.
C2v E C2 v v’
A1 1 1 1 1 Z X2 y2 z2
A2 1 1 -1 -1 Rz xy
B1 1 -1 1 -1 X, Rx xz
B2 1 -1 --1 1 Y, Ry yz
red 9 -1 1 3
Rotational and translational
representations can be directly
obtained from character table
vibrational representations, A1,
B1 and B2

21. Now again refer to the character table for
water molecule.
Now again
vibrational =3A1 +A2 +2B1 + 3B2 -rotational -translational
Therefore, vibrational =3A1 +A2 +2B1 + 3B2 -A2-B1-B2 –A1-B1-B2
• FUNDAMENTAL MODES OF VIBRATIONS ARE= 3*3-6=3
• Check your answer- It is three only.(A and B are one dimensional
representations)
vibrational = 2A1 + B2

22. Predicting IR and Raman active vibrations
1. For a molecular vibration to be observed in the infrared spectrum
(IR active), it must change the dipole moment of the molecule.
The dipole moment vectors have the same symmetry properties as
the cartesian coordinates x, y and z.
2. For a molecular vibration to be observed in the Raman spectra
(Raman active), there must be a change in polarizability of the
molecule.
The polarizability has the same symmetry properties as the quadratic
functions, xy, yz, xz, x2, y2 and z2

23. IR and Raman active vibrations
For water molecule, we have three fundamental modes of vibrations-
1. 2A1 type (doubly degenerate) vibrations.
2. one B2 type
It can be very easily observed from character table, which of the
vibration is IR active or Raman active or both.

24. Now again refer to the character table for water molecule.
C2v E C2 v v’
A1 1 1 1 1 Z X2 y2 z2
A2 1 1 -1 -1 Rz xy
B1 1 -1 1 -1 X, Rx xz
B2 1 -1 --1 1 Y, Ry yz
red 9 -1 1 3
For a molecular vibration to be
observed in the infrared spectrum
(IR active), it must change the
dipole moment of the molecule.
The dipole moment vectors have
the same symmetry properties as
the cartesian coordinates x, y and
z.
IR active vibration

25. Now again refer to the character table for water molecule.
C2v E C2 v v’
A1 1 1 1 1 Z X2 y2 z2
A2 1 1 -1 -1 Rz xy
B1 1 -1 1 -1 X, Rx xz
B2 1 -1 --1 1 Y, Ry yz
red 9 -1 1 3
For a molecular vibration to be
observed in the Raman spectra
(Raman active), there must be a
change in polarizability of the
molecule.
The polarizability has the same
symmetry properties as the
quadratic functions, xy, yz, xz, x2,
y2 and z2
Raman active vibrations A1and
B2 representations

26. Now again refer to the character table for water molecule.
C2v E C2 v v’
A1 1 1 1 1 Z X2 y2 z2
A2 1 1 -1 -1 Rz xy
B1 1 -1 1 -1 X, Rx xz
B2 1 -1 --1 1 Y, Ry yz
red 9 -1 1 3
representation IR active Raman active
A1 yes yes
B2 yes yes
Both
representations
are IR and Raman
active

27. Indeed such vibrations are found in IR and
Raman spectra
1. Symmetric
stretching
vibrations
2. Bending vibration
3. Antisymmetric
stretching vibration

28. But the entire procedure described is
cumbersome, is in it?
• For water molecule, we have constructed a 3×
3 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛 matrices, for 3 atoms of the molecule.(each atom is
decomposed in 3 dimension Cartesian coordinates).
• Think had it been a Benzene molecule, for 12 atoms of C6H6, matrices
of 36× 36 𝑜𝑟𝑑𝑒𝑟 𝑚𝑎𝑡𝑟𝑖𝑥 𝑤𝑜𝑢𝑙𝑑 𝑏𝑒 𝑟𝑒𝑞uired.
• Clearly this transformation and manipulation is not easy to work out.
Than what to do?

29. 1. We have observed that characters of only those atoms become
important, which remain un-shifted during a symmetry
operation.(others do not come in the diagonal of the matrix ).
2. Now number of un-shifted atoms contribute in the character of that
symmetry operation only.
3. Recall that every symmetry operation has a matrix representation

30. Contribution of character per un-shifted atoms
• E=
1 0 0
0 1 0
0 0 1
i =
−1 0 0
0 −1 0
0 0 −1
(cn)z
𝑐𝑜𝑠 𝑠𝑖𝑛 0
−𝑠𝑖𝑛 𝑐𝑜𝑠 0
0 0 1
(E)= 3 (i)= -3 (Cn)= 2cos +1

31. Contribution of character per un-shifted atoms
• xy=
1 0 0
0 1 0
0 0 −1
yz =
−1 0 0
0 −1 0
0 0 −1
(Sn)z=
𝑐𝑜𝑠 𝑠𝑖𝑛 0
−𝑠𝑖𝑛 𝑐𝑜𝑠 0
0 0 1
(xy)= 1 (yz)= 1 (Sn) = 2cos -1

32. Contributed of character per un-shifted atom
Symmetry operation Contribution of character per un-
shifted atom
E (Identity) 3
I (Inversion) -3
Cn (rotation along z axis) 2cos +1
Sn (improper rotation) 2cos -1
 (reflaction) 1

33. It is the easiest way to compute reducible for
any molecule.
• Again, let us apply for earlier problem of water molecule.
Symmetry
operation
Un-shifted
atoms
Contribution of
character per un-
shifted atom
Total
E All three 3 9
C2 One (oxygen
atom)
2cos180+1= 0 -1
yz one 1 1
xz All three 1 3
Result is same as described earlier

34. Take ammonia
molecule as another
example. 3 vertical
planes are as shown.
Perpendicular to the
plane there exists a
three fold axis of
rotation. This
molecule belongs to
point group C3v.

35. reducible for this molecule can be obtained
easily
Symmetry
operation
Un-shifted
atoms
Contribution of
character per
un-shifted atom
total
E All 4(1 N and 3
H)
3 12
C3 One (only N
atom)
2cos120+1=0 0
 Two(lying in the
plane)
1 2

36. Character table for point group C3v is as
following
 red 12 0 2

37. Next we have to decompose reducible
representations as the sum of irreducible rep.
• A1 = 1/6[12*1*1 + 0*1*2 + 2*1*3]= 1/6[12+0+6]= 3
• A2 = 1/6[12*1*1 + 0*-1*2 +2*-1*3]= 1/6[12+0-6]= 1
• E = 1/6[12*2 +0*0*2 + 2*0*3] =1/6[24+0+0]=4
• Final solution is
• red = 3A1+A2+4E How can we see that
this solution has no
computational error?

38. Quite easy
• We know that A stands for one-D and E for 2-D.
• Substitute these values in the solution just obtained.
• red = 3A1+A2+4E = 3*1+ 1+ 4*2= 12
• For ammonia molecule, 4 atoms would contribute in total of 3N type
of motions. Thus 12 such motions are possible.(4*3)
• We can see that this is a solution which matches to the worked out
exercise.

39. Next step is to identify rotational and
translational motion from character table
translational
motion has
the same
symmetry as
A1 and E

40. rotational
motion has
the same
symmetry as
A2 and E

41. Now again refer to the character table for
water molecule.
Now again
vibrational =3A1 +A2 +4E -rotational -translational
Therefore, vibrational =3A1 +A2 +4E -A1-E-A2-E
• FUNDAMENTAL MODES OF VIBRATIONS ARE= 4*3-6=6
• Check your answer- It is six only.(A one dimensional and E being 2D
representations)
vibrational = 2A1 + 2E

42. Predicting IR and Raman activity
Representation IR Raman
A1 Active, belongs to
Cartesian coordinates
Active, Belongs to binary
product
E Active Active

43. thanks
But many more questions are still unanswered
1. We are not able to distinguish between the symmetries of stretching
and bending vibrations.
2. Not able to visualize that how molecule will vibrate when is associated
with a particular representation.
3. Not able to link the experimental data with theoretical considerations.
For that we will have to go in further details of –
Normal coordinate analysis
Coming up next…………………