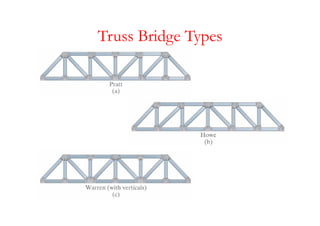
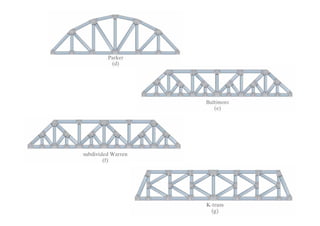
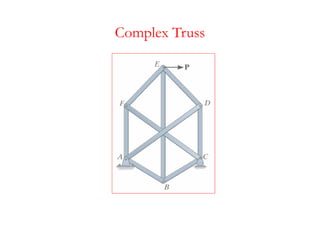
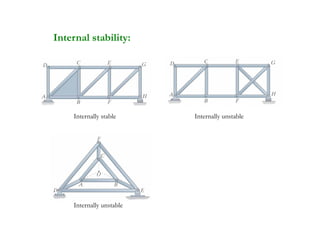
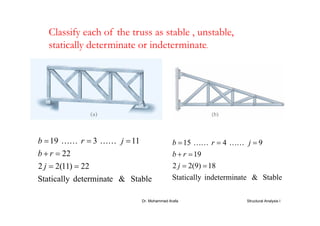
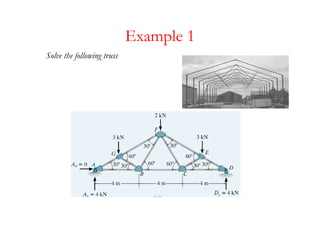
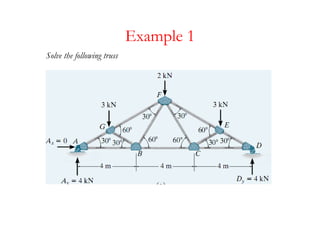
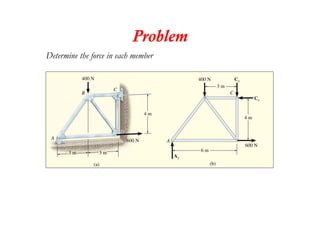
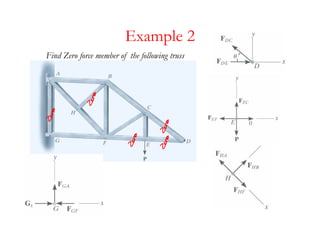
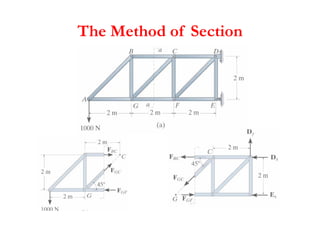
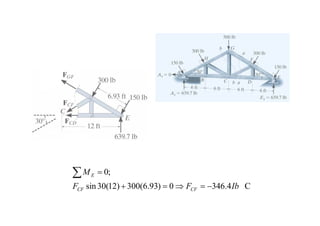
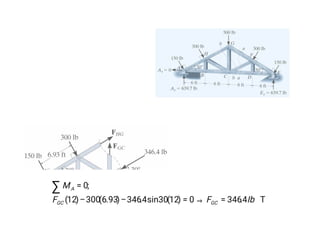
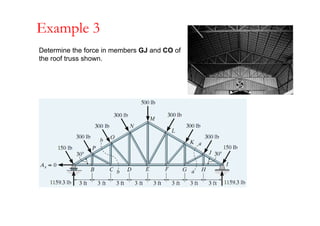
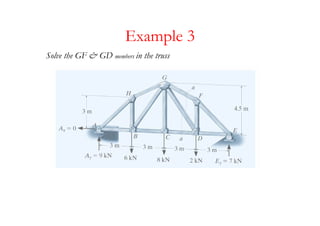
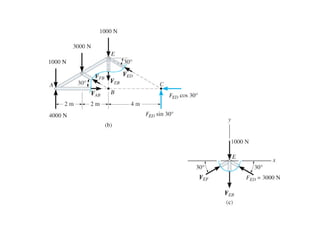
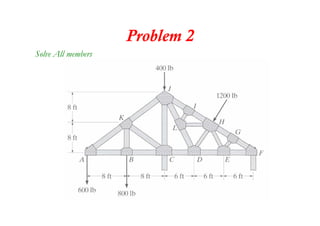
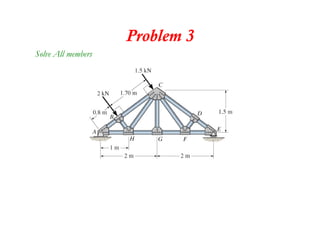
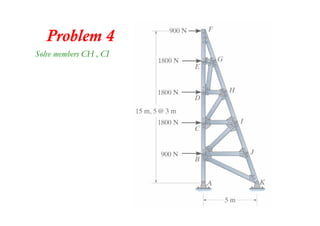
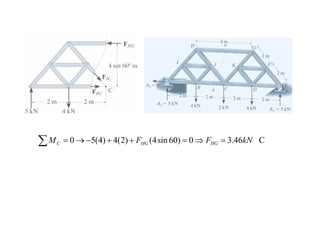
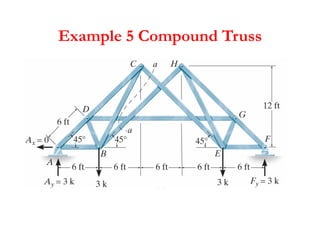
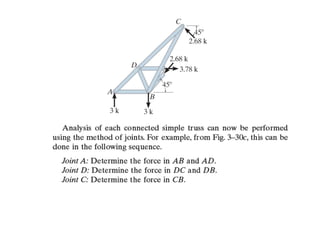
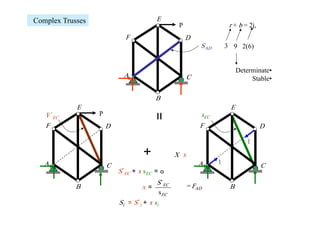
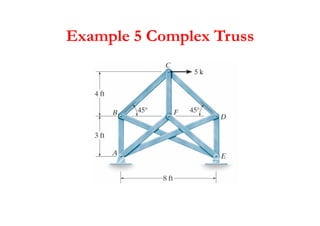
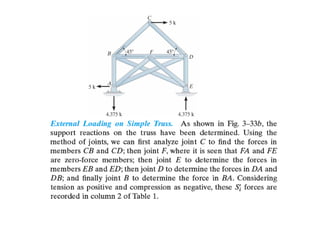
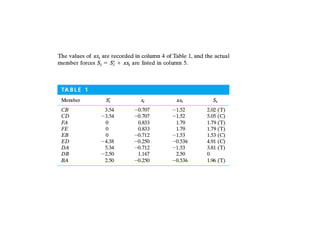
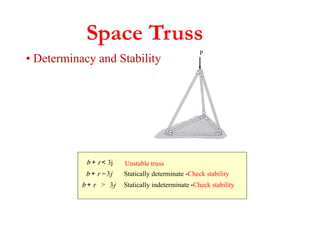
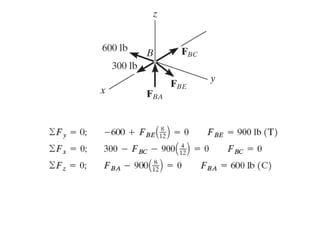
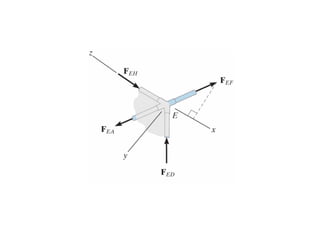
The document discusses various types of trusses used in building structures including simple trusses, compound trusses, and complex trusses. It also covers the assumptions made in truss analysis, classifications of trusses based on stability and determinacy, and different methods for analyzing trusses including the method of joints, method of sections, and analyzing zero force members. Several examples are provided to demonstrate how to apply these analysis methods to solve for unknown member forces in various truss configurations.

1. Chapter 3Chapter 3
TrussesTrusses

2. Trusses in Building

3. Trusses Types for Building
Structural Analysis IDr. Mohammed Arafa

6. ٦ Chapter 2 Dr. Mohammed Arafa

8. Truss Bridge

9. Truss Bridge Types

13. Assumptions for Design
 All members are connected at both ends by smooth
frictionless pins.
 All loads are applied at joints (member weight is
negligible)
 Centroids of all joint members coincide at the joint.
 All members are straight.
 All load conditions satisfy Hookeís law.

14. Classification of coplanar Truss
Simple Truss

15. Compound Truss

16. Stability of Compound Truss

17. Complex Truss

18. Determinacy
For plane truss
If b+r = 2j statically determinate
If b+r > 2j statically indeterminate
Where
b = number of bars
r = number of external support reaction
j = number of joints

19. Stability
For plane truss
If b+r < 2j unstable
The truss can be statically determinate or indeterminate (b+r >=2j)
but unstable in the following cases:
External Stability: truss is externally unstable if all of its
reactions are concurrent or parallel

20. Internal stability:
Internally stable Internally unstable
Internally unstable

21. Classify each of the truss as stable , unstable,
statically determinate or indeterminate.
Stable&edeterminatStatically
22)11(22
22
11319



j
rb
jrb 
Stable&ateindeterminStatically
18)9(22
19
9415



j
rb
jrb 
Structural Analysis IDr. Mohammed Arafa

22. Stable&edeterminatStatically
12)6(22
12
639



j
rb
jrb 
Unstable
16)8(22
15
8312



j
rb
jrb 

23. STEPS FOR ANALYSIS
1. If the support reactions are not given, draw a FBD of the entire
truss and determine all the support reactions using the
equations of equilibrium.
2. Draw the free-body diagram of a joint with one or two unknowns.
Assume that all unknown member forces act in tension (pulling
the pin) unless you can determine by inspection that the forces
are compression loads.
3. Apply the scalar equations of equilibrium,  FX = 0 and
FY = 0, to determine the unknown(s). If the answer is
positive, then the assumed direction (tension) is correct, otherwise
it is in the opposite direction (compression).
4. Repeat steps 2 and 3 at each joint in succession until all the
required forces are determined.
The Method of Joints

24. The Method of Joints
Structural Analysis IDr. Mohammed Arafa

25. Example 1
Solve the following truss

26. Example 1
Solve the following truss

27. T93.6030cos8
;0
C8030sin4
;0
KNFF
F
KNFF
F
ABAB
x
AGAG
y







28. C50.6030sin38
;0
C6.2030cos3
;0
KNFF
F
KNFF
F
GFGF
x
GBGB
y






T33.4
093.660cos6.260cos6.2
;0
T6.2060sin6.260sin
;0
KNF
F
F
KNFF
F
BC
BC
x
BFBF
y








29. Problem
Determine the force in each member

30. Zero Force Member
1- If a joint has only two non-colinear members and there is no
external load or support reaction at that joint, then those two
members are zero-force members

31. Zero Force Member
2- If three members form a truss joint for which two of the
members are collinear and there is no external load or reaction at
that joint, then the third non-collinear member is a zero force
member.

32. Example 2
Find Zero force member of the following truss

33. Method of Section

34. The Method of Section

35. 1. Decide how you need to “cut” the truss. This is based on:
a) where you need to determine forces, and, b) where the total
number of unknowns does not exceed three (in general).
2. Decide which side of the cut truss will be easier to work with
(minimize the number of reactions you have to find).
3. If required, determine the necessary support reactions by
drawing the FBD of the entire truss and applying the EofE.
The Method of Section
STEPS FOR ANALYSIS

36. 4. Draw the FBD of the selected part of the cut truss. We need to
indicate the unknown forces at the cut members. Initially we
assume all the members are in tension, as we did when using the
method of joints. Upon solving, if the answer is positive, the
member is in tension as per our assumption. If the answer is
negative, the member must be in compression. (Please note that you
can also assume forces to be either tension or compression by inspection as was
done in the previous example above.)
5. Apply the equations of equilibrium (EofE) to the selected cut
section of the truss to solve for the unknown member forces.
Please note that in most cases it is possible to write one equation
to solve for one unknown directly.

37. Example 2
Solve the CF & GC members in the truss

38. C4.3460)93.6(300)12(30sin
;0
IbFF
M
CFCF
E



40. Determine the force in members GJ and CO of
the roof truss shown.
Example 3

41. Example 2

42. Example 3

43. Example 3
Solve the GF & GD members in the truss

44. C8.10)6(2)3(7)6(3.56sin0
C83.70)3(7)3(6.26cos0
kNFFM
kNFFM
GFGDo
GFGFD





45. Example 4
Solve the ED & EB members in the truss

47. Example 5
Solve the BC & MC members in the K-truss

48. T21750)20()15(29000 IbFFM BCBCL 
TIbFF MBy 12000BJointAt 
TIbFFF MLMLy 29001200120029000
partcuttingtotalFor the


49. TIbF
CIbF
FFF
FFF
MC
MK
MKMCy
MKMCx
1532
1532
0120029000
00
MJointAt
13
2
13
2
13
3
13
3







50. Problem 2
Solve All members

51. Problem 3
Solve All members

52. Problem 4
Solve members CH , CI

53. Example 4 Compound Truss
Solve the truss

54. C46.30)60sin4()2(4)4(50 kNFFM HGHGC 

55. F
& FF
& FF
& FF
& FF
JC
BJBC
IBIJ
HJHI
AIAB





JJoint
BJoint
IJoint
HJoint
AJoint

56. Example 5 Compound Truss

59. Example 5__Compound Truss
Solve the truss

60. F
& FF
EB
ABAE


BJoint
AJoint
AGAF
AE
& FF
F
AJoint
SolveAfter

61. Complex Truss
iii xsSS  '
Force in members
?
0'


x
xsSS ECECEC

62. 1
1
Complex Trusses
+
=
X x
๐=ECsx+EC´S
=x EC´S
ECs
P
A
B
C
DF
E
r + b = 2j,
3 9 2(6)
•Determinate
•Stable
EC´F P
A
B
C
DF
E
AD= F
ADS
ECs
A
B
C
DF
E
isx+i´S=iS

63. Member
AB
AC
AF
FE
BE
ED
FC
EC
'iS is ixs iS
iii xsSS  '
?
0'


x
xsSS ECECEC

64. Example 5 Complex Truss

68. Example 5b

71. P
b + r < 3j
b + r = 3j
Statically indeterminate -Check stability
• Determinacy and Stability
Space Truss
Unstable truss
b + r > 3j
Statically determinate -Check stability

72. •x, y, z, Force Components
Space Truss
222
zyxl 
)(
l
x
FFx 
)(
l
y
FFy 
)(
l
z
FFz 
222
zyx FFFF 

73. x
y
z
y
z
x
y
z
x
z
x
y
x
y
z
yF
zF
zF
xF
xF
zF
yF
short link
y
x
z
roller
z
x
y
slotted roller
constrained
in a cylinder
y
z
x ball-and -socket
Support Reactions

74. Zero Force Member
1- If all but one of the members connected to a joint lie on the
same plane, and provided no external load act on the joint, then
the member not lying in the plane of the other members must
subjected to zero force.
Fz = 0 , FD = 0

75. Zero Force Member
2- If it has been determined that all but two of several members
connected at a joint support zero force, then the two remaining
members must also support zero force, provided they don’t lie a
long the same line and no external load act on the joint.
Fz = 0 , FB = 0
Fy = 0 , FD = 0

76. Example 6__Space Truss
Structural Analysis IDr. Mohammed Arafa

82. Example 7__Space Truss

85. Copyright © 2009 Pearson Prentice Hall Inc.