1. PRML輪読会 2017
第3章 線形回帰モデル
東京⼤学⼤学院⼯学系研究科
技術経営戦略学専攻
松尾研究室
⼤野峻典

2. 構成
3.1 線形基底関数モデル
3.2 バイアス_バリアンス分解
3.3 ベイズ線形回帰
3.4 ベイズモデル⽐較
3.5 エビデンス近似
3.6 固定された基底関数の限界
2

3. はじめに
• これまで：密度推定やクラスタリングなど 教師なし学習
• 今回：教師あり学習。まずは、回帰の問題。
• 回帰
– D次元の⼊⼒変数のベクトル x から、⽬標変数 t の値を予測（ex. 多項式フィッティン
グ@1章）
• 線形回帰モデル
– パラメータに関して線形であり、解析が容易（⼊⼒変数に関しては⾮線形になりうる）
– 単純には：
• 新しい⼊⼒ x に対する値が対応する t の値の予測値となる関数 y(x) を構成
– 確率論的には：
• x に対する t の値の不確かさを表すために予測分布 p(t|x) をモデル化
• 損失関数の期待値を最⼩化するように, 任意の x の新たな値に対する t を予測可能
3

4. 3.1 線形基底関数モデル
• 最も単純な線形回帰モデル
– パラメータ(w)に関して線形
– ⼊⼒変数(x)に関しても線形
– しかし…表現能⼒に乏しい。↓に拡張
• ⼊⼒変数に関して⾮線形な関数の線形結合
– M: パラメータ数
– Φj(X)： 基底関数
– w0：バイアスパラメータ（任意の固定されたオフセット量）
– パラメータwに関しては線形なので、線形モデル
– →簡略化：
4

5. 3.1 線形基底回帰モデル
• 基底関数の例
– 多項式回帰(1章でみた)：Φj(x) = xj
– ガウス基底関数：
– シグモイド基底関数：
• ただし
– フーリエ基底、ウェーブレット…
• 本章での話は基底関数集合の選択に依存しないので、今後特に指定はしない。
5

6. 3.1.1 最尤推定と最⼩⼆乗法
6
• ⽬標変数tを関数がガウスノイズの和で与えられる時を考える
– εは期待値0で精度(分散-1)がβのガウス確率変数
• つまり, tは以下の分布に従う
• ⼊⼒と⽬標値が与えられた時の尤度関数
– t：⽬標変数{tn}をまとめたベクトル
– X: ⼊⼒ {x1 , … , xN}

7. 3.1.1 最尤推定と最⼩⼆乗法
7
• 尤度関数の対数を取って1変数ガウス分布の標準形(1.46)より以下得る.
– ただし⼆乗和誤差関数：
• wに関して最⼤化したいので、微分して 勾配0になる時考える.
• wについてとくと：
– ただし計画⾏列：

8. • t = (t1,…,tN)T
– → N次元空間のベクトル
• y = ΦwML = [φ1,…,φM] wML
– → M次元空間のベクトル（M個のφの線形結合なので）
• Φj = (φj(x1), …, φj(xN))T
– → N次元空間のベクトル
• yはM(<N)次元空間S上のベクトルなので、yとtの距離が最⼩になるのは、t
のSへの正射影の時とわかる.
3.1.2 最⼩⼆乗法の幾何学
8

9. • 1章でやったように, データが⼤きい時は逐次学習（オンライン学習）便利
– η（イータ）は学習率パラメータ. 収束するように適切に選ぶ.
– τ（タウ）は繰り返しの回数.
– 誤差関数に⼆乗話誤差関数を⽤いており、最⼩平均⼆乗アルゴリズム（LMS）と呼ぶ
3.1.3 逐次学習
9

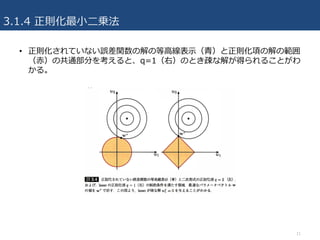
10. 3.1.4 正則化最⼩⼆乗法
10
• 過学習を防ぐため, 誤差関数に正則化項を加える（1.1節）
– （正規化項の最も単純な形）重みベクトルの⼆乗和：
• ↑を⽤いると誤差関数はwの⼆次形式であり, 誤差関数の最⼩値を取る解は閉じた形で求まる.
– データの当てはめに必要と判断されない重みが衰退して0に近づいていく（荷重衰退）
– ⼀般形：

11. 3.1.4 正則化最⼩⼆乗法
11
• 正則化されていない誤差関数の解の等⾼線表⽰（⻘）と正則化項の解の範囲
（⾚）の共通部分を考えると、q=1（右）のとき疎な解が得られることがわ
かる。

12. 3.1.5 出⼒変数が多次元の場合
• wをWとして多次元化（M⾏K列）、tをTとして多次元化（N⾏K列）すると、
対数尤度関数は、
• これを最⼤化するWは,
• 結果は個々の列について評価できる。回帰問題の解は異なる⽬標変数が相互
に影響しないので、疑似逆⾏列 は⼀度計算すれば、全てのベクトルwk
で共有できる。
12

13. 3.2 バイアス-バリアンス分解
• 最尤推定の問題点：
– 過学習を避けるため基底関数の数を限定する → モデルの表現⼒が限られる
– 正規化項を導⼊する → 正則化係数 λ の決定が難しい
– ⇛ これらの問題を回避するためには, ベイズ的なアプローチを⽤いればいい.（3.4節）
• 本節では, （ベイズ的アプローチの前に）まず頻度主義の観点からバイアス
-バリアンスのトレードオフとして知られるモデルの複雑さの問題について
考える.（でベイズに⾏く）
13

14. 3.2 バイアス-バリアンス分解
• 決定理論における標準的な損失関数は⼆乗損失関数で, 最適な予測は条件付
期待値で表せる. (1.5.5節)
• この時, 期待⼆乗損失は以下. (1.5.5節) (h(x)は条件付期待値, y(x)は予測)
• 有限なデータからh(x)を求めているので, y(x) = h(x) とすることは, 未知
のデータに対して期待⼆乗損失を最⼩化する解には, 必ずしもならない…
• 頻度主義的には, データ集合Dによりwが推定されるので予測関数 y(x; D)
とおける。データ集合によって関数が変わり, ⼆乗損失の値も変わる。なの
で, 学習アルゴリズムの性能は, データ集合のとり⽅に関して平均すること
で評価する。
14
y(x)と独⽴でノイズのみに依存y(x)に依存してる.
この項を最⼩化するy(x)が知りたい

15. 3.2 バイアス-バリアンス分解
15
式全体のDに関する期待値を取って
全てのデータ集合のとり⽅に関
する予測値の平均が, 理想的な
回帰関数(条件付平均h(x))から
どれだけ離れているか
各々のデータ集合における解が, 特定の
データ集合の選び⽅に関する期待値の周
りでどれだけ変動するか.
⇛ つまり, データ集合が変わると, 予測
値がどれだけ変わるか
この項を最⼩化するy(x)が知りたい

16. 3.2 バイアス-バリアンス分解
16
この項を最⼩化するy(x)が知りたい
• バイアスとバリアンスをバランスよく⼩さくすることが必要
• 柔軟性の⾼い複雑なモデル：
– バイアス⼩さく, バリアンス⼤きい
• 柔軟性の低い単純なモデル：
– バイアス⼤きく, バリアンス⼩さい
• しかし…データ集合のとり⽅に関する平均にもとづいているが,現実的に場
⾯で1つだけの観測データ集合が与えらると, 有⽤性微妙。
• すべてのデータを1つの⼤きな訓練集合にした⽅が過学習抑制できる。
– ⇛ ベイズ的な線形基底関数の扱い！

17. 3.3 ベイズ線形回帰
• 最尤推定
– モデルの複雑さはデータサイズに依存して適切に決める必要ある
– 正則化項でモデルの複雑さ調整する
– 過学習の可能性
– データをテスト⽤に分けるの計算量もデータももったいない
• ベイズ線形回帰
– パラメータを確率変数として扱う。
– 過学習の回避
– 訓練データだけからモデルの複雑さを⾃動で決定
17

18. 3.3.1 パラメータの分布
• 尤度関数は （3.1節）であり, ガウス分布であ
り指数にwの⼆次の項を持つ。
• wの事前分布を共役なガウス分布として以下のように書ける.
• 事後分布∝尤度関数×事前分布 なのでガウス分布となる. (⼆章より計算)
• 議論を簡単にするため, 期待値0で単⼀精度パラメータαで記述される等⽅的
ガウス分布を本章では考える.
18

19. • 事後分布の対数↑。wに関して最⼤化することは, ⼆乗和誤差関数と⼆次の
正規化項の和を最⼩化することに等しい
3.3.1 パラメータの分布
19

20. 3.3.1 パラメータの分布
20
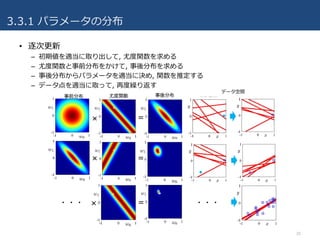
• 逐次更新
– 初期値を適当に取り出して, 尤度関数を求める
– 尤度関数と事前分布をかけて, 事後分布を求める
– 事後分布からパラメータを適当に決め, 関数を推定する
– データ点を適当に取って, 再度繰り返す
データ空間

21. 3.3.2 予測分布
• 実際にはwの値そのものではなく, 新しいxの値に対する t を予測したいこ
とが多い.
• 予測分布：
– ただし
• 結局, 以下の形を取ることがわかる.
21

22. 3.3.2 予測分布
22
例) ガウス基底関数結合モデルのsin(2πx)への当てはめ

23. 3.3.3 等価カーネル
• 訓練データの⽬標値だけから予測
• 線形基底関数モデルに対して、事後分布の平均解を導⼊（ ）
• つまり, 点xでの予測分布の平均は訓練データの⽬標変数tnの線形結合なので、
» ただし
• 平滑化⾏列or等価カネールと⾔う
23

24. 3.3.3 等価カーネル
• ガウス基底関数に対する k(x, xʼ)をプロット
– → xに近い xʼを⼤きく重み付けしていることがわかる
24

25. 3.4 ベイズモデル⽐較
• データ集合 D上のモデル集合{Mi}(i=1,…,L)からモデル選択をベイズ的に
⾏う.
• モデルエビデンス：
– モデルでデータがどれくらい説明できるか、を表す
– 周辺尤度ともよばれる.
• ベイズ因⼦：
25
)|(
)|(
j
i
p
p
MD
MD

26. 3.4 ベイズモデル⽐較
• モデルエビデンスは確率の加法・乗法定理より
– パラメータを事前分布から適当にサンプリングしたときにデータ集合Dが⽣成される確
率 (→ 11章)
• パラメータに関する積分を単純近似することでモデルエビデンスの解釈得る.
簡単のためパラメータが1つしかないモデルを考える. (今後Mの依存省略)
• 例) パラメータ1つのモデル
– 事後分布：最頻値付近で尖って, 幅⊿wposterior
– 事前確率：平坦で, 幅⊿wprior
26
データへの
フィッティング度
ペナルティ項

27. 3.4 ベイズモデル⽐較
• 周辺尤度最⼤化により中間程度の複雑さのモデルが選ばれる。
27

28. 3.5 エビデンス近似
• 線形基底関数モデルを完全にベイズ的に扱うために, 超パラメータα,βに対
しても事前分布を導⼊し, 通常のパラメータwだけでなく, 超パラメータに
関しても周辺化し, 予測する.
• 超パラメータα,βの事前分布を導⼊すれば, 予測分布は同時分布をw,α,βに関
して周辺化することで得られる.(簡単のためxに関する依存省略)
• 事後分布 が の値の周りで鋭く尖っているとき, α, βをそれ
ぞれの値に固定して, 単にwを周辺可することで, 予測分布が得られる.
• を如何に求めるか？α, βの事後分布はベイズの定理より以下のよう
にかける。
– 周辺尤度関数 を最⼤化すれば求められる！
28

29. 3.5.1 エビデンス関数の評価
• 周辺尤度関数 は同時分布をwに関する積分で表現
• これまでの結果より
– M: wの次元数
–
• ただし,
29
← wに関して平⽅完成

30. 3.5.1 エビデンス関数の評価
• wに関する積分は, 多次元ガウス分布の正規化係数に関する標準的な結果を
⽤いるだけで, 次のように評価できる.
• よって, 周辺尤度の対数尤度は,
30

31. 3.5.1 エビデンス関数の評価
• 対数エビデンス関数
31
エビデンスの値を評価することで最適
なMを考えることができる.観測され
たデータを説明できるモデルの中で最
も単純なものが評価される.
今回であればM=3. 平⽅⼆乗誤差は
M=3から8の間で⼀定だが, その中で
最も単純なモデルはM=3.
1章 エビデンス関数の評価

32. 3.5.2 エビデンス関数の最⼤化
• 対数エビデンス関数
– これを最⼤化するα, βの値は,
– λiは βΦTΦ の固有値
• 計算流れ
– パラメータ γを定義
– パラメータ αを最⼤化 → 停留点を求める. αに関して陰関数なので繰り返し法で求める.
• αの初期値を適当に決める → mNとγを求める → それらでαを再推定 → 収束するまで繰返
– パラメータ βを最⼤化 → 停留点を求める. βに関して陰関数なので繰り返し法で求める
• αと同様.
32

33. 3.5.3 有効パラメータ数
33
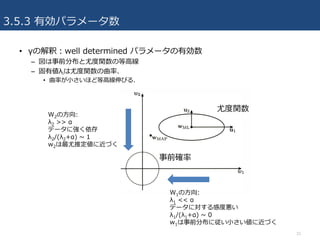
• γの解釈：well determined パラメータの有効数
– 図は事前分布と尤度関数の等⾼線
– 固有値λiは尤度関数の曲率.
• 曲率が⼩さいほど等⾼線伸びる.
尤度関数
事前確率
W2の⽅向:
λ2 >> α
データに強く依存
λ2/(λ2+α) ~ 1
w2は最尤推定値に近づく
W1の⽅向:
λ1 << α
データに対する感度悪い
λ1/(λ1+α) ~ 0
w1は事前分布に従い⼩さい値に近づく

34. 3.5.3 有効パラメータ数
34
• βの解釈：
– 不偏推定量(1章)によく似ている
• 分散の最尤推定値
• 分散の不偏推定量
• β
– 不偏推定量は⾃由度の1つを平均フィッティングと最尤推定のバイアスを除くのに⽤い
ていた。→ βも同様の考え⽅で解釈してみる.
– 最尤推定によりβを推定した場合(3.1.1)：
• ↑事前分布なしの時
– ベイズ推定の結果, γ個のパラメータが有効で残りが無効の場合：
• 有効パラメータ：データにより決定される
• 有効パラメータでない奴：データによらず事前分布により⼩さい値に設定される（⾃由）
• パラメータの決定のために⾃由度γを使⽤しているので, ⾃由度は N-γ

35. 式(3.90)より, この交差点は
エビデンス関数のαに関する微分を0にする点
= αの最適解
3.5.3 有効パラメータ数
35
左図の交差の辺りで, 対数エビデンスが最⼤値に
テスト集合に対する誤差は最⼩に近いことがわかる
対数エビデンス
テストでの誤差
エビデンスの枠組みによるハイパパラメータ値の決定法
=

36. 3.5.3 有効パラメータ数
36
• wiの⼤きさの変化
– αを 0 → ∞ に変化させると, γは 0 → Mに変化する.
– 極限的に全てのパラメータがwell determinedになる.
– αはwiの⼤きさを制御しているといえる.

37. 3.6 固定された基底関数の限界
• ⾮線形基底関数を線形結合したモデルを本章で考えた.
• 利点
– パラメータに関する線形性の仮定より最⼩⼆乗問題の閉じた解が求まる.
– ベイズ推定の計算が簡単になる.
– 基底関数を適切に選ぶことで⼊⼒変数から任意の⾮線形変換モデル化できる.
• ⽋点
– 訓練データ集合を観測する前に基底関数Φj(x)を固定する仮定から, 次元の呪いが問題と
なる(1.4節). ⼊⼒空間の次元数Dに対して, 指数的に基底関数の数を増やさないといけ
ない…
• ただ現実的なデータには⽋点を軽減する2つの性質
– 1. データベクトルは概して本質的な次元数が⼊⼒空間の次元数よりも⼩さい⾮線形多
様体上に⼤体分布してる性質（⼊⼒変数同⼠が強い相関を持っているため.）→ 12章
• 局所的な基底関数を⽤いればいい
• RBF, SVM, RVMでも⽤いられる.
– 2. ⽬的変数がデータ多様体中のほんの少数の可能な⽅向にしか強く依存しない性質.
• ニューラルネットワークでも, ⼊⼒空間中で基底関数が反応する⽅向を選ぶことでこの性質活
⽤
37

38. 参考資料
• パターン認識と機械学習 上
– C.M. ビショップ (著), 元⽥ 浩 (監訳), 栗⽥ 多喜夫 (監訳), 樋⼝ 知之 (監訳), 松本 裕治 (監
訳), 村⽥ 昇 (監訳)
• PRML輪読会3章前半担当分スライド（penzant, SlideShare）
– https://www.slideshare.net/penzant/prml3-48218339
• PRMLの線形回帰モデル（線形基底関数モデル）（Yasunori Ozaki,
SlideShare）
– https://www.slideshare.net/yasunoriozaki12/prml-29439402
• PRML輪読会 3章4節（Heavy Watal）
– https://heavywatal.github.io/lectures/prml-3-4.html
• Prml3.5 エビデンス近似〜（Yuki Matsubara, SlideShare）
– https://www.slideshare.net/yukimatsubara9847/prml35-40730590
38