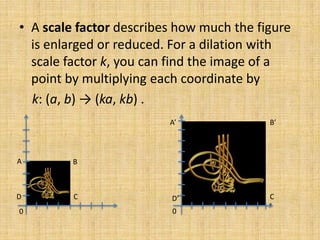
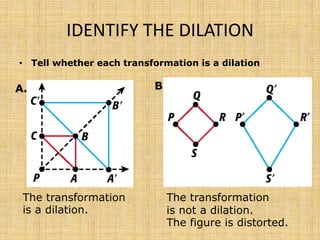
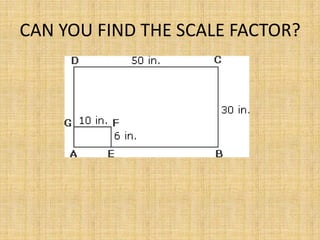
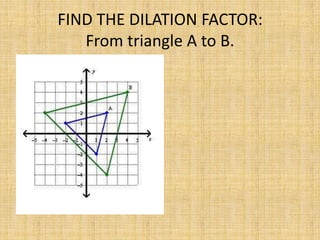
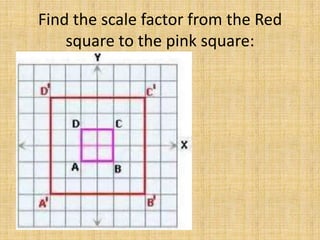
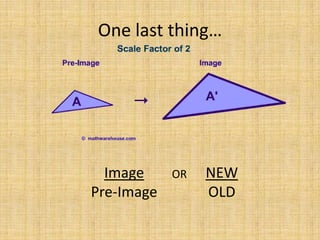
This document discusses dilations, which are transformations that change the size of a figure but not its shape. A dilation is identified by its scale factor, which describes how much the figure is enlarged or reduced. If the scale factor is greater than 1, it is an enlargement, and if it is less than 1, it is a reduction. The document provides examples of identifying dilations, drawing dilations of different figures using given scale factors, and finding the scale factor between two figures. Students are assigned independent practice and homework on dilations.

1. Dilations and Similarity
Mr. Saucedo - GEOMETRY - Milby High School

2. OBJECTIVE:
•To identify and
construct dilations.

3. • A dilation is a transformation that changes the
size of a figure but not its shape.

4. • A scale factor describes how much the figure
is enlarged or reduced. For a dilation with
scale factor k, you can find the image of a
point by multiplying each coordinate by
k: (a, b) → (ka, kb) .
A’
A
C
D’
C
’
B
D
B’
0
0

5. KEY CONCEPT:
• A Dilation stretches or shrinks a figure.
• The Center of Dilation never changes
position. It’s a starting point.
• The Scale Factor tells you how much the
dilation stretches or shrinks.

6. • If the scale factor of a dilation is greater than 1
(k > 1) , it is an enlargement. If the scale factor
is less than 1 (k < 1) , it is a reduction.

7. IDENTIFY THE DILATION
• Tell whether each transformation is a dilation
A.
The transformation
is a dilation.
B.
The transformation
is not a dilation.
The figure is distorted.

8. DRAWING A DILATION
• Draw a dilation
of quadrilateral
ABCD, with
vertices
A(2,1), B(4,1), C(
4,-1), and (1,-1).
Use a scale factor
of k=2.

9. DRAW A DILATION
• A triangle has
the vertices
A(4,-4), B(8,2),
and C(8,-4).
Draw its
dilation with a
scale of ½.

10. CAN YOU FIND THE SCALE FACTOR?

11. FIND THE DILATION FACTOR:
From triangle A to B.

12. Find the scale factor from the Red
square to the pink square:

13. One last thing…
Image
Pre-Image
OR
NEW
OLD

14. INDEPENDENT PRACTICE

15. HOMEWORK
Workbook, Section 6.7. Pages: 121-123
Problems: 2, 4, 6, 8, 9, 10, 11, 12, 13
Pre AP: Add problem 14.