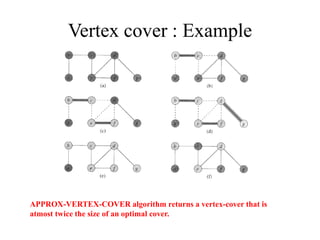
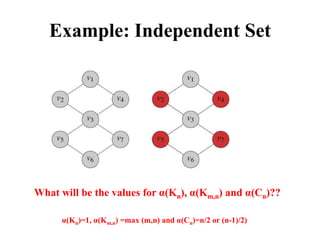
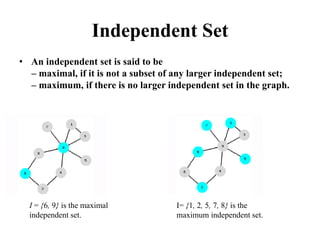
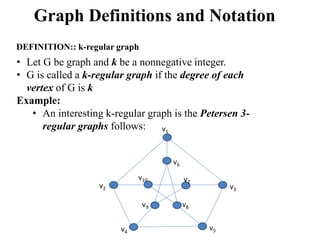
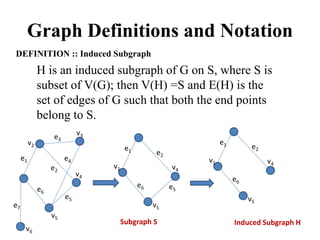
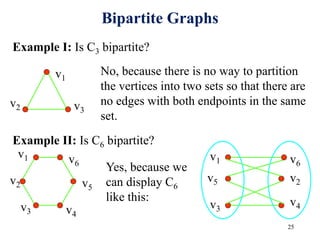
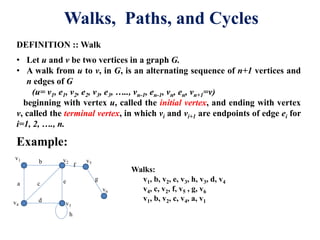
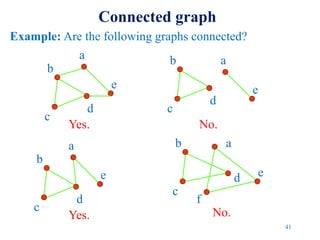
Graph algorithms can be used to model and solve many real world problems. Some famous graph problems include the traveling salesman problem of planning the shortest route to visit all cities once, and the four color theorem about coloring maps with four colors so no adjacent regions have the same color. Graphs are mathematical structures used to represent pairwise relationships between objects. They are made up of vertices connected by edges, and common graph algorithms involve finding shortest paths, matching items, or modeling flows through networks.




































![Vertex cover Algorithm
• APPROX-VERTEX_COVER (G: Graph)
• c ← { }
• E’ ← E[G]
• while E’ is not empty do
• Let (u, v) be an arbitrary edge of E’
• c ← c U {u, v}
• Remove from E’ every edge incident on either
u or v
• return c
Analysis
It is easy to see that the running time of this algorithm is O(V+E),
using adjacency list to represent E’.](https://image.slidesharecdn.com/lecture1-graphalgorithms-basics-220726060354-919c6f50/85/Lecture-1-Graph-Algorithms-Basics-pptx-48-320.jpg)