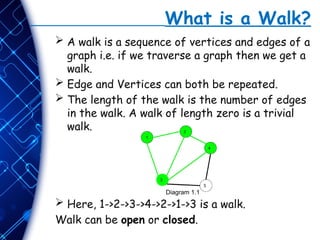
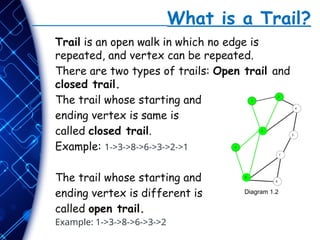
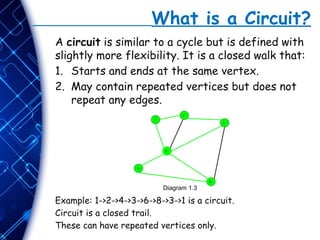
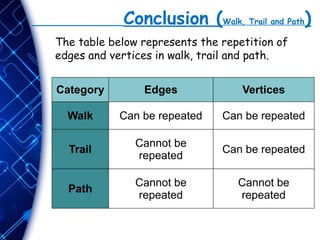
The document provides an overview of graph theory, defining key concepts such as graphs, vertices, edges, and different types of graphs, including directed, undirected, and various specialized graphs. It explains walks, trails, paths, cycles, and circuits, highlighting their definitions and differences regarding the repetition of vertices and edges. The content aims to enhance understanding of graph structures and their practical applications, such as tracking in GPS systems.

1. GRAPH
JOSEPHINE T. CRUZ

2. Objectives
At the end of this lesson you will be
able to:
1. Explain and simulate how to represent
the graph

3. GRAPH
Basic Concept of a Graph
 A graph is determined as a mathematical
structure that represents a particular function
by connecting a set of points. It is used to
create a pairwise relationship between objects.
 The graph is made up of vertices (nodes) that
are connected by the edges (lines).
 a graph is a pictorial representation of any data
in an organised manner.
 The graph shows the relationship between
variable quantities.
 In real-life also the best example of graph
structure is GPS, where you can track the path
or know the direction of the road.

4. GRAPH
Basic Concept of a Graph
 Formally, a graph is denoted as a pair G(V, E).
Where V represents the finite set vertices and E
represents the finite set edges.
Therefore, we can say a graph includes non-empty
set of vertices V and set of edges E.
Example:
Suppose, a Graph G=(V,E), where
Vertices, V={a,b,c,d}
Edges, E={{a,b},{a,c},{b,c},{c,d}}

5. Types of Graph
 The graphs are basically of two types, directed
and undirected. It is best understood by the
figure given below. The arrow in the figure
indicates the direction.
1. In graph theory, a directed graph
is a graph made up of a set of
vertices connected by edges, in
which the edges have a direction
associated with them.
2. The undirected graph is defined
as a graph where the set of nodes
are connected together, in which
all the edges are bidirectional.
Sometimes, this type of graph
is known as the undirected network.

6. Types of Graph
Other types of graphs
 Null Graph: A graph that does not have
edges.
 Simple graph: A graph that is undirected
and does not have any loops or multiple
edges.
 Multigraph: A graph with multiple edges
between the same set of vertices. It has
loops formed.
 Connected graph: A graph where any two
vertices are connected by a path.
 Disconnected graph: A graph where any
two vertices or nodes are disconnected by
a path.

7. Types of Graph
Other types of graphs
 Cycle Graph: A graph that completes a
cycle.
 Complete Graph: When each pair of
vertices are connected by an edge then
such graph is called a complete graph
 Planar graph: When no two edges of a
graph intersect and are all the vertices and
edges are drawn in a single plane, then such
a graph is called a planar graph

8. Complementary Graph
 In graph theory, the complementary graph (or
complement) of a graph , denoted as
𝐺 G, is
formed by creating a new graph with the same
set of vertices as G but with different edges.
In the complement G , an edge exists between
two vertices if and only if that edge does not
exist in G. In other words, for any two
vertices and :
𝑢 𝑣
• If and are connected by an edge in G,
𝑢 𝑣
they are not connected in G .
• If and are not connected by an edge in G,
𝑢 𝑣
they are connected in G.

9. Complementary Graph
Example:
Consider a simple graph G with 4 vertices, labeled
{ , , , , and edges connecting them as follows:
𝐴 𝐵 𝐶 𝐷
Edges in G: ( , ),( , ),( , )
𝐴 𝐵 𝐴 𝐶 𝐵 𝐷
For G, the adjacency relationships are:
• A is connected to B and C
• B is connected to A and D
• C is connected to A
• D is connected to B
To construct G:
• The vertices are the same: { , , , }
𝐴 𝐵 𝐶 𝐷
• Add edges where there are no connections in G:
– A connects to D
– B connects to C
– C connects to D
So, the edges in G are: ( , ),( , ),( , )
𝐴 𝐷 𝐵 𝐶 𝐶 𝐷
The resulting graph G is the complement of G, with edges opposite
to those in G.

10. What is a Walk?
 A walk is a sequence of vertices and edges of a
graph i.e. if we traverse a graph then we get a
walk.
 Edge and Vertices can both be repeated.
 The length of the walk is the number of edges
in the walk. A walk of length zero is a trivial
walk.
 Here, 1->2->3->4->2->1->3 is a walk.
Walk can be open or closed.
Diagram 1.1

11. What is a Trail?
Trail is an open walk in which no edge is
repeated, and vertex can be repeated.
There are two types of trails: Open trail and
closed trail.
The trail whose starting and
ending vertex is same is
called closed trail.
Example: 1->3->8->6->3->2->1
The trail whose starting and
ending vertex is different is
called open trail.
Example: 1->3->8->6->3->2
Diagram 1.2

12. What is a Path?
Path is a walk with no repeated vertices or edges
This directly implies that no edges will ever be
repeated and hence is redundant to write in the
definition of path.
- Vertex not repeated
- Edge not repeated
Example: consider Diagram 1.2 6->8->3->1->2->4 is a Path.
*A Path is a trail in which neither vertices nor
edges are repeated. As path is also a trail, thus
it is also an open walk.
Diagram 1.3

13. What is a Cycle?
A cycle is a closed path in a graph that:
- Starts and ends at the same vertex.
- Has no repeated edges or vertices (except the
starting/ending vertex).
In other words, a cycle is a "simple" closed path where no
vertices or edges (other than the starting/ending vertex)
are revisited.
Cycles are fundamental in graph theory as they help identify
connected structures within a graph.
Example: Consider Diagram 1.2 1->2->4->3->1 is a cycle.
Cycle is a closed path.
These cannot have repeat anything (neither edges nor
vertices).
Note that for closed sequences start and end vertices are the
only ones that can repeat.

14. What is a Circuit?
A circuit is similar to a cycle but is defined with
slightly more flexibility. It is a closed walk that:
1. Starts and ends at the same vertex.
2. May contain repeated vertices but does not
repeat any edges.
Example: 1->2->4->3->6->8->3->1 is a circuit.
Circuit is a closed trail.
These can have repeated vertices only.
Diagram 1.3

15. Conclusion (Walk, Trail and Path)
The table below represents the repetition of
edges and vertices in walk, trail and path.
Category Edges Vertices
Walk Can be repeated Can be repeated
Trail
Cannot be
repeated
Can be repeated
Path
Cannot be
repeated
Cannot be
repeated

16. ! Thank you !