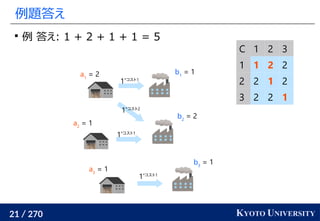
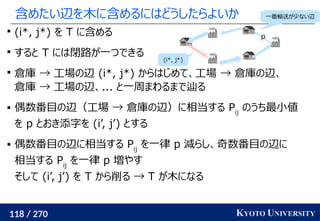
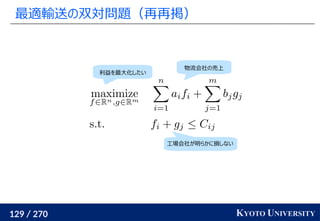
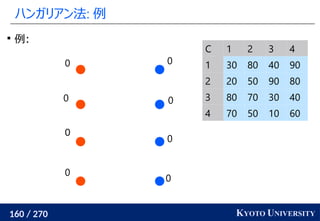
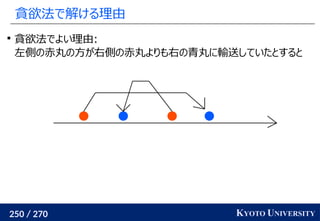
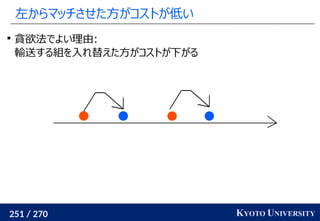
最適輸送問題(Wasserstein 距離)を解く方法についてのさまざまなアプローチ・アルゴリズムを紹介します。
線形計画を使った定式化の基礎からはじめて、以下の五つのアルゴリズムを紹介します。
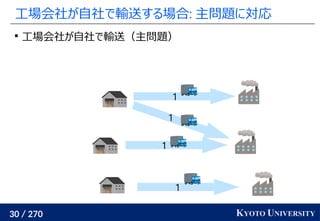
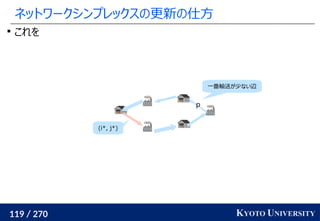
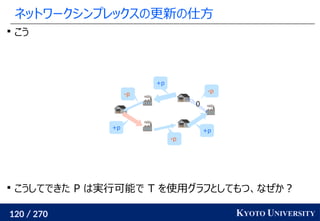
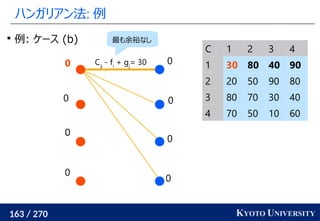
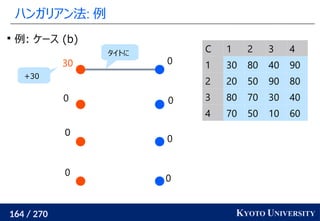
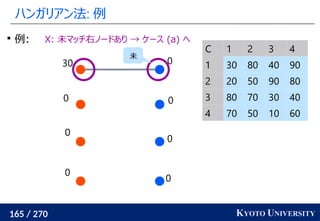
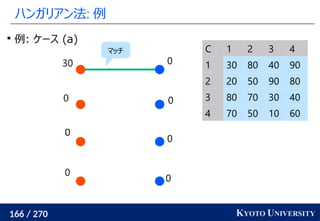
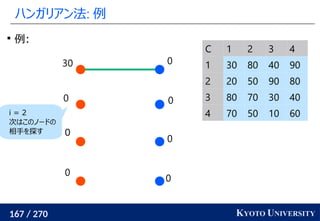
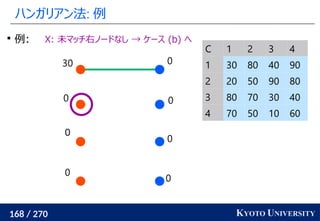
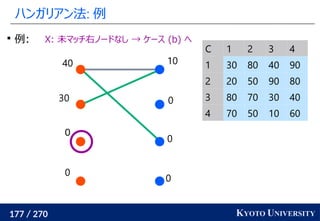
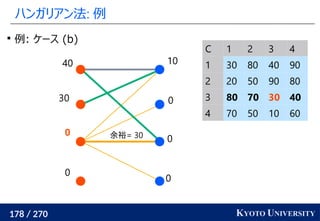
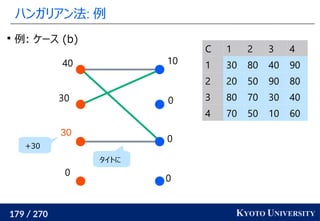
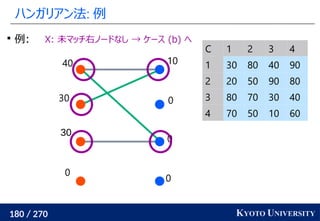
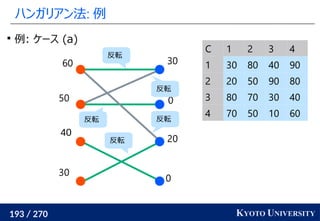
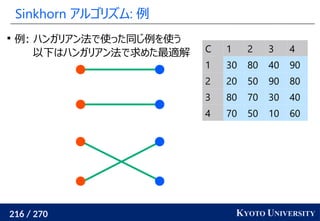
1. ネットワークシンプレックス法
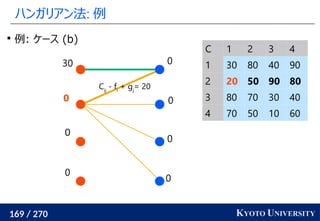
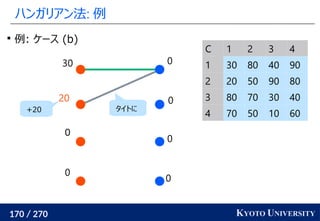
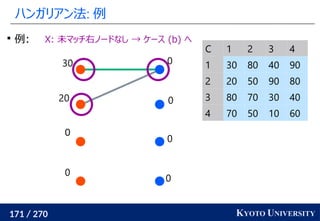
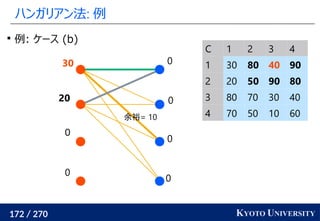
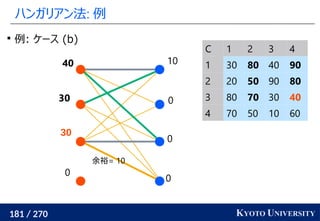
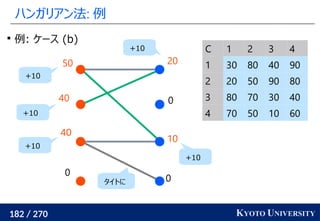
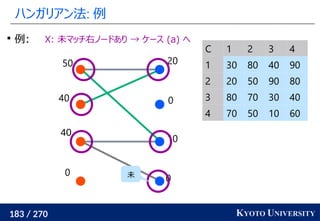
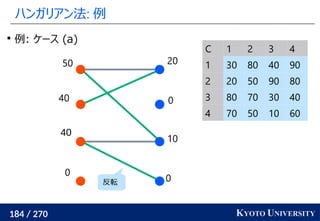
2. ハンガリアン法
3. Sinkhorn アルゴリズム
4. ニューラルネットワークによる推定
5. スライス法
このスライドは第三回 0x-seminar https://sites.google.com/view/uda-0x-seminar/home/0x03 で使用したものです。自己完結するよう心がけたのでセミナーに参加していない人にも役立つスライドになっています。
『最適輸送の理論とアルゴリズム』好評発売中! https://www.amazon.co.jp/dp/4065305144
Speakerdeck にもアップロードしました: https://speakerdeck.com/joisino/zui-shi-shu-song-nojie-kifang










![11 / 270 KYOTO UNIVERSITY
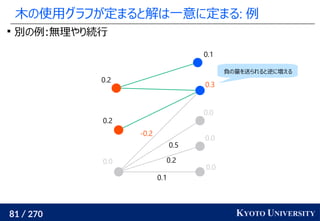
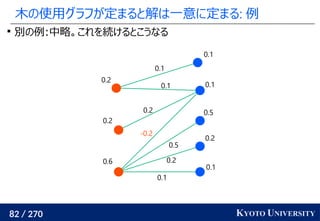
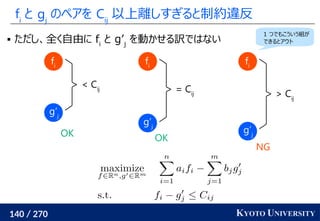
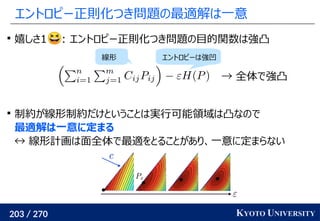
Sinkhorn は微分可能で GPU フレンドリー
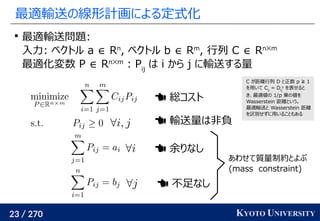
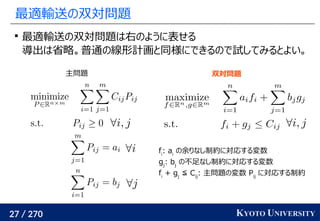
その3: Sinkhorn アルゴリズムは目的関数に正則化を加え、
行列演算で最適輸送を解くアルゴリズム
Sinkhorn が [Cuturi+ 2013] で紹介されたことで
機械学習界隈で最適輸送が使われるようになるキッカケになった
長所 :コストに関して微分可能
GPU 上だと早い
複数の最適輸送を並列に解ける
最適解が唯一に定まる
短所 : 厳密な最適輸送の解ではない
オーバーフローや解の丸めに気をつける必要あり
Marco Cuturi. Sinkhorn Distances: Lightspeed Computation of Optimal Transport. NeurIPS 2013.
Gabriel Peyré, Marco Cuturi. Computational Optimal Transport. 2019.](https://image.slidesharecdn.com/slides-210617083130/85/slide-11-320.jpg)





























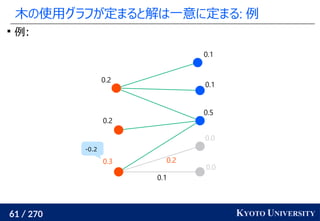
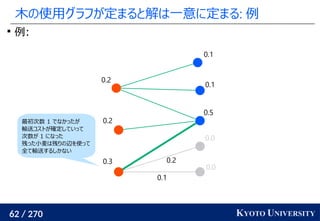
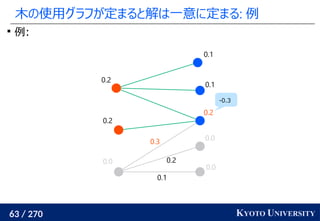
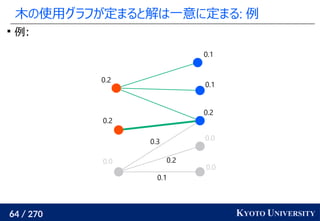
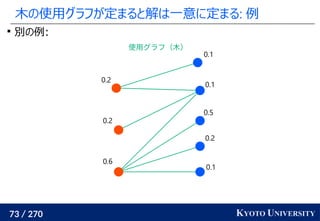
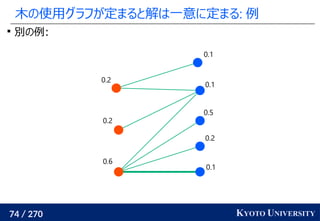
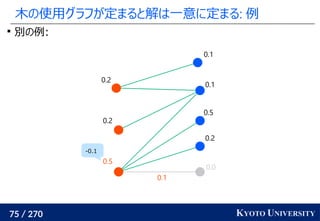
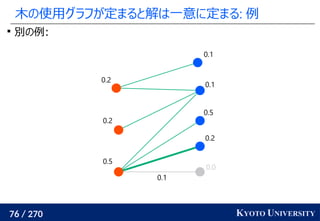
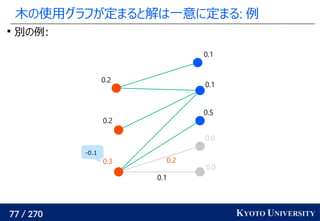
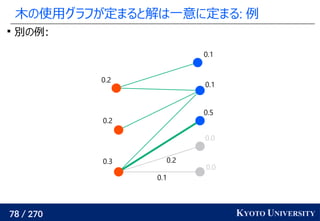
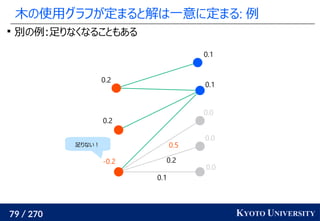
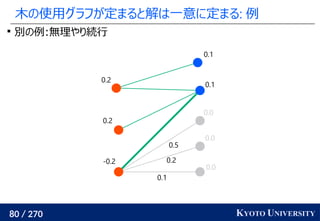









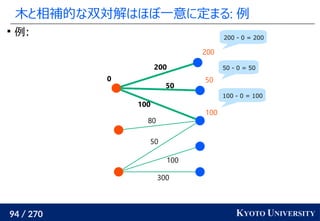
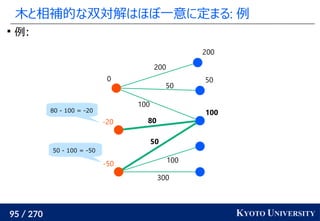
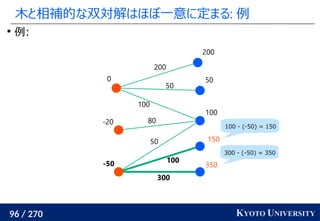
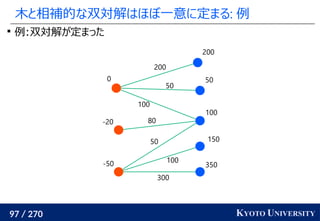



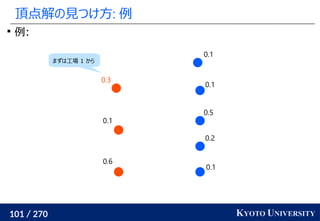
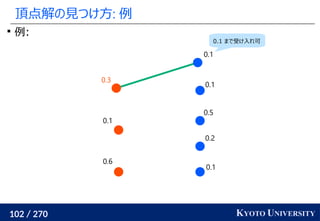
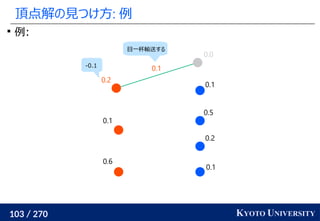
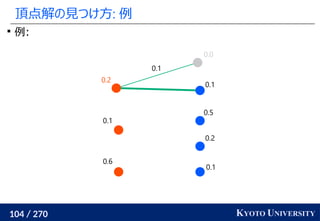
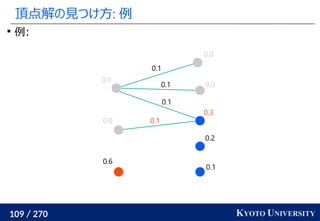
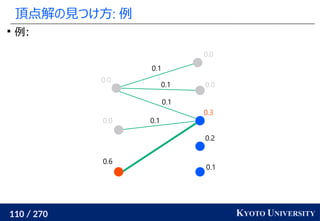
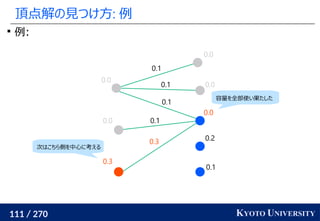
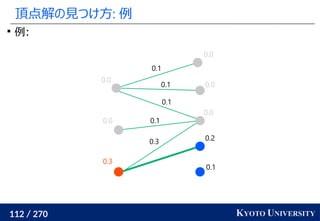




































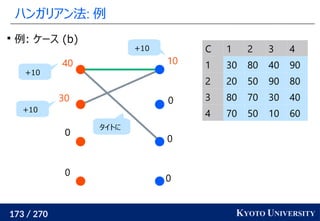
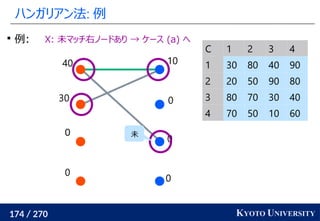
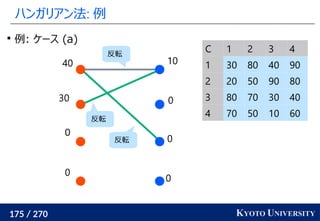
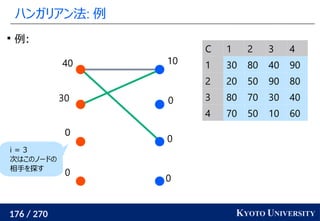





![199 / 270 KYOTO UNIVERSITY
Sinkhorn は微分可能で GPU フレンドリー
その3: Sinkhorn アルゴリズムは目的関数に正則化を加え、
行列演算で最適輸送を解くアルゴリズム
Sinkhorn が [Cuturi+ 2013] で紹介されたことで
機械学習界隈で最適輸送が使われるようになるキッカケになった
長所 :コストに関して微分可能
GPU 上だと早い
複数の最適輸送を並列に解ける
最適解が唯一に定まる
短所 : 厳密な最適輸送の解ではない
オーバーフローや解の丸めに気をつける必要あり
Marco Cuturi. Sinkhorn Distances: Lightspeed Computation of Optimal Transport. NeurIPS 2013.
Gabriel Peyré, Marco Cuturi. Computational Optimal Transport. 2019.](https://image.slidesharecdn.com/slides-210617083130/85/slide-199-320.jpg)













![214 / 270 KYOTO UNIVERSITY
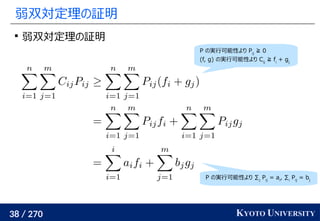
Sinkhorn 変数から元の変数への戻し方
Sinkhorn により (u, v) が求まると、変数変換の式より元の
双対変数は
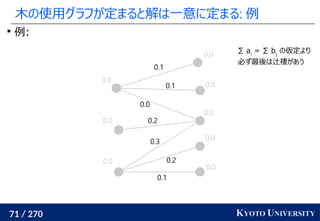
主問題の変数はラグランジュ関数から双対関数を求めた式より
f, g が完璧に収束しない限り、求めた Pij
は厳密には実行可能とは
限らないことに注意
この Pij
から違反分をいい感じに分配して実行可能解を計算する
アルゴリズムも提案されている [Altschuler+ 2017]
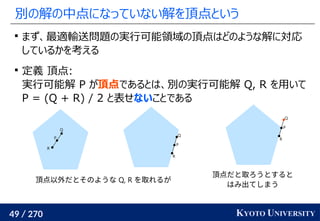
Jason Altschuler, Jonathan Weed, Philippe Rigollet. Near-linear time approximation algorithms for
optimal transport via Sinkhorn iteration. NeurIPS 2017.](https://image.slidesharecdn.com/slides-210617083130/85/slide-214-320.jpg)



![219 / 270 KYOTO UNIVERSITY
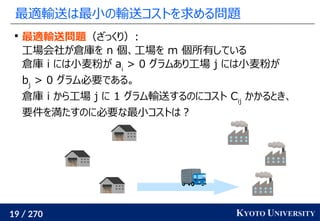
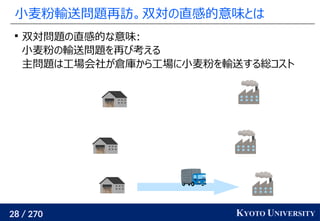
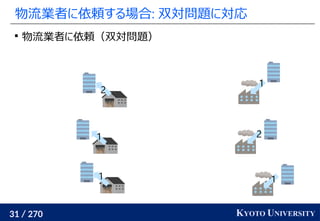
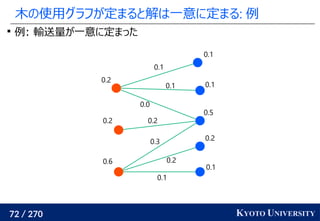
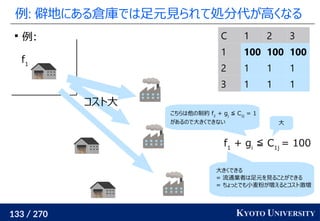
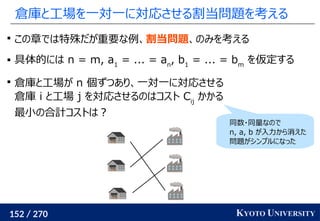
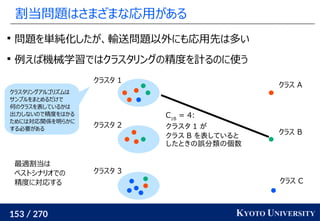
最新の手法でも配置問題に Sinkhorn が使われる
この問題はクラスタリングと見ることもできる [Cuturi+ ICML 2014]
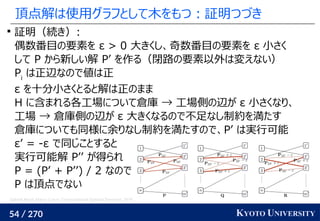
工場がサンプル点で、倉庫がクラスタ中心
クラスタが含むサンプル数(倉庫に入る小麦粉)は決まっている
この発想から、クラスタリングの際に Sinkhorn 法を使う手法が
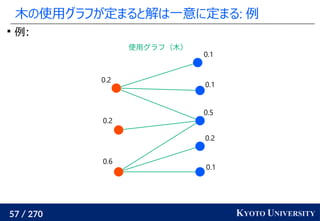
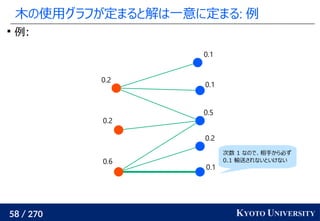
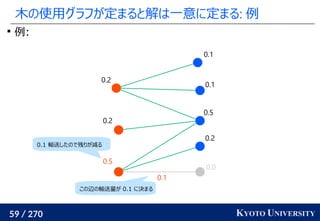
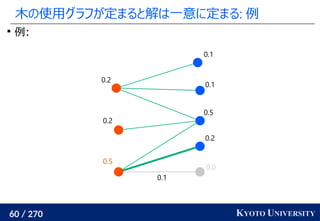
最新の機械学習でも使われている [Caron+ NeurIPS 2020]
Marco Cuturi, Arnaud Doucet. Fast Computation of Wasserstein Barycenters. ICML 2014.
Mathilde Caron, Ishan Misra, Julien Mairal, Priya Goyal, Piotr Bojanowski, Armand Joulin. Unsupervised
Learning of Visual Features by Contrasting Cluster Assignments. NeurIPS 2020.
クラスタ中心](https://image.slidesharecdn.com/slides-210617083130/85/slide-219-320.jpg)
![220 / 270 KYOTO UNIVERSITY
最新の手法でも公平予測問題に Sinkhorn が使われる
他にも、二つの集合の距離を近づけるための微分可ロスとして使われる
例えば、公平性の担保のため、男性についての予測と女性についての
予測分布が同じようにしたい
予測誤差 + 赤と青の最適輸送距離を最小化 [Oneto+ NeurIPS 2020]
Luca Oneto, Michele Donini, Giulia Luise, Carlo Ciliberto, Andreas Maurer, Massimiliano Pontil. Exploiting
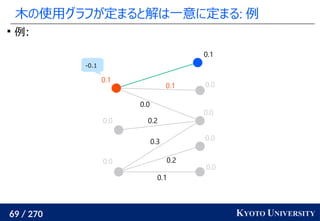
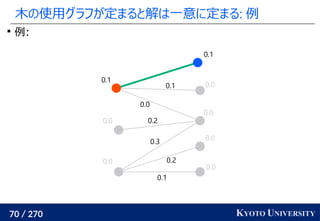
MMD and Sinkhorn Divergences for Fair and Transferable Representation Learning. NeurIPS 2020.
ニューラルネットワーク
入力
d 次元ベクトルが
出てくる
Rd
予測器
出力
各丸は各サンプルの
埋め込み
赤: 女性サンプル
青: 男性サンプル](https://image.slidesharecdn.com/slides-210617083130/85/slide-220-320.jpg)
















![238 / 270 KYOTO UNIVERSITY
パラメータの値を無理やり制限してリプシッツ性を課す
解決策 1: weight clipping [Arjovsky+ 2017]
訓練の際ニューラルネットワークの各パラメータの絶対値が
定数 γ > 0 を越えるたびに絶対値 γ にクリップする(γ:ハイパラ)
こうすると、ニューラルネットワーク f の表現できる関数は制限され
急激な変化をする関数は表せなくなる
γ の設定次第で、何らかの k > 0 について k-リプシッツであることが
保証できる
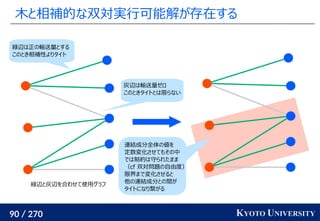
k-リプシッツな関数全てを表現できる訳ではないが、ニューラルネットワー
クの柔軟性よりそれなりに豊富な関数が表現できることが期待できる
Martin Arjovsky, Soumith Chintala, Léon Bottou. Wasserstein GAN. ICML 2017](https://image.slidesharecdn.com/slides-210617083130/85/slide-238-320.jpg)
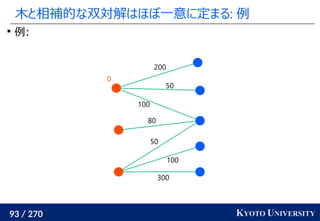
![239 / 270 KYOTO UNIVERSITY
各点での勾配が 1 から離れるとペナルティ
解決策 2: gradient penalty [Arjovsky+ 2017]
f が微分可のとき各点での勾配のノルムが 1 以下 ↔ 1-リプシッツ
色んな点で勾配を評価して 1 から離れていたらペナルティを課す
をロスとして最適化
Ishaan Gulrajani, Faruk Ahmed, Martín Arjovsky, Vincent Dumoulin, Aaron C. Courville.. Improved
Training of Wasserstein GANs. NeurIPS 2017
ハイパラ正則化係数
色んな訓練サンプル
例えば X ∪ Y
勾配を 1 に近づける](https://image.slidesharecdn.com/slides-210617083130/85/slide-239-320.jpg)









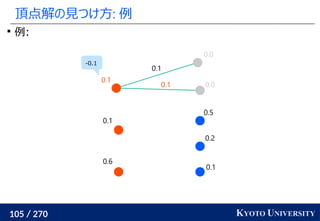
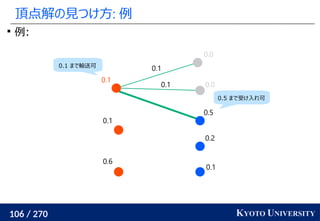
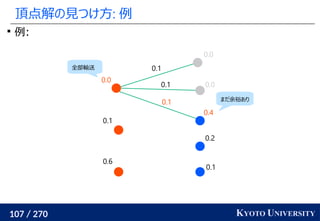
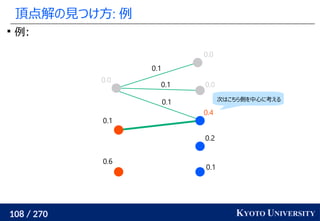
![255 / 270 KYOTO UNIVERSITY
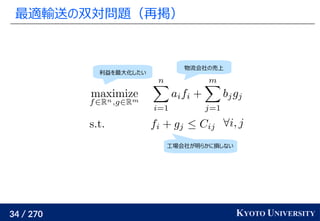
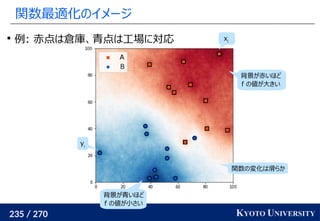
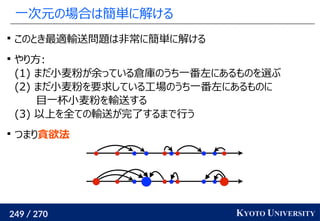
高次元でも一次元に帰着して簡単にする
一次元の場合非常に簡単なことを利用して、
高次元の場合も一次元に帰着する方法が提案されている
Sliced Wasserstein distance [Rabin+ 2011]:
x1
, ..., xn
∈ Rd
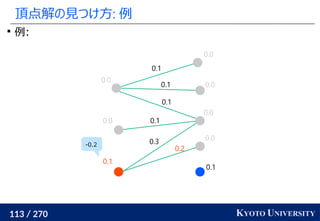
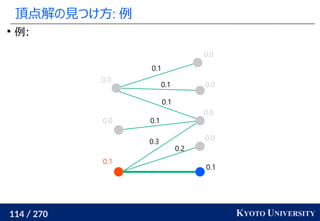
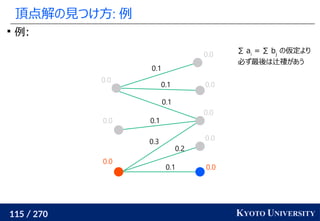
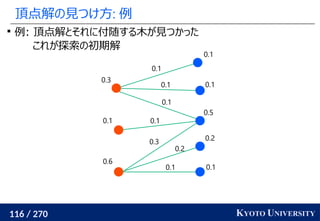
, y1
, ..., ym
∈ Rd
のとき、ランダムな方向 Θ ∈ Rd
に x1
, ..., xn
, y1
, ..., ym
を射影し、一次元にして輸送距離を計算
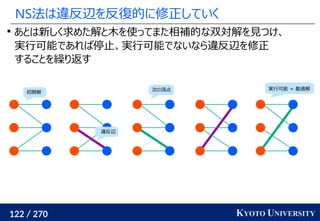
最終的な答えは何度か方向を変えた時の平均値
k 個方向を使うと O(k n log n) 時間
実装は一次元の場合と同等
Julien Rabin, Gabriel Peyré, Julie Delon, Marc Bernot. Wasserstein Barycenter and its Application to
Texture Mixing. 2011.
https://www.programmersought.com/article/67174999352/
ただしこの期待値が
元の空間でのコストの
近似になっている訳ではない](https://image.slidesharecdn.com/slides-210617083130/85/slide-255-320.jpg)
![256 / 270 KYOTO UNIVERSITY
直線に限らず、どんな一次元に射影してもよい
Sliced Wasserstein distance [Rabin+ 2011] では直線に
沿って射影したが、一次元に射影できたらどういう射影でもよい
例えばデータが U 字型だったら U 字に沿った一次元、
一般にはデータのサポートに沿った一次元が良さそう
Generalized sliced Wasserstein [Kolouri+ NeurIPS 2019]
適当な射影関数 Θ: Rd
→ R を使って射影して一次元で解く
ランダムな射影の平均だけでなく、一番青と赤が見分けられるような
射影を学習により見つける方法も提案(判別分析のようなイメージ)
Julien Rabin, Gabriel Peyré, Julie Delon, Marc Bernot. Wasserstein Barycenter and its Application to
Texture Mixing. 2011.
Soheil Kolouri, Kimia Nadjahi, Umut Simsekli, Roland Badeau, Gustavo K. Rohde. Generalized Sliced
Wasserstein Distances. NeurIPS 2019.](https://image.slidesharecdn.com/slides-210617083130/85/slide-256-320.jpg)


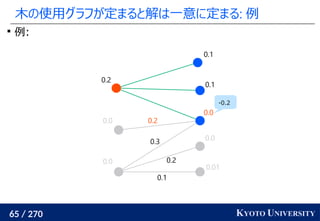
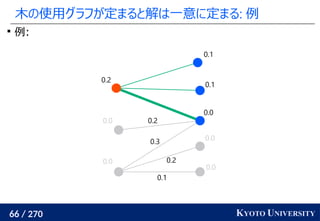
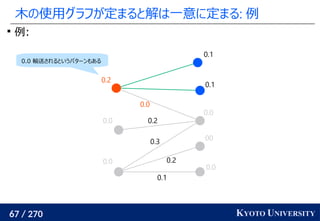
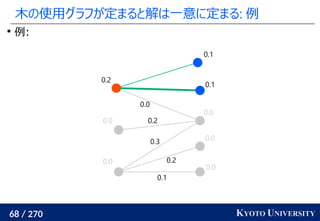
![259 / 270 KYOTO UNIVERSITY
高次元でも木に帰着して簡単にする
一次元の場合と同様に、木に帰着する方法が提案されている
Tree-Sliced Wasserstein [Le+ NeurIPS 2019]:
x1
, ..., xn
∈ Rd
, y1
, ..., ym
∈ Rd
のとき、ランダムな木(例えば
クラスタリング木)のノードに x1
, ..., xn
, y1
, ..., ym
を射影し、
木上で輸送距離を計算
最終的な答えは何度か木を変えた時の平均値
k 個木を使うと O(k n log n) 時間
良い木を使うと元の輸送距離の近似にもなる
Tam Le, Makoto Yamada, Kenji Fukumizu, Marco Cuturi. Tree-Sliced Variants of Wasserstein Distances.
NeurIPS 2019.
http://www.sthda.com/english/articles/31-principal-component-methods-in-r-practical-guide/117-hcpc-hierarchical-clustering-on-principal-components-essentials/](https://image.slidesharecdn.com/slides-210617083130/85/slide-259-320.jpg)
![260 / 270 KYOTO UNIVERSITY
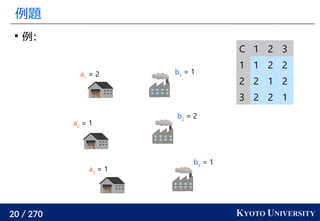
一次元の場合そのものが重要な場合もある
高次元を一次元や木に帰着する場合を主に扱ったが、一次元の
最適輸送そのものが重要なこともある
就活生の特徴量を受け取り自社の適正スコアを出す問題を考える
男性の適正スコアと女性の適正スコアは偏ってはいけないので
最適輸送コストを正則化に加える
データの方を男性と女性の見分けが付かなくなるように最適輸送コスト
で補正するやり方が [Feldman+ KDD 2015] で提案されている
適正スコア
x1 x2
x3
y1
y2
y3
Michael Feldman, Sorelle A. Friedler, John Moeller, Carlos Scheidegger, Suresh Venkatasubramanian.
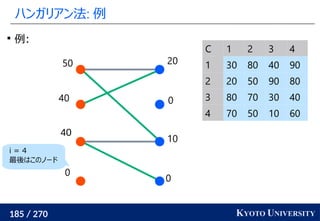
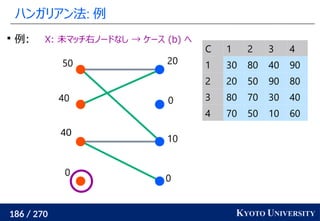
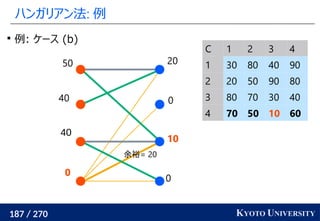
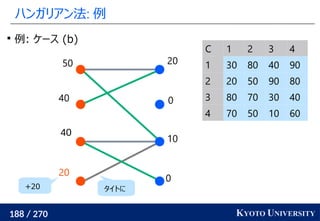
Certifying and Removing Disparate Impact. KDD 2015.](https://image.slidesharecdn.com/slides-210617083130/85/slide-260-320.jpg)









