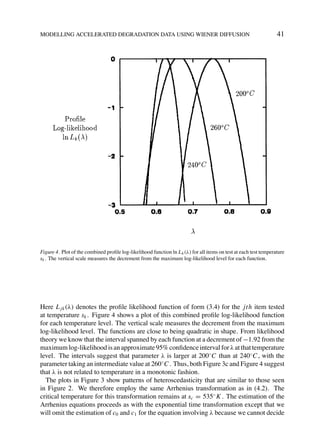
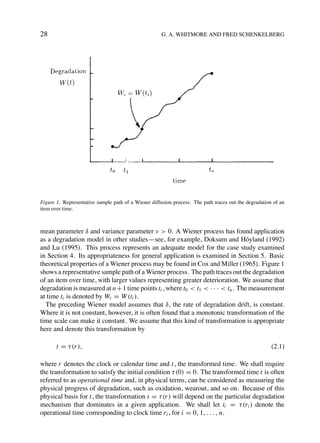
The document presents a statistical model for performance degradation of products using a Wiener diffusion process with time scale transformations, aimed at predicting the lifetime of long-life items under accelerated testing conditions. It explains how the model incorporates Arrhenius extrapolation for high stress testing and provides inference methods for model parameters based on collected degradation test data. A case application demonstrates the model's utility, particularly in evaluating self-regulating heating cables, while addressing challenges faced in practical implementations.



![MODELLING ACCELERATED DEGRADATION DATA USING WIENER DIFFUSION 31
3. Inference
In practice, the linear coefficients of the Arrhenius equations in (2.3) must be estimated
from accelerated degradation test data. We now give new notation to represent these test
data and specify the general characteristics of the degradation test.
We assume that m k new items are placed on test at each of K stress levels, denoted by sk ,
for k = 1, . . . , K . Let Wi jk and ri jk denote the observed degradation level and clock time,
respectively, for the ith reading on the jth item at the kth stress level. Here j = 1, . . . , m k
and i = 0, . . . , n jk . Thus, m k is the number of items on test at the kth stress level and
n jk + 1 is the number of observations made on the jth item at that stress level. We assume
that n jk ≥ 2 for each item so that the data are sufficient for parameter estimation.
We use the method of maximum likelihood to estimate the parameters δ, ν and λ for each
ˆ ˆ ˆ
item. Let these estimates be denoted by (δ jk , ν jk , λ jk ) for the jth item at the kth stress level.
To describe the estimation method, we will suppress the subscripts j and k and focus on
the n + 1 observations (Wi , ri ), i = 0, 1, . . . , n, made on an individual item. Because non-
overlapping increments in a Wiener process are independent, we consider first differences
of the observations. For i = 1, 2, . . . , n, define Wi = Wi − Wi−1 and ti = ti − ti−1 ,
where ti = τ (ri ; λ). The dependence of the differences ti on the unknown parameter λ is
suppressed in this notation. As we have
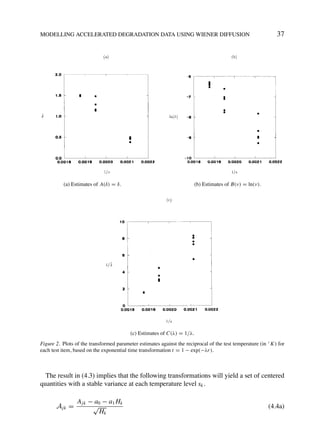
Wi ∼ N (δ ti , ν ti ), (3.1)
the sample likelihood function is
n n
1 1 ( Wi − δ ti )2
L(δ, ν, λ) = (2πν ti )− 2 exp − . (3.2)
i=1
2ν i=1
ti
By basing the sample likelihood function on first differences, the initial observation W0 =
W (t0 ) does not appear explicitly in the function. For the case study in Section 4, the initial
observation for an item is independent of the degradation process parameters and, hence, no
information is lost by omitting this initial reading from the likelihood. In some applications,
there may be a need to model the initial reading and include it in the inference structure.
The likelihood function (3.2) can be maximized directly by using a three-dimensional nu-
merical optimization routine (the approach used in the case study). An alternative approach
is to fix λ initially and then maximize the likelihood function (3.2) with respect to δ and
ν. This optimization yields the following conventional estimators, each being conditional
on λ.
Wn − W 0
ˆ
δ(λ) = (3.3a)
tn − t 0
1 n ˆ
[ Wi − δ(λ) ti ]2
ν (λ) =
ˆ (3.3b)
n i=1
ti](https://image.slidesharecdn.com/modellingwiener-130114183739-phpapp01/85/Modeling-Accelerated-Degradation-Data-Using-Wiener-Diffusion-With-A-Time-Scale-Transformation-5-320.jpg)
![32 G. A. WHITMORE AND FRED SCHENKELBERG
Substituting these conditional estimators back into (3.2) and simplifying, we obtain the
following partially maximized profile likelihood function.
n
n 1
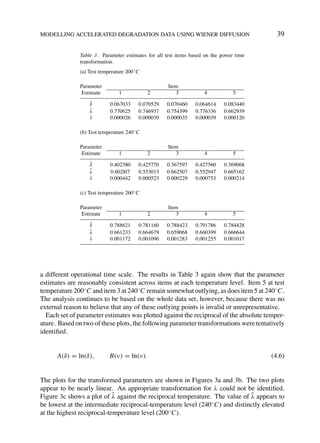
L(λ) = [2π ν(λ)]− 2
ˆ ( ti )− 2 exp(−n/2) (3.4)
i=1
Recall that ti here is a function of λ. The function in (3.4) can be maximized using a
one-dimensional search over λ, yielding the maximum likelihood estimate λ. Substitution ˆ
of this estimate into each of (3.3a) and (3.3b) yields the unconditional maximum likelihood
ˆ
estimates, δ and ν . ˆ
By one of the preceding numerical methods, therefore, we obtain the triplet of parameter
ˆ ˆ ˆ
estimates (δ jk , ν jk , λ jk ) for the jth item at the kth stress level. Continuing to assume that the
transformations A, B, C and H are known for the moment, we can compute the transformed
ˆ ˆ
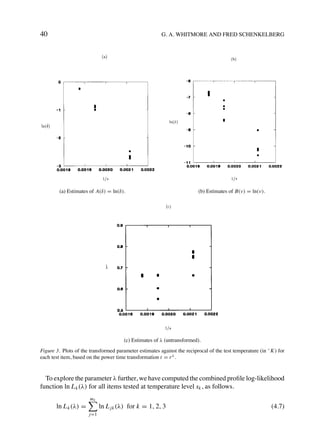
statistics A jk = A(δ jk ), Bjk = B(ˆ jk ), C jk = C(λ jk ), and Hk = H (sk ), for all j and k.
ν
The exact multivariate distribution of the triplets Y jk = (A jk , Bjk , C jk ) is unknown,
although we know from likelihood theory that they will be asymptotically trivariate normal.
Thus, if we let Xk = (1, Hk ) and
a0 b0 c0
B=
a1 b1 c1
then we know that
Y jk ∼ approx. N3 (Xk B, Σk ), (3.5)
where Σk denotes the covariance matrix of the triplet for each item at stress level k. Using
(3.5), the linear coefficients of the Arrhenius equations (2.3) can be estimated by multivariate
regression of the triplets Y jk on the values of Hk (see Johnson and Wichern, 1992, page
314). This regression must take account of the heteroscedastic error structure reflected in
the covariance matrix Σk . The precise form of the covariance matrix will vary from one
application to another. The regression analysis is illustrated in Section 4.
Once the estimated Arrhenius equations are available, the predictive analysis described in
the preceding section can be applied, provided two remaining hurdles are overcome. First,
account must be taken of the sampling errors in the estimated coefficients in (2.3) when
they are used for predictive analysis. Second, the correct transformations A(δ), B(ν), C(λ)
and H (s) must be identified. These two hurdles need to be dealt with on a case-by-case
basis.
In some applications, the sampling errors in the estimated coefficients of (2.3) represent
effects of secondary importance and, hence, can be ignored in predictive analysis. Where
the sampling errors will have a material effect on predictive statements, a strategy is needed
to take their effect into account. Development of exact analytical results appears to be
infeasible. A practical approach might employ sensitivity analysis, simulation or a Bayesian
procedure; these methods being in increasing order of sophistication. The estimator of the
coefficient matrix B in regression model (3.5) is the key input to predictions. The estimator,
ˆ
which we denote by B, has an asymptotic multivariate normal distribution that can be
estimated using conventional regression theory. The estimated distribution can then be](https://image.slidesharecdn.com/modellingwiener-130114183739-phpapp01/85/Modeling-Accelerated-Degradation-Data-Using-Wiener-Diffusion-With-A-Time-Scale-Transformation-6-320.jpg)