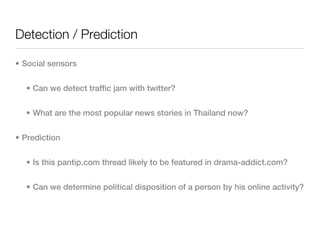
The document discusses social networks and computer science. Some key points: 1. Social networks can be represented as graphs with people as vertices and relationships as edges. Quantitative analysis looks at graph properties and constructs models to explain them. 2. Computer science can help study large-scale social networks through processing power, storage, and algorithms. Areas of study include network structure, how networks change over time, and designing tools to monitor/predict changes. 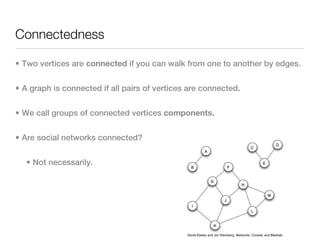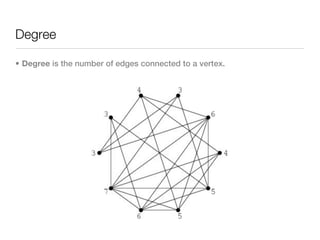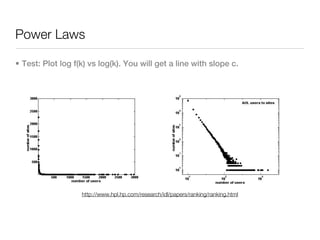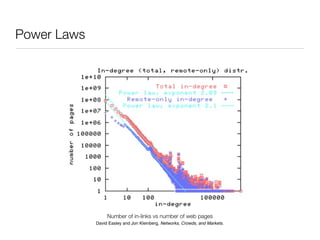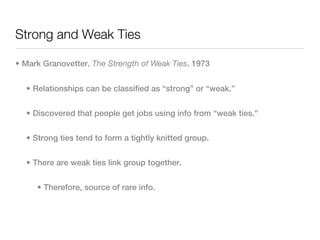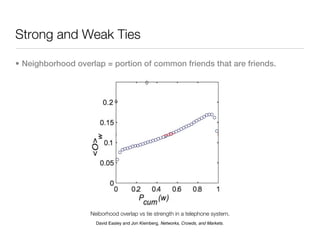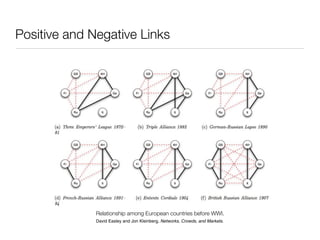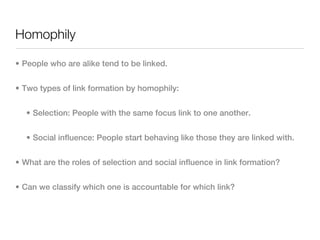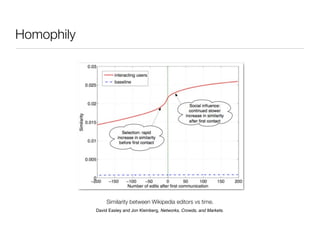3. Structural properties like degree distribution, connected components, and small world phenomena are observed in social networks. The dynamics of link formation, homophily, and positive/negative links are also examined.

1. แผนภาพโดย Steve Jurvetson (http://www.flickr.com/photos/jurvetson/)
Social Networks
dragonmeteor
and Computer Science

2. Social Networks
• Consist of
• People
• Relationships between pairs
• Can be represented by “graphs”
• People = “vertices” (dots)
• Relationships = “edges” (lines) E-mail social network in a company
David Easley and Jon Kleinberg, Networks, Crowds, and Markets.

3. Quantitative Study of Social Networks
• Look at them as graphs.
• Observe graph properties.
• Construct mathematical models to explain properties.
• Test model with new data.

4. Why Compute Science?
• The Internet
• Large social networks
• Massive data
• Can study them in largest scale.
• Human can’t process data by himself.
• The need of efficiency.
The Internet Graph
http://matthewgress.com/galleries/www/tn/Internet
%20Graph%201069646562.LGL.2D.
4096x4096.png.html

5. What CS Has to Offer
• Computers
• Processing power
• Storage
• Problem solving
• Graph algorithms
• CS ways of seeing things (how? > what?)

6. What We Study
• Structure
• Graph properties of social networks
• Process
• How do the graphs change?
• How does information flow?
• Design
• algorithms / tools to moniter/predict changes.

7. Structure

8. Connectedness
• Two vertices are connected if you can walk from one to another by edges.
• A graph is connected if all pairs of vertices are connected.
• We call groups of connected vertices components.
• Are social networks connected?
• Not necessarily.
David Easley and Jon Kleinberg, Networks, Crowds, and Markets.

9. Giant Component
• But most of them have a giant component.
A social network of dating in a public high school.
David Easley and Jon Kleinberg, Networks, Crowds, and Markets.

10. Structure of Online Social Network
• Kumar et at. Structure and Evolution of Online Social Networks. 2006
• Studied Flickr and Yahoo! 360
• The graphs have three parts.
• Singletons: users who only use the site and don’t form links.
• Giant component: users who participate in network evolution.
• Middle region: small components = user who joined because of
offline friend’s invitation.

11. Degree
• Degree is the number of edges connected to a vertex.

12. Power Laws
• What portion of vertices have degree k?
• Let f(k) = such portion.
• In graphs that represent “popularity,” we find that
1
f (k) ∝ c
k
• Examples
• Links among web pages
• Friending in social networks

13. Power Laws
• Test: Plot log f(k) vs log(k). You will get a line with slope c.
http://www.hpl.hp.com/research/idl/papers/ranking/ranking.html

14. Power Laws
Number of in-links vs number of web pages
David Easley and Jon Kleinberg, Networks, Crowds, and Markets.

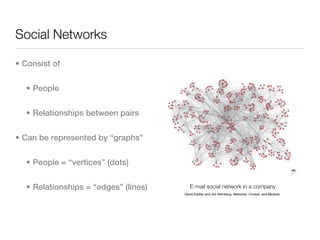
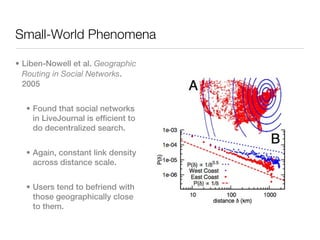
15. Small-World Phenomena
• In social networks, vertices are a few hops from one another.
• Six Degrees of Separation [Stanley Milgram, 1967]
• Had people forward letters to a designated person,
using only contacts that they know on first name basis.
• Median of number of hops = 6
• Study on .NET Messenger Service [Leskovec and Horvitz, 2008]
• Average number of hops = 6.6

16. Strong and Weak Ties
• Mark Granovetter. The Strength of Weak Ties. 1973
• Relationships can be classified as “strong” or “weak.”
• Discovered that people get jobs using info from “weak ties.”
• Strong ties tend to form a tightly knitted group.
• There are weak ties link group together.
• Therefore, source of rare info.

17. Strong and Weak Ties
• Neighborhood overlap = portion of common friends that are friends.
Neiborhood overlap vs tie strength in a telephone system.
David Easley and Jon Kleinberg, Networks, Crowds, and Markets.

18. Strong and Weak Ties
• Implications:
• Social networks tend to be partitioned into tightly knitted group.
• Leads naturally to the problem of graph partitioning.
David Easley and Jon Kleinberg, Networks, Crowds, and Markets.

19. Positive and Negative Links
• Edges can be classified as
• positive: friendship, fandom, following
• negative: animosity, rivalry, conflict

20. Positive and Negative Links
• Structural balance: some types of triangles are more “stable” than others.
David Easley and Jon Kleinberg, Networks, Crowds, and Markets.
• Networks will arrange themselves so that all triangles are type (a) or (c).

21. Positive and Negative Links
Relationship among European countries before WWI.
David Easley and Jon Kleinberg, Networks, Crowds, and Markets.

22. Process

23. Homophily
• People who are alike tend to be linked.
• Two types of link formation by homophily:
• Selection: People with the same focus link to one another.
• Social influence: People start behaving like those they are linked with.
• What are the roles of selection and social influence in link formation?
• Can we classify which one is accountable for which link?

24. Homophily
Friendships among students in a middle school and a high school. The colors are based on race.
David Easley and Jon Kleinberg, Networks, Crowds, and Markets.

25. Homophily
Similarity between Wikipedia editors vs time.
David Easley and Jon Kleinberg, Networks, Crowds, and Markets.

26. Small-World Phenomena
• A series of papers by Jon Kleinberg.
• Milgram asked people to do “decentralized search.”
• Not all graphs are good for this.
• Series of mathematical models of “small-world graphs.”
• Common characteristic
• Constant link density across distance stance.
• E.g. 10 links to 1-2 km, 10 links to 2-4 km, 10 links to 4-8 km.

27. Small-World Phenomena
• Liben-Nowell et al. Geographic
Routing in Social Networks.
2005
• Found that social networks
in LiveJournal is efficient to
do decentralized search.
• Again, constant link density
across distance scale.
• Users tend to befriend with
those geographically close
to them.

28. Power Laws
• A mathematical model for power-law distribution.
• Vertices are to form links sequentially.
• With probability p, link to a random vertex.
• With probability 1-p
• Choose a random vertex.
• Then, link to a random vertex connected to that vertex.
• c = -(1 + 1 / (1-p))

29. Design

30. Prediction
• Use machine learning to predict several aspects discussed previously.
• Examples:
• Link formation. [Liben-Nowell and Kleinberg 2003]
• Positive and negative links. [Leskovec et al. 2010]
• Relationship strength from online activity. [Xiang et al. 2010]
• Selection or social influence? [La Fond and Neville 2010]

31. Detection
• Social networks also provide other types of data.
• Texts from blogs and tweets.
• Pictures for picture sharing sites.
• Geographical location.
• Use the above information to detect events, news cycle, etc.

32. Meme Tracking [Leskovec et al. 2009]
• Extract quotes from blogs, and graph their volumes over time.
• Possible to see news cycles.
J. Leskovec, L. Backstrom, J. Kleinberg. Meme-tracking and the Dynamics of the News Cycle. ACM SIGKDD Intl. Conf. on Knowledge Discovery and Data Mining, 2009.

33. Earthquake Detection [Sakaki et al. 2010]
• User tweets to detect real-time events such as earthquakes and typhoons.
• View human users as sensors.
• Warning after the fact, but 3-6 minutes faster than JMA.

34. Research Ideas

35. Analyze Social Networks/New Media in Thailand
• Facebook, hi5, twitter, wikipedia, etc.
• Graph structures. Homophily.
• Other social science questions.
• What are people using it for?
• How do they represent themselves?
• Are there cultural norms that are particular to Thai people?
• How do blog services like oknation, gotoknow, and exteen differ?

36. Detection / Prediction
• Social sensors
• Can we detect traffic jam with twitter?
• What are the most popular news stories in Thailand now?
• Prediction
• Is this pantip.com thread likely to be featured in drama-addict.com?
• Can we determine political disposition of a person by his online activity?

37. Social Networks and User Generated Content
• Nico Nico Douga (a Japanese video sharing sites)
• How can Youtube and Nico Nico Douga be so different?
• Can we trace the memes?
• Can we determine influential memes?
• Can we predict which video is going to be popular?
• User/content dynamics.
• Can do the same for social networks of artists like pixiv, piapro, and
Deviant Art.