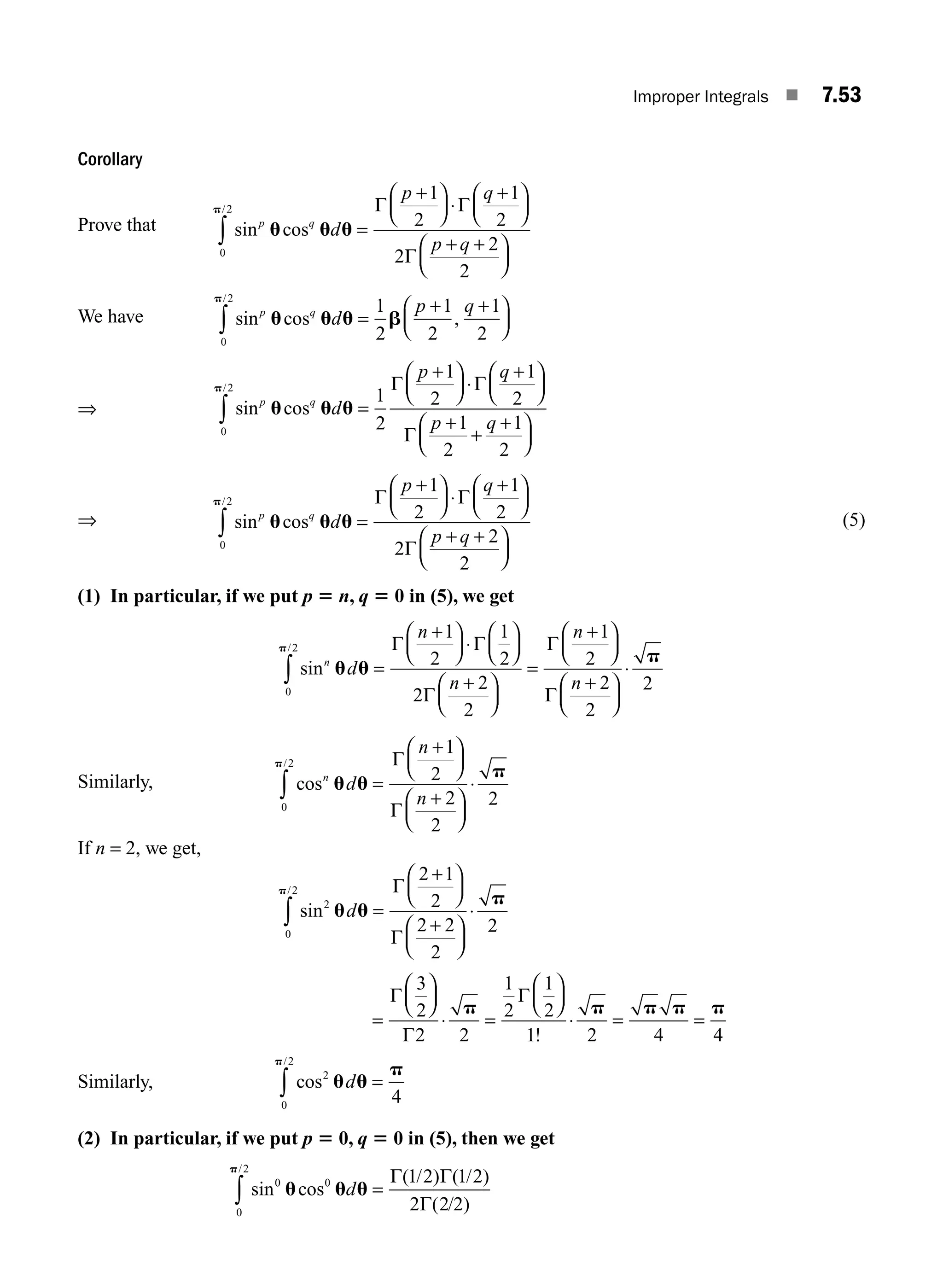
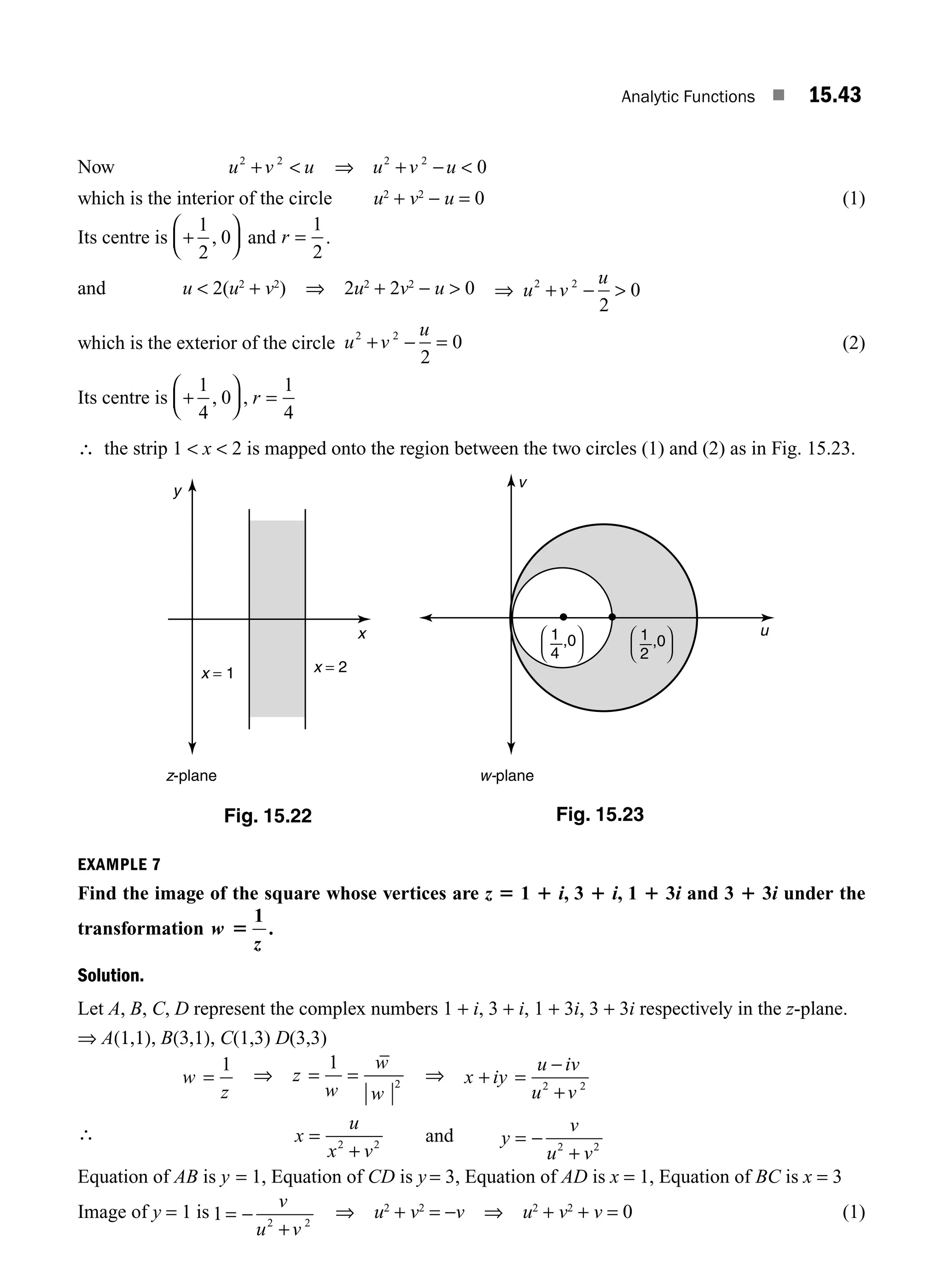
Pearson is a global learning company active in 70 countries, recognized for its collaboration with educators to enhance teaching and learning experiences. The document outlines products and services aimed at improving educational outcomes, particularly in higher education and K-12. It includes a comprehensive guide to engineering mathematics, covering topics from algebra to complex analysis.
























![xxiv n Contents
13.2 Frobenius Method 13.9
Worked Examples13.11
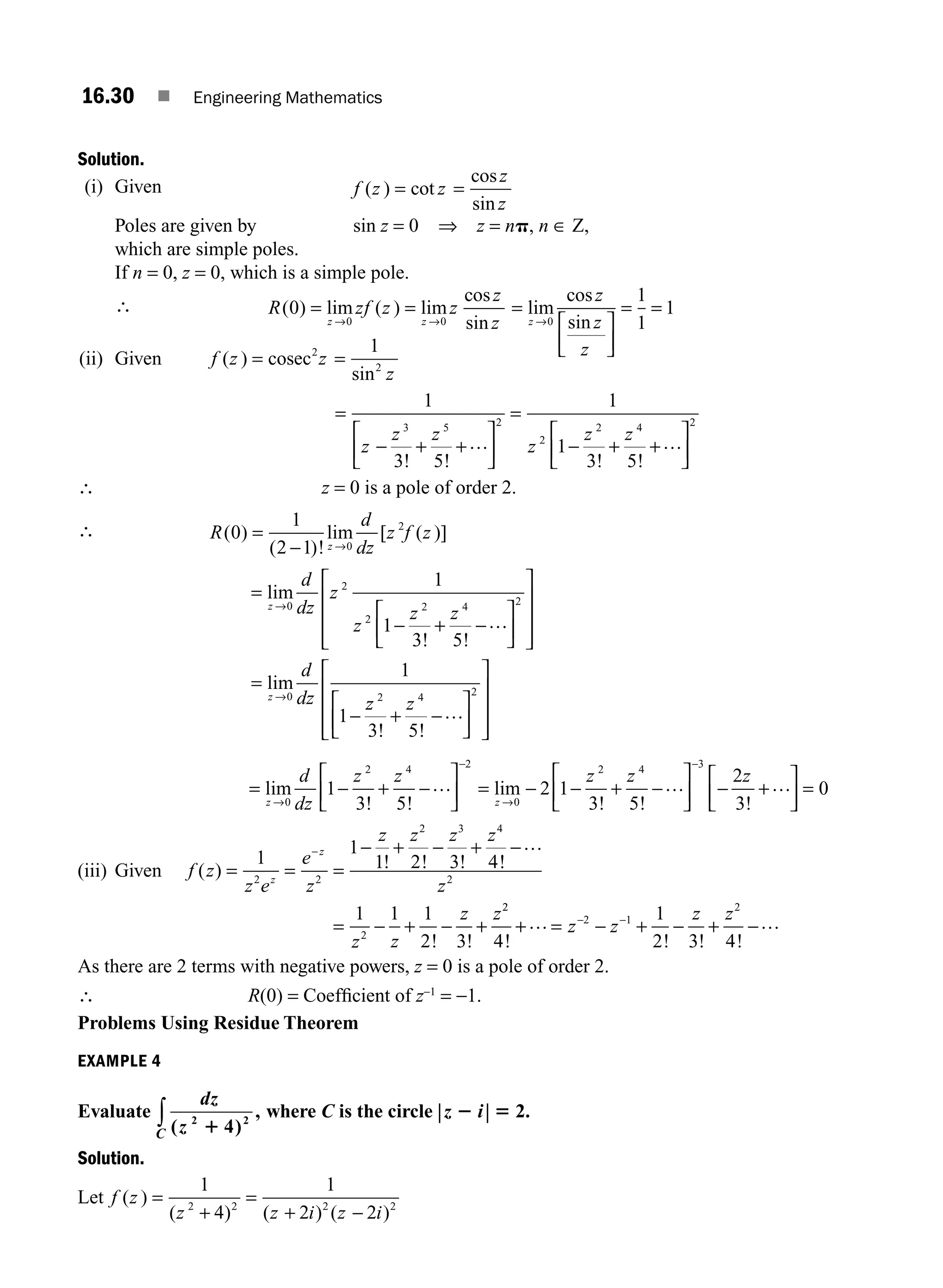
Exercise 13.213.33
Answers to Exercise 13.213.33
13.3 Special Functions 13.34
13.4 Bessel Functions 13.34
13.4.1 Series Solution of Bessel’s Equation 13.34
13.4.2 Bessel’s Functions of the First Kind 13.37
Worked Examples13.39
13.4.3 Some Special Series 13.40
13.4.4 Recurrence Formula for Jn (x)13.41
13.4.5 Generating Function for Jn (x) of Integral Order 13.44
Worked Examples13.46
13.4.6 Integral Formula for Bessel’s Function Jn (x) 13.49
Worked Examples13.53
13.4.7 Orthogonality of Bessel’s Functions 13.56
13.4.8 Fourier–Bessel Expansion of a Function f(x)13.59
Worked Examples13.60
13.4.9 Equations Reducible to Bessel’s Equation 13.62
Worked Examples13.62
Exercise 13.313.65
Answers to Exercise 13.313.66
13.5 Legendre Functions 13.66
13.5.1 Series Solution of Legendre’s Differential Equation 13.66
13.5.2 Legendre Polynomials 13.71
13.5.3 Rodrigue’s Formula 13.71
Worked Examples13.73
13.5.4 Generating Function for Legendre Polynomials 13.74
Worked Examples13.75
13.5.5 Orthogonality of Legendre Polynomials in [-1, 1] 13.77
Worked Examples13.80
13.5.6 Fourier–Legendre Expansion of f(x) in a Series of Legendre
Polynomials13.83
Worked Examples13.83
Exercise 13.413.85
Answers to Exercise 13.413.85
14. Partial Differential Equations 14.1
14.0 Introduction 14.1
14.1 Order and Degree of Partial Differential Equations 14.1
14.2 Linear and Non-linear Partial Differential Equations 14.1
14.3 Formation of Partial Differential Equations 14.2
Worked Examples 14.2
Exercise 14.114.15
Answers to Exercise 14.114.15
A01_ENGINEERING_MATHEMATICS-I _FM - (Reprint).indd 24 3/2/2017 6:17:55 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-25-2048.jpg)












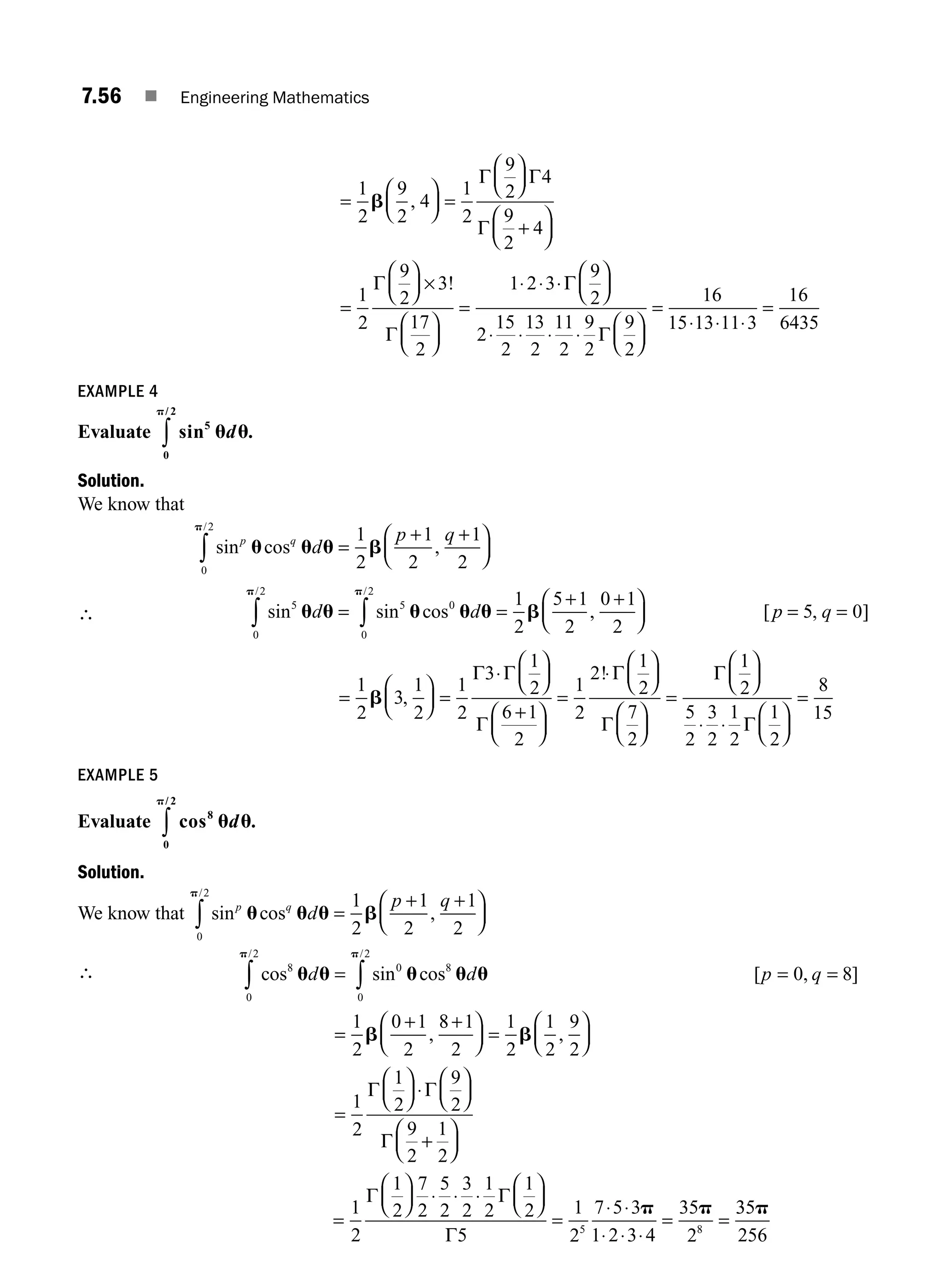
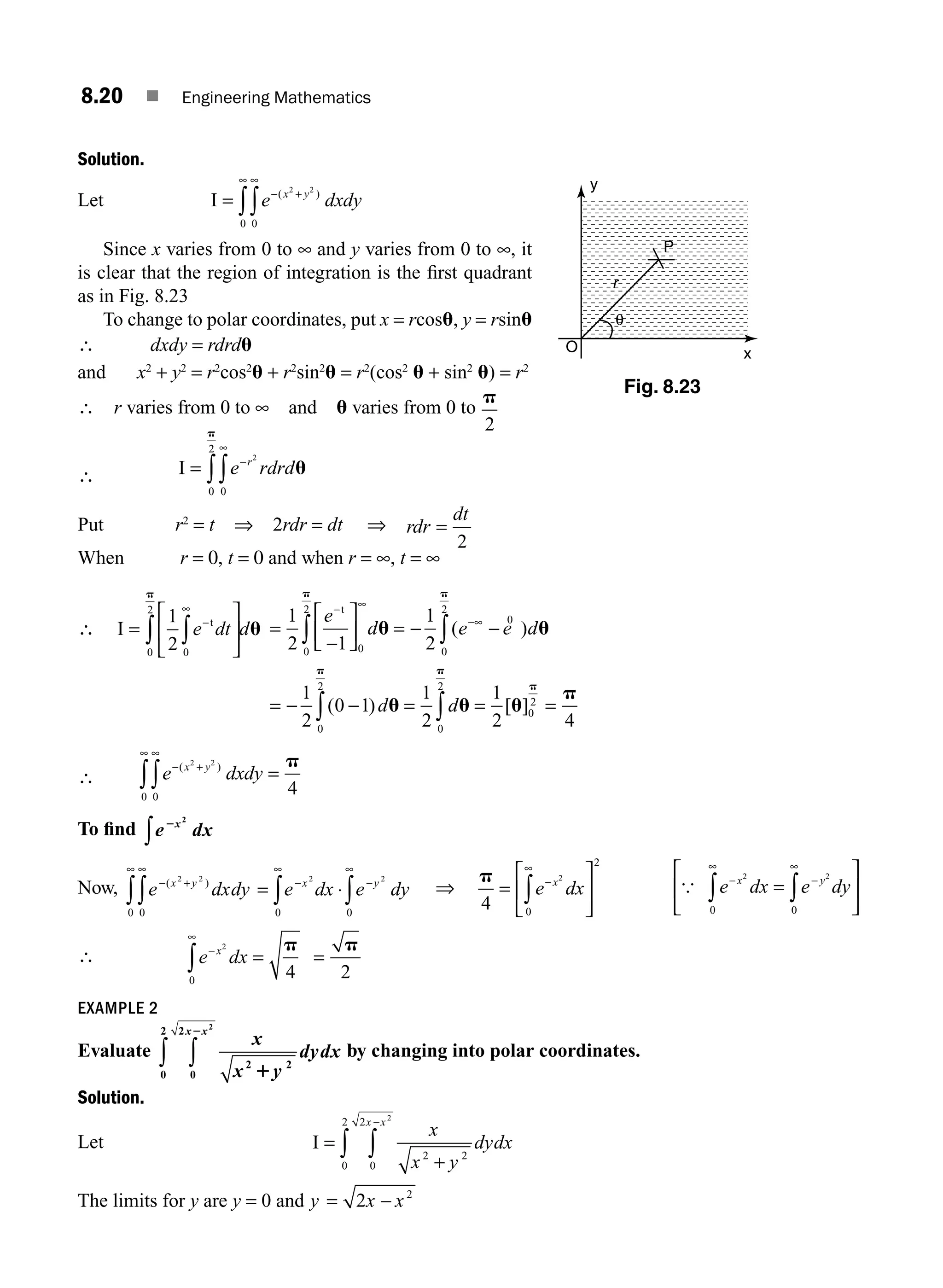
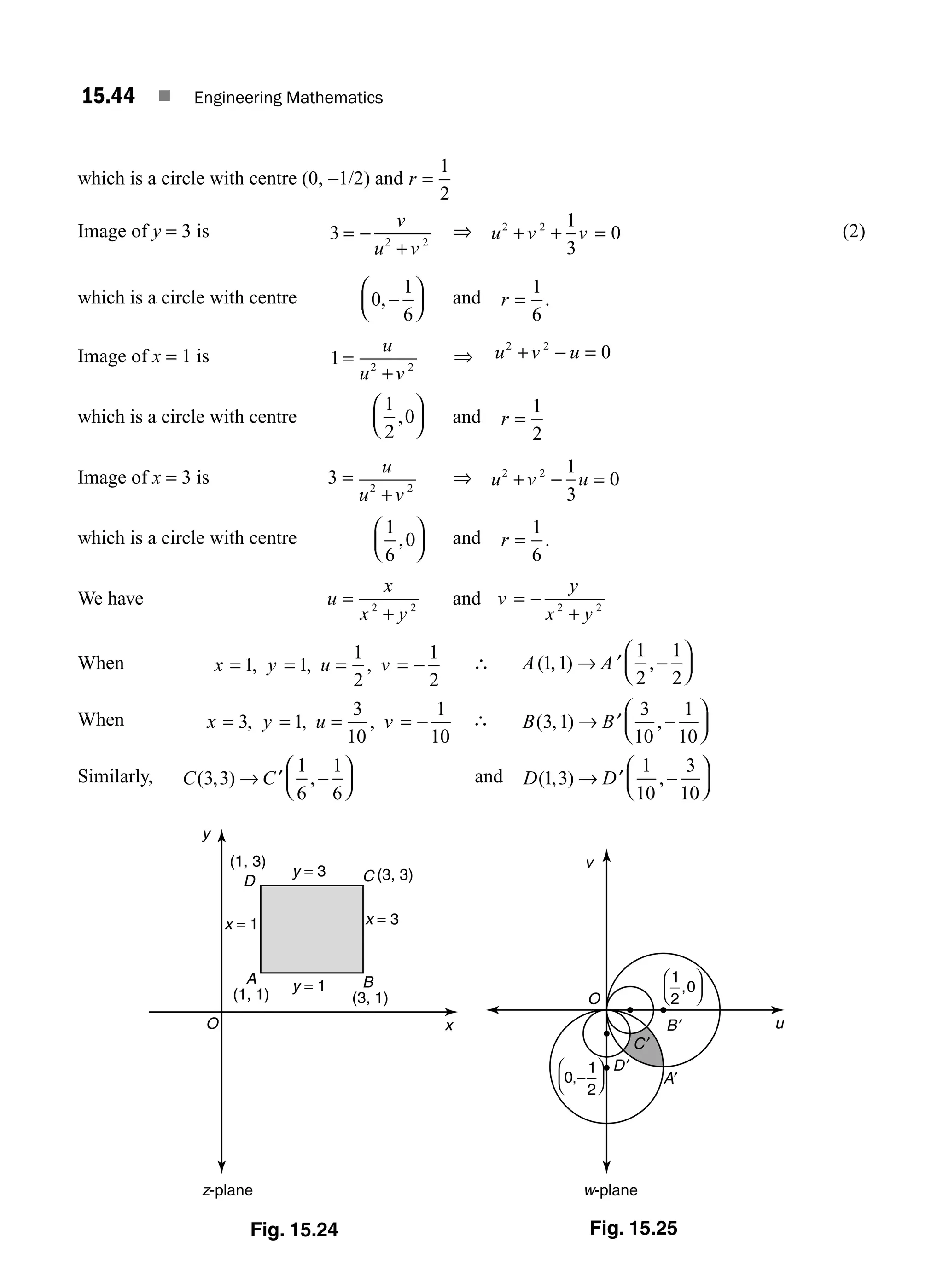
![1.0 INTRODUCTION
The concept of matrices and their basic operations were introduced by the British mathematician
Arthur Cayley in the year 1858. He wondered whether this part of mathematics will ever be used.
However, after 67 years, in 1925, the German physicist Heisenberg used the algebra of matrices in his
revolutionary theory of quantum mechanics. Over the years, the theory of matrices have been found as
an elegant and powerful tool in almost all branches of Science and Engineering like electrical networks,
graph theory, optimisation techniques, system of differential equations, stochastic processes, computer
graphics, etc. Because of the digital computers, usage of matrix methods have become greatly fruitful.
In this chapter, we review some of the basic concepts of matrices. We shall discuss two important
applications of matrices, namely consistency of system of linear equations and the eigen value problems.
1.1 BASIC CONCEPTS
Definition 1.1 Matrix
A rectangular array of mn numbers (real or complex) arranged in m rows (horizontal lines) and
n columns (vertical lines) and enclosed in brackets [ ] is called an m × n matrix.
The numbers in the matrix are called entries or elements of the matrix.
Usually an m × n matrix is written as
A
a a a a
a a a a a
a a a a a
j n
j n
i i i ij in
=
a11 12 13 1 1
21 22 23 2 2
1 2 3
… …
… …
… …
A A A A A
A
A A A
a a a a a
m m m mj mn
1 2 3 … …
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
where aij
is the element lying in the ith
row and jth
column, the first suffix refers to row and the second
suffix refers to column.
The matrix A is briefly written as
A = [aij
]m × n
, i = 1, 2, 3, …, m, j = 1, 2, 3, …, n
If all the entries are real, then the matrix A is called a real matrix.
Definition 1.2 Square Matrix
In a matrix, if the number of rows = number of columns = n, then it is called a square matrix of order n.
If A is a square matrix of order n, then A = [aij
]n × n
, i = 1, 2, 3, …, n; j = 1, 2, 3, …, n.
Definition 1.3 Row Matrix
A matrix with only one row is called a row matrix.
1
Matrices
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 1 5/30/2016 4:34:37 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-38-2048.jpg)
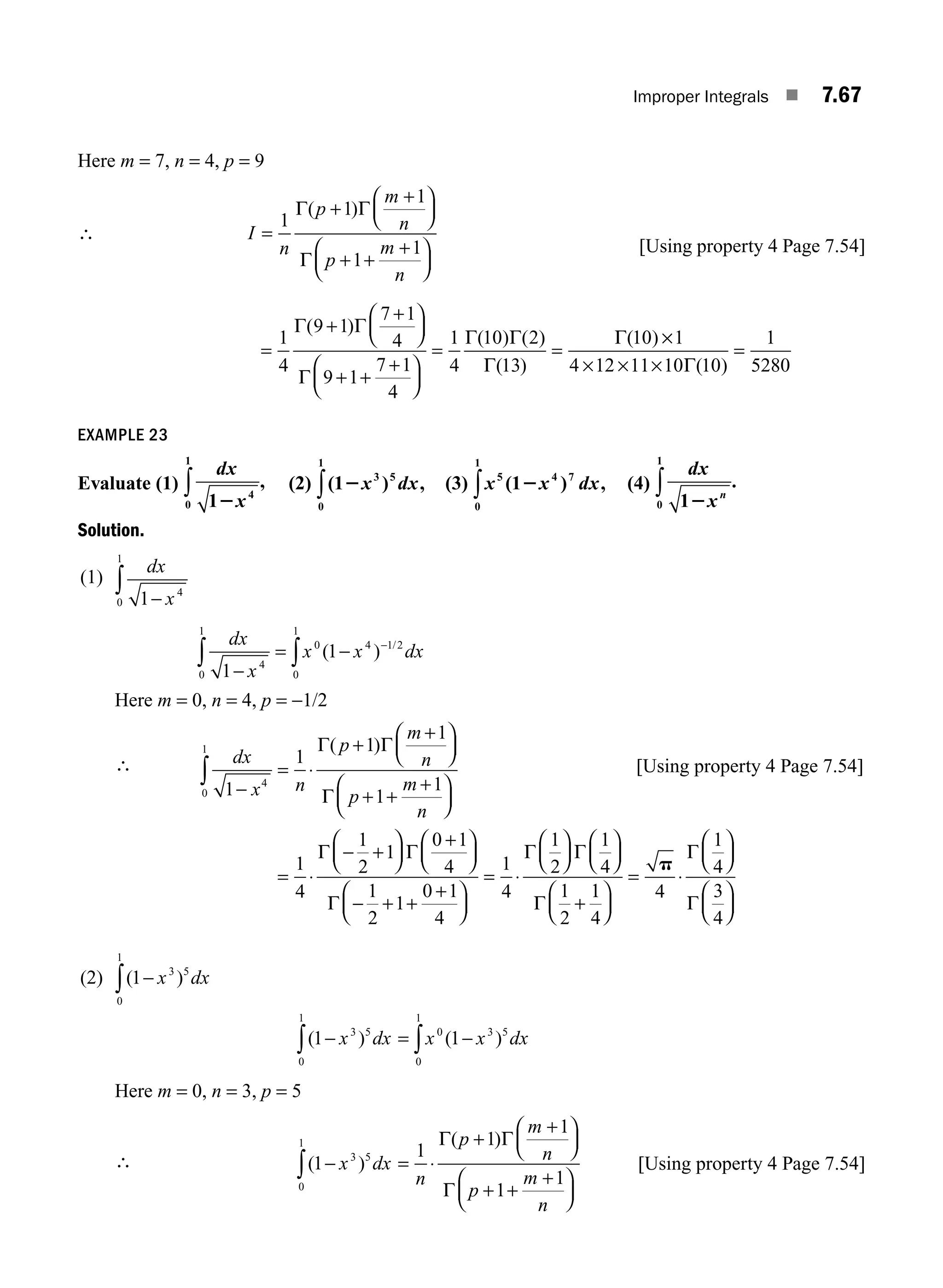
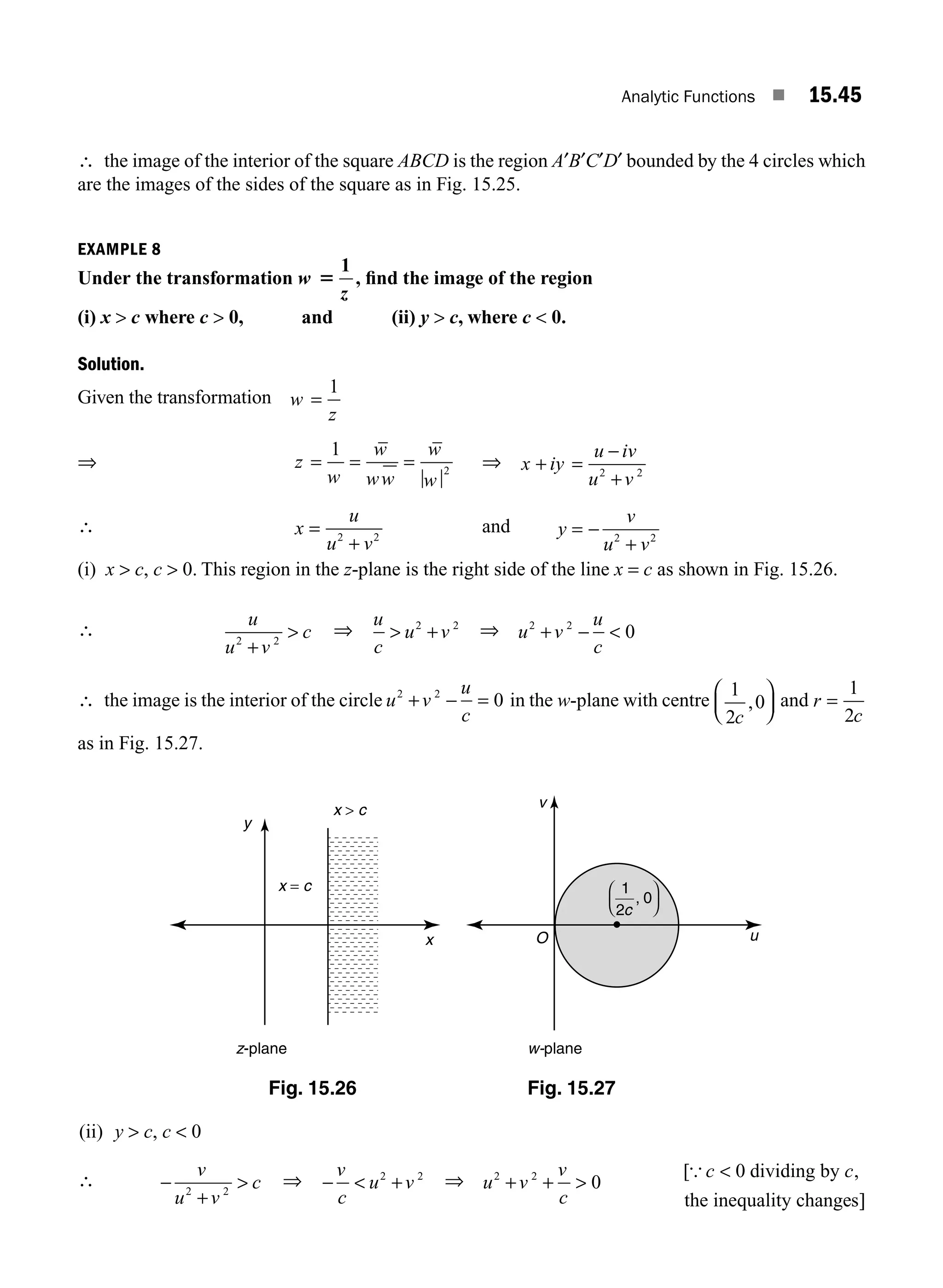
![1.2 ■ Engineering Mathematics
EXAMPLE 1.1
Let A = [a11
a12
a13
… a1n
]. It is a row matrix with n columns. So, it is of type 1 × n.
EXAMPLE 1.2
Let A = [1, 2, 3, 4]. It is a row matrix with 4 columns. So, it is a row matrix of type 1 × 4.
Definition1.4 Column Matrix
A matrix with only one column is called a column matrix.
EXAMPLE 1.3
Let A
a
a
a
an
=
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
11
21
31
1
:
It is a column matrix with n rows. So, it is of type n × 1.
EXAMPLE 1.4
Let A = −
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
1
0
2
1
3
It is a column matrix with 5 rows. So, it is of type 5 × 1.
Definition 1.5 Diagonal Matrix
A square matrix A = [aij
] with all entries aij
= 0 when i ≠ j is is called a diagonal matrix.
In other words a square matrix in which all the off diagonal elements are zero is called a diagonal
matrix.
EXAMPLE 1.5
(1) A
a
ann
=
…
…
…
11 0 0 0
0 0
0 0 0
0 22
a
: : :
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
is a diagonal matrix of order n.
(2) A =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 0 0
0 3 0
0 0 4
is a diagonal matrix of order 3.
(3) A =
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
1 0 0 0
0 2 0 0
0 0 3 0
0 0 0 0
is a diagonal matrix of order 4.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 2 5/30/2016 4:34:38 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-39-2048.jpg)
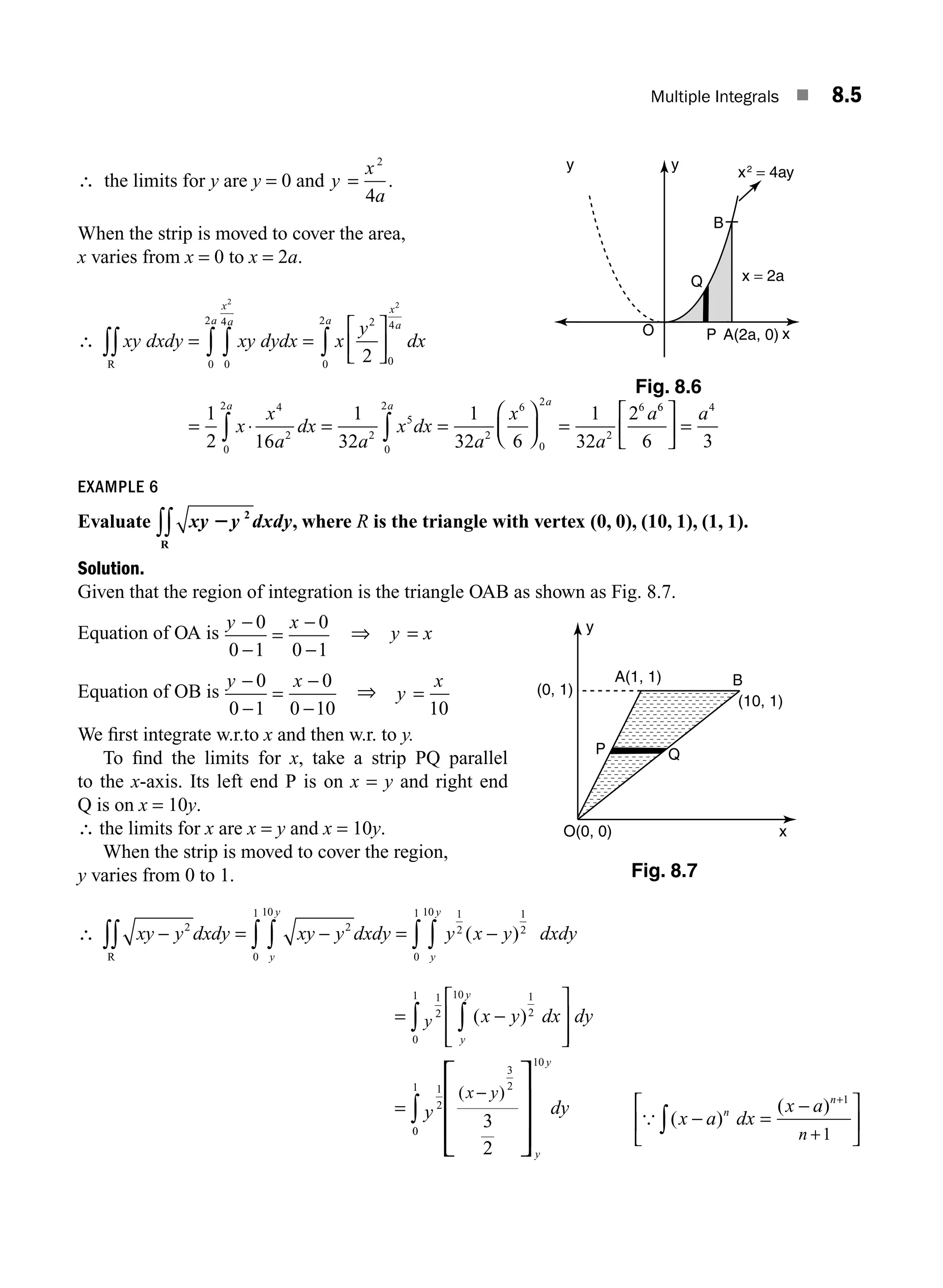
![Matrices ■ 1.3
Definition 1.6 Scalar Matrix
In a diagonal matrix if all the diagonal elements are equal to a non-zero scalar a, then it is called a
scalar matrix.
EXAMPLE 1.6
A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
a
a
a
0 0
0 0
0 0
is a scalar matrix.
Definition 1.7 Unit Matrix or Identity Matrix
In a diagonal matrix, if all the diagonal elements are equal to 1, then it is called a Unit matrix or
identity matrix.
EXAMPLE 1.7
[ ], ,
1
1 0
0 1
1 0 0
0 1 0
0 0 1
⎡
⎣
⎢
⎤
⎦
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
are identity matrices of orders 1, 2, 3 respectively. They are denoted by I1
, I2
, I3
.
In general, In
is the identity matrix of order n.
Definition 1.8 Zero Matrix or Null Matrix
In a matrix (rectangular or square), if all the entries are equal to 0, then it is called a zero matrix or
null matrix.
EXAMPLE 1.8
A B
=
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
⎦
⎥
0 0
0 0
0 0 0 0
0 0 0 0
, are zero matrices of types 2 × 2 and 2 × 4.
Definition 1.9 Triangular matrix
A square matrix A = [aij
] is said to be an upper triangular matrix if all the entries below the main
diagonal are zero.
That is aij
= 0 if i j
A square matrix A = [aij
] is said to be a lower triangular matrix if all the entries above the main
diagonal are zero.
That is aij
= 0 if i j
EXAMPLE 1.9
(1) The matrices A B
=
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
1 2 3
0 1 4
0 0 5
4 1 0 2
0 2 3 1
0 0 0 2
0 0 0 5
and are upper triangular matrices.
(2) The matrices A =
−
⎡
⎣
⎢
⎤
⎦
⎥
2 0
1 0
and B = −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 0 0
2 1 0
0 2 1
are lower triangular matrices.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 3 5/30/2016 4:34:39 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-40-2048.jpg)
![1.4 ■ Engineering Mathematics
1.1.1 Basic Operations on Matrices
Definition 1.10 Equality of Matrices
Two matrices A = [aij
] and B = [bij
] of the same type m × n are said to be equal if aij
= bij
for all i, j and
is written as A = B.
Definition 1.11 Addition of Matrices
Let A = [aij
] and B = [bij
] of the same type m × n. Then A + B = [cij
], where cij
= aij
+ bij
for all i and j
and A + B is of type m × n.
EXAMPLE 1.10
If A =
−
⎡
⎣
⎢
⎤
⎦
⎥
1 2 3
0 1 5
and B =
−
⎡
⎣
⎢
⎤
⎦
⎥
1 2 3
1 0 2
, then A B
+ =
− + + +
+ + −
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
⎦
⎥
1 1 2 2 3 3
0 1 1 0 5 2
0 4 6
1 1 3
We see that A and B are of type 2 × 3 and A + B is also of type 2 × 3.
Definition 1.12 Scalar Multiplication of a Matrix
Let A = [aij
] be an m × n matrix and k be a scalar, then kA = [kaij
].
EXAMPLE 1.11
If A
a a a
a a a
=
⎡
⎣
⎢
⎤
⎦
⎥
11 12 13
21 22 23
, then kA
ka ka ka
ka ka ka
=
⎡
⎣
⎢
⎤
⎦
⎥
11 12 13
21 22 23
.
In particular if k = −1, then − =
− − −
− − −
⎡
⎣
⎢
⎤
⎦
⎥
A
a a a
a a a
11 12 13
21 22 23
.
Multiplication of Matrices
If A and B are two matrices such that the number of columns of A is equal to the number of rows of
B, then the product AB is defined. Two such matrices are said to be conformable for multiplication.
In the product AB, A is known as pre-factor and B is known as post-factor.
Definition 1.13 Let A = [aij
] be an m × p matrix and B = [bij
] be an p × n matrix, then AB is defined and
AB = [cij
] is an m × n matrix, where c a b
ij ik kj
k
p
=
=
∑1
.
That is cij
is the sum of the products of the corresponding elements of the ith
row of A and the jth
column of B.
EXAMPLE 1.12
Let A B
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 2
0 1 3
2 2 1
1 2
3 1
2 1
and
Since A is of type 3 × 3 and B is of type 3 × 2, AB is defined and AB is of type 3 × 2.
AB =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⋅ + ⋅ + ⋅ ⋅ + ⋅ +
1 1 2
0 1 3
2 2 1
1 2
3 1
2 1
1 1 1 3 2 2 1 2 1 1 2
2 1
0 1 1 3 3 2 0 2 1 1 3 1
2 1 2 3 1 2 2 2 2 1 1 1
⋅
⋅ + ⋅ + ⋅ ⋅ + ⋅ + ⋅
⋅ + ⋅ + ⋅ ⋅ + ⋅ + ⋅
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
8 5
9 4
10 7
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 4 5/30/2016 4:34:41 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-41-2048.jpg)
![Matrices ■ 1.5
Note If A and B are square matrices of order n, then both AB and BA are defined, but not necessarily
equal. That is, AB ≠ BA, in general.
So, matrix multiplication is not commutative.
1.1.2 Properties of addition, scalar multiplication and multiplication
1. If A, B, C are matrices of the same type, then
(i) A + B = B + A (ii) A + (B + C) = (A + B) + C
(iii) A + 0 = A (iv) A + (−A) = 0
(v) a(A + B) = aA + aB (vi) (a + b)A = aA + bA
(vii) a(bA) = (ab)A for any scalars a, b.
2. If A, B, C are conformable for multiplication, then
(i) a(AB) = (aA)B = A(aB)
(ii) A(BC) = (AB)C
(iii) (A + B)C = AC + BC, where A and B are of type m × p and C is of type p × n.
(iv) If A is a square matrix, then
A2
= A × A, A3
= A2
× A, …, An
= An − 1
× A
Definition 1.14 Transpose of a Matrix
Let A = [aij
] be an m × n matrix. The transpose of A is obtained by interchanging the rows and
columns of A and it is denoted by AT
.
∴ =
A a
T
ji
[ ] is a n × m matrix.
Properties:
(i) (AT
)T
= A (ii) (A + B)T
= AT
+ BT
(iii) (AB)T
= BT
AT
(iv) (aA)T
= aAT
Definition 1.15 Symmetric Matrix
A square matrix A = [aij
] of order n is said to be symmetric if AT
= A.
This means [aji
] = [aij
] ⇒ aji
= aij
for i, j = 1, 2, …n
Thus, in a symmetric matrix elements equidistant from the main diagonal are the same.
EXAMPLE 1.13
A
a h g
h b f
g f c
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
and B =
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
1 2 3 4
2 0 5 7
3 5 2 8
4 7 8 4
are symmetric matrices of orders 3 and 4.
Definition 1.16 Skew-Symmetric Matrix
A square matrix A = [aij
] of order n is said to be skew-symmetric if AT
= −A.
This means [aji
] = −[aij
] ⇒ aji
= − aij
for all i, j = 1, 2, …, n
In particular, put j = i, then aii
= − aii
⇒ 2aii
= 0 ⇒ aii
= 0 for all i = 1, 2, …, n
So, in a skew-symmetric matrix, the diagonal elements are all zero and elements equidistant from
the main diagonal are equal in magnitude, but opposite in sign.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 5 5/30/2016 4:34:41 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-42-2048.jpg)
![1.6 ■ Engineering Mathematics
EXAMPLE 1.14
A B
=
−
⎡
⎣
⎢
⎤
⎦
⎥ =
−
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
0 1
1 0
0 2 3
2 0 4
3 4 0
and are skew-symmetric matrices of orders 2 and 3.
Definition 1.17 Non-Singular Matrix
A Square matrix A is said to be non-singular if A ≠ 0 ( A means determinant of A).
If A = 0, then A is singular.
Definition 1.18 Minor and Cofactor of an Element
Let A = [aij
] be a square matrix of order n. If we delete the row and column of the element aij
, we get
a square submatrix of order (n − 1).
The determinant of this submatrix is called the minor of the element aij
and is denoted by Mij
.
The cofactor of aij
in A is A M
ij
i j
ij
= − +
( )
1
EXAMPLE 1.15
A = −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 6 2
0 2 4
3 1 2
The cofactor of a11
= 1 is A11
1 1
1
2 4
1 2
= −
−
+
( ) = −4 −4 = −8
The cofactor of a12
= 6 is A12
1 2
1
0 4
3 2
= − +
( ) = − (−12) = 12
The cofactor of a32
= 1 is A32
3 2
1
1 2
0 4
= − +
( ) = − (4 −0) = −4
Similarly, we can determine the cofactors of other elements.
Definition 1.19 Adjoint of a Matrix
Let A = [aij
] be a square matrix. The adjoint of A is defined as the transpose of the matrix of cofactors
of the elements of A and it is denoted by adj A.
Thus, adj A
A A A
A A A
A A A
n
n
n n nn
T
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
11 12 1
21 21 2
1 2
…
…
…
: : :
Properties: If A and B are square matrices of order n, then
(i) adj AT
= (adj A)T
(ii) (adj A) A = A (adj A) = A In
.
(iii) adj(AB) = (adj A) (adj B)
Using property (ii), we define inverse.
Definition 1.20 Inverse of a Matrix
If A is a non-singular matrix, then the inverse of A is defined as
adj A
A
and it is denoted by A−1
.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 6 5/30/2016 4:34:44 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-43-2048.jpg)
![Matrices ■ 1.7
∴ A
A
A
−
=
1 adj
EXAMPLE 1.16
Find the inverse of A = −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 6 2
0 2 4
3 1 2
.
Solution.
Given A = −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 6 2
0 2 4
3 1 2
∴ A = −
1 6 2
0 2 4
3 1 2
= 1(−4 −4) −6(0 − 12) + 2(0 + 6) = −8 + 72 + 12 = 76 ≠ 0
Since A ≠ 0, A is non-singular and hence A−1
exists and A
A
A
−
=
1 adj
.
We shall find the cofactors of the elements of A
A A
A
11
1 1
12
1 2
13
1
2 4
1 2
4 4 8 1
0 4
3 2
0 12 12
= −
−
= − − = − = − = − − =
=
+ +
( ) ( ) , ( ) ( )
(−
−
−
= + = = − = − − = −
= −
+ +
+
1
0 2
3 1
0 6 6 1
6 2
1 2
12 2 10
1
1 3
21
2 1
22
2
) ( ) , ( ) ( )
( )
A
A 2
2
23
2 3
31
3 1
1 2
3 2
2 6 4 1
1 6
3 1
1 18 17
1
6 2
2 4
= − = − = − = − − =
= −
−
+
+
( ) , ( ) ( )
( )
A
A =
= + = = − = − − = −
= −
−
= − −
+
+
( ) , ( ) ( )
( ) (
24 4 28 1
1 2
0 4
4 0 4
1
1 6
0 2
2
32
3 2
33
3 3
A
A 0
0 2
) = −
∴
8 12 6
10 4 17
28 4 2
8 10 28
12 4 4
6 17
=
−
− −
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
− −
− −
−
adj A
T
2
2
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
∴ A −
=
− −
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1
76
8 10 28
12 4 4
6 17 2
1.2 COMPLEX MATRICES
A matrix with at least one element as complex number is called a complex matrix.
Let A = [aij
] be a complex matrix.
The conjugate matrix of A is denoted by A and A aij
= ⎡
⎣ ⎤
⎦.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 7 5/30/2016 4:34:46 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-44-2048.jpg)
![1.8 ■ Engineering Mathematics
EXAMPLE 1.17
A
i i
i
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥
2 2
3 2 0 3
is a complex matrix.
The conjugate of A is A
i i
i
i i
i
=
−
−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
=
−
+
⎡
⎣
⎢
⎤
⎦
⎥
2 2
3 2 0 3
2 2
3 2 0 3
[{ conjugate of a + ib = a − ib]
We denote A
T
( ) by A*.
∴ A* is the transpose of the conjugate of A.
In the above example
A
i i
i
*
=
− +
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 3 2
0
2 3
Note We have A A A A
T T T
⎡
⎣ ⎤
⎦ = ⎡
⎣ ⎤
⎦ ∴ = ⎡
⎣ ⎤
⎦
∗
∴ If A a A a A a
ji
T
ji
T
ji
= = ⎡
⎣ ⎤
⎦
[ ], [ ],
then =[ ] ∴ A ∗
= [ ]
aji
Definition 1.21 Hermitian Matrix
A complex square matrix A is said to be a Hermitian matrix if A* = A and Skew-Hermitian matrix if
A* = −A.
A Hermitian matix is also denoted by AH
.
If A = [aij
], then A aji
* [ ]
= ∴ A* = A ⇒ aji = aij
for all i and j
Put j = i, then aii = aii
⇒ aii
are real numbers.
So, the diagonal elements of a Hermitian matrix are real numbers.
The elements equidistant from the main diagonal are conjugates.
A* = −A ⇒ aji = −aij
for all i and j
Put j = i, then aii = −aii
If aii
= a + ib, then aii = a − ib
∴ a − ib = −(a + ib) ⇒ 2a = 0 ⇒ a = 0
∴ aii
= ib, which is purely imaginary if b ≠ 0 and 0 if b = 0.
∴ the diagonal elements of a Skew-Hermitian matrix are all purely imaginary or 0 and the elements
equidistant from the main diagonal are conjugates with opposite sign.
Properties: If A and B are complex matrices, then
1. A A
( ) = , 2. A B A B
+ = + 3. a a
A A
=
4. AB A B
= 5. (A*).* = A 6. (A + B).* = A* + B*
7. (aA).* = aA * 8. (AB).* = B*A*
Definition 1.22 Unitary Matrix
A complex square matrix is said to be unitary if AA* = A*A = I
From the definition it is obvious that A* is the inverse of A.
∴ A* = A−1
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 8 5/30/2016 4:34:50 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-45-2048.jpg)

![1.10 ■ Engineering Mathematics
WORKED EXAMPLES
EXAMPLE 1
If A
i i
i i
5
1 2 1
2 2
2 3 1 3
5 4 2
⎡
⎣
⎢
⎤
⎦
⎥ , then show that AA* is a Hermitian matrix.
Solution.
Given A
i i
i i
=
+ − +
− −
⎡
⎣
⎢
⎤
⎦
⎥
2 3 1 3
5 4 2
∴ A* = A
i i
i i
T
T
[ ] =
− − −
− − +
⎡
⎣
⎢
⎤
⎦
⎥
2 3 1 3
5 4 2
=
− −
−
− − +
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 5
3
1 3 4 2
i
i
i i
We have to prove AA* is a Hermitian matrix.
That is to prove (AA*)* = AA*
Now AA
i i
i i
i
i
i i
* =
+ − +
− −
⎡
⎣
⎢
⎤
⎦
⎥
− −
−
− − +
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 3 1 3
5 4 2
2 5
3
1 3 4 2
=
+ − + ⋅ + − + − − + − + − + − + +
( )( ) ( )( ) ( )( ) ( ) ( ) (
2 2 3 3 1 3 1 3 2 5 3 1 3 4 2
i i i i i i i i
i
i i i i i i i i
)
( ) ( )( ) ( )( ) ( ) ( )( )
− − + ⋅ + − − − − − + − + − +
⎡
⎣
⎢ 5 2 3 4 2 1 3 5 5 4 2 4 2
⎤
⎤
⎦
⎥
=
+ + + + − − − − + +
− + + − − + − +
2 1 9 1 3 10 5 3 4 10 6
10 5 3 4 10 6 25 4
2 2 2
2 2 2
i i i i
i i i i i +
+
⎡
⎣
⎢
⎤
⎦
⎥
=
− + −
− − −
⎡
⎣
⎢
⎤
⎦
⎥ =
− +
− −
⎡
⎣
⎢
⎤
2
24 14 2 6
14 2 6 46
24 20 2
20 2 46
2
i
i
i
i ⎦
⎦
⎥ = −
[ ]
{ i2
1
∴ ( *)*
AA
i
i
T
=
− +
− −
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
24 20 2
20 2 46
=
− −
− +
⎡
⎣
⎢
⎤
⎦
⎥ =
− +
− −
⎡
⎣
⎢
⎤
⎦
⎥
24 20 2
20 2 46
24 20 2
20 2 46
i
i
i
i
T
= AA*
⇒ (AA*)* = AA*
Hence, AA* is a Hermitian matrix.
EXAMPLE 2
Show that every square complex matrix can be expressed uniquely as P + iQ, where P and Q are
Hermitian matrices.
Solution.
Let A be any square complex matrix.
We shall rewrite A as
A A A i
i
A A
= + + −
⎡
⎣
⎢
⎤
⎦
⎥
1
2
1
2
[ *] ( *)
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 10 5/30/2016 4:34:54 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-47-2048.jpg)
![Matrices ■ 1.11
Put P A A Q
i
A A
= + = −
1
2
1
2
( *), ( *), then A = P + iQ.
We shall now prove P and Q are Hermitian.
Now, P A A A A A A P
*
( *) ( * ( *)* ( * )
*
= +
⎡
⎣
⎢
⎤
⎦
⎥ = +
⎡
⎣
⎢
⎤
⎦
⎥ = + =
1
2
1
2
1
2
∴ P is Hermitian.
and Q A A
i
A A
i
A A
i
A A Q
* ( *) ( * ( *)* [ * ] ( *)
*
= −
⎡
⎣
⎢
⎤
⎦
⎥ = −
[ ]= − − = − =
1
2
1
2
1
2
1
2
i
∴ Q is Hermitian.
We shall now prove the uniqueness of the expression A = P + iQ.
If possible, let A = R + iS (1)
where R and S are Hermitian matrices.
∴ R* = R and S* = S
Now, A* = (R + iS)* = R* + (iS)* = R* − iS* = R − iS [by property] (2)
(1) + (2) ⇒ A + A* = 2R ⇒ R =
1
2
( *)
A A P
+ =
(1) − (2) ⇒ A − A* = 2iS ⇒ S =
1
2i
A A Q
( *)
− =
∴ the expression A = P + iQ is unique.
EXAMPLE 3
If A is any square complex matrix, prove that (1) A 1 A* is Hermitian and (ii) A 5 B 1 C, where
B is Hermitian and C is Skew-Hermitian.
Solution.
Given A is a square complex matrix.
(i) Let P = A + A*
∴ P* = (A + A*)* = A* + (A*)* = A* + A = A + A* = P [by property]
∴ P is Hermitian
Hence, A + A* is Hermitian.
To prove (ii): Since A is square complex matrix, we can write A as
A A A A A
= + + −
1
2
1
2
( *) ( *) = B + C
where B A A
= +
1
2
( *) is Hermitian by part (i) and C A A
= −
1
2
( *)
⇒ C A A A A
* ( *) ( * ( *)*
*
= −
⎡
⎣
⎢
⎤
⎦
⎥ = −
[ ]
1
2
1
2
= − = − − = −
1
2
1
2
[ * ] [ *]
A A A A C
∴ C is Skew- Hermitian.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 11 5/30/2016 4:34:57 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-48-2048.jpg)

![Matrices ■ 1.13
( )
( )
1
36
16 4 1 4 0
0 4 1 4 6
1
36
36 0
0 36
=
+ +
+ +
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
⎦
⎥ =
1 0
0 1
I.
∴ B is unitary.
Hence, (I − A)(I + A)−1
is unitary.
Note Another method: To prove B is unitary, verify B* = B−1
EXERCISE 1.1
1. If A B A B
+ =
⎡
⎣
⎢
⎤
⎦
⎥ − =
⎡
⎣
⎢
⎤
⎦
⎥
7 0
2 5
3 0
0 3
, , find A and B
2. Find x, y, z and w if
3
6
1 2
4
3
x y
z w
x
w
x y
z w
⎡
⎣
⎢
⎤
⎦
⎥ =
−
⎡
⎣
⎢
⎤
⎦
⎥ +
+
+
⎡
⎣
⎢
⎤
⎦
⎥
3. If matrix A has x rows and x +5 columns and B has y rows and 11 − y columns such that both AB and BA
exist, then find x and y.
4. If A =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 3 4
1 2 3
1 1 2
and B = −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 3 0
1 2 1
0 0 2
, then find AB and BA and test their equality.
5. If A =
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
0
2
2
0
tan
tan
a
a
, show that I A I A
+ = −
−
⎡
⎣
⎢
⎤
⎦
⎥
[ ]
cos sin
sin cos
a a
a a
6. If A =
−
⎡
⎣
⎢
⎤
⎦
⎥
cos sin
sin cos
a a
a a
, then verify that AAT
= I2
.
7. If A is a square matrix, then show that A can be expressed as A = P + Q, where P is symmetric and Q is
skew-symmetric.
Hint: Take P
A A
Q
A A
T T
=
+
=
−
⎡
⎣
⎢
⎤
⎦
⎥
2 2
,
8. If A =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 0 1
2 1 3
1 1 0
and f(x) = x2
− 5x + 6, then find f(A).
9. If A =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 1
2 3 0
18 2 10
, then prove that A(adj A) =
0 0 0
0 0 0
0 0 0
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
10. Find the inverse of A =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 0 0
3 3 0
5 2 1
in terms of adj A.
11. Show that A
i i
i i
=
+ − +
+ −
⎡
⎣
⎢
⎤
⎦
⎥
1
2
1 1
1 1
is unitary.
12. If A and B are orthogonal matrices of the same order, prove that AB is orthogonal.
[Hint: AAT
= I, BBT
= I. Compute AB(AB)T
= A(BBT
)AT
= AAT
= I].
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 13 5/30/2016 4:35:03 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-50-2048.jpg)
![1.14 ■ Engineering Mathematics
13. If A and B are Hermitian matrices of the same order, prove that
(i) A + B is Hermitian (ii) AB + BA is Hermitian
(iii) iA is Skew-Hermitian (iv) AB − BA is Skew-Hermitian
14. Find the inverse of the following matrices.
(i)
2 1 4
3 0 1
1 1 2
−
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
(ii)
4 3 3
1 0 1
4 4 3
− −
− − −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
15. If A =
3 3 4
2 3 4
0 1 1
−
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, then show that A3
= A−1
.
ANSWERS TO EXERCISE 1.1
1. A B
=
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
⎦
⎥
5 0
1 4
2 0
1 1
, 2. x = 2, y = 4, z = 1, w = 3 3. x = 3, y = 8
4. AB ≠ BA 8. f A
( ) =
− −
− − −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 3
1 1 10
5 4 4
10. A−
= −
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
1
1 0 0
1
1
3
0
3
2
3
1
14. (i) A−
=
−
−
− − −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
1 6 1
5 8 14
3 1 3
(ii) A−
= − −
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
4 3 3
1 0 1
4 4 3
1.3 RANK OF A MATRIX
Let A = [aij
] be an m × n matrix. A matrix obtained by omitting some rows and columns of A is called
a submatrix of A.
The determinant of a square submatrix of order r is called a minor of order r of A.
EXAMPLE 1.22
Consider A =
−
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 3 4 1
0 3 4 0
3 2 1 2
Omitting the fourth column, we get the submatrix A1
2 3 4
0 3 4
3 2 1
=
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
and A1
2 3 4
0 3 4
3 2 1
=
− −
is a
minor of order 3.
Omitting the first and third columns and the third row, we get the submatrix A2
3 1
3 0
=
−
⎡
⎣
⎢
⎤
⎦
⎥ and
A2
3 1
3 0
=
−
is a minor of order 2. Since A2 = 3 ≠ 0, it is called a non-vanishing minor of order 2.
But
3 4
3 4
0
= , so it is called a vanishing minor of order 2.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 14 5/30/2016 4:35:06 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-51-2048.jpg)



![1.18 ■ Engineering Mathematics
k R4
1
1
2
5
6
3
2
0
1
2
7
6
3
2
0 0
4
6
0
0 0 0 3
− − −
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥ →
∼
R
R R
4 3
+
= B
Given r(A) = 3. So, the number of non-zero rows of B should be 3.
∴ k − 3 = 0 ⇒ k = 3
Definition 1.26 Elementary Matrix
A matrix obtained from a unit matrix by performing a single elementary row (column) transformation
is called an elementary matrix.
Since unit matrices are non-singular square matrices, elementary matrices are also non-singular.
EXAMPLE 1.24
I3
1 0 0
0 1 0
0 0 1
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
z
1 0 0
0 1 1
0 0 1 3 3 2
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥ → +
C C C
This is an elementary matrix.
Similarly,
1 0 0
0 3 0
0 0 1
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
got by R2
→ 3R2
is an elementary matrix.
Definition 1.27 Normal form of a Matrix
Any non-zero matrix A of rank r can be reduced by a sequence of elementary transformations to the
form
Ir 0
0 0
⎡
⎣
⎢
⎤
⎦
⎥, where Ir
is a unit matrix of order r.
This form is called a normal form of A.
Other normal forms are Ir
,
Ir
0
⎡
⎣
⎢
⎤
⎦
⎥, [Ir
, 0].
Theorem 1.1
Let A be an m × n matrix of rank r. Then there exist non-singular matrices P and Q of orders m and n
respectively such that PAQ =
Ir 0
0 0
⎡
⎣
⎢
⎤
⎦
⎥
Note Each elementary row transformation of A is equivalent to pre multiplying A by the corresponding
elementary matrix. Each elementary column transformation is equivalent to post multiplying A
by the corresponding elementary matrix. So, there exists elementary matrices P1
, P2
, …, Pk
and
Q1
, Q2
, …, Qt
such that
P1
P2
… Pk
A Q1
Q2
… Qt
=
Ir 0
0 0
⎡
⎣
⎢
⎤
⎦
⎥
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 18 5/30/2016 4:35:12 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-55-2048.jpg)

![1.20 ■ Engineering Mathematics
1 0 0 0
0 1 0 0
0 0 1 0 4 4 3
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥ → −
C C C
∼
=
= [ : ]
I3 0
This is the normal form of A and so the r(A) = 3
EXAMPLE 2
Let A 5
2 2
1 1 1
1 1 1
3 1 1
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.Find matrices P and Q such that PAQ is in the normal form.Also find rank
of A.
Solution.
Given A =
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥ ×
1 1 1
1 1 1
3 1 1 3 3
Consider A = I3
AI3
⇒
1 1 1
1 1 1
3 1 1
1 0 0
0 1 0
0 0 1
1 0 0
0 1 0
0 0 1
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
A ⎥
⎥
⎥
⎥
Our aim is to reduce the LHS matrix to normal form.
Also row operations to be applied to pre factor and column operations to be applied to post factor.
Apply,
and to post factor
C C C
C C C
2 2 1
3 3 1
1 0 0
1 2 2
3 4 4
→ +
→ +
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 0 0
0 1 0
0 0 1
1 1 1
0 1 0
0 0 1
A
R R R
R R R
2 2 1
3 3 1
3
1 0 0
0 2 2
0 4 4
1
→ −
→ + −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
( )
and to pre factor
0
0 0
1 1 0
3 0 1
1 1 1
0 1 0
0 0 1
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
A
R R R
3 3 2
2
1 0 0
0 2 2
0 0 0
1 0 0
1 1 0
1
→ + −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
= −
−
( )
and to pre factor −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 1
1 1 1
0 1 0
0 0 1
A
R R
2 2
1
2
1 0 0
0 1 1
0 0 0
1 0 0
1
2
1
2
0
1 2 1
→
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
= −
− −
and to pre factor
⎡
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
A
1 1 1
0 1 0
0 0 1
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 20 5/30/2016 4:35:16 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-57-2048.jpg)

![1.22 ■ Engineering Mathematics
R R
R R
2 2
3 3
1
3
1
2
1 0 0 0
0 2 2 3
0 2 1 3
1 0
→
→
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
and to pre factor
0
0
4
3
1
3
0
1 0
1
2
1 1 1 2
0 1 0 0
0 0 1 0
0 0 0 1
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
A
⎥
⎥
C C C
4 4 2
3
2
1 0 0 0
0 2 2 0
0 2 1 0
1 0 0
4
3
1
→ +
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
= −
and to post factor
3
3
0
1 0
1
2
1 1 1
1
2
0 1 0
3
2
0 0 1 0
0 0 0 1
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
A ⎥
⎥
⎥
⎥
⎥
C C C
3 3 2
1 0 0 0
0 2 0 0
0 2 1 0
1 0 0
4
3
1
3
→ −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
= −
and to post factor
0
0
1 0
1
2
1 1 0
1
2
0 1 1
3
2
0 0 1 0
0 0 0 1
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
A ⎥
⎥
⎥
⎥
⎥
R R R
3 3 2
1 0 0 0
0 2 0 0
0 0 1 0
1 0 0
4
3
1
3
0
→ −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
= −
and to pre factor
1
1
3
1
3
1
2
1 1 0
1
2
0 1 1
3
2
0 0 1 0
0 0 0 1
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
A
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
R R
R R
2 2
3 3
1
2
1
1 0 0 0
0 1 0 0
0 0 1 0
1 0
→
→ −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
( )
and to pre factor
0
0
2
3
1
6
0
1
3
1
3
1
2
1 1 0
1
2
0 1 1
3
2
0 0 1 0
0 0 0 1
−
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
−
−
⎡
⎣
⎢
A
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⇒ [I3
: 0] = PAQ,
where P Q
= −
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
=
−
−
1 0 0
2
3
1
6
0
1
3
1
3
1
2
1 1 0
1
2
0 1 1
3
2
0 0 1 0
0 0
,
0
0 1
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
and the rank of A = 3
Remark: To find the rank of a matrix, the simplest method is to reduce to row echelon form.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 22 5/30/2016 4:35:19 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-59-2048.jpg)

![1.24 ■ Engineering Mathematics
17. Reduce to normal form and find the rank of
0 1 2 1
1 2 3 2
3 1 1 3
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
18. If A =
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 2
1 2 3
0 1 1
, then find non-singular matrices P and Q such that PAQ is in normal form and find its
rank.
ANSWERS TO EXERCISE 1.2
1. 3 2. 2 3. 3 4. 2 5. 3
6. 3 7. 3 8. 3 9. 3 10. 2
11. 3 12. 3 13. k = 2 14. a = 4, b = 18 15. a = 4, b = 6
16. [I4
, 0], rank = 4 17. [I3
, 0], rank = 3
18. P Q
= −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 0 0
1 1 0
1 1 1
1 1 1
0 1 1
0 0 1
, and rank = 2.
1.4 SOLUTION OF SYSTEM OF LINEAR EQUATIONS
There are many problems in science and engineering whose solution often depends upon a system of
linear equations.
The equation a1
x1
+ a2
x2
+ … + an
xn
= b is called a non-homogeneous linear equation in n variables
x1
, x2
, …, xn
where b ≠ 0 and at least one ai
≠ 0.
If b = 0, then the equation a1
x1
+ a2
x2
+ … + an
xn
= 0 is called a homogenous linear equation in
x1
, x2
, …, xn
.
1.4.1 Non-homogeneous System of Equations
Consider the system of m linear equations in n variables x1
, x2
, …, xn
a11
x1
+ a12
x2
+ … + a1n
xn
= b1
a21
x1
+ a22
x2
+ … + a2n
xn
= b2
:
am1
x1
+ am2
x2
+ … + amn
xn
= bm
, where at least one bi
≠ 0
If A
a a a
a a a
a a a
B
b
b
b
n
n
m m mn m
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
11 12 1
21 22 2
1 2
1
2
…
…
…
: : : :
,
⎣
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
, ,
X
x
x
xn
1
2
:
then the system of equations can be written as a single matrix equation AX = B.
The matrix A is called the coefficient matrix.
A solution of the system is a set of values of x1
, x2
, …, xn
which satisfy the m equations.
The system of equations is said to be consistent if it has at least one solution.
If the system has no solution, then the system of equations is said to be inconsistent.
The condition for the consistency of the system is given by Rouche’s theorem.
We shall state the theorem without proof.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 24 5/30/2016 4:35:24 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-61-2048.jpg)
![Matrices ■ 1.25
Theorem 1.2 Rouche’s Theorem The system of linear equations AX = B is consistent if and only if the
coefficient matrix A and the augmented matrix [A, B] have the same rank. That is., r(A) = r([A, B])
Working rule:
Let AX = B represent a system of m equations in n variables.
1. Write down the coefficient matrix A and the augmented matrix [A, B]. Find r(A), r([A, B])
2. If r(A) ≠ r([A, B]), then the system is inconsistent. That is it has no solution.
3. If r(A) = r([A, B]) = n, the number of variables, then the system is consistent with unique solution.
4. If r(A) = r([A, B]) n, the number of variables, then the system is consistent with infinite number
of solutions.
If the rank is r, then in this case the solution set will contain n − r parameters or arbitrary constants.
To get the solutions we assign arbitrary values to n − r variables and write down the solutions in
terms of them.
Forexample,thesystemx+y+z=1,2x−y+3z=−1,2x+5y+z=5isconsistentwithinfinitenumberof
solutions.
Here r = 2, n = 3.
∴ the solution set will contain n − r = 3 − 2 = 1 parameter.
We assign an arbitrary value to one variable, say y.
Put y = k and solve for x and z in terms of k.
The solution set is
x = 4 + 2k, y = k, z = −3 − 3k,
where k is any real number.
Note
If m = n, then A is a square matrix and the system of equations AX = B has unique solution if A is
non-singular. That is., A ≠ 0, then r(A) = number of variables n.
The unique solution is X = A−1
B.
1.4.2 Homogeneous System of Equations
Consider the homogeneous system
a11
x1
+ a12
x2
+ … + a1n
xn
= 0
a21
x1
+ a22
x2
+ … + a2n
xn
= 0
:
am1
x1
+ am2
x2
+ … + amn
xn
= 0
If A
a a a
a a a
a a a
X
x
x
x
n
n
m m mn n
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
11 12 1
21 22 2
1 2
1
2
…
…
…
: : : :
,
⎡
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
, then the matrix equation is AX = 0.
For this system x1
= 0, x2
= 0, …, xn
= 0 is always a solution. This is called the trivial solution.
If A ≠ 0, the r(A) = n and the only solution is the trivial solution. So, the condition for
non-trivial solution is A = 0 (or r(A) n).
In solving equations we use only row operations.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 25 5/30/2016 4:35:26 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-62-2048.jpg)
![1.26 ■ Engineering Mathematics
1.4.3 Type 1: Solution of Non-homogeneous System of Equations
WORKED EXAMPLES
(A) Non-homogeneous system with unique solution
EXAMPLE 1
Test for consistency and solve 2x 2 y 1 z 5 7, 3x 1 y 2 5z 5 13, x 1 y 1 z 5 5.
Solution.
The given equations are
x + y + z = 5
2x − y + z = 7
3x + y − 5z = 13
We have rearranged the equation for convenience in reducing to row echelon form.
The coefficient matrix is A = −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 1
2 1 1
3 1 5
and the augmented matrix is
[ , ]
:
:
:
:
:
:
A B = −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
− − −
− − −
⎡
⎣
1 1 1 5
2 1 1 7
3 1 5 13
1 1 1 5
0 3 1 3
0 2 8 2
∼ ⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
→ −
→ −
R R R
R R R
2 2 1
3 3 1
2
3
∼
∼
1 1 1 5
0 1
1
3
1
0 1 4 1
1
3
1
2
1 1 1 5
0 1
1
3
2 2
3 3
:
:
:
:
:
− − −
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→ −
→
R R
R R
1
1
0 0
11
3
0 3 3 2
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
→ +
: R R R
From the last matrix, we find
A ∼
1 1 1
0 1
1
3
0 0
11
3
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 26 5/30/2016 4:35:27 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-63-2048.jpg)
![Matrices ■ 1.27
The number of non-zero rows in the equivalent matrices of A and [A, B] are 3.
∴ r(A) = 3, r([A, B]) = 3
⇒ r(A) = r([A, B]) = 3, the number of variables.
So, the equations are consistent with unique solution.
From the reduced matrix [A, B], we find the given equations are equivalent to
x + y + z = 5, y +
1
3
z = 1 and −
11
3
z = 0 ⇒ z = 0
∴ y = 1 and x + 1 + 0 = 5 ⇒ x = 4.
So, the unique solution is x = 4, y = 1, z = 0.
EXAMPLE 2
Test for the consistency and solve x 1 2y 1 z 5 3, 2x 1 3y 1 2z 5 5, 3x 2 5y 1 5z 5 2,
3x 1 9y 2 z 5 4.
Solution.
The given equations are
x + 2y + z = 3
2x + 3y + 2z = 5
3x − 5y + 5z = 2
3x + 9y − z = 4.
The coefficient matrix is A =
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
1 2 1
2 3 2
3 5 5
3 9 1
The augmented matrix is
[ , ]
:
:
:
:
:
:
A B = ∼
1 2 1 3
2 3 2 5
3 5 5 2
3 9 1 4
1 2 1 3
0 1 0 1
0 11 2
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
− −
− :
:
:
:
−
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→ −
→ −
→ −
−
7
0 3 4 5
2
3
3
1 2 1 3
0
2 2 1
3 3 1
4 4 1
R R R
R R R
R R R
∼
1
1 0 1
0 0 2 4
0 0 4 8
11
3
1 2 1 3
0 1
3 3 2
4 4 2
:
:
:
:
−
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→ −
→ +
−
R R R
R R R
∼
0
0 1
0 0 1 2
0 0 1 2
1
2
1
4
3 3
4 4
:
:
:
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→
→ −
R R
R R
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 27 5/30/2016 4:35:28 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-64-2048.jpg)
![1.28 ■ Engineering Mathematics
⇒ [ , ]
:
:
:
:
A B
R R R
∼
1 2 1 3
0 1 0 1
0 0 1 2
0 0 0 0 4 4 3
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→ −
From this last matrix we find
A ∼
1 2 1
0 1 0
0 0 1
0 0 0
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
The number of non-zero rows in the equivalent matrices of A and [A B] are 3.
∴ r(A) = 3, r([A, B]) = 3
⇒ r(A) = r([A, B]) = 3, the number of variables.
So, the equations are consistent with unique solution
From the reduced matrix [A, B], we find the given equations are equivalent to
x + 2y + z = 3, −y = −1 and z = 2
∴ y = 1, z = 2 and so x + 2 ⋅ 1 + 2 = 3 ⇒ x = −1
So, the unique solution is x = −1, y = 1, z = 2.
EXAMPLE 3
Solve x2
yz 5 e, xy2
z3
5 e, x3
y2
z 5 e using matrices.
Solution.
The given equations are
x2
yz = e (1)
xy2
z3
= e (2)
x3
y2
z = e (3)
Taking logarithm to the base e on both sides of (1), (2) and (3), we get
and
log log log log log
log log log
lo
e e e e e
e e e
x yz e x y z
x y z
2 2
1
2 1
= ⇒ + + =
⇒ + + =
g
g log log log log
log log log
e e e e e
e e
xy z e x y z
x y z e x
2 3
3 2
2 3 1
3
= ⇒ + + =
= ⇒ + 2
2 1
log log
e e
y z
+ =
For simplicity, put x1
= loge
x, y1
= loge
y, z1
= loge
z
∴ the equations are 2x1
+ y1
+ z1
= 1
x1
+ 2y1
+ 3z1
= 1
3x1
+ 2y1
+ z1
= 1
The coefficient matrix is A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 1 1
1 2 3
3 2 1
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 28 5/30/2016 4:35:29 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-65-2048.jpg)
![Matrices ■ 1.29
The augmented matrix is
[ , ]
:
:
:
A B =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 1 1 1
1 2 3 1
3 2 1 1
∼
∼
1 2 3 1
2 1 1 1
3 2 1 1
1 2 3 1
0 3 5 1
0 4 8 2
1 2
:
:
:
:
:
:
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
↔
− − −
− − −
⎡
⎣
⎢
⎢
⎢
R R
⎤
⎤
⎦
⎥
⎥
⎥
→ −
→ −
R R R
R R R
2 2 1
3 3 1
2
3
⇒ − − −
− −
⎡
⎣
⎢
⎢
⎢
⎢
A B
1 2 3 1
0 3 5 1
0 0
4
3
2
3
[ , ]
:
:
:
∼
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥ → −
R R R
3 3 2
4
3
From the last matrix, we find A ∼
1 2 3
0 3 5
0 0
4
3
− −
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
The number of non-zero rows in the equivalent matrices of A and [A, B] are 3.
∴ r(A) = 3, r([A, B]) = 3
⇒ r(A) = r([A, B]) = 3, the number of variables.
So, the equations are consistent with unique solution.
From the reduced matrix [A, B], we find that the given equations are equivalent to
x1
+ 2y1
+ 3z1
= 1 (4)
−3y1
− 5z1
= −1 (5)
and − = − ⇒ =
4
3
2
3
1
2
1 1
z z
Substituting in (5), we get
− − ⋅ = − ⇒ = − = − ⇒ = −
3 5
1
2
1 3 1
5
2
3
2
1
2
1 1 1
y y y
Substituting in (4) we get
⇒
∴
x x x
x x x e
e
1 1 1
1
1
2
1
2
3
1
2
1
1
2
1 1
1
2
1
2
1
2
1
2
+ −
⎛
⎝
⎜
⎞
⎠
⎟ + ⋅ = ⇒ + = ⇒ = − =
= ⇒ = ⇒ =
log 2
2
1
1
2
1
1
2
1
2
1
2
1
1
2
1
2
=
= − ⇒ = − ⇒ = =
= ⇒ = ⇒ = =
−
e
y y y e
e
z z z e e
e
e
log
log
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 29 5/30/2016 4:35:31 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-66-2048.jpg)
![1.30 ■ Engineering Mathematics
So, the unique solution is
x e y
e
z e
= = =
, ,
1
.
(B) Non-homogeneous system with infinite number of solutions
EXAMPLE 4
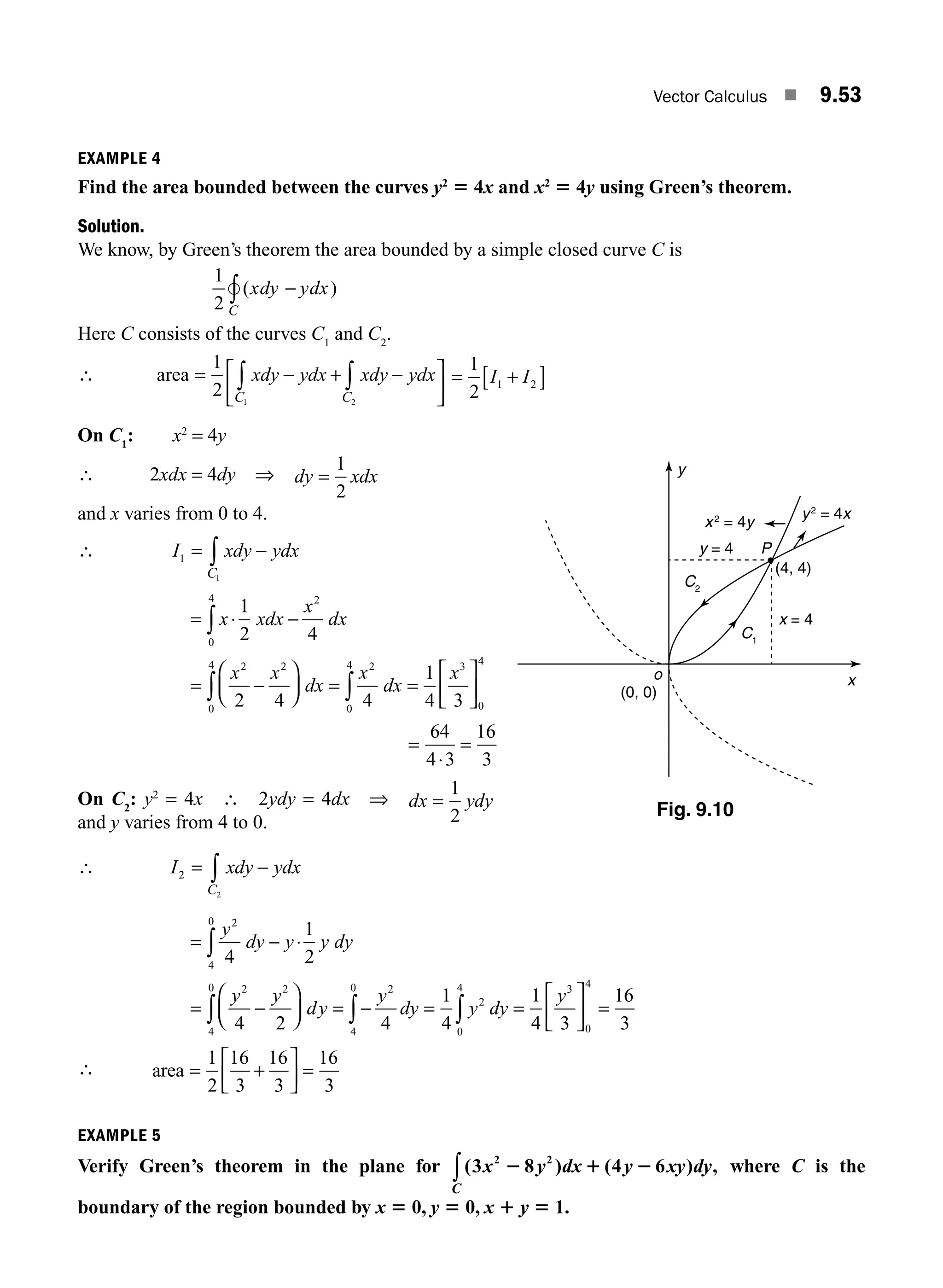
By investigating the rank of relevant matrices, show that the following equations possess a one
parameter family of solutions: 2x 2 y 2 z 5 2, x 12y 1 z 5 2, 4x 2 7y 2 5z 5 2.
Solution.
The given equations are
x +2y + z = 2
2x − y − z = 2
4x − 7y − 5z = 2
The coefficient matrix is A = − −
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 2 1
2 1 1
4 7 5
The augmented matrix is
[ , ]
:
:
:
:
:
:
A B = − −
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
− − −
− − −
1 2 1 2
2 1 1 2
4 7 5 2
1 2 1 2
0 5 3 2
0 15 9 6
∼
⎡
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
→ −
→ −
− − −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
R R R
R R R
2 2 1
3 3 1
2
4
1 2 1 2
0 5 3 2
0 0 0 0
∼
:
:
: R
R R R
3 3 2
3
→ −
From the last matrix we find A ∼
1 2 1
0 5 3
0 0 0
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
The number of non-zero rows of equivalent matrices of A and [A, B] are 2
∴ r(A) = 2, r([A, B]) = 2
⇒ r(A) = r([A, B]) = 2 the number of variables 3.
So, the equations are consistent with infinite number of solutions involving one parameter,
since n − r = 3 − 2 = 1.
From the reduced matrix [A, B], we find that the given equations are equivalent to
x + 2y + z = 2 (1)
− 5y − 3z = − 2 ⇒ 5y + 3z = 2 (2)
Assign arbitrary value to one of the variables.
Put z = k in (2) ∴ 5y + 3k = 2 ⇒ y
k
=
−
2 3
5
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 30 5/30/2016 4:35:33 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-67-2048.jpg)
![Matrices ■ 1.31
Substituting in (1), we get,
x
k
k
x
k
k
k k k
+
−
+ =
= −
−
− =
− + −
=
+
2 2 3
5
2
2
2 2 3
5
10 4 6 5
5
6
5
( )
( )
∴ the solution set is x k
= +
1
5
6
( ), y k z k
= − =
1
5
2 3
( ), , where k is any real number.
EXAMPLE 5
Solve, if the equations are consistent: x 2 y 1 2z 5 1, 3x 1 y 1 z 5 4, x 1 3y 23z 5 2,
5x 2 y 1 5z 5 6.
Solution.
The given equations are
x − y + 2z = 1
3x + y + z = 4
x + 3y − 3z = 2
5x − y + 5z = 6
The coefficient matrix is A =
−
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
1 1 2
3 1 1
1 3 3
5 1 5
The augmented matrix is
[ , ]
:
:
:
:
:
:
A B =
−
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
−
−
−
1 1 2 1
3 1 1 4
1 3 3 2
5 1 5 6
1 1 2 1
0 4 5 1
0 4 5
∼
:
:
:
:
1
0 4 5 1
3
5
1 1 2 1
0 4 5
2 2 1
3 3 1
4 4 1
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→ −
→ −
→ −
−
−
R R R
R R R
R R R
∼
:
:
:
:
1
0 0 0 0
0 0 0 0
3 3 2
4 4 2
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→ −
→ −
R R R
R R R
From the last matrix, we find A ∼
1 1 2
0 4 5
0 0 0
0 0 0
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
The number of non-zero rows of the equivalent matrices of A and [A, B] are 2.
⇒
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 31 5/30/2016 4:35:34 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-68-2048.jpg)
![1.32 ■ Engineering Mathematics
∴ r(A) = 2, r([A, B]) = 2
⇒ r(A) = r([A, B]) = 2 3, the number of variables.
So, the equations are consistent with infinite number of solutions involving one parameter,
since n − r = 3 − 2 = 1.
From reduced matrix [A, B], we find that the given equations are equivalent to
x − y + 2z = 1 (1)
4y − 5z = 1 (2)
Put z = k, in (2) then 4y − 5k = 1 ⇒ y
k
=
+
1 5
4
Substituting in (1), we get
x
k
k x
k
k
k k k
−
1 5
4
2 1 1
1 5
4
2
4 1 5 8
4
5 3
4
+
+ = ⇒ = +
+
− =
+ + −
=
−
∴ the solution set is
x
k
y
k
z k
=
−
=
+
=
5 3
4
1 5
4
, , , where k is any real number.
EXAMPLE 6
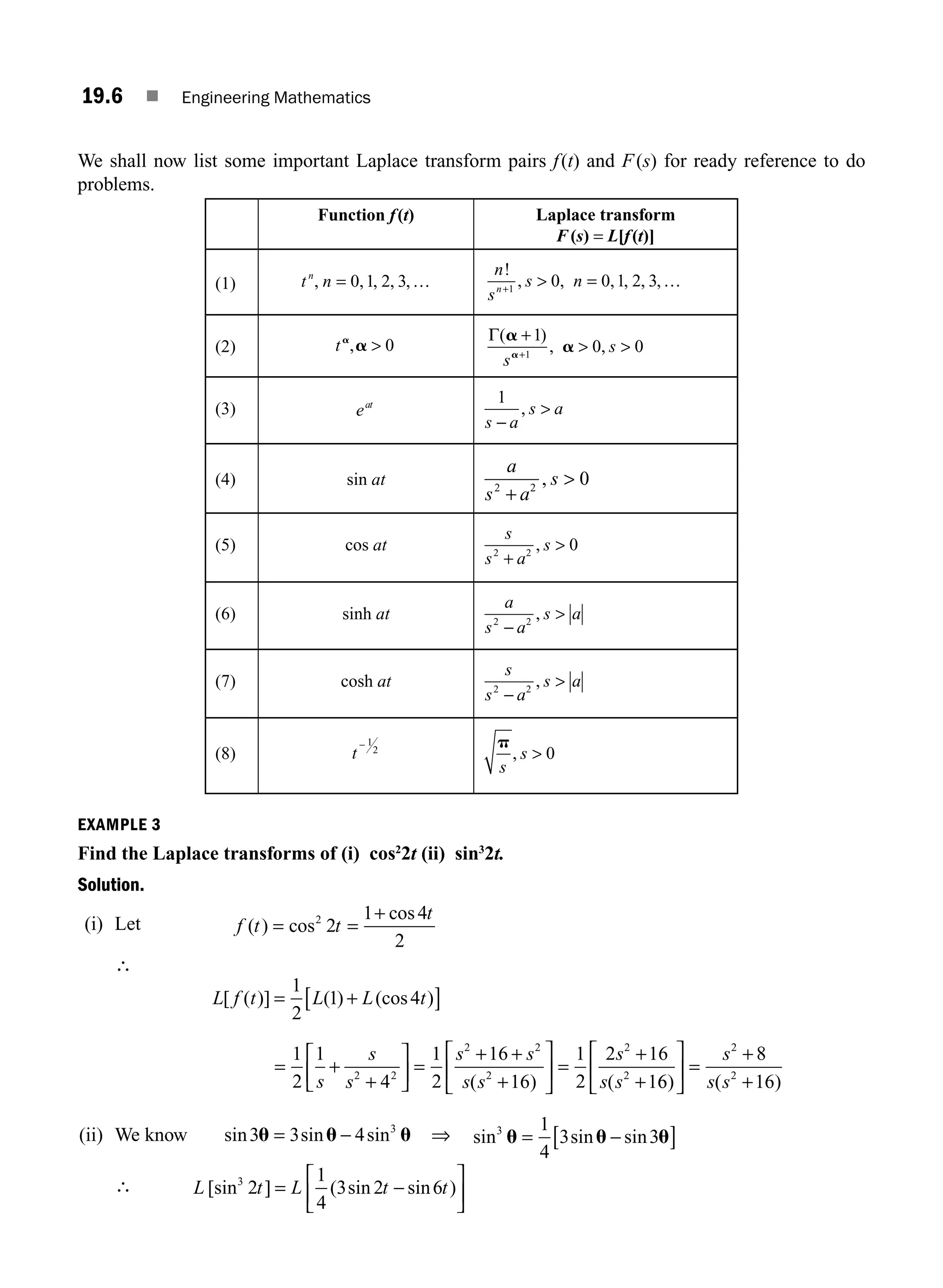
Test the consistency of the system of equations and solve, if consistent: x1
1 2x2
2 x3
2 5x4
5 4,
x1
1 3x2
2 2x3
2 7x4
5 5, 2x1
2 x2
1 3x3
5 3.
Solution.
The given equations are
x1
+ 2x2
− x3
− 5x4
= 4
x1
+ 3x2
− 2x3
− 7x4
= 5
2x1
− x2
+ 3x3
+ 0x4
= 3
The coefficient matrix is A =
− −
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 2 1 5
1 3 2 7
2 1 3 0
The augmented matrix is
[ , ]
:
:
:
:
:
A B =
− −
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
− −
− −
−
1 2 1 5 4
1 3 2 7 5
2 1 3 0 3
1 2 1 5 4
0 1 1 2 1
0
∼
5
5 5 10 5 2
1 2 1 5 4
0 1 1 2 1
0 0 0 0 0
2 2 1
3 3 1
:
:
:
:
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
→ −
→ −
− −
− −
R R R
R R R
∼
⎡
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥ → +
R R R
3 3 2
5
From the last matrix, we find
A ∼
1 2 1 5
0 1 1 2
0 0 0 0
− −
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 32 5/30/2016 4:35:36 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-69-2048.jpg)
![Matrices ■ 1.33
The number of non-zero rows of the equivalent matrices of A and [A, B] are 2.
∴ r(A) = 2, r([A, B]) = 2
⇒ r(A) = r([A, B]) = 2 4, the number of variables.
So, the equations are consistent with infinite number of solutions containing two parameters,
since n − r = 4 − 2 = 2.
From the reduced matrix of [A, B] we find that the given equations are equivalent to
x1
+ 2x2
− x3
− 5x4
= 4 (1)
and x2
− x3
− 2x4
= 1 (2)
Put x3
= k1
, x4
= k2
, then (2) ⇒ x2
− k1
− 2k2
= 1 ⇒ x2
= 1 + k1
+ 2k2
Substituting in (1), we get
x1
+ 2(1 + k1
+ 2k2
) − k1
− 5k2
= 4
⇒ x1
+ 2 + 2k1
+ 4k2
− k1
− 5k2
= 4
⇒ x1
+ k1
− k2
= 2 ⇒ x1
= 2 − k1
+ k2
∴ the solution set is
x1
= 2 − k1
+ k2
, x2
= 1 + k1
+ 2k2
, x3
= k1
, x4
= k2
, where k1
, k2
are any real numbers.
(C) Non-homogeneous system with no solution
EXAMPLE 7
Examine for the consistency of the following equations 2x 1 6y 1 11 5 0, 6x 1 20y 2 6z 1 3 5 0,
6y 2 18z 1 1 5 0.
Solution.
The given equations are
2x + 6y + 0z = −11
6x + 20y − 6z = −3
0x + 6y − 18z = −1
The coefficient matrix is A = −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 6 0
6 20 6
0 6 18
The augmented matrix is
[ , ]
:
:
:
:
:
A B =
−
− −
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
− −
2 6 0 11
6 20 6 3
0 6 18 1
1 3 0
11
2
6 20 6 3
0 6
∼
−
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→
18 1
1
2
1 1
:
R R
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 33 5/30/2016 4:35:37 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-70-2048.jpg)
![1.34 ■ Engineering Mathematics
−
−
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
1 3 0
11
2
0 2 6 30
0 6 18 1
:
:
:
∼
⎥
⎥
⎥
⎥
⎥
→ −
R R R
2 2 1
6
⇒ [ , ]
:
:
:
A B
R R R
∼
1 3 0
11
2
0 2 6 30
0 0 0 91 3
3 3 2
−
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥ → −
From the last matrix, we find A ∼
1 3 0
0 2 6
0 0 0
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
The number of non-zero rows in the equivalent matrices of A and [A, B] are 2 and 3 respectively.
∴ r(A) = 2, r([A, B]) = 3
⇒ r(A) ≠ r([A, B]).
Hence, the equations are inconsistent and the system has no solution.
1.4.4 Type 2: Solution of Non-homogeneous Linear Equations Involving Arbitrary
Constants
WORKED EXAMPLES
EXAMPLE 1
Show that the system of equations 3x 2 y 1 4z 5 3, x 1 2y 2 3z 5 22, 6x 1 5y 1 lz 5 23 has
at least one solution for any real number l. Find the set of solutions when l 5 25.
Solution.
The given equations are
x + 2y − 3z = −2,
3x − y + 4z = 3
6x + 5y + lz = −3
The coefficient matrix is A =
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 2 3
3 1 4
6 5 l
and the augmented matrix is
[ , ]
:
:
:
:
:
:
A B =
− −
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
− −
−
− +
1 2 3 2
3 1 4 3
6 5 3
1 2 3 2
0 7 13 9
0 7 18
l l
∼
9
9
3
6
2 2 1
3 3 1
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
→ −
→ −
R R R
R R R
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 34 5/30/2016 4:35:38 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-71-2048.jpg)
![Matrices ■ 1.35
⇒
1 2 3 2
0 7 13 9
0 0 5 0
− −
−
+
⎡
A B
[ , ]
:
:
:
∼
l
⎣
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥ → −
R R R
3 3 2
From the last matrix we find A ∼
1 2 3
0 7 13
0 0 5
−
−
+
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
l
Case (i): If l + 5 ≠ 0 ⇒ l ≠ −5, the number of non-zero rows in the equivalent matrices of [A, B]
and A are 3.
∴ r(A) = 3, r([A, B]) = 3
⇒ r(A) = r([A, B]) = 3, the number of variables.
So, the equations are consistent with unique solution.
Case (ii): If l + 5 = 0 ⇒ l = −5, then we get
[ , ]
:
:
:
A B ∼
1 2 3 2
0 7 13 9
0 0 0 0
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
and A ∼
1 2 3
0 7 13
0 0 0
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
The number of non-zero rows of equivalent matrices of [A, B] and A are 2.
∴ r(A) = 2, r([A, B]) = 2
⇒ r(A) = r([A, B]) = 2 3, the number of variables.
So, the equations are consistent with infinite number of solutions involving one parameter
since n − r = 3 − 2 = 1.
From cases (i) and (ii), we find that the equations are consistent for all values of l.
We shall now find the solution when l = −5. The solutions will contain one parameter.
In this case from the last matrix [A, B], we find the equations are equivalent to
x + 2y − 3z = −2 (1)
− 7y + 13z = 9 (2)
Put z 5 k in (2), then −7y + 13k = 9 ⇒ = − ⇒ = −
7 13 9
1
7
13 9
y k y k
( )
Substituting in (1) we get
x k k x k k
k k
+ ⋅ − − = − ⇒ = − − − +
= − − + + =
2
1
7
13 9 3 2 2
2
7
13 9 3
1
7
14 26 18 21
1
( ) ( )
[ ]
7
7
4 5
[ ]
− k
∴ the solutions are
x k y k z k
= − = − =
1
7
4 5
1
7
13 9
[ ], [ ], , where k is any real number.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 35 5/30/2016 4:35:39 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-72-2048.jpg)
![1.36 ■ Engineering Mathematics
EXAMPLE 2
Find the values of a and b if the equations x 1 y 1 2z 5 2, 2x 2 y 1 3z 5 2, 5x 2 y 1 az 5 b have
(i) no solutions, (ii) unique solution and (iii) infinite number of solutions.
Solution.
The given equations are
x + y + 2z = 2
2x − y +3z = 2
5x − y + az = b
The coefficient matrix is A
a
= −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 2
2 1 3
5 1
The augmented matrix is
[ , ]
:
:
:
A B
a b
= −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 2 2
2 1 3 2
5 1
∼
∼
1 1 2 2
0 3 1 2
0 6 10 10
2
5
1 1 2
2 2 1
3 3 1
:
:
:
− − −
− − −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
→ −
→ −
a b
R R R
R R R
:
:
:
:
2
0 3 1 2
0 0 8 6 2
3 3 2
− − −
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥ → −
a b R R R
From this matrix, we find A
a
∼
1 1 2
0 3 1
0 0 8
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Case (i): The equations have no solution
⇒ r(A) ≠ r([A, B])
This is possible, if r(A) = 2 and r([A, B]) = 3
⇒ a − 8 = 0 and b − 6 ≠ 0 ⇒ a = 8 and b ≠ 6.
Case (ii): The equations have unique solution ⇒ r(A) = r([A, B]) = 3.
∴ a − 8 ≠ 0 and b is any real number.
∴ a ≠ 8 and b is any real number.
Case (iii): The equations have infinite number of solutions
⇒ r(A) = r([A, B]) = 2 3, the number of variables.
This is possible, if a − 8 = 0 and b − 6 = 0 ⇒ a = 8, b = 6
Thus, no solution ⇒ a = 8, b ≠ 6
Unique solution ⇒ a ≠ 8, b is any real number
Infinite number of solutions ⇒ a = 8, b = 6.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 36 5/30/2016 4:35:40 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-73-2048.jpg)
![Matrices ■ 1.37
EXAMPLE 3
For what values of k, the equations x 1 y 1 z 5 1, 2x 1 y 1 4z 5 k and 4x 1 y 1 10z 5 k2
have
(i) a unique solution, (ii) infinite number of solutions, (iii) no solution and solve them completely
in each case of consistency.
Solution.
The given equations are
x + y + z = 1
2x + y + 4z = k
4x + y + 10z = k2
The coefficient matrix is A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 1
2 1 4
4 1 10
The augmented matrix is
⇒
[ , ]
:
:
:
:
:
:
A B k
k
k
k
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
− −
− −
⎡
⎣
1 1 1 1
2 1 4
4 1 10
1 1 1 1
0 1 2 2
0 3 6 4
2 2
∼ ⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
→ −
→ −
− −
− − −
⎡
⎣
R R R
R R R
k
k k
2 2 1
3 3 1
2
2
4
1 1 1 1
0 1 2 2
0 0 0 4 3 2
∼
:
:
: ( )
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥ → −
− −
− +
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
R R R
A B k
k k
3 3 2
2
3
1 1 1 1
0 1 2 2
0 0 0 3 2
[ , ]
:
:
:
∼
From the last matrix, we find
A ∼
1 1 1
0 1 2
0 0 0
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Since the number of non-zero rows is 2, r(A) = 2
(i) If k2
− 3k + 2 = 0 ⇒ (k − 2)(k − 1) = 0 ⇒ k = 1, k = 2
∴
[ , ]
:
:
:
[ , ]
A B k
r A B
∼
1 1 1 1
0 1 2 2
0 0 0 0
2
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
∴
So, r(A) = r([A,B]) = 2 3, the number of variables.
∴ the system of equations is consistent with infinite number of solutions if k = 1 or k = 2.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 37 5/30/2016 4:35:42 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-74-2048.jpg)
![1.38 ■ Engineering Mathematics
(ii) If k2
− 3k + 2 ≠ 0 ⇒ k ≠ 1 and k ≠ 2, then r([A, B]) = 3
∴ r(A) ≠ r([A, B])
So, the system is inconsistent and has no solution if k ≠ 1 and k ≠ 2.
Now we shall find the solutions if k = 1 and k = 2.
If k = 1, then [ , ]
:
:
:
A B = − −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 1 1
0 1 2 1
0 0 0 0
So, the equivalent equations are x + y + z = 1 and −y + 2z = −1
Put z = k1
, then −y + 2k1
= −1 ⇒ y = 1 + 2k1
∴ x + 1 + 2k1
+ k1
= 1 ⇒ x = −3k1
∴ the solutions are x = 3k1
, y = 1 + 2k1
, z = k1
, where k1
is any real number
If k = 2, then [ , ]
:
:
:
A B = −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 1 1
0 1 2 0
0 0 0 0
So, the equivalent equations are x + y + z = 1 and −y + 2z = 0 ⇒ y = 2z.
Put z = k2
, then y = 2k2
∴ x + 2k2
+ k2
= 1 ⇒ x = 1 − 3k2
∴ the solutions are x = 1 − 3k2
, y = 2k2
, z = k2
, where k2
is any real number.
1.4.5 Type 3: Solution of the System of Homogeneous Equations
WORKED EXAMPLES
EXAMPLE 1
Find all the non-trivial solutions of 7x 1 y 2 2z 5 0, x 1 5y 2 4z 5 0, 3x 2 2y 1 z 5 0.
Solution.
The given equations are
7x + y − 2z = 0
x + 5y − 4z = 0
3x − 2y + z = 0
The coefficient matrix is A =
−
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
7 1 2
1 5 4
3 2 1
Since R. H. S of the equations is zero it is enough, we consider A instead of augmented matrix
[ , ]
:
:
:
A B =
−
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
7 1 2 0
1 5 4 0
3 2 1 0
, because r(A) = r([A, B]) always.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 38 5/30/2016 4:35:43 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-75-2048.jpg)



![1.42 ■ Engineering Mathematics
It is a system of homogeneous equations in a, b, c.
From the given equations, it is obvious that a, b, c cannot be simultaneously zero or no two of them
equal [For if all a, b, c are zero, then x
a
b c
y
b
c a
z
c
a b
=
−
=
−
=
−
, , are indeterminate, do not exist.]
∴ the system of equations (1) has non-trivial solutions
∴ = ⇒
−
−
+ − −
=
⇒ − − − − − + + − − =
⇒ − −
A
x x
y y
z z
yz x y yz x yz z
y
0
1
1
1
0
1 1 0
1
( ) ( )( ) ( )
z
z xy xyz xyz xz
xy yz zx
xy yz zx
− + − − =
⇒ − − − − =
⇒ + + + =
0
1 0
1 0
EXAMPLE 2
Find the values of l for which the equations
( 1) (3 1) 2 0
1) (4 2) ( 3) 0
2 (3 1) 3(
l 2 1 l 1 1 l 5
l 2 1 l 2 1 l 1 5
1 l 1 1 l2
x y z
x y z
x y
(
1
1)z 5 0
are consistent and find x : y : z, when l has the smallest of these values.What happens when l has
the greater of these values?
Solution.
The given equations are
( ) ( )
( ) ( ) ( )
( ) (
l l l
l l l
l l
− + + + =
− + − + + =
+ + + −
1 3 1 2 0
1 4 2 3 0
2 3 1 3
x y z
x y z
x y 1
1 0
)z =
Since the system is homogeneous it is always consistent with at least the trivial solution x = 0, y = 0
and z = 0. It will have non-trivial solution if A = 0
⇒
l l l
l l l
l l
− +
− − +
+ −
=
1 3 1 2
1 4 2 3
2 3 1 3 1
0
( )
⇒ l l l
l l l
l l l
+
− +
+
6 3 1 2
6 4 2 3
6 3 1 3( −
−
= → + +
1
0 1 1 2 3
)
C C C C
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 42 5/30/2016 4:35:51 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-79-2048.jpg)




![Matrices ■ 1.47
Now to solve equation (1), we start with the augmented matrix A I
, 1
[ ] where I1
1
0
0
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
and trans-
form by row operations so that A is reduced to unit matrix in Jordan’s method, then we write the solu-
tion for x x x
11 21 31
, , directly.
The same procedure is applied to solve (2) and (3) by writing A I
, 2
[ ] and A I
, 3
[ ]. In practice, we
will not do this individually and convert A into a unit matrix, but we start with A I I I A I
⏐ 1 2 3
⎡
⎣
⎤
⎦ = ( )
, and
convert A into unit matrix by row operations and find X.
Working rule
Consider the augmented matrix [A, I ], where I is the identity matrix of the same order as A.
By row operations, reduce A into a unit matrix, then correspondingly I will be changed into a
matrix X. This matrix X is the inverse of A. It is advisable to change the pivot element to 1 before
applying row operations at each step.
WORKED EXAMPLES
EXAMPLE 1
Using Gauss–Jordan method, find the inverse of the matrix A 5 2
2 2
1 1 3
1 3 3
2 4 4
.
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Solution.
Given A = −
− −
1 1 3
1 3 3
2 4 4
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
. To find A–1
Consider the augmented matrix
A I
,
:
:
:
[ ]= −
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1 3 1 0 0
1 3 3 0 1 0
2 4 4 0 0 1
∼
1 1 3 1 0 0
0 2 6 1 1 0
0 2 10 2 0 1 2
2 2 1
3 3 1
:
:
:
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
→ −
→ +
R R R
R R R
∼
1 1 3 1 0 0
0 1 3
1
2
1
2
0
0 1 5 1 0
1
2
1
2
1
2
2 2
3 3
:
:
:
− −
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
→
→
R R
R R
[The pivot 2 in R2
is reduced to 1]
∼
1 0 6
3
2
1
2
0
0 1 3
1
2
1
2
0
0 0 2
1
2
1
2
1
2
1
1 1
:
:
:
−
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
→ + −
R R (
( )
→ +
R
R R R
2
3 3 2
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 47 5/30/2016 4:36:00 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-84-2048.jpg)
![1.48 ■ Engineering Mathematics
∼
1 0 6
3
2
1
2
0
0 1 3
1
2
1
2
0
0 0 1
1
4
1
4
1
4
1
2
3 3
:
:
:
−
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
→
R R (The pivot 2 in R3
is
reduced to 1)
∼
1 0 0 0 2
3
2
0 1 0
1
4
5
4
3
4
0 0 1
1
4
1
4
1
4
6
1 1
:
:
:
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
→ + −
(
R R )
)
→ +
R
R R R
3
2 2 3
3
∴ the inverse matrix of A is A −
=
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
1
0 2
3
2
1
4
5
4
3
4
1
4
1
4
1
4
EXAMPLE 2
Find the inverse of the matrix A 5 2
2
4 1 2
2 3 1
1 2 2
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
by Gauss–Jordan method.
Solution.
Given A = −
4 1
2 3
1 2 2
2
1
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
. To find A–1
Consider the augmented matrix
A I
,
:
:
:
[ ] = −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
4 1 2 1 0 0
2 3 1 0 1 0
1 2 2 0 0 1
∼
1
1
4
1
2
1
4
0 0
2 3 1 0 1 0
1 2 2 0 0 1
1
4
1 1
:
:
:
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→
R R (The pivot 4 in R1
is reduced to 1)
∼
1
1
4
1
2
1
4
0 0
0
5
2
2
1
2
1 0
0
9
4
3
2
1
4
0 1
2 2
:
:
:
− −
− −
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
→ +
R R −
−
( )
→ −
2 1
3 3 1
R
R R R
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 48 5/30/2016 4:36:03 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-85-2048.jpg)

![1.50 ■ Engineering Mathematics
The coefficient matrix is
A B X
= −
− − −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
1 1 3
1 3 3
2 4 4
4
2
8
, and
x
y
z ⎥
⎥
∴ the system of equations is AX B X A B
= ⇒ = −1
.
We find A −1
by the method of matrix inverse by Gauss–Jordan method.
Consider the augmented matrix
A I
,
:
:
:
:
:
[ ]= −
− − −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
∼ − −
1 1 3 1 0 0
1 3 3 0 1 0
2 4 4 0 0 1
1 1 3 1 0 0
0 2 6 1 1 0
0
0 2 2 2 0 1 2
1 1 3 1 0 0
0 1 3
1
2
1
2
0
0 1
2 2 1
3 3 1
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
→ −
→ +
∼
− −
−
:
:
:
R R R
R R R
1
1 1 0
1
2
1
2
1
2
1 0 4 2 0
1
2
0 1 3
1
2
1
2
0
0
2 2
3 3
:
:
:
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
→
→
∼ − −
R R
R R
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
→ +
1 1 1 0
1
2
1 1 3
:
R R R
∼ − −
−
1 0 4 2 0
1
2
0 1 3
1
2
1
2
0
0 0
:
:
2
2
1
2
1
2
1
2 3 3 2
:
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥ → +
R R R
∼ − −
− − −
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥ → −
⎛
1 0 4 2 0
1
2
0 1 3
1
2
1
2
0
0 0 1
1
4
1
4
1
4
1
2
3
:
:
: R
⎝
⎝
⎜
⎞
⎠
⎟ R3
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 50 5/30/2016 4:36:06 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-87-2048.jpg)

![1.52 ■ Engineering Mathematics
∴ the system of equation is AX B
= ⇒ X A B
= −1
.
We find A −1
by the method of matrix inverse by Gauss–Jordan method.
Consider the augmented matrix
A I
,
:
:
:
[ ]=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 1 2 1 0 0
2 2 1 0 1 0
1 2 2 0 0 1
∼
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
→
1
1
2
1
1
2
0 0
2 2 1 0 1 0
1 2 2 0 0 1
1
2
1 1
:
:
:
R R
∼ − −
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
→ −
→ −
1
1
2
1
1
2
0 0
0 1 1 1 1 0
0
3
2
1
1
2
0 1
2
2 2 1
3 3
:
:
:
R R R
R R R
R1
∼
−
− −
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
→ −
1 0
3
2
1
1
2
0
0 1 1 1 1 0
0 0
5
2
1
3
2
1
1
2
1 1 2
:
:
:
R R R
R3
3 3 2
3
2
→ −
R R
∼
−
− −
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥ →
1 0
3
2
1
1
2
0
0 1 1 1 1 0
0 0 1
2
5
3
5
2
5
2
5
3 3
:
:
: R R
∼
1 0 0
0
2
5
2
5
3
5
0 1 0
3
5
2
5
2
5
0 0 1
2
5
3
5
2
5
3
2
1 1
:
:
:
−
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
→ −
R R R
R
R R R
3
2 2 3
→ +
∴ the inverse of A is A −
=
−
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
1
2
5
2
5
3
5
3
5
2
5
2
5
2
5
3
5
2
5
M01_ENGINEERING_MATHEMATICS-I _CH01_Part A.indd 52 5/30/2016 4:36:11 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-89-2048.jpg)








![Matrices ■ 1.61
Thus, the eigen values of A are a + ib, a − ib and the corresponding eigen vectors are
X1
1
=
⎡
⎣
⎢
⎤
⎦
⎥
i
and X2
1
=
⎡
⎣
⎢
⎤
⎦
⎥
i
−
EXAMPLE 3
Find the eigen values and eigen vectors of the matrix
3 4 4
1 2 4
1 1 3
2
2
2
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
Solution.
Let A =
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
3 4 4
1 2 4
1 1 3
−
The characteristic equation of A is A I
− =
l 0
⇒
3 4 4
1 2 4
1 1 3
0
− −
− −
− −
=
l
l
l
⇒ l l l
3
1
2
2 3 0
− + − =
S S S
where S1
= sum of main diagonal elements of A = 3 + (−2) + 3 = 4
S2
= sum of minors of diagonal elements of A
=
−
−
+ +
−
−
= − + + − + − + = − + + − =
2 4
1 3
3 4
1 3
3 4
1 2
6 4 9 4 6 4 2 5 2 1
( ) ( )
and S A
3 3 6 4 4 3 4 4 1 2 6 4 4 6
= = − + + − + − + = − − + = −
( ) ( ) ( )
∴ the characteristic equation is l3
− 4l2
+ l + 6 = 0
We choose integer factors of constant term 6 for trial solution. We find l = −1 is a root. To find the
other roots we perform synthetic division
Other roots are given by
⇒
⇒
l l
l l
l
2
5 6 0
2 3 0
2 3
− + =
− − =
=
( )( )
or
−
−
− −
−
1
1 4 1 6
0 1 5 6
1 5 6 0
∴ the eigen values are l = −1, 2, 3 [different roots]
To find eigen vectors:
Let X =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
x
x
x
1
2
3
be an eigen vector corresponding to the eigen value l.
Then ( )
A I X
− = ⇒
− −
− −
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
l
l
l
l
0
3
1
1
4 4
2 4
1 3
0
0
0
1
2
3
x
x
x
⎡
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⇒
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 61 5/30/2016 5:03:38 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-98-2048.jpg)





![Matrices ■ 1.67
Note If B =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
0 5 6
5 0 7
6 7 0
with the eigen vectors as rows, then
B = − − + − − = − =
0 5 0 42 6 35 0 210 210 0
( ) ( )
∴ the vectors X1
, X2
, X3
are linearly dependent. However, any two of them are linearly independent.
Geometrically, it means that all the vectors are coplanar, but any two of them are non-collinear.
In this example we have seen −1 is the only eigen value of 3 × 3 matrix and two linearly
independent eigen vectors.
1.6.4 Properties of Eigen Values
1. A square matrix A and its transpose AT
have the same eigen values.
Proof Eigen values of A are the roots of its characteristic equation
A I
− =
l 0 (1)
We know ( ) ( )
A I A I
T T T
− = −
l l [ ( ) ]
{ A B A B
T T T
+ = +
= − = −
A I A I
T T T
l l [ ]
{ I I
T
=
∴ ( )
A I A I
T T
− = −
l l (2)
For any square matrix B, B B
T
=
∴ ( )
A I A I
T
− = −
l l (3)
From (2) and (3), A I A I
T
− = −
l l .
This shows that the characteristic polynomial of A and AT
are the same.
Hence, the characteristic equations of A and AT
is (1).
∴ A and AT
have the same eigen values. ■
2. Sum of the eigen values of a square matrix A is equal to the sum of the elements on its main
diagonal.
Proof Let A be a square matrix of order n.
Then the characteristic equation of A is A I
− =
l 0
⇒ l l l
n n n n
n
S S S
− + − + − =
− −
1
1
2
2
1 0
... ( ) (1)
where S1
= sum of the diagonal elements of A
If l1
, l2
, …, ln
are the roots of (1), then l1
, l2
, …, ln
are the eigen values of A.
From theory of equations,
sum of the roots of (1) is =
− −
coefficient of
coefficient of
n
n
l
l
1
⇒ l1
+ l2
+ … + ln
= −(−S1
) = S1
∴ the sum of the eigen values = l1
+ l2
+ … + ln
= S1
= sum of the diagonal elements of the matrix A. ■
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 67 5/30/2016 5:03:50 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-104-2048.jpg)
![1.68 ■ Engineering Mathematics
Note Sum of the diagonal elements of A is called the trace of A.
∴ Sum of the eigen values = trace of A
3. Product of the eigen values of a square matrix A is equal to A .
Proof Let A be a square matrix of order n.
Then its characteristic equation is A I
− =
l 0
⇒ l l l
n n n n
n
S S S
− + − + − =
− −
1
1
2
2
1 0
... ( ) (1)
where S A
n = .
If l1
, l2
, …, ln
are the n roots of (1), then from theory of equations,
the product of roots = −
( )
1
constant term
coefficient of
n
n
l
⇒ l l l
1 2
2
1 1 1
… n
n n
n
n
n n
S S S A
= − − = − = =
( ) ( ) ( ) [{ (−1)2n
= 1]
∴ the product of the eigen values = = =
l l l
1 2 … n n
S A . ■
Note If at least one eigen value is 0, then A = 0 ∴ A is a singular matrix.
If all the eigen values are non-zero, then A ≠ 0
∴ A is a non-singular if all the eigen values are non-zero.
4. If l1
, l2
, …, ln
are non-zero eigen values of square matrix of order n, then
1 1 1
1 2
l l l
, , ,
…
n
are
eigen values of A
21
.
Proof Let l be any non-zero eigen value of A, then there exists a non-zero column matrix X such that
AX = lX. Since all the eigen values are non-zero, A is non-singular.
∴ A
−1
exists.
∴ A
−1
(AX) = A
−1
(lX)
⇒ (A
−1
A)X = l(A
−1
X)
⇒ IX = l(A
−1
X)
⇒ X A X X A X A X X
1 1 1
= ⇒ = ⇒ =
− − −
l
l l
( ) .
1 1
[{ l ≠ 0]
So, is an eigen value of A .
1
1
l
−
This is true for all the eigen values of A.
∴ …
1 1 1
1 2
l l l
, , ,
n
are the eigen values of A
−1
. ■
Note that the eigen vector for A
−1
corresponding to
1
l
is also X.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 68 5/30/2016 5:03:53 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-105-2048.jpg)
![Matrices ■ 1.69
5. If l1
, l2
, ???, ln
are the eigen values of A, then
(i) cl1
, cl2
, ???, cln
are the eigen values of cA, where c ≠ 0
(ii) l l l
1 2
m m
n
m
, , ,
… are the eigen values of Am
, where m is a positive integer.
Proof
Let l be any eigen value of A, then there exists a non-zero column matrix X such that
AX = lX (1)
(i) Multiply by c ≠ 0 then c(AX) = c(lX) ⇒ (cA) X = (cl) X
∴ cl is an eigen value of cA.
This is true for all eigen values of A.
∴ cl1
, cl2
, …, cln
are the eigen values of cA.
(ii) Now A2
X = A(AX) = A(lX) = l(AX) = l(lX) = l2
X [using (1)]
∴ A2
X = l2
X ⇒ l2
is an eigen value of A2
.
Similarly, A3
X = A(A2
X) = A(l2
X) = l2
(AX) = l2
(lX) = l3
X
A3
X = l3
X ⇒ l3
is an eigen value of A3
.
Proceeding in this way, we have Am
X = lm
X for any positive integer m.
This is true for all eigen values.
∴ l l l
1 2
m m
n
m
, , ,
… are the eigen values of Am
. ■
6. If l1
, l2
, …, ln
are the eigen values of A, then
(i) l1
2 K, l2
2 K, …, ln
2 K are the eigen values of A 2 KI.
(ii) a l 1 a l 1 a a l 1 a l 1 a a l 1 a l 1 a
0 1 1 1 2 0 2
2
1 2 2 0
2
1 2
2
, , ,
… n n are the eigen values of
a 1 a 1 a
0
2
1 2
A A I.
Proof
Let l be any eigen value of A. Then AX = lX (1)
where X ≠ 0 is a column matrix.
∴ AX − KX = lX − KX
⇒ (A − KI)X = (l − K)X
∴ l − K is an eigen value of A − KI.
This is true for all eigen values of A.
∴ l1
− K, l2
− K, …, ln
− K are the eigen values of A − KI.
(ii) We have AX = lX and A2
X = l2
X.
∴ a0
(A2
X) = a0
(l2
X) and a1
(AX) = a1
(lX)
∴ a0
(A2
X) + a1
(AX) = a0
(l2
X) + a1
(lX)
Adding a2
X on both sides, we get
a0
(A2
X) + a1
(AX) + a2
X = a0
(l2
X) + a1
(lX) + a2
X
⇒ (a0
A2
+ a1
A + a2
I)X = (a0
l2
+ a1
l + a2
)X
This means a0
l2
+ a1
l + a2
is an eigen value of a0
A2
+ a1
A + a2
I.
This is true for all eigen values of A.
∴ + + + + + +
a l a l a a l a l a a l a l a
0 1
2
1 1 2 0 2
2
1 2 2 0
2
1 2
, , ,
… n n
are the eigen values of
a a a
0
2
1 2
A A I
+ + . ■
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 69 5/30/2016 5:03:54 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-106-2048.jpg)



![Matrices ■ 1.73
9.
− − −
− − −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
5 5 9
8 9 18
2 3 7
10.
2 1 1
1 2 1
0 0 1
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
ANSWERS TO EXERCISE 1.5
1. l = 1, 3, −4; eigen vectors
2
1
4
2
1
2
1
3
13
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥ −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, , 2. l = 0, −1, 2; eigen vectors
5
1
0
2
0
1
0
1
2
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥ −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, ,
3. l = −3, −3, 5; eigen vectors
2
1
0
3
0
1
1
2
1
−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
−
−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
, , 4. l = 3, 6, 9; eigen vectors
1
2
2
2
1
2
2
2
1
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥ −
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
, ,
5. l = 2, 2, 8; eigen vectors
1
0
2
1
2
0
2
1
1
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, , 6. l = −2, 3, 6; eigen vectors
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
0
1
1
1
1
1
2
1
, ,
7. l = 1, 1, 4; eigen vectors
1
1
0
0
1
1
1
1
1
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, ,
8. l = 3, 2, 2; eigen vectors X1 2 3
1
1
2
5
2
5
=
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
= =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
and X X
9. l = −1, −1, −1; eigen vectors X1
= X2
= X3
= −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
3
6
2
10. l = 1, 1, 3; eigen vectors X X X
1 2 3
1
0
1
0
1
1
1
1
0
=
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, ,
1.6.5 Cayley-Hamilton Theorem
Theorem 1.4 Every square matrix satisfies its characteristic equation
Proof
Let A aij n n
= [ ] ×
be a square matrix of order n.
Then the Characteristic polynomial is
A I
a a a a
a a a a
a a a a
n
n
n n n nn
− =
−
−
−
l
l
l
l
11 12 13 1
21 22 23 2
1 2 3
…
…
…
:
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 73 5/30/2016 5:04:04 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-110-2048.jpg)
![1.74 ■ Engineering Mathematics
The coefficient of ln
is (−1)n
from the product of (a11
− l) (a22
− l)... (ann
− l).
∴ let A I a a a
n n n
− = − +…+
l l l l
( 1) 1 2
2
n
n
+ +
⎡
⎣ ⎤
⎦
− −
1
(1)
Since the elements of A − lI are at most first degree in l, the elements of adj (A − lI) are ordinary
polynomials in l of degree at most (n − 1).
∴ adj (A − lI) can be written as a matrix polynomial in l of degree n − 1.
Let adj( )
A I B B B B
n n n n
− = + + +
− − − −
l l l l
0
1
1
2
2
3 1
… n (2)
where B0
, B1
,…, Bn − 1
are n × n matrices.
The elements of these matrices are function of aij
.
We know that if A is a n × n matrix, then A A A I
(adj ) (adjA) A
= =
where I is n × n identity matrix.
∴ we have ( ) ( )
A I A I A I I
− − = − =
l l l
adj
Substituting from (1) and (2), we have
( )[ ]
( ) (
A I B B B B B
a
n n n
n n
n n n
− + + + + +
= − + +
− − −
− −
−
l l l l l
l l
0
1
1
2
2
3
2 1
1
1
1
…
a
a a a
n
n n
2
2
1
l l
−
−
+ +
… )
Equating the coefficients of lm
, ln − 1
, ln − 2
… l and term independent of l, we get
−IB0
= (−1)n
, AB0
− IB0
= (−1)n
a1
I,
AB1
− IB2
= (−1)n
a2
I, … , ABn − 2
− IBn − 1
= (−1) an − 1
I, ABn − 1
= (−1)n
an
I
Pre-multiplying the above equation by An
, An − 1
, An − 2
, …, A, I, we get
− = −
− = −
− = −
− −
− −
A B A
A B A B a A
A B A B a A
n n n
n n n n
n n n
0
0
1
1 1
1
1
1
2
2 2
1
1
1
( )
( )
( ) n
n
n
n
A B AB a
AB a
−
− − −
−
− = −
= −
2
2
2 1 1
1
1
1
:
n n n
n n
( )
( )
A
I
Adding we get,
⇒
( ) [ ... ]
...
− + + + =
+ + + =
− −
− −
1 0
0
1
1
2
2
1
1
2
2
n n n n
n
n n n
n
A a A a A a I
A a A a A a I
This means A satisfies the equation l l l
n n n
n
a a a
+ + + + =
− −
1
1
2
2
0
… ,
which is the characteristic equation of A.
Hence, the theorem.
Properties: Cayley–Hamilton Theorem has the following two important properties:
1. To find the inverse of a non-singular matrix A
2. To find higher integral power of A
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 74 5/30/2016 5:04:06 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-111-2048.jpg)
![Matrices ■ 1.75
WORKED EXAMPLES
EXAMPLE 1
Verify that A
1 2
2 1
5
2
⎡
⎣
⎢
⎤
⎦
⎥ satisfies its characteristic equation and hence find A4
.
Solution.
Given A =
−
⎡
⎣
⎢
⎤
⎦
⎥
1 2
2 1
The characteristic equation of A is A I
− =
l 0 ⇒ l l
2
1 2 0
− + =
S S
where S S A
1 2
1 1 0 1 4 5
= + − = = = − − = −
( ) and
∴ the characteristic equation is l2
− 5 = 0 (1)
By Cayley-Hamilton theorem, A satisfies (1). That is A2
− 5I = 0 (2)
We shall now verify this by direct computation.
∴
A A A
I
A I
2
2
1 2
2 1
1 2
2 1
5 0
0 5
1 0
0 1
5
= ⋅ =
−
⎡
⎣
⎢
⎤
⎦
⎥ −
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
− =
5
5 0
0 5
5
1 0
0 1
5 0
0 5
5 0
0 5
0 0
0 0
⎡
⎣
⎢
⎤
⎦
⎥ −
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
⎦
⎥ −
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
⎦
⎥
⇒ A
2
− 5I = 0.
Hence, A satisfies its characteristic equation.
To find A4
: We have A
2
= 5I [from (2)]
∴ A4
= 5A2 =
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
⎦
⎥
5
5 0
0 5
25 0
0 25
.
EXAMPLE 2
Verify Cayley-Hamilton theorem for the matrix A
1 4
2 3
5
⎡
⎣
⎢
⎤
⎦
⎥ and find its inverse. Also express
A5
2 4A4
2 7A3
1 11A2
2 A 2 10I as a linear polynomial in A.
Solution.
Given A =
⎡
⎣
⎢
⎤
⎦
⎥
1 4
2 3
The characteristic equation of A is A I
− =
l 0 ⇒ l l
2
1 2 0
− + =
S S
where S S A
1 2
1 3 4 3 8 5
= + = = = − = −
,
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 75 5/30/2016 5:04:09 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-112-2048.jpg)

![Matrices ■ 1.77
∴ l5
− 4l4
− 7l3
+ 11l2
− l − 10 = (l2
− 4l − 5)(l3
− 2l + 3) + l + 5
Replace l by A, we get
A5
− 4A4
− 7A3
+ 11A2
− A − 10I = (A2
− 4A − 5I) (A3
− 2A + 3I) + A + 5I
= 0 + A + 5I = A + 5I [using (2)]
which is a linear polynomial in A.
EXAMPLE 3
Find the characteristic equation of the matrixA given A
2 1 1
1 2 1
1 1 2
5
2
2 2
2
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
. Hence,find A21
and A4
.
Solution.
Given A =
−
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 1 1
1 2 1
1 1 2
The characteristic equation of A is A I
− =
l 0
⇒
2 1 1
1 2 1
1 1 2
0
− −
− − −
− −
l
l
l
= ⇒ 0
3
1
2
2 3
− + − =
l l l
S S S
where S1
= sum of the diagonal elements of A = 2 + 2 + 2 = 6
S2
= sum of the minors of the diagonal elements of A
=
−
−
+ +
−
−
= − + − + − =
= = − + − + + − =
2 1
1 2
2 1
1 2
2 1
1 2
4 1 4 1 4 1 9
2 4 1 2 1 1 2
3
S A ( ) ( ) ( ) 6
6 1 1 4
− − =
∴ the characteristic equation is l3
− 6l2
+ 9l − 4 = 0
By Cayley-Hamilton theorem, A satisfies its characteristic equation
∴ A3
− 6A2
+ 9A − 4I = 0 (1)
⇒ 4I = A3
− 6A2
+ 9A
Multiply by A−1
, 4IA−1
= A3
A−1
− 6A2
⋅ A−1
+ 9A A−1
⇒ 4A−1
= A2
− 6A + 9I
But A2
2 1 1
1 2 1
1 1 2
2 1 1
1 2 1
1 1 2
4 1 1 2
=
−
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
+ + − − 2
2 1 2 1 2
2 2 1 1 4 1 1 2 2
2 1 2 1 2 2 1 1 4
6 5 5
− + +
− − − + + − − −
+ + − − − + +
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
−
−5
5 6 5
5 5 6
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 77 5/30/2016 5:04:11 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-114-2048.jpg)
![1.78 ■ Engineering Mathematics
∴ 4
6 5 5
5 6 5
5 5 6
6
2 1 1
1 2 1
1 1 2
9
1 0 0
A
1
−
=
−
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
−
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+ 0
0 1 0
0 0 1
6 12 9 5 6 5 6
5 6 6 12 9 5 6
5 6 5 6 6 12 9
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
− + − + −
− + − + − +
− − + − +
=
⎡
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
3 1 1
1 3 1
1 1 3
∴ A
−
=
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1
4
3 1 1
1 3 1
1 1 3
(1) ⇒ A A A I
3 2
6 9 4
= − +
∴ A A A A
A A I A A
A A I
4 3 2
2 2
2
6 9 4
6 6 9 4 9 4
27 50 24
= − +
= − + − +
= − +
[ ]
[Multiplying by A]
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+
27
6 5 5
5 6 5
5 5 6
50
2 1 1
1 2 1
1 1 2
24
1 0 0
−
− −
−
−
−
− −
−
0
0 1 0
0 0 1
162 100 24 135 50 135 50
135 50 162 100 24
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
+ +
+ +
− − −
− − −
−
− − −
−
− −
135 50
135 50 135 50 162 100 24
86 85 85
85 86 85
8
+
+ +
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
5
5 85 86
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
EXAMPLE 4
Use Cayley-Hamilton theorem to find the matrix
A8
2 5A7
1 7A6
2 3A5
1 8A4
2 5A3
1 8A2
2 2A 1 I if the matrix A
2 1 1
0 1 0
1 1 2
5
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
Solution.
Given A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 1 1
0 1 0
1 1 2
The characteristic equation is A I
− =
l 0
⇒ 2 1 1
0 1 0
1 1 2
0 0
3
1
2
2 3
−
−
−
= ⇒ − + − =
l
l
l
l l l
S S S
where S1
= 2 + 1 + 2 = 5
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 78 5/30/2016 5:04:13 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-115-2048.jpg)
![Matrices ■ 1.79
S
S A
2
3
1 0
1 2
2 1
1 2
2 1
0 1
2 4 1 2 7
2 2 1 0 1 1 4 1 3
= + + = + − + =
= = ⋅ − ⋅ + − = − =
( )
∴ the characteristic equation is l3
− 5l2
+ 7l − 3 = 0
By Cayley-Hamilton theorem, we get A3
− 5A2
+ 7A − 3I = 0 (1)
We have to find the matrix
A8
− 5A7
+ 7A6
− 3A5
+ 8A4
− 5A3
+ 8A2
− 2A + I = f(A), say
We shall rewrite this matrix polynomial in terms of
A3
− 5A2
+ 7A − 3I
∴ the polynomial
f(A) = A5
(A3
− 5A2
+ 7A − 3I) + 8A4
− 5A3
+ 8A2
− 2A + I
= 8A4
− 5A3
+ 8A2
− 2A + I [Using (1)]
= 8A(A3
− 5A2
+ 7A − 3I) + 35A3
− 48A2
+ 22A + I
= 35A3
− 48A2
+ 22A + I [Using (1)]
= 35(A3
− 5A2
+ 7A − 3I) + 127A2
− 223A + 106I
= 127A2
− 223A + 106I [Using (1)]
But A2
2 1 1
0 1 0
1 1 2
2 1 1
0 1 0
1 1 2
5 4 4
0 1 0
4 4 5
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
∴ f ( )
A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
127
5 4 4
0 1 0
4 4 5
223
2 1 1
0 1 0
1 1 2
106
1 0 0
0
+ 1
1 0
0 0 1
635 446 106 508 223 508 223
0 127 223 106 0
508
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
− − −
−
+
+
−
− − −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
223 508 223 635 446 106
295 285 285
0 10 0
285 285 295
+
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Note: Otherwise divide l8
− 5l7
+ 7l6
− 3l5
+ 8l4
− 5l3
+ 8l2
− 2l + 1 by l3
− 5l2
+ 7l − 3 and
proceed as in example 2.
EXAMPLE 5
If A
1 0 0
1 0 1
0 1 0
5
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, then show that An
5 An 2 2
1 A2
2 I for n $ 3. Hence, find A50
.
Solution.
Given A =
1 0 0
1 0 1
0 1 0
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 79 5/30/2016 5:04:15 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-116-2048.jpg)

![Matrices ■ 1.81
∴ A A A I
n
= +
−
⎛
⎝
⎜
⎞
⎠
⎟ −
−
2 2
2
2
2
2
n n
⇒ A A I
n
= −
−
⎛
⎝
⎜
⎞
⎠
⎟
2
2
2
2
n n
Putting n = 50, we get A50
= 25A2
− 24I
But A A A
2
1 0 0
1 0 1
0 1 0
1 0 0
1 0 1
0 1 0
1 0 0
1 1 0
1 0 1
= ⋅ =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
∴ A50
25
1 0 0
1 1 0
1 0 1
24
1 0 0
0 1 0
0 0 1
1 0 0
25 1 0
25 0
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
1
1
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
EXAMPLE 6
If A
1 2
2 1
5
2
⎡
⎣
⎢
⎤
⎦
⎥ , then find An
in terms of A and I.
Solution.
Given A =
−
⎡
⎣
⎢
⎤
⎦
⎥
1 2
2 1
The characteristic equation is l2
− 5 = 0 [see example 17]
By Cayley-Hamiltons theorem A2
− 5I = 0 (1)
To find An
, consider the polynomial ln
Dividing ln
by l2
− 5, we get ln
= (l2
− 5) f(l) + al + b (2)
where f(l) is the quotient and al + b is the remainder.
We shall now find the values of a and b.
The eigen values of A are l = −
5 5
,
Substitute l = 5 in (2) then 5 0 5
( ) = + +
n
a b ⇒ a b
5 5
+ = ( )
n
(3)
Substitute l = − 5 in (2), then −
( ) = + −
( )+
5 0 5
n
a b
⇒ − + = −
( )
a b
5 5
n
(4)
(3) + (4) ⇒ 2 5 5
b = ( ) + −
( )
n n
∴ b =
( ) + −
( )
= ( ) + −
5 5
2
5
1 1
2
n n
n n
( ( ) )
(3) − (4) ⇒ 2 5 5 5
a = ( ) − −
( )
n n
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 81 5/30/2016 5:04:22 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-118-2048.jpg)
![1.82 ■ Engineering Mathematics
∴ a =
( ) − −
( )
= ( ) −
5 5
2 5
5
1 1
2
n n
n n
( ( ) )
−
Replacing l by A in (2), we get
∴
A A I A A I A I
A A
n
n
n n n
= − + + = + +
= ( ) − −
⎛
⎝
⎜
⎞
⎠
⎟ + ( ) +
( ) ( )
( ) (
2
5 0
5
1 1
2
5
1
f a b a b
−
−
⎛
⎝
⎜
⎞
⎠
⎟
1
2
)
.
n
I
EXERCISE 1.6
Verify Cayley-Hamilton theorem for the following matrices and hence find their inverses.
1.
1 3 7
4 2 3
1 2 1
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2.
1 0 3
2 1 1
1 1 1
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
3.
−
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 0 3
8 1 7
3 0 8
4.
7 2 2
6 1 2
6 2 1
−
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
5. Verify that the matrix A =
−
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 1 2
1 2 1
1 1 2
satisfies its characteristic equation and hence find A4
.
6. A =
⎡
⎣
⎢
⎤
⎦
⎥
7 3
2 6
, find An
in terms of A and I using Cayley-Hamilton theorem and hence find A3
.
7. Find A4
using Cayley-Hamilton theorem for the matrix A = −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 2 3
2 1 4
3 1 1
. Find A4
+ A3
− 18A2
− 39A + 2I
8. Find the eigen values and eigen vectors of the system of equations 10x1
+ 2x2
+ x3
= lx1
, 2x1
+ 10x2
+ x3
=
lx2
, 2x1
+ x2
+ 10x3
= lx3
[Hint: Equations can be rewritten as (10 − l)x1
+ 2x2
+ x3
= 0, 2x1
+ (10 − l)x2
+ x3
= 0,
2x1
+ x2
+ (10 − l)x3
= 0
If A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
10 2 1
2 10 1
2 1 10
and X =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
x
x
x
1
2
3
then these equations in matrix form is (A − lI)X = 0 and so A I
− =
l 0
is the characteristic equation of A and l = 8, 9, 13. Eigen vectors are given by (I)]
9. If l is an eigen value of a non-singular matrix A, show that
A
l
is an eigen value of the matrix adj A.
Hint: AX = lX ⇒ (adj A) (AX) = (adj A) (lX) A X adj A X
= l( ) ⇒ adj A X
A
X
=
⎤
⎦
⎥
l
( )
(
⎡
⎣
⎢
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 82 5/30/2016 5:04:25 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-119-2048.jpg)

![1.84 ■ Engineering Mathematics
The relation (2) means B is similar to A. Thus, if A is similar to B, then B is similar to A.
Hence, we simply say A and B are similar matrices.
An important property of similarity transformations is that they preserve eigen values, which is
proved in the next theorem.
Theorem 1.5 Similar matrices have the same eigen values.
Proof Let A and B be two similar matrices of order n.
Then B = P−1
AP, by definition.
∴ the characteristic polynomial of B is B I
− l
Now B I P AP I P AP P IP
− = − = −
− − −
l l l
1 1 1
⇒ = −
−
P A I P
1
( )
l
= −
−
P A I P
1
l =
AB A B
[ ]
{
= − = − = −
− −
A I P P A I P P A I I
1 1
l l l
⇒ − =
B I A
l −
− lI =
I
[ ]
{ 1
∴ A and B have the same characteristic polynomial and hence have the same characteristic equation.
So, A and B have the same eigen values.
Note Similar matrices A and B have the same determinant value i.e., A B
= .
For B P AP B P AP P A P A P P A I A
= ⇒ = = = = =
− − − −
1 1 1 1
1.7.2 Diagonalisation of a Square Matrix
Definition 1.36 A square matrix A is said to be diagonalisable if there exists a non-singular matrix P
such that P−1
AP = D, where D is a diagonal matrix. The matrix P is called a modal matrix of A.
The next theorem provides us with a method of diagonalisation.
Theorem 1.6 If A is a square matrix of order n, having n linearly independent eigen vectors and M
is the matrix whose columns are the eigen vectors of A, then M−1
AM = D, where D is the diagonal
matrix whose diagonal elements are the eigen values of A.
Proof Let X1
, X2
, …, Xn
be n linearly independent eigen vectors of A corresponding to the eigen
values l1
, l2
, …, ln
of A.
∴ AXi
= li
Xi
, i = 1, 2, 3, …, n.
Let M = [X1
X2
… Xn
] be the matrix formed with the eigen vectors as columns.
Then AM = [AX1
AX2
AX3
… AXn
]
= [l1
X1
l2
X2
l3
X3
… ln
Xn
]
= …
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
[ ]
X X Xn
n
1 2
1
2
3
0 0 0
0 0
0 0
0 0 0
l
l
l
l
…
…
: : : :
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 84 5/30/2016 5:04:29 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-121-2048.jpg)
![Matrices ■ 1.85
⇒
AM MD where D
M AM D
n
= =
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
,
l
l
l
1
2
1
0 0
0 0
0
: : :
…
−
The matrix M which diagonalises A is called the modal matrix of A and the resulting diagonal matrix
D whose elements are eigen values of A is called the spectral matrix of A.
1.7.3 Computation of the Powers of a Square Matrix
Diagonalisation of a square matrix A is very useful to find powers of A, say Ar
.
By the theorem 1.6, D = M−1
AM
∴ D M AM M AM
M A MM AM M AIAM M A M
2 1 1
1 1 1 1 2
=
=
( ) ( )
( )
− −
− − − −
= =
Similarly, D D D
M A M M AM
M A MM AM M A IAM M A M
3 2
1 2 1
1 2 1 1 2 1 3
=
=
= = =
− −
− − − −
( ) ( )
( )
Proceeding in this way, we can find
∴
D M A M
A MD M where D
r r
r r r
r
r
n
r
=
= =
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
−
−
1
1
1
2
0 0
0 0
0 0
,
l
l
l
…
…
… … … …
…
⎥
⎥
⎥
⎥
⎥
⎥
Note
(1) If the eigen values l1
, l2
, …, ln
of A are different then the corresponding eigen vectors X1
,
X2
, …, Xn
are linearly independent by theorem 1.2.1 (2). So, A can be diagonalised.
(2) Even if 2 or more eigen values are equal, if we can find independent eigen vectors corresponding
to them (see worked example 6), then A can be diagonalised.
Thus, independence of eigen vectors is the condition for diagonalisation.
Working rule to diagonalise a n 3 n matrix A by similarity transformation:
Step 1: Find the eigen values l1
, l2
, …, ln
Step 2: Find linearly independent eigen vectors X1
, X2
, …, Xn
Step 3: Form the modal matrix M = [X1
X2
… Xn
]
Step 4: Find M−1
and AM.
Step 5: Compute M−1
AM = D =
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
l
l
l
1
2
0 0 0
0 0 0
0 0
…
…
… …
: : : : :
n
⇒
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 85 5/30/2016 5:04:31 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-122-2048.jpg)
![1.86 ■ Engineering Mathematics
1.7.4 Orthogonal Matrix
Definition 1.37 A real square matrix A is said to be an orthogonal matrix if AAT
= AT
A = I, where I
is the unit matrix of the same order as A.
From this definition it is clear that AT
= A−1
.
So, an orthogonal matrix is also defined as below.
Definition 1.38 A real square matrix A is orthogonal if AT
= A−1
.
EXAMPLE 1.25
Prove that A
cos sin
sin cos
5
u u
2 u u
⎡
⎣
⎢
⎤
⎦
⎥ is orthogonal.
Solution.
Given A =
−
⎡
⎣
⎢
⎤
⎦
⎥
cos sin
sin cos
u u
u u
∴ A =
−
⎡
⎣
⎢
⎤
⎦
⎥ = +
cos sin
sin cos
cos sin
u u
u u
u u
2 2
1
=
∴ A is non-singular.
Hence, A
adj A
A
A
1
T
T
−
=
= =
−
⎡
⎣
⎢
⎤
⎦
⎥
cos sin
sin cos
u u
u u
[ ]
{ A = 1
∴ A is orthogonal.
1.7.5 Properties of Orthogonal Matrix
1. If A is orthogonal, then AT
is orthogonal.
Proof Given A is orthogonal. ∴ AAT
= AT
A = I
Reversing the roles of A and AT,
we see AT
A = AAT
= I ⇒ AT
is orthogonal.
Note Since AT
= A−1
, it follows A−1
is orthogonal.
2. If A is an orthogonal matrix, then A 1.
56
Proof Given A is orthogonal. Then AAT
= 1
⇒ AAT
= 1 ⇒ A AT
= 1
But we know A A
T
=
∴ A A A A
= = ±
1 1 1
2
⇒ ⇒ =
3. If l is an eigen value of an orthogonal matrix A, then
1
l
is also an eigen value of A.
Proof Given A is orthogonal and l is an eigen value of A.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 86 5/30/2016 5:04:32 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-123-2048.jpg)
![Matrices ■ 1.87
Then AT
= A−1
. By property (4) of eigen values,
1
l
is an eigen value of A−1
and so an eigen value of AT
.
By property (1), A and AT
have same eigen values.
∴
1
l
is an eigen of A and hence l,
1
l
are eigen values of orthogonal matrix A.
4. If A and B are orthogonal matrices, then AB is orthogonal.
Proof Given A and B are orthogonal matrices.
∴ AT
= A−1
and BT
= B−1
Now (AB)T
= BT
AT
= B−1
A−1
= (AB)−1
∴ AB is orthogonal.
5. Eigen values of an orthogonal matrix are of magnitude 1.
Proof Let A be an orthogonal matrix and let l be an eigen value of A.
Then AX = lX, where X ≠ 0 (1)
Taking complex conjugate, we get A X X
= l
But A is real matrix ∴ A A
=
Hence, AX X
= l
Taking transpose, ( ) ( )
AX X
T T
= l
⇒ X A X
T T T
= l ⇒ X A X
T 1 T
−
= l [ ]
{ A A
T
= −1
(2)
Multiplying (2) and (1) we get
⇒
⇒
⇒
( )( ) ( )( )
( )
X A AX X X
X A A X X X
X X X X
T 1 T
T 1 T
T T
−
−
⇒
=
=
=
= =
l l
ll
l
l l
2
2
1 1
[ ]
{ X X as X
T
≠ ≠
0 0
This is true for all eigen values of A.
Hence, eigen values of A are of absolute value 1. ■
1.7.6 Symmetric Matrix
Definition 1.39 Real Square Matrix
The matrix A = [aij
]n × n
is said to be symmetric if AT
= A.
Example:
1 1
1 0
1 1 3
1 0 4
3 4 2
−
−
−
−
⎡
⎣
⎢
⎤
⎦
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, are symmetric matrices.
Note that the elements equidistant from the main diagonal are the same.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 87 5/30/2016 5:04:35 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-124-2048.jpg)
![1.88 ■ Engineering Mathematics
1.7.7 Properties of Symmetric Matrices
1. Eigen values of a symmetric matrix are real.
Proof Let A be a symmetric matrix of order n and l be an eigen value of A.
Then there exists X ≠ 0 such that AX = lX (1)
Taking complex conjugate,
A X X
= l
⇒ AX X
= l [ ]
{ A is real A A
= (2)
Taking transpose, ( ) ( )
AX X
T T
= l ⇒ ( ) ( )
X A X X A X
T T T T T
= =
l l
⇒ [ ]
{ A A
T
=
Post multiplying by X,
⇒
⇒
⇒
⇒
( (
) )
) ( )
( ) ( )
X A)X X) X
X (AX (X X
X ( X X X
X X X X
T T
T T
T T
T T
=
=
=
=
=
l
l
l l
l l
l l l
∴ is
s real
[ ]
{ X X as X
T
≠ ≠
0 0
This is true for all eigen values.
∴ eigen values of a symmetric matrix are real. ■
2. Eigen vectors corresponding to different eigen values of a symmetric matrix are orthogonal
vectors.
Proof Let A be a symmetric matrix of order n. ∴ AT
= A.
Let l1
, l2
be two different eigen values of A. Then l1
, l2
are real, by property (1).
∴ there exist X1
≠ 0, X2
≠ 0 such that
AX1
= l1
X1
(1)
and AX2
= l2
X2
(2)
Premultiplying (1) by X2
T
, we get X AX X X
2
T
2
T
1
( )
1 1
= l
⇒ X AX X X )
T
2
T
1
2 1 1
= l ( (3)
Premultiplying (2) by X1
T
, we get X (AX ) X X
1
T
2 1
T
2
= l2
⇒ X AX X X )
1
T
2 1
T
2
= l2 ( (4)
Taking transpose of (3), we get ( (
X AX ) X X )
2
T
1
T
2
T
1
T
= l1
⇒ X A X X X
1
T T
2 1
T
2
= l1
⇒ X AX (X X )
1
T
2 1
T
2
= l1 (5)
From (4) and (5) we get, l l
1 2
( ) ( )
X X X X
1
T
2 1
T
2
=
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 88 5/30/2016 5:04:38 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-125-2048.jpg)
![Matrices ■ 1.89
⇒ ( )( )
l l
1 2 0
− =
X X
1
T
2
Since l l l l
1 2 1 2 2
0 0
≠ − ≠ =
, , ∴ X X
1
T
⇒ X1
and X2
are orthogonal. ■
Remark: If X1
= (a1
, b1
, c1
) and X2
= (a2
, b2
, c2
) be two 3-dimensional vectors, they are orthogonal if
their dot product is 0 ⇒ a1
a2
+ b1
b2
+ c1
c2
= 0
If we treat them as column matrices, X X
1
1
1
1
2
2
2
2
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
a
b
c
a
b
c
, then the matrix product
X X
1
T
2 1 1 1
2
2
2
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
[ ]
a b c
a
b
c
= + +
a a b b c c
1 2 1 2 1 2
So, X1
and X2
are orthogonal if X X or X X
1
T
2
T
2 1
0 0
= = .
Thus, we can treat column matrices as vectors and verify dot product = 0.
2. The unit vector in X1
is
X1
2 2 2
a b c
1 1
and it is called a normalised vector.
Note For any square matrix eigen vectors corresponding to different eigen values are linearly
independent, but for a symmetric matrix, they are orthogonal, pairwise.
1.7.8 Diagonalisation by Orthogonal Transformation or Orthogonal Reduction
Definition 1.40 A Square Matrix
A is said to be orthogonally diagonalisable if there exists an orthogonal matrix N such that
N−1
AN = D ⇒ NT
AN = D [{ NT
= N−1
]
This transformation which transforms A into D is called an orthogonal transformation.
The next theorem gives a method of orthogonal reduction.
Theorem 1.7 Let A be a symmetric matrix of order n. Let X1
, X2
, …, Xn
be eigen vectors of A which are
pairwise orthogonal. Let N be the matrix formed with the normalised eigen vectors of A as columns.
Then N is an orthogonal matrix such that N−1
AN = D ⇒ NT
AN = D.
N is called normalised modal matrix of A or normal modal matrix of A.
Working rule for orthogonal reduction of a n 3 n symmetric matrix.
Step 1: Find the eigen values l1
, l2
, …, ln
Step 2: Find the eigen vectors X1
, X2
, …, Xn
which are pairwise orthogonal.
Step 3: Form the normalised modal matrix N with the normalised eigen vectors as columns.
Step 4: Find NT
and AN.
Step 5: Compute N AN D
T
n
= =
… …
…
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
l
l
l
1
2
0 0
0 0
0
:
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 89 5/30/2016 5:04:40 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-126-2048.jpg)


![1.92 ■ Engineering Mathematics
So, the normalised modal matrix N =
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
−
−
1
3
1
2
1
6
1
3
1
2
1
6
1
3
0
2
6
∴ NT
=
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
1
3
1
3
1
3
1
2
1
2
0
1
6
1
6
2
6
AN = −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
3 1 1
1 3 1
1 1 3
1
3
1
2
1
6
1
3
1
2
1
6
1
3
0
2
6
⎥
⎥
⎥
⎥
=
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
1
3
4
2
4
6
1
3
4
2
4
6
1
3
0
8
6
∴ N AN
T
=
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
−
−
1
3
1
3
1
3
1
2
1
2
0
1
6
1
6
2
6
1
3
4
2
4
6
1
3
4
2
4
6
1
3
0
0
8
6
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 0 0
0 4 0
0 0 4
, which is a diagonal matrix.
EXAMPLE 2
The eigen vectors of a 3 3 3 real symmetric matrix A corresponding to the eigen values 2, 3, 6
are [1, 0, 21]T
, [1, 1, 1]T
, [21, 2, 21]T
respectively, find the matrix A.
Solution.
Given A is symmetric and the eigen values are different.
So, the eigen vectors are orthogonal pairwise.
The normalised eigen vectors are
1
2
0
1
2
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
,
1
3
1
3
1
3
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
,
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
1
6
2
6
1
6
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 92 5/30/2016 5:06:59 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-129-2048.jpg)


![Matrices ■ 1.95
We shall now choose X3 =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
a
b
c
orthogonal to X2
∴ dot product = 0 ⇒ a + c = 0 and X3
should satisfy equations (2)
∴ a – c = 0 and 0b = 0
Solving, we get a = c = 0 and choose b = 1 ∴ X3
0
1
0
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Thus, the eigen values are 1, 3, 3 and the corresponding eigen vectors are
1
0
1
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
,
1
0
1
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
,
0
1
0
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Clearly they are pairwise orthogonal vectors.
The normalised eigen vectors are
1
2
0
1
2
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
,
1
2
0
1
2
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
,
0
1
0
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
∴ the normalised modal matrix N =
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
1
2
1
2
0
0 0 1
1
2
1
2
0
∴ NT
=
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
1
2
0
1
2
1
2
0
1
2
0 1 0
AN =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
=
2 0 1
0 3 0
1 0 2
1
2
1
2
0
0 0 1
1
2
1
2
0
1
2
3
2
0
0
0 0 3
1
2
3
2
0
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
∴ N AN
T
=
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
1
2
0
1
2
1
2
0
1
2
0 1 0
1
2
3
2
0
0 0 3
1
2
3
2
0
⎦
⎦
⎥
⎥
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
1 0 0
0 3 0
0 0 3
D
∴ N−1
AN = D ⇒ A = ND N−1
∴ A3
= ND3
N−1
= ND3
NT
[
∴
NT
= N−1
]
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 95 5/30/2016 5:07:05 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-132-2048.jpg)
![1.96 ■ Engineering Mathematics
⇒ A3
1
2
1
2
0
0 0 1
1
2
1
2
0
1 0 0
0 27 0
0 0 27
=
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
=
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
1
2
0
1
2
1
2
0
1
2
0 1 0
1
2
1
2
0
0 0 1
1
2
1
2
0
⎥
⎥
⎥
⎥
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
1
2
0
1
2
27
2
0
27
2
0 27 0
14 0 13
0 27 0
13 0 14
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
1.8 REAL QUADRATIC FORM. REDUCTION TO CANONICAL FORM
Definition 1.41 A homogeneous polynomial of second degree in any number of variables is called a
quadratic form.
For example
(i) x xy y
2 2
4 4
+ +
(ii) ax by cz hxy gyz fzx
2 2 2
2 2 2
+ + + + +
(iii) x x x x
1
2
2
2
3
2
4
2
3
+ + +
are quadratic forms in 2, 3 and 4 variables respectively.
Definition 1.42 The general quadratic form in n variables x1
, x2
, …, xn
is a x x
ij i j
i
n
j
n
=
=
∑
∑ 1
1
, where aij
are
real numbers such that aij
= aji
for all i, j = 1, 2, 3, …, n.
Usually the quadratic form is denoted by Q and Q
1
1
=
=
=
∑
∑ a x x
ij i j
i
n
j
n
.
1. Matrix form of Q
If X
n
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
x
x
x
1
2
…
, A
n
2n
n1 n2 nn
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
a a a
a a a
a a a
11 12 1
21 22
…
…
… … … …
…
, where aij
= aji
, then A is a symmetric matrix and the quadratic
form
Q =
=
=
∑
∑ a x
ij ij
i
n
j
n
1
1
can be written as Q = XT
AX.
A is called the matrix of the quadratic form.
For example the quadratic form x2
+ 4xy + 4y2
can be written in the matrix form [ ] .
x y
x
y
1 2
2 4
⎡
⎣
⎢
⎤
⎦
⎥
⎡
⎣
⎢
⎤
⎦
⎥
Here X =
⎡
⎣
⎢
⎤
⎦
⎥
x
y
and A =
⎡
⎣
⎢
⎤
⎦
⎥
1 2
2 4
.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 96 5/30/2016 5:07:07 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-133-2048.jpg)
![Matrices ■ 1.97
Note Since the quadratic form is Q = XT
AX, it is obvious that the characteristics or properties of Q
depend on the characteristics of A.
2. Canonical form of Q
Definition 1.43 A quadratic form Q which contains only the square terms of the variables is said to
be in canonical form.
For example x2
+ y2
, x2
– y2
, x2
+ y2
– 4z2
and x x x x
1
2
2
2
3
2
4
2
2
+ + + are in canonical forms because they
contain only square terms of the variables.
3. Reduction of Q to canonical form by orthogonal transformation
Let Q = XT
AX be a quadratic form in n variables x1
, x2
, …, xn
and A = [aij
] be the symmetric matrix
of order n of the quadratic form. We will reduce A to diagonal form by an orthogonal transformation
X = NY, where N is the normalised modal matrix of A. Then NT
AN = D, where D is the diagonal
matrix containing the eigen values of A.
If l1
, l2
, …, ln
are the eigen values of A, then
D
n
=
…
…
… … … … …
…
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
l
l
l
1
2
0 0 0
0 0 0
0 0 0
∴ Q X AX (NY) A(NY) Y (N AN)Y Y DY
T T T T T
= = = =
If Y =
y
y
y
1
2
…
n
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
, then Q n
n n
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
[ ]
y y y
y
y
y
1 2
1
2
1
2
0 0
0 0
0 0
…
…
…
… … … …
…
…
l
l
l
⎥
⎥
⎥
⎥
= …
…
= …
[ ]
l l l l l l
1 1 2 2
1
2
1 1
2
2 2
2 2
y y y
y
y
y
y y y
n n n
n
n
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
+ + +
This is the required quadratic form.
Note In the canonical form the coefficients are the eigen values of A. Since A is a symmetric matrix,
the eigen values of A are all real. So, the eigen values may be positive, negative or zero. Hence, the
terms of the canonical form may be positive, negative or zero. By using the canonical form or the
eigen values, we can characterise the quadratic form.
Definition 1.44 If A is the matrix of the quadratic form Q in the variables x1
, x2
, …, xn
, then the rank
of Q is equal to the rank of A.
If rank of A n, where n is the number of variables or order of A, then A = 0 and Q is called a
singular form.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 97 5/30/2016 5:07:09 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-134-2048.jpg)
![1.98 ■ Engineering Mathematics
4. Index, signature and rank of quadratic form
Definition 1.45 Let Q = XT
AX be a quadratic form in n variables x1
, x2
, …, xn
.
X = [x1
, x2
, …, xn
]T
and A is the matrix of the quadratic form.
(i) Index of the quadratic form is the number of positive eigen values of A.
(ii) Signature of the quadratic form is the difference between the number of positive and
negative eigen values of A.
(iii) Rank of the quadratic form is the number of positive and negative eigen values of A.
Usually index is denoted by p, signature by s and rank by r.
5. Definite and indefinite quadratic forms
Definition 1.46 Let Q = XT
AX be a quadratic form in n variables x1
, x2
, …, xw
.
i.e., X = [x1
… xn
]T
and A is the matrix of the quadratic form.
(i) Q is said to be positive definite if all the n eigen values of A are positive.
i.e., if r = n and p = n
e.g., y y y
1
2
2
2 2
+ + +
… n is positive definite.
(ii) Q is said to be negative definite if all the n eigen values of A are negative.
i.e., if r = n, p = 0
e.g., − − − −
y y y
1
2
2
2 2
… n is negative definite.
(iii) Q is said to be positive semidefinite if all the n eigen values ofA are ≥ 0 with at least one
eigen value = 0.
i.e., if r n and p = r
e.g., y y y
1
2
2
2 2
+ + +
… r , where r n, is positive semi-definite.
(iv) Q is said to be negative semidefinite if all the n eigen values of A are ≤ 0 with at least one
value = 0.
i.e., if r n and p = 0
e.g., − − − −
y y y
1
2
2
2 2
… r , where r n, is negative semi definite.
(v) Q is said to be indefinite if A has positive and negative eigen values.
e.g., y y y y y
1
2
2
2
3
2
4
2 2
+ − − + +
… n
is indefinite.
6. We can also find the nature of a quadratic form without finding the eigen values of A or without
reducing to canonical form but by using the principal minors of A as below.
Definition 1.47 Let Q = XT
AX be a quadratic form in n variables x1
, x2
, …, xn
and let the matrix of
the quadratic form be
A
n
2n
n1 n2 nn
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
a a a
a a a
a a a
11 12 1
21 22
…
…
… … … …
…
Let D1
= a11 = a11
, D2
=
a a
a a
11 12
21 22
, D3
=
a a a
a a a
a a a
11 12 13
21 22 23
31 32 33
and so on.
Finally Dn
= A .
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 98 5/30/2016 5:07:10 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-135-2048.jpg)

![1.100 ■ Engineering Mathematics
EXAMPLE 2
Write down the quadratic form corresponding to the matrix
2 4 5
4 3 1
5 1 1
.
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Solution.
Let A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 4 5
4 3 1
5 1 1
, which is a 3 × 3 symmetric matrix.
So, the quadratic form has 3 variables x1
, x2
, x3
.
Let X =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
x
x
x
1
2
3
, then the quadratic form is
Q X AX
T
= =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
[ ]
x x x
x
x
x
1 2 3
1
2
3
2 4 5
4 3 1
5 1 1
= + + + + + +
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
= + +
[ ]
(
2 4 5 4 3 5
2 4 5
1 2 3 1 2 3 1 2 3
1
2
3
1 2
x x x x x x x x x
x
x
x
x x x
x x x x x x x x x x
x x x x x x x
3 1 1 2 3 2 1 2 3 3
1
2
1 2 3 1 1 2
4 3 5
2 4 5 4
) ( ) ( )
+ + + + + +
= + + + +
+ + + + +
= + + + + +
3 5
2 3 8 10 2
2
2
3 2 1 3 2 3 3
2
1
2
2
2
3
2
1 2 1 3 2
x x x x x x x x
x x x x x x x x x3
3
Aliter Given A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
a a a
a a a
a a a
11 12 13
21 22 23
31 32 33
2 4 5
4 3 1
5 1 1⎥
⎥
Then the quadratic form in 3 variables x1
, x2
, x3
is
Q X AX
T
= = + + + + +
a x a x a x a x x a x x a x
11 1
2
22 2
2
33 3
2
12 1 2 13 1 3 23 2
2 2 2
( ) ( ) ( ) x
x
x x x x x x x x x
x x x
3
1
2
2
2
3
2
1 2 1 3 2 3
1
2
2
2
3
2
2 3 2 4 2 5 2 1
2 3
= + + + + +
= + +
( ) ( ) ( )
+
+ + +
8 10 2
1 2 1 3 2 3
x x x x x x
EXAMPLE 3
Discuss the nature of the following quadratic forms.
(i) 6x2
+ 3y2
+ 3z2
– 4xy 2 2yz + 4zx
(ii) 6 3 14 4 18 4
1
2
2
2
3
2
2 3 1 3 1 2
x x x x x x x x x
1 1 1 1 1
(iii) xy + yz + zx
(iv) 10x2
+ 2y2
+ 5z2
+ 6yz 2 10zx 2 4xy.
Solution.
(i) The Q.F is 6x2
+ 3y2
+ 3z2
– 4xy − 2yz + 4zx, having 3 variables x, y, z.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 100 5/30/2016 5:07:14 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-137-2048.jpg)
![Matrices ■ 1.101
The matrix of the quadratic form is
A =
−
− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
6 2 2
2 3 1
2 1 3
.
The principal minors are
D1
= |6| = 6 0; D2
6 2
2 3
18 4 14 0
=
−
−
= − =
D A
3
6 2 2
2 3 1
2 1 3
6 9 1 2 6 2 2 2 6 48 8 8 32 0
= =
−
− −
−
= − + − + + − = − − =
( ) ( ) ( )
Since D1
, D2
, D3
are positive, the quadratic form is positive definite.
(ii) The quadratic form is 6 3 14 4 18 4
1
2
2
2
3
2
2 3 1 3 1 2
x x x x x x x x x
+ + + + + , having 3 variables x1
, x2
, x3
.
The matrix of the Q.F is
A =
6 2 9
2 3 2
9 2 14
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
The principal minors are D1
= 6 0; D2
6 2
2 3
= = 18 − 4 = 14 0
and D A
3
6 2 9
2 3 2
9 2 14
= =
= 6(42 − 4) – 2(28 − 18) + 9(4 − 27) = 6(38) – 20 + 9(−23) = 228 – 20 – 207 = 1 0
Since D1
, D2
, D3
are positive, the quadratic form is positive definite.
(iii) The quadratic form is xy + yz + zx in 3 variables x, y, z
The matrix of the quadratic form is A =
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
0
1
2
1
2
1
2
0
1
2
1
2
1
2
0
The principal minors are D1
= 0, D2
=
0
1
2
1
2
0
= −
1
4
0
and D3
0
1
2
1
2
1
2
0
1
2
1
2
1
2
0
= = = − − + −
[ ]= × =
1
8
0 1 1
1 0 1
1 1 0
1
8
0 1 0 1 1 0
1
8
2
1
4
0
( ) ( )
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 101 5/30/2016 5:07:16 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-138-2048.jpg)
![1.102 ■ Engineering Mathematics
Since D1
= 0, D2
0, D3
0, the quadratic form is indefinite.
(iv) The Q.F 10 2 5 6 10 4
2 2 2
x y z yz zx xy
+ + + − − is in three variables x, y, z.
The matrix of the quadratic form A =
− −
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
10 2 5
2 2 3
5 3 5
The principal minors are D1
= 10 0, D2
10 2
2 2
=
−
−
= 20 − 4 = 16 0
D3
10 2 5
2 2 3
5 3 5
=
− −
−
−
= 10(10 − 9) + 2 (−10 + 15) – 5(−6 + 10) = 10 +10 – 20 = 0
Since D1
0, D2
0 and D3
= 0, the quadratic form is positive semi-definite.
EXAMPLE 4
Determine l so that l(x2
1 y2
1 z2
) 1 2xy 2 2yz 1 2zx is positive definite.
Solution.
The matrix of the quadratic form is A = −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
l
l
l
1 1
1 1
1 1
The principal minors are D1
= l, D2
2
1
1
1
= = −
l
l
l ;
D A
3
2
1 1 1
1 1 1 1
= = − − + + − −
= + + − −
=
l l l l
l l l
( ) ( ) ( )
( )( ( ) )
(l
l l l l l
+ − − = + −
1 2 1 2
2 2
)( ( ) ( )
Given the quadratic form is positive definite.
∴ D1
0, D2
0 and D3
0
⇒ l 0, l2
– 1 0 ⇒ (l + 1)(l − 1) 0 ⇒ l 1 (
∴
l 0)
and (l + 1)2
(l − 2) 0 ⇒ l − 2 0 ⇒ l 2 [∴ (l + 1)2
0]
∴ the common values of l are l 2
EXAMPLE 5
Show that the quadratic form ax bx x cx
1
2
1 2 2
2
2 1
2 is positive definite if a . 0 and ac 2 b2
. 0.
Solution.
The matrix of the quadratic form is A =
−
−
⎡
⎣
⎢
⎤
⎦
⎥
a b
b c
The principal minors are D1
= a, D A
2
2
= = =
a b
b c
ac b
−
−
− .
Given a 0 and ac – b2
0. ∴ D1
0 and D2
0.
Hence, the Q.F is positive definite.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 102 5/30/2016 5:07:18 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-139-2048.jpg)


![Matrices ■ 1.105
The normalised modal matrix N =
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
2
6
1
5
2
30
1
6
2
5
1
30
1
6
0
5
30
Then N AN D
T
= =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
8 0 0
0 2 0
0 0 2
The orthogonal transformation X = NY, where Y =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
y
y
y
1
2
3
reduces the given quadratic form to
YT
DY = [y1
y2
y3
]
8 0 0
0 2 0
0 0 2
1
2
3
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
y
y
y
= + +
8 2 2
1
2
2
2
3
2
y y y , which is the canonical form.
∴ rank of the Q.F = 3, index = 3, signature = 3
The Q.F is positive definite, since all the eigen values are positive.
EXAMPLE 7
Find out the type of conic represented by 17x2
2 30xy 1 17y2
5 128 after reducing the quadratic
form 17x2
2 30xy 1 17y2
to canonical form by an orthogonal transformation.
Solution.
Given quadratic form is 17x2
– 30xy + 17y2
The matrix of the Q.F is A =
⎡
⎣
⎢
⎤
⎦
⎥
17 15
15 17
−
−
The characteristic equation of A is A I
− l = 0
⇒
17 15
15 17
0
− −
− −
=
l
l
⇒ 17 15 0 17 15 17 15 2 32
2 2 2 2
− − = ⇒ − = ⇒ − = ± ⇒ =
l l l l
( ) ( ) or .
.
To find eigen vectors:
If X =
⎡
⎣
⎢
⎤
⎦
⎥
x
x
1
2
be an eigen vector corresponding to eigen value l.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 105 5/30/2016 5:07:25 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-142-2048.jpg)
![1.106 ■ Engineering Mathematics
Then ( )
A I X
− ⇒
− −
− −
l
l
l
=
⎡
⎣
⎢
⎤
⎦
⎥
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
⎦
⎥
0
17 15
15 17
0
0
1
2
x
x
⇒ ( )
( )
17 15 0
15 17 0
1 2
1 2
− −
− −
l
l
x x
x x
=
=
⎫
⎬
⎭
+
(I)
Case (i) If l = 2, then equations (I) become
15 15 0 15 15 0
1 2 1 2 1 2
x x x x x x
− = − + = ⇒ =
,
Choosing x1
= 1, we get x2
= 1 ∴ an eigen vector is X1
1
1
=
⎡
⎣
⎢
⎤
⎦
⎥
Case (ii) If l = 32, then equation (I) become
− − = − − = ⇒ = −
15 15 0 15 15 0
1 2 1 2 2 1
x x x x x x
and
Choose x1
= 1, we get x2
= −1 ∴ an eigen vector is X2
1
1
=
⎡
⎣
⎢
⎤
⎦
⎥
−
∴ the normalised eigen vectors are
1
2
1
2
1
2
1
2
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
,
−
The normalised modal matrix
N =
1
2
1
2
1
2
1
2
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⇒ N AN
T
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
1
2
1
2
1
2
1
2
−
17 15
15 17
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
2
1
2
1
2
1
2
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥ =
2 0
0 32
D
The transformation X = NY, where Y =
⎡
⎣
⎢
⎤
⎦
⎥
y
y
1
2
, reduces the given quadratic form to
Y DY which is the cano
T
=
⎡
⎣
⎢
⎤
⎦
⎥
⎡
⎣
⎢
⎤
⎦
⎥ =
[ ] ,
y y
y
y
y y
1 2
1
2
1
2
2
2
2 0
0 32
2 32
+ n
nical form.
But the given quadratic from = 128
∴ 2 32 128
64 4
1
1
2
2
2 1
2
2
2
y y
y y
+ ⇒ + =
= , which represents an ellipse.
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 106 5/30/2016 5:07:28 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-143-2048.jpg)

![1.108 ■ Engineering Mathematics
Case (i) If l = 0, then the equations (I) become
8 6 2 0 4 3 0
6 7 4 0 2 4 3 0
1 2 3 1 2 3
1 2 3 1 2 3
x x x x x x
x x x x x x
− + = ⇒ − + =
− + − = − + =
and
From the first and third equations, we get
⇒
⇒
x x x
x x x
x x x
1 2 3
1 2 3
1 2 3
9 4 2 12 16 6
5 10 10
1 2 2
− +
=
−
=
− +
−
=
−
=
−
= =
Choosing x1
= 1, x2
= 2, x3
= 2, we get an eigen vector X1
1
2
2
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Similarly, we can find for l = =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
3
2
1
2
2
, X and for l = =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
15
2
2
1
3
, X −
∴ the normalised modal matrix N =
1
3
2
3
2
3
2
3
1
3
2
3
2
3
2
3
1
3
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
= −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
3
1 2 2
2 1 2
2 2 1
∴ N AN D
T
= =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
0 0 0
0 3 0
0 0 15
The transformation X = NY, where Y =
y
y
y
1
2
3
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, reduces the quadratic form to the canonical form
Y DY
T
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
[ ]
y y y
y
y
y
1 2 3
1
2
3
0 0 0
0 3 0
0 0 15
= + +
0 3 15
1
2
2
2
2
2
y y y
The transformation is
x
y
z
y
y
y
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
3
1 2 2
2 1 2
2 2 1
1
2
3
−
−
−3
−4
x1
x2
x3
4 −3
2 −4
1
3
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 108 5/30/2016 5:07:33 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-145-2048.jpg)


![Matrices ■ 1.111
∴ the normalised modal matrix is N =
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
1
3
1
2
1
6
1
3
0
2
6
1
3
1
2
1
6
−
−
∴ the diagonal matrix is N AN D
T
= =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
0 0 0
0 1 0
0 0 3
The orthogonal transformation is X = NY
where Y =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
y
y
y
1
2
3
and the canonical form is Y DY
T
= +
y y
2
2
3
2
3
∴ the quadratic form is positive semi-definite.
The transformation X = NY ⇒
x
x
x
y
y
1
2
3
1
2
1
3
1
2
1
6
1
3
0
2
6
1
3
1
2
1
6
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
−
−
y
y3
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
∴ x y y y x y y x y y y
1 1 2 3 2 1 3 3 1 2 3
1
3
1
2
1
6
1
3
2
6
1
3
1
2
1
6
= + − = + = − + +
, and
These equation make the quadratic form = 0
⇒ y y y y
2
2
3
2
2 3
3 0 0 0
+ = ⇒ = =
and
[Since sum of squares of real numbers = 0 ⇒ each number = 0] and y1
can take any real value.
∴ x y x y x y
1 1 2 1 3 1
1
3
1
3
1
3
= −
, ,
= =
Choosing y1 3
= , one set of values of x1
, x2
, x3
is x1
= 1, x2
= 1, x3
= −1.
EXERCISE 1.7
Diagonlaise the following matrices by orthogonal transformation.
1. A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
6 2 2
2 3 1
2 1 3
−
− −
−
2. A =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
10 2 5
2 2 3
5 3 5
− −
− 3. A =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
8 6 2
6 7 4
2 4 3
−
− −
4. A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 1 1
1 2 1
1 1 2
−
− −
−
5. A =
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
7 2 0
2 6 2
0 2 5
−
− −
−
6. A =
−
−
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2 1 1
1 1 2
1 2 1
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 111 5/30/2016 5:07:40 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-148-2048.jpg)
![1.112 ■ Engineering Mathematics
7. Find the symmetric matrix A whose eigen values and eigen vectors are given
(i) eigen values are 0, 2, and eigen vectors
1
1
1
1
−
⎡
⎣
⎢
⎤
⎦
⎥
⎡
⎣
⎢
⎤
⎦
⎥
, .
(ii) eigen values are 1, 2, 3 and eigen vectors
1
1
0
0
0
1
1
1
0
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, , .
8. Reduce the quadratic form 8 7 3 12 8 4
1
2
2
2
3
2
1 2 2 3 3 1
x x x x x x x x x
+ + − − + to the canonical form through an
orthogonal transformation and hence show that it is positive semi-definite.
9. Reduce the quadratic form 2 6 2 8
1
2
2
2
3
2
1 3
x x x x x
+ + + to canonical form by orthogonal reduction.
10. Reduce the quadratic form 3 5 3 2 2 2
1
2
2
2
3
2
2 3 3 1 1 2
x x x x x x x x x
+ + − + − to the canonical form by orthogonal
reduction.
11. Find the nature, index, signature and rank of the following Q.F, without reducing to canonical form.
(i) 3 5 3 2 2 2
1
2
2
2
3
2
2 3 3 1 1 2
x x x x x x x x x
+ + − + − . (ii) 10 2 5 6 10 4
2 2 2
x y z yz zx xy
+ + + − − .
(iii) 3 2 4 8 12
2 2 2
x y z xy xz yz
− − + +
− .
12. Determine the nature of the following quadratic form f(x1
, x2
, x3
) = x x
1
2
2
2
2
+ .
13. Find the nature of the quadratic form 2x2
+ 2xy + 3y2
.
14. Find the index, signature and rank of the Q.F in 3 variables x x x
1
2
2
2
3
2
2 3
+ − .
15. Reduce the quadratic form x x x x x x x x x
1
2
2
2
3
2
1 2 2 3 3 1
5 2 2 6
+ + + + + to canonical form through an orthogonal
transformation.
16. Reduce the quadratic form 2 6 2 8
1
2
2
2
3
2
1 3
x x x x x
+ + + to canonical form.
17. Reduce the given quadratic form Q to its canonical form using orthogonal transformation
Q = x2
+ 3y2
+ 3z2
− 2yz.
ANSWERS TO EXERCISE 1.7
1. l = 2, 2, 8; eigen vectors [0 1 1]T
, [1 1 −1]T
, [2 –1 1]T
2. l = 0, 3, 14; eigen vectors [1 −5 4]T
, [1 1 1]T
, [−3 1 2]T
3. l = 0, 3, 15; eigen vectors [1 2 2]T
, [2 1 −2]T
, [2 −2 1]T
4. l = 1, 1, 4; eigen vectors [1 1 0]T
, [−1 1 2]T
, [1 −1 1]T
, A3
22 21 21
21 22 21
21 21 22
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
− −
−
5. l = 3, 6, 9; eigen vectors [1 2 2]T
, [2 1 −2]T
, [2 −2 1]T
6. D =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 0 0
0 1 0
0 0 4
7. (i) A =
⎡
⎣
⎢
⎤
⎦
⎥
1 1
1 1
(ii)
2 1 0
1 2 0
0 0 2
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
M01_ENGINEERING_MATHEMATICS-I _CH01_Part B.indd 112 5/30/2016 5:07:43 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-149-2048.jpg)








![Sequences and Series ■ 2.5
Hence, the sequence is convergent and converges to
1
2
.
(ii) The given sequence is s
n
n
n
n
= + − =
+ =
− =
⎧
⎨
⎩
2 1
2 1 3
2 1 1
( )
if is even
if is odd
∴ lim lim
n
n
n
if is even
→∞ →∞
=
s n
= 3 3
and lim lim
n
n
n
if is odd
→∞ →∞
=
s n
= 1 1
Since the limit is not unique, the sequence is not convergent. But it oscillates between 1 and 3.
Hence, the sequence is an oscillating sequence.
(iii) The given sequence is 1
3
2
3
3
3
4
3
2 3 4
, , , , .
−
⎧
⎨
⎩
⎫
⎬
⎭
− …
∴ the nth
term is s
n
n
n 1
n
= − ⋅
−
( )
1
3
=
n
n
n
n
3
3
n
n
if is odd
if is even
−
⎧
⎨
⎪
⎪
⎩
⎪
⎪
Now, if n is odd lim lim
n
n
n n
→∞ →∞
= =
s
n
3
0 [by L - Hopital’s rule]
and if n is even lim lim
n
n
n n
→∞ →∞
= −
⎛
⎝
⎜
⎞
⎠
⎟ =
s
n
3
0 [by L - Hopital’s rule]
∴ lim
n
n
→∞
=
s 0
∴ the sequence is convergent and converges to 0.
EXAMPLE 3
Show that the sequence
2 7
3 2
n
n
2
1
⎧
⎨
⎩
⎫
⎬
⎭
is monotonic increasing. Hence or otherwise prove that it is
convergent.
Solution.
Let the given sequence be { }
s
n
n
n =
+
{ }
2 7
3 2
−
∴ s
n
n
n =
−
+
2 7
3 2
To prove it is monotonic increasing sequence, we have to prove s s n
n n N
≤ ∀ ∈
+1
Now s
n
n
n
n
n+ =
+
+ +
=
−
+
1
2 1 7
3 1 2
2 5
3 5
( )
( )
−
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 5 5/12/2016 10:53:07 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-158-2048.jpg)



![Sequences and Series ■ 2.9
The given sequence is 1
2
5
3
11
, , ,…
∴ the sequence is a bounded below by 0 [and above by 1].
Hence, the sequence is convergent
EXERCISE 2.1
1. Show that the sequence n
n +
{ }
1
converges to 1.
2. Show that the sequence
n
n
2
2
2 1
+
⎧
⎨
⎩
⎫
⎬
⎭
converges to
1
2
.
3. Show that the sequence 3
3 1
2
2
n n
n n
+
+
⎧
⎨
⎩
⎫
⎬
⎭
+
converges to 3.
4. Test the convergence of the sequence n
n
− 2
2
+
{ }.
5. Test the convergence of the sequence 3 4
2 1
n
n
+
+
{ }.
6. Test the convergence of the sequence
3 1
2
+
⎧
⎨
⎩
⎫
⎬
⎭
( )
.
− n
n
ANSWERS TO EXERCISE 2.1
4. Converges 5. Converges 6. Converges
2.2 SERIES
Definition 2.8 If { }
un be a sequence of real numbers, then the expression u1
+ u2
+ u3
+ u4
+ … + un
+ …
is called an infinite series and it is denoted by u u
n n
n
or ∑
∑
=
∞
1
.
un
is called the nth
term of the series.
2.2.1 Convergent Series
Definition 2.9 Let u u u u
1 2 3
+ + + +
+… …
n be an infinite series.
If s u u u s
n n n
then
= + +
1 2
…+ , is called the nth
partial sum of the series. If the sequence of partial sums
{ }
sn converges to l, then we say that the series un
n=1
∞
∑ converges to l and it is written as u l
n
n=
∞
∑
1
= .
Then l is called the sum of the series.
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 9 5/12/2016 10:53:28 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-162-2048.jpg)
![2.10 ■ Engineering Mathematics
2.2.2 Divergent Series
Definition 2.10 If the sequence of partial sums { }
sn of the infinite series diverges, then the series un
n=
∞
∑
1
diverges.
That is, if lim ,
n
n n
n
then
→∞
=
∞
= ∞ ∑
s u
1
diverges to ` and if lim ,
n
n
→∞
= ∞
s − then un
n=
∞
∑
1
diverges to −`.
2.2.3 Oscillatory Series
Definition 2.11 If the sequence of partial sums { }
sn of the infinite series diverges, but does not diverge
to + ` or −`, then the sequence { }
sn is said to oscillate. Then we say that the series un
n=
∞
∑
1
is an
oscillatory series.
Examples
(1) 1
1
2
1
2
1
2
1
2
2 3
+ + + + + +
… …
n
(2) 1
1
3
1
3
1
3
1
1
3
2 3
− + − + + +
… − …
( )n
n
(3) 1 1 1 1
− + − +… (4) n
n
!
2
1
n
n
n=
∞
∑ (5)
x
n
n
p
n
−
∞
−
∑
1
1 2 1
( )
=
2.2.4 General Properties of Series
1. The convergence or divergence of an infinite series is unaffected by addition or removal of finite
number of terms.
2. The convergence or divergence of an infinite series is unaffected when each term of the series is
multiplied by a non-zero number.
3. If un
n=
∞
∑
1
and vn
n=
∞
∑
1
are convergent series with sums a and b respectively, then for any pair of real
numbers l and m, the series [ ]
l m
u v
n n
n
±
=
∞
∑
1
converges with sum l m
a b
± .
2.3 SERIES OF POSITIVE TERMS
The discussion of the convergence of any type of series of real numbers depend upon the series of
positive terms. So, we shall discuss in detail the series with positive terms.
Definition 2.12 A series un
n
,
=
∞
∑
1
where u n
n N
∀ ∈
0 , is called a series of positive terms.
A series of positive terms can either converge or diverge to `. It can never oscillate.
2.3.1 Necessary Condition for Convergence of a Series
Theorem 2.1 If the series of positive terms ∑un is convergent, then lim
n
n
→∞
u = 0
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 10 5/12/2016 10:53:35 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-163-2048.jpg)

![2.12 ■ Engineering Mathematics
Choose ε 0, such that l −
ε 0.
Then by the definition of limit, there exists a positive integer n0
such that
u
v
l n n
n
n
for all
− ≥
ε 0
∴ −ε ε
−
u
v
l
n
n
[ ]
{ x a a x a
− ⇒ − +
ε ε ε
⇒ l
u
v
l
−
ε + ε
n
n
⇒ ( ) ( )
l v u l v n n
− + ∀ ≥
ε ε
n n n 0 [ ]
{ v n
n N
≥ ∀ ∈
0
Consider u l v
n n
+
( )
ε
Case (i): If ∑vn is convergent, then ∑vn is a finite number.
∴ ( )
l v
+ ε ∑ n is finite number
But ∑ + ∑
u l v
n n
( )
ε
∴ ∑
un a finite number ∀ ≥
n n0
⇒ ∑
un a finite number as n → ∞
Hence, ∑un is convergent.
Case (ii): If ∑vn is divergent, then ∑ → ∞ → ∞
v n
n as
Consider ( )
l v u n n
− ∀ ≥
ε n n 0
∴ ( )
l v u
− ε ∑ ∑
n n
⇒ ∑ − ∑
u l v
n n
( )
ε ⇒ ∑ → ∞ → ∞
u n
n as
∴ ∑un is divergent. ■
Note
1. If l = 0, then ∑un is convergent if ∑vn is convergent.
2. If l u
= ∞ ∑
, then n is divergent if ∑vn is divergent.
3. In order to discuss the convergence of ∑un by comparison test, we consider ∑vn whose convergence
is known already.
Two standard series used for comparison are the following.
(i) The geometric series with positive terms a ar ar
+ +
+ …
2
, where a 0 and r 0.
It converges if 0 1
r and diverges if r ≥1.
(ii) The p-series is
1
1
1
2
1
3
1 1
1
p p p p p
+ + + + =
=
∞
∑
+… …
n n
n
, where p 0.
It converges if p 1 and diverges if p ≤ 1.
The p-series is also known as harmonic series of order p.
In many problems, the auxiliary series is chosen as the p-series for particular values of p.
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 12 5/12/2016 10:53:58 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-165-2048.jpg)
![Sequences and Series ■ 2.13
For choosing the auxiliary series we write un
in the form f
n
1
⎛
⎝
⎜
⎞
⎠
⎟ , then decide vn
.
For example if u
n
f
n
n p
=
⎛
⎝
⎜
⎞
⎠
⎟
1 1
, Then we take v
n
n p
=
1
, p 0.
WORKED EXAMPLES
EXAMPLE 1
Test the convergence of the series
1
1 2 3
3
2 3 4
5
3 4 6
⋅ ⋅ ⋅ ⋅ ⋅
1 1 1
⋅
….
Solution.
Let the given series be ∑un .
∴ ∑ =
⋅ ⋅
+
⋅ ⋅
+
⋅ ⋅
+
un
1
1 2 3
3
2 3 4
5
3 4 6
…
The numerators 1 3 5 1 1 2 2 1
, , , ( ].
… + −
are in A.P. So, the term is )
th
n n n
= − In the denominator, first
factors are 1, 2, 3,… and the nth
term is n, the second factors are 2, 3, 4,… and the nth
term is (n + 1)
and the third factors are 3, 4, 5,… and the nth
term is n + 2.
Then the nth
term is u
n
n n n
n
n
n
n n
n
n =
+ +
=
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
=
2 1
1 2
2 1
1
2
1
1
1
2
2
3
2
−
−
( )( )
1
1
1
2
1
1
1
2
−
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
n
n n
Take
1
n 2
n 5
n
∴ n
n
u
v n
n
n n
n
=
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
× =
−
2
1
1
2
1
1
1
2
2 1
1
2
2
−
2
2
1
1
1
2
n
n n
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
∴ lim lim ( )
n
n
n
n
→∞ →∞
−
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
= ≠
u
v
n
n n
=
+
2 1
1
2
1
1
1
2
2 0
⎡
⎣
⎢
∴ 1
0
n
→
⎤
⎦
⎥
as n → ∞
∴ by comparison test ∑un and ∑vn behave alike.
But ∑ ∑
v
n
n =
1
2
is convergent, since p = 2 1 in p-series
Hence, ∑un is convergent.
EXAMPLE 2
Test the convergence of
( 1)( 2)
.
2
n 1
n n
n n
1 1
5
⎛
⎝
⎜
⎞
⎠
⎟
∑
∞
Solution.
Let the given series be ∑un . ∴ ∑ =
+ +
⎛
⎝
⎜
⎞
⎠
⎟
=
∞
∑
u
n n
n n
n
n
( )( )
1 2
2
1
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 13 5/12/2016 10:54:04 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-166-2048.jpg)





![Sequences and Series ■ 2.19
Proof
Given ∑un is a series of positive terms and lim .
n
n
n
→∞
+
=
u
u
l
1
Since u n
u
u
l
n
n
n
N
∀ ∈ ⇒
+
0 0 0
1
, .
Since lim ,
n
n
n
→∞
+
=
u
u
l
1
by definition of limit, given ε 0, there exists a positive integer n0
such that
u
u
l n n
n
n+
− ∀ ≥
1
0
ε
⇒ − − ∀ ≥
+
ε ε
u
u
l n n
n
n 1
0
⇒ l
u
u
l n n
− ε ε
+ ∀ ≥
+
n
n 1
0
(i) Let l 1: Choose ε 0 such that l −
ε 1, then
l
u
u
l n m n m
− + ∀ ≥
+
ε ε ε
n
n
for this is
1
0
[ ]
,
Consider l
u
u
n m
− ∀ ≥
+
ε n
n 1
⇒ u
u
l n m
n
n+
− ∀ ≥
1
ε
Replace n by m, m + 1, m + 2, …, n − 1; we get
u
u
l
m
m+
−
1
ε,
u
u
l
u
u
l
u
u
l
m
m
m
m
n
n
, , ,
+
+
+
+
−
− − −
1
2
2
3
1
ε ε … ε
Multiplying all these inequalities, we get
u
u
u
u
u
u
u
u
m
m
m
m
m
m
n
n
+
+
+
+
+
−
⋅ ⋅
1
1
2
2
3
1
… − − −
( )( ) ( )
l l l
ε ε … ε [n − m factors]
⇒
u
u
l n m
m
n
n m
−
( ) ∀ ≥ + ⇒
−
ε 1
⇒
u
u
l
l
n m
m
n
n
m
−
−
∀ ≥ +
ε
ε
1
( )
( )
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 19 5/12/2016 10:54:41 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-172-2048.jpg)
![2.20 ■ Engineering Mathematics
⇒ u
l
l
u n m
m
m
n n
( )
( )
−
−
∀ ≥ + ⇒
ε
ε
1
⇒ u u l
l
n m
n m
m
n
( )
( )
− ⋅
−
∀ ≥ +
ε
ε
1
1
⇒ ∑ − ∑
−
∀ ≥ +
u u l
l
n m
n m
m
n
( )
( )
ε
ε
1
1
But ∑
−
1
( )
l ε n
is an infinite geometric series with r
l
=
−
1
1
ε
{ l
l
− ⇒
−
⎡
⎣
⎢
⎤
⎦
⎥
ε
ε
1
1
1
∴ ∑
−
1
( )
l ε n
converges as n → ∞ ∴ ∑un is convergent if l 1
(ii) Let l , 1: Choose ε 0 such that l +
ε 1.
Then there exists a positive integer k such that
l
u
u
l n k
− ε ε
+ ∀ ≥
+
n
n 1
[for this ε, n0
is k]
Consider u
u
l n k
n
n+
+ ∀ ≥
1
ε .
Replacing n by k, k + 1, k + 2, …, n − 1, we get
u
u
l
u
u
u
u
k
k
k
k
n
n
, ,
+
+
+
+
1
1
2
1
ε + ε …, + ε
−
l l
Multiplying all these inequalities, we get
u
u
u
u
u
u
l l l
k
k
k
k
n
n
+
+
+
−
⋅ + + +
1
1
2
1
… ε ε … ε
( )( ) ( ) [(n−k) factors]
⇒
u
u
l
l
l
k
n
n k
n
k
+ =
+
+
( )
( )
( )
ε
ε
ε
−
⇒ u l
l
u
k
k
n n
+ ⋅
+
( )
( )
ε
ε
1
⇒ u u l
l
n k
k
n
+ ⋅
+
( )
( )
ε
ε
1
⇒ u u l
l
n k
k
n
∑ + ∑
+
( )
( )
.
ε
ε
1
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 20 5/12/2016 10:54:46 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-173-2048.jpg)

![2.22 ■ Engineering Mathematics
∴ u
u
n
n
n
n
n
n
n
n
n
n
+
+
= ⋅
+
+
1
1
1
2 1
1 2
! ( )
( )!
+
=
+
+
( )( )
( )
n n
n n
+1 1
2 1
n
n =
+
⎛
⎝
⎜
⎞
⎠
⎟
= +
⎛
⎝
⎜
⎞
⎠
⎟
n
n
n n
1
1
2
1
2
1
1
n
n
n
n
∴ lim lim [ ]
n
n
n
n
n
→∞
+
→
= +
⎛
⎝
⎜
⎞
⎠
⎟ =
u
u n
e
e
1
1
2
1
1
2
1 2 3
∞
{
∴ by De’Alembert’s ratio test ∑un is convergent.
EXAMPLE 2
Test the convergence or divergence of the series
x x x
x
1 2 2 3 3 4
0
⋅ ⋅ ⋅
1 1 1
2 3
…∞, .
Solution.
Let the given series be ∑un . ∴ ∑ =
⋅
+
⋅
+
⋅
u
x x x
n
1 2 2 3 3 4
2 3
+…
Then u
x
n n
u
x
n n
n
n
n
n
and
=
+
=
+ +
+
( ) ( )( )
1 1 2
1
1
+
∴ u
u
x
n n
n n
x
n
n x n x
n
n
n
n
+
+
=
+
⋅
+
=
+
⋅ = +
⎡
⎣
⎢
⎤
⎦
⎥⋅
1
1
1
1 2 2 1
1
2 1
( )
( )( )
+
∴ lim lim ,
n
n
n
n
→∞
+
→
= +
⎛
⎝
⎜
⎞
⎠
⎟ ⋅ =
u
u n x x
x
1
1
2 1 1
0
∞
∴byDe’Alemberts’ratiotest, ∑un isconvergentif
1
1 1
x
x
⇒ anddivergentif
1
1 1
x
x
⇒ .
If x = 1, then the test fails to give a conclusion.
In this case, the series becomes
1
1 2
1
2 3
1
3 4
⋅
+
⋅
+
⋅
∞
+…
∴ u
n n
n
n
n =
+
=
⎛
⎝
⎜
⎞
⎠
⎟
1
1
1
1
1
2
( )
+
. Take v
n
n =
1
2
∴ u
v
n
n
n
n
n
n
=
⎛
⎝
⎜
⎞
⎠
⎟
× =
+
1
1
1
1
1
1
2
2
+
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 22 5/12/2016 10:55:04 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-175-2048.jpg)





![2.28 ■ Engineering Mathematics
(iii) If l = 1, then the test fails to give a definite conclusion.
Consider ∑
1
n
and ∑
1
2
n
, we find that lim lim
n
n
n
n
n
→∞ →
=
⎛
⎝
⎜
⎞
⎠
⎟ =
u
n
1 1
1
1
∞
and lim lim
n
n
n
n
n
→∞ →
=
⎛
⎝
⎜
⎞
⎠
⎟ =
u
n
1
2
1
1
1
∞
But ∑
1
n
is divergent and ∑
1
2
n
is convergent.
∴ ∑un may be convergent or divergent if l = 1 ■
Note
1. Root test is more general or stronger than the ratio test, because there are cases where the ratio
test fails but root test gives definite conclusion.
2. The root test is used when the general term un
contains index interms of n.
WORKED EXAMPLES
EXAMPLE 1
Test the convergence of 1
1
2
1
1
2
5 n
⎛
⎝
⎜
⎞
⎠
⎟
∞
∑
n
n
.
Solution.
Let the given series be ∑un . ∴ ∑ =
⎛
⎝
⎜
⎞
⎠
⎟
=
∞
∑
u
n
n
n
n
1
1
2
1
+
−
Then u
n
n
n
=
⎛
⎝
⎜
⎞
⎠
⎟
−
1
1
2
+ ⇒ ( )
u
n n
n
n
n n n
1
1
1
1
1
1
2
= +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥ = +
⎡
⎣
⎢
⎤
⎦
⎥
−
−
∴ lim lim [ ]
n
n
n
n
n
→ →
=
⎛
⎝
⎜
⎞
⎠
⎟ = =
∞ ∞
−
−
+
u
n
e
e
e
1
1
1
1 1
1 2 3
{
∴ by Cauchy’s root test, ∑un is convergent.
EXAMPLE 2
Test the convergence of 1
1
3
2
1
1
2
5 n
⎛
⎝
⎜
⎞
⎠
⎟
∞
∑
n
n
.
Solution.
Let the given series be ∑un . ∴ ∑ =
⎛
⎝
⎜
⎞
⎠
⎟
−
=
∞
∑
u
n
n
n
n
1
1
3
2
1
+
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 28 5/12/2016 10:56:20 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-181-2048.jpg)
![Sequences and Series ■ 2.29
Then =
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
−
u
n
n
n
n
n
1
1 1
1
1
3
2
3
2
+ =
⇒ [ ]
u
n
n
n
n
n
1
1
1
1
1
3
2
=
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
+
=
+
⎛
⎝
⎜
⎞
⎠
⎟
=
⎛
⎝
⎜
⎞
⎠
⎟
=
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅
1
1
1
1
1
1
1
1
1
3
2
1
2
1
n n
n
n
n
n
n
+
∴ lim lim
n
n
n
n n
→∞ →∞
=
⎛
⎝
⎜
⎞
⎠
⎟
u
n
e
1
1
1
1
1
1
+
=
∴ by Cauchy’s root test, ∑un is convergent.
EXAMPLE 3
Test the convergence of the series given below
2
1
2
1
3
2
3
2
2
2
1 3
3
2
2 1 2 1
2 2
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
4
3
4
3
4
4
3
1 1
2
⎛
⎝
⎜
⎞
⎠
⎟ ∞
… .
Solution.
Let the given series be ∑un.
∴ ∑ = −
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
− − −
un
2
1
2
1
3
2
3
2
4
3
4
3
2
2
1 3
3
2 4
4
3
− +…
Then u
n
n
n
n
n
n
n
n
n
n
n
n
n n
=
+ +
⎡
⎣
⎢
⎤
⎦
⎥
=
+
⎛
⎝
⎜
⎞
⎠
⎟ −
+
⎡
⎣
⎢
⎤
⎦
⎥ = +
+
−
+ −
( )
1 1
1 1
1
1
1
1
+
−
1
1
1
1
1
1
1
1
1
1
1
n n n n
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥ = +
⎛
⎝
⎜
⎞
⎠
⎟ ⋅ +
⎛
⎝
⎜
⎞
⎠
⎟ − +
+ −
n n n
−
n
n
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
−n
∴ u
n n n
n
n
n n n
1
1
1
1
1
1
1
1
= +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ − +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
=
−
1
1
1
1
1
1
1
1
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ − +
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎩
⎫
⎬
⎭
−
n n n
n
∴ lim lim
n
n
n
n
n
→∞ →∞
= +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
u
n n n
1 1
1
1
1
1
1
1
+
−
= ⋅ − =
−
−
[ ]
e
e
1 1
1
1
1
1
[ , ]
{ 2 3 1 1
e e −
∴ by Cauchy’s root test, ∑un is convergent.
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 29 5/12/2016 10:56:24 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-182-2048.jpg)

![Sequences and Series ■ 2.31
If u x dx
( )
1
∞
∫ diverges (i.e., the value does not exist), then un
n=1
∞
∑ diverges.
Proof
Let {sn
} be the sequence of partial seem of the series un
n=1
∞
∑ .
∴ s u u u u
n n
= + + +
1 2 3
…+ (1)
Let In
n
= = …
u x dx n
( ) , , , ,
2 3 4
1
∫
Since u(x) is monotonic decreasing in [1, `), we have
u n u x u n n x n n
( ) ( ) ( ) ,
≥ ≥ + ≤ ≤
1 1
for N
+ ∈
Also u(x) is positive and integrable on [1, `)
∴ u n dx u x dx u n dx
( ) ( ) ( )
n
n
n
n
n
n
+ +
∫ ∫ ∫
≥ ≥
1 1 1
1
+
+
⇒ u n u x dx u n n
( ) ( ) ( )
≥ ∀
+
∫
n
n
N
1
1
≥ + ∈
Since u(n) = un
, n ∈ N; we have
u u x dx u
n n
n
n
≥ ≥ +
+
∫ ( ) 1
1
Putting n = 1, 2, 3, …, n − 1 and adding, we get
u u u u x dx u x dx u x dx
u u u
1 2 1
1
2
2
3
1
2 3
+ + + ≥ + +
≥ + + +
−
−
∫ ∫ ∫
… …+
…
n
n
n
n
( ) ( ) ( )
⇒ s u x dx s u n
n
n
n N
− ≥ ≥
∫
1
1
1
( ) − ∀ ∈ [From (1)]
⇒ s s u n
n n n
I N
− ≥ ≥ ∀
1 1
− ∈
Taking I N
n n
≥ ∀
s u n
− ∈
1
⇒ s u n
n n
I N
− ∀
1 ≤ ∈
s u
n n
I
≤ + 1
∴ lim lim lim
n
n
n
n
n
I
→∞ →∞ →∞
≤
s u
+ 1
⇒ lim ( )
n
n
→∞
∞
≤ +
∫
s u x dx u
1
1
If u x dx
( )
1
∞
∫ is convergent, then lim
n
n
→∞
s is finite
∴ ∑un is convergent.
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 31 5/12/2016 10:56:35 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-184-2048.jpg)
![2.32 ■ Engineering Mathematics
Taking sn n
I
−1 ≥
⇒ lim lim
n
n
n
n
I
→∞ →
≥
s −
∞
1
⇒ lim ( ) .
n
n
→
−
∞
≥ ∫
∞
s u x dx
1
1
If u x dx
( )
1
∞
∫ does not exist, then lim
n
n
→∞
s −1 does not exist.
∴ un
∑ is divergent.
Thus, un
∑ and u x dx
( )
1
∞
∫ behave alike. ■
WORKED EXAMPLES
EXAMPLE 1
Discuss the convergence of the p-series
1
0
1 n
p
p
n=
∑
∞
, .
Solution.
Let the given series be ∑un . ∴ ∑ =
∞
∑
u
n
n p
n
1
1
=
Then u
n
n p
=
1
. Consider u x
x
x
( ) , [ ,
= ∈ ∞)
1
1
p
u(x) is positive and decreasing function of x for x 1.
∴ by Cauchy’s integral test,
∑un and u x dx
( )
1
∞
∫ behave alike.
Now u x dx
x
dx
( ) .
1 1
1
∞ ∞
∫ ∫
= p
If p 5 1, then u x dx
x
dx
( )
1 1
1
∞
∫ ∫
=
∞
= =
[log ]
x 1
∞
∞
So, the integral diverges. ∴ ∑un diverges if p = 1
If p 1, then u x dx
x
dx
( )
1 1
1
∞
∫ ∫
= p
∞
=
+
⎡
⎣
⎢
⎤
⎦
⎥
=
−
⎡
⎣
⎢
⎤
⎦
⎥ =
− ∞
−
⎛
⎝
⎜
⎞
⎠
⎟ = −
−
=
− +
−
∞
x
p
p x p p
p
p
1
1
1
1
1
1
1
1 1
1
1
1
1
1
−
∞
1
1
1
p −
[{ p − 1 0]
Since the integral exists, by Cauchy’s integral test, ∑un is convergent if p 1.
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 32 5/12/2016 10:56:42 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-185-2048.jpg)
![Sequences and Series ■ 2.33
If p 1, then u x dx
x
dx
( )
1 1
1
∞
∫ ∫
= p
∞
=
− +
⎡
⎣
⎢
⎤
⎦
⎥ = −
( ) =
− + ∞
x
p p
p 1
1
1
1
1
1
−
∞ ∞ [{ 1 − p 0]
∴ the integral does not exist and hence, divergent.
So, ∑un is divergent if p 1.
Thus, ∑un is convergent if p 1 and divergent if p ≤ 1.
EXAMPLE 2
Test the convergence of the series 1
2
1
5
1
10
1
1 2
1 1 1 1
1
1
… …∞
n
.
Solution.
Let the given series be ∑un
∴ ∑ = + + +
+
u
n
n
1
2
1
5
1
10
1
1 2
…+ +…
Then u
n
n =
1
1 2
+
. Consider u x
x
x
( ) ,
=
1
1
1
2
+
≥
∴ u x
( ) is positive and decreasing function of x.
By cauchy’s integral test ∑un and u x dx
( )
1
∞
∫ behave alike.
Now u x dx
x
dx x
( ) tan tan tan .
1
2
1
1
1
1 1
1
1
1
2 4 4
∞ ∞
− −
∫ ∫
= = [ ] = ∞ − = − =
+
− ∞ p p p
∴ u x dx
( )
1
∞
∫ is convergent.
Hence, ∑un is convergent.
EXAMPLE 3
Test the convergence of the series
1
2 2
1
3 3
(log ) ( )
e e
p p
1og
1 1
1
4 4
0
(log )
, .
e
p
1…∞ p
Solution.
Let the given series be un
n=2
∞
∑
∴ u p
n n
e e e
e
n
n
p p p
p
=
∞
∑ = + +
=
2
1
2 2
1
3 3
1
4 4
0
1
(log ) (log ) (log )
,
(log )
+ …∞
,
, p
=
∞
∑ 0
2
n
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 33 5/12/2016 10:56:47 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-186-2048.jpg)
![2.34 ■ Engineering Mathematics
Then u
n n
e
n p
=
1
(log )
Consider u x
x x
p x
e
( )
(log )
, ,
=
1
0 2
p
≥
Clearly u(x) is positive and decreasing function of x for x ≥ 2
∴ by Cauchy’s integral test, ∑un and u x dx
( )
2
∞
∫ behave alike.
Now u x dx
x x
dx
e
( )
(log )
.
2 2
1
∞
∫ ∫
= p
∞
Put t x dt
x
dx
= log ∴ =
1
When x = 2, t = log 2 and when x = `, t = log ` = `
∴ u x dx
t
dt
e
( )
log
2 2
1
∞
∫ ∫
= p
∞
If p 1, then u x dx t dt
t
p
e e
( )
log log
= =
− +
⎡
⎣
⎢
⎤
⎦
⎥
∞
∫
∫
−
∞ − + ∞
p
p
2
2
1
2
1
=
−
⎛
⎝
⎜
⎞
⎠
⎟
−
∞
1
1
1
1
2
p t e
p
log
[{ p − 1 0]
=
− ∞
−
⎡
⎣
⎢
⎤
⎦
⎥ = −
−
⋅ =
−
⋅
− −
1
1
1 1
2
1
1
1
2
1
1
1
1 1
p p p
e e
(log ) ( ) (log ) ( ) (log
p p
e
e 2 1
)p−
∴ the integral u x dx
( )
2
∞
∫ exists and hence, un
n=
∞
2
∑ is convergent for p 1
If p 1, then u x dx
t
dt
e
( )
log
1 2
1
∞
∫ ∫
= p
∞
=
+
⎡
⎣
⎢
⎤
⎦
⎥ =
−
− = ∞
− + ∞
t
p p
e
e
p 1
2
1
1
1
2
−
∞
log
( log ) [{ 1 − p 0]
∴ ∫u x dx
( )
2
∞
does not exist and hence, divergent
∴ ∑un
n=
∞
2
is divergent if p 1
If p 5 1, then u x dx
t
dt
e
( )
log
= ∫
∫
∞
1
2
2
∞
= = ∞ =
(log ) log log log
log
t 2 2
∞
− ∞
∴ ∫u x dx
( )
2
∞
does not exist and hence, divergent
∴
=
∑un
n 2
∞
is divergent if p = 1
Thus, the given series ∑un is convergent if p 1 and divergent if 0 p ≤ 1.
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 34 5/12/2016 10:56:53 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-187-2048.jpg)
![Sequences and Series ■ 2.35
EXAMPLE 4
Using integral test, determine whether the series
ln n
n2
n 1
5
∑ is convergent or divergent.
Solution.
Let the given series be ∑un ∴ ∑ = =
=
∑
u
n
n
n
n
n
e
n
ln
[ln log ]
2
1
∞
Then u
n
n
n =
ln
.
2
Consider u x
x
x
x
( )
ln
,
= ≥
2
2 (1)[ ( ) ]
{ u x x
= 0 1
if =
Clearly u x x
( ) .
0 2
∀ ≥
To prove u(x) is monotonic function of x, test the sign of ′
u x
( ).
Differentiating (1) w.r. to x, we get
′ =
⋅ − ⋅
=
−
= =
−
u x
x
x
x x
x
x x x
x
x x
x
x
x
( )
ln
ln ( ln ) ln
2
4 4 4 3
1
2
2 1 2 1 2
−
If x ≥ 2, then ln ln
x ≥ 2 [{ logarithm is an increasing function]
∴ 2 2 2
ln ln
x ≥ ⇒ −2 2 2
ln ln
x ≤ − ⇒ 1 2 1 4 0
− ≤ −
ln ln
x [{ ln 4 = 1.39]
∴ ′ ∀ ≥
u x x
( ) 0 2
Hence, u x
( ) is decreasing in [2, `)
∴ by Cauchy’s integral test, un
n=
∑
2
∞
and u x dx
( )
ln2
∞
∫ behave alike
But u x dx
x
x
dx
( )
ln
ln ln
=
∫ ∫
∞
2
2
2
∞
. Put ln x t dt
x
dx
= ∴ =
1
When and when
x t x t
= = = = ∞ =
2 2
, ln , ln
∞ ∞
∴ u x dx
t
e
dt te dt x t x e
t
e e
( ) [ ln ]
ln ln ln
2 2 2
1
1
∞ ∞
−
∞
−
∫ ∫ ∫
= = =
=
−
− ⋅
t
t t
t
{ ⇒ =
−
− ∞
−
−
⎡
⎣
⎢
⎤
⎦
⎥
= − +
⎡
⎣ ⎤
⎦
t
t
by Bernoulli’s formula
( )
[ ]
( )
ln
ln
1
1
2
2
e t 2
2
2
1
2
0 2 1 2 1
1
2
2 1
∞
= + +
⎡
⎣ ⎤
⎦ = + = +
−
e e
ln
ln
(ln ) (ln ) (ln )
∴ the integral u x dx
( )
2
∞
∫ is convergent and hence, un
n=
∞
∑
2
is convergent.
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 35 5/12/2016 10:57:00 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-188-2048.jpg)


![2.38 ■ Engineering Mathematics
∴ lim lim
n
n
n
n
→∞
+
→∞
=
+
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅ =
⋅
u
u
n n
n
x
1
2 2
2
2
2
3
2
1
1 2 2
+
2
2
1 1
2 2 2
⋅ =
x x
∴ by the De’Alembert’s ratio test,
∑un is convergent if
1
1 1
2
2
x
x
⇒ ⇒ x x
2
1 0 0 1
− ⇒
[ ]
{ x 0
and divergent if
1
1 1 1
2
2
x
x x
⇒ ⇒
[ ]
{ x 0
Now
1
1 1 1
2
2
x
x x
= ⇒ = ⇒ = [ ]
{ x 0
If x = 1, the test fails to give a definite conclusion.
In this case, we use Raabe’s test.
When x = 1, the series is
∑ = ⋅ +
⋅
⋅
⋅ +
⋅ ⋅
⋅ ⋅
⋅
un
1
2
1
3
1 3
2 4
1
5
1 3 5
2 4 6
1
7
+…
u
u
n n
n
n
n+
=
+
1
2
2 2 2 3
2 1
( )( )
( )
+ + [ ]
from (1)
∴ u
u
n n
n
n n n
n
n
n+
=
+ +
+
=
+ + − +
+
1
2
2
2
1
2 2 2 3
2 1
1
2 2 2 3 2 1
2 1
− −
( )( )
( )
( )( ) ( )
( )
=
=
+ + − + +
( )
+
=
+
+
4 10 6 4 4 1
2 1
6 5
2 1
2 2
2 2
n n n n
n
n
n
( ) ( )
∴ n
u
u
n n
n
n
n+
−
⎛
⎝
⎜
⎞
⎠
⎟ =
+
+
1
2
1
6 5
2 1
( )
( )
=
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
=
+
+
⎛
⎝
⎜
⎞
⎠
⎟
n
n
n
n
n
n
2
2
2 2
6
5
4 1
1
2
6
5
4 1
1
2
+
∴ lim lim
n
n
n
n
→∞ →∞
⎛
⎝
⎜
⎞
⎠
⎟ =
+
+
⎛
⎝
⎜
⎞
⎠
⎟
= =
n
u
u
n
n
+
−
1
2
1
6
5
4 1
1
2
6
4
3
2
1
∴by Raabe’s test ∑un is convergent if x = 1.
Hence, the given series is convergent if 0 x ≤ 1 and divergent if x 1.
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 38 5/12/2016 10:57:17 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-191-2048.jpg)
![Sequences and Series ■ 2.39
EXAMPLE 2
Test the convergence or divergence of
x x x
2
2
4
2 2
6
2
3 4
2 4
3 4 5 6
1 1 1
⋅
⋅
⋅ ⋅ ⋅
2 4 6
3 4 5 6 7 8
2 2 2
8
⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅
x 1….
Solution.
Omitting the first term, let the given series be ∑un
∴ ∑ =
⋅
+
⋅
⋅ ⋅ ⋅
+
⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅
u x x x
n
2
3 4
2 4
3 4 5 6
2 4 6
3 4 5 6 7 8
2
4
2 2
6
2 2 2
8
+…
Then n
n
u
n
n n
x
=
⋅
⋅ ⋅ ⋅ + +
2 4 2
3 4 5 6 2 1 2 2
2 2 2
2 2
…
…
+
( )
( )( )
and u
n n
n n n n
x
n+ =
⋅ ⋅ +
⋅ ⋅ ⋅ + + + +
1
2 2 2 2
2
2 4 2 2 2
3 4 5 6 2 1 2 2 2 3 2 4
…
…
( ) ( )
( )( )( )( )
n
n+4
∴ u
u
n n
n x
n
n+
=
+
+
⋅
1
2 2
2 3 2 4
2 2
1
( )( )
( )
+ (1)
=
+
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅ =
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
n
n n
n
n
x
n n
2
2
2 2
2
3
2
4
2
2
1
2
3
2
4
+
⎞
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅ ≠
2
2
1
0
2 2
n
x
x
,
∴ lim lim
n
n
n
n
→∞
+
→∞
=
+
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅ =
⋅
u
u
n n
n
x
1
2 2
2
3
2
4
2
2
1 2 2
+
2
2
1 1
2 2 2
⋅ =
x x
∴ by De’Alembert’s ratio test,
∑un is convergent if
1
1 1
2
2
x
x
⇒ ⇒ −1 x 1, x ≠ 0.
and divergent if
1
1 1
2
2
x
x
⇒ ⇒ x −1 or x 1.
If x2
= 1, the test fails, so we use Raabe’s test.
In this case, u
u
n n
n
n
n+
=
+
+
1
2
2 3 2 4
2 2
( )( )
( )
+ [From (1)]
∴
u
u
n n
n
n n n
n
n
n+
− =
+ +
+
=
+ + − +
+
1
2
2
2
1
2 3 2 4
2 2
1
2 3 2 4 2 2
2 2
( )( )
( )
( )( ) ( )
( )
−
=
=
+ + − + +
+
=
+
+
4 14 12 4 8 4
2 2
6 8
2 2
2 2
2 2
n n n n
n
n
n
( )
( ) ( )
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 39 5/12/2016 10:57:22 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-192-2048.jpg)
![2.40 ■ Engineering Mathematics
∴ n
u
u
n n
n
n
n
n
n
n
n+
−
⎛
⎝
⎜
⎞
⎠
⎟ =
+
=
+
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
=
1
2
2
2
2
1
6 8
2 2
6
8
2
2
6
( )
( )
+
+
+
+
⎛
⎝
⎜
⎞
⎠
⎟
8
2
2
2
n
n
∴
lim lim
n
n
n
n
→∞
+
→∞
−
⎛
⎝
⎜
⎞
⎠
⎟ =
+
⎛
⎝
⎜
⎞
⎠
⎟
= =
n
u
u
n
n
1
2
1
6
8
2
2
6
4
3
2
1
+
∴ by Raabe’s test ∑un is convergent if x2
1
= ⇒ x = ±1.
∴ the given series is convergent if − ≤
1 1
≤ x [{ when x = 0; it is trivially convergent]
and divergent if x x
−1 1
or .
EXAMPLE 3
Test the convergence of the series ( !)
( )!
.
n
x
n
2
2
1 2
n
n
=
∞
∑
Solution.
The given series be ∑un ∴ ∑ =
=
∞
∑
u n
x
n
n
n
n
( !)
( )!
2
2
1 2
Then u
n x
n
n
n
=
( !)
( )!
2 2
2
and u
n x
n
n x
n
n
n n
+
+ +
=
+
+
=
+
+
1
2 2 2 2 2 2
1
2 1
1
2 2
[( )!]
[ ( )]!
[( )!]
( )!
∴
u
u
n x
n
n
n x
n
n
n
n
n
n
n
+
+
= ⋅
+
+
[ ]
=
1
2 2
2 2 2
2
2
2 2
1
2
2
( !)
( )!
( )!
( )!
( !)
( )!
( )!(
( )( )
( !) ( )
( ) ( )
( )
,
2 1 2 2
1
1
2 1 2 1
1
1
0
2 2 2
2 2
n n
n n x
n n
n x
x
+ +
+
⋅
=
+ +
+
⋅ ≠
⇒ u
u
n
n x
n
n+
=
+
+
⋅
1
2
2 2 1
1
1
( ) (1)
=
+
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅ =
+
⎛
⎝
⎜
⎞
⎠
⎟
+
⋅
2 2
1
1
1
1
2 2
1
1
1
1
2 2
n
n
n
n
x
n
n
x
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 40 5/12/2016 10:57:26 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-193-2048.jpg)



![2.44 ■ Engineering Mathematics
WORKED EXAMPLES
EXAMPLE 1
Test the convergence and divergence of the series
1
2
2
3
3
4
4
5
5
0
2
2
3
3
4
4
1 1 1 1 1
! ! ! !
, .
x x x x x
…
Solution.
Let the given series be ∑un .
∴ ∑ = + + + + +
u x x x x x
n 1
2
2
3
3
4
4
5
5
0
2
2
3
3
4
4
! ! ! !
,
…
Then u
n
n
x u
n
n
x
n
n
n
n
n
n
and
= =
+
+
−
−
+
1
1
1
1
1
!
( )
( )!
∴
u
u
n
n
x
n
n x
n
n x
n
n
n
n
n n
n
n
+
−
−
−
−
= ⋅
+
+
=
+
⋅
1
1
1
1
1
1
1 1
1
!
( )!
( ) ( )
⇒
u
u
n
n
n
x
n
x
n
n
n
n
n
n n
+
−
−
− −
=
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅ =
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅ =
+
⎛
⎝
⎜
⎞
1
1
1
1 1
1
1
1 1
1
1
1
1
1
⎠
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅
1
1
1
n
x
n
(1)
∴ lim lim
n
n
n
n n
→∞
+
→∞
=
+
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅ =
u
u
n
n
x ex
1
1
1
1
1
1 1
∴ by ratio test, ∑un is convergent if
1
1
1
ex
x
e
⇒ and diverges if
1
1
1
ex
x
e
⇒
When x
e
=
1
, the test fails. So, we use logarithmic test.
∴ u
u
n
e
n
n
n
+
−
=
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅
1
1
1
1
1
[ ]
from (1)
∴ log log log
( )log
e e e
e
u
u
e
n
n
n
n
n
n
+
−
⎛
⎝
⎜
⎞
⎠
⎟ = − +
⎛
⎝
⎜
⎞
⎠
⎟
= − − +
⎛
⎝
1
1
1
1
1 1 1
1
⎜
⎜
⎞
⎠
⎟
= − − − + − +
⎛
⎝
⎜
⎞
⎠
⎟
1 1
1 1
2
1
3
1
4
2 3 4
( )
n
n n n n
…
= − − − + + +
⎛
⎝
⎜
⎞
⎠
⎟ = − +
1 1
1
2
1 1
3
1
2
3
2
5
6
2 2 2
n n n n n n
… …
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 44 5/12/2016 10:57:46 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-197-2048.jpg)
![Sequences and Series ■ 2.45
∴ n
u
u
n
n n n
log n
n+
⎛
⎝
⎜
⎞
⎠
⎟ = − +
⎛
⎝
⎜
⎞
⎠
⎟ = − +
1
2
3
2
5
6
3
2
5
6
… …
∴ lim log lim
n
n
n
n
→∞
+
→∞
⎛
⎝
⎜
⎞
⎠
⎟ = − +
⎛
⎝
⎜
⎞
⎠
⎟ =
n
u
u n
1
3
2
5
6
3
2
1
…
∴ by logarithmic test, ∑un is convergent if x
e
=
1
.
∴ the given series is convergent if 0
1
≤
x
e
and divergent if x
e
1
.
EXAMPLE 2
Test the convergence of 1
1
2
2
4
3
6
0
2 2
2
2
3
1 1 1 1
( !)
!
( !)
!
( !)
!
, .
x x x x
…
Solution.
Let ∑un be the series, omitting the first term
u x x x x
n
n=
∞
∑ = + + +
1
2 2
2
2
3
1
2
2
4
3
6
0
( !)
!
( !)
!
( !)
!
,
…
Then u
n
n
x
n
n
=
( !)
( )!
2
2
and u
n
n
x
n
n
+
+
=
+
+
1
2
1
1
2 2
[( )!]
( )!
∴
u
u
n
n
x
n
n x
n n
n
n
n
n
n
+
+
=
( )
⋅
+
+
=
+ +
+
1
2
2 1
2
2 2
1
1
2 1 2 2
1
( !)
!
( )!
[( )!]
( )( )
( )
)
( )( )
( )
( )
2 2
1 2 2 1 1
1
1 2 2 1
1
1
⋅ =
+ +
+
⋅ =
+
+
⋅
x
n n
n x
n
n x
⇒ u
u
n
n
n
n
x
n
n+
=
+
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅
1
4 1
1
2
1
1
1
=
+
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅
4 1
1
2
1
1
1
n
n
x
(1)
∴ lim lim
n
n
n
n
→∞
+
→∞
=
+
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅ =
u
u
n
n
x x
1
4 1
1
2
1
1
1 4
∴ by ratio test, ∑un is convergent if
4
1 4
x
x
⇒ and is divergent if
4
1 4
x
x
⇒ .
When x = 4, the test fails. So, we use logarithmic test.
∴ If x = 4, then
u
u
n
n
n
n
n
n+
=
+
⎛
⎝
⎜
⎞
⎠
⎟
+
⋅ =
+
+
1
4 1
1
2
1
1
1
4
1
1
2
1
1
[ ]
from (1)
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 45 5/12/2016 10:57:53 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-198-2048.jpg)



![Sequences and Series ■ 2.49
x x x x x x
x x
x x
x
n n n n n n
n n
n n
n
( )( )
( )
=
+ ⋅ − − ⋅
+ +
=
−
+
+ + +
+
+
+
1 1 1
1
1
1
1 1
1 (
( )
( )
( )( )
1
1
1 1
0
1
+
=
−
+ +
+
x
x x
x x
n
n
n n
[ ]
{ 0 x x
⇒ −
1 1 0
∴ u u n
n n N
+ ∀ ∈
1
That is the terms are decreasing
and lim lim
n
n
n
n
n
→∞ →∞
=
+
=
u
x
x
1
0 [ , ]
{ 0 1 0
→ → ∞
x x n
n
as
∴ by Leibnitz’s test, the given series is convergent.
EXAMPLE 4
Test the convergence of ( )
( )
.
2
1
1
5
1
1
1
2
3
1
n
n
n
n
( )
⎛
⎝
⎜
⎞
⎠
⎟
∞
∑
Solution.
The given series is −
+
+
+
+
+
−
+
+
+ = −
+
+
−
+
+
+
+
+
1 1
1 1
1 2
1 2
1 3
1 3
1 1
1 1
1 2
1 2
1 3
1 3
2
3
2
3
2
3
2
3
2
3
2
... 3
3
−
⎛
⎝
⎜
⎞
⎠
⎟
...
Consider, the series is
1 1
1 1
1 2
1 2
1 3
1 3
1 4
1 4
1 5
1 5
2
3
2
3
2
3
2
3
2
3
+
+
−
+
+
+
+
+
−
+
+
+
+
+
+…
It is an alternating series with
u
n
n
n =
+
+
1
1
2
3
and u
n
n
n+ =
+ +
+ +
1
2
3
1 1
1 1
( )
( )
=
+ +
+ + +
n n
n n n
2
3 2
2 2
3 3 2
∴ u u
n n
n n n
n
n
n n n n
n n
+ − =
+ +
+ + +
−
+
+
=
+ + + − +
1
2
3 2
2
3
3 2 2
2 2
3 3 2
1
1
1 2 2 1
( )( ) ( )(
( )
( )( )
(
n n n
n n n n
n n n n n n n
3 2
3 3 2
3 5 4 3 3
3 3 2
1 3 3 2
2 2 2 2
+ + +
+ + + +
=
+ + + + + − + 3
3 3 2 3 3 2
1 3 3 2
2 4
2 5 4 3 2
3 3 2
4 3 2
n n n n n n
n n n n
n n n
+ + + + + +
+ + + +
= −
+ + +
)
( )( )
( n
n
n n n n
)
( )( )
1 3 3 2
0
3 3 2
+ + + +
∴ u u n
n n
+ ∀ ≥
1 1.
So, the terms are decreasing.
and lim lim lim
n
n
n n
→∞ →∞ →∞
=
+
+
⎛
⎝
⎜
⎞
⎠
⎟ =
+
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
u
n
n
n
n
n
n
1
1
1
1
1
1
2
3
2
2
3
3
⎜
⎜
⎞
⎠
⎟
=
+
+
⎛
⎝
⎜
⎞
⎠
⎟
=
∞
=
→∞
lim
n
1
1
1
1
1
0
2
3
n
n
n
∴ by Leibnitz’s test, the given series is convergent.
[ ]
{ n is positive
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 49 5/12/2016 10:58:17 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-202-2048.jpg)



![Sequences and Series ■ 2.53
which is an alternating series with
u n n
n n n n
n n
n = + − =
+ −
( ) + +
( )
+ +
( )
2
2 2
2
1
1 1
1
⇒ u
n n
n n n n
n =
+ −
+ +
=
+ +
2 2
2 2
1
1
1
1
(1)
∴ u
n n
n+ =
+ + + +
1 2
1
1 1 1
( ) ( )
It is obvious ( ) ( )
n n n n
+ + + + + +
1 1 1 1
2 2
[{ n ≥ 1]
⇒
1
1 1 1
1
1
2 2
( ) ( )
n n n n
+ + + +
+ +
⇒ u u n
n n N
+ ∀ ∈
1
So, the terms of the series are decreasing
Now lim lim
n
n
n
→∞ →∞
=
+ +
=
∞
=
u
n n
1
1
1
0
2
∴ by Leibnitz’s test, the series is convergent.
To test the conditional convergence of the given series ∑un , we test the convergence of the series
∑ un of absolute terms
Now ∑ = − + −
{ } = + −
( )
=
∞
=
∞
∑ ∑
u n n n n
n
n
n n
( )
1 1 1
2
1
2
1
{ | |
( a 1
− =
⎡
⎣ ⎤
⎦
1) nd
n 2
1 0
n + −
n
∴ u n n
n n
n
n
n n
n
n = + − =
+ +
=
+ +
=
+ +
⎧
⎨
⎩
⎫
⎬
⎭
2
2
2 2
1
1
1
1
1
1
1
1
1
1
[from (1)]
Take v
n
n =
1
∴
u
v
n
n
n
n
n
n
=
+ +
⎧
⎨
⎩
⎫
⎬
⎭
× =
+ +
1
1
1
1
1
1
1
1
2 2
∴ lim lim ( )
n
n
n
n
→∞ →∞
=
+ +
= ≠
u
v n
1
1 1
1
2
0
2
But ∑ = ∑
v
n
n
1
is divergent by p-series, since p = 1
∴ by comparison test, ∑ un is divergent.
Thus, ∑un is convergent and ∑ un is divergent.
Hence, the given series ∑un is conditionally convergent.
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 53 5/12/2016 10:59:11 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-206-2048.jpg)
![2.54 ■ Engineering Mathematics
EXAMPLE 4
Test whether the series is conditionally convergent or not.
1
2
1 2
3
1 2 3
4
1 2 3 4
5
3 3 3 3
2
1
1
1 1
2
1 1 1
1…∞.
Solution.
The given series is
1
2
1 2
3
1 2 3
4
3 3 3
−
+
+
+ +
−…,
which is an alternating series with
u
n
n
n n
n
n
n
n =
+ + + +
+
=
+
+
=
+
1 2 3
1
1
2 1 2 1
3 3 2
…
( )
( )
( ) ( )
(1)
and u
n
n
n
n
n+ =
+
+ +
=
+
+
1 2 2
1
2 1 1
1
2 2
( ) ( )
(2)
∴ u u
n
n
n
n
n n
+ − =
+
+
−
+
1 2 2
1
2 2 2 1
( ) ( )
=
+ − +
+ +
=
+ + + − + +
+
( ) ( )
( ) ( )
( )
( )
n n n
n n
n n n n n n
n
1 2
2 1 2
3 3 1 4 4
2 1
3 2
2 2
3 2 2
2
(
( )
( ) ( )
( )
( ) ( )
n
n n
n n
n n
n n
n
+
=
− − +
+ +
=
− + −
+ +
∀ ∈
2
1
2 1 2
1
2 1 2
0
2
2
2 2
2
2 2
N
∴ u u n
n n N
+ ∀ ∈
1
∴ the terms of the given series ∑un are decreasing
and lim lim
( )
lim
n
n
n n
→∞ →∞ →∞
=
+
=
+
⎛
⎝
⎜
⎞
⎠
⎟
=
∞
=
u
n
n
n
n
2 1
1
2 1
1
1
0
2 2
∴ by Leibnitz’s test, the series ∑un is convergent.
To test the conditional convergence of the given series ∑un, we test the convergence of the series ∑ un
of absolute terms.
∑ = +
+
+
+ +
+
un
1
2
1 2
3
1 2 3
4
3 3 3
…
u
n
n
n
n
n
n
n
n =
+
=
+
⎛
⎝
⎜
⎞
⎠
⎟
=
+
⎛
⎝
⎜
⎞
⎠
⎟
2 1
2 1
1
1
2 1
1
2
2
2 2
( )
[from(1)]
Take v
n
n =
1
∴ u
v
n
n
n
n
n
n
=
+
⎛
⎝
⎜
⎞
⎠
⎟
⋅ =
+
⎛
⎝
⎜
⎞
⎠
⎟
1
2 1
1
1
2 1
1
2
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 54 5/12/2016 10:59:16 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-207-2048.jpg)

![2.56 ■ Engineering Mathematics
We shall now test the convergence of some important series.
1. Binomial series
2. Exponential series
3. Logarithmic series
2.6 CONVERGENCE OF BINOMIAL SERIES
The binomial series 1
1
1
2
1 2
3
1 2 1
2 3
+ +
−
+
− −
+ +
− − − +
n
x
n n
x
n n n
x
n n n n r
r
x
!
( )
!
( )( )
!
( )( ) ( )
!
…
… r
r
+ ∞
…
is absolutely convergent if | |
x 1.
Proof
Let the given series be denoted by ur
r=
∞
∑
1
[omitting the first term].
Then u
n n n n r
r
x
r
r
=
− − − +
( )( ) ( )
!
1 2 1
…
and u
n n n n r n r
r
x
r
r
+
+
=
− − − + −
+
1
1
1 2 1
1
( )( ) ( )( )
( )!
…
∴ u
u
r
n r x
r
r+
=
+
−
⋅
1
1 1 (1)
u
u
r
n r x
r
n
r
x
r
r+
=
+
−
⋅ =
+
−
⋅
1
1 1 1
1
1
1
∴ lim lim
r
r
r
r
→∞
+
→∞
=
+
−
= − =
u
u
r
n
r
x x x
1
1
1
1
1
1
1 1
∴ by the ratio test, the series is convergent if
1
1 1
x
x
⇒ and divergent if
1
1 1
x
x
⇒ .
When x = 1, the test fails.
When x = 1, u
u
r
n r
r
r+
=
+
−
1
1
=
+
−
1
1
1
r
n
r
[using(1)]
∴ lim lim
r
r
r
r
→∞
+
→∞
=
+
−
=
−
= −
u
u
r
n
r
1
1
1
1
1
1
1 1
∴ by ratio test, the series is divergent when x = 1.
∴ the binomial series is absolutely convergent if x 1. ■
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 56 5/12/2016 10:59:29 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-209-2048.jpg)
![Sequences and Series ■ 2.57
Note The sum of the binomial series is (1 + x)n
.
∴ ( )
!
( )
!
( )( )
( )( ) (
1 1
1
1
2
1 2
3
1 2
2 3
+ = + +
−
+
− +
+ +
− − −
x
nx n n
x
n n n
x
n n n n r
n
…
… +
+
+
1)
!
r
xr … if x 1
2.7 CONVERGENCE OF THE EXPONENTIAL SERIES
The exponential series 1
1 2 3
2 3
+ + + + + + ∞
x x x x
n
! ! ! !
… …
n
converges absolutely for all values of x.
Proof
Let the given series be denoted by un
n=
∞
∑
1
[omitting the first term]
Then u
x
n
u
x
n
n
n
n
n
and
= =
+
+
+
! ( )!
1
1
1
∴
u
u
x
n
n
x
x
n
n
n
n
n
+
=
+
⋅ =
1
1
1 1
+
+
( )!
!
∴
u
u
x
n
x
n
n
n
+
=
+
=
+
1
1 1
∴ lim lim
n
n
n
n
R
→∞
+
→∞
=
+
= ∀ ∈
u
u
x
n
x
1
1
0
Here l 1 and so the series ∑un is absolutely convergent for all x ∈R.
Hence, the exponential series is convergent for all values of x ∈R. ■
Note The sum of the exponential series is ex
.
∴ e
x x x x
n
x
x
n
R
= + + + + + + ∞ ∀ ∈
1
1 2 3
2 3
! ! ! !
… …
2.8 CONVERGENCE OF THE LOGARITHMIC SERIES
The logarithmic series x
x x x x
n
− + − + +
−
+
2 3 4
2 3 4
1
… …
( )n n
is convergent for all values of x in
− ≤
1 1
x .
Proof
Let the given series be ∑un.
∴ ∑ = − + − +
u x
x x x
n
2 3 4
2 3 4
…
Now the series of absolute terms is
∑ = + + + +
u x
x x x
n
2 3 4
2 3 4
…
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 57 5/12/2016 10:59:41 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-210-2048.jpg)

![Sequences and Series ■ 2.59
a x a a a x a
n
n
n
( ) ( )
− = + − +
=
∞
∑
0
0 1
a x a a x a
2
2
( ) ( )
− + + − +
… …
n
n
It is called a power series in (x − a) [or about the point a], where a0
, a1
, a2
, , … are real numbers and
x is a real variable.
Definition 2.16 Radius of Convergence of a Power Series
The power series a x
n
n
n=
∞
∑
0
is said to have radius of convergence R if the series converges for all x
satisfying x x
−
R i.e., R R
( ).
This interval is called the interval of convergence of the power series.
2.9.1 Hadmard’s Formula
Theorem 2.2 Consider the power series a x
n
n
n
=
∞
∑
0
. If lim ,
n
n
n
R
→∞
=
a
1
1
then the power series will converge
absolutely if x R and diverge if x R
lim
n
n
n
R
→∞
=
a
1
1
is known as Hadmard’s formula.
Proof
Let the given power series be ∑ =
=
∞
∑
u a x
n n
n
n
0
. Then u a x
n n
n
=
⇒
u a x a x
u a x a x
n n
n
n
n
n
n
n
n n n
n
n
= =
= ⋅ = ⋅
1 1 1 1
∴ lim lim .
n
n
n
n
n
n
R
→∞ →∞
= =
u a x x
1 1
1
{ lim a
R
n
n
1
1
=
⎡
⎣
⎢
⎤
⎦
⎥
∴ by Cauchy’s root test, the series ∑ un is convergent if
x
x
R
R
⇒
1
and divergent if
x
x
R
R
⇒
1 .
∴ ∑un is absolutely convergent if x R
∴ the power series a x
n
n
n=
∞
∑
0
converges absolutely if x R.
That is, the power series converges in the interval −
R R
x . ■
Note
1. The interval (−R, R) is called the interval of convergence of the power series.
At the end points x = −R and x = R, the power series may or may not converge.
∴
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 59 5/12/2016 10:59:59 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-212-2048.jpg)


![2.62 ■ Engineering Mathematics
∴ by Leibnitz’s test, the series is convergent.
When x = −1, the series is
− − − − − = − + + + +
⎛
⎝
⎜
⎞
⎠
⎟
1
1
2
1
3
1
4
1
1
2
1
3
1
4
2 2 2 2 2 2
… …
This series is convergent by p-series, since p = 2 1
Hence, the region of convergence for the given power series is −1 ≤ x ≤ 1.
EXAMPLE 3
Find the radius of convergence of the series
( )
21
8
3
0
n
n
n
n
x
⎛
⎝
⎜
⎞
⎠
⎟
=
∞
∑ and the interval of convergence.
Solution.
The given series is
( )
−
= − + − +
=
∞
∑
1
8
1
8 8 8
3 3
0
6
2
9
3
n n
n
n
x x x x …
Put y x
= 3
(to reduce to usual form)
∴ the series is 1
8 8 8
2
2
3
3
− + − +
y y y …
which is a power series in y with a a
n
n
n n
n
n
=
−
=
−
+
+
+
( ) ( )
1
8
1
8
1
1
1
and
∴ a
a
n
n
n
n
n
n
+
+
+
=
−
×
−
= −
1
1
1
1
8
8
1
8
( )
( )
∴ a
a
n
n+
= − =
1
8 8
∴ the radius of convergence of the series in y is
R = = =
→∞
+
→∞
lim lim
n
n
n
n
a
a 1
8 8
∴ the power series in y converges in the interval −
8 8
y
Now we test the convergence of the series at the end points
When y = 8, the series in y becomes
1 1 1 1 1
− + − + − ∞
… , which is not convergent (it oscillates between −1 and 1)
When y = −8, the series in y becomes
1 1 1 1
+ + + + ∞
… , which is not convergent.
Hence, the power series in y is not convergent at the end points
∴ the interval of convergence for the power series in y is
−8 y 8 ⇒ −
8 8
3
x ⇒ −
2 2
x [ ]
{ y x
= 3
∴ the interval of convergence of the given series is −
2 2
x
and the radius of convergence is 2.
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 62 5/12/2016 11:00:17 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-215-2048.jpg)


![Sequences and Series ■ 2.65
( ) ( )
−
⋅ =
−
= − + − + −
=
∞
=
∞
∑ ∑
2 1
2
1
1
1
2
1
3
1
4
2
1
2
1
2 2 2
n
n
n
n
n
n n
…
This is an alternating series with u
n
n =
1
2
and the terms are decreasing
Now lim lim
n
n
n
→∞ →∞
= =
∞
=
u
n
1 1
0
2
∴ by Leibnitz’s test the series is convergent.
When y = −
1
2
, the series becomes
( )
( )
−
⋅
−
= = + + + +
=
∞
=
∞
∑ ∑
2 1
2
1
1
1
2
1
3
1
4
2
1
2
1
2 2 2
n
n
n
n
n n
…
which is convergent by p-series, since p =
2 1.
∴ the interval of convergence of the power series in y is
− ≤ ≤
1
2
1
2
y ⇒ − ≤ + ≤
1
2
2 1
1
2
x ⇒ − ≤ + ≤
1
4
1
2
1
4
x [dividing by 2]
⇒ − − ≤ ≤ −
1
2
1
4
1
4
1
2
x ⇒ − ≤ ≤ −
3
4
1
4
x
∴ the interval of convergence of the given series is − ≤ ≤ −
3
4
1
4
x
and the radius of convergence is
1
4
, since the centre is −
1
2
EXAMPLE 6
For what values of x, the series
1
1
1
2 1
1
3 1
1
4 1
2 3 4
2
1
2
1
2
1
2
1
x x x x
( ) ( ) ( )
…∞ converges.
Solution.
The given series is
1
1
1
2 1
1
3 1
1
4 1
2 3 4
−
+
−
+
−
+
−
+ ∞
x x x x
( ) ( ) ( )
…
It is defined if x ≠ 1.
Put y
x
=
−
1
1
, then the given series is
y
y y y
+ + + +
2 3 4
2 3 4
…
This is a power series in y.
Here a
n
a
n
n n
and
= =
+
+
1 1
1
1
M02_ENGINEERING_MATHEMATICS-I _XXXX_CH02.indd 65 5/12/2016 11:00:36 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-218-2048.jpg)





![3.0 INTRODUCTION
Calculus is one of the remarkable achievements of the human intellect. It is a collection of fascinating
and exciting ideas rather than a technical tool.
Calculus has two main divisions namely differential calculus and integral calculus. They serve
to solve a variety of priblems that arise in science, engineering and other fields including social
sciences.
Differential calculus had its origin from the problem of tangent to a curve and integral calculus had
its origin from the problem of finding plane area. The concept of derivative which measure the rate of
change of a function is the central idea in differential calculus.
We assume that the reader is familiar with the basic concepts of limit, continuity and differentiability.
In this chapter we deal with successive differentiation, equation of tangent and normal, length of the
tangent, length of the normal, length of the sub-tangent and length of the sub-normal, Rolle’s theorem,
Mean value theorems, Taylor’s series, Maclaurin’s series, Indeterminate forms, Maxima and minima
and curve tracing.
Basic rules of differentiation
If u and v are differentiable functions of x, then
(1)
d
dx
ku k
du
dx
( ) ,
= where k is constant
(2)
d
dx
u v
du
dx
dv
dx
( )
± = ±
(3)
d
dx
u v u
dv
dx
v
du
dx
( )
⋅ = + [product rule]
(4)
d
dx
u
v
v
du
dx
u
dv
dx
v
⎛
⎝
⎜
⎞
⎠
⎟ =
−
2
[quotient rule]
(5)
d
dx
u v x
d
dv
u v x
dv
dx
[ ( ( ))] [ ( ( ))]
= ⋅ [composite function rule]
(6)
d
dx
k
( ) ,
= 0 where k is a constant.
3
Differential Calculus
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 1 5/30/2016 7:06:49 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-224-2048.jpg)


![3.4 ■ Engineering Mathematics
Differentiating w.r.to x,
dy
dx
x x x x x x x x
= − + ⋅ = − +
2 2
2 2
[ sin ] cos sin cos .
Again differentiating w.r.to x,
d y
dx
x x x x x x x
x x x x
2
2
2
2
2 2 1
2
= − + ⋅ + − + ⋅
= − −
[ cos sin ] [ ( sin ) cos ]
cos sin −
− + = − −
2 2 2 4
2
x x x x x x x
sin cos ( )cos sin .
EXAMPLE 2
If y e bx
ax
5 sin , then show that
d y
dx
a
dy
dx
a b y
2
2
2 2
2 ( ) 0.
2 1 1 5
Solution.
Given y e bx
ax
= sin
Differentiating w.r.to x,
dy
dx
e bx b bxe a e b bx a bx
ax ax ax
= ⋅ + ⋅ = +
cos sin [ cos sin ].
Again differentiating w.r.to x,
d y
dx
e b bx b a bx b b bx a bx e a
ax ax
2
2
= − + ⋅ + + ⋅
[ ( sin ) cos ] [ cos sin ]
= − + + +
= − +
e b bx ab bx ab bx a bx
e a b bx a
ax
ax
[ sin cos cos sin ]
[( )sin
2 2
2 2
2 b
b bx
cos ].
L H S
. . ( )
[( )sin cos ]
= − + +
= − + −
d y
dx
a
dy
dx
a b y
e a b bx ab bx a
ax
2
2
2 2
2 2
2
2 2 [
[ { cos sin }] ( ) sin
[ sin sin
e b bx a bx a b e bx
e a bx b bx
ax ax
ax
+ + +
= − +
2 2
2 2
2
2 2 2
0 0
2 2 2
ab bx ab bx a bx a bx b bx
eax
cos cos sin sin sin ]
− − + +
= × = = R.H.S.
.
EXAMPLE 3
If y x
5 2
cos ,
1
then show that (1 ) 0
2
2 1
2 2 5
x y xy .
Solution.
Given y x
= −
cos 1
Differentiating w.r.to x,
dy
dx x
= −
−
1
1 2
.
Squaring,
dy
dx x
⎛
⎝
⎜
⎞
⎠
⎟ =
−
2
2
1
1
⇒ y
x
1
2
2
1
1
=
−
⇒ ( ) .
1 1
2
1
2
− =
x y
Again differentiating w.r.to x,
( ) ( )
1 2 2 0
2
1 2 1
2
− + − =
x y y y x ⇒ ( ) .
1 0
2
2 1
− − =
x y xy [Dividing by 2y1
]
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 4 5/30/2016 7:07:02 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-227-2048.jpg)
![Differential Calculus ■ 3.5
EXAMPLE 4
If y
x
x
5
log
2
, then show that x
d y
dx
x
d y
dx
x
dy
dx
y
3
3
3
2
2
2
6 4 4 0.
1 1 2 5
Solution.
Given y
x
x
e
=
log
2
.
Differentiating w.r.to x,
dy
dx
x
x
x x
x
x x x
x
x x
x
x
x
e
e e e
=
⋅ − ⋅
=
− ⋅
=
−
=
−
2
4 4 4
1
2 2 1 2 1 2
log log [ log ] log
3
3
.
Again differentiating w.r.to x,
d y
dx
x
x
x x
x
x x x
x
x
e
e
2
2
3 2
6
2 2
6
2
2
1 2 3
2 3 1 2
=
−
⎛
⎝
⎜
⎞
⎠
⎟ − −
=
− − −
=
( log )
( log ) [
[ log ] log
− +
=
−
5 6 6 5
6 4
e e
x
x
x
x
Again differentiating w.r.to x,
d y
dx
x
x
x x
x
x x x x
x
x
e
e
3
3
4 3
8
3 3 3
8
3
6
6 5 4
6 24 20 26 24
=
⋅ − −
=
− +
=
−
( log )
log [ l
log ] log
e e
x
x
x
x
8 5
26 24
=
−
∴ L.H.S = + + −
x
d y
dx
x
d y
dx
x
dy
dx
y
3
3
3
2
2
2
6 4 4
=
−
+
−
+
−
−
=
x x
x
x x
x
x x
x
x
x
e e e e
3
5
2
4 3 2
26 24 6 6 5 4 1 2
4
[ log ] [ log ] [ log ] log
2
26 24 6 6 5 4 1 2
4
1
26
2 2 2 2
2
−
+
−
+
−
−
= −
log ( log ) ( log ) log
[
e e e e
x
x
x
x
x
x
x
x
x
2
24 36 30 4 8 4
30 30 36 36
log log log log ]
log log
e e e e
e e
x x x x
x x
+ − + − −
=
− + −
x
x2
0
= = R.H.S.
EXAMPLE 5
If x a y b
5 u 5 u
cos sin
3 3
, then find
d y
dx
2
2
.
Solution.
Given x a y b
= =
cos sin
3 3
u u
and , which are parametric equations.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 5 5/30/2016 7:07:04 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-228-2048.jpg)




![3.10 ■ Engineering Mathematics
Differentiating w.r.to x successively, we get
y ax b a
1 = − + ⋅
sin( ) = − + = + +
⎛
⎝
⎜
⎞
⎠
⎟
a ax b a ax b
sin ) cos
(
p
2
y a ax b a
2
2
= − + +
⎛
⎝
⎜
⎞
⎠
⎟ ⋅
sin
p
= + + +
⎛
⎝
⎜
⎞
⎠
⎟
a ax b
2
2 2
cos
p p
= + + ⋅
⎛
⎝
⎜
⎞
⎠
⎟
a ax b
2
2
2
cos
p
:
y a ax b n
n
n
= + + ⋅
⎛
⎝
⎜
⎞
⎠
⎟
cos
p
2
Particular case:
If a b
= =
1 0
, , then y x
= cos . ∴ y x n
n = + ⋅
⎛
⎝
⎜
⎞
⎠
⎟
cos
p
2
.
7. Find the nth
derivative of e bx c
ax
sin( ).
1
Solution.
Let y e bx c
ax
= +
sin( )
Differentiating w.r.to x, successively we get
y e bx c b bx c e a
ax ax
1 = + ⋅ + + ⋅
cos( ) sin( ). = + + +
e b bx c a bx c
ax
[ cos( ) sin( )]
If a r b r
= =
cos , sin
u u, then
( ) cos sin (cos sin )
a b r r r r r
2 2 2 2 2 2 2 2 2 2 2
+ = + = + =
u u u u ⇒ r a b
= +
( )
2 2 1 2
and tanu =
b
a
, ∴ u =
⎛
⎝
⎜
⎞
⎠
⎟
−
tan 1 b
a
.
∴ y e r bx c r bx c
ax
1 = + + +
[ sin cos( ) cos sin( )]
u u
= + + +
re bx c bx c
ax
[sin cos( ) cos sin( )]
u u = + +
re bx c
ax
sin( )
u
∴ y r e bx c b bx c e a
ax ax
2 = + + ⋅ + + + ⋅
[ cos( ) sin( ) ]
u u
= + + + + +
re r bx c r bx c
ax
[ sin cos( ) cos sin( )]
u u u u
= + + +
r e bx c
ax
2
sin( )
u u = + +
r e bx c
ax
2
2
sin( ).
u
Similarly, y r e bx c
ax
3
3
3
= + +
sin( )
u
:
y r e bx c n
n
n ax
= + +
sin( )
u
⇒ y a b e bx c n
b
a
n
n ax
= + ⋅ + +
⎛
⎝
⎜
⎞
⎠
⎟
−
( ) sin tan
2 2 2 1 .
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 10 5/30/2016 7:07:26 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-233-2048.jpg)
![Differential Calculus ■ 3.11
8. Find the nth
derivative of e bx c
ax
cos( ).
1
Solution.
Let y e bx c
ax
= +
cos( )
Differentiating w.r.to x, successively we get
y e bx c b bx c e a
ax ax
1 = − + ⋅ + + ⋅ ⋅
( sin( ) ) cos( )
⇒ y e a bx c b bx c
ax
1 = + − +
[ cos( ) sin( )]
Put a r b r
= =
cos , sin
u u, then r a b
2 2 2
= + ⇒ = +
r a b
( )
2 2 1 2
and tanu =
b
a
⇒ u =
⎛
⎝
⎜
⎞
⎠
⎟
−
tan 1 b
a
.
∴ y e r bx c r bx c
ax
1 = + − +
[ cos cos( ) sin sin( )]
u u
= + − +
re bx c bx c
ax
[cos cos( ) sin sin( )]
u u = + +
re bx c
ax
cos( )
u
y r e bx c b bx c e a
ax ax
2 = − + + ⋅ + + + ⋅
[ ( sin( ) ) cos( ) ]
u u
= + + − + +
= + + −
re a bx c b bx c
re r bx c r
ax
ax
[ cos( ) sin( )]
[ cos cos( ) si
u u
u u n
n sin( )]
u u
bx c
+ +
= + + − + +
r e bx c bx c
ax
2
[cos cos( ) sin sin( )]
u u u u
⇒ y r e bx c
ax
2
2
= + + +
cos( )
u u = + +
r e bx c
ax
2
2
cos( )
u .
Similarly, y r e bx c
ax
3
3
3
= + +
cos( )
u
:
y r e bx c n
n
n ax
= + +
cos( )
u
⇒ y a b e bx c n
b
a
n
n ax
= + ⋅ + +
⎛
⎝
⎜
⎞
⎠
⎟
−
( ) cos tan
2 2 2 1 .
WORKED EXAMPLES
1. The nth
derivative using partial fractions
EXAMPLE 1
Find the nth
derivative of (i)
x
x
( 2)2
2
(ii) 2
(2 1)( 1)
x
x x
1 2
.
Solution.
(i) x
x
( )
− 2 2
. Let y
x
x
=
−
( )
2 2
Split the R.H.S into partial fractions. to reduce to the form
1
( )
ax b m
+
⎛
⎝
⎜
⎞
⎠
⎟
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 11 5/30/2016 7:07:31 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-234-2048.jpg)
![3.12 ■ Engineering Mathematics
Let x
x
( )
− 2 2
= A
x
B
x
( ) ( )
−
+
−
2 2 2
⇒ x A x B
= − +
( ) .
2
Put x = 2, then 2 0
= × +
A B ⇒ B = 2.
Equating the coefficients of x, A = 1.
∴ x
x x x
( ) ( ) ( )
−
=
−
+
−
2
1
2
2
2
2 2
∴ y
x x
=
−
+
−
1
2
2
2 2
( ) ( )
then y
n
x
n
x
n
n
n
n
n
=
−
−
+ ⋅
− +
−
+ +
( ) !
( )
( ) ( )!
( )
1
2
2
1 1
2
1 2
. [Refer formula 2]
(ii) 2
2 1 1
x
x x
( )( )
+ −
. Let y
x
x x
=
+ −
2
2 1 1
( )( )
Split the R.H.S into partial fractions.
Let
2
2 1 1
x
x x
( )( )
+ −
= A
x
B
x
2 1 1
+
+
−
⇒ 2 1 2 1
x A x B x
= − + +
( ) ( )
Put x = −
1
2
, then 2
1
2
1
2
1
−
⎛
⎝
⎜
⎞
⎠
⎟ = − −
⎛
⎝
⎜
⎞
⎠
⎟
A ⇒ − = −
3
2
1
A ⇒ A =
2
3
Put x = 1, then 2 1 2 1 1 3 2
2
3
⋅ = ⋅ + ⇒ = ⇒ =
B B B
( )
∴ 2
2 1 1
2
3
1
2 1
2
3
1
1
x
x x x x
( )( )
+ −
= ⋅
+
+ ⋅
−
∴ y
x x
= ⋅
+
+ ⋅
−
2
3
1
2 1
2
3
1
1
Hence, y
n
x
n
x
n
n n
n
n
n
= ⋅
−
+
+
−
−
+ +
2
3
1 2
2 1
2
3
1
1
1 1
( ) !
( )
( ) !
( )
. [Refer formula 3]
=
−
+
+
−
−
+
+ +
( ) !
( )
( ) !
( )
1 2
3 2 1
2 1
3 1
1
1 1
n n
n
n
n
n
x
n
x
.
EXAMPLE 2
Find the nth
derivative of
x
x x
4
( 1)( 2)
2 2
.
Solution.
Let y =
x
x
4
( 1)( 2)
− −
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 12 5/30/2016 7:07:37 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-235-2048.jpg)
![Differential Calculus ■ 3.13
Split the R.H.S into partial fractions.
Since the degree of the Nr. is greater than the degree of Dr., it is an improper fraction.
We divide x4
by ( )( )
x x x x
− − = − +
1 2 3 2
2
and then split the proper fraction into partial
fractions.
Dividing
∴
x
x x
x x
x
x x
4
2
1 2
3 7
15 14
1 2
−
( ) −
( )
= + + +
−
− −
( )( )
Let
15 14
1 2 1 2
x
x x
A
x
B
x
−
− −
=
−
+
−
( )( )
⇒ 15 14 2 1
x A x B x
− = − + −
( ) ( )
Put x = 1, then 15 1 14 1 2 0
⋅ − = − + ⋅
A B
( ) ⇒ A = −1
Put x = 2, then 15 2 14 2 1
⋅ − = −
B( ) ⇒ B = 16
∴
15 14
1 2
1
1
16
2
x
x x x x
−
− −
= −
−
+
−
( )( ) ( )
∴
x
x x
x x
x x
4
2
1 2
3 7
1
1
16
2
( )( )
− −
= + + −
−
+
−
∴ y x x
x x
= + + −
−
+
−
2
3 7
1
1
16
2
Hence, y
n
x
n
x
n
n
n
n
n
= − ⋅
−
−
+
−
−
+ +
1
1
1
16
1
2
1 1
( ) !
( )
( ) !
( )
=
−
−
+
−
−
+
+ +
( ) !
( )
( ) !
( )
,
1
1
16 1
2
2
1
1 1
n
n
n
n
n
x
n
x
n
2. The nth
derivatives of trigonometric functions
If y is a simple power of sine or cosine or product of sine and cosine, then they can be expressed as a
sum of sines and cosines of multiple angles and nth
derivative can be found.
EXAMPLE 3
Find the nth
derivative of (i) sin2
x (ii) sin3
x.
Solution.
(i) sin2
x
Let y x
= sin2
=
−
= −
1 2
2
1
2
2
2
cos cos
x x
∴ y x n
n
n
= − +
⎛
⎝
⎜
⎞
⎠
⎟
1
2
2 2
2
cos
p
= − +
⎛
⎝
⎜
⎞
⎠
⎟
−
2 2
2
1
n
x n
cos
p
. [Refer the formula 5]
x x
x x x
x x x
x x
x x x
2
2 4
4 3 2
3 2
3 2
3 7
3 2
3 2
3 2
3 9 6
+ +
− +
− +
−
− +
⎯⎯⎯⎯⎯⎯⎯
⎯⎯⎯⎯⎯⎯⎯⎯⎯
⎯⎯
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
7 6
7 21 14
15 14
2
2
x x
x x
x
−
− +
−
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 13 5/30/2016 7:07:40 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-236-2048.jpg)
![3.14 ■ Engineering Mathematics
(ii) sin3
x
Let y x
= sin3
⇒ = −
1
4
3 3
[ sin sin ]
x x = −
3
4
1
4
3
sin sin
x x [ sin sin sin ]
{ 3 3 4 3
x x x
= −
Hence, y x n x n
n
n
= +
⎛
⎝
⎜
⎞
⎠
⎟ − +
⎛
⎝
⎜
⎞
⎠
⎟
3
4 2
1
4
3 3
2
sin sin
p p
[Refer the formula 5]
EXAMPLE 4
Find the nth
derivative of (i) cos4
x (ii) sinx sin2x sin3x.
Solution.
(i) cos4
x
Let y x
= cos4
= (cos )
2 2
x =
+
⎡
⎣
⎢
⎤
⎦
⎥
cos
2
1 2
2
x
= + +
[ cos cos ]
2
1
4
1 2 2 2
x x
= + +
+
⎡
⎣
⎢
⎤
⎦
⎥ = + + +
1
4
1
2
2
1
4
1 4
2
1
4
1
8
1
2
2
1
8
4
cos
cos
cos cos
x
x
x x
⇒ y x x
= + +
3
8
1
2
2
1
8
4
cos cos
Hence, y x
n
x
n
n
n n
= ⋅ +
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟
1
2
2 2
2
1
8
4 4
2
cos cos .
p p
(ii) sin sin2 sin3
x x x
Let y x x x
= sin sin sin
2 3
We know that sin sin cos cos
A B A B A B
= −
( )− +
( )
⎡
⎣ ⎤
⎦
1
2
and sin cos sin sin
A B A B A B
= +
( )+ −
( )
⎡
⎣ ⎤
⎦
1
2
∴ y x x x
= −
[ ]
1
2
5
sin cos cos = −
{ }
1
2
5
sin cos sin cos
x x x x
= − −
[ ]
⎧
⎨
⎩
⎫
⎬
⎭
1
2
1
2
2
1
2
6 4
sin sin sin
x x x = − −
1
4
2
1
4
6 4
sin (sin sin )
x x x
Hence, y x
n
x
n
x
n
n
n n n
= +
⎛
⎝
⎜
⎞
⎠
⎟ − +
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
1
4
2 2
2
1
4
6 6
2
1
4
4 4
2
sin sin sin
p p p
⎜
⎜
⎞
⎠
⎟ [Refer formula 5]
⇒ y x
n
x
n
x
n
n
n n n n
= +
⎛
⎝
⎜
⎞
⎠
⎟ − ⋅ +
⎛
⎝
⎜
⎞
⎠
⎟ + +
− − −
2 2
2
3 2 6
2
4 4
2 2 1
sin sin sin
p p p
2
2
⎛
⎝
⎜
⎞
⎠
⎟
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 14 5/30/2016 7:07:44 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-237-2048.jpg)
![Differential Calculus ■ 3.15
EXAMPLE 5
Find the nth
differential coefficient of sin cos
3 5
u u.
Solution.
Let y = sin cos
3 5
u u and let x i ei
= + =
cos sin
u u u
∴ 1 1
x i
=
+
cos sin
u u
= = −
1
e
e i
i
i
u
u
u u
= cos sin
∴ x
x
+ =
1
2cosu and x
x
i
− =
1
2 sinu.
By De−Moivre’s theorem,
x n i n
n
= +
cos sin
u u and 1
x
n i n
n
= −
cos sin
u u
x
x
n
n
n
+ =
1
2cos u and x
x
i n
n
n
− =
1
2 sin u
∴ 2
1
5 5
5
cos u = +
⎛
⎝
⎜
⎞
⎠
⎟
x
x
and 2
1
3 3 3
3
i x
x
sin u = −
⎛
⎝
⎜
⎞
⎠
⎟
∴ 2 2
1 1
3 3 3 5 5
3 5
i x
x
x
x
sin cos
u u
⋅ = −
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⇒ − = −
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥ +
⎛
⎝
⎜
⎞
⎠
⎟
i x
x
x
x
x
x
2
1 1 1
8 3 5
3 2
sin cos
u u = −
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
x
x
x
x
2
2
3 2
1 1
= − + −
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟
x x
x x
x
x
6 2
2 6
2
2
3
3 1
2
1
= + + − − −
x x x x x
8 6 4 4 2
2 3 6 3 + + + − − −
3
6 3 1 2 1
2 4 4 6 8
x x x x x
= −
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟
x
x
x
x
x
x
x
x
8
8
6
6
4
4
2
2
1
2
1
2
1
6
1
− = + ⋅ − ⋅ − ⋅ ⋅
i i i i i
2 2 8 2 2 6 2 2 4 6 2 2
8 3 5
sin cos sin sin sin sin
u u u u u u
⇒ − = + − − ⋅
2 8 2 6 2 4 6 2
7 3 5
sin cos sin sin sin sin
u u u u u u [dividing by 2i]
∴ sin cos [sin sin sin sin ]
3 5
7
1
2
8 2 6 2 4 6 2
u u u u u u
= − + − −
= + − −
1
2
6 2 2 4 2 6 8
7
[ sin sin sin sin ]
u u u u
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 15 5/30/2016 7:07:49 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-238-2048.jpg)
![3.16 ■ Engineering Mathematics
∴ y = + − −
1
2
6 2 2 4 2 6 8
7
[ sin sin sin sin ]
u u u u
∴ y
n n n
n
n n n
= ⋅ +
⎛
⎝
⎜
⎞
⎠
⎟ + ⋅ +
⎛
⎝
⎜
⎞
⎠
⎟ − ⋅ +
⎛
⎝
1
2
6 2 2
2
2 4 4
2
2 6 6
2
7
sin sin
u
p
u
p
u
p
⎜
⎜
⎞
⎠
⎟ − +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
8 8
2
n n
sin u
p .
EXAMPLE 6
If y
x
x
5
log
, then prove that y
n
x
x
n
n
n
n
5
2
2 2 2 2
1
( 1) !
log 1
1
2
1
3
1
.
1 e ⋅⋅⋅
⎡
⎣
⎢
⎤
⎦
⎥
Solution.
Given y
x
x
e
=
log (1)
Differentiating w.r.to x, we get
y
x x
x
x
e
1 2
1 1 1
= ⋅ + ⋅ −
⎛
⎝
⎜
⎞
⎠
⎟
log = − =
−
−
1 1 1 1
1
2 2 2
x x
x
x
x
e e
log
( ) !
[log ].
Again differentiating w.r.to x, we get
y
x x
x
x
e
2 2 3
1
1 1
1
2
= − ⋅ + − ⋅ −
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎩
⎫
⎬
⎭
( ) (log )
= − − −
⎧
⎨
⎩
⎫
⎬
⎭
( ) (log )
1
1 2
1
3 3
x x
x
e
=
−
− −
⎧
⎨
⎩
⎫
⎬
⎭
=
−
− −
⎧
⎨
⎩
⎫
⎬
⎭
( )
log
( ) !
log
1 2
1
1
2
1 2
1
1
2
2
3
2
3
x
x
x
x
e e
Again differentiating w.r.to x, we get
y
x x
x
x
e
3
2
3 4
1 2
1 1
1
1
2
3
= − ⋅ + − −
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
( ) ! log
= − − − −
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎩
⎫
⎬
⎭
( ) ! log
1 2
1 3
1
1
2
2
4 4
x x
x
e
=
− ×
− − −
⎧
⎨
⎩
⎫
⎬
⎭
( ) !
log
1 2 3
1
1
2
1
3
3
4
x
x
e =
−
− − −
⎧
⎨
⎩
⎫
⎬
⎭
( ) !
log .
1 3
1
1
2
1
3
3
4
x
x
e
Proceeding in this way or by induction, we get
y
n
x
x
n
n
n
n e
=
−
− − − ⋅⋅⋅−
⎡
⎣
⎢
⎤
⎦
⎥
+
( ) !
log
1
1
1
2
1
3
1
1
.
EXERCISE 3.2
1. Find the nth
derivative of (i) x x
2
3
sin (ii) x x
2
4
cos (iii) sin sin
3 2
x x.
2. Find the nth
derivative of x x x
e
4 2
3 5 2
+ + −
log ( ) .
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 16 5/30/2016 7:07:52 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-239-2048.jpg)

![3.18 ■ Engineering Mathematics
Inductive step: We assume that the theorem is true for n = k (1).
i.e., p(k) is true ⇒ y uv kC u v kC u v
k k k k k
= + + +
−
1 1 1
… is true (2)
To prove p(k + 1) is true.
That is to prove
y uv C u v C u v C u v
k k
k
k
k
k
k
k k
+ +
+ +
−
+
+ +
= + + + +
1 1
1
1 1
1
2 2 1
1
1 1
… .
Differentiating (2) w.r.to x, we get
y uv u v kC u v u v kC u v u v kC
k k k k k k k k
+ + − − − −
= + + + + + + +
1 1 1 1 1 2 1 2 2 1 3 2
[ ] [ ] … 1
1 1 2 1
1 1
[ ]
[ ]
u v u v
kC u v u v
k k
k k k
−
+
+
+ +
⇒ y uv kC u v kC kC u v kC kC u v u
k k k k k k k
+ + − −
= + + + + + + + +
1 1 1 1 2 1 2 1 1 1
1
( ) ( ) ( )
… k
k v
+1
⇒ y uv C u v C u v C u v u v
k k
k
k
k
k
k
k k k
+ +
+ +
−
+
+
= + + + + +
1 1
1
1 1
1
2 2 1
1
1 1
… [ ]
{ n
r
n
r
n
r
C C C
+
−
= +
1
1
∴ P(k + 1) is true.
Thus, P(k) is true ⇒ p(k + 1) is true.
∴ By induction p(n) is true for all values of n ∈ N.
Hence, the theorem is true for all values of n ∈ N.
∴ y uv C u v C u v C u v u v
n n
n
n
n
n
n
r r n r n
= + + + + + +
− − −
1 1 1 2 2 2
… … .
WORKED EXAMPLES
EXAMPLE 1
If y m x
5 2
cos( sin )
1
, then prove that (1 ) 0.
2
2 1
2
2 2 1 5
x y xy m y Hence prove that
(1 ) (2 1) ( ) 0
2
2 1
2 2
2 2 1 1 2 5
1 1
x y n xy m n y
n n n
.
Solution.
Given y m x
= −
cos( sin )
1
⇒ cos sin
− −
=
1 1
y m x (1)
Differentiating (1) w.r.to x, we get
−
−
⋅ = ⋅
−
1
1
1
1
2 2
y
dy
dx
m
x
⇒
−
−
⋅ =
−
1
1 1
2 1 2
y
y
m
x
Squaring,
y
y
m
x
1
2
2
2
2
1 1
−
=
−
⇒ ( ) ( )
1 1
2
1
2 2 2
− = −
x y m y .
Differentiating w.r.to x, we get
( )
1 2 2 2
2
1 2 1
2 2
1
− − = −
x y y xy m yy
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 18 5/30/2016 7:08:00 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-241-2048.jpg)
![Differential Calculus ■ 3.19
Dividing by 2 1
y on both sides,
( )
1 2
2 1
2
− − = −
x y xy m y ⇒ ( )
1 0
2
2 1
2
− − + =
x y xy m y (2)
Differentiating (2) w.r.to x, n times by Leibnitz’s theorem, we get,
( ) ( ) ( ) [ ]
1 2 2 1 0
2
2 1 1 2 1 1
2
− + − + − − + ⋅ ⋅ + =
+ + +
x y C x y C y xy C y m y
n
n
n
n
n n
n
n n
⇒ ( )
( )
1 2 2
1
1 2
0
2
2 1 1
2
− − − ⋅
−
⋅
− − + =
+ + +
x y nx y
n n
y xy ny m y
n n n n n n
⇒ ( ) ( ) [ ( ) ]
1 2 1 1 0
2
2 1
2
− − + + − − − =
+ +
x y n xy m n n n y
n n n
⇒ ( ) ( ) ( )
1 2 1 0
2
2 1
2 2
− − + + − + − =
+ +
x y n xy m n n n y
n n n
⇒ ( ) ( ) ( ) .
1 2 1 0
2
2 1
2 2
− − + + − =
+ +
x y n xy m n y
n n n
EXAMPLE 2
If y a x b x
5 1
cos(log ) sin(log ) , then show that x y n xy n y
n n n
2
2 1
2
(2 1) ( 1) 0
1 1
1 1 1 1 5 .
Solution.
Given y a x b x
= +
cos(log ) sin(log ) (1)
Differentiating (1) w.r.to x, we get
y a x
x
b x
x
1
1 1
= − ⋅ + ⋅
( sin(log )) cos(log ) = − +
1
x
a x b x
[ sin(log ) cos(log )]
⇒ xy a x b x
1 = − +
sin(log ) cos(log ).
Again differentiating w.r.to x, we get
xy y a x
x
b x
x
2 1
1 1
+ = − ⋅ + −
cos(log ) ( sin(log ))
= − +
1
x
a x b x
[ cos(log ) cos(log ) = −
y
x
⇒ x y xy y
2
2 1
+ = − ⇒ x y xy y
2
2 1 0
+ + = (2)
Differentiating (2) w.r.to x, n times by Leibnitz’s theorem, we get,
x y C xy C y xy C y y
n
n
n
n
n n
n
n n
2
2 1 1 2 1 1
2 2 1 0
+ + +
+ + + + ⋅ ⋅ + =
⇒ x y nxy
n n
y xy ny y
n n n n n n
2
2 1 1
2 2
1
1 2
0
+ + +
+ + ⋅
−
⋅
+ + + =
( )
⇒ x y n xy n n n y
n n n
2
2 1
2 1 1 1 0
+ +
+ + + − + + =
( ) [ ( ) ]
⇒ x y n xy n n n y
n n n
2
2 1
2
2 1 1 0
+ +
+ + + − + + =
( ) ( )
⇒ x y n xy n y
n n n
2
2 1
2
2 1 1 0
+ +
+ + + + =
( ) ( ) .
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 19 5/30/2016 7:08:04 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-242-2048.jpg)
![3.20 ■ Engineering Mathematics
EXAMPLE 3
If y x x
m
5 1 1
1 2
( ) , then prove that (1 ) (2 1) ( ) 0
2
2 1
2 2
1 1 1 1 2 5
1 1
x y n xy n m y
n n n .
Solution.
Given y x x
m
= + +
( )
1 2
(1)
Differentiating (1) w.r.to x, we get
y m x x
x
x
m
1
2
1
2
1 1
1
2 1
2
= + +
( ) +
+
⋅
⎛
⎝
⎜
⎞
⎠
⎟
−
= + +
( ) +
+
⎛
⎝
⎜
⎞
⎠
⎟
−
m x x
x
x
m
1 1
1
2
1
2
= + +
( ) + +
+
⎛
⎝
⎜
⎞
⎠
⎟
−
m x x
x x
x
m
1
1
1
2
1 2
2
=
+ +
( )
+
=
+
m x x
x
my
x
m
1
1 1
2
2 2
Squaring, y1
2
=
+
m y
x
2 2
2
1
⇒ ( )
1 2
1
2 2 2
+ =
x y m y
Again differentiating w.r.to x,
( )
1 2 2 2
2
1 2 1
2 2
1
+ + =
x y y xy m yy ⇒ ( )
1 2
2 1
2
+ + =
x y xy m y [dividing by 2 1
y ]
⇒ ( )
1 0
2
2 1
2
+ + − =
x y xy m y . (2)
Differentiating (2) w.r.to x, n times by Leibnitz’s theorem, we get,
( )
1 2 2 1 0
2
2 1 1 2 1 1
2
+ + + + + ⋅ ⋅ − =
+ + +
x y nC xy nC y xy nC y m y
n n n n n n
⇒ ( )
( )
1 2 2
1
1 2
0
2
2 1 1
2
+ + +
−
⋅
+ + − =
+ + +
x y nx y
n n
y xy ny m y
n n n n n n
⋅
⇒ ( ) ( ) [ ( ) ]
1 2 1 1 0
2
2 1
2
+ + + + − + − =
+ +
x y n xy n n n m y
n n n
⇒ ( ) ( ) ( )
1 2 1 0
2
2 1
2 2
+ + + + − + − =
+ +
x y n xy n n n m y
n n n
⇒ ( ) ( ) ( )
1 2 1 0
2
2 1
2 2
+ + + + − =
+ +
x y n xy n m y
n n n
.
Problems to find y n (0)
EXAMPLE 4
If y x
5 2
(sin )
1 2
, then prove that (1 ) 2 0
2
2 1
2 2 2 5
x y xy . Hence show that
(1 ) (2 1) 0
2
2 1
2
2 2 1 2 5
1 1
x y n xy n y
n n n
and find y n
(0).
Solution.
Given y x
= −
(sin )
1 2
(1)
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 20 5/30/2016 7:08:08 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-243-2048.jpg)
![Differential Calculus ■ 3.21
Differentiating (1) w.r.to x, we get
y
x
x
1
1
2
2
1
=
−
−
sin (2)
Squaring, y
x
x
1
2
1 2
2 2
4
1
=
−
−
(sin )
( )
⇒ ( )
1 4
2
1
2
− =
x y y (3)
Differentiating (3) w.r.to x, we get
( )
1 2 2 4
2
1 2 1
2
1
− − =
x y y xy y ⇒ ( ) .
1 2
2
2 1
− − =
x y xy [dividing by 2y1
] (4)
Differentiating (4) w.r.to x, n times using Leibnitz’s theorem, we get
( ) ( ) ( ) [ ]
1 2 2 1 0
2
2 1 1 2 1 1
− + − + − − + ⋅ ⋅ =
+ + +
x y nC x y nC y xy nC y
n n n n n
⇒ ( )
( )
1 2 2
1
1 2
0
2
2 1 1
− − − ⋅
−
⋅
− − =
+ + +
x y nxy
n n
y xy ny
n n n n n
⇒ ( ) ( ) [ ( ) ]
1 2 1 1 0
2
2 1
− − + − − + =
+ +
x y n xy n n n y
n n n
⇒ ( ) ( ) [ ]
1 2 1 0
2
2 1
2
− − + − − + =
+ +
x y n xy n n n y
n n n
⇒ ( ) ( )
1 2 1 0
2
2 1
2
− − + − =
+ +
x y n xy n y
n n n
(5)
To find y n (0)
Put x = 0 in (5), we get y n y
n n
+ − =
2
2
0 0 0
( ) ( ) .
Put x = 0 in (2), we get y1
1
0
2 0
1 0
0
( )
sin
=
−
=
−
.
Put x = 0 in (4), we get y2 0 2 0
( ) − = ⇒ y2 0 2
( ) = .
We have y n y
n n
+ − =
2
2
0 0 0
( ) ( ) ⇒ y n y
n n
+ =
2
2
0 0
( ) ( ).
If n is odd, n = 1, 3, 5, 7, …, then we have
y y
3 1
0 0 0
( ) ( )
= = , y y y y
5
2
3 7
2
5
0 3 0 0 0 5 0 0
( ) ( ) , ( ) ( )
= = = = and so on.
∴ If n is odd, yn ( ) .
0 0
=
If n is even, n = 2, 4, 6, 8, …, then we have y2 0 2
( ) = y y
4
2
2
2
0 2 0 2 2
( ) ( ) ,
= = ⋅
y y
6
2
4
2 2
0 4 0 2 2 4
( ) ( )
= = ⋅ ⋅ , y y
8
2
6
2 2 2
0 6 0 2 2 4 6
( ) ( )
= = ⋅ ⋅ ⋅ and so on.
∴ If n is even, y n
n ( ) ( )
0 2 2 4 6 2
2 2 2 2
= ⋅ ⋅ ⋅ ⋅⋅⋅ −
∴ y
n n
n
n ( )
( ) , if
, .
0
2 2 4 6 2
0
2 2 2 2
=
⋅ ⋅ ⋅ ⋅⋅⋅ −
⎧
⎨
⎩
iseven
if isodd
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 21 5/19/2016 2:15:20 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-244-2048.jpg)
![3.22 ■ Engineering Mathematics
EXAMPLE 5
Find the value of the nth
derivate of ea x
sin 1
2
for x 5 0.
Solution.
Let y = ea x
sin−1
(1)
Differentiating w.r. to x, we get
y1
= ea x
sin−1
a
x
ay
x
1 1
2 2
−
=
−
(2)
⇒ (1 − x2
)y1
2
= a2
y2
Again differentiating w.r. to x, we get
(1 − x2
)2y1
y2
− 2xy1
2
= a2
. 2yy1
⇒ (1 − x2
)y2
− xy1
= a2
y ⇒ (1 − x2
) y2
− xy1
− a2
y = 0 (3)
Differentiating (3) w.r. to x, n times using Leibnitz’s theorem, we get
(1− x2
) yn + 2
+ n
C1(−2x)yn + 1
+ n
C2(−2) yn
− [xyn+1
+ n
C1. 1. yn
] − a2
yn
= 0
⇒ (1 − x2
) yn + 2
− 2nx yn + 1
− 2
1
1 2
n n
yn
( )
.
−
− xyn+1
− nyn
− a2
yn
= 0
⇒ (1 − x2
) yn + 2
− (2n + 1) x yn+1
− [n (n − 1) + n + a2
] yn
= 0
⇒ (1 − x2
) yn + 2
− (2n + 1) xyn+1
− (n2
+ a2
) yn
= 0 (4)
Put x = 0 in (4), then
y n a y
n n
+ − + =
2
2 2
0 0 0
( ) ( ) ( )
⇒ y n a y
n n
+ = +
2
2 2
0 0
( ) ( ) ( ) (5)
Put x = 0 in (1), then y( )
0 1
=
Put x = 0 in (2), then y1 0
( ) = a
Put x = 0 in (3), then y a y
2
2
0 0
( ) ( )
= ⇒ y a a
2
2 2
0 1
( ) = ⋅ =
Putting n = 1, 3, 5, 7, … in (5) we get
y a y a a a a
3
2 2
1
2 2 2 2
0 1 0 1 1
( ) ( ) ( ) ( ) ( )
= + ⋅ = + ⋅ = +
y a y a a a
5
2 2
3
2 2 2 2
0 3 0 1 3
( ) ( ) ( ) ( )( )
= + ⋅ = + +
y a y a a a a
7
2 2
5
2 2 2 2 2 2
0 5 0 1 3 5
( ) ( ) ( ) ( )( )( )
= + ⋅ = + + +
and so on.
If n is odd, y a a a n a
n ( ) ( )( ) [( ) ]
0 1 3 2
2 2 2 2 2 2
= + + ⋅⋅⋅ − +
Putting n = 2, 4, 6, 8, … in (5), we get
y a y a a
4
2 2
2
2 2 2
0 2 0 2
( ) ( ) ( ) ( )
= + = +
y a y a a a
6
2 2
4
2 2 2 2 2
0 4 0 2 4
( ) ( ) ( ) ( )( )
= + = + +
y a y a a a a
8
2 2
6
2 2 2 2 2 2 2
0 6 0 2 4 6
( ) ( ) ( ) ( )( )( )
= + = + + +
and so on.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 22 5/19/2016 2:15:25 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-245-2048.jpg)
![Differential Calculus ■ 3.23
If n is even, y a a a a n a
n ( ) ( )( )( ) [( ) ].
0 2 4 6 2
2 2 2 2 2 2 2 2 2
= + + + ⋅⋅⋅ − +
y
a a a n a n
n ( )
( )( ) [( ) ],
( )(
0
2 4 2
2 2 2 2 2 2 2
=
+ + ⋅⋅⋅ − +
+ +
if iseven
1 3
2 2 2
a a a
a2 2 2
[(n 2) ], if isodd
)⋅⋅⋅ − +
⎧
⎨
⎪
⎩
⎪ a n
EXAMPLE 6
Considering x x x
n n n
2
5 ⋅ and using Leibnitz’s theorem prove that
1
1
( 1)
1 2
( 1) ( 2)
1 2 3
(2 )!
( !)
2
2
2 2
2 2
2 2 2
2 2 2 2
1 1
2
1
2 2
1 5
n n n n n n n
n
⋅ ⋅ ⋅
⋅⋅⋅ .
Solution.
Let y x n
= 2
Differentiating w.r.to x, n times we get
y n n n n n x
n
n n
= − − ⋅⋅⋅ − + −
2 2 1 2 2 2 1 2
( )( ) ( )
= − − ⋅⋅⋅ +
2 2 1 2 2 1
n n n n xn
( )( ) ( )
=
− − ⋅⋅⋅ + ⋅⋅⋅ ⋅
⋅ ⋅ ⋅⋅⋅
2 2 1 2 2 1 2 1
1 2 3
n n n n n
n
xn
( )( ) ( )
⇒ y
n
n
x
n
n
=
( )!
( !)
2 (1)
Also y x n
= 2
= ⋅
x x
n n
. Let u x v x
n n
= =
and ∴ y uv
=
By Leibnitz’s theorem,
y uv nc u v nc u v nc u v u v
n n n n n n n
= + + +⋅⋅⋅+ +
− − − −
1 1 1 2 2 2 1 1 1
u nxn
1
1
= −
, u n n xn
2
2
1
= − −
( )
u n n n xn
3
3
1 2
= − − ⋅⋅⋅
−
( )( ) ,
u n n n n n x
n
n n
−
− −
= − − ⋅⋅⋅ − −
2
2
1 2 3
( )( ) [ ( )] ( )
= − − ⋅⋅⋅ ⋅
n n n x
( )( )
1 2 3 2
=
− − ⋅⋅⋅ ⋅ ⋅ ⋅
⋅
=
⋅
n n n
x
n
x
( )( ) !
1 2 4 3 2 1
1 2 1 2
2 2
u n n n n n x
n
n n
−
− −
= − − ⋅⋅⋅ − − ⋅
1
1
1 2 2
( )( ) [ ( )] ( )
= − − ⋅⋅⋅ =
n n n x n x
( )( ) !
1 2 2
∴ u n
n = !
Similarly, if v xn
= , then v n
n = !
∴ y x n nC nx n x nC n n x
n
x
n
n n n
= + ⋅ + ⋅ − ⋅
⋅
− −
! ! ( )
!
1
1
2
2 2
1
1 2
+ − −
⋅ ⋅
+⋅⋅⋅+
−
nC n n n x
n
x n x
n n
3
3 3
1 2
1 2 3
( )( )
!
!
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 23 5/19/2016 2:15:29 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-246-2048.jpg)

![Differential Calculus ■ 3.25
3.2 APPLICATIONS OF DERIVATIVE
3.2.1 Geometrical Interpretation of Derivative
Let f be a differentiable function on [a, b].
The graph of f is the set {( , ) ( ), [ , ]}
x y y f x x a b
= ∈ .
That is y f x
= ( ) is the equation of the graph of f,
Let c, c h a b
+ ∈[ , ].
So, that P c f c
( , ( )) and Q c h f c h
( , ( ))
+ + be the
corresponding points of the curvey f x
= ( ).
Then the slope of the chord
PQ
f c h f c
c h c
=
+ −
+ −
( ) ( )
=
+ −
f c h f c
h
( ) ( )
Suppose the point Q moves along the curve towards
P, then the chord PQ approaches to a definite line PT
in the limit as Q P
→ .
This line PT is called the tangent line to the curve at P.
∴ lim( ) lim
( ) ( )
Q p h
PQ
f c h f c
h
→ →
=
+ −
slope of chord
0
= f c
′( ), if the limit exists.
So, when f c
′( ) exists, it is the slope of the tangent PT at P.
∴ the equation of the tangent at P is.
y f c f c x c
− = −
( ) ( )( )
′ .
3.2.2 Equation of the Tangent and the Normal to the Curve y = f(x)
1. The equation of the tangent at ( , )
1 1
x y
The given curve is y f x
= ( ).
Let P x y
( , )
1 1
be any point on the curve.
Let m be the slope of the tangent at ( , )
x y
1 1 . ∴ m
dy
dx x y
=
( , )
1 1
∴ the equation of the tangent at P x y
( , )
1 1
is y y m x x
− = −
1 1
( ).
2. The equation of the normal at ( , )
1 1
x y
The normal at P x y
( , )
1 1
is a straight line through P and perpendicular to the tangent at P.
∴ If m1
is the slope of the normal at P, then m m
⋅ = −
1 1 ⇒ m
m
1
1
= − .
That is the slope of the normal = −
1
the slope of the tangent
.
Fig. 3.1
y
P
T o
θ
Q
x
C C + n
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 25 5/19/2016 2:15:40 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-248-2048.jpg)


![3.28 ■ Engineering Mathematics
∴ the roots are x1 1 2
3
2
= , ,
When x y
1 1
1 1 6 13 10 5 3
= = − + − + =
,
When x y
1 1
4 3 2
2 2 6 2 13 2 10 2 5
= = − × + × − × +
, = − + − + =
16 48 52 20 5 5.
When x y
1 1
4 3 2
3
2
3
2
6
3
2
13
3
2
10
3
2
5
= =
⎛
⎝
⎜
⎞
⎠
⎟ − ×
⎛
⎝
⎜
⎞
⎠
⎟ + ×
⎛
⎝
⎜
⎞
⎠
⎟ − × +
, = − + − + =
1
16
81 324 468 240 80
15
16
[ ] .
∴ the points are ( , ),( , ), , .
1 3 2 5
3
2
15
16
⎛
⎝
⎜
⎞
⎠
⎟
At these points the tangents to the curve are parallel to the line y x
= 2 .
Now we have to prove that at two of these points, the tangents are equal.
At the point (1, 3)
The equation of the tangent is
y x
− = −
3 2 1
( ) ⇒ y x
− = −
3 2 2 ⇒ 2 1 0
x y
− + = (2)
At the point ( , )
2 5
The equation of the tangent is
y x
− = −
5 2 2
( ) ⇒ y x
− = −
5 2 4 ⇒ 2 1 0
x y
− + = (3)
The equations (2) and (3) are the same.
∴ the tangents at the points ( , )
1 3 , ( , )
2 5 are the same.
EXAMPLE 3
Find the equations of the tangents from the origin to the curve y x x
5 2
4 2
3 5
.
Solution.
The given curve is y x x
= −
4 2
3 5
. (1)
Let a tangent from the origin to the curve touch it at the point P x y
( , )
1 1 .
∴ OP is a tangent to the curve and y x x
1
3
1
5
1
4 2
= − (2)
The slope of OP =
y
x
1
1
, sin ( , ) ( , )
ce x y
1 1 0 0
≠
[ ]
But the slope of OP
dy
dx x y
=
( , )
1 1
.
Differentiating (1) w.r.to x, we get
dy
dx
x x
= −
12 10
2 4 .
At the point P x y
( , )
1 1 : dy
dx
x x
= −
12 10
1
2
1
4.
∴ 12 10
1
2
1
4 1
1
x x
y
x
− = ⇒ 12 10
1
3
1
5
1
x x y
− = (3)
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 28 5/19/2016 2:16:00 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-251-2048.jpg)


![Differential Calculus ■ 3.31
Solution.
Given curve is x y a
3 3 3
+ = (1)
Also given ( , )
x y
1 1
is a point on (1). ∴ x y a
1
3
1
3 3
+ = (2)
Differentiating (1) w.r.to x, we get
3 3 0
2 2
x y
dy
dx
+ = ⇒ y
dy
dx
x
2 2
= − ⇒ dy
dx
x
y
=
− 2
2
.
At the point P x y
( , )
1 1 :
dy
dx
x
y
= − 1
2
1
2
.
∴ the slope of the tangent at the point ( , )
x y
1 1 is m
x
y
= − 1
2
1
2
.
∴ the equation of the tangent at the point ( , )
x y
1 1
is
y y
x
y
x x
− = − −
1
1
2
1
2 1
( ) ⇒ y y y x x x
1
2
1
3
1
2
1
3
− = − +
⇒ x x y y x y
1
2
1
2
1
3
1
3
+ = + ⇒ x x y y a
1
2
1
2 3
+ = [using (2)]
This tangent meets the curve in ( , )
h k . ∴ x h y k a
1
2
1
2 3
+ = (3)
( , )
h k is a point on the curve ∴ h k a
3 3 3
+ = (4)
( ) ( )
3 4
− ⇒ x h y k h k
1
2
1
2 3 3
0
+ − − =
⇒ h x h k y k
( ) ( )
1
2 2
1
2 2
0
− + − = ⇒ h x h k y k
( ) ( )
1
2 2
1
2 2
− = − − (5)
( ) ( )
2 3
− ⇒ x y x h y k
1
3
1
3
1
2 2
1
2
0
+ − − =
⇒ x x h y y k
1
2
1 1
2
1 0
( ) ( )
− + − = ⇒ x x h y y k
1
2
1 1
2
1
( ) ( )
− = − − (6)
∴ ( )
( )
5
6
⇒
h x h
x x h
k y k
y y k
( )
( )
( )
( )
1
2 2
1
2
1
1
2 2
1
2
1
−
−
=
− −
− −
⇒ h x h
x
k y k
y
( ) ( )
1
1
2
1
1
2
+
=
+ ⇒ h
x
h
x
k
y
k
y
1
2
1
2
1
2
1
2
+ = +
⇒ h
x
k
y
h
x
k
y
1 1
2
1
2
2
1
2
0
− + − = ⇒ h
x
k
y
h
x
k
y
h
x
k
y
1 1 1 1 1 1
0
− + −
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ =
⇒ h
x
k
y
h
x
k
y
1 1 1 1
1 0
−
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎡
⎣
⎢
⎤
⎦
⎥ =
⋅
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 31 5/19/2016 5:01:16 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-254-2048.jpg)
![3.32 ■ Engineering Mathematics
⇒ 1
1 1
+ +
h
x
k
y
= 0 {
h
x
k
y
h k x y
1 1
1 1
0
− ≠
⎡
⎣
⎢
⎤
⎦
⎥
as and are different points
( , ) ( , )
∴
h
x
k
y
1 1
1 0
+ + =
EXAMPLE 6
If the tangent at three points t1
, t2
, t3
on the curve x
t
t
y
t
t
5
1
5
1
2
3
3
3
1
,
1
are concurrent, Prove
that t t t
1 2 3 0
1 1 5 .
Solution.
The equation of the curve is given in parametric form
x
t
t
=
+
2
3
1
(1) and y
t
t
=
+
3
3
1
(2)
First we find the equation of the tangent at any point ‘t’ on the curve.
Differentiating (1) and (2) w.r.to t, we get
dx
dt
t t t t
t
t t t
t
t t
t
=
+ − ⋅
+
=
+ −
+
=
−
+
( )
( ) ( ) ( )
1 2 3
1
2 2 3
1
2
1
3 2 2
3 2
4 4
3 2
4
3 2
.
.
( )
( ) ( ) (
dy
dt
t t t t
t
t t t
t
t
t
=
+ − ⋅
+
=
+ −
+
=
+
1 3 3
1
3 3 3
1
3
1
3 2 3 2
3 2
2 5 5
3 2
2
3
)
)2
∴
dy
dx
dy dt
dx dt
t
t
t t
t
t
t t
t
t
= =
+
−
+
=
−
=
−
/
/
( )
( )
.
3
1
2
1
3
2
3
2
2
3 2
4
3 2
2
4 3
∴ slope of the tangent at ‘t’ is m
t
t
=
−
3
2 3
.
∴ the equation of the tangent at ‘t’ is
y
t
t
t
t
x
t
t
−
+
=
−
−
+
⎛
⎝
⎜
⎞
⎠
⎟
3
3 3
2
3
1
3
2 1
⇒
( ) ( )
1
1
3
2
1
1
3 3
3 3
3 2
3
+ −
+
=
−
+ −
+
⎡
⎣
⎢
⎤
⎦
⎥
t y t
t
t
t
t x t
t
⇒
( ) [( ) ]
1
3
2
1
3 3
3
3 2
+ − =
−
+ −
t y t
t
t
t x t
⇒ ( )( ) ( ) ( )
1 2 2 3 1 3
3 3 3 3 3 3
+ − − − = + −
t t y t t t t x t
⇒ ( )( ) ( )
1 2 3 1 2 3
3 3 3 3 6 3
+ − = + + − −
t t y t t x t t t
⇒ ( )( ) ( ) ( )
1 2 3 1 1
3 3 3 3 3
+ − = + − +
t t y t t x t t
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 32 5/19/2016 5:01:22 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-255-2048.jpg)
![Differential Calculus ■ 3.33
⇒ ( )
2 3
3 3
− = −
t y tx t [Dividing by (1 + t3
)]
⇒ 3 2 0
3 3
tx t y t
+ − − =
( ) ⇒ ( ) .
y t tx y
− + − =
1 3 2 0
3
∴ the equation of the tangent at t1
, t2
, t3
are
( ) , ( ) , ( ) .
y t xt y y t xt y y t xt y
− + − = − + − = − + − =
1 3 2 0 1 3 2 0 1 3 2 0
1
3
1 2
3
2 3
3
3
Given that the three tangents at t1
, t2
, t3
are concurrent.
Let (x1
, y1
) be the point of concurrency.
∴ the point (x1
, y1
) will satisfy the equations of the tangents at t1
, t2
, t3
.
∴ ( ) ,
y t x t y
1 1
3
1 1 1
1 3 2 0
− + − = ( )
y t x t y
1 2
3
1 2 1
1 3 2 0
− + − = and ( ) .
y t x t y
1 3
3
1 3 1
1 3 2 0
− + − =
These three equations imply that t1
, t2
, t3
are the roots of the equation
( )
y t x t y
1
3
1 1
1 3 2 0
− + − =
∴ sum of the roots = −
coeff
coeff
t
t
2
3
⇒ t t t
y
1 2 3
1
0
1
0.
+ + =
−
=
EXERCISE 3.4
1. Find the equation of tangents to the curve y x x
= − −
( )( )
3
1 2 at the point where it meets the x-axis.
2. Find the equation of the tangents from the origin to the curvey x
= +
2 1
2
.
3. Find the equation of normal to the curve 3 8
2 2
x y
− = which is parallel to the line x + 3y = 4.
4. Find the equation of the tangent to the curve y x x
= −
7 2
at the point (3, 12) on it. Also find the
equation of the normal at the point.
5. Find the points on the curve y x x
2 2
2 3
= −
( ) at which the tangents are parallel to the x-axis.
6. Find the points on the curve y x a x
3 2
2
= −
( ), where the tangents are parallel to y-axis.
7. If the tangent at (x1
, y1
) on the curve y3
+ x3
– 9xy + 1 = 0 is parallel to the x-axis, prove that at
the point
d y
dx x
2
2
1
3
18
27
=
−
.
8. Find the equation of the tangent to the curve x
t
t
y
t
t
=
−
+
=
+
−
1
1
1
1
, at the point t = 2.
9. Find the abscissa of the point on the curve ay2
= x3
at which the normal cuts off equal intercepts
on the coordinate axes.
[Hint: A line makes equal intercepts if its slope = 1 or −1].
10. If the tangent at (1, 3) on the parabola y = 4x − x2
cuts the parabola y = x2
− 6x + k at two different
points, find the values of k.
11. Find the equation of the tangent to the curve x2
+ 4y2
=16 at the point which is such that it is the
mid point of the portion of the tangent intercepted between the coordinate axes.
12. Find the points on x2
= y3
at which the normal pass through (0, 4).
13. The curve y = ax2
+ bx + c passes through the points (−1, 0) and (0, −2). The tangent to the curve
at the latter point makes 135° with the x-axis.
14. If p, q are the lengths of the perpendiculars from the origin to the tangent and normal at a point
on x y a
2 3 2 3 2 3
/ / /
+ = , then prove that 4 2 2 2
p q a
+ = .
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 33 5/19/2016 5:01:29 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-256-2048.jpg)









![Differential Calculus ■ 3.43
ANSWERS TO EXERCISE 3.6
I.
1.
p
4
2. tan− ⎛
⎝
⎜
⎞
⎠
⎟
1 21
20
3. tan− ⎛
⎝
⎜
⎞
⎠
⎟
1 1
3
and tan− ⎛
⎝
⎜
⎞
⎠
⎟
1 1
2
4. tan− ⎛
⎝
⎜
⎞
⎠
⎟
1 3
4
and
p
2
5. 0, the curves touch each other. 6. tan ( )
/
−1 13
2
7. tan ,tan ( )
− −
⎛
⎝
⎜
⎞
⎠
⎟
1 1
6
13
2 8.
p
2
3
5
1
, tan− ⎛
⎝
⎜
⎞
⎠
⎟ 9.
p
2
10.
p
4
1
3
1
, tan− ⎛
⎝
⎜
⎞
⎠
⎟ 11. tan− ⎛
⎝
⎜
⎞
⎠
⎟
1 7
11
13. tan− ⎛
⎝
⎜
⎞
⎠
⎟
1 3
4
II.
1. y = x + 1 2. y = 0 3. y x
− + =
p
3
0 4. 4x − y = 1.
3.3 MEAN-VALUE THEOREMS OF DERIVATIVES
The mean−value theorems for derivatives play an important role in calculus because many basic
properties of functions can be deduced from it. However, mean−value theorems are obtained from a
special case due to the French Mathematician Michael Rolle.
3.3.1 Rolle’s Theorem
Let f be a real function defined on the closed interval [a, b] such that
(i) f is continuous on [a, b]
(ii) f is derivable in the open interval (a, b) and
(iii) f(a) = f(b), then there exists at least one point c a b
∈( , ) such that ′
f c
( ) 0
5 .
Geometrical Meaning of Rolle’s Theorem
If y f x
= ( ) be a continuous curve with end points A B
and , having tangent at every point between
A B
and and the ordinates of A B
and are equal, then there exists at least one point Pon the curve
between A B
and such that the tangent at Pis parallel to the x-axis.
The geometrical meaning is clear from the diagrams.
y
o a b x
A B
P
y
o a b x
A
B
P1
P2
Fig. 3.6 Fig. 3.7
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 43 5/19/2016 5:02:53 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-266-2048.jpg)
![3.44 ■ Engineering Mathematics
Algebraic Meaning
If a and b are two consecutive roots of the polynomial equation f x
( ) ,
= 0 then there is at least one root
of ′ =
f x
( ) ,
0 between a and b.
Physical Meaning
The instantaneous rate of change of f at some point c between a and b is zero.
WORKED EXAMPLES
EXAMPLE 1
Test the application of Rolle’s theorem for the following functions.
(i) x on[ 1, 1]
2 (ii) cos
1
on[ 1, 1]
x
2
(iii) x2
on[2, 3] (iv) tan on[0, ].
x p
Solution.
(i) Let f x x x
( ) , 1 1.
= − ≤ ≤ Then f is continuous on [ , ]
−1 1
and f f
( ) , ( )
− = − = = =
1 1 1 1 1 1 ∴ f f
( ) ( ).
− =
1 1
We have f x
x x
x x
( ) =
− − ≤
≤ ≤
⎧
⎨
⎩
if
if
1 0
0 1
∴ ′ =
− −
⎧
⎨
⎩
f x
x
x
( )
1 1 0
1 0 1
if
if
∴ ′ ≠ ′
− +
f f
( ) ( )
0 0 ∴ ′
f ( ) .
0 does not exist
Hence, the second condition is not satisfied.
So, Rolle’s theorem can not be applied.
(ii) Let f x
x
x
( ) cos , [ , ]
= ∈ −
1
1 1
f f
( ) cos( ) cos , ( ) cos
− = − = =
1 1 1 1 1 ∴ f f
( ) ( )
− =
1 1
But f is not continuous at x = 0. So, ′
f ( ) .
0 does not exist
∴ Rolle’s theorem can not be applied
(iii) Let f x x x
( ) , [ , ]
= ∈
2
2 3 and f is continuous and differentiable on [2, 3]
But f ( )
2 2 4
2
= = and f f f
(3) 3 (2) (3).
= ∴
2
9
= ≠
Hence, Rolle’s theorem can not be applied.
(iv) Let f x x x
( ) tan ,
= ≤ ≤
0 p
When x x
= = = ∞
p p
2 2
, tan tan and so, the function f x
( ) is discontinuous at
p
2
.
Hence, first condition is not satisfied.
But f f
( ) ( )
0 0 0
= =
and p ∴ f f
( ) ( ).
0 = p
Hence, Rolle’s theorem can not be applied.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part A.indd 44 5/19/2016 5:03:09 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-267-2048.jpg)
![Differential Calculus ■ 3.45
EXAMPLE 2
If a0
, a1
, a2
, … an
are real numbers such that
a
n
a
n
a
n
a
a
n
n
0 1 2 1
1 1 2
0
1
1 1
2
1 1 1 5
2
… , then there
exists at least one x in (0, 1) such that a x a x a x a x a
n n n
n n
0 1
1
2
2
1 0.
1 1 1 1 1 5
2 2
2
…
Solution.
Consider the function
f x a
x
n
a
x
n
a
x
n
a
x
a x x
n n n
n n
( ) , ,
=
+
+ +
−
+ + + ∈[ ]
+ −
−
0
1
1 2
1
1
2
1 1 2
0 1
…
Then f(0) = 0
and f
a
n
a
n
a
n
a
a
n
n
( )
1
1 1 2
0
0 1 2 1
=
+
+ +
−
+ + + =
−
… [Given]
∴ f f
( ) ( ).
0 1
=
Since f(x) is a polynomial, it is continuous in [0,1] and differentiable in (0, 1).
So, all the conditions of Rolle’s theorem are satisfied.
Hence, by Rolle’s theorem, there exists at least one x ∈( , )
0 1 such that f′(x) = 0.
But ′ =
+
+
+ +
−
−
+ + +
− −
−
f x a
n x
n
a
nx
n
a
n x
n
a
x
a
n n n
n n
( )
( ) ( )
0 1
1
2
2
1
1
1
1
1
2
2
…
= + + + + +
− −
−
a x a x a x a x a
n n n
n n
0 1
1
2
2
1
…
∴ a x a x a x a x
n n
n n
0 1
1
1 0 0 1
+ + + + = ∈
−
−
… for at least one ( , ).
EXAMPLE 3
Using Rolle’s theorem, prove that there is no real a for which the equation x x a
2
3 0
2 1 5 has
two different roots in [ 1, 1].
2
Solution.
Suppose there is a real a for which x x a
2
3 0
− + = has two different roots a b
, in [−1, 1].
Then the interval [ , ]
a b is contained in the interval [−1, 1]
i.e., [a, b] ⊆ [−1, 1].
Consider f x x x a x
( ) . [ , ].
= − + ∈
2
3 a b
Since f x
( ) is a polynomial in x, it is continuous and differentiable in (a b
, ).
Given a and b are the roots of f(x) = 0.
∴ f f
( ) ( )
a b
= =
0 0
and ⇒ f f
( ) ( ).
a b
=
So, the condition of Rolle’s theorem are satisfied by f(x) in [ a b
, ].
∴ by Rolle’s theorem, there exists at least one c ∈[ , ]
a b such that ′ =
f c
( ) 0 .
Now ′ = −
f x x
( ) 2 3 ∴ f c c
′( ) = −
2 3
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 45 5/19/2016 1:07:04 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-268-2048.jpg)
![3.46 ■ Engineering Mathematics
and ′ = ⇒ − = ⇒ =
f c c c
( ) .
0 2 3 0
3
2
But c c
= ∉ −
[ ] ∉
3
2
1 1
, [ , ]
andso, a b .
This is a contradiction. So, our assumption is wrong
i.e., there is no a for which x x a
2
3 0
− + = has two different roots in [−1, 1].
EXAMPLE 4
Prove that between any two roots of e x
x
sin 1
5 , there is at least one root of e x
x
cos 1 0
1 5 .
Solution.
Let a and b be any two roots of e x
x
sin = 1.
∴ e e
a a
a a
sin sin
= ⇒ = −
1 and e e
b b
b b
sin sin
= ⇒ = −
1
⇒ e−
− =
a
a
sin 0 and e−
− =
b
b
sin .
0 (1)
Consider the function f x e x x
x
( ) sin , [ , ]
= − ∈
−
a b
Then f e
( ) sin
a a
a
= − =
−
0 and f e
( ) sin
b b
b
= − =
−
0
∴
f f
( ) ( ).
a b
=
Since e x
−
and sinx are continuous in [ , ]
a b and differentiable in ( a b
, ),
f x
( )is continuous in [ , ]
a b and differentiable in ( a b
, ).
Hence, all the conditions of Rolle’s theorem are satisfied.
∴ by Rolle’s theorem, there is a c ∈( , )
a b such that ′ =
f c
( ) 0
But ′ = − −
−
f x e x
x
( ) cos ∴ f c e c
c
′( ) cos
= − −
−
∴ f c e c e c e c
c c c
′( ) cos cos cos .
= ⇒ − − = ⇒ − − = ⇒ + =
−
0 0 1 0 1 0
∴ c is a root of e x c
x
cos ( , )
+ = ∈
1 0 and a b
Thus, between any two roots of e x
x
sin = 1, there is a root of e x
x
cos + =
1 0.
EXAMPLE 5
If f x
x
x
x
( )
sin sin sin
cos cos cos
tan tan tan
, 0
2
5
a b
a b
a b
a b
p
. Show that ′
f x
( ) 0
5 has a root between a and b.
Solution.
Consider f(x) in [a, b].
∴
f ( )
sin sin sin
cos cos cos
tan tan tan
a
a a b
a a b
a a b
= = 0
[{ C1
= C2
]
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 46 5/19/2016 1:07:09 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-269-2048.jpg)
![Differential Calculus ■ 3.47
and f ( )
sin sin sin
cos cos cos
tan tan tan
b
b a b
b a b
b a b
= = 0 [{ C1
= C3
]
∴ f f
( ) ( )
a b
=
Since sinx, cosx, tanx are continuous and differentiable in 0
2
,
p
⎛
⎝
⎜
⎞
⎠
⎟ and [ , ] ,
a b
p
⊂
⎛
⎝
⎜
⎞
⎠
⎟
0
2
, it follows
that f(x) is continuous and differentiable in ( , )
a b .
So, all the three conditions of Rolle’s theorem are satisfied by f(x) in [ , ]
a b .
∴ by Rolle’s theorem, there is a c ∈( , )
a b such that ′ =
f c
( ) 0 .
⇒ f x
′( ) = 0 has a root c between α and β.
3.3.2 Lagrange’s Mean Value Theorem
Let f be a real function defined on the closed interval [ , ]
a b such that
(i) f is continuous on [ , ]
a b and (ii) f is derivable in the open interval (a, b).
Then there exists at least one point c a b
∈( , ) such that
′
f c
f b f a
b a
( )
( ) ( )
5
2
2
Proof Consider F x f x Ax x a b
( ) ( ) , [ , ]
= + ∈ , where A is chosen such that
F a F b
( ) ( )
=
Since f and x are continuous on [a, b] and derivable in (a, b), F is continuous on [a, b] and derivable
in (a, b).
Further F a F b
( ) ( )
=
⇒ F a Aa F b Ab
( ) ( )
+ = +
⇒ A a b f b f a
( ) ( ) ( )
− = − ⇒ A
f b f a
b a
= −
−
[ ]
−
( ) ( )
. (1)
So, F satisfies all the conditions of Rolle’s theorem on [a, b].
∴ by Rolle’s theorem, there exists at least one c a b
∈( , ) such that ′ =
F c
( ) 0 .
But ′ = ′ +
F x f x A
( ) ( ) ∴ ′ = ′ +
F c f c A
( ) ( )
∴ ′ =
F c
( ) 0 ⇒ ′ + =
f c A
( ) 0 ⇒ ′ = −
f c A
( )
⇒ ′ =
−
−
f c
f b f a
b a
( )
( ) ( )
[using (1)]
Geometrical meaning of Lagrange’s Mean Value Theorem
If y f x
= ( ) is a continuous curve with A and B as end points and at each point between A and B, the
curve has a tangent, then there is atleast one point P on the curve between A and Bat which the tangent
is parallel to the chord AB.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 47 5/19/2016 1:07:15 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-270-2048.jpg)
![3.48 ■ Engineering Mathematics
A is (a, f(a)) and B is (b, f(b). So, slope of chord AB
f b f a
b a
=
−
−
( ) ( )
.
Slope of the tangent at the point P c f c
( , ( )) is f c
′( )
y
o a c b x
A
B
P
y
o a b x
A
B
Fig. 3.8 Fig. 3.9
∴ f c
f b f a
b a
′( )
( ) ( )
.
=
−
−
Physical meaning of Lagrange’s Mean Value Theorem
The instantaneous rate of change of f at some point between a and b is equal to the average rate of
change of f on [a, b].
Another form of Lagrange’s Mean Value Theorem
If b a h
− = , then b a h h
= +
, 0, then c a b c a h
∈ ⇒ = +
( , ) , .
u u
0 1
Lagrange’s mean value theorem is
′ + =
+ −
f a h
f a h f a
h
( )
( ) ( )
u
⇒ f a h f a hf a h
( ) ( ) ( ), .
+ = + ′ +
u u
0 1
Deductions of Lagrange’s Mean Value Theorem
(1) Iff isacontinuousonaclosedinterval[a,b]andderivablein(a,b)suchthat ′ = ∀ ∈
f x x a b
( ) ( , )
0 ,
then f is constant on [a, b].
i.e., f x k x a b
( ) [ , ]
= ∀ ∈
In particular, f x f a x a b
( ) ( ) [ , ]
= ∀ ∈
(2) If f and g are real functions which are continuous on [a, b] and derivable in (a, b) such that
′ = ′ ∀ ∈
f x g x x a b
( ) ( ) ( , ), then
f x g x k x a b
( ) ( ) [ , ],
− = ∀ ∈ where k is a constant.
(3) If f is continuous at c and if lim ( )
x c
f x l
→ −
′ = and lim ( ) ,
x c
f x l
→ +
=
′ then ′
f c
( ) exists and ′ =
f c l
( ) .
Proof Given lim ( )
x c
f x l
→
=
′
∴ lim ( )
x c
f x l
→ −
=
′ and lim ( ) .
x c
f x l
→ +
=
′
a c a + h
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 48 5/19/2016 1:07:20 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-271-2048.jpg)
![Differential Calculus ■ 3.49
Consider lim ( ) .
x c
f x l
→ +
=
′
So, there exists an interval ( , ),
c c h h
+ 0 where ′
f x
( ) exists for every x c c h
∈ +
( , ).
∴ f is continuous in [ , ]
c c h
+ .
If x is a point in this interval., by Lagrange’s mean value theorem
f x f c
x c
f t c t x
( ) ( )
( ), .
−
−
= ′
lim
( ) ( )
lim ( ) lim ( )
x c x c x c
f x f c
x c
f t f x l
→ + → + →
−
−
= ′ = ′ =
+
⇒ ′ =
+
f c l
( )
Similarly, we can prove that
f c l f c l
′ ′
( ) ( ) .
− = ∴ =
WORKED EXAMPLES
EXAMPLE 1
Find c of Lagrange’s mean value theorem for the following functions
(i) x x x
( 1)( 2) in 0,
1
2
2 2
⎡
⎣
⎢
⎤
⎦
⎥
(ii) x x
3
in [1,2].
1
Solution.
(i) Let f(x) = x(x − 1) (x − 2), x ∈ 0
1
2
,
⎡
⎣
⎢
⎤
⎦
⎥. (1)
Since f(x) is a polynomial function, it is continuous on 0
1
2
,
⎡
⎣
⎢
⎤
⎦
⎥ and differentiable in 0
1
2
,
⎛
⎝
⎜
⎞
⎠
⎟ .
So, the conditions of Lagrange’s mean value theorem are satisfied.
∴ by Lagrange’s mean value theorem, there exists c ∈ 0
1
2
,
⎛
⎝
⎜
⎞
⎠
⎟ such that
f c
f b f a
b a
′( )
( ) ( )
=
−
−
(2)
Here a b
= =
0
1
2
, . Now f(a) = f(0) = 0
and f(b) = f
1
2
⎛
⎝
⎜
⎞
⎠
⎟ =
1
2
1
2
1
1
2
2
−
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟ = −
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟ =
1
2
1
2
3
2
3
8
.
Differentiating (1) w.r.to x, we get
f x x x x x x
x x x x x x
′ ⋅ ⋅ ⋅
( ) {( ) ( ) } ( )( )
= − + − + − −
= − + − + − + =
1 1 2 1 1 2 1
2 3 2 3
2 2 2
x
x x
2
6 2
− +
∴ f c c c
′( ) = − +
3 6 2
2
c x c + h
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 49 5/19/2016 1:07:25 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-272-2048.jpg)
![3.50 ■ Engineering Mathematics
∴ (1) ⇒ 3 6 2
3
8
0
1
2
0
3
4
2
c c
− + =
−
−
= ⇒ 3 6
5
4
0
2
c c
− + =
∴
c =
± −
=
± −
=
±
= ± = ±
6 36 4 3
5
4
6
6 36 15
6
6 21
6
1
21
6
1 0 76
⋅ ⋅
. .
Clearly, 1 0 76 1 76 0
1
2
0
1
2
+ = ∉
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
. . , ,
and 1 0.76 = 0.24 ∈ ∴ c = 0 24
.
(ii) Let f x x x x
( ) , [ , ]
= +
3
1 2
∈ .
Since f(x) is a polynomial, it is continuous on [1, 2] and differentiable in (1, 2).
So, the conditions of Lagrange’s mean value theorem are satisfied.
∴ by Lagrange’s mean value theorem, there exists a c ∈( , )
1 2 such that
′ =
−
−
f c
f b f a
b a
( )
( ) ( )
(1)
Here a =1, b = 2.
Now f(1) = 1 + 1 = 2 and f (2) = 23
+ 2 = 10
f x x
′( ) = +
3 1
2
∴ f c c
′( ) = +
3 1
2
∴ (1) ⇒ 3 1
10 2
2 1
8
2
c + =
−
−
= ⇒ 3 7 0
2
c − = ⇒ c c
2 7
3
7
3
1 53
= ⇒ = ± = ± . .
But c = − ∉
1 53 1 2
. ( , ) and c = ∈
1 53 1 2
. ( , ) ∴ c =
7
3
EXAMPLE 2
Using Lagrange’s mean value theorem prove that tan tan
1 1
2 2
b2 a b2 a
, where b a
.
Solution.
Consider f x x x
( ) tan , [ , ]
= ∈
−1
a b . Clearly [ , ] ,
a b
p p
⊆ −
⎛
⎝
⎜
⎞
⎠
⎟
2 2
Since tan−1
x is continuous on [ , ]
a b and ′ =
+
f x
x
( ) ,
1
1 2
f x
( ) is continuous on [ , ]
a b and
differentiable in ( , ).
a b
So, the condition of Lagrange’s mean value theorem are satisfied.
∴ by Lagrange’s mean value theorem, there exists c ∈( , )
a b such that
′ =
−
−
f c
f b f a
b a
( )
( ) ( )
. (1)
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 50 5/19/2016 1:07:30 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-273-2048.jpg)
![Differential Calculus ■ 3.51
Here a b
= =
a b
, .
∴ f f
( ) tan ( ) tan
a a b b
= =
− −
1 1
, and ′ =
+
f c
c
( )
1
1 2
∴ (1) ⇒
1
1 2
1 1
+
=
−
−
− −
c
tan tan
b a
b a
⇒ tan tan
− −
− =
−
+
1 1
2
1
b a
b a
c
Since 0
1
1
1 0
2
+
−
c
and b a , we have 0
1 2
−
+
−
b a
b a
c
.
∴ tan tan .
− −
− −
1 1
b a b a b a
if
Note In particular, if a b
= = − −
− −
0 0 0
1 1
, , ,
x x x
then tan tan ⇒ tan , .
−
1
0
x x x
if
EXAMPLE 3
If 0 ,
a b then prove that
b a
b
b a
b a
a
2
1
2
2
1
2 2
1
tan tan
1
.
2
1 1
2
Deduce that
(i)
4
3
25
tan
4
3 4
1
6
(ii)
4
1
5
tan 2
4
1
2
.
1 1
p
1
p
1
p
1
p
1
2 2
Solution.
Consider the function f x x x a b
( ) tan , [ , ]
= ∈
−1
. Then ′ =
+
∈
f x
x
x a b
( ) , ( , ).
1
1 2
Clearly f x
( ) is continuous on [ , ]
a b and differential in ( , ).
a b
So, the conditions of Lagrange’s mean value theorem are satisfied.
∴ by Lagrange’s mean value theorem, there exists c a b
∈( , ), such that
f c
f b f a
b a
′( )
( ) ( )
=
−
−
(1)
where f a a f b b
( ) tan , ( ) tan
= =
− −
1 1
and ′ =
+
f c
c
( )
1
1 2
∴ (1) ⇒
1
1 2
+ c
=
tan tan
− −
−
−
1 1
b a
b a
⇒
b a
c
b a
−
+
= −
− −
1 2
1 1
tan tan (2)
Since a c b a b c
and , , are positive numbers, a c b
2 2 2
.
∴ 1 1 1
2 2 2
+ + +
a c b ⇒
1
1
1
1
1
1
2 2 2
+
+
+
a c b
.
We have b a b a
∴ −
. .
0
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 51 5/19/2016 1:07:37 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-274-2048.jpg)

To deduce (i): Put a = 1 and b =
4
3
in (3)
∴
4
3
1
1
16
9
4
3
1
4
3
1
1 1
1 1
−
+
−
−
+
− −
tan tan
⇒
3
25
4
3 4
1
6
1
−
−
tan
p
⇒
p p
4
3
25
4
3 4
1
6
1
+ +
−
tan .
To deduce (ii): Put a = 1 and b = 2 in (3)
∴
2 1
1 4
2 1
2 1
1 1
1 1
−
+
−
−
+
− −
tan tan
⇒
1
5
2
4
1
2
1
−
−
tan
p
⇒
p p
4
1
5
2
4
1
2
1
+ +
−
tan .
EXAMPLE 4
If f R
:[0, 4] → is differentiable, then prove that [ (4)] [ (0)] 8 ( ) ( )
2 2
f f f a f b
2 5 ′
for a b
, (0, 4)
∈ .
Solution.
Given f is a real function defined on [ , ]
0 4 and differentiable and so it is continuous on [ , ]
0 4 .
So, the conditions of Lagrange’s mean value theorem are satisfied.
∴ by Lagrange’s mean value theorem, there exists a ∈( , )
0 4 , such that
′ =
−
−
f a
f f
( )
( ) ( )
4 0
4 0
. ⇒ f f f a
( ) ( ) ( )
4 0 4
− = ′ . (1)
Since f is continuous on [ , ]
0 4 , it takes all values between its maximum and minimum values.
In particular, there is b ∈( , )
0 4 such that f f
f b
( ) ( )
( )
4 0
2
+
= .
⇒ f f f b
( ) ( ) ( )
4 0 2
+ = (2)
( ) ( )
1 2
× ⇒ [ ( ) ( )][ ( ) ( )] ( ) ( )
f f f f f a f b
4 0 4 0 4 2
− + = ′
⇒ [ ( )] [ ( )] ( ) ( ), , ( , )
f f f a f b a b
4 0 8 0 4
2 2
− = ′ ∈ .
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 52 5/19/2016 1:07:42 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-275-2048.jpg)
![Differential Calculus ■ 3.53
3.3.3 Cauchy’s Mean Value Theorem
Let f and g be two functions defined on [a, b] such that
(i) f and g are continuous on [a, b] (ii) f and g are differentiable in (a, b)
and (iii) g x x a b
′ ≠ ∈
( ) ( , )
0 ∀ .
Then, there exists at least one c a b
∈( , ) such that
f c
g c
f b f a
g b g a
′
′
( )
( )
( ) ( )
( ) ( )
5
2
2
.
Proof Consider the function F x f x Ag x x a b
( ) ( ) ( ), [ , ]
= + ∈
where A is chosen such that F a F b
( ) ( )
=
⇒ f a Ag a f b Ag b
( ) ( ) ( ) ( )
+ = +
⇒ A g a g b f b f a
[ ( ) ( )] ( ) ( )
− = −
⇒ A
f b f a
g a g b
=
−
−
( ) ( )
( ) ( )
⇒ A
f b f a
g b g a
= −
−
−
[ ( ) ( )]
( ) ( )
(1)
Since f and g are continuous on [a, b] and differentiable in (a, b), F is continuous on [a, b] and
differentiable in (a, b) and F(a) = F(b).
So, F satisfies the conditions of Rolle’s theorem.
∴ by Rolle’s theorem, there exists c a b
∈( , ) such that F c
′( ) = 0.
But F x f x Ag x
′ ′ ′
( ) ( ) ( )
= + ⇒ F c f c Ag c
′ ′ ′
( ) ( ) ( )
= +
∴ F c
′( ) = 0 ⇒ ′ + =
f c Ag c
( ) ( )
′ 0 ⇒ f c Ag c
′ ′
( ) ( )
= − ⇒
f c
g c
A
′
′
( )
( )
= −
∴
f c
g c
′
′
( )
( )
=
−
−
f b f a
g b g a
( ) ( )
( ) ( )
[using (1)].
Corollary: If f(a) = 0, g(a) = 0, then
f c
g c
f b
g b
a c b
′
′
( )
( )
( )
( )
, .
=
Note The corollary can be algebraically interprepted as below:
If the polynomial equations f(x) = 0, g(x) = 0 have a common root a, then
f x
g x
f c
g c
( )
( )
( )
( )
=
′
′
for some c a x
∈( , ) .
Formula:
1. If F x
f x f x f x
g x g x g x
h x h x h x
( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
=
1 2 3
1 2 3
1 2 3
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 53 5/19/2016 1:07:47 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-276-2048.jpg)
![3.54 ■ Engineering Mathematics
where fi
, gi
, hi
, i = 1, 2, 3 are differentiable functions of x, then
F x
f x f x f x
g x g x g x
h x h x h x
f
′( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
(
=
′ ′ ′
+
1 2 3
1 2 3
1 2 3
1 x
x f x f x
g x g x g x
h x h x h x
f x f x f
) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( )
2 3
1 2 3
1 2 3
1 2
′ ′ ′ +
3
3
1 2 3
1 2 3
( )
( ) ( ) ( )
( ) ( ) ( )
x
g x g x g x
h x h x h x
′ ′ ′
2. If F x
f x f x
g x g x
( )
( ) ( )
( ) ( )
= 1 2
1 2
, then F x
f x f x
g x g x
f x f x
g x g x
′( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
.
=
′ ′
+
′ ′
1 2
1 2
1 2
1 2
The formula can be used column wise also.
WORKED EXAMPLES
EXAMPLE 1
Verify Cauchy’s mean value theorem for f(x) 5 x3
, g(x) 5 x2
in [1, 2].
Solution.
Given f(x) = x3
and g(x) = x2
in [1, 2].
f (x), g(x) being polynomials, they are continuous on [1, 2] and differentiable in (1, 2)
and g x x
′( ) = ≠
2 0 for ∀x ∈( , )
1 2
So, all the conditions of Cauchy’s mean value theorem are satisfied.
∴by Cauchy’s mean value theorem, there exists c ∈( , )
1 2 such that
f c
g c
f b f a
g b g a
′
′
( )
( )
( ) ( )
( ) ( )
.
=
−
−
(1)
Here a = 1, b = 2.
∴ f(a) = 1 and f(b) = 23
= 8, g(a) = 1 and g(b) = 22
= 4
f x x
′( ) = 3 2
and g x x
′( ) = 2 ∴ f c c
′( ) = 3 2
and g c c
′( ) = 2
∴(1) ⇒
3
2
8 1
4 1
7
3
2
c
c
=
−
−
= ⇒
3
2
7
3
c = ⇒ c =
14
9
1 2
∈( , )
Hence, the theorem is verified.
EXAMPLE 2
Verify Cauchy’s mean value theorem and find c, if f x e g x e x a b
x x
( ) , ( ) , [ , ].
5 5 2
∈
Solution.
Given f x e g x e x a b
x x
( ) ( ) , [ , ]
= = −
and ∈ .
Both f and g are continuous on [a, b] and differentiable in (a, b) and g x e x a b
x
′ ∈
( ) ( , )
= − ≠ ∀
−
0 .
So, all the conditions of Cauchy’s mean value theorem are satisfied.
∴ by Cauchy’s mean value theorem, there exists c in (a, b) such that
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 54 5/19/2016 1:07:51 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-277-2048.jpg)
![Differential Calculus ■ 3.55
f c
g c
f b f a
g b g a
′
′
( )
( )
( ) ( )
( ) ( )
=
−
−
. (1)
But f(a) = ea
and f(b) = eb
, g a e a
( ) = −
and g b e b
( ) = −
f x ex
′( ) = and g x e x
′( ) = − −
∴ f c ec
′( ) = and ′ = − −
g c e c
( )
∴ (1) ⇒
e
e
e e
e e
c
c
b a
b a
−
=
−
−
− − −
⇒ − =
−
−
=
−
−
e
e e
e e
e e
e e
e e
c
b a
b a
b a
a b
a b
2
1 1
⋅ ⋅ = − +
ea b
⇒ e e
c a b
2
= +
∴ 2
2
c a b c
a b
a b
= + ⇒ =
+
∈( , )
Hence, the theorem is verified.
EXAMPLE 3
If 0
2
a b
p
, using Cauchy’s mean value theorem, prove that
sin sin
cos cos
cot
a 2 b
b2 a
5 u for
some u a b
∈( )
, .
Solution.
Consider the functions f(x) = sin x and g(x) = cos x, x ∈[ ],
a b
, where [ , ]
a b ⊆ 0
2
,
p
⎛
⎝
⎜
⎞
⎠
⎟
Boththefunctions f and g arecontinuouson [ , ]
a b anddifferentiablein( , )
a b and ′ = − ≠
g x x
( ) sin 0
in ( , )
a b .
So, all the conditions of Cauchy’s mean value theorem are satisfied.
∴ by Cauchy’s mean value theorem there exists u ∈( , )
a b such that
′
′
=
−
−
f
g
f f
g g
( )
( )
( ) ( )
( ) ( )
u
u
b a
b a
(1)
But f ( ) sin
a a
= and f ( ) sin
b b
= ; g g
( ) cos ( ) cos
a a b b
= =
and
′ =
f x x
( ) cos and ′ = −
g x x
( ) sin . ∴ ′ =
f ( ) cos
u u and ′ = −
g ( ) sin
u u
∴ (1) ⇒ cos
sin
sin sin
cos cos
u
u
b a
b a
−
=
−
−
⇒ − =
−
−
cot
sin sin
cos cos
u
b a
b a
⇒
sin sin
cos cos
cot
a b
b a
u
−
−
= , u a b
∈[ , ].
EXAMPLE 4
Using mean value theorem, show that x x x
x
e
+ −
log (1 )
2
2
if x 0.
Solution.
Consider the function f(x) = loge
(1 + x), x ≥ 0
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 55 5/19/2016 1:08:00 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-278-2048.jpg)
![3.56 ■ Engineering Mathematics
∴ f x
x
f x
x
x
′
+
′′ = −
( ) , ( )
( )
,
=
+
1
1
1
1
0
2
We know that f(x) = f(0) + xf ′(ux), 0 u 1
∴ f(0) = log(1 + 0) = 0, f x
x
′ =
( )
u
u
1
1+
∴ loge
(1 + x) = 0
1
1 1
+
+
=
+
x
x
x
x
u u
Since u 0, x 0, 1 + ux 1 ⇒
1
1
1
1
+ +
u u
x
x
x
x
⇒ (1)
∴ loge
(1 + x) x ⇒ x loge
(1 + x) (2)
Again f x f xf
x
f x
( ) ( ) ( ) ( )
= + ′ + ′′
0 0
2
2
u , up to second derivative 0 u 1
But f ′(0) = 1, f ″(ux) = −
+
1
1 2
( )
ux
∴ log
( )
,
e x x
x
x
x
x
x
1 0 1
2
1
1 2 1
0 1
2
2
2
2
+
( ) = + + −
+
( )
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
= −
+
⋅
u u
u
⇒ loge
(1 + x) − x = −
+
x
x
2
2
2 1
( )
u
(1) ⇒
x
x
x
x
x
x
x
x
x
1 1 2 1 2
2
2
2
2
2
2
+ u u u
⇒
+
⇒ −
+
−
( ) ( )
∴ loge
(1 + x) – x − ⇒ −
x
x x
x
e
2 2
2
1
2
log ( )
+ (3)
From (2) and (3), we get x x x
x
e
+ −
log ( )
1
2
2
if x 0.
EXERCISE 3.7
I. Verify Rolle’s theorem for the following functions.
1. f x x x x x
( ) , ,
= + − − ∈ − −
⎡
⎣
⎢
⎤
⎦
⎥
2 4 2 2
1
2
3 2
. 2. f x e x x
x
( ) cos , ,
= ∈ −
⎡
⎣
⎢
⎤
⎦
⎥
p p
2 2
3. f x x x
( ) , [ , ]
= − ∈ −
4 2 2
2
4. f x x x
( ) sin , [ , ]
= ∈
2
0 p
5. f x x x
( ) , [ , ]
= − ∈ −
1 1 1
4
5
6. f x
x x
x x
( )
,
,
=
+ ≤ ≤
− ≤
⎧
⎨
⎩
2
1 0 1
3 1 2
7. f x a x b
m n
( ) ( ) ( )
x = − − where m and n are positive integers.
8. f x x a x n
( ) ( )
= −
−
2 1 2
n
in [0, a]. 9. f x
x ab
x a b
e
( ) log
( )
=
+
+
2
in [a, b], a, b 0.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 56 5/19/2016 1:09:06 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-279-2048.jpg)
![Differential Calculus ■ 3.57
II. 1. Find c of Rolle’s theorem for the function f x e x x x
x
( ) (sin cos ), ,
= − ∈
⎡
⎣
⎢
⎤
⎦
⎥
p p
4
5
4
2. Considering the function f x x x
e
( ) ( )log ,
= − 2 show that the equation x x
e
log x = −
2 has a root
between 1 and 2.
3. Apply Rolle’s theorem for sin cos
x x
2 and find x such that 0
4
x
p
.
III. Verify Lagrange’s mean value theorem for the following functions.
1. f x x x x x
( ) ( )( )( ), [ , ]
= − − − ∈
1 2 4 0 4 2. f x x x
( ) , [ , ]
= ∈ −
2 3
1 1
3. f x
x
x
x
x
( )
cos ,
,
[ , ]
=
≠
=
⎧
⎨
⎪
⎩
⎪
−
1
0
0 0
1 1
in 4. f(x) = loge
x in [1, e].
IV.
1. Verify Lagrange’s mean value theorem and find the point on the curve y
x
x
=
−
1
between the
points A(2, −2) and B 5
5
4
,
−
⎛
⎝
⎜
⎞
⎠
⎟ at which the tangent is parallel to the chord AB.
2. Prove that
p p
3
1
5 3
3
5 3
1
8
1
− −
−
cos by Lagrange’s mean value theorem.
3. For any two real numbers a and b (a b), prove that a2
+ ab + b2
= 3c2
, for some c ∈ (a, b) using
Lagrange’s mean value theorem.
4. For the quardratic function f ( ) , ( , )
x lx mx n x a b
= + + ∈
2
, find u of Lagrange’s mean value
theorem.
5. If f(x) and g(x) are continuous on a ≤ x ≤ b and derivable in a x b, then prove that
f a f b
g a g b
b a
f a f c
g a g c
( ) ( )
( ) ( )
( )
( ) ( )
( ) ( )
= −
′
′
. [Hint: Consider f(x) =
f a f x
g a g x
( ) ( )
( ) ( )
, x ∈ [a, b].
6. For what values of a, m, b does the function f x x x a
( ,
)
,
,
=
=
+ +
+ ≤ ≤
⎧
⎨
⎪
⎩
⎪
3 0
3 0 1
1 2
2
x
x
mx b x
−
satisfy the hypothesis of Lagrange’s mean value theorem on the interval [0, 2].
7. Find u of Lagrange’s mean value theorem for f x x x x
( ) , [ , ]
= − + ∈
3 2 4 2 3
2
V. Using Lagrange’s mean value theorem, prove the following
1.
x
x
x x x
e
1
1 0
+
+
log ( ) , 2. 0
1
1
1
1 0
+
−
log ( )
,
e x x
x
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 57 5/19/2016 1:09:09 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-280-2048.jpg)
![3.58 ■ Engineering Mathematics
3. 0
1 1
1 0
−
x
e
x
x
e
x
log , [Hint: Take f x ex
( ) = in [0, x]]
4. If f x x
( ) cos
= , applying Lagrange’s mean value theorem in [ , ]
0 h prove that lim
x → +
=
0
1
2
u .
[Hint: f h f hf h
( ) ( ) ( ),
= + ′
0 0 1
u u ]
ANSWERS TO EXERCISE 3.7
II. 1. c = p, 3. x =
p
6
IV
. 1. 3
3
2
, −
⎛
⎝
⎜
⎞
⎠
⎟ 4. u =
1
2
6. a = 3, b = 4, m = 1 7. u =
1
2
3.4 MONOTONIC FUNCTIONS
Monotonic functions form an important class of functions in Mathematics. Because most of the
functions that occur in various fields, in practice, are monotonic functions or sum of monotonic
functions.
It will be seen that all bounded monotonic functions are integrable. In this section, we use mean
value theorems to deduce the properties of monotonic functions, using sign of derivative.
3.4.1 Increasing and Decreasing Functions
Definition 3.1 Let f be a function defined on [ , ]
a b .
If for every pair of points x x a b
1 2
, [ , ]
∈
(i) x x f x f x
1 2 1 2
⇒ ≤
( ) ( ), then f is increasing (or non−decreasing) on [a, b].
(ii) x x f x f x
1 2 1 2
⇒ ( ) ( ), then f is strictly increasing on [a, b].
(iii) x x f x f x
1 2 1 2
⇒ ( ( )
) ≥ , then f is decreasing (or non−increasing) on [a, b].
(iv) x x f x f x
1 2 1 2
⇒
( ) ( ) , then f is strictly decreasing on [a, b].
A function f which is either increasing or decreasing on [a, b] is called a monotonic function on [a, b].
If f is strictly increasing or strictly decreasing on [a, b], then f is called strictly monotonic.
3.4.2 Piece−wise Monotonic Function
Definition 3.2 A function f is said to be piece−wise monotonic on [a, b] if the interval [a, b] can
be partitioned into finite number of sub−intervals such that in each of the open sub−intervals f is
monotonic
That is f is piece−wise monotonic on [a, b] if its graph consists of a finite number of monotonic
pieces.
Note
(1) A characteristic property of monotonic function is that it has it finite left and right limits at each
interior point.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 58 5/19/2016 1:09:12 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-281-2048.jpg)
![Differential Calculus ■ 3.59
If f is increasing on [a, b] and c a b
∈( , ), then f c
( )
− and f c
( )
+ exist and
f c f c f c
( ) ( ) ( )
− ≤ ≤ +
Further f a f a
( ) ( )
≤ + and f b f b
( ) ( )
− ≤ .
(2) If f is strictly increasing and continuous on [a, b], then f a b f a f b
:[ , ] [ ( ), ( )]
→ is bijective and
f f a f b a b
−
→
1
:[ ( ), ( )] [ , ] exists and f −1
is continuous and strictly increasing on [ ( ), ( )]
f a f b .
Similarly, we can state (1) and (2) for decreasing functions.
3.4.3 Test for Increasing or Decreasing Functions
Theorem 3.2 Let f be continuous on the closed interval [ , ]
a b and let f9(x) exist for each point
x a b
∈( , ) .
y
x
b
a
o
Increasing
Fig. 3.10
y
x
o
Strictly increasing
Fig. 3.11
y
x
D
a
o
Strictly increasing
Fig. 3.12
y
x
a b
o
Decreasing
Fig. 3.13
y
x
b
a
o
Strictly decreasing
Fig. 3.14
y
e x
a c
o
b d
Piece-wise monotonic
Fig. 3.15
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 59 5/19/2016 1:09:17 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-282-2048.jpg)
![3.60 ■ Engineering Mathematics
(i) If ′
f x x a b
( ) 0 ( , )
. ; e , then f is strictly increasing on [a, b].
(ii) If ′ ≥
f x x a b
( ) 0 ( , )
; e , then f is increasing on [a, b].
(iii) If ′
f x x a b
( ) 0 ( , )
; e , then f is strictly decreasing on [a, b].
(iv) If ′ ≤
f x x a b
( ) 0 ( , )
; e , then f is decreasing on [a, b].
(v) If ′
f x x a b
( ) 0 ( , )
5 ; e , then f is constant on [a, b].
Proof Given f is continuous on [a, b] and f x
′( ) exists for each x a b
∈( , ).
Let x x a b
1 2
, [ , ]
∈ be any two points with x x
1 2
.
Applying Lagrange’s mean value theorem for f on [ , ]
x x
1 2 , there is c x x
∈( , )
1 2 such that
f c
f x f x
x x
′( )
( ) ( )
=
−
−
2 1
2 1
⇒ f x f x x x f c
( ) ( ) ( ) )
2 1 2 1
− = − ′( (1)
(i) Let ′
f c
( ) 0
Since ′
f c
( ) 0 and x x
2 1 0
− , we have from (1)
f x f x
( ) ( )
2 1 0
− ⇒
f x f x
( ) ( )
2 1 ⇒ f x f x
( ) ( )
1 2
Thus, x x
1 2
⇒
f x f x
( ) ( )
1 2 So, by definition, f is strictly increasing on [a, b]
(ii) Let ′ ≥
f c
( ) 0
Since ′ ≥
f c
( ) 0 and x x
1 2 0
− , we have from (1)
f x f x f x f x
( ) ( ) ( ) ( )
2 1 2 1
0
− ≥ ⇒ ≥ ⇒ f x f x
( ) ( )
1 2
≤
Thus, x x f x f x
1 2 1 2
⇒ ≤
( ) ( ) By definition, f is increasing on [a, b].
Similarly, we can prove (iii), (iv) and (v).
Corollary: If f and gare continuous functions on [a, b] such that f x g x x a b
′ ′
( ) ( ) ( , ),
= ∀ ∈ then
f x g x k x a b
( ) ( ) [ , ]
− = ∀ ∈ , where k is a constant.
WORKED EXAMPLES
EXAMPLE 1
Determine the interval of monotonicity of the following functions
(i) 2 9 24 7
3 2
x x x
2 2 1 (ii) 2 ln
2
x x.
2
Solution.
(i) Let f x x x x
( ) = − − +
2 9 24 7
3 2
∴ ′ = − − = − −
f x x x x x
( ) ( )
6 18 24 6 3 4
2 2
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 60 5/19/2016 1:09:24 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-283-2048.jpg)
![Differential Calculus ■ 3.61
∴ ′
f x
( ) 0 if ( )( )
x x
− +
4 1 0 ⇒ x −1 or x 4.
∴ the function is strictly increasing in the interval ( , ]
−∞ −1 and [ , )
4 ∞ .
⇒ ′
f x
( ) 0 if ( )( )
x x
− +
4 1 0 ⇒ −
1 4
x
∴ the function is strictly decresing in the interval − ≤ ≤
1 4
x .
(ii) Let g x x x x
( ) ,
= −
2 1 0
2
n ∴ ′ = −
g x x
x
( ) 4
1
[ log ]
{ 1nx x
e
=
and ′
g x
( ) 0 if 4
1
0
x
x
− ⇒ 4 1 0
2
x − ⇒ ( )( ) ,
2 1 2 1 0 0
x x x
+ − .
Since x x
+
0 2 1 0
, and so, 2 1 0
x − ⇒
x
1
2
.
∴ the function is strictly increasing in the interval
1
2
, ∞
⎡
⎣
⎢
⎞
⎠
⎟ .
Now ′
g x
( ) 0 if 4
1
0
x
x
− ⇒ 4 1 0
2
x − ⇒ ( )( )
2 1 2 1 0
x x
+ −
Since x x
+
0 2 1 0
, and so, 2 1 0
x − ⇒
x
1
2
.
∴ the function is strictly decreasing in the interval 0
1
2
≤
x .
EXAMPLE 2
Prove that x x x x
sin cos
1
2
cos2
1 1 is strictly increasing in 0,
2
p
⎛
⎝
⎜
⎞
⎠
⎟ .
Solution.
Let f x x x x x x
( ) sin cos cos ,
= + + ≤ ≤
1
2
0
2
2 p
.
∴ ′ = + ⋅ − + ⋅ −
f x x x x x x x
( ) cos sin sin cos ( sin )
1
1
2
2 = −
x x x x
cos cos sin
⇒ f x x x x
′( ) cos ( sin )
= − , 0
2
x
p
.
For 0
2
x
p
, cosx 0 and to decide the sign of x x
− sin , we consider the function
g x x x
( ) sin
= − in 0
2
≤ ≤
x
p
∴ ′ = −
g x x
( ) cos
1 = 2
2
0
2
sin
x
in 0
2
x
p
.
∴ g x
( ) is strictly increasing in 0
2
≤ ≤
x
p
.
− 1 4 ∞
−∞ x
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 61 5/19/2016 1:09:34 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-284-2048.jpg)
![3.62 ■ Engineering Mathematics
∴ g x g
( ) ( )
0 for x 0, x ∈
⎛
⎝
⎜
⎞
⎠
⎟
0
2
,
p
.
But g( ) sin
0 0 0 0
= − = ∴ g x
( ) 0 for x 0, in 0
2
x
p
Hence, ′
f x
( ) 0 in 0
2
x
p
. ∴ f x
( ) is strictly increasing in 0
2
,
p
⎛
⎝
⎜
⎞
⎠
⎟ .
EXAMPLE 3
If f x
x
x
x
x
( ) sin
, 0
2
1, 0
5
p
5
≤
⎧
⎨
⎪
⎩
⎪
then prove that (i) f is strictly increasing in 0,
2
p
⎡
⎣
⎢
⎤
⎦
⎥ and (ii) 1
sin 2
x
x
p
.
Solution.
Given f x
x
x
x
x
( ) sin
,
,
=
≤
=
⎧
⎨
⎪
⎩
⎪
0
2
1 0
p
lim ( ) lim
sin
x x
f x
x
x
→ + → +
= =
0 0
1 and f f x f
x
( ) lim ( ) ( )
0 1 0
0
= ⇒ =
→ +
∴ the function is continuous at x = 0 from the right and hence continuous in the interval 0
2
,
p
⎡
⎣
⎢
⎤
⎦
⎥.
Now ′ =
⋅ − ⋅
f x
x x x
x
( )
sin cos
sin
1
2
= −
cos
sin
[tan ]
x
x
x x
2
, 0
2
x
p
.
For 0
2
x
p
,
cos
sin
x
x
2
0
and to decide the sign of tan x x
− , we consider the function
g x x x
( ) tan
= − in 0
2
≤
x
p
∴ ′ = −
g x x
( ) sec2
1 =
tan2
0
x in 0
2
x
p
.
∴ g x
( ) is strictly increasing in 0
2
≤
x
p
. So, g x g
( ) ( )
0 for x 0.
But g(0) = tan0 − 0, ∴ g x
( ) 0 ⇒ tan x x
− 0 for 0
2
x
p
.
Hence, ′
f x
( ) 0 for 0
2
x
p
. ∴ f x
( ) is strictly increasing in 0
2
≤
x
p
.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 62 5/19/2016 1:09:43 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-285-2048.jpg)
![Differential Calculus ■ 3.63
Hence, 0
2
x
p
⇒ f f x f
( ) ( )
0
2
⎛
⎝
⎜
⎞
⎠
⎟
p
⇒ 1 2
2
x
x
sin
sin
p
p
⇒ 1
2
x
x
sin
p
.
EXAMPLE 4
Use the function f x x x
x
( ) , 0
1/
5 , to determine the bigger of the two numbers
(i) e e
p
p
and (ii) (202) and (303
303 202
) .
Solution.
Given f x x x
x
( ) ,
=
1
0.
Taking logarithm to the base e on both sides, we get
log ( ) log
e e
x
f x x
= 1
=
1
x
x
e
log .
∴ Differentiating w.r.to x,
1 1 1 1
2
f x
f x
x x
x
x
e
( )
( ) log
′ = ⋅ + −
⎛
⎝
⎜
⎞
⎠
⎟ ⇒
f x
f x x
x
e
′( )
( )
[ log ]
= −
1
1
2
⇒ f x f x
x
x
x
x
x
e
x
e
′( ) ( ) [ log ] [ log ].
/
= − = −
⋅
1
1 1
2
1
2
∴ f x
′( ) 0 if
x
x
x
x
e
1
2
1 0
/
[ log ]
− ⇒ 1 0
−
loge x ⇒ log .
e x x e
⇒
1 (
∴
e 1)
∴ f(x) is strictly decreasing for all x e
≥ .
(i) Since p e, we have
f f e e e
( ) ( ) / /
p p p
⇒
1 1
Raising to the power pe on both sides we have
( ) ( )
/ /
p p
p p p p
1 1
e e e e
e e
⇒
∴ ep
is the bigger number.
(ii) Since 303 202, we have
f (303) f(202) ⇒ ( ) ( )
/ /
303 202
1303 1202
⇒ [( ) ] [( ) ]
/ ( )( ) / ( )( )
303 202
1303 303 202 1202 303 202
⇒ ( ) ( )
303 202
202 303
∴ ( )
202 303
is the bigger number.
EXAMPLE 5
Prove that
tan
tan
2
1
2
1
x
x
x
x
for 0
2
1 2
x x
p
.
Solution.
We know that for x x
1 2 0
2
, ,
∈
p
⎛
⎝
⎜
⎞
⎠
⎟, tanx1
, tanx2
are positive.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 63 5/19/2016 1:09:49 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-286-2048.jpg)


![3.66 ■ Engineering Mathematics
ANSWERS TO EXERCISE 3.8
2. (a) Increases ∀ ∈
x R 6. Decreases
(b) Increases in (−1, 0) and decreases in (0, 1)
(c) Increases ∀ ∈
x R
3.5 GENERALISED MEAN VALUE THEOREM
In many applications it is useful to approximate a continuous function by a polynomial function
which is the simplest continuous function. Taylor’s and Maclaurin’s theorems are important tools
which provide such an approximation for real functions. Mean value theorems relate the value of the
functions and its first order derivative, where as, Taylor’s and Maclaurin’s theorems generalise this
relation to higher order derivatives. Hence these theorems can be considered as “Generalised mean
value theorems”.
3.5.1 Taylor’s Theorem with Lagrange’s form of Remainder
If f is a real function defined on [ , ]
a a h
+ such that
(i) The ( )
n th
−1 derivative f n
( )
−1
is continuous on [ , ]
a a h
+
and (ii) The nth
derivative f n
( )
exists in [ , ],
a a h
+ then there exists a number u between 0 and 1 such
that
f a h f a
h
f a
h
f a
h
f a
h
n
f
n
( ) ( )
!
( )
!
( )
!
( )
( )!
(
+ = + + +
+ +
−
−
1 2 3
1
2 3
1
′ ′′ ′′′
… n
n
n
n
a
h
n
f a h
−
+ +
1
0 1
) ( )
( )
!
( ),
u u
Proof
Given f is a real function defined on [ , ]
a a h
+ such that the (n – 1)th
derivative f n
( )
−1
is continuous and
so, f f f f n
, , , ( )
′ ′′ … −1
are continuous.
Consider the function
f( ) ( ) ( ) ( )
( )
!
( )
( )
!
( )
x f x a h x f x
a h x
f x
a h x
f x
= + + − +
+ −
+
+ −
′ ′′ ′′′
2 3
2 3
+ +
+ −
−
+
+ −
−
−
… ( )
( )!
( )
( )
!
( )
a h x
n
f x
a h x
n
A
n
n
n
1
1
1
(1)
where A is a constant to be determined such that f f
( ) ( )
a a h
= + .
⇒ f a
h
f a
h
f a
h
n
f a
h
n
A f a h
n
n
n
( )
!
( )
!
( )
( )!
( )
!
(
( )
+ + + +
−
+ = +
−
−
1 2 1
2 1
1
′ ′′ … )
) (2)
Since f f f f n
, , , ( )
′ ′′ … −1
are continuous on [ , ]
a a h
+ and a h x a h x a h x n
+ − + − + −
, ( ) , ( )
2
…, are
continuous, we get f is continuous on [ , ]
a a h
+ .
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 66 5/19/2016 5:07:15 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-289-2048.jpg)
![Differential Calculus ■ 3.67
Further f f f f n
, , , ( )
′ ′′ … −1
and a h x a h x a h x n
+ − + − + −
, ( ) , ( )
2
… are derivable in ( , )
a a h
+ and
also we get f is derivable in ( , ).
a a h
+
Further f f
( ) ( ).
a a h
= +
So, f satisfies the conditions of Rolle’s theorem.
∴ by Rolle’s theorem, there exists a c a a h
∈ +
( , ) such that ′ =
f ( ) .
c 0
Since a c a h
+ , we can write c a h
= +
u u
, .
0 1
∴ ′ + =
f u u
( ) , .
a h 0 0 1
Now
f′ ′ ′ ′′ ′′ …
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
x f x f x a h x f x a h x f x
a h x n
= − + + − − + − +
+
+ − −2
(
( )!
( )
( )
( )!
( )
( )
( )
( ) ( )
n
f x
a h x
n
f x
a h x
n
n
n
n
n
−
−
+ −
−
+
+ −
−
−
−
−
−
2 2
1
1
2
1
1
!
!
( )
( )
!
( )
( )!
( )
( )
( )
( )
f x
n a h x
n
A
a h x
n
f x
a h x
n
n
n
n
n
−
+ −
=
+ −
−
−
+ −
−
− −
1
1
1
1
1
1
( )!
n
A
−
∴ ′ + =
f u
( )
a h 0
⇒
( )
( )!
( )
( )
( )!
( )
a h a h
n
f a h
a h a h A
n
n
n
n
+ − −
−
+ −
+ − −
−
=
− −
u
u
u
1 1
1 1
0
⇒
( )
( )!
( )
( )
( )!
( )
h h
n
f a h
h h A
n
n
n
n
−
−
+ =
−
−
− −
u
u
u
1 1
1 1
⇒ A f a h
n
= +
( )
( ).
u
Substituting in (2), we get
f a h f a
h
f a
h
f a
h
f a
h
n
f
n
( ) ( )
!
( )
!
( )
!
( )
( )!
(
+ = + + + +
+
−
−
1 2 3
1
2 3
1
′ ′′ ′′′ …
n
n
n
n
a
h
n
f a h
−
+ +
1
0 1
) ( )
( )
!
( ),
u u
This is called Taylor’s theorem.
Note
(1) The ( )
n th
+1 term
h
n
f a h
n
n
!
( ),
( )
+
u u
0 1, is called the Lagrange’s Remainder after n terms in
the Taylor’s series expansion of f a h
( )
+ and it is denoted by Rn .
(2) If n = 1, then we get
f a h f a hf a h
( ) ( ) ( ),
+ = + ′ +
u u
0 1
which is Lagrange’s mean value theorem.
(3) If we put a h x
+ = or h x a
= − , that is if the interval is taken as [ , ],
a x then Taylor’s theorem takes
another form
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 67 5/19/2016 5:07:33 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-290-2048.jpg)
![3.68 ■ Engineering Mathematics
f x f a
x a
f a
x a
f a
x a
f a
x
( ) ( )
( )
!
( )
( )
!
( )
( )
!
( )
(
= +
−
+
−
+
−
+
+
1 2 3
2 3
′ ′′ ′′′ …
−
−
−
+
−
+ −
−
−
a
n
f a
x a
n
f a x a
n
n
n
n
)
( )!
( )
( )
!
( ( ))
( ) ( )
1
1
1
0 1
u u
This is called Taylor’s formula about the point a.
If the reminder Rn → 0 as n → ∞, we get Taylor’s series.
3.5.2 Taylor’s Series
If f is a real function defined on [ , ]
a a h
+ such that
(i) f has derivatives of all orders in the interval [ , ]
a a h
+ and
(ii) the remainder after n terms
R
h
n
f a h n
n
n
n
= + → → ∞
!
( ) ,
( )
u 0 as
then f a h f a
h
f a
h
f a
h
n
f a
n
n
( ) ( )
!
( )
!
( )
!
( )
( )
+ = + + + + + ∞
1 2
2
′ ′′ … …
This infinite series is called Taylor’s series.
Taylor’s series about the point a is
f x f a
x a
f a
x a
f a
x a
n
f a
n
n
( ) ( )
( )
!
( )
( )
!
( )
( )
!
( )
( )
= +
−
+
−
+ +
−
+ ∞
1 2
2
′ ′′ … …
Instead of the interval [ , ]
a a h
+ , if the interval is [0, x], then we get Maclaurin’s theorem and
Maclaurin’s series.
3.5.3 Maclaurin’s Theorem with Lagrange’s Form of Remainder
If f is a real function defined on [0, x] such that
(i) The ( )
n −1 th
derivative f n
( )
−1
is continuous on [ , ]
0 x and (ii) The nth
derivative f n
( )
exists in [ , ]
0 x ,
then there exists a number u between 0 and 1 such that
f x f
x
f
x
f
x
n
f
x
n
f
n
n
n
( ) ( )
!
( )
!
( )
( )!
( )
!
( ) (
= + ′ + ′′ + +
−
+
−
−
0
1
0
2
0
1
0
2 1
1
… n
n
x
)
( ),
u u
0 1
.
If the reminder term Rn → 0 as n → ∞, we get Maclaurin’s series.
3.5.4 Maclaurin’s Series
If f is a real function defined on [ , ]
0 x such that (i) f has derivatives of all orders
and (ii) the reminder term
R
x
n
f h
n
n
n
= →
!
( )
( )
u 0 as n → ∞,
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 68 5/19/2016 5:07:46 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-291-2048.jpg)
![Differential Calculus ■ 3.69
then f x f
x
f
x
f
x
n
f
n
n
( ) ( )
!
( )
!
( )
!
( )
( )
= + + +⋅⋅⋅+ +⋅⋅⋅
0
1
0
2
0 0
2
′ ′′
This infinite series is called Maclaurin’s series.
It is also known as the Maclaurin’s series expansion for f x
( ) in powers of x.
Remark: (1) It should be noted that technically there is no distinction betweenTaylor’s and Maclaurin’s
series. Each of which seeks to express the value of the function at any point (in an interval) interms
of the value of the various derivatives of the function at another point and the distance between the
two points.
(2) In order to expand a given function as an infinite series using Taylor’s series or Maclaurin’s
series, it is necessary to verify Rn → 0 as n → ∞. However in practical situations we will be dealing
with functions involving trigonometric, exponential, logarithmic or algebraic functions which satisfy
this condition. Hence, we obtain the expansion formally assuming this condition.
WORKED EXAMPLES
EXAMPLE 1
Expand sin x as a finite series in powers of x, with remainder in Lagrange’s form. Hence find
the series for sin x.
Solution.
Let f x x
( ) sin
= .
∴ ′ = = +
⎛
⎝
⎜
⎞
⎠
⎟
f x x x
( ) cos sin
p
2
, ′′ = − = +
⎛
⎝
⎜
⎞
⎠
⎟
f x x x
( ) sin sin
2
2
p
′′′ = − = +
⎛
⎝
⎜
⎞
⎠
⎟
f x x x
( ) cos sin ,
3
2
p
…, f x
n
x
n
( )
( ) sin
= +
⎛
⎝
⎜
⎞
⎠
⎟
p
2
.
By Maclaurin’s theorem with Lagrange’s reminder, we have
f x f
x
f
x
f
x
n
f
x
n
n
n
n
( ) ( )
!
( )
!
( )
( )!
( )
!
( )
= + + +⋅⋅⋅+
−
+
−
−
0
1
0
2
0
1
0
2 1
1
′ ′′ f
f x
n
( )
( ),
u u
0 1
⇒ sin sin( )
!
sin
!
sin
!
sin
x
x x x
= + +
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟ +
0
1 2
0
2
2
2
0
3
3
2
2 3
p p p
+
+
⎛
⎝
⎜
⎞
⎠
⎟ +
0 …
+
−
−
+
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟
−
x
n
n x
n
n
x
n n
1
1
1
2
0
2
0 1
( )!
sin
( )
!
sin ,
p p
u u
= − + − +
−
−
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
−
x
x x x
n
n
x
n
n
x
n n
3 5 1
3 5 1
1
2 2
! ! ( )!
sin ( )
!
sin
… p p
u
⎞
⎞
⎠
⎟
, .
0 1
u
Here R
x
n
n
x
n
n
= +
⎛
⎝
⎜
⎞
⎠
⎟
!
sin
p
u
2
and f is in [ , ]
0 x .
∴ R
x
n
n
x
x
n
n
n n
= +
⎛
⎝
⎜
⎞
⎠
⎟ ≤
!
sin
!
p
u
2
, since sin
n
x
p
u
2
1
+
⎛
⎝
⎜
⎞
⎠
⎟ ≤ .
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 69 5/19/2016 5:07:59 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-292-2048.jpg)
![3.70 ■ Engineering Mathematics
Let u
x
n
n
n
=
!
, then u
x
n
n
n
+
+
=
+
1
1
1
( )!
.
∴
u
u
x
n
n
x
x
n
n
n
n
n
+
+
=
+
⋅ =
+
1
1
1 1
( )!
!
( )
∴ lim lim
n
n
n
n
u
u
x
n
→∞
+
→∞
=
+
=
1
1
0 ∴ lim
n
n
u
→∞
= 0. [by the result quoted below]
Hence, Rn → 0 as n → ∞ ∴ sin
! ! !
x x
x x x
= − + − +
3 5 7
3 5 7
…
Result: If { }
un
is a sequence such that lim ,
n
n
n
u
u
l l
→∞
+
=
1
0 1, then lim
n
n
u
→∞
= 0.
EXAMPLE 2
Find the Taylor’s series expansion of cos x about x 5
p
4
.
Solution.
Let f(x) = cosx
The Taylor’s series expansion of f(x) about x =
p
4
is f(x) = f
p
4
⎛
⎝
⎜
⎞
⎠
⎟ +
1
1!
x −
⎛
⎝
⎜
⎞
⎠
⎟
p
4
f ′
p
4
⎛
⎝
⎜
⎞
⎠
⎟ +
1
2!
x −
⎛
⎝
⎜
⎞
⎠
⎟
p
4
2
f ″
p
4
⎛
⎝
⎜
⎞
⎠
⎟ +
1
3 4
3
!
x −
⎛
⎝
⎜
⎞
⎠
⎟
p
f ′″
p
4
⎛
⎝
⎜
⎞
⎠
⎟
x f
p p
1
4 4 4
4
4
+ −
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
!
( )
+ …
we have f(x) = cosx , f ′
p
4
⎛
⎝
⎜
⎞
⎠
⎟ = cos
p
4
⎛
⎝
⎜
⎞
⎠
⎟ =
1
2
f(x) = −sin x, f ′
p
4
⎛
⎝
⎜
⎞
⎠
⎟ = −sin
p
4
⎛
⎝
⎜
⎞
⎠
⎟ = −
1
2
f x
″( ) = −cosx, f ″
p
4
⎛
⎝
⎜
⎞
⎠
⎟ = − cos
p
4
⎛
⎝
⎜
⎞
⎠
⎟ = −
1
2
f x
″′( ) = sinx, f ″′
p
4
⎛
⎝
⎜
⎞
⎠
⎟ = sin
p
4
⎛
⎝
⎜
⎞
⎠
⎟ =
1
2
f(4)
(x) = cosx, f(4)
p
4
⎛
⎝
⎜
⎞
⎠
⎟ = cos
p
4
⎛
⎝
⎜
⎞
⎠
⎟ =
1
2
and so on
∴ Taylor’s series is
f x
( ) =
1
2
+ x
x
x
−
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟ +
−
⎛
⎝
⎜
⎞
⎠
⎟
−
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟
p
p
p
4
1
2
4
2
1
2
1
3 4
1
2
3
! ! 2
2
1
4 4
1
2
4
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
!
...
x
p
⇒ sinx =
1
2
1
4
1
2 4
1
3 4
1
4 4
2 3
− −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟
x x x x
p p p p
! ! !
4
4
−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
...
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 70 5/19/2016 5:08:28 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-293-2048.jpg)
![Differential Calculus ■ 3.71
EXAMPLE 3
Using Taylor’s theorem, prove that x
x
x x
x x
2 2 1
3 3 5
6
sin
6 120
for x 0.
Solution.
Let f x x
( ) sin .
= To prove x
x
x x
x x
− − +
3 3 5
6 6 120
sin for x 0
For proving this inequality in terms of x, we consider Maclaurin’s formula upto third and fifth
degree terms with Lagrange’s reminder.
Maclaurin’s series upto the third term with Lagrange’s reminder is
f x f
x
f
x
f
x
f x
( ) ( )
!
( )
!
( )
!
( )
= + + +
0
1
0
2
0
3
2 3
1
′ ′′ ′′′ u , 0 1
1
u
We have f x x
( ) sin
= , f ( ) sin
0 0 0
= =
∴ ′ =
f x x
( ) cos , ′ = =
f ( ) cos
0 0 1
′′ = −
f x x
( ) sin , ′′ = − =
f ( ) sin
0 0 0
′′′ = −
f x x
( ) cos , ′′′ = − = −
f ( ) cos
0 0 1
f x x
( )
( ) sin
4
= , f ( )
( ) sin
4
0 0 0
= =
f x x
( )
( ) cos
5
= , f ( )
( ) cos
5
0 0 1
= =
and f x x
( )
( ) sin
6
= − , f ( )
( ) sin
6
0 0 0
= − =
∴ sin
! ! !
( cos )
x
x x x
x
= + ⋅ + ⋅ + −
0
1
1
2
0
3
2 3
1
u = −
x
x
x
3
1
6
cos ( )
u .
We have for x
x
x
x
− −
0
3 6
3
1
3
,
!
cosu [whether cosu1x is +ve or –ve]
⇒ x
x
x x
x
− −
3
1
3
6 6
cosu ⇒ sin x x
x
≥ −
3
6
(1)
Also Maclaurin’s series up to fifth degree term with Lagrange’s reminder is
f x f
x
f
x
f
x
f
( ) ( )
!
( )
!
( )
!
( )
= + + +
0
1
0
2
0
3
0
2 3
′ ′′ ′′′ + +
x
f
x
f x
4
4
5
5
2 2
4
0
5
0 1
!
( )
!
( ),
( ) ( )
u u
⇒ sin ( )
!
( )
!
( )
!
( )
!
(cos ),
x x
x x x x
x
= + + + + − + +
0 1
2
0
3
1
4
0
5
0 1
2 3 4 5
2 2
u u
= − +
x
x x
x
3 5
2 2
6 120
0 1
cos ,
u u
We have − ≤ ≤
1 1
2
cosu x and x 0. ∴
x
x
x
5
2
5
120 120
cosu ≤
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 71 5/19/2016 5:08:56 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-294-2048.jpg)
![3.72 ■ Engineering Mathematics
∴ x
x x
x x
x x
− + ≤ − +
3 5
2
3 5
6 120 6 120
cosu ∴ sin x x
x x
≤ − +
3 5
6 120
(2)
From (1) and (2), we get x
x
x x
x x
− ≤ ≤ − +
3 3 5
6 6 120
sin .
But equality holds only when x = 0 . ∴ x
x
x x
x x
− − +
3 3 5
6 6 120
sin for x 0.
EXAMPLE 4
Showthat log (1 ) log 2
2 8 192
2 4
e
x
e
e
x x x
1 5 1 1 2 1…andhencededucethat
e
e
x x
x
x
1
1
2 4 48
3
1
5 1 2 1…
Solution.
Let f x e
e
x
( ) log ( )
= +
1
Maclaurin’s series for f x
( ) is
f x f
x
f
x
f
x
f
x
f
( ) ( )
!
( )
!
( )
!
( )
!
( )
( )
= + + + + +
0
1
0
2
0
3
0
4
0
2 3 4
4
′ ′ ′′′ … (1)
we have f x e
e
x
( ) log ( )
= +
1
∴ f x
e
e
x
x
′( ) =
+
⋅
1
1
f x
e e e e
e
x x x x
x
′′
⋅
( )
( )
( )
=
+ −
+
1
1 2 =
+ −
+
=
+
e e e
e
e
e
x x x
x
x
x
2 2
2 2
1 1
( ) ( )
.
′′′ =
+ ⋅ − + ⋅
+
f x
e e e e e
e
x x x x x
x
( )
( ) ( )
( )
1 2 1
1
2
4
=
+ + −
+
( ) [ ]
( )
1 1 2
1 4
e e e e
e
x x x x
x
⇒ f x
e e
e
e e
e
x x
x
x x
x
′′′( )
( )
( ) ( )
=
−
+
=
−
+
1
1 1
3
2
3
and f x
e e e e e e e
e
x x x x x x x
x
( )
( )
( ) [ ] ( ) ( )
( )
4
3 2 2 2
6
1 2 3 1
1
=
+ − − − + ⋅
+
⋅
=
+ + − − −
+
( ) [( )( ) ( )]
( )
1 1 2 3
1
2 2 2
6
e e e e e e e
e
x x x x x x x
x
⇒
f x
e e e e e e
e
x x x x x x
x
( )
( )
( )( ) ( )
( )
4
2 2
4
1 2 3
1
=
+ − − −
+
.
∴ f e e
( ) log ( ) log
0 1 1 2
= + = , f ′( )
0
1
1 1
1
2
=
+
= , f ′′( )
( )
0
1
1 1
1
4
2
=
+
=
f ′′′( )
( )
,
0
1 1
1 1
0
3
=
−
+
= f ( )
( )
( )[ ] ( )
( )
4
4
0
1 1 1 2 3 1 1 1
1 1
2
16
1
8
=
+ − − −
+
= − = −
⋅ .
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 72 5/19/2016 5:09:15 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-295-2048.jpg)

![3.74 ■ Engineering Mathematics
EXERCISE 3.9
1. Find the Taylor’s series expansion of loge
sin x about x = 3 [or in powers of (x − 3].
2. Find the Taylor’s series expansion of sin x about x =
p
4
.
3. Write down the Taylor’s series up to x4
for tan x +
⎛
⎝
⎜
⎞
⎠
⎟
p
4
.
4. Expand f x x x e x
( ) sin
= − −
2 2
by Taylor’s formula up to x4
.
5. Prove that 1
2
1
2
0
2 2
+ + ≤ ≤ + + ≥
x
x
e x
x
e x
x x
for .
6. If f x x x
e
( ) log ( ),
= +
1 0 using Maclaurin’s theorem, then show that for 0 1
u .
log ( )
( )
e x x
x x
x
1
2 3 1
2 3
3
+ = − +
+ u
.
Deduce that log ( )
( )
e x x
x x
x
1
2 3 1
2 3
3
+ − +
+ u
for x ≥ 0.
7. Write down Maclaurin’s formula for the function f x x
( ) = +
1 with Lagrange’s reminder R3.
Estimate the error in the approximation 1 1
2 8
2
+ + −
x
x x
~ when x = 0 2
. .
8. Using Maclaurin’s series expand tanx up to the term containing x5
.
9. Write Taylor’s series for f x x
( ) ( )
= −
1 5 2
with Lagrange’s form of remainder up to 3 terms in the
interval [ , ]
0 1
10. Apply Taylor’s theorem to express x about the point x = 1, up to third degree.
11. Expand loge x as a Taylor’s series in powers of ( )
x −1 and hence evaluate log .
e 1 1 to 4 places of
decimals.
12. Calculate the approximate value of 10 to four decimal places using Taylor’s series.
ANSWERS TO EXERCISE 3.9
1. loge
sinx = loge
sin3 + cot3(x – 3) −
cos
( )
cos cot
( )
ec ec
2
2
2
3
3
3
3
3 3
3
3
x x
− + −
cos ( cot )
(
ec2 2
3 1 3 3
12
3
x
−
+
− )
)4
+…
2. sinx =
1
2
1
4
1
2 4
1
3 4
1
4 4
2 3
+ −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟
x x x x
p p p p
! ! !
4
4
+
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
…
3. tanx x +
⎡
⎣
⎢
⎤
⎦
⎥
p
4
= 1 + 2x + 2x2
+
8
3
x3
+
10
3
x4
+…
4. f x x x
( ) = − +
3 4
5
6
… 6. log ( )
e x x
x x
1
2 3
2 3
+ = − + for x ≥ 0.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 74 5/19/2016 5:09:43 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-297-2048.jpg)
![Differential Calculus ■ 3.75
7. the error is less than
1
2 103
.
8. tan x x
x x
= + +
3 2
3
2
15
9. ( )
! ( ) !
,
1 1
5
2
15
4 2
15
8
1
1 3
0 1
5 2
2
1 2
3
− = − + ⋅ −
−
x x
x
x
x
u
u
10. x x
x x
x
x
= + −
( )−
−
( ) +
−
( ) − + −
[ ] ⋅
−
−
1
1
2
1
1
4
1
2
3
8
1
3
15
16
1 1
1
2 3
7 2
4
! !
( )
( )
u
4
4
0 1
!
, .
u
11. 0 0953
. 12. 3 1623
.
3.5.5 Expansion by Using Maclaurin’s Series of Some Standard Functions
Sometimes for a given function f obtaining the derivatives f f f
′, ′′ ′′′ …
, , would be difficult for writing
the Maclaurin’s series. In such cases, we use Maclaurin’s series expansion of some standard functions,
when we require few terms of the resulting series.
We list the Maclaurin’s series expension of some of the standard functions.
1. ( )
( )
!
( )( )
!
,
1 1
1
2
1 2
3
1
2 3
+ = + +
−
+
− −
+
x nx
n n
x
n n n
x x
n …
2. e
x x x
x R
x
= + + + + ∈
1
1 2 3
2 3
! ! !
,
…
3. log ( ) ,
e x x
x x x
x
1
2 3 4
1
2 3 4
+ = − + − +
…
4. sin
! ! !
x x
x x x
= − + − +
3 5 7
3 5 7
… 5. cos
! !
x
x x x
= − + − +
1
2 4 6
2 4 6
…
6. sinh
! !
x x
x x
= + + +
3 5
3 5
… 7. cosh
! !
x
x x
= + + +
1
2 4
2 4
…
8. tan
! !
−
= − + +
1
3 5
3 5
x x
x x …
9. sin ,
−
= + +
⋅
⋅
+
⋅ ⋅
⋅ ⋅
+
1
3 5 7
1
2 3
1 3
2 4 5
1 3 5
2 4 6 7
x x
x x x … −1 ≤ x ≤ 1
10. cos ,
−
= − − −
⋅
⋅
−
⋅ ⋅
⋅ ⋅
−
1
3 5 7
2
1
2 3
1 3
2 4 5
1 3 5
2 4 6 7
x x
x x x
p … −1 ≤ x ≤ 1
WORKED EXAMPLES
EXAMPLE 1
Expand log (1 sin )
2 6 12
2 3 4
e x x
x x x
1 5 2 1 2 1….
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 75 5/19/2016 5:09:54 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-298-2048.jpg)

![Differential Calculus ■ 3.77
EXAMPLE 3
Show that
e x x
x x x
n
x
n
n
cos 1 2 cos
4 2!
2 cos
2
4 3!
2 cos
3
4 !
2
1/ 2
2 3
3/ 2 /
5 1
p
1
p
1
p
1 1
⋅ ⋅ … 2
2
cos
4
np
1
⎛
⎝
⎜
⎞
⎠
⎟ ….
Solution.
Let f x e x
x
( ) cos
= =
+
⎡
⎣
⎢
⎤
⎦
⎥
−
e
e e
x
ix ix
2
= +
+ −
1
2
1 1
[ ]
( ) ( )
e e
x i x i
f x i e i e
x i x i
9( ) [( ) ( ) ]
( ) ( )
= + + −
+ −
1
2
1 1
1 1
f x i e i e
x i x i
′′( ) [( ) ( ) ]
( ) ( )
= + + −
+ −
1
2
1 1
2 1 2 1
f x i e i e
x i x i
′′′( ) [( ) ( ) ]
( ) ( )
= + + −
+ −
1
2
1 1
3 1 3 1
: :
f x i e i e
n n x i n x i
( ) ( ) ( )
( ) [( ) ( ) ]
= + + −
+ −
1
2
1 1
1 1
∴ f i i
n n n
( )
( ) [( ) ( ) ]
0
1
2
1 1
= + + −
But 1 2
4 4
+ = +
⎡
⎣
⎢
⎤
⎦
⎥
i i
cos sin
p p
and ( ) cos sin
1 2
4 4
2
+ = +
⎡
⎣
⎢
⎤
⎦
⎥
i
n
i
n
n n p p
For, let 1+ = +
i r i
(cos sin )
u u . ∴r r
cos sin
u u
= =
1 1
and
⇒ r r r
2 2 2 2 2 2 2
2 2
cos sin (cos sin
u u u u
+ = ⇒ + =
) ⇒ r r
2
2 2
= ⇒ =
and tanu u
p
= ⇒ =
1
4
∴ 1 2
4 4
+ = +
⎡
⎣
⎢
⎤
⎦
⎥
i i
cos sin
p p
and ( ) cos sin
1 2
4 4
2
+ = +
⎡
⎣
⎢
⎤
⎦
⎥
i
n
i
n
n n p p
[by De−movire’s theorem]
Similarly, ( ) cos sin
1 2
4 4
2
− = −
⎡
⎣
⎢
⎤
⎦
⎥
i
n
i
n
n n p p
∴ f
n
i
n n
i
n
n n n
( ) / /
( ) cos sin cos sin
0
1
2
2
4 4
2
4 4
2 2
= +
⎫
⎬
⎭
+ −
⎫
⎬
⎭
⎧
⎨
⎩
⎧
⎨
p p p p
⎩
⎩
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
= + + −
⎫
⎬
⎭
⎧
⎨
⎩
=
1
2
2
4 4 4 4
1
2
2 2
2 2
⋅ ⋅ ⋅
n n
n
i
n n
i
n n
/ /
cos sin cos sin cos
p p p p p
4
4
⇒ f
n
n n
( ) /
( ) cos
0 2
4
2
=
p
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 77 5/19/2016 5:10:30 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-300-2048.jpg)
![3.78 ■ Engineering Mathematics
Maclaurin’s series is
f x f
x
f
x
f
x
f
x
n
f
n
n
( ) ( )
!
( )
!
( )
!
( )
!
( )
= + + + + + +
0
1
0
2
0
3
0 0
2 3
′ ′′ ′′′ ⋅⋅⋅ ⋅⋅⋅
⋅
But f(0) = 1.
∴ f f f f n
′ ′′ ′′′ ⋅⋅⋅
( ) cos , ( ) cos , ( ) cos , , (
/ / ( )
0 2
4
0 2
4
0 2
3
4
12 3 2
= = =
p p p
0
0 2
4
2
) cos
/
= n np
∴ e x
x x x x
n
x
n
n
cos
!
cos
!
cos
!
cos
!
/ / /
= + + + + +
1
1
2
4 2
2
2
4 3
2
3
4
2
1 2
2 3
3 2
p p p … 2
2
4
cos
np
+…
3.5.6 Expansion of Certain Functions Using differential Equations
WORKED EXAMPLES
EXAMPLE 1
Expand cos( sin )
1
m x
2
as a power series.
Solution.
Let y = cos( sin )
m x
−1
(1)
Differentiating w.r.to x, we get
y m x
m
x
1
1
2
1
= −
−
−
sin( sin ).
⇒ 1 2
1
1
− = − −
x y m m x
sin( sin ).
Squaring, ( ) ( ) sin ( sin )
1 2
1
2 2 2 1
− = − −
x y m m x = − −
m m x
2 2 1
1
[ cos ( sin )]
⇒ ( ) ( )
1 1
2
1
2 2 2
− = −
x y m y (2)
Differentiating w.r.to x, we get
( ) ( ) ( )
1 2 2 2
2
1 2 1
2 2
1
− + − = −
x y y y x m yy
⇒ 2 1 2 2
2
1 2 1
2 2
1
( )
− − = −
x y y xy m yy
Dividing by 2y1
, we get
( )
1 2
2 1
2
− − = −
x y xy m y ⇒ ( )
1 0
2
2 1
2
− − + =
x y xy m y (3)
Differentiating n times using Leibnitz’s theorem, we get
( ) ( ) ( ) { }
1 2 2 1 0
2
2 1 1 2 1 1
2
− + − + − − + + =
+ + +
x y nC x y nC y xy nC y m y
n n n n n n
⋅ ⋅
⇒ ( )
( )
1 2 2
1
2
0
2
2 1 1
2
− + −
−
− − + =
+ + +
x y nxy
n n
y xy ny m y
n n n n n n
1⋅
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 78 5/19/2016 5:10:39 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-301-2048.jpg)
![Differential Calculus ■ 3.79
⇒ ( ) ( ) ( )
1 2 1 0
2
2 1
2 2
− − + + − − + + =
+ +
x y n xy n n n m y
n n n
⇒ ( ) ( ) ( )
1 2 1 0
2
2 1
2 2
− − + − − =
+ +
x y n xy n m y
n n n (4)
Putting x = 0, we get y(0) = cos (0) = 1 ∴ y m
1 0
0
1 0
0
( )
sin
= −
−
=
From (3), we get ( ) ( ) ( )
1 0 0 0 0 0
2
2
− − + =
y m y ⇒ y m y m
2
2 2
0 0
( ) ( )
= − = −
From (4), we get ( ) ( ) ( ) ( )
1 0 0 0 0 0
2
2 2
− − − − =
+
y n m y
n n ⇒ y n m y
n n
+ = −
2
2 2
0 0
( ) ( ) ( ) (5)
Putting n = 1, 2, 3, 4, … in (5), we get
y m y
3
2
1
0 1 0 0
( ) ( ) ( )
= − =
y m y m m m m
4
2 2
2
2 2 2 2 2 2
0 2 0 2 2
( ) ( ) ( ) ( )( ) ( )
= − = − − = −
y m y
5
2 2
3
0 3 0 0
( ) ( ) ( )
= − =
y m y
6
2 2
4
0 4 0
( ) ( ) ( )
= −
= − − = − − −
( ) ( ) ( )( )
4 2 2 4
2 2 2 2 2 2 2 2 2 2
m m m m m m and so on.
∴ Maclaurin’s series for y = f(x) is
f x f
x
f
x
f
x
f
x
f
x
( ) ( )
!
( )
!
( )
!
( )
!
( )
!
( )
= + + + + +
0
1
0
2
0
3
0
4
0
5
2 3 4
4
5
′ ′′ ′′′ f
f
x
f
( ) ( )
( )
!
( )
5
6
6
0
6
0
+ +⋅⋅⋅
⇒ cos( sin ) ( )
!
( )
!
( )
!
( )
!
( )
m x y
x
y
x
y
x
y
x
y
x
−
= + + + + +
1
1
2
2
3
3
4
4
0
1
0
2
0
3
0
4
0
5
5
5
6
6
5
0
6
0
!
( )
!
( )
y
x
y
+ +⋅⋅⋅
= + + − + + − + + −
1
1
0
2 3
0
4
2
5
0
6
2
2
3 4
2 2 2
5 6
2 2
x x
m
x x
m m
x x
m m
! !
( )
! !
( )
! !
[ (
× × × −
− − +
2 4
2 2 2
)( )]
m ⋅⋅⋅
⇒ cos( sin )
!
( )
!
( )( )
!
m x m
x
m m
x
m m m
x
−
= − + − − − − +
1 2
2
2 2 2
4
2 2 2 2 2
6
1
2
2
4
2 4
6
⋅⋅
⋅⋅
Note Deduce the series for cos mu
Put u u
= ⇒ =
−
sin sin
1
x x
∴ cos( )
!
sin
( )
!
sin
( )( )
!
sin
m
m m m m m m
u u u
= − +
−
−
− −
1
2
2
4
2 4
6
2
2
2 2 2
4
2 2 2 2 2
6
6
u +⋅⋅⋅
EXAMPLE 2
Expand sin[ln ( 2 1)]
2
x x
1 1 as a power series using Maclaurin’s series up to x5
.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 79 5/19/2016 5:10:51 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-302-2048.jpg)
![3.80 ■ Engineering Mathematics
Solution.
Let y x x
= + +
sin[ln( )]
2
2 1 (1)
⇒ y x
= +
sin[ln( ) ]
1 2
= +
sin[ ln( )]
2 1
x
Differentiating w.r.to x,
⇒ y x
x
1 2 1
2
1
= +
+
cos[ ln( )]⋅ (2)
⇒ ( ) cos[ ln( )]
x y x
+ = +
1 2 2 1
1
Squaring, ( ) cos [ ln( )]
x y x
+ = +
1 4 2 1
2
1
2 2
= − +
4 1 2 1
2
[ sin ( ln( ))]
x
( ) [ ].
x y y
+ = −
1 4 1
2
1
2 2
Differentiating w.r.to x, we get
( ) ( ) ( )
x y y y x yy
+ + + = −
1 2 2 1 4 2
2
1 2 1
2
1
⋅
⇒ 2 1 2 1 8
2
1 2 1
2
1
( ) ( )
x y y x y yy
+ + + = −
⇒ ( ) ( )
x y x y y
+ + + = −
1 1 4
2
2 1 [dividing by 2y1
]
⇒ ( ) ( )
x y x y y
+ + + + =
1 1 4 0
2
2 1 (3)
Differentiating n times, using Leibnitz’s formula, we get
( ) ( ) ( )
x y nC x y nC y x y nC y y
n n n n n n
+ + + + + + + + =
+ + +
1 2 1 2 1 1 4 0
2
2 1 1 2 1 1 ⋅ ⋅
⇒ ( ) ( )
( )
( )
x y n x y
n n
y x y ny y
n n n n n n
+ + + +
−
+ + + + =
+ + +
1 2 1 2
1
1 2
1 4 0
2
2 1 1
⋅
⋅
⇒ ( ) ( )( ) ( ( ) )
x y n x y n n n y
n n n
+ + + + + − + + =
+ +
1 2 1 1 1 4 0
2
2 1
⇒
( ) ( )( ) ( )
x y n x y n y
n n n
+ + + + + + =
+ +
1 2 1 1 4 0
2
2 1
2
⇒ ( ) ( )( ) ( )
x y n x y n y
n n n
+ = − + + − +
+ +
1 2 1 1 4
2
2 1
2
(4)
Put x = 0, then (1) ⇒ y( ) sin[ln( )] sin .
0 1 0 0
= = =
(2) ⇒ y1 0 2 1
2
0 1
2 0 2
( ) cos[ ln( )] cos
=
+
= =
⋅
(3) ⇒ y y y
2 1
0 0 4 0 0
( ) ( ) ( )
+ + = ⇒ y 2 0 2 0 0
( ) + + = ⇒ = −
y2 0 2
( )
(4) ⇒ y n y n y
n n n
+ +
= − + − +
2 1
2
0 2 1 0 4 0
( ) ( ) ( ) ( ) ( ) (5)
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 80 5/19/2016 5:11:10 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-303-2048.jpg)
![Differential Calculus ■ 3.81
Putting n = 1, 2, 3, … in (5), we get
y y y
y
3 2
2
1
2
4
0 2 1 0 1 4 0 3 2 1 4 2 6 10 4
0
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
= − + − + = − − − + = − = −
= −
− + − + = − − − − = + =
= − +
( ) ( ) ( ) ( ) ( ) ( )
( ) ( )
4 1 0 2 4 0 5 4 8 2 20 16 36
0 6 1
3
2
2
5
y y
y y
y y
4
2
3
0 3 4 0 7 36 13 4 252 52 200
( ) ( ) ( ) ( ) ( )
− + = − − − = − + = −
and so on.
∴ Maclaurin’s series for y = f(x) is
f x f
x
f
x
f
x
f
x
f
x
( ) ( )
!
( )
!
( )
!
( )
!
( )
!
( )
= + + + + +
0
1
0
2
0
3
0
4
0
5
2 3 4
4
5
′ ′′ ′′′ f
f ( )
( )
5
0 +…
= + + + + + +
y
x
y
x
y
x
y
x
y
x
y
( )
!
( )
!
( )
!
( )
!
( )
!
( )
0
1
0
2
0
3
0
4
0
5
0
1
2
2
3
3
4
4
5
5
…
= + + − + − + + − +
0
1
2
2
2
3
4
4
36
5
200
2 3 4 5
x x x x x
! !
( )
!
( )
! !
( )
× × …
∴ sin[ln( )]
! ! !
x x x x x x x
2 2 3 4 5
1 2
4
3
36
4
200
5
+ + = − − + − +…
= − − + − +
2
2
3
3
2
5
3
2 4 5
3
x x x x x …
EXERCISE 3.10
I. Using Maclaurin’s series expand the following functions in powers of x.
(a) log ( )
e
x
e
1+ (b) e x
sin
(c) e x
x
sec (d) e x
x
sin
(e)
x
x
sin
(f) e x
x
cos (g) log sec
e x (h) cos sinh
x x
II. Forming differential equations prove the following.
(a) tan−
= − + −
1
3 5
3 5
x x
x x …
(b) (sin )
! !
.
! !
−
= + + + +
1 2
2
2
4
2 2
6
2 2 2
8
2
2
2 2
4
2 2 4
6
2 2 4 6
8
x
x x x x
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅⋅⋅
(c) e x x
x x x x
x
e
log ( )
! ! ! !
1
2
2
3
9
5
35
6
2 3 5 6
+ = + + + − +⋅⋅⋅
(d) e x x
x x
x cos
cos( sin ) cos
!
cos
!
cos
a
a a a a
= + + + +
1
2
2
3
3
2 3
⋅⋅⋅
(e) sin−
= + + + +
1
3 5 7
1
2 3
1 3
2 2 5
1 3 5
2 4 6 7
x x
x x x
⋅
⋅
⋅
⋅ ⋅
⋅ ⋅
⋅⋅⋅
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 81 5/19/2016 5:11:24 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-304-2048.jpg)

![Differential Calculus ■ 3.83
These indeterminate forms cannot be evaluated by ordinary methods of limits.
A special method was devised by the French mathematician “L’Hopital”, a student of the famous
mathematician Johann Bernoulli.
Theorem 3.3 L’Hopital’s rule for
0
0
form
Let f and g be the two functions defined in a neighbourhood ( , )
a a
− +
d d of a, except possibly at a,
d 0, such that
(i) lim ( ) , lim ( )
x a x a
f x g x
→ →
= =
0 0
(ii) f and g are differentiable in ( , )
a a
− +
d d except possibly at a.
i.e., f x
′( ) and g x
′( ) exist and g x
′( ) ,
≠ 0 for every x a a
∈ − +
( , )
d d , except at x a
=
and
(iii) lim
( )
( )
x a
f x
g x
→
′
′
exists, then lim
( )
( )
lim
( )
( )
x a x a
f x
g x
f x
g x
→ →
=
′
′
.
Proof Given f and g are defined and differentiable in a neighbourhood ( , )
a a
− +
d d of a, except
possibly at x a
= . We shall define F and G in ( , )
a a
− +
d d such that
F x
f x x a a x a
x a
( )
( ) ( , )
,
=
∀ ∈ − + ≠
=
⎧
⎨
⎩
d d and
when
0
G x
g x x a a x a
x a
( )
( ) ( , )
,
=
∀ ∈ − + ≠
=
⎧
⎨
⎩
d d and
when
0
Clearly F and G are continuous and derivable on ( , )
a a
− +
d d except possibly at a.
Now lim ( ) lim ( ) ( )
x a x a
F x f x F a
→ →
= =
and lim ( ) lim ( ) ( )
x a x a
G x g x G a
→ →
= =
∴ F and G are continuous at a also.
If x a, then in the interval [ , ]
a x , F and G satisfy the conditions of Cauchy’s mean value theorem.
∴
F x F a
G x G a
F c
G c
( ) ( )
( ) ( )
( )
( )
−
−
=
′
′
for some c a x
∈( , )
Given F a
( ) = 0 and G a
( ) = 0.
∴
F x
G x
F c
G c
( )
( )
( )
( )
=
′
′
, a c x
We have F x f x
( ) ( )
= and G x g x x a a
( ) ( ) ( , )
= ∀ ∈ + d
∴ F c f c
′ ′
( ) ( )
= and G c g c
′ ′
( ) ( )
= { c a x
∈
[ ]
( , )
a − δ a x a + δ
M03_ENGINEERING_MATHEMATICS-I _CH03_Part B.indd 83 5/19/2016 5:11:50 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-306-2048.jpg)

![Differential Calculus ■ 3.85
Note
(1) Clearly f x g x
( ), ( ) are positive functions. ∴ lim
( )
( )
lim
( )
( )
x a x a
f x
g x
g x
f x
→ →
=
1
1
0
0
form
⎡
⎣
⎢
⎤
⎦
⎥
So, we can use L’Hopital’s rule for
0
0
form.
All other indeterminate forms can be rewritten as
0
0
form or
∞
∞
form and can be evaluated using
L’Hopital’s rule.
(2) While evaluating some of the limits the usage of standard limits such as
lim
sin
1
0
x
x
x
→
5 , limtan 1
0
x
x
→
5 , lim 1
1
, lim(1 )
0
1
x
x
x
x
x
e x e
→ →
⎛
⎝
⎜
⎞
⎠
⎟ = +
∞
1 5
and the series expansions of e x x x x
x n
,(1 ) , log(1 ), sin , cos ,
1 1 etc. may be used.
WORKED EXAMPLES
Type I: Problems of the type
0
0
,
∞
∞
, ∞ − ∞ × ∞
, 0
EXAMPLE 1
Evaluate lim
x
ax bx
e e
x
→0
2
.
Solution.
The given limit is lim
x
ax bx
e e
x
→
−
0
.
Here f x e e
ax bx
( ) = − and g x x
( ) = .
∴ lim ( ) lim( )
x x
ax bx
f x e e
→ →
= − = − =
0 0
1 1 0 and lim ( ) lim
x a x
g x x
→ →
= =
0
0
∴ lim
( )
( )
x
f x
g x
→0
is
0
0
form.
By L’Hopital’s rule, we have
lim
( )
( )
lim
( )
( )
x x
f x
g x
f x
g x
→ →
=
0 0
′
′
= lim
x
ax bx
ae be
ae be a b
→
−
= − = −
0
0 0
1
EXAMPLE 2
Evaluate lim
log ( )
x
x
e
xe x
x
→
⎡
⎣
⎢
⎤
⎦
⎥
0 2
1
2 1
.
Solution.
The given limit is lim
log ( )
x
x
e
xe x
x
→
− +
⎡
⎣
⎢
⎤
⎦
⎥
0 2
1
.
Here f x xe x
x
e
( ) log ( )
= − +
1 and g x x
( ) = 2
.
lim ( ) lim[ log ( )] . log
x x
x
e e
f x xe x
→ →
= − + = − =
0 0
1 0 1 1 0 and lim ( ) lim
x x
g x x
→ →
= =
0 0
2
0
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 85 5/19/2016 1:06:51 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-308-2048.jpg)
![3.86 ■ Engineering Mathematics
∴ lim
( )
( )
x
f x
g x
→0
is
0
0
form.
By L’Hopital’s rule,
lim
( )
( )
lim
( )
( )
x x
f x
g x
f x
g x
→ →
=
0 0
′
′
=
⋅ + ⋅ −
+
→
lim
x
x x
x e e
x
x
0
1
1
1
2
=
+ −
+
→
lim
( )
x
x
x e
x
x
0
1
1
1
2
0
0
form
⎡
⎣
⎢
⎤
⎦
⎥
=
+ + ⋅ −
−
+
→
lim
( )
( )
( )
x
x x
x e e
x
0
2
1 1
1
1
2
, by L’Hopital’s rule
=
+ +
+
→
lim
( )
( )
x
x
x e
x
0
2
2
1
1
2
=
+
=
2 1
2
3
2
.
EXAMPLE 3
Evaluate lim
tan
tan
x
x x
x x
→0 2
2
.
Solution.
The given limit is lim
tan
tan
x
x x
x x
→
−
0 2
.
Here f x x x
( ) tan
= − and g x x x
( ) tan
= 2
.
lim ( ) lim (tan )
x x
f x x x
→ →
= − =
0 0
0 and lim ( ) lim tan
x x
g x x x
→ →
= =
0 0
2
0
∴ lim
( )
( )
x
f x
g x
→0
is
0
0
form.
By L’Hopital’s rule,
lim
( )
( )
lim
( )
( )
x x
f x
g x
f x
g x
→ →
=
0 0
′
′
=
−
+
→
lim
sec
sec tan
x
x
x x x x
0
2
2 2
1
2
=
−
+
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→
lim sec
tan
sec
x
x
x x
x
x
0
2
2
2
1
1
2
[Dividing Nr. and Dr. by sec2
x ]
=
−
+
⎡
⎣
⎢
⎤
⎦
⎥
→
lim
( cos )
sin cos
x
x
x x x x
0
2
2
1
2
=
+
⎡
⎣
⎢
⎤
⎦
⎥
→
lim
sin
sin
x
x
x x x
0
2
2
2
0
0
form
⎛
⎝
⎜
⎞
⎠
⎟
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 86 5/19/2016 1:06:57 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-309-2048.jpg)
![Differential Calculus ■ 3.87
=
+ + ⋅
→
lim
sin cos
cos sin
x
x x
x x x x
0
2
2 2 2 2 1
, [by L’Hopital’s rule]
=
+ +
→
lim
sin
cos sin
x
x
x x x x
0
2
2 2 2 2
=
+ +
⎛
⎝
⎜
⎞
⎠
⎟
→
lim
sin
cos
sin
x
x
x
x
x
x
0
2
2
1 2
2
2
[Dividing Nr. and Dr. by 2x ]
=
+ +
=
1
1 1 1
1
3
. { lim
sin
x
x
x
→
=
⎡
⎣
⎢
⎤
⎦
⎥
0
2
2
1
EXAMPLE 4
Evaluate lim
x
n
x
x
e
→∞
.
Solution.
The given limit is lim
x
n
x
x
e
→∞
.
Here f x xn
( ) = and g x ex
( ) = .
∴ lim ( )
x
f x x
→∞
∞
= = ∞ and lim ( )
x
g x e
→∞
∞
= = ∞
∴ lim
( )
( )
x
f x
g x
→∞
is
∞
∞
form.
By L’Hopital’s rule,
lim
( )
( )
lim
( )
( )
x x
f x
g x
f x
g x
→∞ →∞
=
′
′
=
→∞
−
lim
x
n
x
nx
e
1
∞
∞
⎡
⎣
⎢
⎤
⎦
⎥
form
Now applying L’Hopital’s rule ( )
n −1 times, we get f x n
n
( )
( ) !
= and g x e
n x
( )
( ) = .
∴ lim
( )
( )
lim
( )
( )
( )
( )
x x
n
n
f x
g x
f x
g x
→∞ →∞
= = = =
∞
=
→∞ ∞
lim
! ! !
x x
n
e
n
e
n
0 .
EXAMPLE 5
Evaluate limlog tan
tan
x
x x
→0
2 3 .
Solution.
The given limit is limlog tan
tan
x
x x
→0
2 3 .
We know that log
log
log
b
e
e
a
a
b
= , using change of base rule in quotient form.
∴ log tan
log tan
log tan
tan 2 3
3
2
x
e
e
x
x
x
=
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 87 5/19/2016 1:07:04 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-310-2048.jpg)
![3.88 ■ Engineering Mathematics
∴ limlog tan lim
log tan
log tan
tan
x
x
x
e
e
x
x
x
→ →
=
0
2
0
3
3
2
∞
∞
⎡
⎣
⎢
⎤
⎦
⎥
form
=
⋅ ⋅
⋅ ⋅
→
lim tan
sec
tan
sec
x
x
x
x
x
0
2
2
1
3
3 3
1
2
2 2
[by L’Hopital’s rule]
=
→
3
2
2 3
3 2
0
2
2
lim
tan sec
tan sec
x
x x
x x
=
→
3
2
2
2
2
3
3
3
0
2
2
lim
sin
cos
cos
sin
cos
cos
x
x
x
x
x
x
x
⇒ limlog tan lim
sin cos
sin cos
tan
x
x
x
x
x x
x x
→ →
=
0
2
0
3
3
2
2 2 2
2 3 3
=
→
3
2
4
6
0
lim
sin
sin
x
x
x
0
0
form
⎡
⎣
⎢
⎤
⎦
⎥
= = × =
→
3
2
4 4
6 6
3
2
4
6
1
0
lim
cos
cos
x
x
x
. [by L’Hopital’s rule]
EXAMPLE 6
Evaluate limlog ( ) cot
x
e x x
→1
1
2
2
p
.
Solution.
The given limit is limlog ( )cot
x
e x x
→
−
1
1
2
p
.
Now limlog ( )cot
x
e x x
→
−
1
1
2
p
= × = −∞ ×
log cot
e 0
2
0
p
form.
So, we have to rewrite as
0
0
or
∞
∞
form.
∴ limlog ( )cot lim
log ( )
tan
x
e
x
e
x x
x
x
→ →
− =
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1 1
1
2
1
2
p
p
∞
∞
⎡
⎣
⎢
⎤
⎦
⎥
form
=
−
−
⋅
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→
lim
( )
sec
x
x
x
1 2
1
1
2 2
p p
, [by L’Hopital’s rule]
= −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
→
2 2
1
1
2
p
p
lim
cos
x
x
x
0
0
form
⎛
⎝
⎜
⎞
⎠
⎟
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 88 5/19/2016 1:07:09 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-311-2048.jpg)
![Differential Calculus ■ 3.89
= −
−
⎛
⎝
⎜
⎞
⎠
⎟ ⋅
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→
2
2
2 2 2
1
1
p
p p p
lim
cos sin
x
x x
[by L’Hopital’s rule]
= × −
⎛
⎝
⎜
⎞
⎠
⎟ ⋅ =
2
2
2 2 2
0
p
p p p
cos sin
EXAMPLE 7
Evaluate lim
sin
x x x
→
⎛
⎝
⎜
⎞
⎠
⎟
0 2 2
1 1
2 .
Solution.
The given limit is lim
sin
x x x
→
−
⎛
⎝
⎜
⎞
⎠
⎟
0 2 2
1 1
Now lim
sin
x x x
→
−
⎛
⎝
⎜
⎞
⎠
⎟
0 2 2
1 1
= ∞ − ∞ form. So, we have to rewrite as
0
0
or
∞
∞
form.
∴ lim
sin
lim
sin
sin
x x
x x
x x
x x
→ →
−
⎡
⎣
⎢
⎤
⎦
⎥ =
−
0 2 2 0
2 2
2 2
1 1 0
0
form
⎛
⎝
⎜
⎞
⎠
⎟
=
−
→
lim
sin
sin
x
x
x
x
0
2
2
2
1
0
0
form
⎛
⎝
⎜
⎞
⎠
⎟ [dividing Nr. and Dr. by x2
]
=
− ⋅
→
lim
sin cos sin
sin cos
x
x x x x x
x
x x
0
2 2
4
2 2
2
[by L’Hopital’s rule]
=
−
×
→
lim
sin [ cos sin ]
sin cos
x
x x x x x
x x x
0 4
2
2
=
−
→
lim
cos sin
cos
x
x x x
x x
0 3
=
−
→
lim
tan
x
x x
x
0 3
0
0
form
⎡
⎣
⎢
⎤
⎦
⎥
=
−
→
lim
sec
x
x
x
0
2
2
1
3
[by L’Hopital’s rule]
=
−
→
lim cos
x
x
x
0
2
2
1
1
3
=
−
→
lim
cos
cos
x
x
x x
0
2
2 2
1
3
= −
⎛
⎝
⎜
⎞
⎠
⎟
→
lim
sin
cos
x
x
x x
0
2
2 2
3
= −
⎛
⎝
⎜
⎞
⎠
⎟ =
−
⋅ = −
→
1
3
1
3
1
1
3
0
2
lim
tan
x
x
x
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 89 5/19/2016 1:07:15 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-312-2048.jpg)
![3.90 ■ Engineering Mathematics
Type II: Problems of the type 0 , ,1
8 8
∞ ∞
If A f x
x a
g x
= [ ]
→
lim ( )
( )
is one of these forms, we take logarithm and rewrite log lim ( ) log ( )
e
x a
e
A g x f x
= ⋅
→
in the form
0
0
or
∞
∞
and evaluate.
EXAMPLE 8
Evaluate lim
sin
0
1/
x
x
x
x
→
⎛
⎝
⎜
⎞
⎠
⎟
1
.
Solution.
The given limit is lim
sin
x
x
x
x
→ +
⎛
⎝
⎜
⎞
⎠
⎟
0
1
.
Let A
x
x
x
x
=
⎛
⎝
⎜
⎞
⎠
⎟
→ +
lim
sin
0
1
( )
1∞
form
∴ log lim log
sin
e
x
e
A
x
x
x
=
⎛
⎝
⎜
⎞
⎠
⎟
→ +
0
1
∞⋅
( )
0form
Since limlog
sin
log
x
e e
x
x
→
⎛
⎝
⎜
⎞
⎠
⎟ = =
0
1 0 and lim
x x
→
= ∞
0
1
, were write in the form
0
0
or
∞
∞
.
∴ log lim
log
sin
e
x
e
A
x
x
x
=
⎛
⎝
⎜
⎞
⎠
⎟
→ +
0
0
0
form
⎡
⎣
⎢
⎤
⎦
⎥
=
− ⋅
⎡
⎣
⎢
⎤
⎦
⎥
→ +
lim
sin cos sin
x
x
x
x x x
x
0
2
1
1
1
, [by L’Hopital’s rule]
=
−
→ +
lim
cos sin
sin
x
x x x
x x
0
0
0
form
⎡
⎣
⎢
⎤
⎦
⎥
=
− + ⋅ −
+ ⋅
→ +
lim
( sin ) cos cos
cos sin
x
x x x x
x x x
0
1
1
, [by L’Hopital’s rule]
=
−
+
→ +
lim
sin
cos sin
x
x x
x x x
0
0
0
form
⎡
⎣
⎢
⎤
⎦
⎥
=
− + ⋅
− + ⋅ +
→ +
lim
[ cos sin ]
( sin ) cos cos
x
x x x
x x x x
0
1
1
, [by L’Hopital’s rule]
=
− +
− +
=
→ +
lim
[ cos sin ]
sin cos
x
x x x
x x x
0 2
0
2
= 0.
∴ loge A A e
= ⇒ = =
0 1
0
.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 90 5/19/2016 1:07:22 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-313-2048.jpg)
![Differential Calculus ■ 3.91
EXAMPLE 9
Evaluate lim (sec )
/2
cot
x
x
x
→p
.
Solution.
The given limit is lim sec
cot
x
x
x
→
( )
p 2
.
Let A x
x
x
= ( )
→
lim sec
cot
p 2
∞
( )
0
form
∴ log lim log sec
cot
e
x
e
x
A x
= ( )
→p 2
=
→
lim cot log sec
x
e
x x
p 2
[ ]
0⋅∞form
=
→
lim
logsec
tan
x
x
x
p 2
∞
∞
⎡
⎣
⎢
⎤
⎦
⎥
form
=
⋅
→
lim sec
sec tan
sec
x
x
x x
x
p 2 2
1
[by L’Hopital’s rule]
=
→
lim
tan
sec
x
x
x
p 2 2
= ⋅
→
lim
sin
cos
cos
x
x
x
x
p 2
2
= lim sin cos
x
x x
→
= ⋅ =
p 2
1 0 0
∴ loge A A e
= ⇒ = =
0 1
0
EXAMPLE 10
Evaluate lim
/
x
x x x x x
a b c d
→
⎡
⎣
⎢
⎤
⎦
⎥
0
1
4
1 1 1
, where a, b, c, d are positive numbers.
Solution.
The given limit is lim
/
x
x x x x x
a b c d
→
+ + +
⎡
⎣
⎢
⎤
⎦
⎥
0
1
4
Let A
a b c d
x
x x x x x
=
+ + +
⎡
⎣
⎢
⎤
⎦
⎥
→
lim
/
0
1
4
[1∞
form]
∴ log limlog
/
e
x
e
x x x x x
A
a b c d
=
+ + +
⎡
⎣
⎢
⎤
⎦
⎥
→0
1
4
=
+ + +
⎡
⎣
⎢
⎤
⎦
⎥
→
lim log
x
e
x x x x
x
a b c d
0
1
4
[∞⋅0form]
⇒ log lim
log
e
x
e
x x x x
A
a b c d
x
=
+ + +
⎡
⎣
⎢
⎤
⎦
⎥
→0
4 0
0
form
⎡
⎣
⎢
⎤
⎦
⎥
=
+ + +
+ + +
→
lim
[ log log log log ]
x
x x x x
x
e
x
e
x
e
x
e
a b c d
a a b b c c d d
0
1
4
1
4
1
×
[by L’Hospital’s
rule]
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 91 5/19/2016 1:07:29 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-314-2048.jpg)
![3.92 ■ Engineering Mathematics
=
+ + +
+ + +
= +
1
1
4
0 0 0 0
0 0 0 0
a b c d
a a b b c c d d
a
e e e e
e
[ log log log log ]
[log log
g log log ] log ( ) log ( ) /
e e e e e
b c d abcd abcd
+ + = =
1
4
14
⇒ log log ( ) /
e e
A abcd
= 1 4
⇒ A abcd
= ( ) /
1 4
.
EXAMPLE 11
Evaluate lim( ) .
/log ( )
x
x
x e
→1
2 1 1
12 2
Solution.
The given limit is lim( ) .
/log ( )
x
x
x e
→ −
−
−
1
2 1 1
1
Let A x
x
x
e
= −
→ −
−
lim( ) .
/log ( )
1
2 1 1
1 [00
form]
∴ log lim[log ( ) ]
/log ( )
e
x
e
x
A x e
= −
→ −
−
1
2 1 1
1
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥
→ −
lim
log ( )
log ( )
x
e
e
x
x
1
2
1
1
1
∞
∞
form
⎡
⎣
⎢
⎤
⎦
⎥
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥
→ −
lim
log ( )
log ( )
x
e
e
x
x
1
2
1
1
∞
∞
form
⎡
⎣
⎢
⎤
⎦
⎥
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→ −
lim
( )
( )
( )
,
x
x
x
x
1
2
1
1
2
1
1
1
[by L’ Hopital’s rule]
=
−
+ −
⎡
⎣
⎢
⎤
⎦
⎥ =
+
⎡
⎣
⎢
⎤
⎦
⎥ =
⋅
+
=
→ − → −
lim
( )
( )( )
lim
x x
x x
x x
x
x
1 1
2 1
1 1
2
1
2 1
1 1
1
1
∴ loge
A = 1 ⇒ A = e1
= e
Type III: Problems to find the limit using the expansions of sin x, cos x, tan x, ex
, loge
(1 1 x)
We know
(1) sin
! !
x x
x x
= − + −
3 5
3 5
… (2) cos
! !
x
x x
= − + −
1
2 4
2 4
…
(3) tan x x
x
x
= + + +
3
5
3
2
15
… (4) e
x x x x
x
= + + + + +
1
1 2 3 4
2 3 4
! ! ! !
…
(5) log ( )
e x x
x x x
1
2 3 4
2 3 4
+ = − + − +…
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 92 5/19/2016 1:07:34 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-315-2048.jpg)


![Differential Calculus ■ 3.95
Definition 3.3 Let f be the function defined on [ , ]
a b and let c a b
∈( , ).
Then (i) f is said to have a relative maximum (or local maximum) at c, if there is a neighbourhood
( , )
c c
− +
d d of c such that f x f c x c c
( ) ( ) ( , )
∀ ∈ − +
d d , x c
≠ .
That is f c
( ) is the greatest value in a neighbourhood of c.
(ii) f is said to have a relative minimum (or local minimum) at c, if there is a neighbourhood
( , )
c c
− +
d d of c such that f x f c x c c
( ) ( ) ( , )
∀ ∈ − +
d d , x c
≠ .
That is f c
( ) is the least value in a neighbourhood of c.
Note (1) If f c
( ) is a relative maximum or relative minimum, then f c
( ) is called an extreme value
of f at c or extremum of f at c.
Definition3.4 Let f be defined on[ , ]
a b . f is said to have an absolute maximum (or global maximum)
on [ , ]
a b if there is at least one point c a b
∈[ , ] such that f x f c x a b
( ) ( ) [ , ]
≤ ∀ ∈ .
Inotherwords, the largest value of f on [ , ]
a b is called the absolute maximum
Definition 3.5 Let f be defined on [ , ]
a b . f is said to have an absolute minimum (or global minimum)
on [ , ]
a b if there is at least one point c a b
∈[ , ] such that f x f c x a b
( ) ( ) [ , ]
≥ ∀ ∈ .
That is the least value of f on [ , ]
a b is called the absolute minimum (or global minimum).
Note
1. Given a function f defined on [ , ]
a b , the absolute maximum and the absolute minimum need not
exist.
For example: If f x x
x
x
( ) =
≤
=
⎧
⎨
⎪
⎩
⎪
1
0 1
0 0
if
if
Then f has no absolute maximum on [ , ]
a b .
However, if f is continuous on a closed and
bounded interval [ , ]
a b , then absolute maximum
and absolute minimum exist.
2. From the definition of maximum and minimum
it is obvious that f c
( ) is an extreme value of f at
c, iff f x f c
( ) ( )
− keeps the same sign for all x,
other than c, in some neighbourhood of c.
Theorem 3.6 A necessary condition for the existence of an extremum at an interior point
Let f be a function defined on the interval [ , ]
a b and c a b
∈( , ). If f(c) is an extremum at c and if f c
′( )
exists, then f c
′( ) = 0 .
y
x
o
a C1 C2 Ca b
( ) ( ) ( )
Fig. 3.16
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 95 5/19/2016 1:08:49 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-318-2048.jpg)
![3.96 ■ Engineering Mathematics
3.7.1 Geometrical Meaning
Let y f x
= ( ) be the graph of f on [ , ]
a b , then P c f c
( , ( )) is a point on the curve y f x
= ( ).
If f c
( ) is a maximum value, then in ( , ]
c c
− d the curve is
increasing and so f x
′( ) 0 in ( , )
c c
− d and decreasing in
( , )
c c + d .
That is f x
′( ) 0 in ( , )
c c + d .
If f c
′( ) exists, then f c
′( ) must be zero.
That is the tangent is parallel to the x-axis, because it is
increasing up to the point P and momentarily at rest at P and then
decreasing.
Similarly, if f c
( ) is a minimum value, then f c
′( ) = 0 .
Note
1. The points where f x
′( ) = 0 are called stationary points of f.
2. The converse of the above theorem is not true.
Similarly, if f c
′( ) = 0, then f c
( ) is not an extremum.
For example: Consider f x x
( ) = 3
.
f x x f
′ ′
( ) ( ) .
= ∴ =
3 0 0
2
But f ( )
0 is neither a maximum nor a minimum because there is no
neighbourhood of 0 in which f x f
( ) ( )
− 0 keeps the same sign for x ≠ 0.
For, f x x
( ) = 3
0 if x 0 and f x x
( ) =
3
0 if x 0.
3. It is possible that f c
( ) is an extreme value of f
even if f c
′( ) does not exist.
For example: Consider f x x
( ) = .
We know that f ′( )
0 does not exist.
But f ( )
0 is a minimum value of f x
( ) .
In fact, f ( )
0 is the absolute minimum.
Definition 3.6 Critical Points
Let f be a function defined on [ , ]
a b . The points x a b
∈[ , ] at which f x
′( ) = 0 or f x
′( ) does not exist
are called critical points of f.
For f x x
( ) = , x = 0 is a critical point but not a stationary point.
3.7.2 Tests for Maxima and Minima
(1) Second Derivative Test
Let f be a function defined on [ , ]
a b and let f be twice differentiable in a neighbourhood ( , )
c c
− +
d d
of c a b
∈( , ) and f c
′( ) = 0. Suppose f c
″( ) ≠ 0 , then
Fig. 3.17
y
x
P
c − δ c + δ
c
x
y
o
−δ δ
Fig. 3.18
x
y = −x
y = x
y
o
Fig. 3.19
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 96 5/19/2016 1:09:01 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-319-2048.jpg)
![Differential Calculus ■ 3.97
1. f c
( ) is a maximum if f c
″( ) 0 and 2. f c
( ) is a minimum if f c
″( ) 0 .
Note If f c
″( ) = 0 , then the second derivative test cannot be applied.
In this case, we use the following general test involving higher derivatives or the first derivative
test.
(2) General Test
Let f be differentiable n times and f c f c f c f c
n n
′ ″ ...,
( ) , ( ) , ( ) ( )
= = ≠
−
( ) ( )
0 0 0
1
and .
If n is even, then
1. f c
( ) is a maximum if f c
n
( )
( ) 0 2. f c
( ) is a minimum if f c
n
( )
( ) 0.
If n is odd, then f c
( ) is neither a maximum nor a minimum.
(3) First Derivative Test
Let f be defined on [a,b] and c ∈ (a,b).
Let f be differentiable in a neighbourhood ( , )
c c
− +
d d of c, except possibly at c.
(i) If f x x c
′( )
0 for and f x x c
′( )
0 for in the neighbourhood of c, then f c
( ) is a
maximum value.
That is, f x
′( ) changes from positive to negative in the neighbourhood of c as x increases.
(ii) If f x x c
′( )
0 for and f x x c
′( )
0 for in the neighbourhood of c, then f c
( ) is a
minimum value.
That is, f x
′( ) changes from negative to positive in the neighbourhood of c as x increases.
SUMMARY
To find the maximum and minimum values of a function f on [ , ]
a b .
(i) Find the critical points. That is, find the points where f x
′( ) = 0 or f x
′( ) does not exist.
(ii) Use the second derivative test or the first derivative test and decide the maximum and minimum.
(iii) Absolute maximum will occur at a relative maximum or at the end points.
Absolute minimum will occur at a relative minimum or at the end points.
WORKED EXAMPLES
EXAMPLE 1
Find the maxima and minima of the function 10 24 15 40 108
6 5 4 3
x x x x
2 1 2 1 .
Solution.
Let f x x x x x
( ) .
= − + − +
10 24 15 40 108
6 5 4 3
∴ f x x x x x
′( ) = − + −
60 120 60 120
5 4 3 2
= − + −
60 2 2
5 4 3 2
( )
x x x x
f x x x x x
″( ) [ ]
= − + −
60 5 8 3 4
4 3 2
.
For maxima or minima f x
′( ) = 0
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 97 6/3/2016 7:51:08 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-320-2048.jpg)
![3.98 ■ Engineering Mathematics
∴ 60 2 2 0
5 4 3 2
( )
x x x x
− + − = ⇒ x x x x
5 4 3 2
2 2 0
− + − =
⇒ x x x x
2 3 2
2 2 0
[ ]
− + − = ⇒ x x x x
2 2
2 2 0
[ ( ) ( )]
− + − =
⇒ x x x
2 2
2 1 0
( )( )
− + = ⇒ x = 0 2
or [{ x2
1 0
+ ≠ ]
When x = 2, f ″( ) ( )
2 60 5 2 8 2 3 2 4 2 60 20 0
4 3 2
= ⋅ − ⋅ + ⋅ − ⋅ = × .
When x = 2, the function is minimum.
The minimum value is f ( )
2 10 2 24 2 15 2 40 2 108
6 5 4 3
= ⋅ − ⋅ + ⋅ − ⋅ +
= − + − + =
640 324 240 320 108 344.
When x = 0, ′′ =
f x
( ) 0, the test fails.
Note ′′′ = − + −
f x x x x
( ) [ ]
60 20 24 6 4
3 2
∴ ′′′ = − ≠
f ( )
0 240 0 .
So, f ( )
0 is neither a maximum nor a minimum.
EXAMPLE 2
Find the maximum and minimum values of f x x x
( ) , [ , ]
5 2 2
4 4 4
2
∈ . Also find the absolute
maximum and absolute minimum, if they exist.
Solution.
Let f x x x
( ) , [ , ]
= − ∈ −
4 4 4
2
.
We know 4 4
2 2
− = −
x x if 4 0
2
− ≥
x
⇒ x x
2
4 0 2 2
− ≤ ⇒ − ≤ ≤
and 4 4
2 2
− = − −
x x
( ), if 4 0
2
−
x .
⇒ x2
4 0
− ⇒ −
x x
2 2
or
∴ f x
x x
x x x
( ) =
− − ≤ ≤
− −
⎧
⎨
⎪
⎩
⎪
4 2 2
4 2 2
2
2
if
if or
∴ f x
x x
x x x
′( ) =
− −
−
⎧
⎨
⎩
2 2 2
2 2 2
if
if or
f x
x
x x
″( ) =
− −
−
⎧
⎨
⎩
2 2 2
2 2 2
if
if or
∴ f x x
′( ) ( , )
= ⇒ = ∈ −
0 0 2 2 .
At x = −2 2
, , f x
′( ) does not exist. [Since, f is continuous at x = 2 and f ′( )
2 4
− = − , f ′( )
2 4
+ =
∴ f ′( )
2 does not exist. Similarly, f ′( )
−2 does not exist]
The critical points are x = −
0 2 2
, , .
x
o
(0, −4)
(0, 4)
(−2, 0)
x = −4 x = 4
(2, 0)
y
Fig. 3.20
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 98 5/19/2016 1:09:20 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-321-2048.jpg)
![Differential Calculus ■ 3.99
When x f x
= = −
0 2 0
, ( )
″ .
∴ f x
( ) has a maximum at x = 0 and the maximum value = 4.
Since f x
′( ) does not exist at x x
= − =
2 2
, , we use the first derivative test.
In a neighbourhood of −2,
f x x
′( ) −
0 2
if and f x x
′( ) .
−
0 2
if
So, f ( )
−2 is a minimum.
Similarly, in a neighbourhood of 2,
f x x
′( )
0 2
if and f x x
′( ) .
0 2
if
So, f ( )
2 is a minimum and the minimum value is zero.
The least value of f x
( ) in [ , ]
−4 4 is 0. ∴ the absolute minimum = 0.
Though f ( )
0 4
= is a relative maximum, it is not the absolute maximum.
Absolute maximum occur at the end points x = 4 or x = −4 and the value is
f ( ) .
4 4 4 4 16 12 12
2
= − = − = − =
EXAMPLE 3
In a submarine cable the speed of signalling varies as x
x
e
2 1
log ,
⎛
⎝
⎜
⎞
⎠
⎟ where x is the ratio of the
radius of the core to that of the covering. Find the values of x for which the speed of signaling is
maximum.
Solution.
Let S be the speed of signalling in a submarine cable.
Then S kx
x
kx x
e e
=
⎛
⎝
⎜
⎞
⎠
⎟ = −
2 2
1
log log , where x 0, k 0
∴
dS
dx
k x
x
x x kx x
e e
= − ⋅ + ⋅
⎡
⎣
⎢
⎤
⎦
⎥ = − +
2 1
2 1 2
log [ log ].
For maximum or minimum,
dS
dx
= 0
⇒ − + =
kx x
e
[ log ]
1 2 0
⇒ 1 2 0
+ =
loge x ⇒ loge x x e
e
= − ⇒ = =
−
1
2
1
1
2
[ ]
{ kx ≠ 0
Now
d S
dx
k x
x
x
e
2
2
2
1
1 2 1
= − ⋅ ⋅ + + ⋅
⎡
⎣
⎢
⎤
⎦
⎥
( log ) = − + + = − +
k x k x
e e
[ log ] [ log ]
2 1 2 3 2
When x
e
=
1
,
d S
dx
k
e
e
= − +
⎡
⎣
⎢
⎤
⎦
⎥
3 2
1
0
2
2
log .
∴when x
e
=
1
, S is maximum.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 99 5/19/2016 1:09:29 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-322-2048.jpg)
![3.100 ■ Engineering Mathematics
EXAMPLE 4
A factory D is to be connected by a road with a straight railway line on which a town A is
situated. The distance DB of the factory to the railway line is 5 3 km. Length AB of the railway
line is 20km. Freight charges on the road are twice the charges on the railway. At what point
P PA PB
( )
on the railway line should the road DP be connected so as to ensure minimum
freight charges from the factory to the town.
Solution.
D is the factory, A is the town and AB is the straight railway line.
Given DB = 5 3 km.
Let BP x
= , then PA x
= −
20 and DP x
= +
2
75 is the road.
Let k be the freight charge on railway. Then 2k is the freight charge on road.
If F is the total freight charges, then F k x k x x
= + + − ≤ ≤
2 75 20 0 20
2
( ), .
∴
dF
dx
k
x
x k
= ⋅
+
⋅ + −
2
1
2 75
2 1
2
( )
=
+
−
⎡
⎣
⎢
⎤
⎦
⎥
k
x
x
2
75
1
2
.
For maximum or minimum,
dF
dx
= 0
⇒ k
x
x
2
75
1 0
2
+
−
⎡
⎣
⎢
⎤
⎦
⎥ = ⇒
2
75
1 0
2
x
x +
− =
⇒ 2 75
2
x x
= + ⇒ 4 75
2 2
x x
= + ⇒ 3 75 25 5
2 2
x x x
= ⇒ = ⇒ = [ ]
{ x 0
Now d F
dx
k x x
x
x
x
2
2
2
2
2
2
75 2 2
2
2 75
75
=
+ ⋅ − ⋅
+
⎡
⎣
⎢
⎤
⎦
⎥
+
( )
=
+ −
⎡
⎣ ⎤
⎦
+ +
=
+
k x x
x x
k
x
2 75 2
75 75
150
75
2 2
2 2 2 3 2
( )
( ) ( )
.
/
When x
d F
dx
k k
= =
+
=
5
150
25 75
150
10
0
2
2 3 2 3
,
( ) /
∴ when x = 5, F is minimum.
So, the freight charge will be minimum if the road is connected to the railway line at a distance 5 km
from Bor 15 km from the town A.
EXAMPLE 5
A rectangular sheet of metal has four equal square portions removed at the corners and the sides
are then turned up so as to form an open rectangular box. Show that when the volume contained
in the box is a maximum, the depth will be
1 2 2
b
a b a ab b
1 2 2 2
⎡
⎣
⎤
⎦
, where a and b the sides of
the original rectangle.
B
D
x A
P 20 − x
90°
x2
+ 75
3
5
Fig. 3.21
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 100 5/19/2016 1:09:38 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-323-2048.jpg)
![Differential Calculus ■ 3.101
Solution.
Given a and b be the sides of the rectangular sheet of metal.
Let x be the side of square cut off from the corners.
∴ the dimensions of the box formed by folding up the sides are a x b x
− −
2 2
, and x.
The volume of the box V x a x b x
= − −
( )( )
2 2
⇒ V x ab a b x x
= − + +
[ ( ) ]
2 4 2
⇒ V abx a b x x
= − + +
2 4
2 3
( )
∴
dV
dx
ab a b x x
= − + +
4 12 2
( ) .
For maximum or minimum,
dV
dx
= 0
12 4 0
2
x a b x ab
− + + =
( )
⇒ x
a b a b ab
=
+ ± + −
4 16 48
24
2
( ) ( )
=
+ ± + −
=
+ ± + + −
4 4 3
24
2 3
6
2
2 2
( ) ( )
( )
a b a b ab
a b a b ab ab
=
+ ± + −
= + + + −
⎡
⎣
⎤
⎦
+ − + −
⎡
⎣
⎤
⎦
a b a b ab
a b a b ab a b a b ab
2 2
2 2 2 2
6
1
6
1
6
or .
Now
d V
dx
x a b
2
2
24 4
= − +
( ) = − +
4 6
[ ( )].
x a b
When x a b a b ab
= + − + −
( )
1
6
2 2
,
d V
dx
a b a b ab
a b
a b a b ab
2
2
2 2
2 2
4 6
6
4
=
+ − + −
⎛
⎝
⎜
⎞
⎠
⎟ − +
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
= + − + − −
( )
(a
a b a b ab
+
⎡
⎣
⎤
⎦
= − + −
) .
4 0
2 2
∴ when the depth is
1
6
2 2
a b a b ab
+ − + −
⎡
⎣
⎤
⎦
, V is maximum.
EXAMPLE 6
A cone circumscribed a sphere of radius r. Prove that when the volume of the cone is minimum,
its height is 4r and the semi−vertical angle is sin .
21 1
3
⎛
⎝
⎜
⎞
⎠
⎟
x x
x
x
x a − 2x
b − 2x
Fig. 3.22
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 101 5/19/2016 1:09:45 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-324-2048.jpg)
![3.102 ■ Engineering Mathematics
Solution.
Let the sphere be of radius r. Let the cone be of radius R and height h.
Let the semi−vertical angle of the cone be u. Let V be the volume of the cone.
Then Volume V R h
=
1
3
2
p .
Let O be centre of the sphere. D be the centre of the
base circle of the cone.
∴ OD r AD h
= =
and
∴ OA h r
= −
From Δ = ⇒ =
ABD
BD
AD
BD h
, tan tan
u u
From Δ =
AEO
EO
EA
, tanu.
But EA OA r h r r h r rh r h hr
= − = − − = + − − = −
2 2 2 2 2 2 2 2
2 2
( )
∴ tanu =
r
h hr
2
2
−
∴ BD h
r
h hr
= ⋅
−
2
2
=
−
hr
h hr
2
2
.
∴
V
h r
h hr
h
=
−
1
3 2
2 2
2
p . =
−
=
−
1
3 2
1
3 2
2
3
2
2
p p
r
h
h h r
r
h
h r
( ) ( )
∴
dV
dh
r h r h h
h r
=
− − ⋅
−
p 2 2
2
3
2 2 1
2
[( ) ]
( )
=
− −
−
=
−
−
p p
r h h r h
h r
r h h r
h r
2
2
2
2
2 4
3 2
4
3 2
[ ]
( )
( )
( )
.
For maximum or minimum
dV
dh
= 0
⇒
pr h h r
h r
2
2
4
3 2
0
( )
( )
−
−
= ⇒ h h r
( )
− =
4 0 ⇒ h − 4r = 0 ⇒ h r
= 4 [{h ≠ 0]
Now
d V
dh
r h r h r h rh h r
h r
2
2
2 2 2
4
3
2 2 4 4 2 2
2
=
− ⋅ − − − −
−
p [( ) ( ) ( ) ( )]
( )
=
− − − − −
−
pr h r h r h r h rh
h r
2 2
4
3
2 2 2 2 2 4
2
( )[( ) ( ) ( )]
( )
⇒
d V
dh
r h r h h r
h r
2
2
2 2
3
3
2 2 2 4
2
=
− − −
−
p [ ( ) ( )]
( )
.
When h r
= 4 , d V
dh
r r r h
r r
r
r
r
2
2
2 2
3
2
3
2 4 2 2 0
4 2 3
2
2 3
0
=
− − ×
−
= ⋅ =
p p p
( )
( )
A
B C
E
O
θ
D
R
r
h
r
90°
Fig. 3.23
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 102 5/19/2016 1:09:54 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-325-2048.jpg)
![Differential Calculus ■ 3.103
∴ when h r
= 4 , V is minimum.
Now sinu =
OE
OA
r
h r
r
r r
=
−
=
−
=
4
1
3
⇒ u =
⎛
⎝
⎜
⎞
⎠
⎟
−
sin .
1 1
3
EXERCISE 3.12
1. Find the maximum and minimum values of x x x
5 4 3
5 5 1
− + − .
2. Find the maximum and minimum values of
x x
x x
2
2
1
1
+ +
− +
.
3. Find the maximum and minimum values of a x b x
2 2 2 2
sin cos .
+
4. If xy = 4, find the maximum and minimum values of 4 9
x y
+ .
5. Find the maximum and minimum values of x x
− 2
on [ , ].
−2 2
6. An isosceles triangle with vertex ( , )
0 2 is inscribed in the ellipse
x y
2 2
9 4
1
+ = . Find the equation
of the base if the area of the triangle is a maximum.
7. A manufacturer plans to construct a cylindrical can to hold one cubic meter of liquid. If the cost
of constructing the top and bottom of the can is twice the cost of constructing the side, what are
the dimensions of the most economical can?
8. Find the rectangle of maximum area with sides parallel to the coordinate axes which can be
inscribed in the figure bounded by two parabolas 3 12 2
y x
= − and 6 12
2
y x
= − .
9. The cost of fuel in running an engine is proportional to the square of the speed and is Rs. 48
per hour for speed of 16 km/hr and other costs per hour amount Rs. 300. What is the most
economical speed and the cost of a journey of 400 km.
10. Show that the function sin ( cos )
x x
1+ is a maximum when x =
p
3
. Does this function have
minimum at x = 0 orp?
11. Let f x
x a a x
x x
( )
, .
=
− + − −
− ≥
⎧
⎨
⎪
⎩
⎪
2 9 9 2
2 3 2
2
if
if
Find the values of a if f x
( ) has a local minimum at x = 2.
[ ( )
lim ( )
Hint: if
if and
f x x a a r
x x f x f
x
= − + − −
= − ≥ ≥
→ −
2 9 9 2
2 3 2
2
2
(
( )]
2
12. Find the maximum possible slope for a tangent line to the curve y
e x
=
+ −
8
1 3
.
13. Find the area of the largest rectangle with lower base on the x-axis and the upper vertices on
y x
= −
12 2
.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 103 5/19/2016 1:10:01 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-326-2048.jpg)
![3.104 ■ Engineering Mathematics
ANSWERS TO EXERCISE 3.12
1. Maximum at x = 2, Maximum value = −9
Minimum at x = 3, Minimum value = −28
No extremum at x = 0
3. Maximum at x =
p
2
, Maximum value = a
Minimum at x = p, Minimum value = b
5. Maximum at x = −2, x =
1
2
and x = 2, Maximum values are 6, 4 and 2
Minimum at x = 0 and x = 1, Minimum values are 0, 0
6. y + =
1 0, 7. h r
= 4 8. 16
9. 40 km per hour and Rs. 6000.
10. x f
= = − + =
p p p p
, ( ) sin ( cos )
″ 4 1 0
Hence, f x
( ) is neither a maximum nor a minimum at x = p.
12. So, the greatest possible slope is when x e
= log 3 and greatest slope = 2.
13. Maximum area = 32 sq.unit.
3.8 ASYMPTOTES
The study of asymptotes is yet another aspect of characterizing the shape of a curve. In this section we
study rectilinear asymptote. Roughly, an asymptote to an infinite curve is a straight line touching the
curve at an infinite distance from the origin.
In order that a curve to have asymptote it should extend up to infinity. Closed curves like circle and
ellipse will not have asymptotes. But every curve extending up to infinity need not have asymptotes
for example parabola y ax
2
4
= extends up to infinity, yet it has no asymptote.
We shall now formally define an asymptote.
Definition 3.7 A point P x y
( , ) on an infinite curve is said to tend to infinity (i.e., P→ ∞) along the
curve as either x or y or both tend to ∞ or −∞ as P moves along the curve.
Definition 3.8 Asymptote
A straight line at a finite distance from the origin is called an asymptote of an infinite curve, if when a
point P on the curve tends to ∞ along the curve, the perpendicular distance from P to the line tends to 0.
An asymptote parallel to the x-axis is called a horizontal asymptote and an asymptote parallel to
the y-axis is called a vertical asymptote.
An asymptote which is not parallel to either axis will be called an oblique asymptote.
Theorem 3.7 If y mx c
= + (where m and c are finite) is an asymptote of an infinite curve, then
m
y
x
x
=
⎛
⎝
⎜
⎞
⎠
⎟
→∞
lim and c y mx
x
= −
→∞
lim( ),
where P x y
( , ) is any point on the infinite curve.
Proof Given P x y
( , ) be any point on the infinite curve.
2. Maximum at x = 1, Maximum value = 3
Minimum at x = −1, Minimum value =
1
3
4. Maximum at x = 3, Maximum value = −24
Minimum at x = 3, Minimum value = 24
11. a ∈ −∞ − ∞
( , ] [ , ).
1 10
∪
M03_ENGINEERING_MATHEMATICS-I _CH03_Part C.indd 104 5/19/2016 1:10:07 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-327-2048.jpg)


![Differential Calculus ■ 3.107
EXAMPLE 4
Find the asymptote of the curve y
x
x
x
5
2
1
2
3
5 .
Solution.
The given curve is y
x
x
x
=
−
+
2
3
5 .
When x y
= → ∞
3, . ∴ x = 3 is a vertical asymptote.
Now
lim lim lim .
x x x
y
x
x
x
x
x
→∞ →∞ →∞
=
−
+
⎛
⎝
⎜
⎞
⎠
⎟ =
−
+
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
→ ∞
2
3
5
2
1
3
5
∴ there is no horizontal asymptote.
To find the oblique asymptote
We know m
y
x x
x x
=
⎛
⎝
⎜
⎞
⎠
⎟ =
−
+
⎛
⎝
⎜
⎞
⎠
⎟ =
∞
+ =
→∞ →∞
lim lim
2
3
5
2
5 5
And
c y mx
x
x
x x
x
x
x x x
= − =
−
+ −
⎛
⎝
⎜
⎞
⎠
⎟ =
−
⎛
⎝
⎜
⎞
⎠
⎟ =
→∞ →∞ →∞
lim( ) lim lim l
2
3
5 5
2
3
i
im .
x
x
→∞
−
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
=
−
=
2
1
3
2
1 0
2
∴ y x
= +
5 2 is an oblique asymyptote.
EXAMPLE 5
Find the asymptotes if any, of the curve y xe x
5 1/
.
Solution.
The given curve is y xe x
= 1/
.
When x
x
→ → ∞
0
1
+ , . ∴ → ∞
e x
1/
and lim lim (
/
x x
x
y xe
→ + → +
= ⋅∞
0 0
1
0 form)
=
∞
∞
⎛
⎝
⎜
⎞
⎠
⎟
→ +
lim
/
/
x
x
e
x
0
1
1
form
=
−
= = ∞
→ +
→ +
lim
( / )
, [
lim .
/
/
x
x
x
x
e x
x
e
0
1 2
2
0
1
1
1
by L hopital s rule]
’ ’
∴ as x y
→ + → ∞
0 , . Hence, x = 0 is a vertical asymptote.
It can be seen that as x y
→ ∞ → ∞
, and so, there is no horizontal asymptote.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 107 5/19/2016 7:42:17 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-330-2048.jpg)

![Differential Calculus ■ 3.109
+ + ′ + ′′ +
⎡
⎣
⎢
⎤
⎦
⎥ + =
−
− − −
x m
c
x
m
c
x
m
n
n n n
2
2 2
2
2 2
1
2
0
f f f
( ) ( )
!
( ) .
… …
⇒ x m x c m m
n
n
n
n n
f f f
( ) [ ( ) ( )]
+ ′ +
−
−
1
1
+ ′′ + ′ +
⎡
⎣
⎢
⎤
⎦
⎥ + =
−
− −
x
c
m c m m
n
n n n
2
2
1 2
2
0
!
( ) ( ) ( ) .
f f f …
Dividing by xn
, we get
f f f
n n n
m
x
c m m
( ) [ ( ) ( )]
+ ′ + −
1
1
+ ′′ + ′ +
⎡
⎣
⎢
⎤
⎦
⎥ + =
− −
1
2
0
2
2
1 2
x
c
m c m m
n n n
!
( ) ( ) ( )
f f f … (3)
Also from (2), we get
f f f
n n n
y
x x
y
x x
y
x
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ + =
− −
1 1
0
1 2 2 … . (4)
y = mx + c is an asymptote if lim .
x
y
x
m
→
⎛
⎝
⎜
⎞
⎠
⎟ =
∞
Hence, from (4), we get fn m
( ) .
= 0 (5)
The real values of m are the slopes of the asymptotes.
Substituting (5) in (3), we get
1 1
2
1 2
2
1 2
x
c m m
x
c
m c m m
n n n n n
[ ( ) ( )]
!
( ) ( ) ( )
′ + + ′′ + ′ +
⎡
⎣
⎢
⎤
⎦
⎥
− − −
f f f f f +
+ =
… 0.
Multiplying by x and taking limit as x → ∞, we get
c m m
n n
′ + =
−
f f
( ) ( )
1 0
⇒ c
m
m
n
n
= −
′
−
f
f
1( )
( )
if ′ ≠
fn m
( ) .
0 (6)
If m1
, m2
, …, mr
are the real roots of fn m
( ) ,
= 0 then the corresponding values of c from (6)
are c1
, c2
, …, cr
∴ the asymptotes are
y m x c y m x c y m x c
r r
= + = + = +
1 1 2 2
, , , .
…
Note
(1) Suppose ′ =
fn m
( ) 0 and fn m
− ≠
1 0
( ) then c is infinite and hence, there is no asymptote to the
curve, in this case.
(2) Suppose ′ =
fn m
( ) 0 and fn m
( ) = 0 then c m m
n n
f f
( ) ( )
+ =
−1 0 is an identity.
If ′ =
fn m
( ) 0, then fn m
( ) = 0 has repeated roots.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 109 5/19/2016 7:42:26 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-332-2048.jpg)



![Differential Calculus ■ 3.113
When t x y
= − → ∞ → ∞
1, and , we get an asymptote.
We know that y mx c
= + is an asymptote if m
y
x
x
=
→∞
lim and c y mx
x
= −
→∞
lim( )
where (x, y) is a point on the curve.
We have m
y
x
x
=
⎛
⎝
⎜
⎞
⎠
⎟
→∞
lim =
+
+
+
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
→−
lim
t
t
t
t
t
1
2
2
3
2
1
1
( , ).
{ asx t
→ ∞ → −1
=
+ − +
⎡
⎣
⎢
⎤
⎦
⎥ =
− + − − − +
−
→−
lim
( )( ) (( ) )[( ) ( ) ]
( )
t
t t t
t
1
2 2
2
2 2
2 1 1 2 1 1 1
1 2
2
1 2 1 1 1 9
= + + + =
( )( ) .
and c y mx
x
= −
→∞
lim( ) = −
=
+
+
−
+
⎡
⎣
⎢
⎤
⎦
⎥
→∞
→−
lim( )
lim
x
t
y x
t
t
t
t
9
2
1
9
1
1
2 2
3
=
+
→−
lim
( )(
t
t 2 1
1
2
+
+ − +
+ +
=
+ − + − +
→−
t t t
t t
t t t t t
t
3 2
3
1
2 2 2
9 1
1 1
2 1 9 1
) ( )
( )( )
lim
[( )( ) ]( )
(
( )( )
1 1 3
+ +
t t
=
+ − + −
+
=
− + + − + −
→−
→−
lim
( )( )
( )
lim
t
t
t t t t
t
t t t t t
1
2 2 2
3
1
4 3 2 2
2 1 9
1
2 2 2 9
9
1
6 2 2
1
2
3
1
4 3 2
3
t
t
t t t t
t
t
( )
lim
+
=
− + − +
+
→−
0
0
form
⎡
⎣
⎢
⎤
⎦
⎥
=
− − −
→−
lim
t
t t t
t
1
3 2
2
4 3 12 2
3 [by L’Hopital’s rule]
=
− − − − − −
−
=
− − + −
=
−
=
4 1 3 1 12 1 2
3 1
4 3 12 2
3
12 9
3
1
3 2
2
( ) ( ) ( )
( )
.
∴ the asymptote is y x
= +
9 1.
3.8.3 Another Method for Finding the Asymptotes
Let the equation of the curve be nth
degree in x and y.
Suppose the nth
degree curve can be put in the form ( )
ax by c P F
n n
+ + + =
− −
1 1 0, where Pn−1 and Fn−1
denote polynomials of degree ( )
n −1 in x and y.
Any line parallel to ax by c
+ + = 0 that cut the curve in two points at infinity is an asymptote and
it is given by ax by c
F
P
y
a
b
x
n
n
+ + +
⎛
⎝
⎜
⎞
⎠
⎟ =
=− →∞
−
−
lim ,
1
1
0 if the limit is finite.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 113 5/19/2016 7:42:49 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-336-2048.jpg)

![Differential Calculus ■ 3.115
∴ x y
+ = ±2 2 are two asymptotes.
Now the equation is of the form
( )
x y P F
n n
+ + + =
− −
2 2 0
1 2
∴ x y
+ + =
2 2 0 ia an asymptote.
Hence, x y x y
+ = ± + + =
2 2 2 2 0
, are the three asymptotes. [Work out this by the general
method]
EXAMPLE 3
Find the asymptotes of x x y xy x xy
3 2 2 2
2 2 0.
2 1 1 2 1 5
Solution.
It is a third degree equation in x and y.
Since the coefficient of x3
is constant there is no asymptote parallel to the x-axis.
Since the coefficient of y 3
is x, asymptote parallel to the y-axis is x = 0.
That is the y-axis itself.
Factorising the third degree terms
x x xy y x x y
( ) ( )
2 2
2 2 0
− + + − + = ⇒ x x y x x y
( ) ( )
− + − + =
2
2 0
⇒ x y x x y x
( ) ( )
− − − + =
2
2 0 ⇒ ( ) ( ) .
y x y x
x
− − − + =
2 2
0
Asymptote parallel to y x
− = 0 is given by ( ) ( ) lim
y x y x
x
y x
− − − + =
= →∞
2 2
0
⇒ ( ) ( )
y x y x
− − − =
2
0
⇒ ( )[( ) ]
y x y x
− − − =
1 0 ⇒ y x y x
− = − − =
0 1 0
,
∴ the asymptotes are x y x y x
= − = − − =
0 0 1 0
, , .
3.8.4 Asymptotes by Inspection
In certain cases, we can find the asymptotes of an rational algebraic equation without any calculations.
If the equation can be rewritten in the form F F
n n
+ =
−2 0, where Fn is a polynomial of degree n in x
and y and Fn−2 is a polynomial of degree almost n − 2.
If Fn can be factored into linear factors so that no two of them represent parallel straight lines, then
Fn = 0 gives all the asymptotes.
For example: The equation of the hyperbola
x
a
y
b
2
2
2
2
1
− = is of the F F
n n
+ =
−2 0, where
F
x
a
y
b
x
a
y
b
x
a
y
b
n = − = −
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
2
2
2
2
.
So, the asymptotes are
x
a
y
b
x
a
y
b
− = + =
0 0
and .
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 115 5/19/2016 7:43:03 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-338-2048.jpg)

![Differential Calculus ■ 3.117
Now the equation can be rewritten as
xy x y xy y x y
( ) ( )
− + + + − =
2
0
This is of the form ( ) .
x y P F
n n
− + =
− −
1 1 0
∴ the asymptote parallel to x y
− = 0 is
x y
F
P
x y
n
n
− + =
= →∞
−
−
lim 1
1
0 ⇒ x y
xy y x y
xy
x y
− +
+ + −
⎡
⎣
⎢
⎤
⎦
⎥ =
= →∞
lim
2
0
⇒ x y
x x x x
x
x
− +
+ + −
⎡
⎣
⎢
⎤
⎦
⎥ =
→∞
lim
2 2
2
0 ⇒x y
x
x
x
− +
⎛
⎝
⎜
⎞
⎠
⎟ =
→∞
lim
2
0
2
2
⇒ x y
− + =
2 0.
∴ the asymptotes are y x x y
= − = − + =
0 1 0 2 0
, , .
The curve cannot have more than 3 asymptotes.
∴ their combined equation is
y x x y
( )( )
− − + =
1 2 0 ⇒ ( )( )
xy y x y
− − + =
2 0
⇒ x y xy xy xy y y
2 2 2
2 2 0
− + − + − = ⇒ x y xy xy y y
2 2 2
2 0
− + + − = .
∴ A x y xy xy y y
≡ − + + − =
2 2 2
2 0.
The curve is
C x y xy xy y x y
≡ − + + + − =
2 2 2
0.
The point of intersection of the asymptotes lie on the curve.
C A
− = 0. ⇒ x y
+ = 0,
which is a straight line and the number of points of intersection is 3(3 – 2) = 3.
EXAMPLE 6
Show that the four asymptotes of the curve
( )( 4 ) 6 5 3 2 3 1 0
2 2 2 2 3 2 2 2 2
x y y x x x y xy y x xy
2 2 1 2 2 1 2 1 2 5
cut the curve again in eight points which lie on a conic.
Solution.
The given curve is ( )( ) .
x y y x x x y xy y x xy
2 2 2 2 3 2 2 2 2
4 6 5 3 2 3 1 0
− − + − − + − + − =
Put x y m
= =
1, in the fourth degree terms, we get f4
2 2
1 4
( ) ( )( )
m m m
= − − .
Put x y m
= =
1, in the third degree terms, we get f3
2
6 5 3
( )
m m m
= − − .
∴
′ = − + − −
= − − + = −
f4
2 2
2 2 2
1 2 4 2
2 1 4 2 5 2
( ) ( )( ) ( )( )
[ ] [ ]
m m m m m
m m m m m
∴ c
m
m
m m
m m
= −
′
= −
− −
−
⎡
⎣
⎢
⎤
⎦
⎥
f
f
3
4
2
2
6 5 3
2 5 2
( )
( ) ( )
.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 117 5/19/2016 7:43:16 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-340-2048.jpg)
![3.118 ■ Engineering Mathematics
Solving f4 0
( ) ,
m = we get
( )( )
1 4 0
2 2
− − =
m m ⇒ 1 0 4 0
2 2
− = − =
m m
or ⇒ m m
= ± = ±
1 2
or .
When m c
= − = −
− − − −
− − −
⎡
⎣
⎢
⎤
⎦
⎥ = −
+ −
− ⋅
=
1
6 5 1 3 1
2 1 5 2 1
6 5 3
2 3
8
2
2
,
( ) ( )
( )( ( ) ) ( ) 2
2 3
4
3
×
= .
∴ asymptote is y x
= − +
4
3
⇒ y x
+ − =
4
3
0.
When m c
= = −
− ⋅ − ⋅
⋅ ⋅ − ⋅
= −
−
⋅
=
1
6 5 1 3 1
2 1 5 1 2 1
2
2 3
1
3
2
2
,
( )
( )
( )
.
∴ the asymptote is y x
= +
1
3
⇒ y x
− − =
1
3
0.
When m c
= − = −
− − − −
− − −
= −
+ −
− −
=
2
6 5 2 3 2
2 2 5 2 2
6 10 12
4 5 8
2
2
,
[ ( ) ( ) ]
( )[ ( ) ]
[ ]
[ ]
−
−
×
= −
4
4 3
1
3
.
∴ the asymptote is y x
= − −
2
1
3
⇒ y x
+ + =
2
1
3
0.
When m c
= = −
− × − ⋅
⋅ − ⋅
2
6 5 2 3 2
2 2 5 2 2
2
2
,
[ ]
( )
= −
− −
−
[ ]
( )
6 10 12
4 5 8
= −
×
= −
16
4 3
4
3
.
∴ the asymptote is y x
= −
2
4
3
⇒ y x
− + =
2
4
3
0.
The fourth degree equation has 4 asymptotes.
∴ the combined equation of the asymptotes is
y x y x y x y x
+ −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟ − +
⎛
⎝
⎜
⎞
⎠
⎟ =
4
3
1
3
2
1
3
2
4
3
0
⇒ y x y x y x y x y x y x
2 2 2 2
1
3
4
3
4
9
4
4
3
2
1
3
2
4
9
− − + − − +
⎡
⎣
⎢
⎤
⎦
⎥ − + + + − +
⎡
( ) ( ) ( ) ( )
⎣
⎣
⎢
⎤
⎦
⎥ = 0
⇒ ( )( ) ( )( ) ( )( ) ( )
y x y x y x y x y x y x y x
2 2 2 2 2 2 2 2 2 2
4
4
3
2
1
3
2
4
9
− − + − + + − − + −
− + − − + + − + − − +
1
3
4
4
9
2
1
9
2
4
27
2 2
( )( ) ( )( ) ( )( ) ( )
y x y x y x y x y x y x y x
− − − − − + − − − − −
4
3
4
16
9
2
4
9
2
16
27
2 2
( )( ) ( )( ) ( )( ) ( )
y x y x y x y x y x y x y x
+ − + + + − + =
4
9
4
16
27
2
4
27
2
16
81
0
2 2
( ) ( ) ( )
y x y x y x
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 118 5/19/2016 7:43:23 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-341-2048.jpg)
![Differential Calculus ■ 3.119
⇒ ( )( )
x y y x xy x x y y x xy x
2 2 2 2 2 3 2 2 2
4 3 6 5
17
9
2
9
5
3
4
3
16
81
0
− − − + − + + + − − =
∴ A x y y x xy x x y y x xy x
≡ − − − + − + + + − − =
( )( )
2 2 2 2 2 3 2 2 2
4 3 6 5
17
9
2
9
5
3
4
3
16
81
0
C x y y x x x y xy y x xy
≡ − − + − − + − + − =
( )( )
2 2 2 2 3 2 2 2 2
4 6 5 3 2 3 1 0.
The points of intersection lie on the curve C A
− = 0.
⇒ 2
17
9
2
9
3
5
3
4
3
1
16
81
0
2 2 2 2
y y x x xy xy x
− − − + − + − + =
⇒
1
9
11
9
4
3
4
3
65
81
0
2 2
y x
xy
x
− + + − =
⇒ y x xy x
2 2
11 12 12
65
9
0
− + + − = .
which is a hyperbola. [
∴
h2
− ab 0]
EXAMPLE 7
Determine the asymptotes of the curve
4 17 4 4 2 2 0
4 4 2 2 2 2 2
( ) ( ) ( )
x y x y x y x x
1 2 2 2 1 2 5 and show that they pass through the points
of intersection of the curve with the ellipse x y
2 2
4 4
1 5 .
Solution.
The given curve is
4 17 4 4 2 2 0
4 4 2 2 2 2 2
( ) ( ) ( )
x y x y x y x x
+ − − − + − =
Put x y m
= =
1, in the fourth degree terms, we get f4
4 2
4 1 17
( ) ( )
m m m
= + −
∴ ′ = −
f4
3
16 34
( )
m m m
Put x y m
= =
1, in the third degree terms, we get f3
2
4 4 1
( ) ( )
m m
= − − .
∴ c
m
m
= −
′
f
f
3
4
( )
( )
=
−
−
=
−
−
4 4 1
16 34
2 4 1
8 17
2
3
2
3
( ) ( )
m
m m
m
m m
Solving, f4 0
( )
m = , we get
4 1 17 0
4 2
( )
+ − =
m m ⇒ 4 17 4 0
4 2
m m
− + =
⇒ 4 16 4 0
4 2 2
m m m
− − + = ⇒ 4 4 1 4 0
2 2 2
m m m
( ) ( )
− − − =
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 119 5/19/2016 7:43:29 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-342-2048.jpg)
![3.120 ■ Engineering Mathematics
⇒ ( )( )
4 1 4 0
2 2
m m
− − = ⇒ 4 1 0
2
m − = or m2
4 0
− = ⇒ m = ±
1
2
or m = ± 2.
When m = −
1
2
, c =
⋅ −
⎛
⎝
⎜
⎞
⎠
⎟ −
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
−
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟
=
⋅ −
⎡
⎣
2 4
1
2
1
8
1
2
17
1
2
2 4
1
4
1
2
3
⎢
⎢
⎤
⎦
⎥
− +
=
1
17
2
0.
∴ the asymptote is y
x
y x
= − ⇒ + =
2
2 0 .
When m =
1
2
, c =
⋅
⎛
⎝
⎜
⎞
⎠
⎟ −
⎡
⎣
⎢
⎤
⎦
⎥
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
=
2 4
1
4
1
8
1
2
17
1
2
0
3
. ∴ the asymptote is y
x
y x
= ⇒ − =
2
2 0 .
When m = −2, c =
⋅ −
− − −
2 4 4 1
8 2 17 2
3
( )
( ) ( )
=
×
− +
=
−
= −
2 15
64 34
30
30
1.
∴ the asymptote is y x y x
= − − ⇒ + + =
2 1 2 1 0.
When m = 2, c =
⋅ −
× − ×
2 4 4 1
8 2 17 2
3
( )
=
×
−
= =
2 15
64 34
30
30
1.
∴ the asymptote is y x y x
= + ⇒ − + =
2 1 2 1 0
( ) .
The 4th
degree equation has 4 asymptotes.
Now the combined equation of the asymptotes is
( )( )[ ( )][ ( )]
2 2 2 1 2 1 0
y x y x y x y x
+ − + + − + =
⇒ ( )[ ( ) ]
4 2 1 0
2 2 2 2
y x y x
− − + =
⇒ ( )[ ( )]
4 4 4 1 0
2 2 2 2
y x y x x
− − + + =
⇒ ( )( )
4 4 4 1 0
2 2 2 2
y x y x x
− − − − =
⇒ ( )( ) ( ) ( )
4 4 4 4 4 0
2 2 2 2 2 2 2 2
y x y x x y x y x
− − − − − − =
⇒ 4 17 4 16 4 4 0
4 2 2 4 2 3 2 2
y x y x xy x y x
− + − + − + =
⇒ 4 17 16 4 4 0
4 4 2 2 2 3 2 2
( )
x y x y xy x y x
+ − − + − + =
∴ A x y x y xy x y x
≡ + − − + − + =
4 17 16 4 4 0
4 4 2 2 2 3 2 2
( )
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 120 5/19/2016 7:43:38 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-343-2048.jpg)


![Differential Calculus ■ 3.123
Theorem 3.8 Criterion for Concavity
Let f be defined on [a, b] and let f″ exist in (a, b).
1. If f″ (x) 0 ∀ x a b
∈( , ), then the graph of f, viz, the curve y f x
= ( ) is concave down in ( , ).
a b
2. If f″ (x) 0 ∀ x a b
∈( , ), then the graph of f, viz, the curve y f x
= ( ) is concave up in ( , ).
a b
Definition 3.10 Point of Inflexion
A point P on the curve y f x
= ( ) is said to be a point of inflexion, if the curve has a tangent at the point
P and the curve changes from concave up to concave down or vice versa at the point P.
Criteria for point of inflexion (or inflection)
1. If f be a function such that f″(c) = 0 and f″′(c) ≠ 0 then the point ( , ( ))
c f c is a point of inflexion
on the curve y f x
= ( ).
2. Let f be a function such that f″(x) changes sign in a neighbourhood ( , )
c c
− +
d d of c as x
increases, then the point ( , ( ))
c f c is a point of inflexion on the curve y f x
= ( ).(even if f″(c) = 0
or f″(c) does not exist).
Note
1. The position of the point of inflexion on a curve is independent of the position of x and y axes.
Therefore, the point of inflexion is unaffected by the
interchange of these x and y axes. When
dy
dx
= ∞, we may
use
dx
dy
d x
dy
,
2
2
to determine the point of inflexion.
2. At a point of inflexion, the curve crosses the tangent at the
point.
For example, for the curve y x x
= =
3
0
, is a point of
inflexion, the tangent at the point is x-axis
x
O
y
y = x3
Fig. 3.27
x = a x = b
Concave up
x = a x = b
Concave down
Fig. 3.25 Fig. 3.26
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 123 5/19/2016 8:44:58 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-346-2048.jpg)
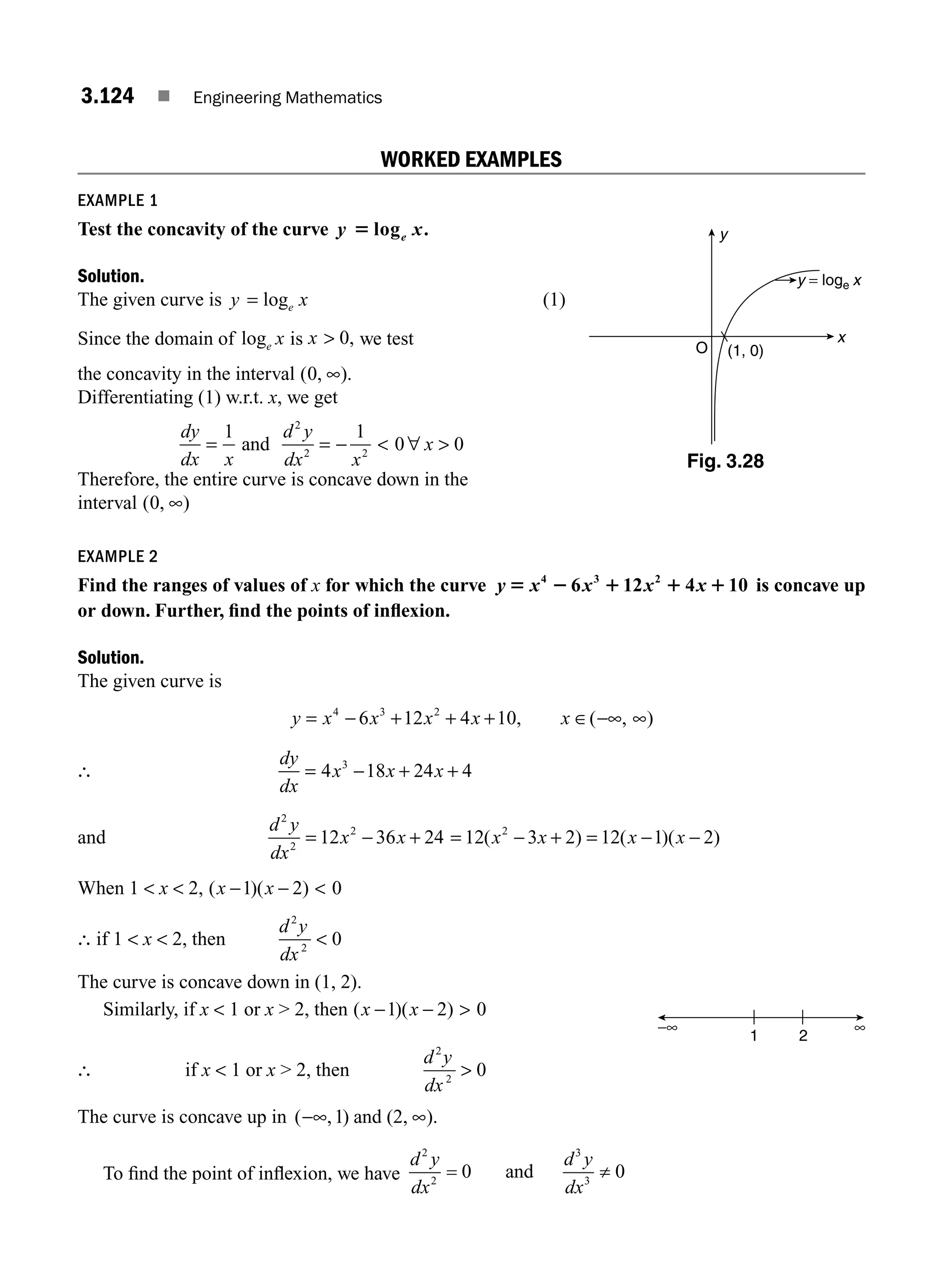
![Differential Calculus ■ 3.125
Now,
d y
dx
2
2
0
= ⇒ 12 1 2 0 1 2
( )( )
x x x
− − = ⇒ = or
and
d y
dx
3
3
= 24 36
x −
When x
d y
dx
= = ⋅ − = − ≠
1 24 1 36 12 0
3
3
,
When x
d y
dx
= = ⋅ − = ≠
2 24 2 36 12 0
3
3
,
When x = 1 and x = 2, the curve has the points of inflexion.
When x y
= = − × + × + × + =
1 1 6 1 12 1 4 1 10 21
, .
When x y
= = − × + × + × + =
2 2 6 2 12 2 4 2 10 34
4 3 2
,
The points of inflexion on the curve are (1, 21) and (2, 34).
EXAMPLE 3
Test the concavity of the curve x y a x y a
2 2 3
1 1 5
( ) and show that the points of inflexion lie on
the line x y a
1 5
4 3 .
Solution.
The given curve is
x y a x y a
2 2 3
+ + =
( )
⇒ y x a a a x
( )
2 2 3 2
+ = − ⇒ y
a a x
x a
=
−
+
2
2 2
( )
(1)
Differentiating (1) w.r. to x
dy
dx
a x a a x x
x a
a x a ax x
x
=
+ − − −
+
=
− − − +
2 2 2
2 2 2
2 2 2 2
2
1 2
2 2
[( )( ) ( ) ]
( )
[ ]
( +
+
=
− −
+
a
a x ax a
x a
2 2
2 2 2
2 2 2
2
)
[ ]
( )
and
d y
dx
a x a x a x ax a x a x
x a
2
2
2 2 2 2 2 2 2 2
2 2 4
2 2 2 2 2
=
+ − − − − + ⋅
+
[( ) ( ) ( ) .( ) ]
( )
=
=
+ + − − − −
+
a x a x a x a x x ax a
x a
2 2 2 2 2 2 2
2 2 4
2 4 2
( )[ ( )( ) ( )]
( )
=
− + − − + +
+
=
− − + +
2 2 4 2
2 3 3
2 3 2 2 3 3 2
2 2 3
2 3 3 2
a x ax a x a x ax a x
x a
a x a ax
[ ]
( )
[ a
a x
x a
2
2 2 3
]
( )
+
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 125 5/19/2016 8:45:04 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-348-2048.jpg)
![3.126 ■ Engineering Mathematics
=
− + + +
+
= −
+
+
− + −
2 3
2
2 3 3
2 2 3
2
2 2 3
2 2
a x a ax x a
x a
a x a
x a
x ax a
[ ( ) ( )]
( )
( )
( )
3
3
2
4
2
2 2 3
2 2
ax
a x a
x a
x ax a
⎡
⎣ ⎤
⎦ = −
+
+
− +
⎡
⎣ ⎤
⎦
( )
( )
∴
d y
dx
x a x ax a
2
2
2 2
0 4 0
= ⇒ + − + =
( )[ ] ⇒ x a x a a
+ = − =
0 4
2
or 0
2
x +
Now, x a x a
+ = ⇒ = −
0
and x a a
2
4
− x + =
2
0
⇒ x
a a a
=
+ −
4 16 4
2
2 2
=
+
= ±
4 2 3
2
2 3
a a
a
( )
∴ x a x a x a
= − = − = +
, ( ) , ( )
2 3 2 3
and
d y
dx
a
x a
x a x a x a
2
2
2
2 2 3
2
2 3 2 3
= −
+
+ − − − +
( )
( )[ ( ) ][ ( ) ]
If x −a, all the three factors are negative.
⇒ ( )[ ( ) ] [ ( ) ]
x a x a x a
+ − − − +
2 3 2 3 0 and
a
x a
2
2 2 3
2
0
−
+
( )
always
∴
d y
dx
2
2
0
If − −
a x a
d y
dx
( ) ,
2 3 0
2
2
then
If ( ) ( ) ,
2 3 2 3 0
2
2
− +
a x a
d y
dx
then
If x a
d y
dx
+
( ) ,
2 3 0
2
2
then
∴ the curve is concave up in the intervals ( , ), [( ) , ( ) ]
−∞ − − +
a a a
2 3 2 3 and concave down in the
intervals [ , ( ) ] [( ) , )
− − + ∞
a a a
2 3 2 3
and
The points of inflexion are at x a a a
= − − +
, ( ) , ( ) .
2 3 2 3
When x a y
a a a
a a
a
= − =
+
+
=
,
( )
2
2 2
When x a y
a a a
a a
a
a
a
= − =
− −
− +
=
−
− + +
=
( ) ,
[ ( ) ]
( )
[ ]
[ ]
(
2 3
2 3
2 3
3 1
4 4 3 3 1
3
2
2 2 2
3
2
−
−
−
1
8 4 3
)
⇒ y
a a
=
−
−
=
−
−
∴ − = − = −
( )
[ ]
( )
( )
[ ( ) ( )]
3 1
4 2 3
3 1
2 3 1
3 1 4 2 3 2 2 3
2
2
−∞ ∞
−a (2 − 3)a (2 + 3)a
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 126 5/19/2016 8:45:07 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-349-2048.jpg)
![Differential Calculus ■ 3.127
=
−
=
+
− +
=
+
a a a
2 3 1
3 1
2 3 1 3 1
3 1
4
( )
( )
( )( )
( )
When x a
= +
( ) ,
2 3 y
a a a
a a
a
a
y
a
=
− +
+ +
=
− −
+ + +
=
− +
2
2 2 2
3
2
2 3
2 3
3 1
4 3 4 3 1
3 1
4 2
[ ( ) ]
( )
[ ]
( )
( )
( +
+
=
− +
+
3
3 1
2 3 1 2
)
( )
( )
a
=
−
+
=
− −
+ −
=
− −
a a a
2 3 1
3 1
2 3 1 3 1
3 1
4
( )
( )
( )( )
( )
Thus, the points of inflexion are the points A(−a, a), B 2 3
4
3 1
−
( ) +
( )
⎛
⎝
⎜
⎞
⎠
⎟
a
a
,
and C = 2 3
4
3 1
+
( ) − −
( )
⎛
⎝
⎜
⎞
⎠
⎟
a
a
,
To prove the points A, B, and C are collinear, we have to prove the slope of AB = the slope BC.
Now, the slope of AB =
+ −
− +
a
a
a a
4
3 1
2 3
( )
=
+ −
− +
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥ = −
a
a
4
3 1 4
2 3 1
1
4
3 3
3 3
1
4
( )
( )
and slope of BC =
− − − +
+ − −
=
− − + +
⎡
⎣
⎤
⎦
+ − −
⎡
⎣
⎤
⎦
=
a a
a a
a
a
4
3 1
4
3 1
2 3 2 3
4
3 1 3 1
2 3 2 3
( ) ( )
( ) ( )
−
− = −
1
4
2 3
2 3
1
4
∴ slope of AB = slope of BC
Therefore, the points A, B, C are collinear.
The equation of the line in which the points of inflexion is
y a x a
− = − +
1
4
( ) ⇒ 4 4
y a x a
− = − − ⇒ x y a
+ =
4 3
EXERCISE 3.14
1. Show that y x
= 4
is concave upwards at the origin.
2. Find the intervals in which the curve y x x x
= − + −
3 40 3 20
5 3
is concave upwards or
downwards.
3. Find the intervals in which the curve y x x
= −
3 2
2 3
is concave upwards or concave downwards.
4. Show that the curve y
x
x
=
+
6
3
2
has three points of inflexion and they are collinear.
5. Find the points of inflexion of the curve y x x
2 2
1
= +
( ) .
[ ( ) ( )
∴ + = + + = +
3 1 3 1 2 3 2 2 3
2
⇒
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 127 5/19/2016 8:45:10 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-350-2048.jpg)

![Differential Calculus ■ 3.129
6. Sign of
dy
dx
Determine the intervals of increasing, decreasing, Critical points etc.
7. Sign of
d y
dx
2
2
Intervals of concavity upwards and downwards and point of inflexion.
8. Loop
If the curve intersects the line of symmetry at two points A and B , then there is a loop
between A and B .
Note
However, the order of the steps can be interchanged depending on the nature of the equation of the curve.
WORKED EXAMPLES
EXAMPLE 1
Trace the curve y x
2 3
5 . [It is called the semi-cubical parabola]
Solution.
The given curve is y x
2 3
= .
1. Symmetry
The given equation is even degree in y, so the curve is symmetrical about the x-axis.
2. Origin: it is a point on the curve.
3. Tangent at the origin:
The tangent at the origin is got by equating the lowest degree terms to zero.
That is y y
2
0 0
= ⇒ =
∴ the x-axis is the tangent at the origin.
4. Region
y x x
2 3
0 0 0
≥ ⇒ ≥ ⇒ ≥ . ∴ the curve lies on the right side of y-axis.
5. Sign of
dy
dx
y x y
dy
dx
x
2 3 2
2 3
= ⇒ = ⇒
dy
dx
x
y
=
3
2
2
∴ if y 0,
dy
dx
0 That is, the curve is increasing for all x ≥ 0 and y 0.
So, the curve is increasing in the first quadrant.
Also if y 0,
dy
dx
0 i.e., the curve is decreasing for all x ≥ 0 and y 0.
So, the curve is decreasing in the 4th
quadrant.
M03_ENGINEERING_MATHEMATICS-I _CH03_Part D.indd 129 5/19/2016 8:45:18 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-352-2048.jpg)
![3.130 ■ Engineering Mathematics
6. Sign of
d y
dx
2
2
d y
dx
y x x
dy
dx
y
2
2
2
2
3
2
2
=
⋅ − ⋅
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
− ⋅
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
3
2
2 2
2
xy x
dy
dx
y
= −
⎡
⎣ ⎤
⎦
3
2
4 3
3
2 3
x
y
y x = ⋅ −
⎡
⎣ ⎤
⎦
3
4
4 3
3
3 3
x
y
x x = = = ⋅ =
3
4
3
4
3
4
1 3
4
4
3
4
2
4
3
x
y
x
yy
x
y x
x
y
.
∴
d y
dx
2
2
0
if y 0 (as already x 0) and
d y
dx
2
2
0
if y 0.
∴ the curve is concave up if y 0 and concave
down if y 0.
So, the curve is concave up in the first quadrant and the
curve is concave down in the fourth quadrant.
7.Asymptotes
It has no asymptotes.
With these information we shall draw the curve.
The curve is as shown in Fig. 3.29.
EXAMPLE 2
Trace the curve y a x x
2 3
2
( ) .
2 5 [This curve is called the Cissoid of Diocles]
Solution.
The given equation of the curve is y
x
a x
2
3
2
=
−
. (1)
1.Symmetry
The equation is even degree in y, so the curve is symmetrical about the x-axis.
2. Origin: It is a point on the curve.
The tangent at the origin is given by y y
2
0 0
= ⇒ = That is the x-axis is the tangent at the origin.
3. Region:
y
x
a x
x
x a
2
3 3
0
2
0
2
0
≥ ⇒
−
≥ ⇒
−
≤ ⇒
x
x a
x a
3
2
0 0 2
−
≤ ⇒ ≤ .
∴ the curve lies between the lines x = 0 and x a
= 2 .
4.Asymptote
When x a
→ 2 , y → ∞ ∴ x a
= 2 is a vertical asymptote.
5. Sign of
dy
dx
Differentiating (1) with respect to x, we get
x
y
o
Fig. 3.29
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 130 5/19/2016 8:48:06 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-353-2048.jpg)
![Differential Calculus ■ 3.131
2
2 3 1
2
6 2
2
2 3
2
2 3
2
y
dy
dx
a x x x
a x
ax x
a x
=
− ⋅ − −
−
=
−
−
( ) ( )
( ) ( )
⇒
dy
dx
x a x
y a x
x a x
y a x
=
−
−
=
−
−
2 3
2 2
3
2
2
2
2
2
( )
( )
( )
( )
Since 0 2 3 0
≤ −
x a a x
, and ( ) .
2 0
2
a x
−
∴
dy
dx
0 if y 0
and
dy
dx
0 if y 0
∴ the curve is increasing in the first quadrant and the curve is decreasing in the 4th
quadrant
Also it touches x a
= 2 at infinity
With these informations, we can draw the curve.
The curve is as shown in Fig. 3.30.
EXAMPLE 3
Trace the curve y
x a x
a x
2
2 2 2
2 2
5
2
1
( )
. [This curve is called Lemniscate of Bernoulli]
Solution.
The given equation of the curve is y
x a x
a x
2
2 2 2
2 2
=
−
+
( )
(1)
1. Symmetry
The equation is even degree in x and y .
So, the curve is symmetrical about the x-axis as well as the y-axis.
When ( , )
x y is replaced by ( , )
− −
x y equation is unaltered.
∴ the curve is symmetrical about the origin.
2. Origin
Origin is a point on the curve.
3. Tangent at the origin
We have
y
x a x
a x
2
2 2 2
2 2
=
−
+
( )
⇒ y a x x a x
2 2 2 2 2 4
( )
+ = − ⇒ a x y x y x
2 2 2 2 2 4
( )
− = +
Tangent at the origin is got by equating the lowest degree terms to zero.
i.e., x y
2 2
0
− = ⇒ = ±
y x
∴ y x
= and y x
= − are the tangents at the origin.
Fig. 3.30
x
y
o
x = 2a
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 131 5/19/2016 8:48:10 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-354-2048.jpg)
![3.132 ■ Engineering Mathematics
4. Special points
To find the point of intersection with the x-axis, put y = 0 in (1)
∴ x a x
2 2 2
0
( )
− = ⇒ x2
0
= or a x
2 2
0
− = ⇒ x = 0 0
, or x a
= ±
So, the curve passes through the origin twice and the points ( , ), ( , )
−a a
0 0 .
To find the intersection with the y-axis, put x = 0 in (1).
∴ y = 0
So, it meets the y-axis only at the origin.
5. Region
y
x a x
a x
2
2 2 2
2 2
=
−
+
( )
y x a x
a x
2 2 2 2
2 2
0 0
0
≥ ⇒ − ≥
⇒ − ≥
( )
⇒ x a a x a
2 2
0
− ≤ ⇒ − ≤ ≤ .
∴ the curve lies between x = −a and x = a.
6. Loop
Since the curve meets the line of symmetry, the
x-axis, at O( , ), ( , ), ( , )
0 0 0 0
A a B a
− there is a loop
between O and A and a loop between O and B.
With these informations, we shall draw the curve.
The curve is as shown in Fig. 3.31.
EXAMPLE 4
Trace the curve x y axy a
3 3
3 0
1 5 , . [This curve is called the Folium of Descartes]
Solution.
The given equation of the curve is x y axy a
3 3
3 0
+ =
, (1)
1. Symmetry
The equation is unaltered if x and y are interchanged.
So, the curve is symmetric about the line y x
= .
2. Origin
Origin lies on the curve.
3. Tangent at the origin
Tangents at the origin are got by equating the lowest degree terms to zero
∴ xy = 0 ⇒ x = 0, y = 0
So, the y-axis and the x-axis are the tangents at the origin.
y
x
A
B
O
y = −x
y = x
(a, 0)
(−a, 0)
Fig. 3.31
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 132 5/19/2016 8:48:14 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-355-2048.jpg)


![Differential Calculus ■ 3.135
Solution.
The equation of the given curve is y
x
x
=
+
−
2
2
1
1
(1)
1. Symmetry
Since the equation is even degree in x, the curve is symmetrical about the y-axis.
2.Asymptotes
When x = −1 and x y
= → ∞
1,
∴ x = −1 and x = 1 are vertical asymptotes.
lim lim lim
x x x
y
x
x
x
x
→∞ →∞ →∞
=
+
−
=
+
−
=
2
2
2
2
1
1
1
1
1
1
1
∴ y = 1 is the horizontal asymptote.
3. Region
y
x
x
=
+
−
2
2
1
1
⇒ y x x
( )
2 2
1 1
− = + ⇒ x y y
2
1 1
( )
− = + ⇒ x
y
y
2 1
1
=
+
−
Series x
y
y
y y
2
0
1
1
0 1 1
≥ ⇒
+
−
≥ ⇒ ≤ − ≥
or
The curve lies in the part of y ≤ −1 and y 1
i.e., the curve lies above the line y = 1 and below the line y = −1 for all x ≠ ±1
4. Sign of
dy
dx
y
x
x
dy
dx
x x x x
x
x x x
x
=
+
−
=
− ⋅ − +
−
=
− − −
2
2
2 2
2 2
2 2
1
1
1 2 1 2
1
2 1 1
( ) ( )( )
( )
[ ]
( 2
2 2 2 2
1
4
1
−
= −
−
) ( )
x
x
∴
dy
dx
x
0 if 0 and
dy
dx
x
0 if 0
So, the curve is increasing if x 0 and is decreasing if x 0
When x y
= = −
0 1
, . In the interval (−1, 1) the curve increases upto the point (0, −1) and then
decreases.
If −
1 1
x , then x y
2
1 0 0
− ∴
.
So, in this part, the curve lies below the x-axis.
If x 1, then
dy
dx
0 and so, the curve is decreasing.
If x −1,then
dy
dx
0 and so, the curve is increasing.
∴
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 135 5/19/2016 8:48:26 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-358-2048.jpg)
![3.136 ■ Engineering Mathematics
5. Sign of
d y
dx
2
2
We have
dy
dx
x
x
= −
−
4
1
2 2
( )
∴ d y
dx
x x x x
x
x x
2
2
2 2 2
2 4
2 2
4 1 1 2 1 2
1
4
1 1
=
− − ⋅ − ⋅ −
⎡
⎣ ⎤
⎦
−
= −
− − −
( ) ( )( )
( )
( )[ 4
4
1
4 1 3
1
2
2 4
2
2 3
x
x
x
x
]
( )
( )
( )
−
=
+
−
If x 1,
d y
dx
2
2
0
∴ the curve is concave up [∴ x2
− 1 0]
If x −1,
d y
dx
2
2
0
∴ the curve is concave up
6.Assymptotes
x = −1, x = 1 are the vertical asymptotes. y = 1 is the horizontal asymptote.
The curve lies in the region y −1 and y 1 and decreasing if x 1 and concave up.
Increasing if x −1 and concave up
We draw the curve.
The curve is as shown in Fig. 3.34.
y
x
y = 1
x = 1
y = −1
x = −1
O
(0, 1)
(0, −1)
Fig. 3.34
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 136 5/19/2016 8:48:28 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-359-2048.jpg)
![Differential Calculus ■ 3.137
3.10.2 Procedure for Tracing of Curve Given by Parametric Equations x 5 f(t), y 5 g(t)
If the current coordinates (x, y) of the curve are expressed interms of another variable t, then t is called
the parameter and the equations x = f(t), y = g(t) are called the parametric equations of the curve.
1. Symmetry
(i) If f(−t) = f(t) and g(−t) = −g(t), then the curve is symmetrical about the x-axis.
(ii) If f(−t) = −f(t) and g(−t) = g(t), then the curve is symmetrical about the y-axis.
(iii) If f(−t) = f(t) and g(−t) = g(t), then the curve is symmetrical in the opposite quadrants.
2. Special points
To find the points of intersection with x-axis, put y = 0 ⇒ g(t) = 0
To find the points of intersection with the y-axis, put x = 0 ⇒ f(t) = 0.
3. Region
Determine the limits of x and y and hence the limt of t
4. Sign of derivative
dy
dx
Find
dx
dt
and dy
dx
and the values of t for which x and y are increasing or decreasing.
Find the tangent parallel to the axes.
i.e.,
dy
dx
= 0 or ∞.
Also check for concavity. i.e.,
d y
dx
2
2
0
or 0
5. Period
If x and y are periodic functions of t with a common period, study the curve in this period.
Note If it is possible to eliminate the parameter t and get the Cartesian form, then we can trace the
curve by the first method.
WORKED EXAMPLES
EXAMPLE 7
Trace the curve x a t
a t
y a t
e
5 1 5
cos log tan ; sin .
2 2
2
[This curve is called the tractrix]
Solution
Given x a t
a t
y a t
e
= + =
cos log tan sin .
2 2
2
and
Let x = f(t) and y = g(t).
1. Symmetry
f t a t
a t
a t
a t
f t
e e
( ) cos( ) log tan cos log tan ( )
− = − + −
⎛
⎝
⎜
⎞
⎠
⎟ = + =
2 2 2 2
2 2
and g t a t a t g t
( ) sin( ) sin ( ).
− = − = − = −
∴ the curve is symmetrical about the x-axis.
2. Intersection with the axes
To find the intersection with the x-axis, put y = 0 ∴ a t t
sin , , , ...
= ⇒ =
0 0 2
p p
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 137 5/19/2016 8:48:29 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-360-2048.jpg)

![Differential Calculus ■ 3.139
EXAMPLE 8
Trace the curve x a y a
5 u 2 u 5 2 u
( sin ), ( cos ).
1 [This curve is called a cycloid]
Cycloid is a curve traced out by a fixed point on the circumference of a circle when it rolls on a
fixed straight line without slipping.
This fixed line is called the base of the curve.
Solution.
Given parametric equations are x a y a
= − = −
( sin ) ( cos )
u u u
and 1
Let x f
= ( )
u and y g
= ( )
u
1. Symmetry
f a
( ) ( sin( ))
− = − − −
u u u = − + = − − = −
a a f
( sin ) ( sin ) ( )
u u u u u
g a
( ) ( cos( ))
− = − −
u u
1 = − =
a g
( cos ) ( )
1 u u
∴ the curve is symmetric about the y-axis.
We shall consider the graph for u ≥ 0.
2. To find the point of intersection with the x-axis
Put y a
= ⇒ − = ⇒ =
0 1 0 1
( cos ) cos
u u ⇒ u p p
= 0 2 4
, , ,…
When u = 0, x y
= =
0 0
and
∴ the origin corresponds to u = 0 and the origin lies on the curve.
Since − ≤ ≤
1 1
cosu , 0 2
≤ ≤
y a.
When u p
= 2 , x a a
= − =
( sin )
2 2 2
p p p and y a
= − =
( )
1 1 0.
∴ the points of intersections with x-axis are ( , ) , )
0 0 2 0
and ( pa .
When u p p p p
= = =
, x a a
( sin )
− and y a a
= − =
( cos )
1 2
p , which is the maximum value of y.
3. Sign of the derivative
dx
d
a a
u
u
u
= − =
( cos ) sin
1 2
2
2
and
dy
d
a
u
u
= sin
If 0
u p, then
dx
du
0 and
dy
du
0
∴ x increases from 0 to 2ap and y increases from
0 to 2a.
We shall draw one arch of the curve between
u = 0 and u p
= 2 .
i.e., between the points ( , )
0 0 and ( , )
2 0
ap on the
curve.
We see that the curve increases from ( , )
0 0
to ( , )
a a
p 2 and decreases from ( , )
a a
p 2 to
( , )
2 0
ap as in Fig. 3.37.
x
y = 2a
(2aπ, 0)
(aπ, 2a)
O
Fig. 3.37
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 139 5/19/2016 8:48:39 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-362-2048.jpg)

![3.142 ■ Engineering Mathematics
(v) When u is replaced by p and r is replaced by –r and if the equation is unaltered, then the
curve is symmetrical about the pole.
2. Pole
If r = 0 for u a
= , then the curve passes through the pole and the line u a
= is tangent at the
pole.
3. Region
If r is imaginary for values of u lying between u u u u
= =
1 2
, ,
and then the curve does not lie
between the lines u u u u
= =
1 2
, .
and
4. Points of intersection
Determine the points where the curve meets the lines u u
p
u
p
u p u
p
= = = = =
0
4 2
3
2
, , , ,
5. Tangent line
Find the values of f with the formula tanf
u
= r
d
dr
where f is the angle between the tangent at
the point p r
( , )
u and the radius vector OP.
6. Loop
If a curve meets a line u a
= at A and B and the curve is symmetrical about the line, then a loop
of the curve exists between A and B.
WORKED EXAMPLES
EXAMPLE 1
Trace the curve r a
5 1 u
(1 cos ). [This curve is called a cardioid]
Solution.
The given curve is r a
= +
( cos )
1 u
1. Symmetry
If u is replaced by −u, then r a
= + −
( cos( ))
1 u = a( cos )
1+ u
Therefore, the equation is unaltered. Hence, the curve is symmetrical about the initial line u = 0.
2. r = ⇒ + ⇒ = −
0 1 0 1
cos cos
u u
= ⇒ u p
=
∴ the tangent at the pole is the line u p
=
3. When u = 0, r a
= 2 , which is the maximum value of r.
When u varies from 0 to p, r decreases from 2a to 0.
4. We know that tan f
u
= r
d
dr
.
Therefore,
dr
d
a
u
u
= −
( sin ) ⇒
d
dr a
u
u
= −
1
sin
∴ tan ( cos )
sin
f u
u
= +
−
⎛
⎝
⎜
⎞
⎠
⎟
a
a
1
1
= − = − = +
⎛
⎝
⎜
⎞
⎠
⎟
2
2
2
2 2
2 2 2
2
cos
sin cos
cot tan
u
u u
u p u
f
p u
=
2 2
+
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 142 5/19/2016 8:48:47 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-365-2048.jpg)
![Differential Calculus ■ 3.143
When u f
p
= =
0
2
,
∴ the tangent at the point (2a, 0) is perpendicular to the initial line u = 0
u
p p p
p
: 0
points:
3 2
2
3
2
3
2 2
0
r a
a
a
a
O
:
A B C D
The curve is as in figure A to O
By symmetry about u = 0, by reflecting the point ABCDO about u = 0,
we get the full curve as in Fig. 3.41.
O
θ = π θ = 0
A
a
2a
B
C
D
x
y
2π
3 π
3
2
3a
2
a
(2a, 0)
θ =
θ =
Fig. 3.41
EXAMPLE 2
Trace the curve r a
5 u
sin .
3 [This curve is called 3 leaved rose]
Solution.
The given curve is r a
= sin3u.
1. Symmetry
When u is replaced by p u
− , r a a a
= − = − =
sin ( ) sin( ) sin
3 3 3 3
p u p u u
So, the equation is unaltered.
Hence, the curve is symmetrical about the line u
p
=
2
(i.e., y-axis)
2. The maximum value of r is a, when sin 3u is maximum,
That is, when sin 3u = 1.
⇒ 3
2
5
2
9
2
u
p p p
= , , ,..... ⇒ u
p p p
= ……
6 6
9
6
, , ,
5
⇒ u = ° °
30 150 270
° ...
, , ,
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 143 5/19/2016 8:48:51 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-366-2048.jpg)


![3.146 ■ Engineering Mathematics
EXERCISE 3.15
Trace the following curves
1. y
x
a x
2
3
2
=
−
2. a y x a x
2 2 2 2 2
= −
( ) 3. y
x a x
a x
2
2
=
−
+
( )
4. y
x
x
2
2
2 1
1
=
−
−
5. x y a
2
3
2
3
2
3
+ = 6. y x x a
2 2 2 2
= −
7. y
x
x
2
3
1
=
−
8. x x y a x y
2 2 2 2 2 2
( ) ( )
+ = − 9. r a
= sin 2u
10. r a
= −
( cos
1 u) 11. r = −
1 2sinu 12. x
at
t
y
at
t
a
=
+
=
+
3
1
3
1
0
3
2
3
, ,
[Hint: Folium of Descartes]
13. y a x x a x a
2 2
0
( ) ( ), .
− = + 14. xy a a x a
2 2
0
= −
( ),
15. x a
= =
cos .
3 3
u u
, sin
y a
ANSWERS TO EXERCISE 3.15
1.
x
y
O
x = 2a
2.
x
y
y = x
y = −x
O
20
(a, 0)
(−a, 0)
3.
x
y
y = x
y = −x
x = −a
4.
(−1, 0) (1, 0)
(0, 1)
(0, −1)
1
x = −1
x = 1
x
y
1
2
2
( , 0)
x =
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 146 5/19/2016 8:49:02 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-369-2048.jpg)
![3.148 ■ Engineering Mathematics
11.
π
2
θ = 0
y
x
θ =
3π
2
θ =
13. y
x
y = −x
y = x
x = a
O
B A
(a, 0)
(−a, 0)
14.
x
y
O (a, 0)
x = a
x = 0
15.
x
O
y
(0, a)
(a, 0)
(−a, 0)
(0, −a)
SHORT ANSWER QUESTIONS
1. Find the first two differential coefficients of y e x
x
5 ?
2
3
cos .
2. Find
d y
dx
y x x
3
3
3
if log
5 . 3. If y 5 a cos mx 1 b sin mx, then prove that
d y
dx
m y
2
2
2
0
1 5 .
4. If y 5 e ax b
x
3
( )
1 , then prove that
d y
dx
dy
dx
y
2
2
6 9 0
2 1 5 .
5. Show that the length of the sub-tangent at any point of the curve xm
yn
5 am 1 n
varies as the abscissa.
6. For the catenary y 5 c cos h
x
c
, prove that the length of the normal is
y
c
2
.
7. Find the equation of the tangent at the point (2, 22) on the curve y
x
x
2
3
4
5
2
.
8. Show that the curves y 5 x2
and 6y 5 7 2 x3
cut orthogonally at the point (1, 1).
9. If y 5 sin21
x, then prove that (1 2 x2
)
d y
dx
x
dy
dx
2
2
0
2 5 .
10. Find ‘c’ of Lagrange’s mean value theorem for f(x) 5 ln x in [1, e].
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 148 5/19/2016 8:49:06 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-371-2048.jpg)

![3.150 ■ Engineering Mathematics
12. lim
cos sin
sin
x
x
→
−
0
x x
x x
2
= __________
13. lim
x
x
→∞
4
2
ex
is __________
14. lim
cos
x→
−
0
3 1
2
x
x
is __________
15. The curve y = x4
at the origin is concave __________
B. Choose the correct answer
1. x x
1
, x 0, is a decreasing function if
(a) x e (b) x e (c) x
e
1
(d) x
e
1
2. The value of lim
x→
p
4
(tan x)tan2x
is
(a)
1
e
(b) e (c) e (d)
1
e
3. The vertical and horizontal asymptotes of y =
x
x − 2
are
(a) x = 2, y = 1 (b) x = 2, y = −1 (c) x = 2, y = −1 (d) x = 2, y = 2
4. The equation of the normal to the curve x2
= 4y passing through the point (1, 2) is
(a) x + y + 3 = 0 (b) x − y − 3 = 0 (c) x + y − 3 = 0 (d) None of these
5. The two curves x3
− 3xy2
+ 2 = 0 and 3x2
y − y3
− 2 = 0
(a) cut at right angles (b) touch each other
(c) cut at an angle
p
4
(d) None of these
6. If f(x) = x3
+ 3x, then the value of c ∈ (0, 4) such that
f f
f c
( ) ( )
( )
4 0
4 0
−
−
= ′ is
(a)
19
3
(b)
4
3
(c)
4
3
(d) None of these
7. If f(x) = x3
− 6x2
− 36x + 7, then f(x) is strictly increasing for the value of x.
(a) x −1 and x 5 (b) x −2 and x 6
(c) x −3 and x 3 (d) x −4 and x 1
8. Maximum value of f(x) =
x
x x
2
4
+ +
on [−1, 1] is
(a) −
1
4
(b) −
1
3
(c)
1
6
(d)
1
5
9. The curve y = 3x5
− 40x3
+ 3x − 20 is concave up in the intervals
(a) (−2, 0) and (2, ∞) (b) (−3, 0) and (1, ∞)
(c) (0, 2) and (2, ∞) (d) None of these
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 150 5/19/2016 8:49:11 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-373-2048.jpg)

![3.152 ■ Engineering Mathematics
24. The equation of the asymptotes of x3
+ y3
= 3axy, a 0, is
(a) x − y − a = 0 (b) x + y + a = 0 (c) x + y − a = 0 (d) x − y + a = 0
25. The asymptotes of the curve (y − x)2
(y − 2x) − (y − x)(y − 6x) + x − 5y + 3 = 0 parallel to the line y − x = 0
are
(a) y − x − 1 = 0 and y − x + 1 = 0 (b) y − x − 2 = 0 and y − x + 2 = 0
(c) y − x − 1 = 0 and y − x − 4 = 0 (d) None of these
ANSWERS
A. Fill up the blanks
1.
x
a
x
b
+ = 1 2. t =
1
2
3. a 4. b
a
x
2
2
5. 2 x
6. 1 7. x = −2 8. x = 1 9. y = ±x 10. [−1, 1]
11. ep
12. −
1
3
13. 0 14. −
9
2
15. up
B. Choose the correct answer
1. (b) 2. (a) 3. (a) 4. (c) 5. (a) 6. (b) 7. (b) 8. (a) 9. (c) 10. (a)
11. (b) 12. (a) 13. (b) 14. (a) 15. (b) 16. (b) 17. (d) 18. (c) 19. (b) 20. (b)
21. (c) 22. (b) 23. (c) 24. (b) 25. (c)
M03_ENGINEERING_MATHEMATICS-I _CH03_Part E.indd 152 5/19/2016 8:49:15 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-375-2048.jpg)

![4.2 ■ Engineering Mathematics
Theorem 4.1 The curvature of a circle at any point is a constant and is equal to the reciprocal of the
radius of the circle.
Proof Consider a circle with centre C and radius r. Let P and Q be two neighbouring points on the
circle.
Let the angles which the tangents at P, Q make with x-axis
be c, c + Δc ∴ ˆ
PCQ = Δc
Arc AP = s and arc AQ = s + Δs so that arc PQ = Δs
But we know arc Δs = rΔc [From trigonometry]
∴
Δ
Δ
c
s r
=
1
∴ lim [ ]
Δ
Δ
Δ
s s r
r
→
=
0
1
c
{ the radius is constant
⇒
d
ds r
c
=
1
∴ curvature at the point P is a constant =
1
r
Hence, curvature at any point of the circle is a constant =
1
r
= reciprocal of its radius
Note If r → ∞, the curvature tends to zero. i.e., when radius r → ∞, the circle approaches a straight
line.
Hence, the curvature of a straight line is zero at any of its points. In otherwords, the straight line
does not bend at any point.
Definition 4.2 Radius of Curvature
If the curvature at a point P on a curve is k, then 1
k
is called the radius of curvature at P (if k ≠ 0).
Radius of curvature is denoted by Greek letter r.
Thus, r
c
= =
1
k
ds
d
.
Note From the definition of curvature it is obvious that we should know the intrinsic equation of the
curve. This is not easy in many cases. Generally, equation of a curve is given in Cartesian or polar
coordinates. So, we shall derive formula for radius of curvature for Cartesian equation of a given curve.
4.1.2 Radius of Curvature for Cartesian Equation of a Given Curve
Let y = f(x) be the equation of a curve, then we know that at the point (x, y),
dy
dx
= tanc, where c is the
angle made by the tangent at (x, y) with the positive direction of the x-axis.
∴
d y
dx
d
dx
d
ds
ds
dx
2
2
2
2
1
=
= +
sec
( tan )
c
c
c
c
C
r
A P
Q
Δψ
ψ + Δψ
ψ
X
Y
O
Fig. 4.2
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 2 5/12/2016 10:08:27 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-377-2048.jpg)
![4.4 ■ Engineering Mathematics
4.1.3 Radius of Curvature for Parametric Equations
If the equation of curve is given by parametric equations x f t y g t
= =
( ), ( ), then we find
dx
dt
dy
dt
,
∴
Let
dx
dt
x
dy
dt
y
dy
dx
dy
dt
dx
dt
y
x
= ′ = ′
= =
′
′
,
∴ d y
dx
d
dx
dy
dx
d
dt
y
x
dt
dx
x y y x
x
2
2
2
1
=
⎛
⎝
⎜
⎞
⎠
⎟ =
′
′
⎛
⎝
⎜
⎞
⎠
⎟ ⋅
=
′ ′′ − ′ ′′
′
⋅
( ) ′
′
=
′ ′′ − ′ ′′
′
x
x y y x
x
( )3
∴ the radius of curvature r =
+
′
′
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
′ ′′ − ′ ′′
1
2 3 2
y
x
x y y x
/
(
( )
′
x 3
=
′ + ′
′ ′′ − ′ ′′
( )
[ ]
/
x y
x y y x
2 2 3 2
in magnitude
Note Radius of curvature for parametric equations can be obtained by using formula (1).
WORKED EXAMPLES
EXAMPLE 1
Find the radius of curvature at the point
1
4
1
4
1
, .
⎛
⎝
⎜
⎞
⎠
⎟ on x y
1 5
Solution.
The given curve is x y
+ = 1 (1)
Differentiating w.r.to x, we get
⇒
1
2
1
2
0
x y
dy
dx
dy
dx
y
x
+ ⋅ =
= − =
−
= −
= − = − −
x
x
y x
x
x
1
1 1
1
1
1 1 2
[ ( ) ]
/
From
= − − ⋅
⎛
⎝
⎜
⎞
⎠
⎟ =
−
d y
dx
x
1
2
1
2
2
2
3 2
/
x
x3 2
/
At the point
1
4
1
4
, ,
⎛
⎝
⎜
⎞
⎠
⎟
dy
dx
= − = − = −
1
1
14
1 2 1
/
and
d y
dx
2
2 3 2
3 2
1
2
1
4
4
2
4 2
2
4
=
⋅
⎛
⎝
⎜
⎞
⎠
⎟
= =
⋅
=
/
/
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 4 5/12/2016 10:08:39 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-379-2048.jpg)
![Applications of Differential Calculus ■ 4.5
∴ y y
1 2
1 4
= − =
and
∴ the radius of curvature r =
+
=
+
= =
( ) ( )
/ /
1 1 1 2 2
4
1
2 3 2
2
3 2
2
y
y y
1
2
EXAMPLE 2
Find the radius of curvature at the point
3
2
3
2
a a
,
⎛
⎝
⎜
⎞
⎠
⎟ on the curve x y axy
3 3
3
1 5 .
Solution.
The given curve is x y axy
3 3
3
+ = . (1)
Differentiating w.r.to x, we get
3 3 3 1
2 2
x y
dy
dx
a x
dy
dx
y
+ = + ⋅
⎡
⎣
⎢
⎤
⎦
⎥
⇒
dy
dx
y ax ay x
[ ]
2 2
− = − ⇒ dy
dx
ay x
y ax
=
−
−
2
2
(2)
Differentiating (2) w.r.to x, we get
d y
dx
y ax a
dy
dx
x ay x y
dy
dx
a
y ax
2
2
2 2
2 2
2 2
=
− −
⎛
⎝
⎜
⎞
⎠
⎟ − − −
⎛
⎝
⎜
⎞
⎠
⎟
−
( ) ( )
( )
At the point
3
2
3
2
a a
, ,
⎛
⎝
⎜
⎞
⎠
⎟
dy
dx
a
a a
a
a
a
=
⋅ −
− ⋅
= −
3
2
9
4
9
4
3
2
1
2
2
and d y
dx
a
a
a
a a
a a
a a
a
2
2
2 2 2
2
9
4
3
2
3
3
2
9
4
3
9
4
=
− ⋅
⎛
⎝
⎜
⎞
⎠
⎟ − − − −
⎛
⎝
⎜
⎞
⎠
⎟ − −
−
( ) ( )
3
3
2
2 2
a
⎛
⎝
⎜
⎞
⎠
⎟
=
− − −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
⎛
⎝
⎜
⎞
⎠
⎟
=
− ⋅ ⋅
⎛
⎝
⎜
⎞
⎠
⎟
( )
4
3
4
3
4
3
4
4 2
3
4
3
2 2
2 2
2
a
a a
a
a
a
a2
2 2 2
4
8
3
4
32
3
⎛
⎝
⎜
⎞
⎠
⎟
=
−
= −
a
a a
∴ y y
a
1 2
1
32
3
= − = −
and
∴ =
+
the radius of curvature r
( ) /
1 1
2 3 2
2
y
y
=
+
−
=
− ×
= −
( ) /
1 1
32
3
2 2 3
32
3
8 2
3 2
a
a a
Since r is positive, r =
3
8 2
a
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 5 5/12/2016 10:08:44 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-380-2048.jpg)

![Applications of Differential Calculus ■ 4.7
At the point (a, 0),
dy
dx
= ∞ ∴ = ⇒ =
dx
dy
x
0 0
1
So, we use the formula r =
+
( ) /
1 1
2 3 2
2
x
x
Now dx
dy
a
b
y
x
= − ⋅
2
2
Differentiating w.r.to y, we get
d x
dy
a
b
x y
dx
dy
x
2
2
2
2 2
1
= − ⋅
⋅ − ⋅
⎡
⎣
⎢
⎤
⎦
⎥
At the point (a, 0), d x
dy
a
b
a
a
a
b
2
2
2
2 2 2
= − = − ∴ x x
a
b
1 2 2
0
= = −
and
∴ the radius of curvature r =
+
−
= −
( ) /
1 0 3 2
2
2
a
b
b
a
Since r is positive, r =
b
a
2
, which is the length of the semi-latus rectum of the ellipse.
EXAMPLE 5
For the curve y
x
x
5
1
a
a
, if r is the radius of curvature at any point (x, y), show that
2
2 3 2 2
r
5 1
a
y
x
x
y
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
/
.
Solution.
The given curve is y
ax
a x
=
+
(1)
Differentiating w.r.to x, we get
dy
dx
a a x x
a x
a
a x
=
+ −
+
=
+
[( ) ]
( ) ( )
⋅ ⋅
1 1
2
2
2
and d y
dx
a
a x
2
2
2
3
2
= −
+
( )
At the point (x, y), y
a
a x
y
a
a x
1
2
2 2
2
3
2
=
+
= −
+
( ) ( )
and
∴ the radius of curvature r =
+
=
+
+
⎡
⎣
⎢
⎤
⎦
⎥
−
+
( ) ( )
( )
/
/
1
1
2
1
2 3 2
2
4
4
3 2
2
3
y
y
a
a x
a
a x
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 7 5/12/2016 10:09:07 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-382-2048.jpg)
![4.8 ■ Engineering Mathematics
Since r is positive,
r =
+ +
⎡
⎣ ⎤
⎦
+
⎡
⎣ ⎤
⎦
+
=
+ +
⎡
⎣ ⎤
⎦
( )
( )
( )
( )
/
/
/
a x a
a x
a
a x
a x a
4 4 3 2
4 3 2
2
3
4 4 3 2
2 2a
a a x
2 3
⋅ +
( )
⇒ 2 4 4 3 2
3 3
r
a
a x a
a a x
=
+ +
⎡
⎣ ⎤
⎦
+
( )
( )
/
⇒
2
2 3 4 4
3 3 2 3
r
a
a x a
a a x
⎛
⎝
⎜
⎞
⎠
⎟ =
+ +
⎡
⎣ ⎤
⎦
+
⎡
⎣ ⎤
⎦
/
/
( )
( )
raising to the pow
wer
dividing t
2
3
4 4
2 2
2
2
2
2
⎡
⎣
⎢
⎤
⎦
⎥
=
+ +
+
=
+
+
+
( )
( )
( )
( )
a x a
a a x
a x
a
a
a x
e
erm by term
[ ]
We have y
ax
a x
=
+
⇒ =
+
y
x
a
a x
and
x
y
a x
a
=
+
∴ 2
2 3 2 2
r
a
x
y
y
x
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
/
EXAMPLE 6
If r r
1 2
, be the radii of curvatures at the ends of a focal chord of a parabola whose latus rectum
is 2l, prove that ( ) ( )
/ / /
r 1 r 5
2 2 2
1
2 3
2
2 3 2 3
l .
Solution.
Let the parabola be y ax
2
4
= (1)
We know that 4a is the length of the latus rectum.
Given 2l is the latus rectum.
∴ 4 2
2
a l a
l
= ⇒ =
Let S be the focus (a, 0).
Let PQ be the focal chord.
Let P be ( , )
at at
2
2 and Q be ( , )
at at
1
2
1
2 .
The Slope of PQ =
−
−
=
−
−
=
−
+ −
=
+
y y
x x
at at
at at
a t t
a t t t t
t t
1 2
1 2
1
1
2 2
1
1 1
1
2 2
2
2
( )
( )( )
[
[ ]
{ t t
1 ≠
Slope of SP =
−
−
=
−
=
−
2 0 2
1
2
1
2 2 2
at
at a
at
a t
t
t
( )
Since slope of PQ = Slope of SP
O
P(at2
, 2at)
Q(at1
2
, 2at1
)
(a, 0)
S
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 8 5/12/2016 10:09:13 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-383-2048.jpg)
![Applications of Differential Calculus ■ 4.9
⇒
2 2
1
1
2
t t
t
t
+
=
−
∴ t t t t
2
1
1
− = +
( ) ⇒ t tt t
2
1
2
1
− = + ⇒ t t
1 1
= − ⇒ t
t
1
1
= − (2)
The radius of curvature at ( , )
at at
2
2 is r = +
2 1 2 3 2
a t
( ) /
∴ At the point P( , ),
at at
2
2 r1
2 3 2
2 1
= +
a t
( ) /
⇒ r1
2
3 2 3 2 1
2 1
−
− −
= +
( ) ( )
/
a t ⇒ r1
2
3
2 3
2
2
1
−
−
=
+
( ) /
a
t
At the point Q (at at
1
2
1
2
, ), r 2 1
2 3 2
2 1
= +
a t
( ) /
⇒ r2
2
3 2 3
1
2 1
2 1
− −
( )
= +
−
( ) /
a t
= +
⎛
⎝
⎜
⎞
⎠
⎟ =
+
= ⋅
+
−
−
−
−
−
−
( ) ( )
( )
( )
/ / /
2 1
1
2
1
2
1
2 3
2
1
2 3
2 1
2
2 3
2
2
a
t
a
t
t
a
t
t
[Using (2)]
∴ r r
1
2
3
2
2
3 2 3
2
2 3
2
2
2
1
1
2
1
− −
− −
+ =
+
+ ⋅
+
( ) ( )
/ /
a
t
a
t
t
∴
=
+
+
+
⎛
⎝
⎜
⎞
⎠
⎟
=
+
+
= =
−
− − −
( )
( ) ( )
/
/ / /
2
1
1 1
2
1
1
2
2 3
2
2
2
2 3
2
2
2 3 2
a
t
t
t
a
t
t
a l 3
3
1
2
3
2
2
3 2 3
r r
− −
−
+ = l /
[{ 2a = l]
EXAMPLE 7
Prove that the radius of curvature at any point of the cycloid x 5 u1 u
a( )
sin , y 5 2 u
a( )
1 cos is
4
2
acos
u
.
Solution.
The given curve is x a y a
= + = −
( sin ) ( cos )
u u u
and 1
∴
dx
d
a a
dy
d
a
u
u
u
u
u
= + = =
( cos ) cos sin
1 2
2
2
and
∴
dy
dx
dy
d
dx
d
= u
u
= = =
a
a
a
a
sin
cos
sin cos
cos
tan
u
u
u u
u
u
2
2
2
2 2
2
2
2
2 2
∴
d y
dx
d
d
dy
dx
d
dx
2
2
=
⎛
⎝
⎜
⎞
⎠
⎟ ⋅
u
u
= ⋅ ⋅ =
sec
sec
2
2
4
2
1
2
1
2
2
2
4
u
u
u
a
a
cos
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 9 5/12/2016 10:09:20 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-384-2048.jpg)

![Applications of Differential Calculus ■ 4.11
Differentiating w.r.to x,
2 4
y
dy
dx
= ⇒ dy
dx y
=
2
and d y
dx y
dy
dx y
2
2 2 3
2 4
= − ⋅ = −
Let (a, b) be the point on the curve at which the radius of curvature is 4 2.
Since (a, b) is on y2
= 4x, b a
2
4
= (2)
At the point (a, b),
dy
dx b
d y
dx b
= = −
2 4
2
2 3
, ∴ y
b
y
b
1 2 3
2 4
= = −
and
r =
+
( ) =
+
⎛
⎝
⎜
⎞
⎠
⎟
−
= −
+
= −
+
1
1
4
4
4
4
4
1
2 3 2
2
2
3 2
3
2 3 2
3
2 3 2
y
y
b
b
b
b
b
/
/
/ /
( ) ( )
4
4
Since r is positive, r =
+
( ) /
b2 3 2
4
4
Given r = 4 2
∴
( ) /
b2 3 2
4
4
4 2
+
= ⇒ ( ) /
4 4 16 2
3 2
a + = ⇒ 4 1 16 2
3 2 3 2
/ /
( )
a + =
⇒ 4 1 16 2
3 3 2
( )
a + = × [squaring both sides]
⇒ ( )
a a a
+ =
×
= = + = ⇒ =
1
16 2
4
8 2 1 2 1
3
2
3
3
⇒
(2) is b a b b
2 2
4 4 2
= ⇒ = ⇒ = ±
∴ the points are (1, 2) and (1, −2).
4.1.4 Centre of Curvature and Circle of Curvature
Let Γ be a simple curve having tangent at each point. At any point P on this curve we can draw a circle
having the same curvature at P as the curve Γ.
This circle is called the circle of curvature and its centre is called the centre of curvature and its
radius is the radius of curvature of Γ at P.
How to draw the circle of curvature is given in the next definition.
Definition 4.3 Let Γ be a simple curve and let P be a point of Γ.
Draw the normal at P to the curve Γ in the direction of the concavity of the curve (which is the positive
direction of the normal) and cut off a segment PC = r, the radius of curvature of Γ at P.
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 11 5/12/2016 10:09:30 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-386-2048.jpg)
![4.12 ■ Engineering Mathematics
The point C is called the centre of curvature of the given curve at P.
The circle with centre C and radius r (passing through P) is
called the circle of curvature of the given curve at P.
Note
1. From the definition of circle of curvature it follows that at the
given point, the curvature of the curve and curvature of the
circle are the same.
2. It is quite possible that the circle of curvature at a point crosses
the curve as in Fig. 4.4, just as a tangent line crosses the curve
at the point of inflexion.
4.1.5 Coordinates of the Centre of Curvature
Let P (x, y) be the point on y f x
= ( ). Let C ( , )
x y be the centre
of curvature at P.
Then PC = r.
Let the tangent at P make an angle c with the x-axis.
Then = c [{ angle between two lines = angle
between their perpendiculars]
From the right angle CNP
NP
NP
Δ , sin sin
c
r
r c
= ⇒ =
Now x x
= = − = − = −
OM OL ML OL NP r c
sin
and y y
= = + = +
MC MN MC r c
cos
Since tan ,
sin , cos
c
c c
= =
=
+
=
+
dy
dx
y
y
y y
1
1
1
2
1
2
1
1
1
and r =
+
( ) /
1 1
2 3 2
2
y
y
∴ x x
y
y
y
y
= −
+
⋅
+
( ) /
1
1
1
2 3 2
2
1
1
2 ⇒ x x
y y
y
= −
+
1 1
2
2
(1 )
(1)
and y y
y
y y
= +
+
⋅
+
( ) /
1 1
1
1
2 3 2
2 1
2
⇒ y y
y
y
= +
(1+ )
1
2
2
(2)
Thus, the centre of curvature ( , )
x y is given by (1) and (2).
∴ the equation of the circle of curvature at P is ( ) ( )
x x y y
− + − =
2 2 2
r
Note The centre of the curvature formula holds if y2 0 0
or .
P ρ
C
tangent at P
circle of
curvature
Fig. 4.4
N
M L
P(x, y)
ψ
X
Y
O
ψ
ρ
C(x, y)
Fig. 4.5
1 1
2
+ y
ψ
y1
1
Fig. 4.6
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 12 5/12/2016 10:09:38 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-387-2048.jpg)

![4.14 ■ Engineering Mathematics
Now dy
dx
a x
x
a
x
a x
= −
−
( )
= − = − ⋅ −
1 1 1 2
/ [from (1)]
∴
d y
dx
a x
a
x
2
2
3 2 3 2
12
2
= − − =
− −
( / )
/ /
At the point
a a
4 4
,
⎛
⎝
⎜
⎞
⎠
⎟
dy
dx
a
a
= − = −
/
/
4
4
1
and
d y
dx
a a a
a a a
2
2
3 2
2 4 2
4 2 4
= ⋅
⎛
⎝
⎜
⎞
⎠
⎟ = ⋅
⋅
=
− /
∴ y y
a
1 2
1
4
= − =
and
∴ the radius of curvature r =
+
=
+
= =
( ) ( )
/
/ /
1 1 1
4
2
2
1
2 3 2
2
3 2
y
y a
a a
2
At the point
a a
4 4
, ,
⎛
⎝
⎜
⎞
⎠
⎟ the coordinates of the centre of curvature ( , )
x y is given by
x
y
= −
+
= −
− +
= + =
= +
+
= +
x
y y
y
a
a
a a a
y
y
y
a
1 1
2
2
1
2
2
1
4
1 1 1
4 4 2
3
4
1
4
( ) ( )( )
/
( ) 1
1 1
4 4 2
3
4
+
= + =
a
a a a
∴ the centre of curvature is ( , ) ,
x y
a a
=
⎛
⎝
⎜
⎞
⎠
⎟
3
4
3
4
∴ the circle of curvature at
a a
4 4
,
⎛
⎝
⎜
⎞
⎠
⎟ is
( ) ( )
x x y y
− + − =
2 2 2
r ⇒ x
a
y
a a
−
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟ =
3
4
3
4 2
2 2 2
.
EXAMPLE 3
Find the centre of curvature and equation of the circle of curvature at the point P on the curve
y ex
5 where the curve crosses the y-axis.
Solution.
The given curve is y ex
= (1)
∴
dy
dx
ex
= and
d y
dx
ex
2
2
=
Also given P is the point on the y-axis where the curve crosses it.
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 14 5/12/2016 10:09:49 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-389-2048.jpg)

![4.16 ■ Engineering Mathematics
14. Find the radius of curvature at y a
= 2 on the curve y ax
2
4
= .
15. Prove that at the point x =
p
2
of the curve y x x
= −
4 2
sin sin , r =
5 5
4
.
16. Prove that the radius of curvature at any point (x, y) on
x
a
y
b
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ =
1 2 1 2
1
/ /
is r =
+
2 3 2
( )
.
/
ax by
ab
17. Show that the radius of curvature at the point ( cos , sin )
a a
3 3
u u on the curve x y a
2 3 2 3 2 3
/ / /
+ = is
3a sin u cos u.
18. Prove that the radius of curvature at any point of the astroid x y a
2 3 2 3 2
/ /
+ = is three times the
length of the perpendicular from the origin to the tangent at that point.
19. Find the radius of curvature and the curvature at the point (0, c) on the curve y c
x
c
= cosh .
20. If r is the radius of curvature at any point P on the parabola y ax
2
4
= and S is its focus, show
that r2
varies as (SP)3
.
21. Find r for the curve x a t t t y a t t t
= + = −
(cos sin ), (sin cos ).
22. Show that the radius of curvature at any point of the curve x ae
= −
u
u u
(sin cos ),
y ae
= +
u
u u
(sin cos ) is twice the perpendicular distance from the origin to the tangent at the point.
23. Show that the measure of curvature of the curve
x
a
y
b
+ = 1 at any point (x, y) on it is
ab
ax by
2 3 2
( )
.
/
+
24. Find the centre of curvature of the hyperbola
x
a
y
b
2
2
2
2
1
− = at the point ( , tan )
a b
sec u u .
25. Find the centre of curvature of y ax
2
4
= at an end of the latus rectum.
26. Find the centre of curvature at (c, c) on xy c
= 2
.
27. Find the circle of curvature at
1
4
1
4
1
, .
⎛
⎝
⎜
⎞
⎠
⎟ + =
on x y
28. Find the circle of curvature for the curve x y xy
3 3
3
+ = at the point 3
2
3
2
,
⎛
⎝
⎜
⎞
⎠
⎟ on it.
29. Find the coordinates of the centre of curvature of the curve x y a xy
4 4 2
2
+ = at (a, a).
30. If the centre of curvature of the ellipse
x
a
y
b
2
2
2
2
1
+ = at one end of the minor axis lies at the other
end. Find the eccentricity of the ellipse.
[Hint At (0, b), the centre of curvature is (0, −b)∴ =
r 2b compute r and find e]
31. Find the equation of the circle of curvature at (3, 6) on y x
2
12
= .
32. Find the equation of the circle of curvature at (c, c) on xy = c2
.
33. Find the radius of curvature and centre of curvature at any point (x, y) on the curve y c
x
c
= log .
sec
34. Find the radius of curvature and centre of curvature of the curve x y
4 4
2
+ = at the point (1, 1).
ANSWERS TO EXERCISE 4.1
1. 6 2. c 3.
1 2 2 2 3 2
ab
a b
( sin cos ) /
u u
+ 4. a
x
a
cosh2
5. c 7. a 8. c 2 9.
2 2
3
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 16 5/12/2016 10:10:10 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-391-2048.jpg)
![Applications of Differential Calculus ■ 4.17
10. 2a 11. 2 12. 2 1 2
a t
( )
+ 13. asec2
u
14. r = 4 2
a . 15. r =
5 5
4
16. r= +
2 3 2
ab
ax by
( ) .
/
17. 3asinθcosθ
18. r = 3p 19. Curvature =
1
c
20. r2 3
(SP)
=
4
a
21. at
22. r = 2p 24. x
a b
a
y
a b
b
=
+
=
− +
2 2
3
2 2
3
sec u u
;
( )
tan 25. ( , )
5 2
a a
−
26. ( , )
2 2
c c 27. x y
−
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟ =
3
4
3
4
1
2
2 2
28. x y x y
2 2 21
8
432
128
0
+ − + + =
( ) 29.
6
7
6
7
a a
,
⎛
⎝
⎜
⎞
⎠
⎟ 30.
1
2
31. ( ) ( )
x y
− + + =
15 6 288
2 2
32. ( ) ( )
x c y c c
− + − =
2 2 2
2 2 2
33. c
x
c
x c
x
c
y c
sec , tan ,
− +
⎛
⎝
⎜
⎞
⎠
⎟ 34.
2
3
2
3
2
3
, ,
⎛
⎝
⎜
⎞
⎠
⎟
4.1.6 Radius of Curvature in Polar Coordinates
Let the equation of the curve in polar coordinates be r = f(u)
Let P(r, u) be any point on the curve
Let r be the radius of curvature at the point P.
Let O be the pole and OA be the initial line. Draw the tangent at P and it meets OA at the point B.
Let PB make an angle c with OA.
Let C be a fixed point on the curve from which the arc length is measured.
Let CP = s and CQ = s + Δs. so that the arc PQ = Δs.
Let AOP=u and f the angle between the tangent at P and the radius vector OP
∴ the radius of curvature is r
c
=
ds
d
and from Fig. 4.7 c = u + f
[ From Δ OPB]
∴
d
d
d
d
c
u
f
u
= +
1
We know tanf = r
d
dr
r
dr
d
u
u
=
Differentiating with respect to u, we get
sec2
2
2
2
f
f
u
u u u
u
d
d
dr
d
dr
d
r
d r
d
dr
d
=
⋅ −
⎛
⎝
⎜
⎞
⎠
⎟
=
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
dr
d
r
d r
d
dr
d
u u
u
2 2
2
2
Q
P
O B A
C
r
r +
Δr
θ
φ
ψ
Δs
s
Fig. 4.7
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 17 5/12/2016 10:10:19 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-392-2048.jpg)
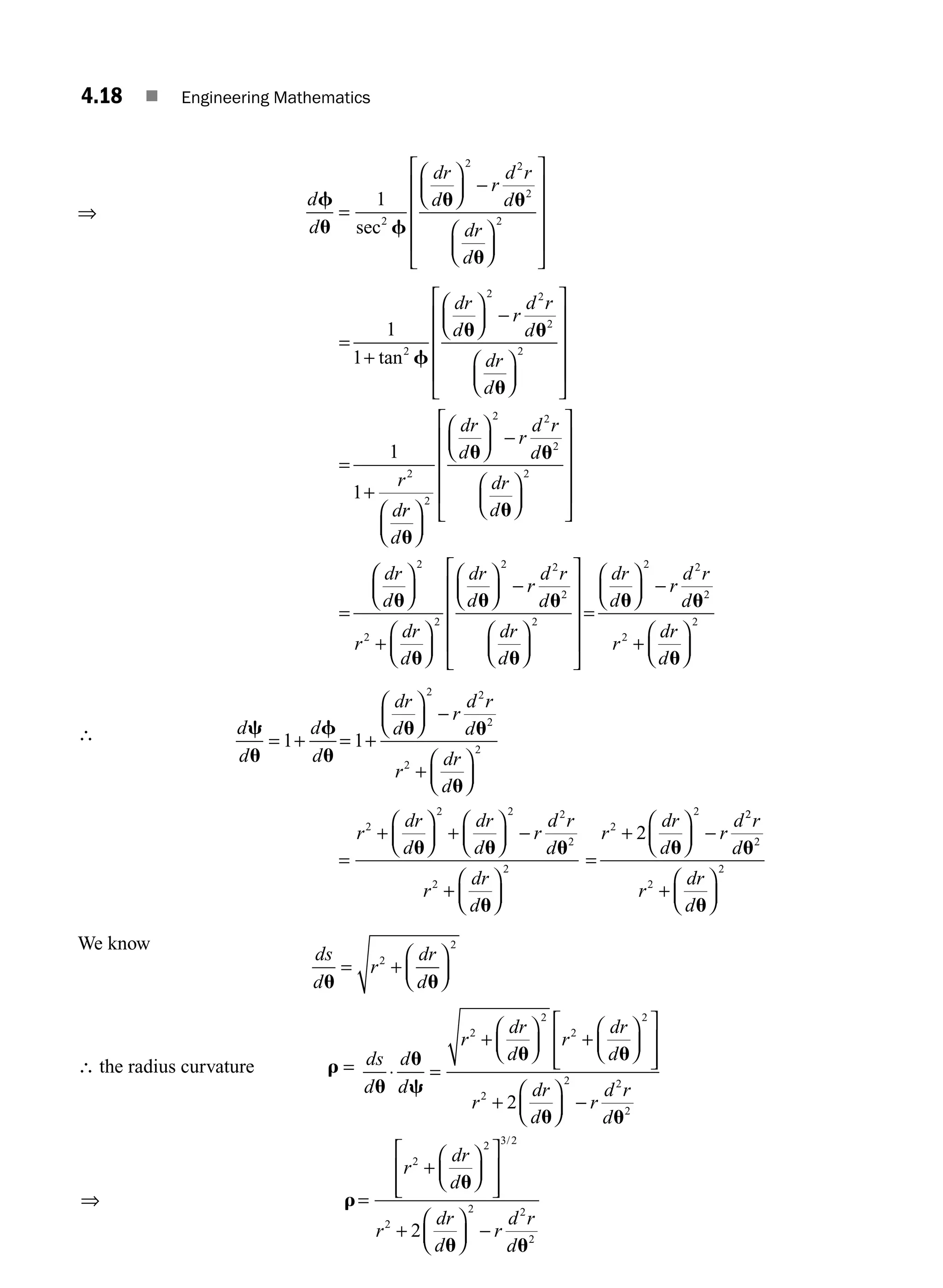
![Applications of Differential Calculus ■ 4.19
⇒ =
+
r
r r
2
1
1
2 3 2
2
1
2
2
1 2
2
2
2
⎡
⎣ ⎤
⎦
+ −
= =
/
.
r r rr
r
dr
d
r
d r
d
where and
u u
WORKED EXAMPLES
EXAMPLE 1
Find the radius of curvature of the cardioid r = a (1 + cos u) and show that
r2
r
is a constant.
Solution.
The given equation is
r = a (1 + cos u) (1)
The radius curvature is r =
r r
r r rr
2
1
2
3
2
2
1
2
2
2
+
( )
+ −
Differentiating (1) with respect to u, we get
r
dr
d
a a
1 = = − = −
u
u u
( sin ) sin and r
d r
d
a
2
2
2
= = −
u
u
cos
Now r r r a
a a
a
2
1
2 2 2 2
2 2 2 2
2 2 2
1
1 2
+ = +
= + +
= + + +
sin
( cos ) sin
cos cos sin
u
u u
u u u
u
u u u u
⎡
⎣ ⎤
⎦
= + + +
⎡
⎣ ⎤
⎦ = +
[ ]=
a a ar
2 2 2 2
1 2 2 1 2
cos sin cos cos
∴ r r ar
2
1
2
3
2
3
2
2
+
⎡
⎣ ⎤
⎦ = [ ]
and r r rr r a r a
a
2
1
2
2
2 2 2
2
2 2
1
+ − = + − −
=
sin ( cos )
(
u u
+
+ + + ⋅ +
= + +
cos ) sin ( cos )cos
cos sin
u u u u
u u u
2 2 2
2 2 2
2 1
1 2
a a a
a + 2cos +co
os +cos
+3cos
u u
u u u
u
2
2 2 2
2
1 2
3 1 3
⎡
⎣ ⎤
⎦
= + +
⎡
⎣ ⎤
⎦
= + =
a
a a
(cos sin )
( cos ) r
r [ cos sin ]
{ 2 2
1
u u
+ =
∴ the radius of curvature is r =
[ ]
2
3
3
2
ar
ar
⇒ r
r
=
( ) = =
2
3
8
9
8
9
2
3
2
2
ar
ar
ar
r
a
( )
,
⇒ constant
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 19 5/12/2016 10:10:26 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-394-2048.jpg)
![4.20 ■ Engineering Mathematics
EXAMPLE 2
Find the radius of curvature at any point on the curve rn
= an
sinnu, where a is a constant.
Solution.
The given curve is
rn
= an
sin nu
Taking log on both sides, we get
⇒
log log log sin
log log log sin
e
n
e
n
e
e e e
r a n
n r n a n
= +
= +
u
u (1)
The radius of curvature at any point is
r =
+
+ −
( )
r r
r r rr
2
1
2
3
2
2
1
2
2
2
(2)
Differentiating (1) with respect to u, we get
⇒
n
r
dr
d n
n n
dr
d
r n r r n
r
d r
d
r
⋅ = ⋅
= =
= = −
1 1
1
2
2
2
u u
u
u
u u
u
sin
cos
cot cot
cos
⇒
e
ec ec
2 2 2
n n n
dr
d
nr n r n
u u
u
u u
⋅
⎡
⎣ ⎤
⎦ + = − +
cot cos cot
Now r r r r n r n r n
2
1
2 2 2 2 2 2 2 2
1
+ = + = + =
cot ( cot )
u u u
cosec
∴ r r r
2
1
2 3 2 2
+
⎡
⎣ ⎤
⎦ =
/
c
cosec cosec
2
3
2 3 3
n r n
u u
⎡
⎣ ⎤
⎦ =
and r r r r r r n r nr n r n
r r n
2
1
2
2
2 2 2 2 2
2 2 2
2 2
+ − = + − − +
= +
cot ( cot )
cot
u u u
cosec
u
u u
u u
u
+
= + +
= +
nr n
r n nr n
r n nr
2 2
2 2 2 2
2 2 2
1
cosec
cosec
cosec cose
( cot )
c
c cosec
2 2 2
1
n n r n
u u
= +
( )
Substituting in (2), we get
r
u
u
u
=
+
=
+
r n
n r n
r n
n
3 3
2 2
1 1
cosec
cosec
cosec
( )
=
+
⋅ =
+
⋅ =
+
− +
r
n n
r
n
a
r
a r
n
n
n
n n
1
1
1 1
1
sin u
[Using (1)]
Note
1. When n = 1, the given curve is r = a sinu
which is a circle and the radius of curvature is r =
+
=
+
a
r a
−1 1
1 1 2
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 20 5/12/2016 10:10:29 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-395-2048.jpg)

![4.22 ■ Engineering Mathematics
4.1.7 Radius of Curvature at the Origin
Newton’s Method
1. If the curve y = f(x) passes through the origin and the x-axis is tangent at the origin O(0,0), then
at the point O(0,0), the radius of curvature r =
→
lim
x
x
y
0
2
2
Proof
Let y = f(x) be the equation of the curve.
Since the x-axis is a tangent at the origin O(0, 0) to the curve, we have
dy
dx
y
= ⇒ =
0 0
1
The radius of curvature r =
+
=
( )
1 1
1
2
2 2
3
2
y
y y
∴ at the origin O(0, 0), r =
1
2
y
(1)
Now consider
lim lim
x x
x
y
x
y
→ →
=
0
2
0
1
2
2
2 [By L’ Hopital’s rule]
⇒ lim
x
x
y y
→
=
0
2
2
2
1
(2)
∴ from (1) and (2), we get at the origin O(0, 0), r =
⎛
⎝
⎜
⎞
⎠
⎟
→
lim
x
x
y
0
2
2
2. If the curve y = f(x) passes through the origin and the y-axis is tangent at the origin O(0, 0), then
at O(0, 0), r =
→
lim
y
y
x
0
2
2
.
Proof
The curve is y = f(x)
Since the y-axis is tangent at the origin O(0, 0) to the curve
dy
dx
dx
dy
x
= ∞ ⇒ = ⇒ =
0 0
1
But, the radius of curvature r =
+
=
( )
1 1
1
2
3
2
2 2
x
x x
∴ at the origin O(0, 0), r =
1
2
x
(1)
Now, consider
lim lim
lim
y y
y
y
x
y
dx
dy
→ →
→
⎛
⎝
⎜
⎞
⎠
⎟ =
⋅
[ ]
=
0
2
0
0
2
2
2
By L’Hopital’s rule
y
y
x x x
y
1
0
2 2
1 1
=
⎡
⎣
⎢
⎤
⎦
⎥ = [ ]
→
lim By L’Hopital’s rule
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 22 5/12/2016 10:10:38 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-397-2048.jpg)
![Applications of Differential Calculus ■ 4.23
From (1) and (2), we get, at the origin O(0, 0), r =
→
lim
y
y
x
0
2
2
.
3. If the curve y = f(x) passes through the origin O(0, 0), but neither the x-axis nor the y-axis is a
tangent at the origin, then at the origin O(0, 0), r =
+
⎡
⎣ ⎤
⎦
1 2
3
2
p
q
, where p f q f
= ′ = ′′
( ), ( )
0 0 .
Proof
In this case we use Maclaurin’s series expansion for f(x)
∴ y f x f
x
f
x
f
= = + ′ + ′′ +⋅⋅⋅
( ) ( )
!
( )
!
( )
0
1
0
2
0
2
Putting p f q f
= ′ = ′′
( ), ( )
0 0 , we get
y px
q
x
= + +⋅⋅⋅
2
2
[{ f(0) = 0]
Thus, at the origin O(0, 0), r =
+
⎡
⎣ ⎤
⎦
1 2
3
2
p
q
.
Note
1. In this case we may not be able to find y1
, y at the origin O(0, 0) in the usual way.
So, we substitute
y px
q
x
= + +⋅⋅⋅
2
2
in the given equation and equate the like coefficients of p and q.
2. If the curve passes through the origin, then the equation of the tangent at the origin is obtained by
equating the lowest degree terms to zero.
WORKED EXAMPLES
EXAMPLE 1
Find the radius of curvature at the origin for x y x y
3 3 2
2 6 0
1 2 1 5 .
Solution.
The given curve is
x y x y
3 3 2
2 6 0
+ − + = (1)
Since there is no constant term in the equation, it passes through the origin (0, 0).
The tangent at the origin O(0, 0) is obtained by equating the lower degree term to zero.
In (1) the lowest degree term is 6y
∴ y = 0 is the tangent at the origin. i.e., the x-axis the tangent at the origin.
∴ the radius of curvature r =
⎛
⎝
⎜
⎞
⎠
⎟
→
lim
x
x
y
0
2
2
⇒ 2
0
2
r =
⎛
⎝
⎜
⎞
⎠
⎟
→
lim
x
x
y
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 23 5/12/2016 10:10:43 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-398-2048.jpg)


![4.26 ■ Engineering Mathematics
⇒
1 1
2 2 2
p r
=
sin f
= = +
( )
= +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
1 1
1
1
1
1
2
2
2
2
2
2
r r
r r
dr
d
cosec f f
u
cot
∴ 1 1 1
2 2 4
2
p r r
dr
d
5 1
u
⎛
⎝
⎜
⎞
⎠
⎟
which is called the p – r equation or pedal equation of a curve, r = f(u).
WORKED EXAMPLES
EXAMPLE 1
Find the p – r equation of the cardioid r a
5 2 u
( ).
1 cos
Solution.
The given equation is
r a
= −
( cos )
1 u (1)
The pedal equation of the curve (1) is
1 1 1
2 2 4
2
p r r
dr
d
= +
⎛
⎝
⎜
⎞
⎠
⎟
u
Differentiating (1) with respect to u, we get
dr
d
a a
u
u u
= − −
[ ]=
( sin ) sin
∴ the pedal equation is
1 1 1
2 2 4
2 2
p r r
a
= + sin u =
+
=
−
( ) +
=
+ − +
⎡
r a
r
a a
r
a
2 2 2
4
2 2 2 2
4
2 2 2
1
1 2
sin
cos sin
cos cos sin
u
u u
u u u
⎣
⎣ ⎤
⎦
=
+ + −
⎡
⎣ ⎤
⎦ = −
r
a
r
a
r
4
2 2 2
4
2
4
1 2 2
1
cos sin cos
( cos )
u u u
u
1 2 2
2
2 4 3
2
3
p
a
r
r
a
r
p
r
a
= ⋅ = =
⇒ .
p
P
M
O T A
r
φ
180
−
φ
ψ
Fig. 4.8
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 26 5/12/2016 10:11:01 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-401-2048.jpg)

![4.28 ■ Engineering Mathematics
Which is a parabola and the p – r equation is
pa r r p a r p ar
− − +
−
= = ⇒ = ⇒ =
1
2
1
2
1
1
2 2 1 2
5. When m = −1, the curve is
r a
r a
a
r
− −
= − ⇒ = ⇒ =
1 1 1 1
cos( ) cos cos
u u u, a straight line.
and the p – r equation is
pa r p a
− − +
= = ⇒ =
1 1 1
1
When m = −2, the curve is
⇒
r a
r a a
r a
− −
= −
= = ⇒ =
2 2
2 2 2
2 2
2
1 1
2
1
2
2
cos(
cos
sec
sec
u
u
u
u
)
which is a rectangular hyperbola and the p – r equation is
pa r r
p
a r
pr a
− − + −
= = ⇒ = ⇒ =
2 2 1 1
2
2
1
4.1.9 Radius of Curvature Using the p 2 r Equation of a Curve
Let r f
= ( )
u be the equation of the curve.
We know that the radius of curvature at any point ( , )
r u is
r
u
u u
=
+
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
+
⎛
⎝
⎜
⎞
⎠
⎟ −
=
+
r
dr
d
r
dr
d
r
d r
d
r r
2
2
2
2 2
2
2
1
2
3 2
2
/
[ ]
]
/
3 2
2
1
2
2
2
r r rr
+ −
For some curves, it is not easy to find r using the above formula. In such cases, we find r using the
(p – r) equation of the curve.
Prove that the radius curvature r5r
dr
dp
Proof
Let O be the pole and OA be the intial line. Let P r
( , )
u be any point on the curve r f
= ( )
u
Let r be the radius of curvature at P.
Let PT be the tangent at the point P and it meets OA at T.
Draw OM perpendicular to PT
Let OP = r and OM = p
∠AOP = u. Let ∠ OPT = f and ∠PTA = c
∴ c u f
= +
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 28 5/12/2016 10:11:19 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-403-2048.jpg)
![Applications of Differential Calculus ■ 4.29
From ΔOPM,
OM
OP
= =
sin sin
f f
⇒ p r
We know sinf
u
= r
d
ds
and cosf =
dr
ds
∴ tanu
u
u
= = ⋅
r
d
dr
r
dr
d
1
We have p = rsinf
Differentiating with respect to r, we get
dp
dr
r
d
dr
r
dr
ds
d
dr
r
d
ds
r
d
ds
r
d
ds
r
d
ds
d
ds
= +
= +
= + = +
cos sin
f
f
f
f u
f u f u
⎡
⎡
⎣
⎢
⎤
⎦
⎥ = + =
r
d
ds
r
d
ds
( )
u f
c
ds
d
r
dr
dP
r
dr
dP
ds
d
c
r r
c
= = =
⎡
⎣
⎢
⎤
⎦
⎥
⇒ {
∴ the radius of curvature at the point P r
( , )
u on the curve is r = r
dr
dP
WORKED EXAMPLES
EXAMPLE 3
Find the radius curvature at any point on the cardioid r a
5 2 u
( )
1 cos using the p – r equation
of the curve.
Solution.
The given curve is r a
= −
( cos )
1 u
The p – r equation is
p
r
a
2
3
2
= (1) [Refer worked example 1, page 4.26]
Let r be the radius curvature at any point P r
( , )
u on the curve,
∴ r = r
dr
dp
Now p
r
a
2
3
2
= ⇒ r ap
3 2
2
=
P
O T
M
p
A
r
θ
φ
ψ
Fig. 4.9
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 29 5/12/2016 10:11:30 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-404-2048.jpg)
![4.30 ■ Engineering Mathematics
Differentiating w.r.to p, we get
∴ 3 2 2
4 4
2
2
3
2
2
3
2
1
2
r
dr
dp
a p r
dr
dp
ap
r
a
r
r
a
ar
= ⋅ ⇒ = = ⋅ =
( )
[using (1)]
∴ the radius of curvature r =
2
3
2ar
EXAMPLE 4
Find the (p – r) equation of the curve x y ax
2 2
1 5 and hence, deduce its radius of curvature.
Solution.
The given curvature is x y ax
2 2
+ = .
Put x r y r
= =
cos , sin .
u u
∴ Its polar equation is
r r ar
r ar r ar r
2 2 2 2
2 2 2 2
cos sin cos
(cos sin ) cos cos
u u u
u u u u
+ =
⇒ + = ⇒ = ⇒ = a
acosu
The (p – r) equation is
1 1 1
2 2 4
2
p r r
dr
d
= +
⎛
⎝
⎜
⎞
⎠
⎟
u
We have r a
= cosu ∴
dr
d
a
u
u
= − sin
⇒
1 1 1 1
1
2 2 4
2 2
4
2 2 2
4
2 2 2 2
2
p r r
a
r
r a
r
a a
a
= + = +
= + =
sin [ sin ]
[ sin ]
u u
u u
cos
[
[ sin ]
( )
cos2 2
4
2
4
4 2 2 2
1
u u
+
=
= ⇒ =
r
a
r
r a p r ap
The radius of curvature is r = r
dr
dp
Differentiating (1) w.r to p, we get
∴ the radius of curvature
2
2
2 2
r
dr
dp
a
dr
dp
a
r
r
a
r
a
= ⇒ =
= ⋅ =
r
Note that r = a cos u is a circle of diameter a. So, the radius =
a
2
. Hence, r =
a
2
.
EXERCISE 4.2
1. Find the radius of curvature of the rectangular hyperbola r a
2 2
2
= sec u.
2. Find the radius of curvature at the point ( , )
r u on the curve r a n
n n
= cos u.
∴
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 30 5/12/2016 10:11:36 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-405-2048.jpg)

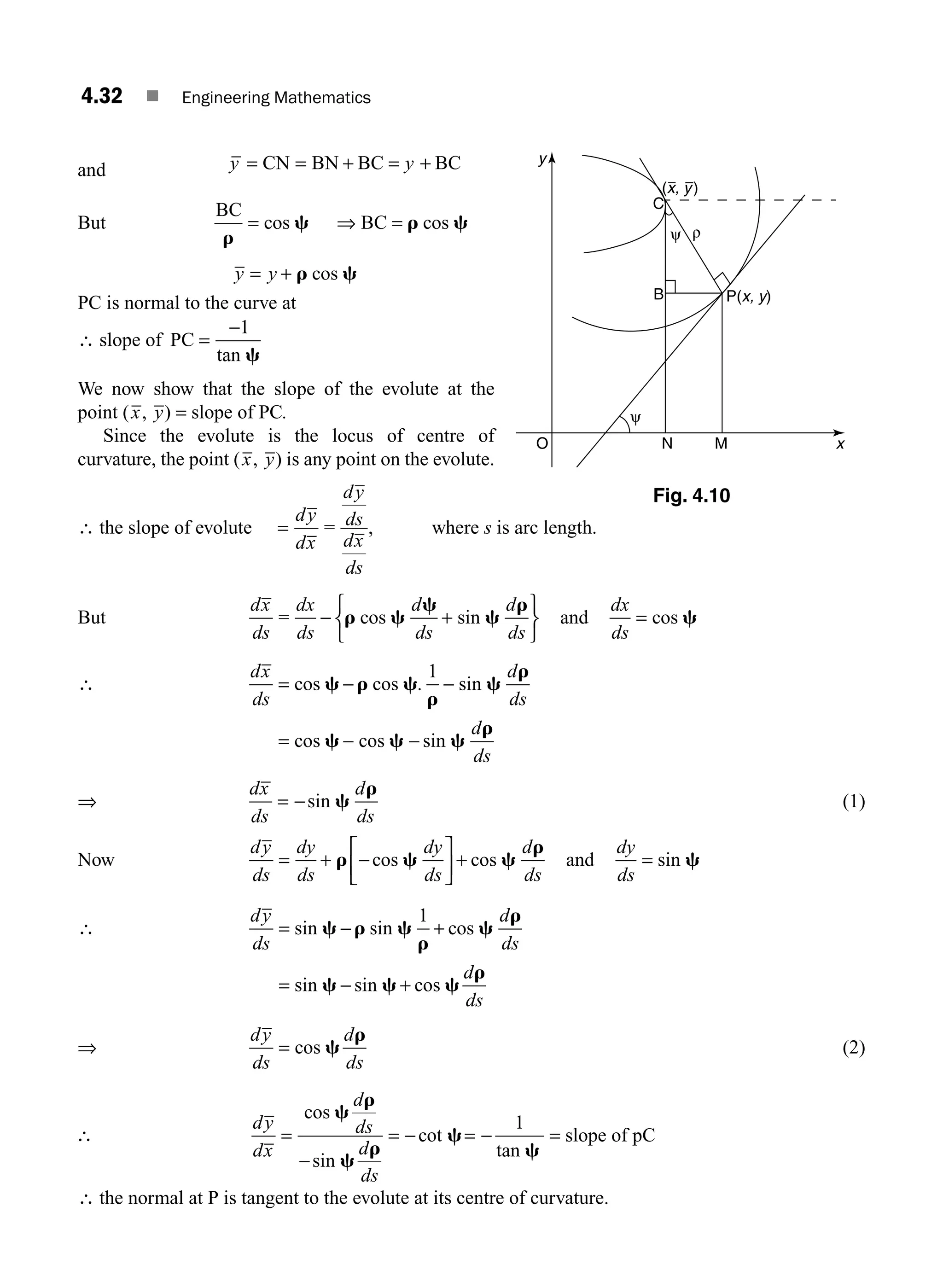
![Applications of Differential Calculus ■ 4.33
Property 2
The length of an arc of the evolute is equal to the difference between the radii of curvature of the given
curve which are tangent to the arc at its extremities, provided that along the arc of the given curve, r
increases or decreases.
Proof
We know the differential arc length of any curve is
ds dx dy
( ) = ( ) + ( )
2 2 2
Let C1
C2
be an arc of the evolute, C1
C2
are the centres of curvature of P1
P2
respectively.
For the evolute if s′ is the arc length of evolute measured from the fixed point A and (x, y) is any-
point on the evolute.
∴ ds dx dy
dx
ds
d
ds
dy
ds
d
ds
′
( ) = ( ) + ( )
= − =
2 2 2
sin c
r
c
r
and cos
(3)
But [from property (1)]
Squaring and adding, we get
dx
ds
dy
ds
d
ds
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟
2 2 2
r
(4)
But ds
ds
dx
ds
dy
ds
′
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
2 2 2
[Dividing (3) by ds]
⇒ =
⎛
⎝
⎜
⎞
⎠
⎟
d
ds
r
2
Using (4)
⇒
ds
ds
d
ds
′
= ±
r
⇒ ds d
′ = ± r
∴ integrating, ′ = ±
s c
r +
If arc AC1
= s1
′ and arc AC2
= s2
′ , then arc C1
C2
= s2
′ − s1
′
If r1
and r2
are radii of curvatures at the points to P1
, P2
on the given curve, then
′ =
s c
1 1
± +
r and ′ = ± +
s c
2 2
r ∴ ′ − ′ = ± −
( )
s s
2 1 2 1
r r
∴ arc C C
1 2 2 1
= −
r r
Hence, the result.
Note
For a given curve Γ there is only one evolute C. But there are many curves for which C is the
evolute. So, there are many involutes.
C1
C2
y
x
ρ1
P1
P2
ρ2
s1
′
A
O
Fig. 4.11
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-A.indd 33 5/12/2016 10:11:53 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-408-2048.jpg)


![4.36 ■ Engineering Mathematics
and d y
dx
b
a
b a
b
a
b
b
2
2
2
2 2 2
= −
−
−
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
=
−
sin cos
cos
sin
sin
u u
u
u
u
2
2
2
2 2
2 3 2 3
1
a
b b
b
b
a
[ sin cos ]
sin sin
u u
u u
+
= −
∴ y
b
a
y
b
a
1 2 2 3
= − = −
cos
sin sin
u
u u
and
The centre of curvature ( , )
x y at the point P is given by
x x
y y
y
a
b
a
b
a
= −
+
= −
−
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
1 1
2
2
2 2
2 2
1
1
( )
cos
cos
sin
cos
sin
u
u
u
u
u
⎞
⎞
⎠
⎟
−
= − +
⎛
⎝
⎜
⎞
⎠
⎟
=
b
a
a a
b
a
a
2 3
2
2 2
2 2
1
1
sin
cos cos sin
cos
sin
cos
u
u u u
u
u
u
u u u u
u u u
u
− −
= − −
= −
a
b
a
a
b
a
a
b
a
cos sin cos
cos ( sin ) cos
cos c
2
2
3
2
2
3
3
2
1
o
os cos
3
2 2
3
u u
=
−
a b
a
⇒ x
a b
a
=
−
2 2
3
cos u (1)
and y y
y
y
b
b
a
b
a
b
a
b
= +
+
= +
+
−
= −
1
1
1
2
2
2
2
2
2
2 3
2 3
sin
cos
sin
sin
sin
sin
u
u
u
u
u
u
1
1
2
2
2
2
2
3 2
+
⎛
⎝
⎜
⎞
⎠
⎟
= − −
b
a
b
a
b
b
cos
sin
sin sin sin cos
u
u
u u u u
= − −
= − =
−
b
a
b
b
a
b
b a
b
sin ( cos ) sin
sin sin sin
u u u
u u u
1 2
2
3
3
2
3
2 2
3
⇒ y
a b
b
= −
−
2 2
3
sin u (2)
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-B.indd 36 5/12/2016 10:26:45 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-411-2048.jpg)

![4.38 ■ Engineering Mathematics
and y y
y
y
c
t
t
ct
= +
+
= +
+
1 1
1
2
1
2
2
4
3
= + + = + = +
c
t
c
t
t
c
t
ct
t
c
t
t
2
1
3
2 2 2
3
4
4
4
( ) ( )
⇒ y
c
t
t t
= +
2
3
3
2 6
( ) (3)
∴ x y
c
t
t t t
c
t
t t t
c
t
t
+ = + + +
= + + + = +
2
3 1 3
2
1 3 3
2
1
3
4 2 6
3
2 4 6
3
2 3
[ ]
[ ] ( )
⇒ x y
c t
t
+ =
+
⎛
⎝
⎜
⎞
⎠
⎟
2
1
2 3
⇒ ( ) /
/
x y
c t
t
+ =
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
1 3
1 3 2
2
1
(4)
Also x y
c
t
t t t
c
t
t t t
c
t
t
c
− = + − −
= − + − = − =
−
2
3 1 3
2
1 3 3
2
1
2
1
3
4 2 6
3
2 4 6
3
2 3
[ ]
[ ] ( )
t
t
t
2 3
⎡
⎣
⎢
⎤
⎦
⎥
⇒ ( ) /
/
x y
c t
t
− =
⎛
⎝
⎜
⎞
⎠
⎟
−
⎡
⎣
⎢
⎤
⎦
⎥
1 3
1 3 2
2
1
(5)
Eliminating t from (4) and (5), we get the equation of the evolute.
Now, ( ) ( )
/ /
/
x y x y
c t
t
t
t
+ − − =
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟ −
−
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
2 3 2 3
2 3 2 2 2 2
2
1 1
⎦
⎦
⎥
=
⎛
⎝
⎜
⎞
⎠
⎟
+ − −
⎡
⎣
⎢
⎤
⎦
⎥
c t t
t
2
1 1
2 3 2 2 2 2
2
/
( ) ( )
=
⎛
⎝
⎜
⎞
⎠
⎟ ⋅ =
c t
t
c
2
4
2 3 2
2
/ 2
2 3
2 3
2
3
1
1
3 2 3
2
4 4 4
/
/
/
( )
⋅ = =
−
c c
⇒ ( ) ( ) ( )
/ / /
x y x y c
+ − − =
2 3 2 3 2 3
4
∴ the locus of ( , )
x y is ( ) ( ) ( ) ,
/ / /
x y x y c
+ − − =
2 3 2 3 2 3
4
which is the equation of the evolute.
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-B.indd 38 5/12/2016 10:27:02 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-413-2048.jpg)




![Applications of Differential Calculus ■ 4.43
Infact, the envelope of a family of curves f x y
( , , )
a = 0, a is a parameter, is the locus of their
isolated characteristic points.
(3) Not every single parameter family has envelope. For example, the family of concentric circles
x y
2 2 2
+ = a has no envelope, as there is no characteristic point.
WORKED EXAMPLES
EXAMPLE 1
Find the envelope of the family lines y mx a m b
= ± −
2 2 2
, where m is the parameter.
Solution.
Given family is y mx a m b
= ± −
2 2 2
, m is the parameter
⇒ y mx a m b
− ± −
= 2 2 2
⇒ ( )
y mx a m b
− = −
2 2 2 2
⇒ y mxy m x a m b
2 2 2 2 2 2
2
− + = −
⇒ m x a mxy y b
2 2 2 2 2
2 0
( ) ( )
− − + + =
This is quadratic in m
Here A B C
= − = − = +
x a xy y b
2 2 2 2
2
, ,
∴ the envelope is B AC
2
4 0
− =
⇒ 4 4 0
2 2 2 2 2 2
x y x a y b
− − + =
( )( )
⇒ x y x y b x a y a b
2 2 2 2 2 2 2 2 2 2
0 4
− + − − =
( ) [ ]
÷ by
⇒ b x a y a b
2 2 2 2 2 2
0
− − = ⇒ b x a y a b
2 2 2 2 2 2
− = ⇒ x
a
y
b
2
2
2
2
1
− =
which is a hyperbola.
EXAMPLE 2
Find the envelope of the straight lines represented by x y
cos sin sec ,
a 1 a 5 a
a where a is the
parameter.
Solution.
Given family is x y a
cos sin sec
a a a
+ = , where a is the parameter
Dividing by cos a, x y a
+ =
tan sec
a a
2
= +
a( tan )
1 2
a
⇒ a y a x
tan tan ( )
2
0
a a
− + − = , which is a quadratic in tan a
Here A B C
= = − = −
a y a x
, ,
∴ the envelope is B AC
2
4 0
− = ⇒ y a a x y a a x
2 2
4 0 4
− − = =
( ) ( )
⇒ −
which is a parabola.
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-B.indd 43 5/12/2016 10:27:42 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-418-2048.jpg)

![Applications of Differential Calculus ■ 4.45
( )cos ( )sin
1 2
a a
+
⇒ y a
(cos sin ) [cos cos sin sin ]
2 2
2 2 2
a a a a a a
+ = +
⇒ y a
= − +
⎡
⎣ ⎤
⎦
(cos sin )cos sin cos
2 2 2
4
a a a a a
= +
a[cos sin cos ]
3 2
3
a a a (4)
∴
x y a
a
− = + − −
= −
[sin sin cos cos sin cos ]
[sin cos ]
3 2 3 2
3
3 3
a a a a a a
a a
⇒
x y
a
−
⎛
⎝
⎜
⎞
⎠
⎟ = −
1 3
/
sin cos
a a (5)
and
x y a
a
+ = + + +
⎡
⎣ ⎤
⎦
= +
sin sin sin cos sin
(sin cos )
3 2 2 3
3
3 3
a a a a a a
a a
cos
∴
x y
a
+
⎛
⎝
⎜
⎞
⎠
⎟ = +
1 3
/
sin cos
a a (6)
Squaring and adding (5) and (6), we get
⇒
( ) ( )
(sin cos ) (sin cos )
sin
/
/
/
/
x y
a
x y
a
−
+
+
= − + +
= +
2 3
2 3
2 3
2 3
2 2
2
a a a a
a c
cos sin cos sin cos sin cos
(cos sin )
(
2 2 2
2 2
2 2
2 2
a a a a a a a
a a
− + +
= + =
−
x y)
) ( )
/ / /
2 3 2 3 2 3
2
+ + =
x y a
which is the envelope.
4.3.2 Envelope of Two Parameter Family of Curves
1. Let f x y
( , , , )
a b = 0 (1)
be a 2-parameter family of curves, where a, b are the parameters such that
f (a, b) = 0 (2)
Find b in terms of a from (2) and substitute in (1) and thus the problem is reduced to one
parameter family and proceed as above.
2. The following method is more convenient in many cases. For a fixed point (x, y) of the envelope
treating b as a function of a differentiate (1) and (2) w.r.to a and eliminate
d
d
b
a
from these equations.
Using this relation with (1) and (2), eliminate a and b. The eliminant, if exists, gives the envelope.
WORKED EXAMPLES
EXAMPLE 1
Find the envelope of the famly of straight lines
x y
a b
1 51, where ab c a b
5 2
and , are parameters,
c is a constant.
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-B.indd 45 5/12/2016 10:27:58 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-420-2048.jpg)

![Applications of Differential Calculus ■ 4.47
Substitute in (1), then we get
x
c x
y
c y
x y c
n n n n n n
n
n
n
n
n
n
/ / / /
+ + + +
+ + +
⋅
+
⋅
= ⇒ + =
1 1 1 1 1 1
1 1 1
1
which is the required envelope.
Note
Some of the important particular cases are
1. For n = 1, we get
x
a
y
b
a b c
+ = + =
1, . Then the envelope is x y c
+ =
2. For n = 2, we get
x
a
y
b
a b c
+ = + =
1 2 2 2
, . Then the envelope is x y c
2 3 2 3 2 3
/ / /
,
+ = which is the
astroid.
3. For n = 3, we get
x
a
y
b
a b c
+ = + =
1 3 3 3
, . Then the envelope is x y c
3 4 3 4 3 4
/ / /
+ =
4. For n = 1 and c = 1, we get
x
a
y
b
a b
+ = + =
1 1
, . Then the envelope is x y
+ = 1
EXAMPLE 3
Prove that the envelope of the system of lines
x
l
y
m
1 5 1,where the parameters l and m are connected
by
l
a
m
b
1 5 1 is the curve
x y
a b
1 51.
Solution.
Given
x
l
y
m
+ = 1 (1) and
l
a
m
b
+ = 1 (2)
Treating m as a function of l, differentiate (1) and (2) w.r.to l.
∴ − − ⋅ =
x
l
y
m
dm
dl
2 2
0 ⇒ dm
dl
m x
l y
= −
2
2
(3)
and
1 1
0
a b
dm
dl
+ ⋅ = ⇒
dm
dl
b
a
= − (4)
From (3) and (4) we get,
− = − = =
m x
l y
b
a
x
bl
y
am
x
l
bl
y
m
bm
2
2 2 2
⇒ ⇒
∴
x
l
bl
y
m
am
x
l
y
m
bl am
= =
+
+ bl am
=
+
1
[using (1)]
Now
l
a
m
b
+ = 1 ⇒ bl am ab
+ = .
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-B.indd 47 5/12/2016 10:28:10 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-422-2048.jpg)



![Applications of Differential Calculus ■ 4.51
⇒
y t x t t t x
x x
x
y
x
= − + + = − −
−
⎛
⎝
⎜
⎞
⎠
⎟
−
− −
⎡
⎣
⎢
⎤
⎦
⎥
=
−
[ ] [ ( )]
( )
/
2 2
2
3
2
3
2
2 2
1 2
=
2
2
3
2
3
2
1 2
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎡
⎣
⎢
⎤
⎦
⎥
/
( )
x
[Using (2)]
Squaring, y
x
x
2 2
2
3
4
9
2
=
−
⎛
⎝
⎜
⎞
⎠
⎟ −
⎡
⎣
⎢
⎤
⎦
⎥
( )
⇒ y x
2 3
4
27
2
= −
( ) ⇒ = −
27 4 2
2 3
y x
( ) ,
which is the evolute of the parabola.
EXAMPLE 3
Find the evolute of the hyperbola
x
a
y
b
2
2
2
2
1
− 5 as the envelope of its normals.
Solution.
The equation of the hyperbola is
x
a
y
b
2
2
2
2
1
− =
We have x a
= sec ,
u y b
= tanu, as parametric equation of the hyperbola.
We shall find the equation of the normal at the point “u”
dx
d
a
dy
d
b
u
u u
u
u
= =
sec tan sec .
and 2
∴ dy
dx
dy
d
dx
d
b
a
= =
u
u
u
u u
sec
sec tan
2
= = = =
b
a
b
a
b
a
sec
tan cos
cos
sin sin
u
u u
u
u u
1
slope of the tangent.
∴ the slope of the normal = −
a
b
sinu
∴ the equation of the normal at the point ‘u’ is
y b
a
b
x a
− = − −
tan
sin
( sec )
u
u
u
⇒ by b a x a
− = − +
2 2
tan sin tan
u u u
⇒ a x by a b
sin ( )tan
u u
⋅ + = +
2 2
⇒ ax by a b
cos cot ( )
u u
+ = +
2 2
(1)
where u is the parameter.
⇒
M04_ENGINEERING_MATHEMATICS-I _CH04_Part-B.indd 51 5/12/2016 10:28:31 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-426-2048.jpg)








![5.4 ■ Engineering Mathematics
WORKED EXAMPLES
EXAMPLE 1
Text the continuity of the function
f x y
xy
x y
x y
x y
( , )
( , ) ( , )
( , ) ( , )
5 1
5
2 2
0 0
0 0 0
if
if
≠
⎧
⎨
⎪
⎩
⎪
at the origin.
Solution.
Given f x y
xy
x y
x y
x y
( , )
( , ) ( , )
( , ) ( , )
= +
≠
=
⎧
⎨
⎪
⎩
⎪
2 2
0 0
0 0 0
if
if
∴ lim ( , ) lim
( , ) ( , ) ( , ) ( , )
f x y
xy
x y
x y x y
→ →
=
+
0 0 0 0 2 2
We shall verify
lim ( , ) ( , )
( , ) ( , )
x y
f x y f
→
=
0 0
0 0 by ∈ − d definition
Let ∈ 0 be given.
Then
f x y f
xy
x y
x y
x y
( , ) ( , )
− =
+
− =
+
0 0 0
2 2 2 2
[
∴
f(0,0) = 0]
But x x y y x y
+ +
2 2 2 2
and
∴
x y x y
x y
x y
x y
+
+
+
2 2
2 2
2 2
⇒
∴ f x y f x y
( , ) ( , )
− ∈ ⇒ + ∈
0 0 2 2
Take d d
= ∈ − + −
, ( ) ( )
then x y
0 0
2 2
Thus, f x y f x y
( , ) ( , ) ( ) ( )
− ∈ − + −
0 0 0 0
2 2
if d
∴ by definition lim ( , ) ( , ) .
( , ) ( , )
x y
f x y f
→
= =
0 0
0 0 0
Hence, is continuous at
f x y
( , ) ( , ).
0 0
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 4 5/12/2016 10:24:10 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-435-2048.jpg)

![5.6 ■ Engineering Mathematics
EXERCISE 5.1
1. Evaluate the following limits, if they exist.
(i) lim
x
y
xy
x y
→
→
+
0
0
2 2
(ii) lim
x
y
xy
x y
→
→
+
0
0
3
2 6
(iii) lim
( )
( )
x
y
x y
y x
→
→
−
−
2
2
2
2
2. Test continuity of the following
(i) f x y
x y x y
x y
( , )
( , ) ( , )
( , ) ( , )
=
+ ≠
=
⎧
⎨
⎩
2
4 1 2
0 1 2
if
if
(ii) f x y
xy
x y
x y
x y
( , )
,
,
= +
≠ ≠
= =
⎧
⎨
⎪
⎩
⎪
2
2 2
0 0
0 0 0
if
if
(iii) f x y
x y
x y
x y
x y
( , )
( , ) ( , )
( , ) ( , )
=
−
+
≠
=
⎧
⎨
⎪
⎩
⎪
2 2
2 2
0 0
0 0 0
if
if
ANSWERS TO EXERCISE 5.1
1. (i) does not exist. (ii) does not exist (iii) does not exist.
2. (i) not continuous
(ii) not continuous
[Hint limit does not exist. Choose paths y = x, x = y3
]
(iii) not continuous
5.2 PARTIAL DERIVATIVES
Functions of two or more independent variables appear in many practical problems more often than
functions of one independent variable. The concept of derivative of a single variable function f(x)
is extended to functions of two or more variables. Suppose f(x, y) is a function of two independent
variables x and y, we treat y as constant and find the derivative of f(x, y) w.r.to x, then the derivative is
called a partial derivative. Partial derivatives find applications in a wide variety of fields like fluid
dynamics, electricity, physical sciences, econometrics, probability theory etc.
Definition 5.6 Let z = f(x, y) be a real function of two independent variables x and y. Let (x0
, y0
) be a
point in the domain of f. The partial derivative of f(x, y) w.r.to x at (x0
, y0
) is the limit
lim
( , ) ( , )
,
0
0 0 0 0
h
f x h y f x y
h
→
1 2
if the limit exists.
Then it is denoted by
∂
∂
f
x
⎛
⎝
⎜
⎞
⎠
⎟
( , )
x y
0 0
or
∂
∂
z
x
⎛
⎝
⎜
⎞
⎠
⎟
( , )
x y
0 0
or fx
(x0
, y0
).
Similarly, partial derivative of f(x, y) w.r.to y at (x0
, y0
) is the limit
lim
( , ) ( , )
,
k→
+ −
0
0 0 0 0
f x y k f x y
k
if the limit exists.
It is denoted by ∂
∂
∂
∂
f
y
z
y
f x y
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
( , ) ( , )
( , )
x y x y
y
or or
0 0 0 0
0 0
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 6 5/12/2016 10:24:19 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-437-2048.jpg)


![Differential Calculus of Several Variables ■ 5.9
∴
f x y x
y
x
f
x
x
y
x
y
x
nx
y
x
( , ) =
⎛
⎝
⎜
⎞
⎠
⎟
= ⋅ ′
⎛
⎝
⎜
⎞
⎠
⎟
−
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
−
n
n n
F
F F
∂
∂ 2
1 ⎞
⎞
⎠
⎟
∴ x
f
x
x y
y
x
nx
y
x
∂
∂
= − ′
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
−
n n
F F
1
(1)
∂
∂
f
y
x
y
x x
x
y
x
= ⋅ ′
⎛
⎝
⎜
⎞
⎠
⎟ ⋅ = ′
⎛
⎝
⎜
⎞
⎠
⎟
−
n n
F F
1 1
∴ y
f
y
x y
y
x
∂
∂
= ′
⎛
⎝
⎜
⎞
⎠
⎟
−
n
F
1 (2)
(1) + (2) ⇒ x
f
x
y
f
y
nx
y
x
∂
∂
∂
∂
+ =
⎛
⎝
⎜
⎞
⎠
⎟
n
F = n f x y
( , )
This theorem can be extended to homogeneous function of any number of variables.
If f(x, y, z) is a homogeneous function of degree n in three independent variables x, y, z and differenti-
able then x
f
x
y
f
y
z
f
z
nf
∂
∂
∂
∂
∂
∂
+ + = . ■
WORKED EXAMPLES
EXAMPLE 1
If u 5 log (x3
1 y3
1 z3
2 3xyz), then prove that
(i) ∂
∂
∂
∂
∂
∂
u
x
u
y
u
z x y z
1 1 5
1 1
3 (ii) ∂
∂
∂
∂
∂
∂
x y z
u
x y z 2
1 1 52
1 1
⎛
⎝
⎜
⎞
⎠
⎟
2
9
( )
Solution.
Given u = log (x3
+ y3
+ z3
− 3xyz)
∴
∂
∂
u
x x y z xyz
x yz
x yz
x y z xyz
=
+ + −
− =
−
+ + −
1
3
3 3
3
3
3 3 3
2
2
3 3 3
[ ]
[ ]
Similarly,
∂
∂
∂
∂
u
y
y zx
x y z xyz
u
z
z xy
x y z xyz
=
−
+ + −
=
−
+ + −
3
3
3
3
2
3 3 3
2
3 3 3
[ ] [ ]
and
∴ ∂
∂
∂
∂
∂
∂
u
x
u
y
u
z
x y z yz zx xy
x y z xyz
1 1 5
1 1 2 2 2
1 1 2
3[
3
2 2 2
3 3 3
]
We know that
x y z xyz x y z xy yz zx x y z
3 3 3 2 2 2
3
+ + − = + + − − − + +
( )( )
∴ ∂
∂
∂
∂
∂
∂
u
x
u
y
u
z
x y z xy yz zx
x y z x y z xy yz
+ + =
+ + − − −
+ + + + − − −
3 2 2 2
2 2 2
( )
( )( z
zx x y z
)
=
+ +
3
Let
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 9 5/12/2016 10:24:31 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-440-2048.jpg)
![5.10 ■ Engineering Mathematics
(ii) ⇒
∂
∂
+
∂
∂
+
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟ =
+ +
x y z
u
x y z
3
(1)
Operating
∂
∂
+
∂
∂
+
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟
x y z
on both sides, we get
∂
∂
+
∂
∂
+
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟ =
∂
∂
+
∂
∂
+
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟
=
∂
∂ + +
x y z
u
x y z x y z
x x y
2
3
3
z
z y x y z z x y z
x
x y z
⎛
⎝
⎜
⎞
⎠
⎟ +
∂
∂ + +
⎛
⎝
⎜
⎞
⎠
⎟ +
∂
∂ + +
⎛
⎝
⎜
⎞
⎠
⎟
=
∂
∂
+ + +
∂
∂
−
3 3
3 3
1
( )
y
y
x y z
z
x y z
x y z x y z x y
( ) ( )
( ) ( ) (
+ + +
∂
∂
+ +
= − + + ⋅ − + + ⋅ − +
− −
− −
1 1
2 2
3
3 1 3 1 3 +
+ ⋅
= −
+ +
−
+ +
−
+ +
= −
+ +
−
z
x y z x y z x y z x y z
)
( ) ( ) ( ) ( )
2
2 2 2 2
1
3 3 3 9
EXAMPLE 2
If u 5 (x 2 y) (y 2 z) (z 2 x), then prove that (i)
∂
∂
∂
∂
∂
∂
u
x
u
y
u
z
1 1 50 (ii) x
u
x
y
u
y
z
u
z
u
∂
∂
∂
∂
∂
∂
1 1 5 3
Solution.
Given u = (x − y) (y − z) (z − x)
∴
∂
∂
u
x
y z x y z x
= − − − + − ⋅
( )[( )( ) ( ) ]
1 1
= − − + + − = − + − − = − − +
( )( ) ( )( ) ( )
y z x y z x y z y z y z x y z yx zx
2 2 2
2 2
Similarly,
∂
∂
∂
∂
u
y
z x zy xy
u
z
x y xz yz
= − − + = − − +
2 2 2 2
2 2 2 2
and
(i)
∂
∂
∂
∂
∂
∂
u
x
u
y
u
z
y z yx zx z x zy x y xz yz
+ + = − − + + − − + − − + =
2 2 2 2 2 2
2 2 2 2 2 0
(ii) u is a homogeneous function of degree 3, since
u xt yt zt tx ty ty tz tz tx t x y y z z x
t
( , , ) ( ) ( ) ( ) ( ) ( ) ( )
(
= − − − = − − −
=
3
3
x
x y y z z x t u x y z
− − − =
) ( ) ( ) ( , , )
3
So, by Euler’s theorem, we get
x
u
x
y
u
y
z
u
z
u
∂
∂
∂
∂
∂
∂
+ + = 3
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 10 5/12/2016 10:24:35 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-441-2048.jpg)

![5.12 ■ Engineering Mathematics
and
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
u
z
u
x
x
z
u
y
y
z
u
z
z
z
= ⋅ + ⋅ + ⋅
1
1
1
1
1
1
⇒
∂
∂
∂
∂
∂
∂
u
z
u
y
u
z
= − +
1 1
(3)
(1) + (2) + (3) ⇒
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
u
x
u
y
u
z
u
x
u
z
u
x
u
y
u
y
u
z
+ + = − − + − + =
1 1 1 1 1 1
0
EXAMPLE 5
If u
x y
x y
5
1
1
2
sin ,
1 ⎛
⎝
⎜
⎞
⎠
⎟
then prove that x
u
x
y
u
y
u
∂
∂
∂
∂
1 5
1
2
tan .
Solution.
Given u
x y
x y
=
+
+
⎛
⎝
⎜
⎞
⎠
⎟
−
sin 1
⇒ sinu
x y
x y
=
+
+
Let f x y
x y
x y
f x y u
( , ) ( , ) sin
=
+
+
∴ =
∴ f tx ty
tx ty
tx ty
t
x y
x y
t f x y
( , ) ( , )
/ /
=
+
+
=
+
+
⎛
⎝
⎜
⎞
⎠
⎟
=
1 2 1 2
∴ f is a homogeneous function of degree
1
2
By Euler’s theorem, we get x
f
x
y
f
y
f
∂
∂
∂
∂
+ =
1
2
⇒ x
x
u y
y
u u f u
∂
∂
∂
∂
(sin ) (sin ) sin [ sin ]
+ = =
1
2
since
⇒ x u
u
x
y u
u
y
u
cos cos sin
∂
∂
∂
∂
+ =
1
2
⇒ x
u
x
y
u
y
u
u
∂
∂
∂
∂
+ =
1
2
sin
cos
⇒ x
u
x
y
u
y
u
∂
∂
∂
∂
+ =
1
2
tan
Another result on homogeneous functions which follow from Euler’s theorem is given below.
Theorem 5.2
If u(x, y) is homogeneous function of degree n in x and y with all first and second derivatives
continuous, then
x
u
x
xy
u
x y
y
u
y
n n u
2
2
2
2
2
2
2
2 1
∂
∂
∂
∂ ∂
∂
∂
1 1 5 2
( )
Proof Given u(x, y) is a homogeneous function of x and y of degree n.
So, by Euler’s theorem x
u
x
y
u
y
nu
∂
∂
∂
∂
+ = (1)
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 12 5/12/2016 10:24:45 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-443-2048.jpg)
![Differential Calculus of Several Variables ■ 5.13
Differentiating (1) partially w.r.to x, we get
⇒
x
u
x
u
x
y
u
x y
n
u
x
x
u
x
y
u
x y
n
u
x
∂
∂
∂
∂
∂
∂ ∂
∂
∂
∂
∂
∂
∂ ∂
∂
∂
2
2
2
2
2
2
1
+ + =
+ = −
( )
Multiplying by x, x
u
x
xy
u
x y
n x
u
x
2
2
2
2
1
∂
∂
∂
∂ ∂
∂
∂
+ = −
( ) (2)
Now differentiating (1) w.r.to y, we get
⇒
x
u
y x
y
u
y
u
y
n
u
y
x
u
x y
y
u
y
n
u
y
⋅ + ⋅ + =
+ = −
∂
∂ ∂
∂
∂
∂
∂
∂
∂
∂
∂ ∂
∂
∂
∂
∂
2 2
2
2 2
2
1
( ) assu
uming
∂
∂ ∂
∂
∂ ∂
2 2
u
x y
u
y x
=
⎡
⎣
⎢
⎤
⎦
⎥
Multiplying by y, xy
u
x y
y
u
y
n y
u
y
∂
∂ ∂
∂
∂
∂
∂
2
2
2
2
1
+ = −
( ) (3)
(2) + (3) ⇒ x
u
x
xy
u
x y
y
u
y
n x
u
x
y
u
y
n n
2
2
2
2
2
2
2
2 1 1
∂
∂
∂
∂ ∂
∂
∂
∂
∂
∂
∂
+ + = − +
⎡
⎣
⎢
⎤
⎦
⎥ = −
( ) ( ) u
u [ ( )]
Using 1
⇒ x u xyu y u n n u
2 2
2 1
xx xy yy
+ + = −
( )
WORKED EXAMPLES
EXAMPLE 6
If z xf
y
x
y
x
5 1
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
g , then show that x
z
x
xy
z
x y
y
z
y
2
2
2
2
2
2
2
2 0
∂
∂
∂
∂ ∂
∂
∂
1 1 5 .
Solution.
Given z xf
y
x
g
y
x
=
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
Let u xf
y
x
v g
y
x
z u v
=
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟ ∴ = +
, (1)
u tx ty tx f
ty
tx
t x f
y
x
tu
( , ) =
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥ =
∴ u is homogeneous of degree 1.
By theorem 5.2
x
u
x
xy
u
x y
y
u
y
n n u
2
2
2
2
2
2
2
2 ( 1) 0
∂
∂
∂
∂ ∂
∂
∂
1 1 5 2 5 [{ n = 1] (2)
∴
v x y g
y
x
v tx ty g
ty
tx
g
y
x
v x y
( , )
( , ) ( , )
=
⎛
⎝
⎜
⎞
⎠
⎟
=
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟ =
Now
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 13 5/12/2016 10:24:49 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-444-2048.jpg)
![5.14 ■ Engineering Mathematics
∴ v is homogeneous of degree 0.
∴ x
v
x
xy
v
x y
y
v
y
n n v
2
2
2
2
2
2
2
2 1 0
∂
∂
∂
∂ ∂
∂
∂
+ + = − =
( ) [{ n = 0] (3)
(2) + (3) ⇒ x
x
u v xy
x y
u v y
y
u v
2
2
2
2
2
2
2
2 0
∂
∂
∂
∂ ∂
∂
∂
( ) ( ) ( )
+ + + + + =
⇒ x
z
x
xy
z
x y
y
z
y
2
2
2
2
2
2
2
2 0
∂
∂
∂
∂ ∂
∂
∂
+ + =
EXAMPLE 7
If u5 2
2 2
x
y
x
y
x
y
2 1 2 1
tan tan , then find the value of x
u
x
2
2
2
∂
∂
1 2
2
2
2
2
xy
u
x y
y
u
y
∂
∂ ∂
+
∂
∂
.
Solution.
Given u x y x
y
x
y
x
y
( , ) tan tan
= −
− −
2 1 2 1
∴ u tx ty t x
ty
tx
t y
tx
ty
t x
( , ) tan tan
tan
=
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
=
− −
−
2 2 1 2 2 1
2 2 1 y
y
x
y
x
y
t u x y
−
⎡
⎣
⎢
⎤
⎦
⎥ =
−
2 1 2
tan ( , )
∴ u(x, y) is homogeneous of degree 2 and it is differentiable twice, partially.
∴ by theorem 5.2,
x
u
x
xy
u
x y
y
u
y
u u
2
2
2
2
2
2
2
2 2 2 1 2
∂
∂
∂
∂ ∂
∂
∂
+ + = − =
( )
EXAMPLE 8
If u 5 xy
, then show that (i) uxy
5 uyx
(ii) uxxy
5 uxyx
Solution.
Given u = xy
∴ ux
= yxy − 1
[treating y as constant] (1)
and uy
= xy
loge
x [treating x as constant] (2)
Differentiating (1) again w.r.to x, uxx
= y(y − 1)xy − 2
Differentiating again w.r.to y, we get
u y y x x x y y
xxy
y 2
e
y 2
1) log 1 ( 1 1
= − + ⋅ + − ⋅
− −
( [ ) ]
[ ( ]
= − + −
−
x y y x y
y 2
e
1) log 2 1 (3)
Differentiating (1) w.r.to y, we get
u y x x x u x y x
xy
y
e
y
xy
y
e
= ⋅ + ⋅ = +
− − −
1 1 1
1 1
log [ log ]
⇒ (4)
Differentiating (2) w.r.to x, we get
u x
x
x y x u x y x
yx
y
e
y
yx
y
e
= ⋅ + ⋅ = +
− −
1
1
1 1
log [ log ]
⇒ (5)
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 14 5/12/2016 10:24:52 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-445-2048.jpg)
![Differential Calculus of Several Variables ■ 5.15
From (4) and (5), we get uxy
= uyx
, which is (i)
Again differentiating (4) w.r.to x, we get
⇒
u x y
x
y x y x
x y y y
xyx
y
e
y
y
= ⋅
⎡
⎣
⎢
⎤
⎦
⎥ + + ⋅ −
= ⋅ + − +
− −
−
1 2
2
1
1 1
1 1
( log ) ( )
( )( lo
og )
[ ( )( log )] [ ( )log
e
y
xyx
y
e
y
e
x x
u x y y y x x y y x y
−
− −
= + − + = − +
2
2 2
1 1 1 2 −
−1] (6)
From (3) and (6), we get uxxy
= uxyx
, which is (ii)
EXAMPLE 9
If r x y z
2 2 2 2
5 1 1 , then prove that
∂
∂
∂
∂
∂
∂
2
2
2
2
2
2
2
r
x
r
y
r
z r
1 1 5 .
Solution.
Given r x y z
2 2 2 2
= + + ∴ 2 2
r
r
x
x
r
x
x
r
∂
∂
⇒
∂
∂
= =
∴ ∂
∂
∂
∂
2
2 2 2
2 2
3
1
r
x
r x
r
x
r
r x
x
r
r
r x
r
=
⋅ −
=
− ⋅
=
−
Similarly,
∂
∂
∂
∂
2
2
2 2
3
2
2
2 2
3
r
y
r y
r
r
z
r z
r
=
−
=
−
and
∴
∂
∂
∂
∂
∂
∂
2
2
2
2
2
2
2 2 2 2 2 2
3
2 2 2 2
3
3
r
x
r
y
r
z
r x r y r z
r
r x y z
r
+ + =
− + − + −
=
− + +
=
( ) 3
3 2 2
2 2
3
2
3
r r
r
r
r r
−
= =
5.2.4 Total Derivatives
Let u = f(x, y) be a function of 2 variables x, y. If x and y are continuous functions of t then z will be
ultimately a function of t only or z is a composite function of t. Then we can find the ordinary
derivative
du
dt
which is called the total derivative of u to distinguish it from the partial derivatives ∂
∂
∂
∂
u
x
u
y
, .
We have
du
dt
u
x
dx
dt
u
y
dy
dt
= +
∂
∂
∂
∂
This is also know as chain rule for one independent variable.
Proof u = f(x, y), x = F(t), y = G(t).
Giving increment Δt to t will result in increments Δx, Δy and Δu in x, y and u.
∴ Δ Δ Δ
Δ Δ Δ Δ
u f x x y y f x y
f x x y y f x y y f x y y f
= + + −
= + + − + + + −
( , ) ( , )
( , ) ( , ) ( , ) (x
x y
, )
∴ Δ
Δ
Δ Δ Δ
Δ
Δ
Δ
u
t
f x x y y f x y y
t
f x y y f x y
t
=
+ + − +
+
+ −
( , ) ( , ) ( , ) ( , )
=
+ + − +
+
+ −
f x x y y f x y y
x
x
t
f x y y f x y
y
y
t
( , ) ( , ) ( , ) ( , )
Δ Δ Δ
Δ
Δ
Δ
Δ
Δ
Δ
Δ
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 15 5/12/2016 10:25:04 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-446-2048.jpg)
![5.16 ■ Engineering Mathematics
∴
du
dt
u
t
t x y
t
= → → →
→
lim , , ,
Δ
Δ
Δ
Δ Δ Δ
0
0 0 0
as
∴
du
dt
f
x
dx
dt
f
y
dy
dt
du
dt
u
x
dx
dt
u
y
dy
dt
u f
= + =
∂
∂
+
∂
∂
=
∂
∂
∂
∂
or [ ]
{ (1)
Cor (1) In differential form the result (1) can be written as
df
f
x
dx
f
y
dy du
u
x
dx
u
y
dy
= + = +
∂
∂
∂
∂
∂
∂
∂
∂
or
du is called the total differential of u.
Similarly, if u = f(x, y, z) of 3 independent variable x, y, z, then the total differential is
du
u
x
dx
u
y
dy
u
z
dz
= + +
∂
∂
∂
∂
∂
∂
Note: The function z = f(x, y) is differentiable at the point (x0
, y0
) if the first partial derivatives fx
, fy
exist at (x0
, y0
) and are continuous at (x0
, y0
) and
dz f x y dx f x y dy
x y
= +
( , ) ( , ) .
0 0 0 0
From this result, it follows that if f(x, y) is differentiable at (x0
, y0
), then f is continuous at
(x0
, y0
).
Cor (2) If u = f(x, y) where x and y are function of t1
, t2
, then u is ultimately a function of t1
, t2
and so
z is a composite function of t1
, t2
.
Then we have partial derivatives of u w.r.to t1
, t2
∴
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
u
t
u
x
x
t
u
y
y
t
u
t
u
x
x
t
u
y
y
t
1 1 1 2 2 2
= + ⋅ = + ⋅
and
These are chain rules for two independent variables.
Cor (3) Differentiation of implicit functions
The equation f(x, y) = 0 defines y implicitly as a function of x. Suppose the function f(x, y) is differen-
tiable, then the total differential
⇒
df
df
dx
dx
df
dy
dy
=
+ =
0
0
⇒
∂
∂
∂
∂
f
x
f
y
dy
dx
+ = 0
⇒
dy
dx
f
x
f
y
dy
dx
f
f
f
=
−
= − ≠
∂
∂
∂
∂
⇒ x
y
y
if 0
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 16 5/12/2016 10:25:07 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-447-2048.jpg)
![Differential Calculus of Several Variables ■ 5.17
WORKED EXAMPLES
EXAMPLE 1
If u 5 x2
y3
, x 5 log t, y 5 et
, then find
d
d
u
t
.
Solution.
Given u = x2
y3
, x = log t, y = et
. So, u is ultimately a function of t
We know du
u
x
dx
u
y
dy
= +
∂
∂
∂
∂
∴ du
dt
u
x
dx
dt
u
y
dy
dt
= +
∂
∂
∂
∂
.
But ∂
∂
∂
∂
u
x
xy
u
y
x y
dx
dt t
dy
dt
e
= = ⋅ = =
2 3
1
3 2 2
, , , t
∴
du
dt
xy
t
x y e
t e
t
t e e
t
t
= ⋅ +
= ⋅ ⋅ + ⋅ ⋅ =
2
1
3
2
1
3
2
3 2 2
2
t
3t 2t t
log (log ) (log )e
e t e
e t
t
t t
t t
t
3 3
+ = +
3 2 3
2
3
(log )
log
[ log ]
EXAMPLE 2
If u x y
5 2
2
sin ( ),
1
where x = 3t, y = 4t3
, then show that
du
dt
5
2
3
1
1 1
2
t
t
, .
−
Solution.
Given u = sin−1
(x − y), where x = 3t, y = 4t3
We know du
u
x
dx
u
y
dy
= +
∂
∂
∂
∂
∴ du
dt
u
x
dx
dt
u
y
dy
dt
= +
∂
∂
∂
∂
But
∂
∂
∂
∂
u
x x y
u
y x y
=
− −
=
− −
−
1
1
1
1
1
2 2
( )
,
( )
( ) and dx
dt
dy
dt
t
= =
3 12 2
,
∴
du
dt x y
t
t
x y
=
− −
− =
− −
1
1
3 12
3 1
1
2
2
2
2
( )
( )
( )
( )
− 4
Now 1 − (x − y)2
= 1 − (3t − 4t3
)2
= 1 − (9t2
+ 16t6
− 24t4
) = 1 − 9t2
+ 24t4
− 16t6
Since sum of the coefficients of R. H. S = 0, t2
= 1 will satisfy the polynomial 1 − 9t2
+ 24t4
− 16t6
∴ 1 1 16 8 1
1 16 8 1
2 2 4 2
2 4 2
− − = − − + −
= − − − +
= −
( ) ( )( )
( )( )
( )(
x y t t t
t t t
t2
1 4
− t
t2
− = − −
1 1 1 4
2 2 2 2
) ( )( )
t t
1 16 24 9 1
0 16 8 1
16 8 1 0
− −
− −
− −
∴
du
dt
t
t t t
t
=
−
− −
=
−
−
3 1 4
1 1 4
3
1
1 4 0
2
2 2 2 2
2
( )
( )( )
[ ]
since
EXAMPLE 3
Find
du
dx
if u 5 cos (x2
1 y2
) and a2
x2
1 b2
y2
5 c2
.
Solution.
Given u = cos (x2
+ y2
) and a2
x2
+ b2
y2
= c2
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 17 5/12/2016 10:25:12 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-448-2048.jpg)

![Differential Calculus of Several Variables ■ 5.19
=
⎛
⎝
⎜
⎞
⎠
∂
∂
u
x
⎟
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟ +
2
2 2
2
2 2
[cos sin ] [sin cos ]
u u u u
∂
∂
u
y
⇒
∂
∂
∂
∂
∂
∂
∂
∂
u
r r
u u
x
u
y
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
2
2
2 2 2
1
u
EXAMPLE 5
If u f
y x
xy
z x
zx
5
2 2
,
⎛
⎝
⎜
⎞
⎠
⎟, then prove that x
u
x
y
u
y
z
u
z
2 2 2
0
∂
∂
∂
∂
∂
∂
1 1 5 .
Solution.
Given u f
y x
xy
z x
zx
=
− −
⎛
⎝
⎜
⎞
⎠
⎟
,
Put r
x y
xy y x
s
z x
zx x z
=
−
= − =
−
= −
1 1 1 1
and
∴ u is a function of r, s and r and s are functions of x, y, z
We know du
u
r
dr
u
s
ds
= +
∂
∂
∂
∂
∴ ∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
u
x
u
r
r
x
u
s
s
x
u
y
u
r
r
y
u
s
s
y
u
z
u
= ⋅ + ⋅ = ⋅ + ⋅ =
, ,
r
r
r
z
u
s
s
z
⋅ + ⋅
∂
∂
∂
∂
∂
∂
But
and
r
y x
r
x x
r
y y
r
z
s
x z
s
x x
= − = + = − =
= − = −
1 1 1 1
0
1 1 1
2 2
2
∴
∂
∂
∂
∂
∂
∂
∴
∂
∂
, ,
,
∂
∂
∂
∂
∂
s
y
s
z z
= =
0
1
2
,
∴
∂
∂
∂
∂
∂
∂
u
x
u
r x
u
s x
= ⋅ + −
⎛
⎝
⎜
⎞
⎠
⎟
1 1
2 2
⇒ x
u
x
u
r
u
s
2 ∂
∂
∂
∂
∂
∂
= − (1)
∂
∂
∂
∂
∂
∂
u
y
u
r y
u
s
= ⋅ −
⎛
⎝
⎜
⎞
⎠
⎟ + ⋅
1
0
2
⇒ y
u
y
u
r
2 ∂
∂
∂
∂
= − (2)
and
∂
∂
∂
∂
∂
∂
u
z
u
r
u
s z
= ⋅ + ⋅
⎛
⎝
⎜
⎞
⎠
⎟
0
1
2 ⇒ z
u
z
u
s
2 ∂
∂
∂
∂
= (3)
(1) + (2) + (3) ⇒ + + = − − + =
x
u
x
y
u
y
z
u
y
u
r
u
s
u
r
u
s
2 2 2
0
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 19 5/12/2016 10:25:22 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-450-2048.jpg)






![5.26 ■ Engineering Mathematics
ANSWERS TO EXERCISE 5.2
11. 0
17. 8e4t
18. 3 sin t cos t (b3
sin t − a3
cos t)
20. 4e2t
24. 2 2 1 4 1
2
2
2
2
x u
u v
yu
u v
( )
,
+
+
+
+
27. t3
(4 + t) et
28. 2
2
t
t t t
[ sinh cosh ]
−
29.
e
t
e
t
t
t t
3 2
2
cos [ ]
⎛
⎝
⎜
⎞
⎠
⎟ −
32.
∂
∂
∂
∂
u
x
x
u
v
x
x
v
= =
−
3 2
,
33. 0
5.3 JACOBIANS
Jacobians have many important applications such as functional dependence, transformation of vari-
able in multiple integrals, problems in partial differentiation and in the study of existence of implicit
functions determined by a system of functional equations.
Definition 5.8
(1) If u and v are continuous functions of two independent variables x and y, having first order partial
derivatives, then the determinant
∂
∂
∂
∂
∂
∂
∂
∂
u
x
u
y
v
x
v
y
is called the Jacobian determinant or Jacobian of u
and v with respect to x and y and is denoted by ∂
∂
( , )
( , )
u v
x y
or J
u v
x y
,
,
⎛
⎝
⎜
⎞
⎠
⎟ or J.
Thus, ∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
( , )
( , )
u v
x y
u
x
u
y
v
x
v
y
=
(2) If u, v, w are continuous functions of three independent variables x, y, z having first order partial
derivatives then the Jacobian of u, v, w with respect to x, y, z is defined as
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
( , , )
( , , )
u v w
x y z
u
x
u
y
u
z
v
x
v
y
v
z
w
x
w
y
w
z
=
Similarly, we can define Jacobians for functions of 4 or more variables.
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 26 5/12/2016 9:35:41 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-457-2048.jpg)

![5.28 ■ Engineering Mathematics
∴
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
u
x
u
p
p
x
u
q
q
x
v
x
v
p
p
x
v
q
q
x
= ⋅ + ⋅ = ⋅ + ⋅
and
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
u
y
u
p
p
y
u
q
q
y
v
y
v
p
p
y
v
q
q
y
= ⋅ + ⋅ = ⋅ + ⋅
and
∴
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
( , )
( , )
( , )
( , )
u v
p q
p q
x y
u
p
u
q
v
p
v
q
p
x
p
y
q
x
q
y
⋅ =
=
=
⋅ + ⋅ +
⋅ + ⋅
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
u
p
p
x
u
q
q
x
u
p
p
y
u
q
q
y
v
p
p
x
v
q
q
x
v
v
p
p
y
v
q
q
y
u
x
u
y
v
x
v
y
u v
x y
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
+
= =
( , )
( , )
∴
∂
∂
∂
∂
∂
∂
( , )
( , )
( , )
( , )
( , )
( , )
u v
x y
u v
p q
p q
x y
= ⋅ ■
Note Extension to three variables
(1) ∂
∂
∂
∂
( , , )
( , , )
( , , )
( , , )
u v w
x y z
x y z
u v w
⋅ = 1 and (2) ∂
∂
∂
∂
∂
∂
( , , )
( , , )
( , , )
( , , )
( , , )
( , , )
u v w
x y z
u v w
p q r
p q r
x y z
= ⋅
Property 3 If u and v are functions of two independent variables x and y and u and v are functionally
dependent [i.e., f(u, v) = 0], then
∂
∂
( , )
( , )
.
u v
x y
= 0
Proof If u and v are not independent, then there is a relation between u and v. Let f(u, v) = 0 be the
relation between u and v.
Differentiating with respect to x and y we have,
∂
∂
∂
∂
f
u
u
f
v
v
∂ + ∂ = 0
∴
∂
∂
∂
∂
∂
∂
∂
∂
f
u
u
x
f
v
v
x
+ ⋅ = 0 (1) and
∂
∂
∂
∂
∂
∂
∂
∂
f
u
u
y
f
v
v
y
⋅ + ⋅ = 0 (2)
Eliminating
∂
∂
∂
∂
f
u
f
v
, from (1) and (2), we get
∂
∂
∂
∂
∂
∂
∂
∂
u
x
u
y
v
x
v
y
= 0 ⇒ ∂
∂
( , )
( , )
u v
x y
= 0 ■
Note
(1) The converse of property 3 is also true.
(2) The property can be extended to functions of more than two variables.
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 28 5/12/2016 9:35:51 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-459-2048.jpg)



![5.32 ■ Engineering Mathematics
and y r
= sin sin
u f
∴
∂
∂
∂
∂
∂
∂
∂
∂
y
r
y
r
y
r
z r
z
r
= = =
=
=
sin sin , cos sin , sin cos
cos
cos
u f
u
u f
f
u f
u
u
u
u
u
f
, sin ,
∂
∂
∂
∂
z
r
z
= − = 0
∴ J =
−
sin cos cos cos sin sin
sin sin cos sin sin cos
cos
u f u f u f
u f u f u f
r r
r r
u
u u
−r sin 0
Expanding using third row, we get
J = + + +
cos [ cos sin cos cos sin sin ] sin [ sin cos
u u u f u u f u u f
r r r r
2 2 2 2 2 2
r
r
r r
sin sin ]
sin [cos (cos sin ] sin [sin (cos
2 2
2 2 2 2 2 2 2
u f
u u f f u u f
= + + +
+
= + =
sin )]
sin [cos sin ] sin
2
2 2 2 2
f
u u u u
r r
Note This is the transformation of cartesian coordinates to spherical polar coordinates (r, u, f)
dx dy dz dr d d r dr d d
= = ⋅
J u f u u f
2
sin
EXAMPLE 6
In cylindrical polar coordinates x 5 r cos f, y 5 r sin f, z 5 z, show that
∂
∂
( )
( , , )
.
x y z
z
, ,
r f
5 r
Solution.
We have
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
( , , )
( , , )
x y z
z
x x x
z
y y y
z
z z z
z
r f
r f
r f
r f
=
Given x
x x x
z
=
= = − =
r f
r
f
f
r f
cos
cos , sin ,
∂
∂
∂
∂
∂
∂
0
and y = r f
sin
∴ ∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
y y y
z
z z
z z z
z
r
f
f
r f
r f
= = =
=
= = =
sin , cos ,
, ,
0
0 0 1
(ρ, φ, z)
P
z
Z
Y
M
X
ρ
φ
(x, y, z)
∴
Fig. 5.4
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 32 5/12/2016 9:36:35 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-463-2048.jpg)
![Differential Calculus of Several Variables ■ 5.33
∴ ∂
∂
( , , )
( , , )
cos sin
sin cos
cos sin (
x y z
z
r f
f r f
f r f
r f r f r
=
−
= + =
0
0
0 0 1
2 2
c
cos sin )
2 2
f f r
+ =
Note This is the transformation of cartesian coordinate to cylindrical coordinates (r, f, z).
dx dy dz d d dz d d dz
= =
J r f r r f
EXAMPLE 7
If u
yz
x
v
zx
y
w
xy
z
5 5 5
, , , then show that
∂
∂
( )
( )
.
u v w
x y z
, ,
, ,
5 4
Solution.
We have,
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
( , , )
( , , )
u v w
x y z
u
x
u
y
u
z
v
x
v
y
v
z
w
x
w
y
w
z
=
Given u
yz
x
u
x
yz
x
u
y
z
x
= =
−
=
∴
∂
∂
∂
∂
2
, and
∂
∂
u
z
y
x
=
v
zx
y
v
x
z
y
v
y
zx
y
= = = −
∴
∂
∂
∂
∂
, 2
and
∂
∂
v
z
x
y
=
w
xy
z
w
x
y
z
w
y
x
z
w
z
xy
z
= = = = −
∴
∂
∂
∂
∂
∂
∂
, and 2
∴ ∂
∂
( , , )
( , , )
u v w
x y z
yz
x
z
x
y
x
z
y
zx
y
x
y
y
z
x
z
xy
z
x y z
yz xz x
=
−
−
−
=
−
2
2
2
2 2 2
1
y
y
zy zx xy
zy xz xy
−
−
[Take from I row
from II row and
1
1 1
2
2 2
x
y z
from III row]
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 33 5/12/2016 9:36:41 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-464-2048.jpg)
![5.34 ■ Engineering Mathematics
=
−
−
−
x y z
x y z
2 2 2
2 2 2
1 1 1
1 1 1
1 1 1
[Take from I column
from II
yz
zx c
column and from III column]
xy
= − + − − − − + + = + +
1 1 1 1 1 1 1 1 1 0 2
( ) ( ) ( ) 2
2 4
=
EXAMPLE 8
If u 5 x 1 y 1 z, uv 5 y 1 z, uvw 5 z, then find ∂
∂
( )
( )
.
x y z
u v w
, ,
, ,
Solution.
Given u = x + y + z, uv = y + z, uvw = z
∴ u = x + uv ⇒ x = u − uv
y = uv − z = uv − uvw and z = uvw
Now x = u − uv ∴
∂
∂
∂
∂
∂
∂
x
u
v
x
v
u
x
w
= − = − =
1 0
, and
y = uv − uvw ∴
∂
∂
∂
∂
∂
∂
y
u
v vw
y
v
u uw
y
w
uv
= − = − = −
, and
and z uvw
= ∴
∂
∂
∂
∂
∂
∂
z
u
vw
z
v
uw
z
w
uv
= = =
, , and
∴
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
( , , )
( , , )
x y z
u v w
x
u
x
v
x
w
y
u
y
v
y
w
z
u
z
v
z
w
v
= =
− −
1 u
u
v vw u uw uv
vw uw uv
0
− − −
=
− −
− − −
=
− −
uv
v u
v vw u uw
vw uw
uv
uv
v u
v u
vw u
1 0
1
1
1 0
0
3
[ ]
Taking out from C
w
w
uv v u uv uv u uv uv u v
1
1
2 2 3
2
3
R R R
Expanding by C
→ +
= − + = − + =
[( ) ] ( ) [ ]
EXAMPLE 9
If u
x y
xy
v x y
5
1
2
5 1
2 2
1
1 1
, tan tan find ∂
∂
( )
( )
u, v
x, y
.
Solution.
Given u
x y
xy
=
+
−
1
and v x y
= +
− −
tan tan
1 1
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 34 5/12/2016 9:36:47 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-465-2048.jpg)

![5.36 ■ Engineering Mathematics
∴
∂
∂
( )
( , , )
F, G, H
u v w
x
u y
z w v
=
− +
1 0
2 1
1
= − − + − − = − + + −
x vy w uv z x w vy z uv
{ ( )} ( ) ( )
1 1 2 1 2
∴
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
( )
( , , )
F, G, H
F F F
G G G
H H H
x y z
x y z
x y z
x y z
u
= =
−1 0
0
0 0
0 0
2
v
u
u vu u v
= =
( )
∴ ∂
∂
( , , )
( , , )
( ) [ ( ) ] [ ]
x y z
u v w
x vy w uv z
u v
x w vy uv z
=
− + − − +
=
− − + −
1 1 2 1 2
3
2
u
u v
2
EXAMPLE 11
If x 1 y 1 z 2 u 5 0, y 1 z 1 uv 5 0, z 2 uvw 5 0 then find
∂
∂
( )
)
.
x, y, z
(u, v, w
Solution.
Given x + y +z − u = 0, y + z − uv = 0, z − uvw = 0
These equations implicitly define x, y, z interms of u, v, w
Let f1
= x + y + z − u, f2
= y + z − uv and f3
= z − uvw
To find ∂
∂
( , , )
( , , )
.
x y z
u v w
By the Jacobian of implicit functions, we have
∂
∂
∂
∂
∂
∂
( , , )
( , , )
( )
( , , )
( , , )
( , , )
( ,
f f f
u v w
f f f
x y z
x y z
u v
1 2 3 3 1 2 3
1
= − ⋅
,
, )
w
∴
∂
∂
∂
∂
∂
∂
( , , )
( , , )
( )
( , , )
( , , )
( , , )
( , ,
x y z
u v w
f f f
u v w
f f f
x y
= −1 3
1 2 3
1 2 3
z
z)
We have f1
= x + y + z − u
∴ ∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
f
x
f
y
f
z
f
u
f
v
f
w
1 1 1 1 1 1
1 1 1 1 0 0
= = = = − = =
, , , ,
and
f2
= y + z − uv
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
f
x
f
y
f
z
f
u
v
f
v
u
f
w
2 2 2 2 2 2
0 1 1 0
= = = = − = − =
, , , ,
and
and f3
= z − uvw
∴
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
f
x
f
y
f
z
f
u
vw
f
v
uw
f
w
uv
3 3 3 3 3 3
0 0 1
= = = = − = − = −
, , , ,
and
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 36 5/12/2016 9:36:58 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-467-2048.jpg)
![Differential Calculus of Several Variables ■ 5.37
∴
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
( , , )
( , , )
f f f
x y z
f
x
f
y
f
z
f
x
f
y
f
z
f
x
f
1 2 3
1 1 1
2 2 2
3 3
=
∂
∂
∂
∂
y
f
z
3
1 1 1
0 1 1
0 0 1
1
= =
∂
∂
( , , )
( , , )
( )[( )( )]
f f f
u v w
v u
vw uw uv
u uv u
1 2 3 2
1 0 0
0 1
=
−
− −
− − −
= − − − = − v
v
∴
∂
∂
( , , )
( , , )
( )
( )
x y z
u v w
u v
u v
= − ⋅
−
=
1
1
3
2
2
EXERCISE 5.3
1. If x = sin u cos v, y = sin u sin v, then find ∂
∂
( , )
( , )
.
x y
u v
2. If x = er
sec u, y = er
tan u, then show that
∂
∂
( , )
( , )
sec
x y
r
e r
u
u
= 2
. Verify
∂
∂
∂
∂
( , )
( , )
( , )
( , )
x y
r
r
x y
u
u
⋅ = 1.
3. If x = u(1 + v), y = v (1 + u), then find ∂
∂
( , )
( , )
x y
u v
and show that
∂
∂
∂
∂
( , )
( , )
( , )
( , )
.
x y
u v
u v
x y
⋅ = 1
4. If x = u + v, y = u − v, then find ∂
∂
( , )
( , )
x y
u v
and prove that
∂
∂
∂
∂
( , )
( , )
( , )
( , )
.
x y
u v
u v
x y
⋅ = 1
5. If x = e2u
cos v, y = e2u
sin v, then find ∂
∂
( , )
( , )
x y
u v
and ∂
∂
( , )
( , )
u v
x y
.
6. If x = u − v2
, y = u + v2
, then find ∂
∂
( , )
( , )
x y
u v
.
7. If u = x2
+ y2
+ z2
, v = x + y + z, w = xy + yz + zx, then show that
∂
∂
( , , )
( , , )
.
u v w
x y z
= 0 Is u, v, w
functionally related? If so find the relation between them.
8. If u = y + z, v = x +2z2
, w = x − 4yz − zy2
, then find ∂
∂
( , , )
( , , )
u v w
x y z
.
9. If u
y
x
v
x y
x
= =
+
2 2 2
2 2
, , then find ∂
∂
( , )
( , )
u v
x y
.
10. If u3
+ v3
= x + y, u2
+ v2
= x3
+ y3
, then prove that ∂
∂
( , )
( , )
( )
( )
.
u v
x y
y x
uv u v
=
−
−
1
2
2 2
11. If x = v2
+ w2
, y = w2
+ u2
, z = u2
+ v2
, then prove that ∂
∂
( , , )
( , , )
x y z
u v w
= 0.
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 37 5/12/2016 9:37:08 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-468-2048.jpg)

![Differential Calculus of Several Variables ■ 5.39
f a h b k f a b h
x
k
y
f a b
h
x
k
y
( , ) ( , ) ( , )
!
+ + = + +
⎛
⎝
⎜
⎞
⎠
⎟
+ +
⎛
⎝
⎜
⎞
⎠
⎟
∂
∂
∂
∂
∂
∂
∂
∂
1
2
2
2 3
1
3
f a b h
x
k
y
f a b
( , )
!
( , )
+ +
⎛
⎝
⎜
⎞
⎠
⎟ +
∂
∂
∂
∂
…
i.e., x y xx
f a h b k f a b h f a b k f a b h f
( , ) ( , ) ( , ) ( , )
!
[ (
+ + = + +
⎡
⎣ ⎤
⎦ +
1
2
2
a
a b hk f a b k f a b
h f a b h k f a b
, ) ( , ) ( , )]
!
[ ( , ) ( ,
+ +
+ +
2
1
3
3
2
3 2
xy yy
xxx xxy )
) ( , ) ( , )]
+ + +
3 2 3
hk f a b k f a b
xyy yyy
…
Modified forms
1. Put x = a + h, y = b + k, then h = x − a, k = y − b
∴ the Taylor’s series can be written as
f x y f a b x a f a b y b f a b
x a f a
( , ) ( , ) {( ) ( , ) ( ) ( , )}
!
{( ) ( ,
= + − + −
+ −
x y
xx
1
2
2
b
b x a y b f a b y b f a b
) ( )( ) ( , ) ( ) ( , )}
+ − − + − +
2 2
xy yy
… (1)
This series is known as the Taylor’s series expansion of f(x, y) in the neighbourhood of (a, b) or
about the point (a, b).
2. Putting a = 0, b = 0, we get the expansion of f(x, y) in the neighbourhood of (0, 0)
f x y f xf yf
x f xy f
( , ) ( , ) [ ( , ) ( , )]
!
[ ( , ) ( ,
= + +
+ +
0 0 0 0 0 0
1
2
0 0 2 0
2
x y
xx xy 0
0 0 0
2
) ( , )]
+ +
y f yy
…
This is called Maclaurin’s series for f(x, y) in powers of x and y.
Note Taylor’s formula gives polynomial approximation to a function of two variables about a given
point.
WORKED EXAMPLES
EXAMPLE 1
Expand tan21 y
x
about (1, 1) upto the second degree terms.
Solution.
We know the expansion of f(x, y) about the point (a, b) as Taylor’s series is
f x y f a b x a f a b y b f a b
x a f a
( , ) ( , ) [( ) ( , ) ( ) ( , )]
!
[( ) ( ,
= + − + −
+ −
x y
xx
1
2
2
b
b x a y b f a b y b f a b
) ( )( ) ( , ) ( ) ( , )]
+ − − + − +
2 2
xy yy
…
Here (a, b) 5 (1, 1)
∴ f x y f x f y f
x f
( , ) ( , ) [( ) ( , ) ( ) ( , )]
!
[( ) ( ,
= + − + −
+ −
1 1 1 1 1 1 1 1
1
2
1 1
2
x y
xx 1
1 2 1 1 1 1 1 1 1
2
) ( )( ) ( , ) ( ) ( , )]
+ − − + − +
x y f y f
xy yy
…
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 39 5/12/2016 9:37:27 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-470-2048.jpg)
![5.40 ■ Engineering Mathematics
Given f x y
y
x
f
( , ) tan , ( , ) tan
= = =
− −
1 1
1 1 1
4
p
∴ f
y
x
y
x
y
x y
f
f
y
x
x
x x
y
=
+
−
⎛
⎝
⎜
⎞
⎠
⎟ =
−
+
=
−
+
= −
=
+
⋅
1
1
1 1
1
1 1
1
2
1
1
1
2
2
2 2 2
2
2
( , )
=
=
+
=
+
=
x
x y
f
2 2
1 1
1
1 1
1
2
y ( , )
f
x y y x
x y
xy
x y
f
xx xx
= −
+ ⋅ − ⋅
+
⎧
⎨
⎩
⎫
⎬
⎭
=
+
=
⋅ ⋅
( )
( ) ( )
( , )
2 2
2 2 2 2 2 2
0 2 2
1 1
2 1 1
1
1 1
1
2
2
( )
+
=
f
y
y
x y
f
x y y
xy xy
=
−
+
⎛
⎝
⎜
⎞
⎠
⎟ =
−
+
=
=
( + − − −
∂
∂ 2 2 2
2 2
1 1
1 1
1 1
0
1
, ( , )
( )
)( ) ( )2
2
2 2 2
2 2
2 2 2
y
x y
y x
x y
( ) ( )
+
=
−
+
f
y
x
x y
f
x y x y
x y
yy yy
=
+
⎛
⎝
⎜
⎞
⎠
⎟ =
−
= −
=
( + ⋅ − ⋅
+
∂
∂ 2 2 2
2 2
2 2
1 1
2
2
1
2
0 2
, ( , )
)
( )
) ( )
2 2 2 2
2
=
−
+
xy
x y
∴ f x y x y
x x
( , ) ( ) ( )
( ) ( )(
= + − −
⎛
⎝
⎜
⎞
⎠
⎟ + − ⋅
⎡
⎣
⎢
⎤
⎦
⎥
+ − ⋅ + −
p
4
1
1
2
1
1
2
1
2
1
1
2
1
2
y
y y
− ⋅ + −
−
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥ +
1 0 1
1
2
2
) ( ) …
⇒ tan ( ) ( ) ( ) ( )
−
= − − + − + − − −
1 2 2
4
1
2
1
1
2
1
1
4
1
1
4
1
y
x
x y x y
p
EXAMPLE 2
Expand ex
cos y near the point 1
4
,
p
⎛
⎝
⎜
⎞
⎠
⎟ by Taylor’s series as far as quadratic terms.
Solution.
We know Taylor’s series about the point (a, b) is
f x y f a b x a f a b y b f a b
x a f a
( , ) ( , ) [( ) ( , ) ( ) ( , )]
!
[( ) ( ,
= + − + −
+ −
x y
xx
1
2
2
b
b x a y b f a b y b f a b
) ( )( ) ( , ) ( ) ( , )]
+ − − + − +
2 2
xy yy
…
Here (a, b) 5 1
4
,
p
⎛
⎝
⎜
⎞
⎠
⎟
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 40 5/12/2016 9:37:37 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-471-2048.jpg)
![Differential Calculus of Several Variables ■ 5.41
∴ f x y f x f y f
( , ) , ( ) , ,
=
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
1
4
1 1
4 4
1
4
p p p p
x y ⎟
⎟
⎡
⎣
⎢
⎤
⎦
⎥
+ −
⎛
⎝
⎜
⎞
⎠
⎟ + − −
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
1
2
1 1
4
2 1
4
1
4
2
( ) , ( ) ,
x f x y f
xx xy
p p p
⎠
⎠
⎟
⎡
⎣
⎢ + −
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
⎤
⎦
⎥ +
y f
p p
4
1
4
2
yy , …
Given f x y e y f e
e
f e y f
( , ) cos , , cos
cos , ,
=
⎛
⎝
⎜
⎞
⎠
⎟ = ⋅ =
= ⋅
⎛
⎝
⎜
⎞
⎠
x
x
x
x
1
4 4 2
1
4
p p
p
⎟
⎟ = ⋅ =
= −
⎛
⎝
⎜
⎞
⎠
⎟ = − ⋅ = −
=
e
e
f e y f e
e
f e
cos ,
sin , , sin
co
p
p p
4 2
1
4 4 2
y
x
y
xx
x
s
s , , cos ,
cos ,
y f e
e
f e y f e
xx
yy
x
xy
1
4 4 2
1
4
p p
p
⎛
⎝
⎜
⎞
⎠
⎟ = ⋅ =
= − ⋅
⎛
⎝
⎜
⎞
⎠
⎟ = − ⋅s
sin
sin , , cos
p
p p
4 2
1
4 4 2
= −
= −
⎛
⎝
⎜
⎞
⎠
⎟ = − ⋅ = −
e
f e y f e
e
xy
x
yy
∴ e y
e
x
e
y
e
x
e
x y
x
cos ( )
( ) ( )
= + − + −
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
+ − ⋅ + − −
2
1
2 4 2
1
2
1
2
2 1
2
p
p
p p
4 2 4 2
2
1 1
2
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥ +
= + − −
e
y
e
e
x
…
( ) y
y x x y y
−
⎛
⎝
⎜
⎞
⎠
⎟ + − − − −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
p p p
4
1
2
1 1
4
1
2 4
2
2
( ) ( )
EXAMPLE 3
Expand ex
loge
(1 1 y) in powers of x and y upto terms of third degree.
Solution.
Required the expansion in powers of x and y and so Maclaurin’s series is to be used.
We know f x y f x f y f x f xy f
( , ) ( , ) [ ( , ) ( , )] [ ( , ) ( ,
= + + + +
0 0 0 0 0 0
1
2
0 0 2 0 0
2
x y xx xy )
) ( , )]
+ y f
2
0 0
yy
+ + + + +
1
3
0 0 3 0 0 3 0 0 0 0
3 2 2 3
!
[ ( , ) ( , ) ( , ) ( , )]
x f x y f xy f y f
xxx xxy xyy xyy
…
…
Here (a,b) 5 (0, 0)
Given f(x, y) = ex
log (1 + y), f(0, 0) = e0
log (1 + 0) = 0,
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 41 5/12/2016 9:37:41 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-472-2048.jpg)
![5.42 ■ Engineering Mathematics
∴ f e y
f e
y
f e y
f e
y
f
e
x
x
x
x
x
y
xx
xy
yy
= +
= ⋅
+
= +
= ⋅
+
= −
log( ),
,
log( ),
,
1
1
1
1
1
1
x
x
x
x
x
y
f e y
f e
y
f
e
y
f
( )
,
log ( ),
,
( )
,
1
1
1
1
1
2
2
+
= +
= ⋅
+
= −
+
=
xxx
xxy
xyy
yyy
2
2
1 3
e
y
x
( )
,
+
fx
(0, 0) = 0
fy
(0, 0) = 1
fxx
(0, 0) = 0
fxy
(0, 0) = 1,
fyy
(0, 0) = −1
fxxx
(0, 0) = 0
fxxy
(0, 0) = 1,
fxyy
(0, 0) = −1,
fyyy
(0, 0) = 2
∴
f x y x y x xy y
x x y xy
( , ) [ ( )]
[
= + ⋅ + ⋅ + ⋅ + ⋅ + ⋅ −
+ ⋅ + ⋅ +
0 0 1
1
2
0 2 1 1
1
6
0 3 1 3
2 2
3 2 2
2 3
1 2
( ) ]
− + ⋅
y
⇒ e y y xy y x y xy y
x
log( )
1
1
2
1
2
1
2
1
3
2 2 2 3
+ = + − + − +
EXAMPLE 4
Expand x2
y 1 3y 2 2 in powers of x 2 1 and y 1 2 using Taylor’s theorem.
Solution.
We know
f x y f a b x a f a b y b f a b
x a f a
( , ) ( , ) [( ) ( , ) ( ) ( , )]
!
[( ) ( ,
= + − + −
+ −
x y
xx
1
2
2
b
b x a y b f a b y b f a b
x a f a b
) ( )( ) ( , ) ( ) ( , )]
!
[( ) ( ,
+ − − + −
+ −
2
1
3
2
3
xy yy
xxx )
) ( ) ( ) ( , )
( )( ) ( , ) ( ) (
+ − −
+ − − + −
3
3
2
2 3
x a y b f a b
x a y b f a b y b f
xxy
xyy yyy a
a b
, )]+…
Here (a, b) 5 (1, 22)
Given f(x, y) = x2
y + 3y − 2, f(1, −2) = −2 − 6 − 2 = −10
∴ f xy f
f x f
f y f
x x
y y
xx x
= − = ⋅ ⋅ − = −
= + − = + =
=
2 1 2 2 1 2 4
3 1 2 1 3 4
2
2
, ( , ) ( )
, ( , )
, x
x ( , ) ( )
1 2 2 2 4
− = − = −
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 42 5/12/2016 9:37:45 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-473-2048.jpg)
![Differential Calculus of Several Variables ■ 5.43
yy yy
xy xy
x
, ( , )
, ( , )
0 1 2 0
2 1 2 2 1 2
= − =
= − = ⋅ =
f f
f x f
f x
xx xxx
= − =
0 1 2 0
, ( , )
f
f f
f f
f f
xxy xxy
xyy xyy
yyy yyy
= − =
= − =
= − =
2 1 2 2
0 1 2 0
0 1 2 0
( , )
( , )
( , )
∴ x y y x y
x x y
2
2
3 2 10 1 4 2 4
1
2
1 4 2 1 2
+ − = − + − − + + ⋅
+ − − + − +
[( )( ) ( ) ]
[( ) ( ) ( )( )⋅
⋅ + + ⋅
+ − ⋅ + − + ⋅ + − + ⋅ +
2 2 0
1
6
1 0 3 1 2 2 3 1 2 0 0
2
3 2 2
( ) ]
[( ) ( ) ( ) ( )( ) ]
y
x x y x y +
+
= − − − + + − − + − + + − +
…
10 4 1 4 2 2 1 2 1 2 1 2
2 2
( ) ( ) ( ) ( )( ) ( ) ( )
x y x x y x y
Note Since the given function is 3rd
degree in x, y, the expansion terminates with 3rd
degree terms.
EXAMPLE 5
If f(x, y) 5 tan21
(xy) compute an approximate value of f(0.9, 21.2).
Solution.
We shall use Taylor’s series to find the approximate value. The point (0.9, −1.2) is close to the point
(1, −1). So, we shall find the Taylor’s series about (1, −1).
f x y f x f y f x f
( , ) ( , ) [( ) ( , ) ( ) ( , )]
!
[( )
= − + − − + + − + −
1 1 1 1 1 1 1 1
1
2
1 2
x y xx (
( , )
( )( ) ( , ) ( ) ( , )]
1 1
2 1 1 1 1 1 1 1
2
−
+ − + − + + − +
x y f y f
xy yy
…
Here (a, b) 5 (1, 21)
Given f x y xy f
f
x y
y f
( , ) tan , ( , ) tan ( )
, ( , )
= − = − =
−
=
+
⋅ − =
− −
1 1
2 2
1 1 1
4
1
1
1 1
p
x x
−
−
=
+
⋅ − =
=
+ ⋅ − ⋅
+
1
2
1
1
1 1
1
2
1 0 2
1
2 2
2 2 2
2 2 2
f
x y
x f
f
x y xy y
x y
y y
xx
, ( , )
( )
( )
=
=
−
+
− = − = −
2
1
1 1
2
4
1
2
3
2 2 2
xy
x y
f
( )
( , )
xx
f
y
y
x y
f
x y y x y
x y
xy xy
=
+
⎛
⎝
⎜
⎞
⎠
⎟ − =
=
+ ⋅ − ⋅
+
∂
∂ 1
1 1 0
1 1 2
1
2 2
2 2 2
2 2 2
( , )
( )
( )
=
=
−
+
1
1
2 2
2 2 2
x y
x y
( )
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 43 5/12/2016 9:37:48 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-474-2048.jpg)
![5.44 ■ Engineering Mathematics
f
x y x x y
x y
x y
x y
f
yy yy
=
+ ⋅ − ⋅
+
=
−
+
− = =
( )
( ) ( )
( , )
1 0 2
1
2
1
1 1
2
4
2 2 2
2 2 2
3
2 2 2
1
1
2
∴ tan ( ) ( ) ( ) ( )
−
=
−
+ −
−
⎛
⎝
⎜
⎞
⎠
⎟ + + + − ⋅ + + + ⋅
1 2 2
4
1
1
2
1
1
2
1
2
1
1
2
0 1
1
2
xy x y x y
p ⎡
⎡
⎣
⎢
⎤
⎦
⎥
f x y xy x y x y
( , ) tan [ ( ) ( )] [( ) ( ) ]
= =
−
+ − − + + + − + +
−1 2 2
4
1
2
1 1
1
4
1 1
p
Put x 5 0.9, y 5 21.2
∴ f ( . , . ) ( . . ) ( . . )
0 9 1 2
4
1
2
0 1 0 2
1
4
0 01 0 04
− = − + − + +
p
=
−
− + = − − + = −
p
4
0 1
2
0 05
4
0 7854 0 05 0 0125 0 8229
. .
. . . .
Note We have approximated tan−1
xy by a second degree polynomial in x and y. Using this polynomial
we have found the approximate value of f(0.9, −1.2) = −0.8229
But by direct computation f(0.9, −1.2) = tan−1
(−1.08) = tan−1
1.08 = −0.8238
correct upto 4 decimal places.
The error is only 0.0009, which is negligible.
EXERCISE 5.4
1. Using Taylor’s series, verify that log ( )
( ) ( )
1
2 3
2 3
+ + = + −
+
+
+
−
x y x y
x y x y …
2. Using Taylor’s series, verify that tan ( )
( ) ( )
−
+ = + −
+
+
+
−
1
3 5
3 5
x y x y
x y x y …
3. Expand 1
1+ −
x y
by Taylor’s series upto second degree terms.
4. Find the Taylor’s series expansion of sin x sin y as a polynomial in x and y upto second degree.
5. Expand ex
sin y about the point −
⎛
⎝
⎜
⎞
⎠
⎟
1
4
,
p
upto third degree terms using Taylor’s series.
6. Expand sin (xy) in powers of (x − 1) and y −
⎛
⎝
⎜
⎞
⎠
⎟
p
2
upto the second degree terms.
7. Expand ex
cos y in powers of x and y at (0, 0) upto third degree term, by Taylor’s theorem.
8. Expand exy
in powers of (x − 1) and (y − 1) upto third degree terms, by Taylor’s series.
ANSWERS TO EXERCISE 5.4
3. 1 − x + y + x2
− 2xy + y2
4. xy
5.
1
2
1 1
4
1
2
1 1
4
1
2 4
2
e
x y x x y y
+ + + −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢ + + + + −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
( ) ( ) ( )
p p p
⎜
⎜
⎞
⎠
⎟
2
+ + + − −
⎛
⎝
⎜
⎞
⎠
⎟ − + −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
1
6
1
1
2
1
4
1
2
1
4
1
6 4
3 2
2
( ) ( ) ( )
x x y x y y
p p p
⎠
⎠
⎟
3
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 44 5/12/2016 9:37:54 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-475-2048.jpg)
![Differential Calculus of Several Variables ■ 5.45
6. 1
8
1
2
1
2
1
2 2
2
2
2
− − − − −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟
p p p p
( ) ( )
x x y y
7. 1
1
2
1
6
3
2 2 3 2
+ + − + − +
x x y x xy
( ) ( ) …
8. e x y x x y y
x
{ ( ) ( ) [( ) ( )( ) ( ) ]
[( ) (
1 1 1
1
2
1 4 1 1 1
1
6
1 9
2 2
3
+ − + − + − + − − + −
+ − + x
x y x y y
− − + − − + − +
1 1 9 1 1 1
2 2 3
) ( ) ( )( ) ( ) ] }
…
5.5 MAXIMA AND MINIMA FOR FUNCTIONS OF TWO VARIABLES
You have learned maxima and minima of a function f(x) of a single variable in x. We shall extend these
ideas to a function f(x, y) of two variables in x and y. We shall derive the conditions of maxima and
minima as an application of quadratic form.
Definition 5.9 Let f(x, y) be a continuous function defined in a closed and bounded domain D of the
xy-plane and let (a, b) be an interior point of D.
(i) f(a, b) is said to be a local maximum or relative maximum value of f(x, y) at the point (a, b), if
there exists a neighbourhood N of (a, b) such that f(x, y) f(a, b) for all points (x, y) in N, other
than the point (a, b). And,
(ii) f(a, b) is said to be a local minimum or relative minimum if f(x, y) f(a, b) for all points (x, y)
in N, other than the point (a, b)
Note
(1) A common name for relative maximum or relative minimum is extreme value.
A relative maximum or relative minimum is simply referred to as maximum or minimum.
(2) In contrast, the greatest value of f(x, y) over the entire domain including the boundary is called
the global maximum or the absolute maximum value of f(x, y) on D and smallest value of
f(x, y) over the entire domain D is called the global minimum or absolute minimum.
Fig. 5.5 Fig. 5.6
(a, b)
(x, y)
Z
X
Y
Maximum
z = f(x, y)
(a, b)
(x, y)
Z
X
Y
Minimum
z = f(x, y)
M05_ENGINEERING_MATHEMATICS-I _CH05_Part A.indd 45 5/12/2016 9:37:58 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-476-2048.jpg)


![5.48 ■ Engineering Mathematics
At the point (22, 1)
r = 6 × (−2) = −12 0, s = 0 and t = 6 ⋅ 1 = 6
∴ rt − s2
= −12 × 6 − 0 = −72 0
∴ (−2, 1) is a saddle point.
At the point (2, 21)
r = 6 ⋅ 2 = 12 0, s = 0 and t = 6(−1) = −6
∴ rt − s2
= 12(−6) − 0 = −72 0
∴ (2, −1) is a saddle point.
At the point (22, 21)
r = 6(−2) = −12 0, s = 0, and t = 6(−1) = −6
∴ rt − s2
= (−12)(−6) − 0 = 72 0 and r 0
∴ (−2, −1) is a maximum point.
Maximum value = f(−2, −1) = (−2)3
+ (−1)3
− 12(−2) − 3(−1) + 20 = −8 − 1 + 24 + 3 + 20 = 38
EXAMPLE 2
Discuss the maxima and minima of f(x, y) 5 x3
y2
(1 2 x 2 y).
Solution.
Given f(x, y) = x3
y2
(1 − x − y) = − −
x y x y x y
3 2 4 2 3 3
∴ f x y x y x y f x y x y x y
x y
= − − = − −
3 4 3 2 2 3
2 2 3 2 2 3 3 4 3 2
,
r f xy x y xy s f x y x y x y
t f x x
= = − − = = − −
= = − −
xx xy
yy
6 12 6 6 8 9
2 2
2 2 2 3 2 3 2 2
3 4
,
6
6 3
x y
To find the stationary points, solve fx
= 0 and fy
= 0
∴ 3x2
y2
− 4x3
y2
− 3x2
y3
= 0 ⇒ x y x y
2 2
(3 4 3
− − =
) 0 (1)
⇒ x y x y
= = − − =
0 0 3 4 3 0
, or
and 2 2 3 0
3 4 3 2
x y x y x y
− − = ⇒ x y x y
3
2 2 3 0
[ ]
− − = (2)
∴ x y x y
= = − − =
0 0 2 2 3 0
, or
We find that (0, 0) satisfies the equations (1) and (2)
Solving 3 4 3 0 4 3 3
− − = ⇒ + =
x y x y (3)
and 2 2 3 0 2 3 2
− − = ⇒ + =
x y x y (4)
(3) − (4) ⇒ 2x = 1 ⇒ x =
1
2
When x y y
= ⇒ + = ⇒ =
1
2
4 2
1
2
3 2
1
3
, ( ) .
When x = 0, (3) ⇒ y = 1 and (4) ⇒ 2.0 + 3y = 2 ⇒ y =
2
3
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 48 5/12/2016 9:40:46 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-479-2048.jpg)
![Differential Calculus of Several Variables ■ 5.49
When y = 0, (3) ⇒ x =
3
4
and (4) ⇒ x = 1
∴ the stationary points are ( , ), , , , , ( , ), , , ( , )
0 0
1
2
1
3
0
2
3
0 1
3
4
0 1 0
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
At the points (0, 0), 0
2
3
0 1
3
4
0 1 0
, , ( , ), , ( , )
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟ and
r = 0, s = 0, t = 0 ∴ rt − s2
= 0
∴ we cannot say maximum or minimum. Further investigation is required.
At the point
1
2
1
3
,
⎛
⎝
⎜
⎞
⎠
⎟
r
s
= ⋅
⎛
⎝
⎜
⎞
⎠
⎟ − ⋅ ⋅ − ⋅ ⋅ = − − = −
= ⋅ ⋅ −
6
1
2
1
3
12
1
4
1
9
6
1
2
1
27
1
3
1
3
1
9
1
9
0
6
1
4
1
3
2
8
8
1
8
1
3
9
1
4
1
9
1
2
1
3
1
4
1
12
⋅ ⋅ − ⋅ ⋅ = − − = −
t = ⋅ − ⋅ − ⋅ ⋅ = − − = −
2
1
8
2
1
16
6
1
8
1
3
2
8
1
8
2
8
1
8
∴ rt s
− = −
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟ −
−
⎛
⎝
⎜
⎞
⎠
⎟ = − =
2
2
1
9
1
8
1
12
1
72
1
144
1
144
0
∴ rt − s2
0 and r 0
∴ the point
1
2
1
3
,
⎛
⎝
⎜
⎞
⎠
⎟ is a maximum point.
The maximum value = ⋅ − −
⎛
⎝
⎜
⎞
⎠
⎟ = ⋅ =
1
8
1
9
1
1
2
1
3
1
72
1
6
1
432
EXAMPLE 3
Find the maximum and minimum values of sin x sin y sin (x 1 y), 0 x, y p.
Solution.
Given f(x, y) = sin x sin y sin (x 1 y)
∴ f y x x y x y x
y x x y y
x = + + +
= + + =
sin [sin cos( ) sin( )cos ]
sin sin( ) sin sin(2
2x y
+ )
f x y x y x y y x x y
r f y
y
xx
= + + + = +
= =
sin [sin cos( ) sin( )cos ] sin sin( )
sin
2
c
cos( ) sin cos( )
2 2 2 2
x y y x y
+ ⋅ = +
⇒ s f y x y x y y x y y
= = + + + = + +
xy sin cos( ) sin( )(cos ) sin( )
2 2 2
⇒ s x y
t f x x y
= +
= = +
sin( )
sin cos( )
2 2
2 2
yy
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 49 5/12/2016 9:40:49 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-480-2048.jpg)


![5.52 ■ Engineering Mathematics
⇒ f f f x y z
x x y y z z and
+ = + = + = =
lf lf lf f
0 0 0 0
, , ( , , )
⇒
f f f
x y z
x
x
y
y
z
z
and
f f f
l f
= = = − =
( , , ) 0
Solving these equations, we find the values of x, y, z, which are the stationary points of F, giving the
maximum and minimum values of f(x, y, z).
Note This method does not specify the extreme value obtained is a maximum or minimum. It is
usually decided from the physical and geometrical considerations of the problem.
A method on the basis of quadratic form is given below to decide maxima or minima at the
stationary point for constrained maxima and minima.
5.5.6 Method to Decide Maxima or Minima
We shall see sufficient conditions given by quadratic form of the differentials.
1. For unconstrained functions.
Let u = f(x, y) be a function of two variables.
∴ the total differential du = fx
dx + fy
dy
Necessary conditions for maxima or minima of u = f(x, y) is
du = 0 ⇒ f dx f dy
x y
+ = 0
⇒ fx
= 0, fy
= 0, since dx, dy may take any value.
The sufficient condition for minimum is d2
u 0 and maximum is d2
u 0.
Thus, du = 0 and d2
u 0 are the necessary and sufficient conditions for minimum.
Similarly, du = 0 and d2
u 0 are the necessary and sufficient conditions for maximum.
Now, d2
u = d(fx
) dx + d(fy
) dy
= +
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟
= +
∂
∂
∂
∂
∂
∂
∂
∂
f
x
dx
f
y
dy dx
f
x
dx
f
y
dy dy
f dx f
x x y y
xx x
( y
y xy yy xy yx
xx xy
Assuming
dy dx f dx f dy dy f f
f dx f dx dy
) ( ) [ ]
( )
+ + =
= + +
2
f
f dxdy f dy
f dx f dx dy f dy
xy yy
xx xy yy
+
= + +
( )
( ) ( )
2
2 2
2
Thus, d2
u is a quadratic form in dx, dy.
The matrix of the quadratic form is called the Hessian matrix.
H
xx xy
xy yy
=
f f
f f
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
Its principal minors are D1
= fxx
= r
D
xx xy
xy yy
xx yy xy
2
2 2
= = − = −
f f
f f
f f f rt s
( )
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 52 5/12/2016 9:40:58 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-483-2048.jpg)
![Differential Calculus of Several Variables ■ 5.53
For minimum d2
u 0
i.e., the quadratic form is positive definite.
∴ D1
0, D2
0 ⇒ r 0 and rt − s2
0
For maximum, d2
u 0
⇒ D1
0, D2
0 ⇒ r 0 and rt − s2
0
This can be extended to three or more variables.
The necessary and sufficient conditions are (i) for maximum du = 0 and d2
u 0
and (ii) for minimum du = 0 and d2
u 0.
2. If u = f(x, y, z), then du = fx
dx + fy
dy + fz
dz and
d u f dx f dy f dz f dydz f dxdz f dxdy
d
2
xx yy zz yz zx xy
= + + + + +
( ) ( ) ( )
2 2 2
2 2 2
u
u f f f
= ⇒ = = =
0 0 0 0
x y z
, ,
which gives the stationary points.
The matrix of the quadratic form in dx, dy, dz is the
Hessian H
xx xy xz
yx yy yz
zx zy zz
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
f f f
f f f
f f f
The principal minors are D1
= fxx
, D
xx xy
yx yy
2 =
f f
f f
and D H
3 =
At a stationary point (a, b, c), if D1
0, D2
0, and D3
0, then u is minimum.
If D1
0, D2
0, and D3
0 then u is maximum.
In the same way we can extend to function of n variables f(x1
, x2
, …, xn
)
3. We shall now see how the Hessian changes in the discussion of constrained maxima and
minima.
For example, consider the quadratic form in two variables.
Q = ax2
+2hxy + by2
with linear constraint ax + by = 0 ⇒ y
x
= −
a
b
∴ Q = + −
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟ = − +
ax hx
x
b
x x
h b
2
2 2
2
2 2
2 2
a
b
a
b b
b ab a
[ ]
a
Since
x2
2
b
0, Q 0 or 0 if ab2
− 2hab + ba2
0 or 0
We can easily see that − [ab2
− 2hab + ba2
] =
0 a b
a
b
a h
h b
∴ Q if
0
0
0
a b
a
b
a h
h b
and Q if
0
0
0
a b
a
b
a h
h b
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 53 5/12/2016 9:41:01 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-484-2048.jpg)


![5.56 ■ Engineering Mathematics
WORKED EXAMPLES
EXAMPLE 1
A rectangular box, open at the top, is to have a volume of 32 cc. Find dimensions of the box which
requires least amount of material for its construction.
Solution.
Let x, y, z be the length, breadth and height of the box. Given volume of the box is 32 cc.
⇒ xyz = 32, x, y, z 0 (1)
We want to minimize the amount of material for its construction. i.e., surface area of the box is to be
minimized.
Surface area S = xy + 2xz + 2yz [{ top is open] (2)
We shall solve by two methods.
Method 1 xyz = 32 ⇒ z
xy
=
32
∴ S = + +
xy x y
xy
2
32
( ) ⇒ S = + +
⎛
⎝
⎜
⎞
⎠
⎟
xy
x y
64
1 1
∴
∂
∂
S
x
y
x
= −
64
2
and
∂
∂
S
y
x
y
= −
64
2
To find stationary points, solve
∂
∂
S
x
= 0 and ∂
∂
S
y
= 0
⇒ y
x
x
y
− = − =
64
0
64
0
2 2
and
⇒ x y
2
64
= and xy2
64
= (3)
∴ x y xy
2 2
= ⇒ x = y [ , ]
{ x y
0 0
∴ (3) ⇒ x x y
3
64 4 4
= ⇒ = ∴ =
∴ stationary point is (4, 4)
Now r
S
x x
= =
∂
∂
2
2 3
128
, s
S
x y
t
S
y y
= = = =
∂
∂ ∂
∂
∂
2 2
2 3
1
128
and
∴ at the point (4, 4), r = =
128
4
2 0
3
, s t
= = =
1
128
4
2
3
and
∴ rt − s2
= 2 ⋅ 2 − 1 = 3 0
Since r 0 and rt − s2
0, it is a minimum point
When x = 4, y = 4, z = =
32
16
2
∴ dimensions of the box are x = 4 cms, y = 4 cms and z = 2 cms.
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 56 5/12/2016 9:41:11 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-487-2048.jpg)
![Differential Calculus of Several Variables ■ 5.57
Method 2 Lagrange’s method
We have to minimise S = xy + 2xz + 2yz (1)
Subject to xyz = 32 ⇒ xyz − 32 = 0 (2)
Form the auxiliary function
F(x, y, z) = xy + 2xz + 2yz + l(xyz − 32)
where l is the Lagrange’s multiplier.
∴ F
F
x
y z yz F
F
y
x z xz F
F
z
x y xy F
x y z
= = + + = = + + = = + + =
∂
∂
∂
∂
∂
∂
2 2 2 2
l l l f
l
, , and
To find stationary points, solve Fx
= 0, Fy
= 0, Fz
= 0, f = 0
Fx
= 0 ⇒ y + 2z + lyz = 0
⇒ y + 2z = −lyz ⇒ xy + 2zx = −lxyz [multiplying by x] (3)
Fy
= 0 ⇒ x + 2z + lxz = 0
⇒ x + 2z = − lxz ⇒ xy + 2zy = −lxyz [multiplying by y] (4)
and Fz
= 0 ⇒ 2x + 2y + lxy = 0
⇒ 2x + 2y = −lxy ⇒ 2xz + 2yz = −lxyz [multiplying by z] (5)
From (3), (4) and (5)
⇒ xy zx xy zy xz yz
xy zx xy zy zx zy x y
+ = + = +
+ = + ⇒ = ⇒ =
2 2 2 2
2 2 2 2
and xy zx xz yz
+ = +
2 2 2 ⇒ xy yz x z
= ⇒ =
2 2
∴ x y z
= = 2 (6)
Substituting in (2), we get
2 2 32
z z z
⋅ ⋅ = ⇒ 4 32
3
z = ⇒ z z
3
8 2
= ⇒ =
∴ (6) ⇒ x = 4, y = 4
∴ the stationary point is (4, 4, 2)
So, the dimensions are 4 cms, 4 cms, 2 cms.
Remark We have not justified S is minimum at (4, 4, 2). We shall use the bordered Hessian to decide.
H
x y z
x xx xy xz
y yx yy yz
z zx zy zz
=
0 f f f
f
f
f
F F F
F F F
F F F
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
When x = 4, y = 4, z = 2, Fx
= 0 ⇒ 4 +4 + 8l = 0 ⇒ l = −1
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 57 5/12/2016 9:41:13 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-488-2048.jpg)



![Differential Calculus of Several Variables ■ 5.61
The stationary points are given by x y z
= ± = ± = ±
1
2
1
2
1
2
, ,
These give 8 stationary points. We want the maximum value of T = 400 xyz2
, and so we must have
xy positive. This will occur at 4 of the points.
i.e., at the points
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
, , , , , , , , , , ,
⎛
⎝
⎜
⎞
⎠
⎟
−
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟ − − −
2
2
⎛
⎝
⎜
⎞
⎠
⎟
∴ maximum T C
= × ⋅ ⋅ = °
400
1
2
1
2
1
2
50
EXAMPLE 4
Find the volume of the largest rectangular parallelopiped that can be inscribed in the ellipsoid
x
a
y
b
z
c
2
2
2
2
2
2
1
1 1 5 .
Solution.
Given the ellipsoid
x
a
y
b
z
c
2
2
2
2
2
2
1
+ + =
By the symmetry of the ellipsoid, for the largest parallelopiped, the edges must be parallel to the
coordinate axes and the centre coincides with the centre (0, 0, 0) of the ellipsoid.
Let P (x, y, z) be the coordinates of a vertex on the
ellipsiod, then the dimensions of the rectangular
parallelopiped (or cuboid) are 2x, 2y, 2z respectively.
∴ volume V = 2x ⋅ 2y ⋅ 2z
= 8xyz
Let f( , , )
x y z
x
a
y
b
z
c
= + + − =
2
2
2
2
2
2
1 0 (1)
We want to maximize V subject to f(x, y, z) = 0
Form the auxiliary equation F(x, y, z) =V + lf (x, y, z),
where l is the Lagrange’s multiplier.
⇒ F( , , )
x y z xyz
x
a
y
b
z
c
= + + + −
⎛
⎝
⎜
⎞
⎠
⎟
8 1
2
2
2
2
2
2
l
∴ F yz
x
a
x = +
8 2 2
l
, F zx
y
b
F xy
z
c
F
y z
, and
= + = + =
8 2 8 2
2 2
l l
f
l
To find stationary points solve Fx
= 0, Fy
= 0, Fz
= 0, f = 0
∴ F yz
x
a
x = ⇒ + =
0 8 2 0
2
l
⇒ 4 2
yz
x
a
= −
l
⇒ 4
2
2
xyz
x
a
= −l [multiplying by x]
⇒ − =
4 2
2
xyz x
a
l
(2)
Z
P
O
X
Y
Fig. 5.8
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 61 5/11/2016 4:42:57 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-492-2048.jpg)
![5.62 ■ Engineering Mathematics
F xz
y
b
y = ⇒ + =
0 8 2 0
2
l ⇒ −
4 2
2
xyz y
b
l
= [multiplying by y] (3)
F xy
z
a
z = ⇒ + =
0 8 2 0
2
l ⇒ −
4 2
2
xyz z
b
l
= [multiplying by z] (4)
∴ From (2), (3) and (4), we get
x
a
y
b
z
c
2
2
2
2
2
2
= =
We have
x
a
y
b
z
c
2
2
2
2
2
2
1
+ + =
∴
x
a
x
a
x
a
2
2
2
2
2
2
1
+ + = ⇒ 3 1
3 3
2
2
2
2
x
a
x
a
x
a
= ⇒ = ⇒ = ±
Similarly, y
b
= ±
3
and z
c
= ±
3
∴ So, the stationary points are given by
x
a
y
b
z
c
= ± = ± = ±
3 3 3
, ,
∴ there are 8 stationary points.
Since we want maximum value of V, choose the points with the product of xyz positive.
This will occur at 4 of the points. They are
a b c a b c
3 3 3 3 3 3
, , , , , ,
⎛
⎝
⎜
⎞
⎠
⎟
− −
⎛
⎝
⎜
⎞
⎠
⎟
− −
⎛
⎝
⎜
⎞
⎠
⎟
− −
⎛
⎝
⎜
⎞
⎠
⎟
a b c a b c
3 3 3 3 3 3
, , , , ,
∴ maximum V =
8
3 3
abc
EXAMPLE 5
Divide the number 24 into three parts such that the continued product of the first, square of the
second and the cube of the third may be maximum.
Solution.
Let 24 be divided into 3 parts x, y, z, so that
x + y + z = 24 where x, y, z 0
∴ x + y + z − 24 = 0 (1)
and the product is xy2
z3
We have to maximize this product subject to (1)
Let f(x, y, z) = xy2
z3
and f (x, y, z) = x2
+ y2
+ z2
− 24
Form the auxiliary function
F(x, y, z) = f(x, y, z) + lf(x, y, z)
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 62 5/11/2016 4:43:03 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-493-2048.jpg)

![5.64 ■ Engineering Mathematics
∴ the bordered Hessian matrix is
H =
0 1 1 1
1 0 2 12 2 12
1 2 12 2 12 2 12
1 2 12 2 12 2 12
4 3 4 3
4 3 3 3 4 3
4 3 4 3 7 2
⋅ ⋅
⋅ ⋅ ⋅
⋅ ⋅ ⋅
⎡
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
The principal bordered minors are D1
0 1
1 0
1 0
= =
⎡
⎣
⎢
⎤
⎦
⎥ −
D2
4 3
4 3 3 3
3 3 4 3 4 3
0 1 1
1 0 2 12
1 2 12 2 12
1 2 12 2 12 1 2 12
= ⋅
⋅ ⋅
= − ⋅ − ⋅ + ⋅ ⋅
= −
[ ] [ ]
8
8 12 16 12 16 12 24 12 0
3 3 3 3
⋅ + ⋅ + ⋅ = ⋅
D3 =
⋅ ⋅
⋅ ⋅ ⋅
⋅ ⋅ ⋅
0 1 1 1
1 0 2 12 2 12
1 2 12 2 12 2 12
1 2 12 2 12 2 12
4 3 4 3
4 3 3 3 4 3
4 3 4 3 7 2
2
4 3 4 3
4 3 3
4 3 6 2
3 3 2
0 1 0 0
1 0 2 12 2 12
1 2 12 8 12 0
1 2 12 0 2 12
=
⋅ ⋅
⋅ − ⋅
⋅ − ⋅
→ −
C C C
C
C C C
4 4 2
→ −
= −
⋅ ⋅
− ⋅
− ⋅
1
1 2 12 2 12
1 8 12 0
1 0 2 12
4 3 4 3
3
6 2
1
expanding by R
= − ⋅ ⋅ ⋅ −
( )
1 2 12 2 12
1 2 12
1 1 0
1 0 4
3 3 4 2 [Taking out 23
⋅123
from c2
and 24
⋅122
from c3
]
= − ⋅ − − −
= − ⋅ + =
( ) [ ( )] [ ]
( ) [ ]
1 2 12 1 12 4 1 2
1 2 12 12 12
7 5
3
7 5
expanding by R
(
( )
− ⋅ ⋅
1 2 12 24 0
7 5
Since D1
0, D2
0 and D3
0, f(x, y, z) is maximum at (4, 8, 12).
EXAMPLE 6
Find the maximum value of xm
yn
zp
subject to x 1 y 1 z 5 a.
Solution.
Let f(x, y, z) = xm
yn
zp
(1)
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 64 5/11/2016 4:43:14 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-495-2048.jpg)
![Differential Calculus of Several Variables ■ 5.65
Maximize (1) subject to f(x, y, z) = x + y + z − a = 0 (2)
Form the auxiliary function
F(x, y, z) = f(x, y, z) + lf(x, y, z)
where l is the Lagrange’s multiplier.
⇒ F m n p
( , , ) ( )
x y z x y z x y z a
= + + + −
l
∴ F mx y zp
x
n n
= +
−1
l, F nx y z F px y z F
p
y
m n p
z
m n
, and
= + = + =
− −
1 1
l l f
l
To find stationary points, solve Fx
= 0, Fy
= 0, Fz
= 0, f = 0
F mx y z mx y z
x
n n p n n p
= ⇒ + = ⇒ = −
− −
0 0
1 1
l l (2)
Similarly, Fy = 0 ⇒ nx y z
m n p
−
= −
1
l (3)
Fz = 0 ⇒ px y z
m n p−
= −
1
l (4)
∴ From (2), (3) and (4), we get
mx y z nx y z px y z
m n p m n p m n p
− − −
= =
1 1 1
⇒ m
x
n
y
p
z
x y z
= = [ ]
dividing by m n p
⇒
x
m
y
n
z
p
x y z
m n p
a
m n p
= = =
+ +
+ +
=
+ +
∴ x
am
m n p
y
an
m n p
z
ap
m n p
=
+ +
=
+ +
=
+ +
, ,
Stationary point is
am
m n p
an
m n p
ap
m n p
+ + + + + +
⎛
⎝
⎜
⎞
⎠
⎟
, ,
Maximum value of f
am
m n p
an
m n p
ap
m n p
=
+ +
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟
m n p
=
⋅
+ +
+ +
+ +
a m n p
m n p m n p
m n p m n p
( )
EXERCISE 5.5
1. Find the extreme values of the function f(x, y) = x3
+ y3
− 3x − 12y + 20.
2. Find the maximum and minimum values of x2
− xy + y2
− 2x + y.
3. Find the maximum and minimum values of x3
+ 3xy2
− 15y2
+ 72x.
4. Find the maxima and minima of the function x3
y2
(12 − x − y).
5. Find the extreme values of the function x xy y
x y
2 2 1 1
+ + + + .
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 65 5/11/2016 4:43:19 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-496-2048.jpg)


![5.68 ■ Engineering Mathematics
WORKED EXAMPLES
EXAMPLE 1
The dimensions of a cone are given by radius 5 4 cm, and altitude 5 6 cm. What is the error in
calculation of its volume, if there is a shortage of 0.01 cm in the measures used.
Solution.
Let r be the radius and h be the height of the cone in centimetre.
∴ The volume of the cone V r h
=
1
3
2
p (1)
The differential relation is
dV
v
r
dr
V
h
dh
= +
∂
∂
∂
∂
The error relation is
Δ Δ Δ
V
V
r
r
V
h
h
= +
∂
∂
∂
∂
(2)
From equation (1), we get
∂
∂
∂
∂
V
r
h r
V
h
r
= =
1
3
2
1
3
2
p p
and
∴ Δ Δ Δ
V hr r r h
= +
1
3
2
1
3
2
p p
Given r = 4 cm and h = 6 cm, Δr = Δh = −0.01 = −
1
100
∴ ΔV = × × −
⎛
⎝
⎜
⎞
⎠
⎟ + −
⎛
⎝
⎜
⎞
⎠
⎟
= − + = −
2
3
6 4
1
100 3
4
1
100
300
48 16
64
300
2
p p
p p
[ ] =
= −
16
75
p
cm3
∴ the volume is decreased by
16
75
p
cm3
.
EXAMPLE 2
The torsional rigidity of length of a wire is obtained from the formula N
Il
t r
5
p
8
2 4
. If l is decreased
by 2%,r is increased by 2% and t is increased by 1.5%,then show that the value of N is diminished
by 13% approximately.
Solution.
Given N
Il
t r
=
8
2 4
p
(1)
Taking logarithm on both sides of equation (1), we get
log log log log log
e e e e e
N I l t r
= + − −
8 2 4
p
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 68 5/11/2016 4:43:27 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-499-2048.jpg)


![Differential Calculus of Several Variables ■ 5.71
⇒
Δf
f u v
= +
⎛
⎝
⎜
⎞
⎠
⎟
d
1 1
∴ the relative error in f is d
1 1
u v
+
⎛
⎝
⎜
⎞
⎠
⎟.
EXAMPLE 5
If a triangle be slightly disturbed so as to remain inscribed in the same circle, then prove that
Δ Δ Δ
a
A
b
B
c
C
cos cos cos
1 1 5 0.
Solution.
We know from trigonometry that
a
A
b
B
c
C
R
sin sin sin
= = = 2
⇒ a R A b R B
= =
2 2
sin , sin
(1)
and c = 2R sin C
When the triangle inscribed in the circle of radius R is slightly disturbed, the sides and angles will be
slightly changed. Here R is constant, since the circle is not changed.
Taking differentials to the relation (1), we get
da R A dA db R B dB dc R C dC
= ⋅ = ⋅ = ⋅
2 2 2
cos , cos cos
and
∴ the error relations are
∴
Δ Δ Δ Δ Δ Δ
Δ
Δ
Δ
a R A A b R B B c R C C
a
A
R A
b
B
= ⋅ = ⋅ = ⋅
=
2 2 2
2
cos , cos cos
cos
,
cos
and
=
= =
2 2
R B
c
C
R C
Δ
Δ
Δ
and
cos
∴
Δ Δ Δ
Δ Δ Δ
a
A
b
B
c
C
R A B C
cos cos cos
[ ]
+ + = + +
2
But
∴ A B C dA dB dC A B C
+ + = + + + = + + =
p, 0 0
and Δ Δ Δ
Hence,
Δ Δ Δ
a
A
b
B
c
C
R
cos cos cos
+ + = ⋅ =
2 0 0
EXAMPLE 6
The angles of a triangle ABC are calculated from the sides a, b, and c. If small errors
d d d
a b c
, , and are made in the measurements of the sides, then show that the error in the angle
A is approximately d 5 d 2 d 2 d
A
a
a b c c c
2Δ
( cos cos ).
A
A
R
B
B
C
C
c
a
b
Fig. 5.9
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 71 5/11/2016 4:43:39 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-502-2048.jpg)
![5.72 ■ Engineering Mathematics
Solution.
From trigonometry, we know that the relation between sides and angle A of a triangle is
a b c bc A
2 2 2
2
= + − cos .
Taking differentials, we get
⇒
2 2 2 2
ada bdb cdc A bdc cdb bc AdA
ada bdb cdc b
= + − + −
= + −
[cos ( ) ( sin )]
cos A
Adc c Adb bc AdA
bc AdA ada bdb cdc b Adc c Adb
− +
= − − + +
cos sin
sin cos cos
Since area of ΔABC is
Δ Δ
= ⇒ =
1
2
2
bc A bc A
sin sin
∴ 2Δ⋅ = − − − −
dA ada b c A db c b A dc
( cos ) ( cos )
Given that the errors in a, b and c are d d d
a b c
, and respectively.
So, the error in A is dA
∴ 2Δd d d d
A a a b c A b c b A c
= − − − −
( cos ) ( cos )
We know by projection formula that
b c A a C b c A a C
= + ⇒ − =
cos cos cos cos
and c = a cos B + b cos A ⇒ c b A a B
− =
cos cos
∴ 2Δd d d d d d d
A a a a C b a B c a a C b B c
= − − = − −
cos cos ( cos cos )
⇒ d d d d
A
a
a C b B c
= − ⋅ − ⋅
2Δ
[ cos cos ]
EXERCISE 5.6
1. The pressure p and the volume v of a gas are connected by pv1.4
= c, a constant. Find the percent-
age increase in pressure corresponding to
1
2
% diminish in the volume.
2. If q is calculated from q r h
= K 2
, where K is a constant, then show that a small % error in r is
four times as serious as the same % error in h.
3. Find the percentage error in the area of an ellipse if one per cent error is made in measuring the
major and minor axes.
4. The resistance of a circuit was found by using the formula C
E
R
= . If there be possible errors of
1
10
amperes in C and
1
20
volt in E, what is the possible error in R, given C = 18 amp, E = 100 volts.
M05_ENGINEERING_MATHEMATICS-I _CH05_Part B.indd 72 5/11/2016 4:43:47 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-503-2048.jpg)




![6.0 INTRODUCTION
Calculus is one of the remarkable achievements of human intellect. It is a collection of fascinating
and exciting ideas rather than a technical tool. Calculus has two main divisions ‘differential calculus’
and ‘integral calculus’.
Both had their origin from geometrical problems.
Integral calculus had its origin from the problem of area and differential calculus had its origin
from the problem of tangent to a curve.
The term integration means summation. Infact definite integral is the process of finding a limit of a sum.
The integration symbol ‘∫’ was divised by stretching the summation symbol ‘S’ conveying the
meaning of the process.
6.1 INDEFINITE INTEGRAL
We consider indefinite integral as reverse process of differentiation.
Definition 6.1
If f(x) is continuous function of x such that F′(x) 5 f(x) in [a, b], then F(x) 1 c is defined as the
indefinite integral of f(x) and is denoted by f x dx
( )
∫ .
Thus, f x dx F x c
( ) ( )
= +
∫
Here f(x) is called the integrand and the arbitrary constant c is called the constant of integration,
dx indicates that the variable of integration is x. f(x)dx is called an element of integration.
F(x) is called an antiderivative or primitive of f(x).
F(x) + c is referred to as the most general primitive.
Note In computing indefinite integral, no interest is shown on the interval [a, b]. It is to be understood
that f x dx F x c
( ) ( )
= +
∫ is valid in some suitable sub-interval.
Leibnitz used the symbol f x dx
( )
∫ to denote general primitive of f.
6.1.1 Properties of Indefinite Integral
From the definition of indefinite integral, we have the following properties
1.
d
dx
f x dx f x
( ) ( )
∫
⎡
⎣
⎤
⎦ =
2. d f x f x c
( ( )) ( )
= +
∫
3. d f x dx f x dx
( ) ( )
∫
( )=
4. [ ( ) ( )] ( ) ( )
f x g x dx f x dx g x dx
± = ±
∫ ∫
∫
5. kf x dx k f x dx
( ) ( ) ,
= ∫
∫ where k is a constant.
6
Integral Calculus
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 1 5/19/2016 4:42:30 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-508-2048.jpg)
![6.2 ■ Engineering Mathematics
Table of Integrals
Now we list the standard indefinite integrals derived from the derivatives of standard functions
1. x dx
x
n
n
n
n
=
+
≠ −
+
∫
1
1
1
if 2.
dx
x
x c
e
= +
∫ log
3. e dx e c
x x
= +
∫ 4. sin cos
x dx x c
= − +
∫
5. cos sin
xdx x c
= +
∫ 6. tan log sec
xdx x c
e
= +
∫
7. sec log sec tan
log tan
x dx x x c
x
c
e
e
= + +
+
⎛
⎝
⎜
⎞
⎠
⎟ +
∫
or
p
4 2
8. cos log cos cot
log tan
ec ec
or
x dx x x c
x
c
e
e
= − + +
+
∫
2
9. cot log sin
xdx x c
= +
∫ 10. sec tan
2
xdx x c
= +
∫
11. cos cot
ec2
xdx x c
= − +
∫ 12. sec tan sec
x x dx x c
= +
∫
13. cos cot cos
ec ec
x x dx x c
= − +
∫ 14.
dx
a x a
x
a
c a
2 2
1
1
0
+
= + ≠
−
∫ tan ,
15.
dx
a x a
a x
a x
c
e
2 2
1
2
−
=
+
−
+
∫ log 16.
dx
x a a
x a
x a
c
e
2 2
1
2
−
=
−
+
+
∫ log
17.
dx
a x
x
a
c a x a a
2 2
1
0
−
= + −
−
∫ sin , , .
18.
dx
x a
x x a c x a
e
2 2
2 2
0
−
= + − +
∫ log ,
19.
dx
a x
x a x c
e
2 2
2 2
+
= + + +
∫ log 20.
dx
x x a a
x
a
c
2 2
1
1
−
= +
−
∫ sec
21. [ ( )] )
[ ( )]
f x f x dx
f x
n
c n
n
n
′( =
+
+ ≠ −
+
∫
1
1
1
if 22.
f x
f x
dx f x c
e
′( )
( )
log ( )
∫ = +
23. a x dx
x a x a x
a
c
2 2
2 2 2
1
2 2
− =
−
+ +
−
∫ sin
24. a x dx
x x a a
x x a c
e
2 2
2 2 2
2 2
2 2
+ =
+
+ + +
( ) +
∫ log
25. x a dx
x x a a
x x a c
e
2 2
2 2 2
2 2
2 2
− =
−
− + −
( ) +
∫ log
26. If f x dx F x c f ax b dx
a
F ax b c
( ) ( ) , ( ) ( )
= + + = + +
∫
∫ then
1
27. a dx
a
a
c a a
x
x
e
= + ≠
∫ log
, ,
0 1
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 2 5/19/2016 4:42:35 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-509-2048.jpg)
![Integral Calculus ■ 6.3
In the above formula the derivative of the R.H.S is the integrand.
In the evaluation of the integrals, three main techniques are used.
They are 1. Integration by substitution
2. Integration by partial fractions
3. Integration by parts
6.1.2 Integration by Parts
If u and v are differentiable function of x, then uv dx uv u v dx
= − ∫
∫ 1 1
′
where u
du
dx
v v dx
′ = = ∫
, 1
Integration by parts is used when the integrand is a product of two functions.
The success of this method depends upon the proper choice of u as that function which comes first
in the word ‘ILATE’, where
I – inverse circular function, L – logarithmic function
A – algebraic function, T – Trigonometric function
E – exponential function
6.1.3 Bernoulli’s Formula
If u and v are differentiable functions of x, then
uv dx uv u v u v u v
= − + − +
∫ 1 2 3 4
′ ″ ″′ …
where primes denote differentiation and suffixes denote integration.
That is u
du
dx
u
d u
dx
u
d u
dx
′ ″ ″′ …
= = =
, , ,
2
2
3
3
and v vdx v v dx v v dx v v dx
1 2 1 3 2 4 3
= = = =
∫ ∫ ∫ ∫
, , , , …
If u is a polynomial in x, then Bernoulli’s formula terminates.
6.1.4 Special Integrals
1. e f x f x dx e f x c
x x
[ ( ) ( )] ( )
+ = +
∫ ′
2. e bx dx
e
a b
a bx b bx
ax
ax
cos [ cos sin ]
=
+
+
∫ 2 2
3. e bx dx
e
a b
a bx b bx
ax
ax
sin [ sin cos ]
=
+
−
∫ 2 2
Solution.
To prove e bx dx
e
a b
a bx b bx
ax
ax
sin [ sin cos ]
=
+
−
∫ 2 2
Let I e bx dx
ax
= ∫ sin .
It is a product of two functions. So, we use integration by parts to evaluate the integral.
Taking u e u ae
ax ax
= =
, .
′
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 3 5/19/2016 4:42:36 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-510-2048.jpg)
![6.4 ■ Engineering Mathematics
and v bx v vdx bx dx
bx
b
= = = = −
∫
∫
sin , sin
cos
1
[ I uv u v dx
e
bx
b
ae
bx
b
dx
e
ax ax
ax
= −
= −
⎡
⎣
⎢
⎤
⎦
⎥ − −
⎡
⎣
⎢
⎤
⎦
⎥
= −
∫
∫
1 1
′
cos cos
cos
s
cos
cos sin sin
bx
b
a
b
e bx dx
e bx
b
a
b
e bx
b
ae
bx
b
ax
ax ax
ax
+
= − + −
⎧
⎨
⎩
⎫
∫
∫ ⎬
⎬
⎭
dx [Again integrating by parts]
I
e bx
b
a
b
e bx
a
b
e bx dx
ax
ax ax
= − + − ∫
cos
sin sin
2
2
2
⇒ I
e
b
a bx b bx
a
b
I
ax
= − −
2
2
2
[ sin cos ]
⇒ 1
2
2 2
+
⎛
⎝
⎜
⎞
⎠
⎟ = −
a
b
I
e
b
a bx b bx
ax
[ sin cos ]
⇒
a b
b
I
e
b
a bx b bx
ax
2 2
2 2
+
⎛
⎝
⎜
⎞
⎠
⎟ = −
[ sin cos ] ⇒ I
e
a b
a bx b bx
ax
=
+
−
2 2
[ sin cos ]
[ e bx dx
e
a b
a bx b bx
ax
ax
sin [ sin cos ]
=
+
−
∫ 2 2
Similarly, (2) is
e bx dx
e
a b
a bx b bx
ax
ax
cos [ cos sin ]
=
+
+
∫ 2 2
Remember as below:
e bx dx
e
a b
a bx
d
dx
bx
e bx dx
e
a
ax
ax
ax
ax
sin sin (sin )
cos
=
+
−
⎡
⎣
⎢
⎤
⎦
⎥
=
∫ 2 2
2
2 2
+
−
⎡
⎣
⎢
⎤
⎦
⎥
∫ b
a bx
d
dx
bx
cos (cos )
WORKED EXAMPLES
EXAMPLE 1
Evaluate e x x dx
x
2
2 3
cos sin .
∫
Solution.
Let I e x x dx
x
= ∫
2
2 3
cos sin
We know sin cos [sin( ) sin( )]
A B A B A B
= + + −
1
2
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 4 5/19/2016 4:42:39 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-511-2048.jpg)
![Integral Calculus ■ 6.5
[ sin cos [sin( ) sin( )]
3 2
1
2
3 2 3 2
x x x x x x
= + + − = +
1
2
5
[sin sin ]
x x
[
I e x x dx
x
= +
∫
2 1
2
5
(sin sin ) = +
= ⋅
+
− + ⋅
∫
∫
1
2
5
1
2
1
2 4 25
2 5 5 5
1
2
2 2
2
e x dx e x dx
e
x x
e
x x
x
sin sin
[ sin cos ]
2
2
2 2
4 1
2
58
2 5 5 5
10
2
x
x x
x x c
e
x x
e
x x
+
− +
= − + −
[ sin cos ]
[ sin cos ] [ sin cos ]
]+ c
EXAMPLE 2
Evaluate x x dx
2 1
tan .
2
∫
Solution.
Let I x x dx
= −
∫
2 1
tan
Take u x v x
= =
−
tan 1 2
and [ u
x
v x dx
x
′ =
+
= =
∫
1
1 3
2 1
2
3
and
Integrating by parts, we get
I uv u v dx
= − ∫
1 1
′ = ⋅ −
+
−
∫
tan
( )
1
3
2
3
3
1
1 3
x
x
x
x
dx
= −
+
= −
+ −
+
=
−
−
∫
∫
x
x
x
x
dx
x
x
x x x
x
dx
x
3
1
3
2
3
1
2
2
3
3
1
3 1
3
1
3
1
1
3
tan
tan
( )
tan−
−
− −
+
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎩
⎫
⎬
⎭
∫
1
2
1
3 1
x x
x
x
dx
⇒ I
x
x
x
x c
e
= − − +
⎡
⎣
⎢
⎤
⎦
⎥ +
−
3
1
2
2
3
1
3 2
1
2
1
tan log ( )
⇒ x x dx
x
x
x
x c
e
2 1
3
1
2
2
3 6
1
6
1
tan tan log ( )
− −
= − + + +
∫
EXAMPLE 3
Evaluate x x dx
n
log .
e
∫
Solution.
Let I x x dx
n
e
= ∫ log
Take u x v x
e
n
= =
log and [ u
x
v x dx
x
n
n
n
′ = = =
+
+
∫
1
1
1
1
and
Integrating by parts, we get
I uv u v dx
= − ∫
1 1
′ = ⋅
+
− ⋅
+
+ +
∫
loge
n n
x
x
n x
x
n
dx
1 1
1
1
1
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 5 5/19/2016 4:42:42 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-512-2048.jpg)
![6.6 ■ Engineering Mathematics
=
+
−
+
=
+
−
+ +
+
=
+
+ +
+
∫
x x
n n
x dx
x x
n n
x
n
c
x
n
e n
n
e
n
n
1
1 1
1
1
1
1
1
1 1
log
log
( ) ( )
1
1 1
2
1
2
1 1 1
1 1
log
( ) ( )
[( )log ]
e
n n
e
x
n
x
n
c
x
n
n x c
+
−
+
+ =
+
+ − +
+ +
[ x x dx
x
n
n x c
n
n
log
( )
[( )log ]
=
+
+ − +
+
∫
1
2
1
1 1
EXAMPLE 4
Evaluate 3 2
x
x dx
sin .
∫
Solution.
Let I x dx
x
= ∫3 2
sin
Take u v x
x
= =
3 2
, sin [ u v
x
x
e
′ −
= =
3 3
2
2
1
log
cos
and
Integrating by parts, we get
I
x x
dx
x
x x
e
x
e
= −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟
= − +
∫
3
2
2
3 3
2
2
3
2
2
1
2
cos
log
cos
cos log 3
3 3 2
3 2
2
1
2
3 3
2
2
3 3
2
2
x
x
e
x x
e
x dx
x x x
dx
cos
cos
log
sin
log
sin
∫
∫
= − + −
⎡
⎣
⎢
⎤
⎤
⎦
⎥
= − + − ( ) ∫
3 2
2
1
4
3 3 2
1
4
3 3 2
2
x
e
x
e
x
x
x x dx
cos
(log ) sin log sin
⇒ I
x
x I
x
e
x
e
= − + − ( )
3 2
2
1
4
3 3 2
1
4
3
2
cos
(log ) sin log
?
⇒ 1
1
4
3
3 2
2
1
4
3 3 2
2
+
⎛
⎝
⎜
⎞
⎠
⎟ = − +
(log )
cos
(log ) sin
e
x
e
x
I
x
x
?
⇒
4 3
4
3 2
2
1
4
3 3 2
2
+
⎛
⎝
⎜
⎞
⎠
⎟ = − +
(log ) cos
(log ) sin
e
x
e
x
I
x
x
?
[ I x x c
x
e
e
=
+
− + +
3
4 3
2 2 3 2
2
(log )
[ cos log sin ]
EXAMPLE 5
Evaluate x e dx
x
3 2
2
∫ .
Solution.
Let I x e dx
x
= −
∫
3 2
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 6 5/19/2016 4:42:45 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-513-2048.jpg)
![Integral Calculus ■ 6.7
By Bernoulli’s formula,
I uv u v u v u v
= − + − +
1 2 3 4
′ ″ ″′ …
where u x v e x
= = −
3 2
and
[ u x u x u
′ ″ = ″′
= =
3 6 6
2
, , and v e dx
e
x
x
1
2
2
2
= =
−
−
−
∫
v
e
dx
e e
x x x
2
2 2 2
2
2
1
2 2 2
=
−
=
− −
=
−
− − −
∫ ( ) ( ) ( )
, v
e
dx
e e
x x x
3
2
2
2
2
2
3
2 2 2 2
=
−
=
− −
=
−
− − −
∫ ( ) ( ) ( ) ( )
v
e
dx
e e
x x x
4
2
3
2
3
2
4
2 2 2 2
=
−
=
− −
=
−
− − −
∫ ( ) ( ) ( ) ( )
[ I x
e
x
e
x
e e
c
x x x x
=
−
−
−
+
−
−
−
+
− − − −
3
2
2
2
2
2
3
2
4
2
3
2
6
2
6
2
( ) ( ) ( )
= − − − −
⎡
⎣
⎢
⎤
⎦
⎥ +
−
e
x x x
c
x
2
3 2
2
3
4
6
8
6
16
[ x e dx
e
x x x c
x
x
3 2
2
3 2
8
4 6 6 3
−
−
∫ = − + + + +
[ ]
EXAMPLE 6
Evaluate x x dx
2
2
sin .
∫
Solution.
Let I = x x dx
2
2
sin
∫
By Bernoulli’s formula,
I = uv1
− u′v2
+ u″v3
− u′″v4
+…
Where u = x2
and v = sin 2x
∴ u′ = 2x, u″ = 2, u′″ = 0 and v1
= sin
cos
2
2
2
x dx
x
= −
∫
V2
= −
cos sin
2
2
2
4
x
dx
x
= −
∫
V3
= − = −
⎛
⎝
⎜
⎞
⎠
⎟ =
∫
sin cos
cos
2
4
1
4
2
2
1
8
2
x x
x
∴ I x
x
x
x x
c
x x
x
=
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟ + +
= − +
2
2 2
2
2
2
2
4
2
2
8
1
2
2
2
− −
cos sin cos
cos s
sin cos
2
1
4
2
x x c
+ +
=
1
4
2 2 1 2 2
2
x x x x c
sin ( )cos
+ −
⎡
⎣ ⎤
⎦ +
EXAMPLE 7
Evaluate e
x
x
dx
x 1
1 2
2
2
1
⎛
⎝
⎜
⎞
⎠
⎟
∫ .
Solution.
Let I e
x
x
dx e
x
x
dx
x x
=
−
+
⎛
⎝
⎜
⎞
⎠
⎟ =
−
+
∫ ∫
1
1
1
1
2
2 2
2 2
( )
( )
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 7 5/19/2016 4:42:48 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-514-2048.jpg)
![6.8 ■ Engineering Mathematics
=
+ −
+
=
+
−
+
⎡
⎣
⎢
⎤
⎦
⎥
∫ ∫
e
x x
x
dx e
x
x
x
dx
x x
( )
( ) ( )
1 2
1
1
1
2
1
2
2 2 2 2 2
If f x
x
f x
x
x
( ) , ( )
( )
=
+
= −
+
1
1
2
1
2 2 2
then ′
[ I e f x f x dx
x
= +
∫ [ ( ) )]
′( = + =
+
+
e f x c
e
x
c
x
x
( )
1 2
EXAMPLE 8
Evaluate
e x x
x
dx
x
( )
( ) /
3
2 3 2
1
1
1 1
1
∫ .
Solution.
Let I e
x x
x
dx e
x x
x
dx e
x
x
x x x
=
+ +
+
=
+ +
+
=
+
∫ ∫
( )
( )
[ ( ) ]
( ) (
/ /
3
2 3 2
2
2 3 2 2
1
1
1 1
1 1
1
1
1
1 2 2 3 2
) ( )
/ /
+
+
⎡
⎣
⎢
⎤
⎦
⎥
∫ x
If f x
x
x
( )
( )
,
/
=
+
2 1 2
1
then f x
x x x x
x
′( )
( ) ( )
( )
/ /
/
=
+ ⋅ − ⋅ + ⋅
+
⎡
⎣ ⎤
⎦
−
2 1 2 2 1 2 1
2 1 2 2
1 1
1
2
1 2
1
=
+ − +
+
=
+ −
+
+
=
−
( ) ( )
( )
( )
( )
/ /
/
/
x x x
x
x
x
x
x
x
2 1 2 2 1 2 2
2
2 1 2
2
2 1 2
2
2
1 1
1
1
1
1
+
+ −
+
=
+
1
1
1
1
2
2 3 2 2 3 2
x
x x
( ) ( )
/ /
[ I e f x f x dx
x
= +
∫ [ ( ) ( )]
′ = + =
+
+
e f x c e
x
x
c
x x
( )
( ) /
1 2 1 2
EXAMPLE 9
Evaluate e
x x
x
dx
x
tan ( )
.
2
?
1 1
1
1 1
1
2
2
∫
Solution.
Let I e
x x
x
dx
x
=
+ +
+
−
∫
tan ( )
1 1
1
2
2
⋅
Put t x dt
dx
x
= ∴ =
+
−
tan 1
2
1
and x t
= tan
[ I e t t dt
t
= + +
∫ [ tan tan ]
1 2
= + = +
∫ ∫
e t t dt e t t dt
t t
[sec tan ] [tan sec ]
2 2
If f t t
( ) tan ,
= then f t t
′( ) sec
= 2
[ I e f t f t dt
t
= +
∫ [ ( ) ( )]
′ = + = + = +
−
e f t c e t c xe c
t t x
( ) tan tan 1
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 8 5/19/2016 4:42:51 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-515-2048.jpg)
![Integral Calculus ■ 6.9
EXERCISE 6.1
Evaluate the following integrals:
1. x x dx
2
3
sin
∫ 2. x x dx
2 1
tan−
∫ 3. x x dx
2 1
sec−
∫
4. e x dx
x
2
4
cos
∫ 5. x x dx
e
log
∫ 6. x x dx
2
sin
∫
7. log x dx
( )
∫
2
8. x e dx
x
5 2
∫ 9. e x dx
x
3
5
sin
∫
10. x x dx
3
cos
∫ 11. e x x dx
x
2
3 5
sin cos
∫ 12. x e dx
x
2 5
−
∫
13. e
x
x
dx
x +
+
⎛
⎝
⎜
⎞
⎠
⎟
∫
1
2 2
( )
14. e
x x
x
dx
x
2
2
3 3
2
+ +
+
⎛
⎝
⎜
⎞
⎠
⎟
∫ ( )
15. e
x
x
dx
x 1
1
+
+
⎛
⎝
⎜
⎞
⎠
⎟
∫
sin
cos
16. e x x dx
x
4
6 2
cos cos
∫ 17. sin−
∫
1
x dx 18. a x dx
2 2
+
∫
19. x x dx
4
sin
∫ 20. x x dx
2
2
cos
∫
ANSWERS TO EXERCISE 6.1
1. − + + +
1
3
3
2
9
3
2
9
3
2
x x x x x c
cos sin cos 2.
x
x
x
x c
3
1
2
2
3
1
3 2
1
2
1
tan log( )
−
− − +
⎡
⎣
⎢
⎤
⎦
⎥ +
3.
x
x
x
x c
3
1
2
2
3
1
3
1
3
1 2
sec ( )
−
−
−
− +
⎡
⎣
⎢
⎤
⎦
⎥ + 4.
e
x x c
x
2
20
2 4 4 4
[ cos sin ]
+ +
5.
x
x
x
c
2 2
2 4
log − + 6. 2 2 2
x x x x c
sin cos ( )
+ − +
7. x x x x x c
(log ) log
2
2 2
− + + 8. e x x x x x
x
2 5 4 3 2
5
2
5
2
15
4
15
4
15
8
− + − + −
⎡
⎣
⎢
⎤
⎦
⎥
9.
e
x x c
x
3
34
3 5 5 5
[ sin cos ]
− + 10. x x x x x x x c
3 2
3 6
sin cos sin cos
+ − − +
11.
e
x x
e
x x c
x x
2 2
6
8 4 8
8
2 2
[sin cos ] [sin cos ]
− − − + 12. e
x x
c
x
−
− + −
⎡
⎣
⎢
⎤
⎦
⎥ +
5
2
5
2
25
2
125
13. e
x
x
c
x −
+
⎛
⎝
⎜
⎞
⎠
⎟ +
1
1
14. e
x
x
c
x +
+
⎛
⎝
⎜
⎞
⎠
⎟ +
1
2
15. e
x
c
x
⋅ +
tan
2
16.
e
x x
e
x x c
x x
4 4
40
8 2 8
16
4 4
[cos sin ] [cos sin ]
+ + + +
17. x x x c
sin−
+ − +
1 2
1 18.
x a x a
x a x c
e
2 2 2
2 2
2 2
+
+ + + +
log
19. x x x x x x c
2 4 2
4 6 12 24
( )sin ( )cos
− − − + + 20.
1
4
1 2 2 2 2
2
( )sin cos
+ +
⎡
⎣ ⎤
⎦ +
x x x x c
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 9 5/19/2016 4:42:58 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-516-2048.jpg)
![6.10 ■ Engineering Mathematics
6.2 DEFINITE INTEGRAL (NEWTON–LEIBNITZ FORMULA)
Definition 6.2
If f(x) is a continuous function on [a, b] and F x f x
′( ) ( )
= on [a, b], then the definite integral
f x dx
a
b
( )
∫ is defined as F(b) 2 F(a).
[ f x dx F b F a
a
b
( ) ( ( )
= −
∫ )
Note
1. The difference F(b) − F(a) is written symbolically F x a
b
( )
[ ] .
Hence, the definite integral f x dx F x F b F a
a
b
a
b
( ) ( ) ( ) ( )
= [ ] = −
∫
2. Newton–Leibnitz formula gives a practical method of computing definite integrals when an
anti derivative of the integrand is known.
3. In a definite integral f x dx
a
b
( ) ,
∫ when substitution or transformation of variable is made, it should
be either an increasing function or a decreasing function in the given interval.
6.2.1 Properties of Definite Integral
If f(x) is a continuous and integrable function of x in [a, b], then the following properties are satisfied.
1. f x dx f x dx
a
b
b
a
( ) ( )
= −∫
∫
2. f x dx f x dx f x dx a c b
c
b
a
c
a
b
( ) ( ) ( ) ,
= +
∫
∫
∫
3. f x dx f a b x dx
a
b
a
b
( ) ( )
= + −
∫
∫
4. f x dx f a x dx
a
a
( ) ( )
= −
∫
∫ 0
0
5. f x dx f x dx
a
a
a
( ) ( )
= ∫
∫
−
2
0
if f(x) is an even function of x (i.e., f(−x) = f(x) ∀ x ∈[−a, a])
and f x dx
a
a
( ) =
−
∫ 0 if f(x) is an odd function of x (i.e., f(−x) = −f(x) ∀ x ∈[−a, a])
6. f x dx f x dx
a
a
( ) ( )
= ∫
∫ 2
0
0
2
if f(2a − x) = f(x) and f x dx
a
( ) =
∫ 0
0
2
if f(2a − x) = −f(x)
7. If f x g x
( ) ( ),
≤ then f x dx g x dx
a
b
a
b
( ) ( )
≤ ∫
∫
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 10 5/19/2016 4:43:01 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-517-2048.jpg)
![Integral Calculus ■ 6.11
Note f x dx f u du f t dt
a
b
a
b
a
b
( ) ( ) ( )
= = ∫
∫
∫
That is the value of a definite integral is unaffected by the change of dummi variable, if the limits and
function are the same.
Periodic Function
Definition 6.3
A real function f is said to be periodic if there exists a positive number T such that
f x T f x x R
( ) ( ) .
+ = ∀ ∈
The smallest such T is called the period of the function.
EXAMPLE
We know
cos( ) cos ,cos( ) cos ,
x x x x
+ = + =
2 4
p p cos( ) cos .
x x
+ =
6p and so on
The smallest one is 2p. So, 2p is the period of cos x.
8. If f(x) is periodic with period T, then
(i) f x dx n f x dx n Z
a
T
a
a nT
( ) ( ) ,
= ∈
∫
∫
+
(ii) f x dx n f x dx n Z
T
nT
( ) ( ) ,
= ∈
∫
∫ 0
0
(iii) f x dx f x dx n Z
a
b
a nT
b nT
( ) ( ) ,
= ∈
∫
∫
+
+
Now we shall prove these formulae.
1. f x dx f x dx
a
b
b
a
( ) ( )
52∫
∫
Proof
Let F x f x a b
′( ) ( ) [ , ]
= on
By Newton–Leibnitz formula,
f x dx F x F b F a
a
b
a
b
( ) ( ) ( ) ( )
= [ ] = −
∫
and f x dx F x F a F b F b F a
b
a
b
a
( ) ( ) ( ) ( ) ( ) ( )
=[ ] = − = − −
[ ]
∫
[ f x dx f x dx
a
b
b
a
( ) ( )
= − ∫
∫ ■
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 11 5/19/2016 4:43:03 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-518-2048.jpg)
![6.12 ■ Engineering Mathematics
2. f x dx f x dx f x dx
c
c
b a
a
a
( ) ( ) ( )
5 1 ∫
∫
∫
Proof
We have
f x dx F b F a
f x dx F c F a
a
b
a
c
( ) ( ) ( )
( ) ( ) ( )
= −
= −
∫
∫
and f x dx F b F c
c
b
( ) ( ) ( )
= −
∫
∴ f x dx f x dx F c F a F b F c
c
b
a
c
( ) ( ) ( ) ( ) ( ) ( )
+ = − + −
∫
∫
= − = ∫
F b F a f x dx
a
b
( ) ( ) ( )
∴ f x dx f x dx f x dx
c
a
a
c
a
b
( ) ( ) ( )
= + ∫
∫
∫ ■
3. f x dx f a b x dx
a
b
a
b
( ) ( )
5 1 2
∫
∫
Proof
R.H.S = f a b x dx
a
b
( )
+ −
∫
Put t a b x dt dx dx dt
= + − ∴ = − ⇒ = −
When x = a, t = b and when x = b, t = a
∴ R.H.S = − = −∫
∫ f t dt f t dt
b
a
b
a
( )( ) ( )
= = =
∫ ∫
f t dt f x dx
a
b
a
b
( ) ( ) L.H.S
[by property 1]
∴ f x dx f a b x dx
a
b
a
b
( ) ( )
= + −
∫
∫ ■
4. f x dx f a x dx
a
a
( ) ( )
5 2
0
0
∫
∫
Proof
In 3, put a = 0, b = a, then a b x a x
+ − = −
∴ f x dx f a x dx
a
a
( ) ( ) .
= −
∫
∫ 0
0
■
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 12 5/19/2016 4:43:07 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-519-2048.jpg)
![Integral Calculus ■ 6.13
5. f x dx f x dx
a
a
a
( ) ( )
5
2
2
0
∫
∫ if f(x) is an even function of x and
f x dx
a
a
( ) 5
2
0
∫ if f(x) is an odd function of x
Proof
f x dx f x dx f x dx
a
a
a
a
( ) ( ) ( )
= + ∫
∫
∫ −
− 0
0
(1) [by property 2]
Let I f x dx
a
=
−
∫ ( )
0
Put x t dx dt
= − ∴ = −
When x = −a, t = a and when x = 0, t = 0
∴ I f t dt
a
= − −
∫ ( )( )
−
0
= − − = − = −
∫ ∫ ∫
f t dt f t dt f x dx
a
a a
( ) ( ) ( )
0
0 0
[by note]
If f(x) is an even function of x, then f(−x) = f(x). ∴ f x dx f x dx
a
a
( ) ( )
= ∫
∫ 0
0
If f(x) is an odd function of x, then f(−x) = −f(x). ∴ f x dx f x dx
a
a
( ) ( )
= −∫
∫
− 0
0
Substituting in (1), we get
f x dx f x dx f x dx
a
a
a
a
( ) ( ) ( )
= + ∫
∫
∫
− 0
0
= ∫
2
0
f x dx
a
( ) if f (x) is an even function of x
and f x dx f x dx f x dx
a
a
a
a
( ) ( ) ( )
= − + ∫
∫
∫
− 0
0
= 0 if f (x) is an odd function of x. ■
6. f x dx f x dx f a x f x
a
a
( ) ( ) ( ) ( )
5 2 5
2 if 2
0
0
2
∫
∫ and
f x dx f a x f x
a
( ) ( ) ( )
5 2 52
0 2
0
2
if
∫
Proof
f x dx f x dx f x dx
a
a
a
a
( ) ( ) ( )
= + ∫
∫
∫
2
0
0
2
(1)
Let I f x dx
a
a
= ∫ ( )
2
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 13 5/19/2016 4:43:10 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-520-2048.jpg)
![6.14 ■ Engineering Mathematics
Put 2a x t dx dt dx dt
− = ∴ − = ⇒ = −
When x = a, t = a and when x = 2a, t = 0
∴ I f a t dt
a
= − −
∫ ( )( )
2
0
= − − = − = −
∫ ∫ ∫
f a t dt f a t dt f a x dx
a
a a
( ) ( ) ( )
2 2 2
0
0 0
∴ I f x dx f a x dx
a
a
a
= = −
∫
∫ ( ) ( )
2
0
2
If f (2a−x) = f (x), then f x dx f x dx
a
a
a
( ) ( )
= ∫
∫ 0
2
.
If f (2a−x) = − f (x) , then f x dx f x dx
a
a
a
( ) ( )
= −∫
∫ 0
2
.
Substituting in (1), we get
f x dx f x dx f x dx f x dx f a x f x
f x
a
a
a a
( ) ( ) ( ) ( ) ( ) ( )
(
= + = − =
∫
∫
∫ ∫
0
0
0
2
0
2 2
if
)
) ( ) ( ) ( ) ( )
dx f x dx f x dx f a x f x
a
a
a
= − = − = −
∫
∫
∫ 0
0
0
2
0 2
if ■
8. ( ) ( ) ( )
i f x dx n f x dx
a
T
a
a nT
5
1
∫
∫
Proof
Given f(x) is periodic with period T.
[ f x T f x x R
( ) ( )
+ = ∀ ∈ and f x rT f x Z
( ) ( )
+ = ∀ ∈
r 1
( )
Now f x dx f x dx f x dx f x dx
a
a nT
a
a T
a rT
a r T
a
( ) ( ) ( ) ( )
( )
+ +
+
+ +
+
∫ ∫ ∫
= + + + + +
… …
1
T
T
a T
a n T
a nT
f x dx
+
+ −
+
∫ ∫
2
1
( )
( )
Consider, I f x dx
a rT
a r T
=
+
+ +
∫ ( )
( )
1
Put x y rT dx dy
= + ∴ =
When x a rT y rT a rT y a
= + + = + ⇒ =
,
When x a r T
= + +
( ) ,
1 y rT a r T y a rT T rT a T
+ = + + = + + = +
( )
1 ⇒ −
[ f x dx f y rT dy
a
a T
a rT
a r T
( ) ( )
( )
= +
+
+
+ +
∫
∫
1
= =
+ +
∫ ∫
f y dy f x dx
a
a T
a
a T
( ) ( ) [using (1)]
Putting r = 1, 2, 3, …, (n − 1) in I, we get
f x dx f x dx f x dx f x dx
a
a T
a T
a T
a
a T
a T
a T
( ) ( ) , ( ) ( ) , ,
= =
+
+
+ +
+
+
∫
∫ ∫
∫
2
2
3
…
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 14 5/19/2016 4:43:14 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-521-2048.jpg)

![6.16 ■ Engineering Mathematics
(1) + (2) ⇒ 2
0
2
I
x x
x x
dx
n n
n n
=
+
+
∫
sin cos
sin cos
p
= = [ ] =
∫dx x 0
2
0
2
2
p
p
p
∴ I =
p
4
⇒
sin
sin cos
n
n n
x
x x
dx
+
=
∫
0
2
4
p
p
Note Since the right hand side is independent of n, this is true for all n.
Similarly,
cos
cos sin
n
n n
x
x x
dx
+
=
∫
0
2
4
p
p
for any n.
EXAMPLE 2
Prove that log tan log .
e e
x dx
1
8
2
0
4
1
p
p
( ) =
∫
Solution.
Let I x dx
e
= +
( )
∫log tan
1
0
4
p
(1)
Also I x dx
e
= + −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
∫log tan
1
4
0
4
p
p
[by property 4]
Now tan
p
4
−
⎛
⎝
⎜
⎞
⎠
⎟
x =
−
+
=
−
+
tan tan
tan tan
tan
tan
p
p
4
1
4
1
1
x
x
x
x
∴ 1
4
1
1
1
+ −
⎛
⎝
⎜
⎞
⎠
⎟ = +
−
+
tan
tan
tan
p
x
x
x
=
+ + −
+
=
+
1 1
1
2
1
tan tan
tan tan
x x
x x
.
∴ I
x
dx
e
=
+
⎛
⎝
⎜
⎞
⎠
⎟
∫log
tan
2
1
0
4
p
(2)
(1) + (2) ⇒ 2 1
2
1
0
4
0
4
I x dx
x
dx
e e
= +
( ) +
+
⎛
⎝
⎜
⎞
⎠
⎟
∫
∫log tan log
tan
p
p
= +
( )+
+
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
∫ log tan log
tan
e e
x
x
dx
1
2
1
0
4
p
= +
( )
+
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
∫ log tan
tan
e x
x
dx
1
2
1
0
4
p
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 16 5/19/2016 4:43:19 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-523-2048.jpg)
![Integral Calculus ■ 6.17
= = [ ] =
⎛
⎝
⎜
⎞
⎠
⎟
∫log log log
e e e
dx x
2 2 2
4
0
4
0
4
p
p
p
∴ I e
=
p
8
2
log
EXAMPLE 3
Prove that
x
x
dx
1
2 1
4
3
4
1
5 p 2
p
p
sin
.
⎡
⎣
⎤
⎦
∫
Solution.
Let I
x
x
dx
=
+
∫ 1
4
3
4
sin
p
p
(1)
First remove x by using property 4.
Here f x
x
x
a b
( )
sin
, ,
= = =
1 4
3
4
+
p p
∴ f a b x f x f x
( ) ( )
+ − = + −
⎛
⎝
⎜
⎞
⎠
⎟ = −
p p
p
4
3
4
∴ f x
x
x
x
x
( )
sin( ) sin
p
p
p
p
− =
−
+ −
=
−
+
1 1
Since f x dx f a b x dx
a
b
a
b
( ) ( )
= + −
∫
∫ , we have I
x
x
dx
=
−
+
∫
p
p
p
1
4
3
4
sin
2
( )
(1) + (2) ⇒ 2
1 1
4
3
4
4
3
4
I
x
x
dx
x
x
dx
=
+
+
−
+
∫ ∫
sin sin
p
p
p
p
p
=
+ −
+
=
+
∫ ∫
x x
x
dx
x
dx
p p
p
p
p
p
1 1
4
3
4
4
3
4
sin sin
=
+ −
⎛
⎝
⎜
⎞
⎠
⎟
∫
p
p
p
p
dx
x
1
2
4
3
4
cos
=
−
⎛
⎝
⎜
⎞
⎠
⎟
∫
p
p
p
p
dx
x
2
1
2 2
2
4
3
4
cos
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 17 5/19/2016 4:43:22 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-524-2048.jpg)
![6.18 ■ Engineering Mathematics
= −
⎛
⎝
⎜
⎞
⎠
⎟
∫
p p
2 4 2
2
4
3
4
sec
x
dx
p
p
=
−
⎛
⎝
⎜
⎞
⎠
⎟
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
p
p
p
p
2
4 2
1
2
4
3
4
tan
x
= − −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
p
p p p p
tan tan
4
3
8 4 8
= − −
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
p
p p
tan tan
8 8
= − − −
⎡
⎣
⎢
⎤
⎦
⎥
p
p p
tan tan
8 8
⇒ 2 2
8
2 2 1
I = = −
( )
p
p
p
tan { tan tan
p
8
22
1
2
2 1
=
°
= −
⎡
⎣
⎢
⎤
⎦
⎥
∴ I = −
( )
p 2 1
EXAMPLE 4
Evaluate log sin
e xdx
0
2
p
∫ .
Solution.
Let I xdx
e
= ∫log sin
0
2
p
(1)
Also I x dx
e
= −
⎛
⎝
⎜
⎞
⎠
⎟
∫log sin
p
p
2
0
2
= ∫log cos
e xdx
0
2
p
(2) [by property 4]
(1) + (2) ⇒ 2
0
2
0
2
I xdx xdx
e e
= +
∫ ∫
log sin log cos
p p
= +
∫(log sin logcos )
e x x dx
0
2
p
= ∫log sin cos
e x x dx
0
2
p
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 18 5/19/2016 4:43:25 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-525-2048.jpg)
![Integral Calculus ■ 6.19
=
⎛
⎝
⎜
⎞
⎠
⎟
∫log
sin
e
x
dx
2
2
0
2
p
[ sin sin cos ]
{ 2 2
x x x
=
= ∫(log sin log )
e e
x dx
2 2
0
2
−
p
= − ∫
∫(log sin ) log
e e
x dx dx
2 2
0
2
0
2
p
p
⇒ 2 2
1 0
2
I I x
e
= − [ ]
log
p
= − −
⎡
⎣
⎢
⎤
⎦
⎥ = −
I I
e e
1 1
2
2
0
2
2
log log
p p
.
where I x dx
e
1
0
2
2
= ∫log sin
p
Put t x
= 2 ∴ = ⇒ =
dt dx dx
dt
2
2
When x = 0, t = 0 and when x =
p
2
, t = p.
∴ I t
dt
e
1
0
2
= ∫log sin
p
= ∫
1
2 0
log sin
e t dt
p
= ⋅ ∫
1
2
2
0
2
log sin
e t dt
p
By property 6
{ f t t
t f t
p p
−
( ) = −
( )
= = ( )
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
logsin
logsin
= log sin
e t dt
0
2
p
∫ = =
∫log sin
e x dx I
0
2
p
∴ 2
2
2
I I e
= −
p
log ⇒ I e
= −
p
2
2
log .
EXAMPLE 5
Show that
log
( )
log
e
e
x
x
x
dx
1
1
5 p
1
1
2
2
0
⎛
⎝
⎜
⎞
⎠
⎟
∫
∞
.
Solution.
Let I
x
x
x
dx
e
=
+
⎛
⎝
⎜
⎞
⎠
⎟
+
∞
∫
log
( )
1
1 2
0
Put x = tanu ∴ dx d
= sec2
u u
When x = = ⇒ =
0 0 0
, tanu u and when x = ∞ = ∞⇒ =
, tanu u
p
2
.
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 19 5/19/2016 4:43:30 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-526-2048.jpg)
![6.20 ■ Engineering Mathematics
∴ I d
e
=
+
⎛
⎝
⎜
⎞
⎠
⎟
+
( )
∫
log tan
tan
sec
tan
u
u
u
u
u
p 1
1
2
2
0
2
=
+
⎛
⎝
⎜
⎞
⎠
⎟
∫log
tan
tan
e d
1 2
0
2
u
u
u
p
=
⎛
⎝
⎜
⎞
⎠
⎟
∫log
sec
tan
e d
2
0
2
u
u
u
p
= ⋅
⎛
⎝
⎜
⎞
⎠
⎟
∫log
cos
cos
sin
e d
1
2
0
2
u
u
u
u
p
=
⎛
⎝
⎜
⎞
⎠
⎟
∫log
sin cos
e d
1
0
2
u u
u
p
=
⎛
⎝
⎜
⎞
⎠
⎟
∫log
sin cos
e d
2
2
0
2
u u
u
p
=
⎛
⎝
⎜
⎞
⎠
⎟
∫log
sin
e d
2
2
0
2
u
u
p
= − ∫
∫log log sin
e e
d d
2 2
0
2
0
2
u u u
p
p
= [ ] − ∫
log log sin
e e d
2 2
0
2
0
2
u u u
p
p
= − ∫
p
u u
p
2
2 2
0
2
log log sin
e e d = −
p
2
2 1
loge I
where I d
e
1
0
2
2
= ∫log sin
p
u u = =
∫ ∫
1
2 0 0
2
log sin log sin
e e
d d
p
p
u u u u = −
p
2
2
loge
[Refer example 4]
[ I e e
= − −
⎛
⎝
⎜
⎞
⎠
⎟
p p
2
2
2
2
log log
= +
p p
2
2
2
2
log log
e e = ploge 2 .
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 20 5/19/2016 4:43:34 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-527-2048.jpg)
![Integral Calculus ■ 6.21
EXAMPLE 6
Prove that
x x x
x
dx
sin sin cos
2
2
2
8
0
2
p
2 p
5
p
p
⎛
⎝
⎜
⎞
⎠
⎟
∫ .
Solution.
Let I
x x x
x
dx
=
⎛
⎝
⎜
⎞
⎠
⎟
−
∫
sin sin cos
2
2
2
0
p
p
p
Put 2 2 2 2
x t dx dt dx dt
− = ∴ = ⇒ =
p
When x t t
= = − ⇒ = −
0 2
2
, p
p
and When x t t
= = − ⇒ =
p p p
p
, 2 2
2
[ I
t t t
t
dt
=
+
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
−
∫
p
p
p p
p
p
2
2
2 2
2
2
2
sin( )sin cos
=
+
⎛
⎝
⎜
⎞
⎠
⎟ − ⋅ −
⎛
⎝
⎜
⎞
⎠
⎟
−
∫
p p
p
p
2
2
2
2
2
2 t t t
t
dt
( sin ) sin sin
=
⋅
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
− −
∫ ∫
p
p
p
p
p
p
p
4
2
2 1
2
2
2
2
2
2
2
sin sin sin
sin sin sin
t t
t
dt t t
⎜
⎜
⎞
⎠
⎟ dt
⇒ I I I
= +
p
4
1
2
1 2
where I
t t
t
dt
1
2
2 2
2
=
⋅
⎛
⎝
⎜
⎞
⎠
⎟
−
∫
sin sin sin
p
p
p
and I t t dt
2
2
2
2
2
=
⎛
⎝
⎜
⎞
⎠
⎟
−
∫ sin sin sin
p
p
?
p
Let f t
t t
t
( )
sin sin sin
=
⎛
⎝
⎜
⎞
⎠
⎟
2
2
p
[ f t
t t
t
( )
sin( )sin sin( )
− =
− −
⎛
⎝
⎜
⎞
⎠
⎟
−
2
2
p
= −
⎛
⎝
⎜
⎞
⎠
⎟
sin sin sin
2
2
t t
t
p
= − f t
( ) [ sin( ) sin ]
{ − = −
t t
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 21 5/19/2016 4:43:37 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-528-2048.jpg)
![6.22 ■ Engineering Mathematics
∴ f t
( ) is an odd function of t. [ I f t dt
1
2
2
0
= =
−
∫ ( )
p
p
[by property 5]
Now, let g t t t
( ) sin sin sin
=
⎛
⎝
⎜
⎞
⎠
⎟
2
2
p
[ g t t t
( ) sin( )sin sin( )
− = − −
⎛
⎝
⎜
⎞
⎠
⎟
2
2
p
=
⎛
⎝
⎜
⎞
⎠
⎟ =
sin sin sin ( )
2
2
t t g t
p
∴ g t
( ) is an even function of t.
[ I g t dt g t dt
2
0
2
2
2
2
= = ∫
∫
−
( ) ( )
p
p
p
=
⎛
⎝
⎜
⎞
⎠
⎟
∫
2 2
2
0
2
sin sin sin
t t dt
p
p
[by property 5]
=
⎛
⎝
⎜
⎞
⎠
⎟
∫
4
2
0
2
sin cos sin sin
t t t dt
p
p
Put u t t
u
= ⇒ =
p
p
2
2
sin sin ∴ =
costdt du
2
p
.
When t u
= = =
0
2
0 0
, sin
p
and when t u
= = =
p p p p
2 2 2 2
, sin
[ I
u
u du
2
0
2
4
2 2
= ⋅ ⋅
∫ p p
p
sin = ∫
16
2
0
2
p
p
u u du
sin .
Integrating by parts, we get
I u u u du
2 2 0
2
0
2
16
1
= −
[ ] − ⋅ −
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
∫
p
p
p
( cos ) ( cos )
=
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
∫
16
0
2
0
2
p
p
[ ] cos
+ udu
= [ ] = −
⎡
⎣
⎢
⎤
⎦
⎥
16 16
2
0
2 0
2
2
p p
p
p
sin sin sin
u = − =
16
1 0
16
2 2
p p
( )
[ I I I
= +
p
4
1
2
1 2 = × + ×
p
p
4
0
1
2
16
2
=
8
2
p
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 22 5/19/2016 4:43:42 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-529-2048.jpg)
![Integral Calculus ■ 6.23
EXAMPLE 7
Prove that cot ( ) log .
2
2 1 5
p
2
1 2
0
1
1
2
2
x x dx e
∫
Solution.
Let I x x dx
= − +
−
∫cot ( )
1 2
0
1
1 =
− +
⎛
⎝
⎜
⎞
⎠
⎟
−
∫tan 1
2
0
1
1
1 x x
dx
=
+ −
− −
⎛
⎝
⎜
⎞
⎠
⎟
−
∫tan
( )
( )
1
0
1
1
1 1
x x
x x
dx
= + −
− −
∫[tan tan ( )]
1 1
0
1
1
x x dx
= + −
− −
∫
∫tan tan ( )
1 1
0
1
0
1
1
x dx x dx
= +
− −
∫
∫tan tan
1 1
0
1
0
1
x dx x dx [by property 4]
= −
∫
2 1
0
1
tan x dx
= ⋅
⎡
⎣ ⎤
⎦ −
+
⋅
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
−
∫
2
1
1
1
0
1
2
0
1
tan x x
x
x dx
= − − +
⎡
⎣ ⎤
⎦
⎧
⎨
⎩
⎫
⎬
⎭
−
2 1 0
1
2
1
1 2
0
1
[tan ] log ( )
e x
= − −
⎧
⎨
⎩
⎫
⎬
⎭
= −
2
4
1
2
2 1
2
2
p p
[log log ] log
e e e
EXAMPLE 8
Prove that tan ( ) log .
−
−
1 2
0
1
1 2
x x dx e
+
∫ 5
Solution.
We know that tan cot tan cot
− − −
⇒ −
1 1 1 1
2 2
u u
p
u
p
u
+ = =
−
∴ − − −
∴ −
− −
−
tan ( ) cot (
tan ( )
1 2 1 2
1 2
0
1
1
2
1
1
x x x x
x x dx
+ = +
+ =
∫
p
)
p
p
p
p
2
1
2
1
2
1 2
0
1
0
1
1 2
0
1
− −
− +
−
cot ( )
cot ( )
−
+
⎡
⎣
⎢
⎤
⎦
⎥
= −
=
∫
∫ ∫
x x dx
dx x x dx
[
[ ] log log log
x e e e
0
1
2
2
2 2
2 2
− − −
p p p
⎛
⎝
⎜
⎞
⎠
⎟ = + = [using worked example 7]
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 23 5/19/2016 4:43:45 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-530-2048.jpg)
![6.24 ■ Engineering Mathematics
EXAMPLE 9
Prove that
x dx
a x b x ab
2 2 2 2
2
0
2
cos sin
.
1
5
p
p
∫
Solution.
Let I
x dx
a x b x
=
+
∫ 2 2 2 2
0 cos sin
p
( )
1
Also I
x dx
a x b x
=
−
− + −
∫
( )
cos ( ) sin ( )
p
p p
2 2 2 2
0
p
[by property 4]
⇒ I
x
a x b x
dx
=
−
( )
+
∫
p
2 2 2 2
0 cos sin
p
( )
2
(1) + (2) ⇒ 2 2 2 2 2
0
I
x x
a x b x
dx
=
+ −
+
∫
p
cos sin
p
=
+
∫
p
1
2 2 2 2
0 a x b x
dx
cos sin
p
Let f x
a x b x
( ) =
+
1
2 2 2 2
cos sin
[ f a x f x
( ) ( )
2 − = −
p =
− + −
1
2 2 2 2
a x b x
cos ( ) sin ( )
p p
=
+
=
1
2 2 2 2
a x b x
f x
cos sin
( )
[ 2 2 2 2 2 2
0
2
I
dx
a x b x
=
+
∫
p
p
cos sin
[by property 6]
⇒ I
dx
x a b x
=
+
∫
p
p
cos [ tan ]
2 2 2 2
0
2
=
+
∫
p
p
sec
[ tan ]
2
2 2 2
0
2
dx
a b x
Put t x dt x dx
= ∴ =
tan sec2
.
When x t
= = =
0 0 0
, tan and when x t
= = = ∞
p p
2 2
, tan
[ I
dt
a b t
=
+
∞
∫
p 2 2 2
0
=
+
∞
∫
p
b
dt
a
b
t
2 2
2
2
0
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
∞
p
b a
b
t
a
b
2
1
0
1
tan = ∞ − = −
⎡
⎣
⎢
⎤
⎦
⎥ =
− −
p p p p
ab ab ab
[tan tan ]
1 1
2
0
2
0
2
.
Note In the interval ( , )
0 p we cannot put t x
= tan as it is not increasing there and discontinuous at
x =
p
2
. So, we reduced the interval ( , )
0 p to 0
2
,
p
⎛
⎝
⎜
⎞
⎠
⎟ by property 6, so that in 0
2
,
p
⎛
⎝
⎜
⎞
⎠
⎟, tan x is strictly
increasing.
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 24 5/19/2016 4:43:50 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-531-2048.jpg)
![Integral Calculus ■ 6.25
Integrals of Periodic Functions
EXAMPLE 10
Evaluate 1 2
0
4
2
p
cos x dx
∫ .
Solution.
Let I x dx
= −
∫ 1 2
0
4
cos
p
= ∫ 2 2
0
4
sin x dx
p
= ∫
2
0
4
sin x dx
p
[ ]
{ x x x x x x x
2
0 0
= = ≥ = −
if and if
But sin x is periodic with period p. That is, T = p in property 8(1).
∴ we have sin x dx
0
4
4
p
∫ = sin x dx
0
p
∫
But sin ( , ) sin sin
x x x x
≥ ∈ =
0 0
if p ∴
[ 4 4
0 0
sin sin
x dx x dx
p p
∫ ∫
= = −
[ ] = − − = − − − =
4 4 0 4 1 1 8
0
cos [cos cos ] [ ]
x
p
p
∴ I = × =
2 8 8 2
EXAMPLE 11
Evaluate sin cos
x x dx
1
p
0
∫ .
Solution.
Let I x x dx
= +
∫ sin cos
0
p
Now sin cos
x x
+ = +
⎡
⎣
⎢
⎤
⎦
⎥
2
1
2
1
2
sin cos
x x
= ⋅ + ⋅
⎡
⎣
⎢
⎤
⎦
⎥ = −
⎛
⎝
⎜
⎞
⎠
⎟
2
4 4
2
4
sin sin cos cos cos
p p p
x x x
But sin cos
x x
+ = −
⎛
⎝
⎜
⎞
⎠
⎟
2
4
cos x
p
is of period p.
[ I x dx
= −
⎛
⎝
⎜
⎞
⎠
⎟
∫
2
4
0
cos
p
p
Put t x
= −
p
4
. [ dt = dx
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 25 5/19/2016 4:43:55 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-532-2048.jpg)
![6.26 ■ Engineering Mathematics
When x t x t
= = − = = − =
0
4 4
3
4
, ,
p
p p
p p
and when .
[ I t dt
=
−
∫
2
4
3
4
cos
p
p
But cost ≥ 0 in −
⎛
⎝
⎜
⎞
⎠
⎟
p p
4 2
, and cost 0 in
p p
2
3
4
,
⎛
⎝
⎜
⎞
⎠
⎟
∴ cos cos ,
t t
= −
⎛
⎝
⎜
⎞
⎠
⎟
in
p p
4 2
, and cos cos ,
t t
= −
⎛
⎝
⎜
⎞
⎠
⎟
in
p p
2
3
4
[ I t dt t dt
= + −
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
∫
∫
−
2
2
3
4
4
2
cos cos
p
p
p
p
= [ ] −[ ]
⎧
⎨
⎩
⎫
⎬
⎭
−
2
4
2
2
3
4
sin sin
t t
p
p
p
p
= − −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥ − −
⎡
⎣
⎢
⎤
⎦
⎥
⎧
⎨
⎩
⎫
⎬
⎭
2
2 4
3
4 2
sin sin sin sin
p p p p
= + − +
⎡
⎣
⎢
⎤
⎦
⎥ =
2 1
1
2
1
2
1 2 2.
EXAMPLE 12
Prove that sin cos
x dx n v v n Z
n v
5 1 2 p
p 1
2 1 0
0
if and
≤ ∈
∫ .
Solution.
Let I x dx
n v
=
+
∫ sin
0
p
= + = +
∫ ∫
+
sin sin
x dx x dx I I
n
n
n v
0
1 2
p
p
p
where I x dx
n
1
0
= ∫ sin
p
. But sin x is periodic with period p.
[ I n x dx
1
0
= ∫ sin
p
[by property 8(i)]
= ∫
n x dx
sin
0
p
[since in
sin , ]
x ( )
0 0 p
= −
[ ] = − − = − − − =
n x n n n
cos [cos cos ] [ ]
0
0 1 1 2
p
p
and I x dx
n
n v
2 =
+
∫ sin
p
p
Put x n y
= +
p [ dx = dy. When x = np, y x n v y v
= = + =
0 and when p , .
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 26 6/3/2016 8:16:38 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-533-2048.jpg)
![Integral Calculus ■ 6.27
[ I n y dy
v
2
0
= +
∫ sin( )
p = =
∫ ∫
sin sin
y dy y dy
v v
0 0
[ , sin ]
{ 0 0
≤ ≤
y v y
p
= −
[ ] = − − = −
cos [cos cos ] cos
y v v
v
0
0 1 .
[ I I I n v
= + = + −
1 2 2 1 cos .
EXERCISE 6.2
Evaluate the following integrals:
1.
dx
x
1
4
3
4
+
∫ cos
p
p
2.
x x
x x
dx n
n
n n
sin
sin cos
,
2
2 2
0
2
0
+
∫
p
3.
log x
x
dx
1 2
0
1
−
∫
4.
cos−
∫
1
0
1
x
x
dx 5.
tan−
∞
+
( )
∫
1
2
0 1
x
x x
dx 6.
x dx
x
1 2
0 +
∫ sin
p
7.
x x
x x
dx
tan
sec tan
+
∞
∫
0
8.
dx
x
dx
1
0
2
+
∫ tan
p
9.
dx
x a x
a
+ +
∫ 2 2
0
10. u u u
p
sin3
0
∫ d 11. cos sin
x x dx
−
∫
0
2
p
12. 1 2
0
100
−
∫ cos x dx
p
13.
x x
x
dx
sin
cos
1 2
0 +
∫
p
14.
x dx
x x
sin cos
+
∫
0
2
p
15. Prove that f x dx f x f x dx
a
a a
( ) [ ( ) ( )] .
−
∫ ∫
= + −
0
Hence, evaluate u u u u
sin cos .
d
−
∫p
p
2
2
ANSWERS TO EXERCISE 6.2
1. 2 2. p2
3. −
p
2
2
log 4.
p
2
2
log 5.
p
2
2
log 6.
p2
2 2
7. p
p
2
1
−
⎛
⎝
⎜
⎞
⎠
⎟ 8.
p
4
9.
p
4
10.
2
3
p
11. 2 2 1
− 12. 200 2
13.
p2
4
14.
p
2 2
2 1
⋅ +
( )
loge 15.
p
4
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 27 5/20/2016 10:09:10 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-534-2048.jpg)
![6.28 ■ Engineering Mathematics
6.3 DEFINITE INTEGRAL f x
a
b
( )dx
∫ AS LIMIT OF A SUM
Let f be a bounded function defined on the finite interval [ , ]
a b .
Divide [ , ]
a b into n sub-intervals by the points x x xn
1 2 1
, , , ,
… − not necessarily equidistant.
Take x a x b
n
0 = =
and .
Now [ , , , , ]
x x x xn
0 1 2
… form a partition P a b
of [ , ] and we have n sub-intervals.
I x x r n
r r r
= =
−
[ , ], , , , ,
1 1 2 3 … , Let dr r r
x x
= − −1 be the length of Ir.
Let cr be any point in Ir. Then form the sum f cr r
r
n
( )
=
∑ d
1
.
This sum is called the Riemann sum of f x a b
( ) ,
on[ ] for the partition P.
The length of the largest sub-interval is denoted by d and is called the norm of the partition.
The function f x
( ) is Reimann integrable if lim ( )
n
r r
r
n
f c
→∞
→ =
∑
d
d
0 1
exists and is independent of the choice
of the interval and the point cr.
This limit is called the definite integral of f x a b
( ) [ , ]
over .
We write f x dx f c
a
b
n
r r
r
n
( ) lim ( )
=
∫ ∑
→∞
→ =
d
d
0 1
In practical applications, for convenience, we take the length of the sub-interval equal to h
b a
n
=
−
,
where n is the number of sub-intervals.
Then x a h x a h x a rh b x a nh
r n
1 2 2
= + = + = + = = +
, , , , ,
… …
and cr is taken as an end point of Ir.
Then f x dx h f a rh
a
b
h
n r
n
( ) lim ( )
= +
∫ ∑
→
→∞ =
−
0
0
1
( )
1
Or
f x dx h f a rh
a
b
n
h r
n
( ) lim ( )
= +
∫ ∑
→∞
→ =
0 1
( )
2
If a b h
n
= = =
0 1
1
, , then [ lim ( )
n
r
n
n
f
r
n
f x dx
→∞
=
−
⎛
⎝
⎜
⎞
⎠
⎟ = ∫
∑
1
0
1
0
1
This formula enables us to evaluate the limit of a certain sums interms of the integrals.
6.3.1 Working Rule
1. First rewrite the given limit of a sum in the form lim
n
r
n
n
f
r
n
→∞
=
⎛
⎝
⎜
⎞
⎠
⎟
∑
1
1
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 28 5/20/2016 10:09:16 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-535-2048.jpg)

![6.30 ■ Engineering Mathematics
Solution.
The given limit is lim
n
r
n
r
n r
→∞
= +
∑
2
3 3
1
Rewrite in the form f
r
n
⎛
⎝
⎜
⎞
⎠
⎟ . So, take out n3
as common.
[ lim lim lim
n
r
n
n
r
n
n
r
n r
r
n
r
n
n
r
n
→∞
=
→∞
=
→∞
+
=
+
⎛
⎝
⎜
⎞
⎠
⎟
=
⎛
∑ ∑
2
3 3
1
2
3
3
3
1
1
1 ⎝
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
=
∑
2
3
1
1
r
n
r
n
Treat
r
n
x
= and
1
n
as dx.
When r = 1, x
n
= →
1
0 as n → ∞ and when r n
= , x
n
n
= = 1
[ lim
log ( )
n
r
n
e
r
n r
x
x
dx
x
x
dx
x
→∞
= +
=
+
=
+
= +
∑ ∫ ∫
2
3 3
1
2
3
0
1 2
3
0
1
3
1
1
3
3
1
1
3
1
⎡
⎡
⎣ ⎤
⎦
′
=
⎡
⎣
⎢
⎤
⎦
⎥
= + − +
[ ]=
0
1
1
3
1 1 1 0
{
f x
f x
dx f x
e
e
( )
( )
log ( )
log ( ) log( )
1
1
3
2
loge
[ lim log
x
e
n n n
n
n
→∞ +
+
+
+
+
+ +
⎡
⎣
⎢
⎤
⎦
⎥ =
1
1
4
8
9
27 2
1
3
2
3 3 3
2
3
…
EXAMPLE 3
Show that lim .
/
n
n
n n
n
n e
→∞
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
1
1
1
2
1
4
1
… 5
Solution.
Let A
n n
n
n
n
n
= +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
→∞
lim
/
1
1
1
2
1
1
…
To convert the product into sum, take logarithm on both sides
log lim log
l
/
e
n
e
n
A
n n
n
n
= +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
=
→∞
1
1
1
2
1
1
…
i
im log
n
e
n n n
n
n
→∞
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
1
1
1
1
2
1
…
[{ loge
is a continuous function]
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 30 5/20/2016 10:09:23 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-537-2048.jpg)
![Integral Calculus ■ 6.31
lim
n n
→∞
=
1
l
log log log
lim
e e e
n
n n
n
n
1
1
1
2
1
+
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟ + + +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
=
…
→
→∞
=
+
⎛
⎝
⎜
⎞
⎠
⎟
∑
1
1
1
n
r
n
e
r
n
log
Treat
r
n
x
= and
1
n
as dx.
When r = 1, x
n
= →
1
0 as n → ∞ and when r n
= , x
n
n
= = 1
[ log log ( )
e e
A x dx
= +
∫ 1
0
1
Integrating by parts, we get
log log ( )
log ( ) log
e e
e e
A x x
x
xdx
x
x
= +
[ ] −
+
= + −
[ ]−
+
∫
1
1
1
1 1 1
1
0
1
0
1
0
1
? ?
∫
∫
∫
∫
= −
+ −
+
= − −
+
⎛
⎝
⎜
⎞
⎠
⎟
= − +
dx
x
x
dx
x
dx
dx
e
e
e
log
log
log
2
1 1
1
2 1
1
1
2
0
1
0
1
0
0
1
0
1
0
1
0
1
1
1
2 1
2 1 0 2
∫ ∫ +
= −[ ] + +
[ ]
= − −
( )+ −
x
dx
x x
e e
e e
log log ( )
log log l
log log
e e
1 2 2 1
= −
⇒ log log log log log log
e e e e e e
A e e
e
A
e
= − = − = =
2 4
4 4
2
⇒
[ lim
/
n
n
n n
n
n e
→∞
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥ =
1
1
1
2
1
4
1
…
EXAMPLE 4
Show that lim
n
n
n n n
n
n
→∞
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
1
1
1
2
1
3
1
2
2
2
2 2
2
2 2
2
…
⎣
⎣
⎢
⎢
⎤
⎦
⎥
⎥
2 2
4
/
.
n
e
5
Solution.
Let A
n n n
n
n
n
= +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
→∞
lim 1
1
1
2
1
3
1
2
2
2
2 2
2
2 2
2
…
n
n n
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
2 2
/
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 31 5/20/2016 10:09:26 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-538-2048.jpg)
![6.32 ■ Engineering Mathematics
To convert the product into sum, take logarithm on both sides
[ log limlog
e
n
e
n
A
n n
n
n
= +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
→∞
1
1
1
2
1
2
2
2
2 2
2
…
⎤
⎤
⎦
⎥
⎥
2 2
n
= +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
→∞
lim log
n
e
n
n n n
n
n
2
1
1
1
2
1
2 2
2
2
2 2
2
… ⎥
⎥
⎥
= +
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎛
⎝
⎜
⎞
⎠
⎟ + + +
⎛
→∞
lim log log log
n
e e e
n n n
n
n
n
2
1
1
2 1
2
1
2 2
2
2
2
2
…
⎝
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
= +
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟ +
→∞
=
→∞
∑
lim log lim log
n
e
r
n
n
e
n
r
r
n n
r
n
r
2
1
1
2 1
2
2
2
1
2
n
n
r
n
2
1
⎛
⎝
⎜
⎞
⎠
⎟
=
∑
Treat
r
n
x
= and
1
n
as dx.
When r = 1, x
n
= →
1
0as n → ∞ and when r n
= , x
n
n
= = 1
[ log log ( )
e e
A x x dx
= +
∫2 1 2
0
1
Put 1 2
2
+ = ∴ =
x t xdx dt.
When x t
= =
0 1
, and when x t
= =
1 2
,
[ log log
e A t dt
= ∫
1
2
Integrating by parts, we get
log log
e e
A t t
t
t dt
= ⋅
[ ] − ⋅
∫
1
2
1
2
1
= − ∫
2 2
1
2
loge dt = −[ ] = − − = −
log log ( ) log
e e e
t
2 4 2 1 4 1
2
1
2
⇒ log log log log
e e e e
A e
e
= − =
4
4
⇒ A
e
=
4
[ lim
n
n
n n n
n
n
→∞
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
1
1
1
2
1
3
1
2
2
2
2 2
2
2 2
2
…
⎣
⎣
⎢
⎢
⎤
⎦
⎥
⎥
=
2 2
4
n
e
.
EXERCISE 6.3
Evaluate the following limits as integrals
1. lim
n n n n
→∞ +
+
+
+ +
⎡
⎣
⎢
⎤
⎦
⎥
1
1
1
2
1
2
… . 2. lim
( )
n
r
n
n r
→∞
=
−
+
⎡
⎣
⎢
⎤
⎦
⎥
∑
1
2 2 1 2
0
1
.
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 32 5/20/2016 10:09:30 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-539-2048.jpg)
![Integral Calculus ■ 6.33
3. lim
[ ( )]
n
r
n
n
n r
→∞
= + −
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
∑
3 1 3
1
. 4. lim
n
n
n
n
n
n
n
→∞
+
+
+
+ +
⎡
⎣
⎢
⎤
⎦
⎥
1 2 2
3 2 3 2 3 2
… .
5. lim
n
r
r
r n
→∞
=
∞
+
⎡
⎣
⎢
⎤
⎦
⎥
∑
3
4 4
1
. 6. lim
( )
n
r
n
r
n r
→∞
= +
∑
2
3
1
.
7. lim
n
r
n
r
n r
→∞
= +
∑ 2 2
1
. 8. lim
n
r
n
n r
n
→∞
=
−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
∑
2 2
2
1
.
9. lim
( )( ) ( )
n
n
n n n n
n
→∞
+ + +
⎡
⎣
⎢
⎤
⎦
⎥
3 3 3 3 3
3
1
1 2 …
. 10. lim
n
r
n
r
n r
→∞
= +
∑
4
5 5
1
.
11. lim
n
r
n
n r
→∞
=
−
−
∑
1
2 2
0
1
. 12. lim
n
n
n n
n
n
→∞
+
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
1
1
1
2
1
2
2
2
2
2
1
… .
13. lim
n
n
n
n
n
n
n
n
n n
→∞
+
+
+
+
+ +
+ −
( )
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
2 2 2 2 2 2 2
1 2 1
… .
ANSWERS TO EXERCISE 6.3
1. loge 2 2.
p
2
3.
1
3
4.
2
3
2 2 1
−
( ) 5.
1
4
2
loge
6.
3
8
7.
1
2
2
loge 8.
p
4
9. 4 3
3
e
p
−
10.
1
5
2
loge
11.
p
2
12. 2 2
2
e
p
−
13.
p
4
6.4 REDUCTION FORMULAE
Integrals of type sin , tan ,
n n n ax
x dx x dx x e dx
∫ ∫
∫ cannot be evaluated directively. Applying integration
by parts, we can reduce an integral with index n 0, called the order of the integral, to an integral
of the reduced order with a smaller index. The relation between the given integral and the reduced
integral of lower order is called the reduction formula.
We derive the reduction formula for some standard integrals
6.4.1 The Reduction Formula for (a) sinn
xdx
∫ and (b) cosn
xdx
∫
(a) sinn
x dx
∫
Solution.
Let I x dx
n
n
= ∫sin = −
∫sin sin
n
x x dx
1
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 33 5/20/2016 10:09:35 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-540-2048.jpg)

![Integral Calculus ■ 6.35
Deduction:
If n is a non-negative integer, then prove that
sin cos
n n
x dx x dx
= ∫
∫ 0
2
0
2
p
p
=
−
⋅
−
−
⋅
−
−
⋅ ⋅
−
⋅
−
−
⋅
−
−
n
n
n
n
n
n
n
n
n
n
n
n
n
1 3
2
5
4
3
4
1
2 2
1 3
2
5
4
4
5
…
…
p
if iseven
⋅
⋅ ⋅
⎧
⎨
⎪
⎪
⎩
⎪
⎪
2
3
1 if is odd
n
Solution.
Let I x dx
n
n
= ∫sin
0
2
p
By reduction formula, we have
I
x x
n
n
n
I
n
n
n
= −
⎡
⎣
⎢
⎤
⎦
⎥ +
−
−
−
sin cos
1
0
2
2
1
p
⇒ I
n
n
I
n
n
I
n n n
= +
−
=
−
− −
0
1 1
2 2
⇒ I
n
n
I
n n
− −
=
−
−
2 4
3
2
, I
n
n
I
n n
− −
=
−
−
4 6
5
4
and so on.
[ I
n
n
n
n
n
n
I I
n =
−
⋅
−
−
⋅
−
−
1 3
2
5
4
1 0
…, the last integral is or
Case 1: If n is even, then
I
n
n
n
n
n
n
I
n =
−
⋅
−
−
⋅
−
−
⋅ ⋅
1 3
2
5
4
3
4
1
2
0
…
But I x dx
0
0
0
2
= ∫sin
p
= [ ] =
x 0
2
2
p
p
[ I
n
n
n
n
n
n
n =
−
⋅
−
−
⋅
−
−
⋅ ⋅
1 3
2
5
4
3
4
1
2 2
… p
, if n is even
Case 2: if n is odd, then
In =
n
n
n
n
n
n
I
−
⋅
−
−
⋅
−
−
⋅ ⋅
1 3
2
5
4
4
5
2
3
1
…
But I x dx
1
0
2
= ∫sin
p
= −
[ ] = − −
⎡
⎣
⎢
⎤
⎦
⎥ = − − =
cos cos cos ( )
x 0
2
2
0 1 0 1 1
p
p
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 35 5/20/2016 10:09:43 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-542-2048.jpg)


![6.38 ■ Engineering Mathematics
Integrating by parts, we get
I x x n x x x x dx
n
n n
= − − − − −
− −
∫
cosec cosec cosec
2 3
2
( cot ) ( ) ( cot )( cot )
= − − −
− −
∫
cosec cosec
n n
x x n x x dx
2 2 2
2
cot ( ) cot
= − − − −
− −
∫
cosec cosec cosec
n n
x x n x x dx
2 2 2
2 1
cot ( ) ( )
= − − − + −
− −
∫ ∫
cosec cosec cosec
n n n
x x n x dx n x dx
2 2
2 2
cot ( ) ( )
= − − − + −
−
−
cosecn
n n
x x n I n I
2
2
2 2
cot ( ) ( )
⇒ ( ) cot ( )
1 2 2
2
2
+ − = − + −
−
−
n I x x n I
n
n
n
cosec
⇒ ( ) cot ( )
n I x x n I
n
n
n
− = − + −
−
−
1 2
2
2
cosec
[ I
x x
n
n
n
I
n
n
n
= −
−
+
−
−
−
−
cosec 2
2
1
2
1
cot
[ cot
cot
n
n
n
x dx
x x
n
n
n
I
∫ = −
−
+
−
−
−
−
cosec 2
2
1
2
1
WORKED EXAMPLES
EXAMPLE 1
Evaluate
x
ax x
dx
a 3
2
0
2
2 −
∫ .
Solution.
Let I
x
ax x
dx
a
=
−
∫
3
2
0
2
2
Put x a
= 2 2
sin u [ dx a d
= 4 sin cos
u u u
When x = = ⇒ =
0 0 0
, sinu u and when x a
= = ⇒ =
2 1
2
, sinu u
p
[ I
a a
a a a
d
=
−
∫
( sin ) sin cos
sin ( sin )
2 4
2 2 2
2 3
2 2 2
0
2
u u u
u u
u
p
?
/
= −
∫
32 2 1
4
7
2
0
2
a a
d
sin cos
sin sin
u u
u u
u
p/
= ∫
16 3
6
0
2
a d
sin cos
cos
u u
u
u
p/
= ∫
16 3 6
0
2
a d
sin
/
u u
p
= =
16
5
6
3
4
1
2 2
5
2
3 3
a a
? ? ?
p
p [{ n = 6 is even]
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 38 5/20/2016 10:09:54 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-545-2048.jpg)
![Integral Calculus ■ 6.39
EXAMPLE 2
Evaluate
dx
x
( )
.
1 2 8
0 +
∞
∫
Solution.
Let I
dx
x
=
+
∫ ( )
1 2 8
0
∞
Put x = tanu [ dx d
= sec2
u u
When x = = ⇒ =
0 0 0
, tanu u and when x = = ⇒ =
∞ ∞
,tanu u
p
2
[ I
d
= +
∫
sec
( tan )
/
2
2 8
0
2
1
u
u
u
p
= ∫
sec
sec
/ 2
16
0
2
u
u
u
p
d
= ∫ cos
/
14
0
2
u u
p
d = =
13
14
11
12
9
10
7
8
5
6
3
4
1
2 2
429
4090
? ? ? ? ? ? ?
p p
[{ n = 14 is even]
EXAMPLE 3
If I
t
t
dt
n
n
=
+
∫ ( )
1 2
, then show that I I
t
n
dt
n n
n
+
+
+ =
+
2
1
1
. Hence, evaluate I6.
Solution.
Given I
t
t
dt
n
n
=
+
∫ ( )
1 2
Put t x dt x dx
= ∴ =
tan sec2
[ I
x
x
x dx x dx
n
n
n
=
+
=
∫ ∫
tan
( tan )
sec tan
1 2
2
⇒ I
x
n
I
n
n
n
=
−
−
−
−
tan 1
2
1
[using reduction formula 6.4.2(a)]
⇒ I I
x
n
n n
n
+ =
−
−
−
2
1
1
tan
⇒ I I
t
n
n n
n
+ =
−
−
−
2
1
1
( )
1
Replacing n by n + 2 in ( ),
1 we get
I I
t
n
n n
n
+ + −
+ −
+ =
+ −
2 2 2
2 1
2 1
⇒ I I
t
n
n n
n
+
+
+ =
+
2
1
1
( )
2
To evaluate I6 . I
t
t
dt
6
6
2
1
=
+
∫
Put n = 6 in ( ),
1 we get
I I
t
6 4
5
5
+ = ⇒ I
t
I
6
5
4
5
= −
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 39 5/20/2016 10:10:00 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-546-2048.jpg)
![6.40 ■ Engineering Mathematics
= − −
⎡
⎣
⎢
⎤
⎦
⎥
t t
I
5 3
2
5 3
= − + = − + −
t t
I
t t
t I
5 3
2
5 3
0
5 3 5 3
.
But I x dx dx x t
0
0 1
= = = = −
∫
∫tan tan
[ I
t t
t t c
6
5 3
1
5 3
= − + − +
−
tan
EXAMPLE 4
If I xdx
n
n
= ∫ tan
/
0
4
p
, then prove that (1) ( )[ ]
n I I
n n
− + =
−
1 1
1 and (2) n I I
n n
[ ]
+ −
+ =
1 2 1.
Hence, evaluate I5.
Solution.
Given I x dx
n
n
= ∫ tan
/
0
4
p
1. To prove ( )[ ]
n I I
n n
2 1 5
2
1 1
1
By reduction formula 6.4.2 (a), we have
I
x
n
I
n n
=
−
⎡
⎣
⎢
⎤
⎦
⎥ −
−
−
tan 1
0
4
2
1
p
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥ −
− −
−
1
1 4
0
1 1
2
n
In
tan tan
p
=
−
− − −
1
1
1 0 2
n
In
( ) =
−
− −
1
1
2
n
In
⇒ I
n
I
n n
=
−
1
1
2
− − ( )
1
⇒ I I
n
n n
+ =
−
−2
1
1
⇒ ( )[ ]
n I I
n n
− + =
−
1 1
2 ( )
2
2. To prove n I I
n n
[ ]
1 2
1 5
1 1 1
The result ( )
1 is true for all n ≥ 2. Replacing n by ( )
n +1 in ( )
2 , we get
( )[ ]
n I I
n n
+ − + =
+ + −
1 1 1
1 1 2 ⇒ n I I
n n
[ ]
+ −
+ =
1 1 1
To find I5
I x dx
5
5
0
4
= ∫tan
p
Put n = 5 in ( )
1 , we get
I I
5 3
1
4
= − = − −
⎡
⎣
⎢
⎤
⎦
⎥
1
4
1
2
1
I = − +
1
4
1
I
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 40 5/20/2016 10:10:05 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-547-2048.jpg)
![Integral Calculus ■ 6.41
But I x dx x
1
0
4
0
4
= = [ ]
∫tan logsec
p
p
= −
⎡
⎣
⎢
⎤
⎦
⎥
logsec logsec
p
4
0
= − =
log log log
e e e
2 1
1
2
2
[ I e e
5
1
2
2
1
4
1
4
2 2 1
= − = −
[ ]
log log
EXAMPLE 5
If u x e dx
n
n x
a
= −
∫
0
, then prove that u n a u a n u
n n n
− + + − =
− −
( ) ( ) .
1 2
1 0
Solution.
Given u x e dx
n
n x
a
= −
∫
0
Take u x v e
n x
= = −
, . Integrating by parts, we get
u x
e
nx
e
dx
n
n
x a
n
x
a
=
−
⎡
⎣
⎢
⎤
⎦
⎥ −
−
−
−
−
∫
1 1
0
1
0
= − − +
− − −
∫
[ ]
a e n x e dx
n a n x
a
0 1
0
⇒ u a e nu
n
n a
n
= − +
−
−1
[ u a e n u
n
n a
n
−
− −
−
= − + −
1
1
2
1
( )
[ u n a u a e nu nu au
n n
n a
n n n
− + = − + − −
−
−
− − −
( ) 1 1 1 1
= − −
−
−
a e au
n a
n 1
= − − − + −
− − −
−
a e a a e n u
n a n a
n
[ ( ) ]
1
2
1
= − + − −
− −
−
a e a e a n u
n a n a
n
( )
1 2 = − − −
a n un
( )
1 2
[ u n a u a n u
n n n
− + + − =
− −
( ) ( )
1 2
1 0
EXAMPLE 6
If I x e dx
n
n x
= ∫ , then show that I nI x e
n n
n x
+ =
−1 . Hence, find I4 .
Solution.
Given I x e dx
n
n x
= ∫
Take u x v e
n x
= =
, . Integrating by parts, we get
I x e n x e dx
n
n x n x
= − ⋅ −
∫
1
= − −
∫
x e n x e dx
n x n x
1
⇒ I x e nI
n
n x
n
= − −1 ( )
1
⇒ I nI x e
n n
n x
+ =
−1
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 41 5/20/2016 10:10:10 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-548-2048.jpg)
![6.42 ■ Engineering Mathematics
To find I x e dx
x
4
4
= ∫
Put n = 4 in ( )
1 .
[ I x e I
x
4
4
3
4
= − = − −
x e x e I
x x
4 3
2
4 3
[ ]
= − +
x e x e I
x x
4 3
2
4 12
= − + −
x e x e x e I
x x x
4 3 2
1
4 12 2
[ ]
= − + −
x e x e x e I
x x x
4 3 2
1
4 12 24
= − + − −
x e x e x e xe I
x x x x
4 3 2
0
4 12 24[ ]
= − + − + ∫
x e x e x e xe e dx
x x x x x
4 3 2
4 12 24 24 [{ I e dx
x
0 = ∫ ]
= − + − +
x e x e x e xe e
x x x x x
4 3 2
4 12 24 24
= − + − +
e x x x x
x
[ ]
4 3 2
4 12 24 24
EXAMPLE 7
If u x x dx n
n
n
= ≥
∫ sin ( )
0
2
0
p
, then prove that u n n u n n
n n
n
+ − =
⎛
⎝
⎜
⎞
⎠
⎟ ≥
−
−
( ) , .
1
2
0
2
1
p
Hence, evaluate u2.
Solution.
Given u x x dx
n
n
= ∫ sin
0
2
p
Take u x v x
n
= =
, sin . Integrating by parts, we get
u x x nx x dx
n
n n
= −
( )
⎡
⎣ ⎤
⎦ − −
−
∫
cos ( cos )
0
2 1
0
2
p
p
= + −
∫
0 1
0
2
n x x dx
n
cos
p
= ⎡
⎣ ⎤
⎦ − −
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
− −
∫
n x x n x x dx
n n
1
0
2 2
0
2
1
sin ( ) sin
p
p
=
⎛
⎝
⎜
⎞
⎠
⎟ −
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
− −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
−
−
∫
n n n x x dx
n
n
p p
p
2 2
0 1
1
2
0
2
sin ( ) sin
⎥
⎥
⇒ u n n n u
n
n
n
=
⎛
⎝
⎜
⎞
⎠
⎟ − −
−
−
p
2
1
1
2
( )
⇒ u n n u n
n n
n
+ − =
⎛
⎝
⎜
⎞
⎠
⎟
−
−
( )
1
2
2
1
p
( )
1
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 42 5/20/2016 10:10:15 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-549-2048.jpg)
![Integral Calculus ■ 6.43
To find u2.
Put n = 2 in ( )
1 , then we get
u u
2 0
2 1
2 2 1 2
2
+ − = ⋅
⎛
⎝
⎜
⎞
⎠
⎟
−
( )
p
⇒ + =
u u
2 0
2 p
But u x dx x
0
0
2
0
2
0 1 1
= = −[ ] = − − =
∫sin cos ( )
p
p
[ u u
2 2
2 1 2
+ ⋅ = ⇒ = −
p p
EXAMPLE 8
If I d
n
n
= ∫u u u
p
sin
0
2
, then prove that I
n
n
I
n
n
n n
=
−
+ ≥
−
1 1
2
2 2
, . Hence, find I4.
Solution.
Given I d
n
n
= ∫u u u
p
sin ,
0
2
= −
∫u u u u
p
sin sin
n
d
2 2
0
2
= −
−
∫u u u u
p
(sin ) ( cos )
n
d
2 2
0
2
1
= −
− −
∫
∫u u u u u u u
p
p
(sin ) (sin ) cos
n n
d d
2 2
0
2
2
0
2
= −
−
−
∫
I d
n
n
2
2
0
2
u u u u u
p
cos [(sin ) cos ]
⇒ I I
n
n n
n n
= −
−
⎡
⎣
⎢
⎤
⎦
⎥ − − +
−
− −
2
1
0
2
1
u u
u
u u u
u
p
cos
(sin )
[ ( sin ) cos ]
(sin ) 1
1
0
2
1
n
d
−
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
∫ u
p
= − +
−
−
−
⎫
⎬
⎪
⎭
⎪
⎧
⎨
⎪
−
−
∫
∫
I
n
d
n
d
n
n n
2
1
0
2
0
2
0
1
1
1
1
u u u u u u
p
p
sin (sin ) cos
/
/
⎩
⎩
⎪
= −
−
+
−
⎡
⎣
⎢
⎤
⎦
⎥
−
I
n
I
n n
n n
n
2
0
2
1
1
1
1
sin u
p
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 43 5/20/2016 10:10:18 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-550-2048.jpg)

![Integral Calculus ■ 6.45
By reduction formula for cotn
x dx
∫ , we have
I
x
n
I
n
n
n
=
−
⎡
⎣
⎢
⎤
⎦
⎥ −
−
−
(cot )
/
/
1
4
2
2
1 p
p
=
−
−
− − −
1
1
0 1 2
n
In
[ ] [Refer page 6.36]
⇒ I
n
I n
n n
=
−
− ≥
−
1
1
2
2 , ( )
1
To find I4 . I x dx
4
4
4
2
= ∫cot
p
p
Put n = 4 in ( )
1 , then I I
4 2
1
3
= − = − − = − + + = − +
1
3
1 1
1
3
2
3
0 0 0
( )
I I I .
But I dx x
0
4
2
4
2
2 4 4
= = [ ] = − =
∫
p
p
p
p
p p p
.
[ I4
2
3 4
3 8
12
= − + =
−
p p
.
6.4.4 The Reduction Formula for sin cos
m n
x xdx
∫ , Where m n
, are Non-negative
Integers
Solution.
Let I x x dx
m n
m n
, sin cos
= ∫
= −
∫sin cos cos
m n
x x x dx
1
= −
∫cos (sin cos )
n m
x x x dx
1
Take u x v x x
n m n
= =
−
cos , sin cos
1
. Integrating by parts, we get
I x
x
m
n x x
x
m
dx
m n
n
m
n
m
, cos
sin
( )cos ( sin )
sin
=
+
− − −
+
−
+
−
+
∫
1
1
2
1
1
1
1
=
+
+
−
+
− +
−
∫
cos sin
sin sin cos
n m
m n
x x
m
n
m
x x x dx
1 1
2 2
1
1
1
=
+
+
−
+
−
− +
−
∫
cos sin
sin ( cos )cos
n m
m n
x x
m
n
m
x x x dx
1 1
2 2
1
1
1
1
=
+
+
−
+
−
−
+
− +
−
∫
∫
cos sin
sin cos sin cos
n m
m n m n
x x
m
n
m
x x dx
n
m
x x
1 1
2
1
1
1
1
1
d
dx
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 45 5/20/2016 10:10:26 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-552-2048.jpg)




![6.50 ■ Engineering Mathematics
⇒ I
x x
m
n
m
I
m n
m n
m n
, ,
(log )
=
+
−
+
+
−
1
1
1 1
(b) x mx dx
n
sin
∫
Solution.
Let I x mx dx
n
n
= ∫ sin
Take u x v mx
n
= =
, sin . Integrating by parts, we get
⇒
I x
mx
m
nx
mx
m
dx
x mx
m
n
m
x
n
n n
n
n
= ⋅ −
⎛
⎝
⎜
⎞
⎠
⎟ − −
⎛
⎝
⎜
⎞
⎠
⎟
= − +
−
−
∫
cos cos
cos
1
1
∫
∫
∫
= − + − −
⎡
⎣
⎢
⎤
⎦
⎥
− −
cos
cos sin
( )
sin
mxdx
x mx
m
n
m
x
mx
m
n x
mx
m
dx
n
n n
1 2
1 Ag
gain integrating by parts
[ ]
= − + −
−
−
x mx
m
n
m
x mx
n n
n
n
cos
sin
( )
2
1 1
m
m
x mxdx
I
x mx
m
n
m
x mx
n n
m
I
n
n
n
n
n
2
2
2
1
2 2
1
−
−
−
∫
= − + −
−
sin
cos
sin
( )
(c) x mx dx
n
cos
∫
Solution.
Let I x mx dx
n
n
= ∫ cos
Take u x v mx
n
= =
, cos . Integrating by parts, we get
⇒
I x
mx
m
nx
mx
m
dx
x mx
m
n
m
x mxdx
x
n
n n
n
n
n
= ⋅ −
= −
= −
−
−
∫
∫
sin sin
sin
sin
sin
1
1
m
mx
m
n
m
x
mx
m
n x
mx
m
dx
x mx
m
n n
n
−
−
− −
−
⎡
⎣
⎢
⎤
⎦
⎥
= −
− −
∫
1 2
1
( cos )
( )
( cos )
sin
+
+ −
−
= − +
− −
−
∫
n
m
x mx
n n
m
x mxdx
I
x mx
m
n
m
x
n n
n
n
n
2
1
2
2
2
1
1
cos
( )
cos
sin
cosm
mx
n n
m
In
−
−
−
( )
1
2 2
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 50 5/20/2016 10:10:44 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-557-2048.jpg)
![Integral Calculus ■ 6.51
6.4.6 The Reduction Formula for (a) e x dx
ax m
sin
∫ and (b) e x dx
ax n
cos
∫
(a) e x dx
ax n
sin
∫
Solution.
Let I e xdx xe dx
n
ax n n ax
= =
∫ ∫
sin sin
Take u x v e
n ax
= =
sin , . Integrating by parts, we get
I x
e
a
n x x
e
a
dx
e x
a
n
a
x xe
n
n
ax
n
ax
ax n
n
= −
= −
−
−
∫
∫
sin sin cos
sin
sin cos
1
1 a
ax
ax n
n
ax
n
dx
e x
a
n
a
x x
e
a
x x x n
= − − − + −
− −
sin
sin cos sin ( sin ) cos ( )
1 1
1 s
sin cos
sin
sin cos
n
ax
ax n
ax n
x x
e
a
dx
e x
a
n
a
e x x
−
−
⎡
⎣ ⎤
⎦
⎧
⎨
⎩
⎫
⎬
⎭
= − +
∫
2
2
1 n
n
a
x n x x e dx
e x
a
a x n
n n ax
ax n
2
2 2
1
2
1
− + −
⎡
⎣ ⎤
⎦
= −
−
−
∫ sin ( )sin cos
sin
sin c
cos sin ( )sin ( sin )
sin
x
n
a
x n x x e dx
e
n n ax
ax n
[ ]+ − + − −
⎡
⎣ ⎤
⎦
=
−
−
∫
2
2 2
1 1
1
1
2 2 2
2
1 1
1
x
a
a x n x
n
a
n xe dx
n n
a
e
n ax ax n
sin cos ( )sin
( )
sin
−
[ ]+ − − + +
− −
x
x dx
∫
∫
e x
a
a x n x
n
a
e x dx
n n
a
I
ax n
ax n
∫
= −
[ ]− +
−
−
sin
sin cos sin
( )
1
2
2
2 2
1
n
n
ax
n
n n
e
a
x a x n x
n
a
I
n n
a
I
−
−
−
= −
[ ]− +
−
2
2
1
2 2 2
1
sin sin cos
( )
⇒ 1
1
2
2
1
2 2 2
+
⎛
⎝
⎜
⎞
⎠
⎟ = −
[ ]+
−
−
−
n
a
I
e x
a
a x n x
n n
a
I
n
ax n
n
sin
sin cos
( )
⇒
n a
a
I
e x
a
a x n x
n n
a
I
n
ax n
n
2 2
2
1
2 2 2
1
+
⎛
⎝
⎜
⎞
⎠
⎟ = −
[ ]+
−
−
−
sin
sin cos
( )
⇒ I
e x
n a
a x n x
n n
n a
I
I
e
n
ax n
n
n
ax
=
+
−
[ ]+
−
+
=
−
−
sin
sin cos
( )
( )
sin
1
2 2 2 2 2
1
n
n
n
x
n a
a x n x
n n
n a
I
−
−
+
−
[ ]+
−
+
1
2 2 2 2 2
1
sin cos
( )
( )
(b) e xdx
ax n
cos
∫
Solution.
Let I e xdx
n
ax n
= ∫ cos = ∫cosn ax
xe dx
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 51 5/19/2016 4:54:07 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-558-2048.jpg)
![6.52 ■ Engineering Mathematics
Take u x v e
n ax
= =
cos , . Integrating by parts, we get
I x
e
a
n x x x
e
a
dx
e x
a
n
a
x
n
n
ax
n
ax
ax n
n
= − −
= +
−
−
∫
cos cos ( sin )
cos
cos si
1
1
n
n
cos
cos sin cos cos ( )co
xe dx
e x
a
n
a
x x
e
a
x x n
ax
ax n
n
ax
n
∫
= + ⋅ − + −
− −
1 1
1 s
s ( sin )sin
cos
cos
n
ax
ax n
ax n
x x x
e
a
dx
e x
a
n
a
e
−
−
−
⎡
⎣ ⎤
⎦
⎧
⎨
⎩
⎫
⎬
⎭
= +
∫
∫
2
2
1
x
x x
n
a
x n x x e dx
e x
a
a
n n ax
ax n
sin cos ( )cos sin
cos
c
− − −
⎡
⎣ ⎤
⎦
=
−
−
∫
2
2 2
1
2
1
o
os sin cos ( )cos ( cos )
c
x n x
n
a
x n x x e dx
e
n n ax
ax
+
[ ]− − − −
⎡
⎣ ⎤
⎦
=
−
∫
2
2 2
1 1
o
os
cos sin ( )cos ( )cos
n
n n ax
x
a
a x n x
n
a
n x n x e
−
−
+
[ ]− + − − −
⎡
⎣ ⎤
⎦
1
2 2
2
1 1 1 d
dx
e x
a
a x n x
n
a
e xdx
n n
a
e
ax n
ax n ax
∫
∫
= +
[ ]− +
−
−
cos
cos sin cos
( )
1
2
2
2 2
1
c
cosn
xdx
−
∫
2
⇒ I
e x
a
a x n x
n
a
I
n n
a
I
n
ax n
n n
= +
[ ]− +
−
−
−
cos
cos sin
( )
1
2
2
2 2 2
1
⇒ 1
1
2
2
1
2 2 2
+
⎛
⎝
⎜
⎞
⎠
⎟ = +
[ ]+
−
−
−
n
a
I
e x
a
a x n x
n n
a
I
n
ax n
n
cos
cos sin
( )
⇒
n a
a
I
e x
a
a x n x
n n
a
I
n
ax n
n
2 2
2
1
2 2 2
1
+
⎛
⎝
⎜
⎞
⎠
⎟ = +
[ ]+
−
−
−
cos
cos sin
( )
[ I
e x
n a
a x n x
n n
n a
I
n
ax n
n
=
+
+
[ ]+
−
+
−
−
cos
cos sin
( )
( )
1
2 2 2 2 2
1
[ e xdx
e x
n a
a x n x
n n
n a
I
ax n
ax n
n
cos
cos
cos sin
( )
( )
∫ =
+
+
[ ]+
−
+
−
−
1
2 2 2 2 2
1
6.4.7 The Reduction Formula for (a) cos sin
m
x n x dx
∫ and (b) cos cos
m
x nxdx
∫
Deduce if f m n x nx dx
m
( , ) cos cos ,
/
= ∫
0
2
p
then prove that f m n
m
m
f m n
( , ) ( , )
=
+
− −
1
1 1 and hence
prove that f n n n
( , ) = +
p
2 1
where m n
, are non-negative integers.
(a) cos sin
m
x nx dx
∫
Solution.
I x nxdx
m n
m
, cos sin
= ∫
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 52 5/19/2016 4:54:10 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-559-2048.jpg)
![Integral Calculus ■ 6.53
Take u x v nx
m
= =
cos , sin
Integrating by parts, we get
I x
nx
n
m x x
nx
n
dx
m n
m m
, cos
cos
cos ( sin )
cos
c
= −
⎛
⎝
⎜
⎞
⎠
⎟ − − −
⎛
⎝
⎜
⎞
⎠
⎟
= −
−
∫
1
o
os cos
cos cos sin
m
m
x nx
n
m
n
x nx xdx
− −
∫
1
Now sin( ) sin( )
n x nx x
− = −
1 = −
sin cos cos sin
nx x nx x
⇒ cos sin sin cos sin( )
nx x nx x n x
= − −1
[ I
x nx
n
m
n
x nx x n x dx
x
m n
m
m
m
,
cos cos
cos sin cos sin( )
cos
= − − − −
[ ]
= −
−
∫
1
1
c
cos
cos sin cos sin( )
nx
n
m
n
x nxdx
m
n
x n xdx
m m
− + −
∫ ∫
−1
1
⇒ I
x nx
n
m
n
I
m
n
I
m n
m
m n m n
, , ,
cos cos
= − − + − −
1 1
⇒ 1 1 1
+
⎛
⎝
⎜
⎞
⎠
⎟ = − + − −
m
n
I
x nx
n
m
n
I
m n
m
m n
, ,
cos cos
⇒
m n
n
I
x nx
n
m
n
I
m n
m
m n
+
= − + − −
, ,
cos cos
1 1
[ I
x nx
m n
m
m n
I
m n
m
m n
, ,
cos cos
= −
+
+
+
− −
1 1
[ cos sin
cos cos
,
m
m
m n
x nxdx
x nx
m n
m
m n
I
∫ = −
+
+
+
− −
1 1
(b) cos cos
m
x nxdx
∫
Solution.
Let I x nxdx
m n
m
, cos cos
= ∫
Take u x v nx
m
= =
cos , cos . Integrating by parts, we get
I
x nx
n
m x x
nx
n
dx
x nx
m n
m
m
m
,
cos sin
cos ( sin )
sin
cos sin
= − −
⎛
⎝
⎜
⎞
⎠
⎟
=
−
∫
1
n
n
m
n
x nx xdx
m
+ −
∫cos sin sin .
1
cos( ) cos( )
n x nx x
− = −
1 = +
cos cos sin sin
nx x nx x
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 53 5/19/2016 4:54:13 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-560-2048.jpg)
![6.54 ■ Engineering Mathematics
[ sin sin cos( ) cos cos
nx x n x nx x
= − −
1
[ I
x nx
n
m
n
x n x nx dx
x nx
n
m n
m
m
m
,
cos sin
cos cos( ) cos
cos sin
= + − −
[ ]
=
−
∫
1
1
+
+ − −
−
∫ ∫
m
n
x n xdx
m
n
x nxdx
m m
cos cos( ) cos cos
1
1
⇒ I
x nx
n
m
n
I
m
n
I
m n
m
m n m n
, , ,
cos sin
= + −
− −
1 1
⇒ 1 1 1
+
⎛
⎝
⎜
⎞
⎠
⎟ = + − −
m
n
I
x nx
n
m
n
I
m n
m
m n
, ,
cos sin
⇒
m n
n
I
x nx
n
m
n
I
m n
m
m n
+
⎛
⎝
⎜
⎞
⎠
⎟ = + − −
, ,
cos sin
1 1
[ I
x nx
m n
m
m n
I
m n
m
m n
, ,
cos sin
=
+
+
+
− −
1 1
Deduction:
Given f m n x nxdx
m
( , ) cos cos
/
= ∫
0
2
p
=
+
⎡
⎣
⎢
⎤
⎦
⎥ +
+
− −
= +
+
− −
cos sin
( , )
( , )
/
m
x nx
m n
m
m n
f m n
m
m n
f m n
0
2
1 1
0 1 1
p
[ f m n
m
m n
f m n
( , ) ( , )
=
+
− −
1 1
If m n
= , then f n n
n
n n
f n n
( , ) ( , )
=
+
− −
1 1
⇒ f n n f n n
f n n
f n n
f
( , ) ( , )
( , )
( , )
(
= − −
= ⋅ − −
= − −
= ⋅
1
2
1 1
1
2
1
2
2 2
1
2
2 2
1
2
1
2
2
2
n
n n
f n n
f n n
f
n
− −
= − −
= − −
=
3 3
1
2
3 3
1
2
4 4
1
2
0 0
3
4
, )
( , )
( , )
( , )
:
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 54 5/19/2016 4:54:16 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-561-2048.jpg)
![Integral Calculus ■ 6.55
But f x xdx
( , ) cos cos
/
0 0 0
0
0
2
= ∫
p
= = [ ] =
∫ dx x
0
2
0
2
2
p
p p
/
/
[ f n n n n
( , ) = ⋅ = +
1
2 2 2 1
p p
EXERCISE 6.4
1. Evaluate the following integrals
(a) sin
/
8
0
2
x dx
p
∫ (b) sin
/
7
0
2
x dx
p
∫ (c) sin cos
/
7 5
0
2
x x dx
p
∫ (d) sin cos
/
6 4
0
2
x x dx
p
∫
(e) sin cos
/
15 3
0
2
x x dx
p
∫ (f)
x
a x
dx
3
2 2 5
0 ( )
+
∞
∫
2. If I a x dx
n
n
a
= −
∫( )
2 2
0
where n is a positive integer, then prove that I
na
n
I
n n
=
+
−
2
2 1
2
1.
3. If I x x dx
n
n
= −
∫
2 3
0
1
1
( ) , prove that I
n
n
I
n n
=
+
−
1
1. Hence, find x x dx
2 3 7
0
1
1
( ) .
−
∫
4. If I x x dx
n
n
= ∫ cos ,
/
0
2
p
show that I n n I
n n
n
+ − =
⎛
⎝
⎜
⎞
⎠
⎟
−
( ) .
1
2
2
p
5. Obtain the reduction formula for I e x dx
n
x n
= −
∞
∫ sin
0
and show that ( ) ( ) .
1 1
2
2
+ = − −
n I n n I
n n
Hence, evaluate I4
.
ANSWERS TO EXERCISE 6.4
1. (a)
35
256
p
(b)
16
35
(c)
1
120
(d)
3
512
p
(e)
1
144
(f)
1
24 6
a
3.
1
24
5.
24
85
6.5 APPLICATION OF INTEGRAL CALCULUS
In this section, we deal with some of the important applications of Integral Calculus.
They are 1. Area of plane curves
2. Length of arc of plane curves
3. Volume of solids of revolution
4. Area of surface of revolution
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 55 5/19/2016 4:54:20 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-562-2048.jpg)
![6.56 ■ Engineering Mathematics
6.5.1 Area of Plane Curves
6.5.1 (a) Area of Plane Curves in Cartesian Coordinates
1. If f x
( ) is continuous, positive and bounded in
[ , ],
a b then f x dx
a
b
( )
∫ geometrically represents
the area bounded by the curve y f x
= ( ), the
x-axis and the abscissae x a
= and x b
=
∴ area A ydx f x dx
a
b
a
b
= =
∫ ∫ ( )
2. If y f x
= ( ) crosses the x-axis (as in Fig 6.2)
at x c
= in [ , ],
a b then the area is given by
= +
∫ ∫
A f x dx f x dx
a
c
c
b
( ) ( ) ,
Since f x dx
c
b
( ) ,
∫ 0 for area, we take the
absolute value.
3. If the area is bounded by the curve x g y
= ( ), the
y-axis and the ordinates y c y d
= =
, , then the
area
A xdy g y dy
c
d
c
d
= =
∫ ∫ ( )
4. Area bounded between two curves
If f x g x x a b
( ) ( ) [ , ],
≤ ∀ ∈ then the area
bounded between the curves y f x
= ( ) and
y g x
= ( ) in [ , ]
a b is
A g x f x dx
a
b
= −
[ ]
∫ ( ) ( )
x = a x = b
y = f(x)
y
O x
Fig. 6.1
O
y
x
x = b
y = a
y = f(x)
y = g(x)
Fig. 6.4
x = a
x = b
x = c
y = f(x)
O
y
x
Fig. 6.2
y
x
O
y = c
y = d
x = g(y)
Fig. 6.3
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 56 5/19/2016 4:54:24 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-563-2048.jpg)

![6.58 ■ Engineering Mathematics
∴ area A = ×
4 Area in the first quadrant
= = −
∫ ∫
4 4
0
2 3 2 3 3 2
0
ydx a x dx
a a
( )
/ / /
Put x a
= sin3
u ∴ =
dx a d
3 2
sin cos
u u u
When x = 0, sinu u
= ⇒ =
0 0 and
When x a
= , sinu u
p
= ⇒ =
1
2
∴ area A a a a d
= −
⎡
⎣ ⎤
⎦
∫
4 3
2 3 2 3 2
0
2 3 2
2
/ /
/ /
sin sin cos
u u u u
p
= −
=
∫
∫
12 1
12
2 2 3 2
0
2
2
2 3
0
2
2
a d
a d
( sin ) sin cos
cos sin cos
/
/
/
u u u u
u u u
p
p
u
u
u u u
p
= ∫
12 2 4
0
2
2
a d
cos sin
/
u u
p
=
−
+ ∫
12
2 1
4 2
2 4
0
2
a d
cos
/
p
p
Using reduction formula
4 is
[ ]
= ⋅ ⋅ ⋅ = =
12
6
3
4
1
2 2
3
8
2
2
a
a n
{ e
even
[ ]
EXAMPLE 3
Show that the area of the loop of the curve ay a x
2 2
( )
5 2
x is
8
15
2
a
.
Solution.
The given curve is ay x a x
2 2
= −
( ) ( )
1
To find the loop of the curve, first trace the curve.
Since the equation is of even degree in y, it is symmetric about the x-axis.
To find the intersection with the x-axis, put y = 0 in ( )
1
[ x a x x a
2
0 0 0
( ) , , .
− = ⇒ =
If x a y
, 2
is negative ⇒ y is imaginary. So, the curve does not exit beyond x a
= .
Tangents at the origin is obtained by equating the lowest degree terms to zero.
[ ay ax y x y x
2 2 2 2
0
− = ⇒ = ⇒ = ±
∴ the loop of the curve is a shown in Fig 6.7.
O
y
y′
x
x′ (a, 0)
(0, a)
(0, −a)
(−a, 0)
Fig. 6.6
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 58 5/19/2016 4:54:31 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-565-2048.jpg)

![6.60 ■ Engineering Mathematics
Put x a
= 2 2
sin u [ dx a d
= 4 sin cos
u u u
When x = = ⇒ =
0 0 0
, sinu u and when x a
= = ⇒ =
2 1
2
2
, sin u u
p
[ A a
a
a a
a d
=
−
∫
2 2
2
2 2
4
2
2
2
0
2
sin
sin
sin
sin cos
u
u
u
u u u
p
=
−
∫
16
1
2 3
2
0
2
a d
sin
sin cos
sin
u
u u
u
u
p
?
= ⋅
∫
16 2 4
0
2
a d
sin
cos
cos
u
u
u
u
p
= = ⋅ ⋅ ⋅ =
∫
16 16
3
4
1
2 2
3
2 4
0
2
2 2
a d a a
sin u u
p
p
p
.
EXAMPLE 5
Compute the area bounded by the curve y x x x
5 2 1 1
4 3 2
2 3 , the x 5 axis and the ordinates
corresponding to the points of minimum of the function.
Solution.
Given y x x x
= − + +
4 3 2
2 3 [
dy
dx
x x x
= − +
4 6 2
3 2
For maximum or minimum
dy
dx
= 0
⇒ x x x
− + =
4 6 2 0
3 2
⇒ 2 2 3 1 0
2
x x x
[ ]
− + = ⇒ 2 2 1 1 0
x x x
( )( )
− − = ⇒ =
x 0
1
2
1
, ,
Now
d y
dx
x x
2
2
2
12 12 2
= − +
When x
d y
dx
= =
0 2 0
2
2
, . [ y is minimum.
When x
d y
dx
= =
⎛
⎝
⎜
⎞
⎠
⎟ − + = − + = −
1
2
12
1
2
12
1
2
2 3 6 2 1 0
2
2
2
, ? ? [ y is maximun.
When x
d y
dx
= = − + =
1 12 1 12 1 2 2 0
2
2
, ? ? [ y is minimum
∴ the minimum points correspond to x = 0 and x = 1 and the curve is above the x-axis in this interval.
∴ required area is A ydx
= ∫
0
1
= − + +
= − + +
⎡
⎣
⎢
⎤
⎦
⎥ = − + + − =
∫( )
x x x dx
x x x
x
4 3 2
0
1
5 4 3
0
1
2 3
5
2
4 3
3
1
5
1
2
1
3
3 0
6 −
− + +
=
15 10 90
30
91
30
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 60 5/19/2016 4:54:40 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-567-2048.jpg)

![6.62 ■ Engineering Mathematics
= − − − + − + −
= × − × + × +
=
1
12
3 1
2
3
3 1
3
2
3 1 3 1
1
12
80
2
3
26
3
2
8 2
4 4 3 3 2 2
( ) ( ) ( ) ( )
2
20
3
52
3
14
20 52 42
3
10
3
− + =
− +
=
EXAMPLE 7
Find the area of the propeller shaded region enclosed by the curves x y
2 5
1 3
0 and x y
2 5
1 5
0.
Solution.
The given curves are
x y x y
− = ⇒ =
1 3 3
0 ( )
1
and x y x y
− = ⇒ =
1 5 5
0 ( )
2
To find the points of intersection solve ( )
1 and ( )
2
∴ x x x x
3 5 3 2
1 0
= ⇒ − =
( )
⇒ x 0 1 1
= − +
, ,
When x y x y
= − = − = =
1 1 1 1
, ,
and when
The curves are symmetric about the origin.
Area bounded by the curves is
A = 2[area in theIquadrant]
= −
( )
= −
⎡
⎣
⎢
⎤
⎦
⎥ = −
⎡
⎣
⎢
⎤
⎦
⎥ =
−
⎡
⎣
⎢
⎤
⎦
⎥ =
∫
2
2
4 6
2
1
4
1
6
2
3 2
12
2
1
3 5
0
1
4 6
x x dx
x x
1
12
1
6
⎛
⎝
⎜
⎞
⎠
⎟ =
EXAMPLE 8
Find the area between the curves y x x x
5 1 1 1
4 3
16 4 and y x x x
5 1 1 1
4 2
6 8 4 .
Solution.
Let f x x x x
( ) = + + +
4 3
16 4
g x x x x
( ) = + + +
4 2
6 8 4
Now f x g x x x x
( ) ( )
− = − +
3 2
6 8
The points of intersection of the two
curves is given by f x g x
( ) ( )
− = 0
⇒ x x x
3 2
6 8 0
− + =
O
(1, 1)
(1, 0)
(−1, −1)
(−1, 0)
y
x
Fig. 6.9
y
x
O
(0, 4)
x = 2 x = 4
Fig. 6.10
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 62 5/19/2016 4:54:48 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-569-2048.jpg)
![Integral Calculus ■ 6.63
⇒ x x x
( )
2
6 8 0
− + =
⇒ x x x
( )( )
+ − =
2 4 0
⇒ x = 0 2 4
, ,
When x = 0, y = 4.
In the interval [ , ]
0 4 , the curves intersect at x = 2.
Required area is A f x g x dx f x g x dx
= − + −
∫ ∫
( ( ) ( )) ( ( ) ( ))
0
2
2
4
Now f x g x dx x x x dx
( ) ( ) ( )
− = − +
∫ ∫
0
2
3 2
0
2
6 8
= − +
⎡
⎣
⎢
⎤
⎦
⎥ = − + = − + =
x x x
4 3 2
0
2 4
3 2
4
6
3
8
4
2
4
2 2 2 2 4 16 16 4
? ?
and ( ( ) ( )) ( )
f x g x dx x x x dx
− = − +
∫ ∫
2
4
3 2
2
4
6 8
= − +
⎡
⎣
⎢
⎤
⎦
⎥
= − − − + −
=
x x x
4 3 2
2
4
4 4 3 3 2 2
4
6
3
8
4
1
4
4 2 2 4 2 2 4 2
1
4
240
( ) ( ) ( )
( ) −
− + = − + = −
2 56 4 12 60 112 48 4
( ) ( )
∴ Area A = + − = + =
4 4 4 4 8.
EXAMPLE 9
Find the area bounded by y x x y x x y x x x
5 5 52 1 1
, [ , ], , [ , ] , [ , ]
∈ ∈ ∈
0 1 1 2 2 4 0 2
2 2
and .
Solution.
The given curves are y x x
= ∈
, [ , ]
0 1
⇒ y x x
2
0 1
= ∈
, [ , ] ( )
1
y x x
= ∈
2
1 2
, [ , ] ( )
2
and y x x
= − + +
2
2 4 ( )
3
= − − + = − − − + = − − +
( ) [( ) ] ( )
x x x x
2 2 2
2 4 1 1 4 1 5
⇒ y x
− = − −
5 1 2
( ) ,
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 63 5/19/2016 4:54:52 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-570-2048.jpg)
![6.64 ■ Engineering Mathematics
Which is a downward parabola with vertex
( , )
1 5 and axis x = 1 as in Fig 6.11.
[ area A y dx y dx y dx
= − −
∫ ∫ ∫
( ) ( )
( )
3
0
2
1
0
1
2
1
2
= − + + − −
∫ ∫ ∫
( )
x x dx xdx x dx
2
0
2
0
1
2
1
2
2 4
= − + +
⎡
⎣
⎢
⎤
⎦
⎥ −
⎡
⎣
⎢
⎤
⎦
⎥ −
⎡
⎣
⎢
⎤
⎦
⎥
x x
x
x x
3 2
0
2 3 2
0
1 3
1
2
3
2
2
4
3 2 3
= − + + ⋅ − − − − −
2
3
2 4 2 0
2
3
1 0
1
3
2 1
3
2 3 3
[ ] [ ]
= − + + − − = − + =
− +
=
8
3
4 8
2
3
7
3
17
3
12
17 36
3
19
3
EXAMPLE 10
For any real t x
e e
y
e e
t t t t
, ,
5
1
5
2
2 2
2 2
is a point on the hyperbola x y
2 2
1
2 5 . Show that the
area bounded by this hyperbola and the lines joining its centre to the points corresponding to
t t
1 1
and2 is t1
.
Solution.
The given equation of the hyperbola is
x y
2 2
1
− = ( )
1
Also given x
e e
y
e e
t R
t t t t
=
+
=
−
∈
− −
2 2
, ; ( )
2
[
e e e e
t t t t
+ −
⎛
⎝
⎜
⎞
⎠
⎟
− −
2 2
, are the coordinates of any
point on the rectangular hyperbola x y
2 2
1
− = .
Centre of the hyperbola is the origin O.
Let P be the point on the hyperbola corresponding
to the parameter t t
= 1.
[ P
e e e e
t t t t
=
+ −
⎛
⎝
⎜
⎞
⎠
⎟
− −
1 1 1 1
2 2
,
O
P
t1
X
Y
Q
R
A
Fig. 6.12
y2
= x
y2
= x
y = −x2
+ 2x + 4
x2
= y
x = 1 x = 2
(1, 5)
x
y
O
Fig. 6.11
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 64 5/19/2016 4:54:55 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-571-2048.jpg)
![Integral Calculus ■ 6.65
Let Q be the point on the curve corresponding to t t
= − 1.
[ Q
e e e e
t t t t
=
+ −
⎛
⎝
⎜
⎞
⎠
⎟
− −
1 1 1 1
2 2
, =
+
−
−
⎛
⎝
⎜
⎞
⎠
⎟
− −
e e e e
t t t t
1 1 1 1
2 2
,
[ P Q
and have same x-coordinates but y-coordinates have opposite signs.
Hence, Q is the image of Pin the x-axis and so PQ is perpendicular to the x-axis
Since the points P Q
and and the curve are symmetric about the x-axis, OP and OQ are symmetric
about the x-axis.
So, the area bounded by OP, OQ and the curve is = 2 (area above x-axis)
Let PQ cuts the x-axis at R.
[ the required area = 2[Areaof the right angled OPR area APR
Δ − ]
where area APR is the area bounded by the curve, the x-axis and the line PR.
Now area of ΔOPR OR PR
= ⋅
1
2
=
+
⋅
−
= −
− −
−
1
2 2 2
1
8
1 1 1 1
1 1
2 2
e e e e
e e
t t t t
t t
( )
and the area APR y
dx
dt
dt
t
= ∫
0
1
[ ]
{ t A
= 0correspondsto
Since y
e e
x
e e dx
dt
e e
t t t t t t
=
−
=
+
∴ =
−
− − −
2 2 2
and [ ]
{ t t P
= 1 correspondsto
[ area APR
e e e e
dt
t t
t t t
=
−
⋅
− −
∫ 2 2
0
1
−
= −
= + −
= +
−
−
⎡
⎣
−
−
−
∫
∫
1
4
1
4
2
1
4 2 2
2
2
0
2 2
0
2 2
1
1
( )
( )
e e dt
e e dt
e e
t
t t
t
t t
t
t t
⎢
⎢
⎤
⎦
⎥
0
1
t
= − − − −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥ = − −
−
−
1
4 2 2
2
1
2
1
2
0
1
8 2
2 2
1
2 2 1
1 1
1 1
e e
t e e
t
t t
t t
− ( )
∴ required area A = − − − −
⎧
⎨
⎩
⎫
⎬
⎭
⎡
⎣
⎢
⎤
⎦
⎥ =
⎛
⎝
⎜
⎞
⎠
⎟
− −
2
1
8
1
8 2
2
2
2 2 2 2 1 1
1 1 1 1
( ) ( )
e e e e
t t
t t t t
=
= t1.
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 65 5/19/2016 4:54:59 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-572-2048.jpg)
![6.66 ■ Engineering Mathematics
EXERCISE 6.5
1. Find the area bounded by the curve x y
+ = 1and the coordinate axes.
2. Find the area bounded by the parabola and its latus rectum.
3. Find the area bounded by the curve y x x
= −
3
4 and the x-axes.
4. Find the area of the curve y x x
2 4 2
9
= −
( ).
5. Find the area bounded by the curve and its asymptote
(i) y
x
x
2
3
2
=
−
(ii) y
a x
a x
2
2
=
−
(iii) xy a a x
2 2
= −
( )
6. Find the area of the loop of the curve
(i) a y x a x
2 2 3
= −
( ) (ii) 3 2 2
ay x x a
= −
( ) (iii) y
a a x
a x
2
2 2 2
2 2
=
−
+
( )
7. Find the area in the I quadrant bounded by y x
2
= , the x-axis and the line x y
− = 2.
8. Find the area bounded by y ax
2
4
= and x by
2
4
= .
9. Find the area bounded by the parabola y x
= 2
and the line 2 3 0
x y
− + = .
10. Show that the larger of the two areas into which the circle x y a
2 2 2
64
+ = is divided by the parabola
y ax
2
12
= is
16
3
8 3
2
a
( )
p − .
11. Find the area bounded by the parabola x y
= −2 2
, x y
= −
1 3 2
.
12. Find the area bounded by x y
2
4
= and y
x
=
+
8
4
2
.
13. Find the area of the region bounded by the parabola y x x
= − − +
2
2 3, the tangent at the point
P( , )
2 5
− on the curve and the y-axis.
14. Find the area of the loop of the curve y x
a x
a x
2 2
=
−
⎛
⎝
⎜
⎞
⎠
⎟
+
.
15. Find the area of the curve y x
= sin bounded by the x-axis (i) in [0, 2p] and (ii) in [−p, p].
16. Compute the area bounded by the curve by y x
= and y x
= 2
.
17. Find the area bounded by the curve x y
2
4
= and the straight line x y
= −
4 2.
18. Show that the parabola y x
2
= divides the circle x y
2 2
2
+ = into two portions whose area are in
the ratio ( ) : ( ).
9 2 3 2
p p
− +
19. Find the area bounded by one arch of the cycloid x a y a
= − = −
( sin ), ( cos )
u u u
1 and its base.
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 66 5/19/2016 4:55:05 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-573-2048.jpg)
![Integral Calculus ■ 6.67
ANSWERS TO EXERCISE 6.5
1.
1
6
2.
8
3
2
a 3. 8 4.
31
4
p
5. (i) 3p (ii) pa2
(iii) pa2
6. (i)
p
8
2
a (ii)
8 3
45
2
a (iii)
1
2
2 2
( )
p − a
7.
10
3
8.
16
3
ab
9.
32
3
11.
4
3
12. 2
4
3
p − 13.
8
3
14.
a2
2
4
( ).
p + 15. (i) 4, (ii) 4
16. 1
3
17. 9
8
6.5.1 (b) Area in Polar Coordinates
Formula: The area bounded by the curve r f
= ( )
u and the radius vectors u a u b
= =
and is
A r d
= ∫
1
2
2
u
a
b
.
Proof
Given r f
= ( )
u is the equation of the curve.
Let A B
and be two points on the curve with radii
vectors u a u b
= =
and
f ( )
u is continuous in [ , ]
a b
Let P r
( , )
u and Q r r
( , )
+ +
Δ Δ
u u be
neighbouring points on the curve.
Let ΔA be the element area of the strip OPQ.
Then Δ Δ
A r
=
1
2
2
u approximately.
∴ Δ Δ
A r
∑ ∑
=
1
2
2
u
The limit of ΔA
∑ as Δu → 0 is the area of OAB.
∴ area of the region OAB =
1
2
2
r du
a
b
∫ = ∫
1
2
2
r du
a
b
. ■
x
B
A
P (r, θ)
Q (r + Δr, θ + Δθ)
Δθ
β
α
O
Fig. 6.13
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 67 5/19/2016 4:55:12 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-574-2048.jpg)

![Integral Calculus ■ 6.69
To find the point of intersection, solve ( )
1 and ( )
2
∴ a a
( cos ) cos
1 2
+ =
u u ⇒ cosu u p
= =
1 0 2
⇒ or
When u
p
= = ⋅ =
3
2
1
2
, r a a [From (1)]
That is the circle lies inside the cardioid.
Required area A = Area of the cardioid − Area of the circle
Area of the cardioid =
3
2
2
pa
[by example 1]
Area of the circle = pa2
, since radius is a.
∴ required area = − =
3
2 2
2
2
2
p
p
p
a
a
a
.
EXAMPLE 3
Find the area of a loop of the curve r a
5 u
sin3 .
Solution.
Given the curve is r a
= sin3u
When u = =
0 0
, r
When u
p p
= = =
6 2
, sin
r a a, which is the
maximum value of r.
When u
p
p
= = =
3
0
, sin
r a
So, as u varies from 0 to
p
6
, x goes from 0 toA
and as u varies from
p
6
to
p
3
, x comes from A
to 0.
So, as u varies from 0
3
to
p
, we get a loop as
in Fig. 6.16.
Area of the loop = ∫
1
2
2
0
3
r du
p
= =
−
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
∫ ∫
1
2
3
2
1 6
2
4
6
6
2 2
0
3 2
0
3
2
a d
a
d
a
sin
cos
sin
u u
u
u
u
u
p p
− ⎥
⎥ = − −
⎡
⎣
⎢
⎤
⎦
⎥ =
0
3 2 2
4 3
2
6
0
12
p
p p p
a a
sin
x
y
A
θ = 0
O
θ =
2
π
θ =
3
π
θ =
6
π
60°
30°
Fig. 6.16
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 69 5/19/2016 4:55:25 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-576-2048.jpg)
![6.70 ■ Engineering Mathematics
EXAMPLE 4
Show that the area between the cardioids r a
5 1 u
( cos )
1 and r a
5 2 u
( cos )
1 is
( )
.
3 8
2
2
p 2
a
Solution.
The given equations of the two cardioids are
r a
= +
( cos )
1 u ( )
1
r a
= −
( cos )
1 u ( )
2
The area common to the cardioids is the two shaded regions as in Fig 6.17, which are equal in area,
because both the curves are symmetric about the initial line.
Common Area A = 2[area of the part above the line of OX ].
The two cardioids interact at u
p p
=
2
3
2
, . since a(1 − cosu) = a(1 + cosu) ⇒ cosu = 0 ⇒ u
p p
=
2
3
2
, .
But area of the loop above the line OX = ⋅ =
∫ ∫
2
1
2
2
0
2
2
0
2
r d r d
u u
p p
where r is from the cardioid ( )
2 .
Now r d a d
2
0
2
2 2
0
2
1
u u u
p p
∫ ∫
= −
( cos ) = − +
= − +
+
⎛
⎝
⎜
⎞
⎠
⎟
=
∫
∫
a d
a d
a
2 2
0
2
2
0
2
2
1 2
1 2
1 2
2
( cos cos )
cos
cos
u u u
u
u
u
p
p
3
3
2
2
2
2
3
2
2
2
4
0
2
2
0
2
− +
⎛
⎝
⎜
⎞
⎠
⎟
= − +
⎛
⎝
⎜
⎞
⎠
⎟
=
∫ cos
cos
sin
sin
u
u
u
u u
u
p
p
d
a
a2
2 2 2
3
2 2
2
2 4
0
3
4
2
3 8
4
⋅ − + −
⎛
⎝
⎜
⎞
⎠
⎟ = −
⎛
⎝
⎜
⎞
⎠
⎟ =
−
p p p p p
sin
sin ( )
a a
x
A
A′
(2a, 0)
(−2a, 0) r = 2a
r = a(1 − cos θ) r = a(1 + cos θ)
r = 2a
θ =
2
π
O
P
Fig. 6.17
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 70 5/19/2016 4:55:30 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-577-2048.jpg)
![Integral Calculus ■ 6.71
∴ area of the loop above the x-axis =
a2
3 8
4
( )
p −
∴ common Area A
a a
= × − = −
2
4
3 8
2
3 8
2 2
( ) ( )
p p .
EXAMPLE 5
Prove that the area of the loop of the curve x y axy
3 3
3
1 5 is
3
2
2
a
.
Solution.
The given curve is x y axy
3 3
3
+ = ( )
1
Transform ( )
1 to polar coordinates by putting x r
5 u
cos and y r
5 u
sin
∴ the equation ( )
1 becomes r r ar
3 3 3 3
3
cos sin cos sin
u u u u
+ =
⇒ r ar
3 3 3 2
3
(cos sin ) cos sin
u u u u
+ =
⇒ r a
(cos sin ) cos sin
3 3
3
u u u u
+ = ⇒ r
a
=
+
3
3 3
sin cos
cos sin
u u
u u
If r = 0, then cos sin
u u = 0 ⇒ = ⇒ = ⇒ =
sin
sin
2
2
0 2 0 2 0
u
u u u p
or 2 =
⇒ u u
p
= 0
2
or = , which are the limits for u.
As u varies from 0 to
p
2
, we get a loop of the curve, because r varies from 0 to 0.
For the figure, refer the Fig 3.32, page 3.133
∴ area of the loop is A r d
= ∫
1
2
2
0
2
u
p/
=
+
=
∫
1
2
9
9
2
2 2 2
3 3 2
0
2
2 2 2
6
a
d
a
sin cos
(cos sin )
sin cos
cos (
/
u u
u u
u
u u
u
p
1
1
9
2 1
3 2
0
2 2 2 2
3
0
2
+
=
+
∫ ∫
tan )
tan sec
( tan )
/ /
u
u
u u
u
u
p p
d
a
d
Put t = +
1 3
tan u ∴ dt d
= 3 2 2
tan sec
u u u ⇒ tan sec .
2 2 1
3
u u5
d dt
When u = = + ⇒ =
0 1 0 1
3
, tan
t t and when u
p p
= = + ⇒ =
2
1
2
3
, tan
t t ∞
∴ A
a
t
dt
= ∫
9
2
1
3
2
2
1
∞
= =
− +
⎡
⎣
⎢
⎤
⎦
⎥
= − ⎡
⎣ ⎤
⎦ = −
−
− +
−
∫
3
2
3
2 2 1
3
2
3
2
1
2
2
1
2 2 1
1
2
1
1
2
a
t dt
a t
a
t
a
t
∞ ∞
∞ ⎡
⎡
⎣
⎢
⎤
⎦
⎥ = − −
⎡
⎣
⎢
⎤
⎦
⎥ = − − =
1
2 2 2
3
2
1
1
3
2
0 1
3
2
∞
∞
a a a
[ ]
M06_ENGINEERING_MATHEMATICS-I _CH06_PART A.indd 71 6/3/2016 8:26:42 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-578-2048.jpg)


![6.74 ■ Engineering Mathematics
∴ s
x
dx
= +
∫ 1
9
4
0
1
= +
⎛
⎝
⎜
⎞
⎠
⎟
=
+
⎛
⎝
⎜
⎞
⎠
⎟
×
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
∫ 1
9
4
1
9
4
9
4
3
2
8
27
1 2
0
1
3 2
0
1
x
dx
x
/
/
1
1
9
4
1
8
27
13 13
8
1
1
27
13 13 8
3 2
+
⎛
⎝
⎜
⎞
⎠
⎟ −
⎡
⎣
⎢
⎤
⎦
⎥ = −
⎡
⎣
⎢
⎤
⎦
⎥ = −
/
[ ]
EXAMPLE 2
Find the length of one loop of the curve 3 2 2
ay x x a
5 2
( ) .
Solution.
Given 3 2 2
ay x x a
= −
( ) (1)
It is even degree in y and so symmetric about the
x-axis.
When y x x a x a a
= − = ⇒ =
0 0 0
2
, ( ) , ,
That is the curve meets the x-axis at x = 0 and
x = a two times
So, we get a loop between x = 0 and x = a as in
Fig 6.19.
Let A be the point (a, 0) on the x-axis
Length of the arc OA
ds
dx
dx
a
= ∫
0
∴ length of the loop = 2 × the length of arc OA
= = +
⎛
⎝
⎜
⎞
⎠
⎟
∫
∫
2 2 1
2
0
0
ds
dx
dx
dy
dx
a
a
dx
Differentiating (1) w.r.to x, we get
6 2 1
2 3
2
ay
dy
dx
x x a x a
x a x x a x a x a
= ⋅ − + − ⋅
= − + + − = − −
( ) ( )
( ) ( ) ( )( )
⇒
dy
dx
x a x a
ay
=
− −
( )( )
3
6
∴
dy
dx
x a x a
a y
⎛
⎝
⎜
⎞
⎠
⎟ =
− −
2 2 2
2 2
3
36
( ) ( )
=
− −
−
=
−
( ) ( )
( )
( )
x a x a
ax x a
x a
ax
2 2
2
2
3
12
3
12
∴ 1 1
3
12
12 3
12
2 2 2
+
⎛
⎝
⎜
⎞
⎠
⎟ = +
−
=
+ −
dy
dx
x a
ax
ax x a
ax
( ) ( )
{ ( )
( )
( )
ax b
ax b
a n
n
n
n
+ =
+
+
⎡
⎣
⎢
⎤
⎦
⎥
+
∫
1
1
1
if ≠ −
y
x
A
x = a
(a, 0)
O
Fig. 6.19
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 74 5/19/2016 3:09:31 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-581-2048.jpg)
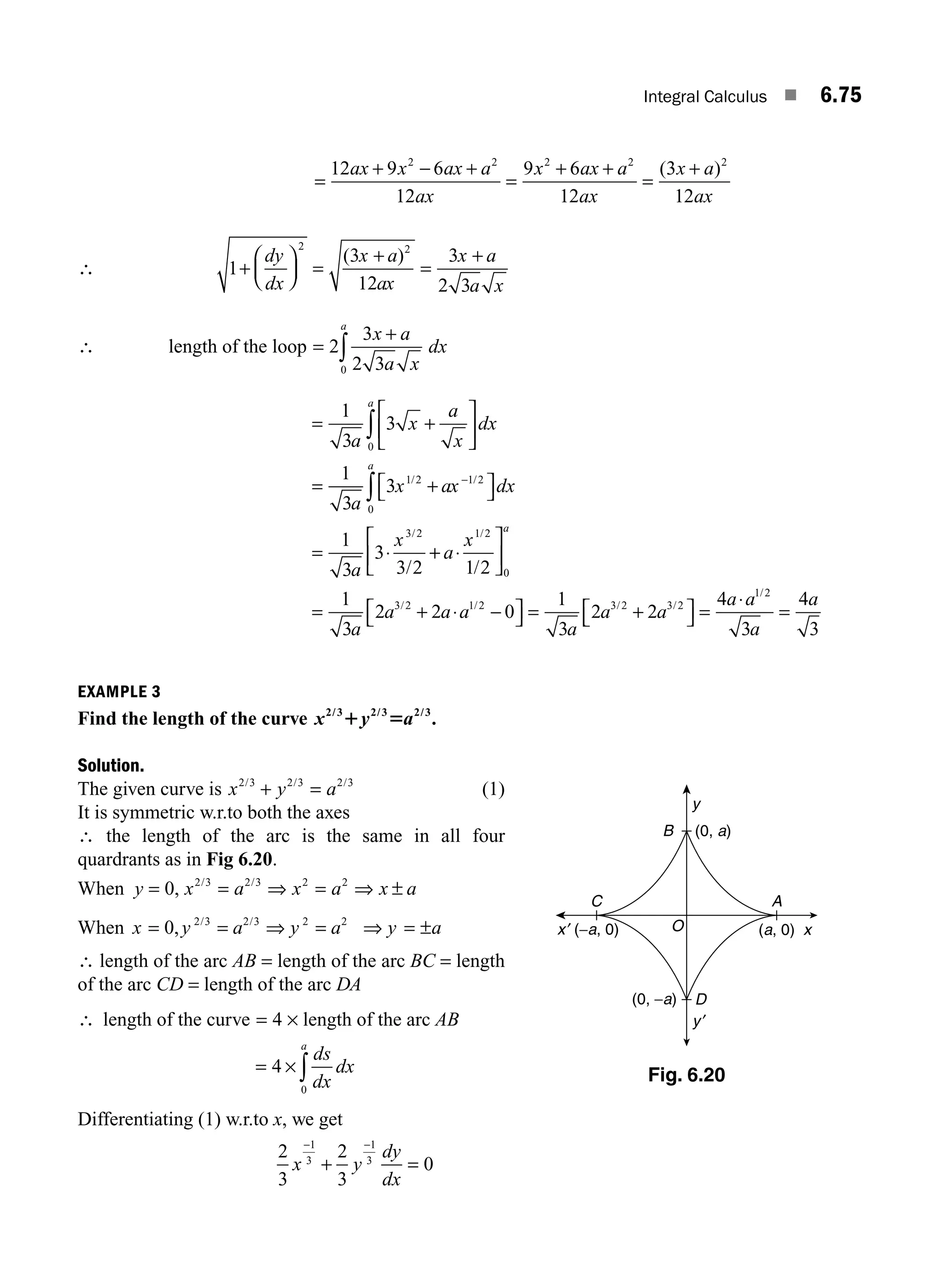
![6.76 ■ Engineering Mathematics
⇒ y
dy
dx
x
− −
= −
1 3 1 3
/ /
⇒
dy
dx
x
y
y
x
= − = −
−
−
+
1 3
1 3
1 3
1 3
/
/
/
/
∴
dy
dx
y
x
⎛
⎝
⎜
⎞
⎠
⎟ =
2 2 3
2 3
/
/
∴ 1 1
2 2 3
2 3
2 3 2 3
2 3
+
⎛
⎝
⎜
⎞
⎠
⎟ = + =
+
dy
dx
y
x
x y
x
/
/
/ /
/
2 3
2 3
=
a
x
/
/
[from (1)]
∴ 1
2 2 3
2 3
1 3
1 3
1 3 1 3
+
⎛
⎝
⎜
⎞
⎠
⎟ = = = −
dy
dx
a
x
a
x
a x
/
/
/
/
/ /
∴ length of the curve is s a x dx
a
= ∫
−
4 1 3
0
1 3
/ /
=
− +
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥ =
− +
4
1
3
1
4
2 3
6
1 3
1 3 1
0
1 3
2 3
0
1 3
a
x
a
x
a
a
a
/
/
/
/
/
/
(a
a a
2 3
0 6
/
)
− =
EXAMPLE 4
Find the length of the curve x a x a y
2 2 2 2 2
8
( )
2 5 .
Solution.
Given curve is x a x a y
2 2 2 2 2
8
( )
− = (1)
The equation of the curve is of even degree in x and y and so the curve is symmetric w.r.to both the
axes.
If y a x x x a a
= − = ⇒ = = −
0 0 0 0
2 2 2
, ( ) , ,
then x or
That is it meets the x-axis at the arigin x = 0 twice,
x = −a and x = a.
If x y
= = ±
0 0
, and if , 0
x a y
= =
∴ the curve passes through the origin and meets the
x-axis at the points A a
( , )
0 andB a
( , )
− 0 .
∴we get two loops of the curve as in Fig 6.21.
∴ total length of the curve is
s = 4 × length of the arc OA
4 4 1
0
2
0
ds
dx
dx
dy
dx
dx
a a
∫ ∫
= +
⎛
⎝
⎜
⎞
⎠
⎟
×
Differentiating (1) w.r.to x, we get
8 2 2 2
2 2 2 2
a y
dy
dx
x x a x x
= − + −
( ) ( )
= − + − = − + = −
2 2 2 4 2 2 2
3 2 3 3 2 2 2
x a x x x a x x a x
[ ]
y
x
O
A
B
(a, 0)
(−a, 0)
Fig. 6.21
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 76 5/19/2016 3:09:40 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-583-2048.jpg)
![Integral Calculus ■ 6.77
∴
dy
dx
x a x
a y
=
−
[ ]
2 2
2
2
8
∴
dy
dx
x a x
a y
⎛
⎝
⎜
⎞
⎠
⎟ =
−
2 2 2 2
2 2
2
8
[ ( )]
( )
=
−
x a x
a a y
2 2 2 2
2 2 2
2
8 8
( )
.
=
−
⋅ −
=
−
−
x a x
a x a x
a x
a a x
2 2 2 2
2 2 2 2
2 2 2
2 2 2
2
8
2
8
( )
( )
( )
( )
[from (1)]
∴ 1 1
2
8
2 2 2 2
2 2 2
+
⎛
⎝
⎜
⎞
⎠
⎟ = +
−
−
dy
dx
a x
a a x
( )
( )
=
− + −
−
8 2
8
2 2 2 2 2 2
2 2 2
a a x a x
a a x
( ) ( )
( )
=
− + − +
−
=
− +
−
8 8 4 4
8
9 12 4
8
4 2 2 4 2 2 4
2 2 2
4 2 2 4
2 2 2
a a x a a x x
a a x
a a x x
a a x
( )
( )
=
=
−
−
( )
( )
3 2
8
2 2 2
2 2 2
a x
a a x
∴ 1
3 2
8
3 2
2 2
2 2 2 2
2 2 2
2 2
2 2
+
⎛
⎝
⎜
⎞
⎠
⎟ =
−
−
=
−
−
dy
dx
a x
a a x
a x
a a x
( )
( )
∴ Length of the curve s
a x
a a x
dx
a
=
−
−
∫
4
3 2
2 2
2 2
2 2
0
=
− +
−
= − +
−
⎡
⎣
⎢
⎤
⎦
∫
∫ ∫
4
2
2 2
2
2
2 2 2
2 2
0
2 2
0
2
2 2
0
( )
a x a
a a x
dx
a
a x dx
a
a x
dx
a
a a
⎥
⎥
=
2
2
2 2
2 2 2
1
0
2 1
a
x a x a x
a
a
x
a
a
−
+
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
+
⎡
⎣
⎢
⎤
⎦
⎥
− −
sin sin
0
0
a
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
= + − + −
⎡
⎣ ⎤
⎦
= +
− − − −
2
0 1 0 1 0
2
2 2
2 1 1 2 1 1
2 2
a
a a
a
a a
(sin sin ) (sin sin )
. .
p p
⎡
⎡
⎣
⎢
⎤
⎦
⎥ = =
2
2
2
a
a a
. p p
EXAMPLE 5
Find the perimeter of the loop of the curve x t
5 2
and y t
t
5 −
3
3
.
Solution.
Given x t
= 2
and y t
t
= −
3
3
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 77 5/19/2016 3:09:44 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-584-2048.jpg)

![Integral Calculus ■ 6.79
2. Find the perimeter of the loop of the curves.
(i) 6 2
2 3
ay x x a
= −
( ) (ii) 9 2 5
2 3
xy x a x a
= − −
( )( )
3. Find the length of the curve x y
= − =
2 2 2 2
u u u
sin , sin as u varies from 0 2
to p.
4. Find the length of the curve x at t y at t
= =
2 2
cos , sin from the origin to the point t = 5.
5. Find the length of the curve x a y a
= + = −
(cos sin ), (sin cos )
u u u u u u from u = 0 to u
p
=
2
.
6. Prove that the length of parabola y2
= 4ax cut off by the latus rectum is 2 2 1 2
a[ log( )]
+ +
7. Find the length of one complete arch of the cycloid x a
= −
( sin )
u u and y a
= −
( cos )
1 u .
ANSWERS TO EXERCISE 6.7
1. (i)
22
3
(ii) 2 1 2
+ +
log( ) (iii)
15
16
2
+
⎛
⎝
⎜
⎞
⎠
⎟
log a
2. (i)
8
3
a
(ii) 4 3
a 3. 8 4.
19
3
a
5.
p2
8
a
7. 8a
6.5.2 (b) Length of the Arc in Polar Coordinates
Let r f
= ( )
u be the equation of the curve. Let A and B be two points on the curve with vectorial angles
a and b. Then the length of the arc AB is s
ds
d
d
= ∫ u
u
a
b
.
We know the differential arc in polars is
( ) ( ) ( )
ds r d dr
2 2 2 2
= +
u
∴
ds
d
r
dr
d
u u
⎛
⎝
⎜
⎞
⎠
⎟ = +
⎛
⎝
⎜
⎞
⎠
⎟
2
2
2
⇒
ds
d
r
dr
d
u u
= +
⎛
⎝
⎜
⎞
⎠
⎟
2
2
∴ s r
dr
d
d
= +
⎛
⎝
⎜
⎞
⎠
⎟
∫
2
2
u
u
a
b
When the limits for r are given, the arc length is s
ds
dr
dr
r
r
= ∫
1
2
= +
⎛
⎝
⎜
⎞
⎠
⎟
∫ 1 2
2
1
2
r
d
dr
dr
r
r
u
.
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 79 5/19/2016 3:09:57 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-586-2048.jpg)

![Integral Calculus ■ 6.81
EXAMPLE 2
Prove that the length of the equiangular spiral r ae
5 u a
cot
between the points with radii vectors
r1
and r2
is r r
1 2
2 a
sec .
Solution.
The equation of the given curve is r = aeu cota
(1)
Since the limits for r are given, the length of the arc is s
ds
dr
dr
r
r
= ∫
1
2
∴ s r
d
dr
dr
r
r
= +
⎛
⎝
⎜
⎞
⎠
⎟
∫ 1 2
2
1
2
u
Differentiating (1) w.r.to u, we get
dr
d
ae
u
a
u a
= cot
cot
⇒
d
ae
u
a
u a
dr
=
1
cot
.cot
=
1
r cot a
∴ r
d
dr
u
a
a
= =
1
cot
tan ⇒ r
d
dr
2
2
2
u
a
⎛
⎝
⎜
⎞
⎠
⎟ = tan
∴ 1 1
2
2
2 2
+
⎛
⎝
⎜
⎞
⎠
⎟ = + =
r
d
d
u
a a
r
tan sec
⇒ 1 2
2
2
+
⎛
⎝
⎜
⎞
⎠
⎟ = =
r
d
dr
u
a a
sec sec
∴ s dr
r
r
= ∫seca
1
2
= sec [ ]
a r r
r
1
2
⇒ s r r
= −
sec [ ]
a 2 1 if r r
2 1
Note: If r r
2 1
, s r r
= 2 1
− seca, since s is positive.
EXERCISE 6.8
1. Find the perimeter of the cardioid r = +
5 1
( cos )
u .
2. Find the length of the parabola r a
( cos )
1 2
+ =
u cut off by its latus rectum.
3. Find the perimeter of the curve r a
= sin3
3
u
.
4. Find the perimeter of the curve r a
= +
(cos sin )
u u 0 ≤ ≤
u p.
ANSWERS TO EXERCISE 6.8
1. 40 2. 2 2 1 2
a + +
⎡
⎣
⎤
⎦
log( ) 3.
3
2
pa
4. 2pa
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 81 5/19/2016 3:10:08 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-588-2048.jpg)
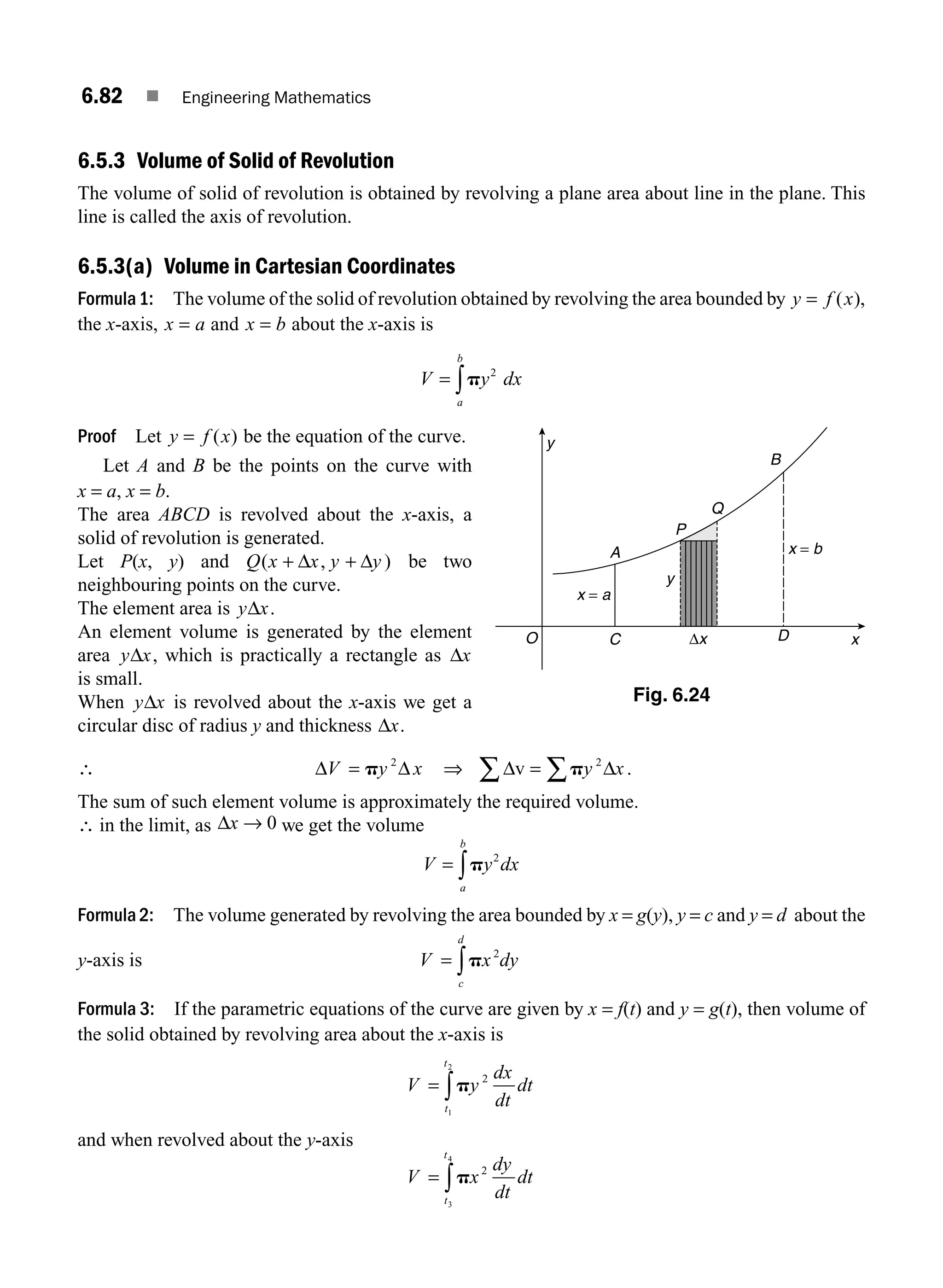
![Integral Calculus ■ 6.83
Formula 4: If f x f x x a b
2 1
( ) ( ) [ , ]
∀ ∈ and the area
bounded by the curves y f x y f x
= =
1 2
( ), ( )
and x = a, x = b (that is area ABCD) is revolved
about the x-axis, the volume of the solid
generated is
V y dx
a
b
= −
∫p(y 2
2
1
2
)
where y f x y f x
1 1 2 2
= =
( ), ( ).
Similarly, the area bounded by the
x g y x h y
= =
( ), ( ) and y c y d
= =
, is revolved
about the y-axis, the volume of the solid generated is
V x dy
c
d
= −
∫p(x2
2
1
2
)
where x1
= g(y) and x2
= h(y)
Formula 5: Solid of revolution about any
line L in the xy plane.
Let y f x
= ( ) be the equation of curve.
The given line L is in the xy plane is taken as the
x-axis.
Let A and B be two points on the curve. Draw AC and BD perpendicular to the line L.
When the area ACDB as in Fig 6.27 is revolved
about the line L, we get the required volume of solid of
revolution.
Let PQNM be the element area perpendicular to CD.
When the element area is revolved about the line L,
we get a circular disc of height PM and width MN.
The element volume ΔV is the volume of the circular
disc
∴ ΔV = p( ) .( )
PM MN
2
The limit of the sum of such element volume is the
volume of the solid of revolution.
∴ Volume V PM d OM
= ∫ p( ) ( )
2
OC
OD
.
WORKED EXAMPLES
EXAMPLE 1
Find the volume of the solid generated by revolving the ellipse
x
a
y
b
a b
2
2
2
2
1
1 5 , be the major
axis.
Solution.
The equation of the ellipse is
x
a
y
b
2
2
2
2
1
+ = (1)
C
D
x
M
N
y
A
P
Q
B
L
y = f(x)
O
Fig. 6.27
y
A B
D
C
x
x = b
y = f1(x)
y = f2(x)
x = b
x = a
x = a
O
Fig. 6.25
Fig. 6.26
y
x
y = c
y
y = d
x = h(y)
x = g(y)
O
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 83 5/19/2016 3:10:20 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-590-2048.jpg)
![6.84 ■ Engineering Mathematics
The x-axis is the major axis.
The ellipse meets the x-axis at x = −a, a.
∴ Volume V y dx
a
a
= ∫ p
−
2
Now
y
b
x
a
y
b
a
a x
2
2
2
2
2
2
2
2 2
1
= ⇒ = −
− ( )
∴ V
b
a
a x dx
a
a
= −
∫
p
2
2
2 2
−
( )
= −
∫
2
2
2
0
2 2
p
b
a
a x dx
a
( ) [{ a x
2 2
= is even function]
=
⎡
⎣
⎢
⎤
⎦
⎥
2
3
2
2
2
3
0
p
b
a
a x
x
a
− = −
⎡
⎣
⎢
⎤
⎦
⎥ = =
2
3
2
2
3
4
3
2
2
2
2 2
2
3
2
p p p
b
a
a a
a b
a
a
ab
. .
Note If revolved about the minor axis (y-axis), Volume =
4
3
2
pa b
EXAMPLE 2
A sphere of radius a is divided into two parts by a plane at a distance
a
2
from the centre. Show
that the ratio of the volume of two parts is 5:27.
Solution.
A sphere of radius a is obtained by revolving the
semi-circular area of radius a as in figure about the
x-axis.
The sphere is cut off by a plane at a distance
a
2
from
the centre (0,0) means the area of the semi-circle is cut
off by the line x
a
=
2
Let V1 andV2 be the two volumes generated by the two
areas A1
and A2
.
Equation of the circle is x y a
2 2 2
+ = ( )
1
[ Volume V1 is generated by the area bounded the portion of the circle ( )
1 and the lines
x
a
=
2
, x = a.
[ Volume V y dx
a
a
1
2
2
= ∫ p = −
∫
p ( )
a x dx
a
a
2 2
2
= −
⎡
⎣
⎢
⎤
⎦
⎥
p a x
x
a
a
2
3
2
3
y
x = a x
(0, 0)
O
A2
A1
x =
2
a
Fig. 6.29
O
y
x
A′ A
(−a, 0) (a, 0)
Fig. 6.28
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 84 5/19/2016 3:10:27 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-591-2048.jpg)

![6.86 ■ Engineering Mathematics
Note Sometimes the spherical cap formula is given in
terms of base radius of the cap and its height h.
If we assume the base radius of the spherical
cap is c. i.e., AC = c
Then OC2
= OA2
+ AC2
= − +
( )
a h c
2 2
⇒ a a ah h c
2 2 2 2
2
= − + +
⇒ 2
2
2 2
2 2
ah h c a
h c
h
= + ⇒ =
+
∴ Volume of the cap =
+
−
⎡
⎣
⎢
⎤
⎦
⎥
ph h c
h
h
2 2 2
3
3
2
( )
= + − = +
p p
h
h
h c h
h
h c
2
2 2 2 2 2
6
3 3 2
6
3
[ ] [ ]
EXAMPLE 4
The area bounded by one arch of the cycloid x a y a
5 u 2 u 5 2 u
( ), ( cos )
sin 1 and its base is
revolved about its base. Find the volume generated.
Solution.
The parametric equations of the cycloid are x a y a
= = −
( ), ( cos )
u u u
− sin 1
The base is the x-axis.
The curve meets the x-axis y = 0 ∴ cosu = 1 ⇒ u = 0, 2p
The volume of the solid generated by revolving the area bounded by one arch of the given curve and
its base (x-axis) about the x-axis is
V y
dx
d
d y
dx
d
d
= ∫
∫ p
u
u p
u
u
p
p
2 2
0
0
2
=
We have
x a
= −
( sin )
u u ∴
dx
d
a
u
u
= −
( cos )
1
∴ V a a d
= −
∫
p u u u
p
2 2
0
2
1 1
( ) ( cos )
− cos
= −
∫
p u u
p
a3 3
0
2
1
( )
cos d =
⎛
⎝
⎜
⎞
⎠
⎟
∫
p
u
u
p
a3 2
3
0
2
2
2
sin d =
⎛
⎝
⎜
⎞
⎠
⎟
∫
8
2
3 6
0
2
p
u
u
p
a sin d
Put t =
u
2
∴ du
1
2
= dt ⇒ d dt
u = 2
When u = =
0 0
, t and when u p p
= =
2 , t
y
x
A
(a − h, 0)
B (a, 0)
O h
a−h
c
a
C
Fig. 6.31
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 86 5/19/2016 3:10:39 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-593-2048.jpg)

![6.88 ■ Engineering Mathematics
= + −
⎡
⎣
⎢
⎤
⎦
⎥
2p 16 4
1
16
4
5
2
4
3
5 3
× . .
= + −
⎡
⎣
⎢
⎤
⎦
⎥ =
+ −
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟ =
2p p p
× 4 1
1
5
2
3
128
15 3 10
15
128
8
15
1024
3 p
p
15
EXAMPLE 6
Find the volume generated when the area bounded by the parabolas y x
2
4
5 2 and y x
2
4 4
5 2
revolves
1. about the common axis of the two curves
2. about the y-axis.
Solution.
The given parabolae are
y x x
2
4 4
= − = − −
( ) (1)
and y x x
2
4 4 4 1
= − = − −
( ) (2)
For the first parabola, the x-axis is the axis and
the vertex is (4, 0).
For the second parabola, the axis is the x-axis
and the vertex is (1, 0).
∴ the common axis is the x-axis.
To find the point of intersection, solve (1) and (2).
∴ 4 4 4 3 0 0
− = − ⇒ = ⇒ =
x x x x
When x = 0, y y
2
4 2
= ⇒ ± .
∴ the points of intersection are (0, 2), (0, −2).
The common area is as shown in the Fig 6.33.
The volume of the solid generated by revolving the common area about the x-axis is the same as
the volume of the solid generated by revolving the area above the x-axis, about the x-axis.
∴ required volume V y dx y dx
= − ∫
∫p p
1
2
2
2
0
1
0
4
, where y x y
1
2
2
2
4 4
= = − 4
− , x
= − − −
∫
∫
p p
( ) ( )
4 4 4
0
1
0
4
x dx x dx
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥ −
−
−
⎡
⎣
⎢
⎤
⎦
⎥
p p
( ) ( )
4
2
4
1
2
2
0
4 2
0
1
x x
= − − − − + − − −
p
p
2
4 4 4 0 2 1 1 1 0
2 2 2 2
[( ) ( ) ] [( ) ( ) ]
= ×
− − + − = − = − =
p
p
p
p p p p
2
0 16 2 0 1
2
16 2 8 2 6
[ ] [ ]
y
x
B
O
C
A
(0, 2)
(0, −2)
(4, 0)
(1, 0)
Fig. 6.33
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 88 5/19/2016 3:10:48 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-595-2048.jpg)

![6.90 ■ Engineering Mathematics
5. The area bounded by the portion of the curve y e x
x
= sin between x = 0 and x = p, revolves about
the x-axis. Find the volume generated.
6. Find the volume of the solid generated by revolving the area of the curve y x
= 3
, y = 0 and x = 2.
7. Find the volume of the solid obtained by revolving the area of the curve y
ax x
a
2
3 4
2
=
−
about the
x-axis.
8. The volume of the solid generated by revolving the area bounded by y x a a
( )
2 2 3
+ = and its
asymptote about the asymptote.
9. The area bounded by y ax
2
4
= and x ay
2
4
= , a 0, revolves about the x-axis. Show that the
volume of the solid formed is V =
96
5
2
pa
.
10. Compute the volume of the solid generated by revolving about the y-axis, the area bounded by
y x
= 2
and 8 2
x y
= .
11. Find the volume of the solid generated when the area of the loop of the curve y x x
2 2
2 1
= −
( )
resolves about the x-axis.
12. Find the volume of a right circular cone of base radius r and height h by integration.
13. When the area of the curve x y a
2 3 2 3 2 3
/
+ =
/ /
in the first quadrant is revolved about the x-axis, find
the volume of the solid generated.
14. Find the volume of the solid generated by revolving the loop of the curve 3 2 2
ay x x a
= −
( ) , about
the x-axis.
15. Find the volume of the solid generated by revolving the catenary y a
x
a
= cosh about the x-axis
between x = 0 and x = b.
16. A bowl has a shape that can be generated by revolving the graph y
x
=
2
2
between y = 0 and y = 5
about the y-axis. Find the volume of bowl.
17. Find the volume of the frustrum of a right circular cone whose lower base has radius R, upper
base is of radius r and height h.
18. If the curve ( )
a x y a x
− 2 2
= revolved about its asymptote, find the volume formed.
19. The area bounded by y x
2
4
= and the line x = 4 above the x-axis is revolved about the x-axis. Find
the volume of the solid generated.
20. Find the volume of the solid if the area included between the curve xy a a x
2 2
= −
( ) and its
asymptote is revolved about the asymptote.
ANSWERS TO EXERCISE 6.9
1.
pa3
15
2.
891
1280
p
3.
64
3
p
4. p 2 2
4
3
log −
⎡
⎣
⎢
⎤
⎦
⎥ 5.
p p
8
1
2
e −
⎡
⎣ ⎤
⎦
6.
64
5
p
7.
pa3
20
8.
p2 2
2
a
9.
96
5
2
pa
10.
24
5
p
11.
p
48
12. pr h
2
. 13.
16
105
3
pa
14.
pa3
36
15. = − +
−
p p
a3
2 2
2
8 2
[ ]
/ /
e e
a b
b a b a
16. 25p 17.
ph
R rh r
3
2 2
[ ]
+ + 18.
p2 3
2
a
19. 32p 20.
p2 3
2
a
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 90 5/19/2016 3:11:03 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-597-2048.jpg)

![6.92 ■ Engineering Mathematics
=
⎡
⎣
⎢
⎤
⎦
⎥
32
3
2
1 2 8
3
0
p u
p
a sin /
( / )
s
×
{ sin
sin
( )
n
n
a a
a
a n
u u u
u
cos d =
+
⎡
⎣
⎢
⎤
⎦
⎥
+
∫
1
1
= −
⎡
⎣
⎢
⎤
⎦
⎥ = − =
8
3 2
0
8
3
1 0
8
3
3 3 3
p p p p
a a a
sin sin [ ]
8 8
EXAMPLE 2
Show that the volume of the solid generated by revolving the lemniscate r a
2 2
2
5 u
cos about the
line u 5
p
2
is 2
8
3
pa
.
Solution.
Given r a
2 2
2
= cos u (1)
Required volume is V r d
= ∫
2
3
3
p
u u
a
b
cos
since the area is revolved about the line u
p
=
⎡
⎣
⎢
⎤
⎦
⎥
2
If we replace r by −r, then
( ) cos cos
− = ⇒ =
r a r a
2 2 2 2
2 2
u u
∴ the equation is unaffected.
When u is changed to −u, the equation is unaffected,
since cos(−2u) = cos 2u.
∴ the curve is symmetric about the initial line and pole respectively.
When r = = ⇒ = ⇒ =
0 2 0 2
2 4
, cos u u
p
u
p
When r a
= = ⇒ = ⇒ =
, cos2 1 2 0 0
u u u
When r a
= − = ⇒ = ⇒ =
, cos2 1 2 0 0
u u u
We get two loops of the curve as in Fig 6.36.
The volume of the solid generated by revolving the area of the lemniscate about the line u
p
=
2
is
equal to 2 times the volume generated by the area above Ox of one loop of the curve revolving about
the line u
p
=
2
.
∴ required volume is V r d
= ∫
2
2
3
3
0
4
×
p
u u
p
cos
Now r a r a r a
2 2 1 2 3 3 3 2
2 2 2
= ⇒ = ⇒ =
cos (cos ) (cos )
/ /
u u u
∴ V a d
= ∫
2
2
3
2
3 3 2
0
×
p
u u u
p
(cos ) cos
/
= −
∫
4
3
1 2
3
2 3 2
0
2
p
u u u
p
a
d
( sin ) cos
/
y
x
θ =
4
π
−
θ =
2
π
θ =
4
π
Fig. 6.36
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 92 5/19/2016 3:16:21 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-599-2048.jpg)


![Integral Calculus ■ 6.95
It is symmetric about the y-axis. Let the line y =
3
2
intersect the parabola at the points A and B
∴the portion of the curve Cut off by the line y =
3
2
is the
arc AOB as in figure.
The surface obtained by revolving arc AOB about the
y-axis, is the same as the surface obtained by revolving
arc OA about the y-axis.
∴ the surface area generated is
S x
ds
dy
dy x
dx
dy
dy
= = +
⎛
⎝
⎜
⎞
⎠
⎟
∫ ∫
2 2 1
0
3 2
0
3 2 2
p p
/ /
we have y
x
=
2
2
∴
dy
dx
x
x
= =
2
2
∴
dx
dy x
dx
dy x
= ⇒
⎛
⎝
⎜
⎞
⎠
⎟ =
1 1
2
2
∴ 1 1
1 1
2
2
2
2
+
⎛
⎝
⎜
⎞
⎠
⎟ = + =
+
dx
dy x
x
x
∴ 1
1 1
2 2
2
2
+
⎛
⎝
⎜
⎞
⎠
⎟ =
+
=
+
dx
dy
x
x
x
x
∴ S x
x
x
dy
=
+
∫
2
1
0
3 2 2
p
/
= +
=
+
⋅
⎡
⎣
⎢
⎤
⎦
⎥
∫
2 2 1
2
2 1
2 3 2
0
3 2
3 2
0
3 2
p
p
y dy
y
/
/ /
( )
( / )
[{ x2
= 2y]
= ⋅ +
⎛
⎝
⎜
⎞
⎠
2
3
2
3
2
1
p
⎟
⎟ − ⋅ +
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
= − = − = −
3 2
3 2
2 3 2 3
2 0 1
2
3
2 1
2
3
2 1
2
3
8 1
/
/
/
( )
[( ) ] [ ] ( )
p p p
=
=
14
3
p
EXAMPLE 2
Find the surface area formed by revolving four-cusped hypocycloid (astroid) x y a
2 3 2 3 2 3
/ / /
1 5
about the x-axis.
Solution.
The given curve is
x y a
2 3 2 3 2 3
/ / /
+ = (1)
The curve is symmetric w.r.to both the axes.
Let x-axis meets the curve at the points A and C and the y-axis meets the curve at B and D
y
x
A
B
x
y = 3/2
O
Fig. 6.38
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 95 5/19/2016 3:16:37 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-602-2048.jpg)
![6.96 ■ Engineering Mathematics
When y x a x a x a
= = ⇒ = ⇒ = ±
0 2 3 2 3 2 2
, / /
∴ A is ( , ),
a C
0 is ( , ).
−a 0
Similarly, B is ( , )
0 a and D is ( , )
0 − a
By symmetry the four arcs AB, BC, CD and DA
are equal.
[ the surface area generated by revolving the
curve about the x-axis is equal to twice the surface
area generated by the arc AB about the x-axis. x varies from 0 to a.
[ Surface area S y
ds
dx
dx
a
= × ∫
2 2
0
p = +
⎛
⎝
⎜
⎞
⎠
⎟
∫
4 1
0
2
p y
dy
dx
dx
a
Differentiating (1) w.r.to x, we get
2
3
2
3
0
1 3 1 3
x y
dy
dx
− −
+ =
/ /
⇒ x y
dy
dx
− −
+ =
1 3 1 3
0
/ /
⇒
dy
dx
x
y
y
x
= − = −
−
−
1 3
1 3
1 3
1 3
/
/
/
/
∴
dy
dx
y
x
⎛
⎝
⎜
⎞
⎠
⎟ =
2 2 3
2 3
/
/
∴ 1 1
2 2 3
2 3
+
⎛
⎝
⎜
⎞
⎠
⎟ = +
dy
dx
y
x
/
/
=
+
=
x y
x
a
x
2 3 2 3
2 3
2 3
2 3
/ /
/
/
/
[ ( )]
Using 1
∴ 1
2 2 3
2 3
1 2 1 3
1 3
+
⎛
⎝
⎜
⎞
⎠
⎟ =
⎡
⎣
⎢
⎤
⎦
⎥ =
dy
dx
a
x
a
x
/
/
/ /
/
We have
x y a
2 3 2 3 2 3
/ / /
+ = ⇒ y a x
2 3 2 3 2 3
/ / /
= − ⇒ y a x
= −
( )
/ / /
2 3 2 3 3 2
[ S a x
a
x
dx
a
= − ⋅
∫
4 2 3 2 3 3 2
1 3
1 3
0
p ( )
/ / /
/
/
= − ⋅
∫
4
1
1 3 2 3 2 3 3 2
0
1 3
pa a x
x
dx
a
/ / / /
/
( )
Let t a x
2 2 3 2 3
= −
/ /
[ 2
2
3
2
3
1
2
3
1
1
3
tdt x dx
x
dx
= − = −
−
−
⇒ tdt
x
dx
= −
−
1
3
1
1
3
⇒ − =
3
1
1
3
tdt dx
x
−
When x = 0, t a t a
2 2 3 1 3
= ⇒ =
/ /
and when x = a, t a a
= − =
2 3 2 3
0
/ /
[ S a t tdt
a
= −
∫
4 3
1 3 2 3 2
0
1 3
p / /
( ) ( )
/
= −
=
=
⎡
⎣
⎢
⎤
⎦
⎥
∫
∫
12
12
12
5
1 3 4
0
1 3 4
0
1 3
5
0
1 3
1 3
1
p
p
p
a t dt
a t dt
a
t
a
a
a
/
/
/
/
/
/3
3
12
5
0
12
5
12
5
1 3
1 3 5 1 3 5 3 2
= −
⎡
⎣
⎢
⎤
⎦
⎥ =
⋅
=
p
p p
a
a a a a
/
/ / /
( )
O
y
y′
x
x′ (a, 0)
B(0, a)
D(0, −a)
A
C
(−a, 0)
Fig. 6.39
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 96 5/19/2016 3:16:50 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-603-2048.jpg)
![Integral Calculus ■ 6.97
EXAMPLE 3
Find the surface generated by revolving the portion of the curve y x
2
4
5 1 cut off by the straight
line x 5 2, about the x-axis.
Solution.
The given curve is y x
2
4
= + (1)
is a parabola with vertex ( , ).
−4 0
It is symmetric about the x-axis. Let A be the vertex.
∴ A is ( , ).
−4 0
Let the straight line x = 2 intersect the parabola at
the points B B
, .
′
The straight line x = 2 meets the x-axis at ( , ).
2 0
The required surface area generated by revolving
the arc AB about the x-axis.
x varies from −4 to 2.
∴ Surface area is S y
ds
dx
dx y
dy
dx
dx
= = +
⎛
⎝
⎜
⎞
⎠
⎟
− −
∫ ∫
2 2 1
4
2 2
4
2
p p
Differentiating (1) w.r.to x, we get
2 1
1
2
1
4
2
2
y
dy
dx
dy
dx y
dy
dx y
= ⇒ = ⇒
⎛
⎝
⎜
⎞
⎠
⎟ =
∴ 1 1
1
4
4 1
4
2
2
2
2
+
⎛
⎝
⎜
⎞
⎠
⎟ = + =
+
dy
dx y
y
y
∴ 1
4 1
2
2 2
+
⎛
⎝
⎜
⎞
⎠
⎟ =
+
dy
dx
y
y
∴ S y
y
y
dx
=
+
−
∫
2
4 1
2
2
4
2
p = +
= + +
= +
=
+
−
−
−
+
∫
∫
∫
p
p
p
p
4 1
4 4 1
4 17
4 17
2
4
2
4
2
4
2
1 2 1
y dx
x dx
x dx
x
( )
( )( / )
4
4 12 1
4 17
4 3 2
6
4 2 1
4
2
3 2
4
2
(( / ) )
( )
( / )
[(
/
+
⎡
⎣
⎢
⎤
⎦
⎥
=
+
×
⎡
⎣
⎢
⎤
⎦
⎥
= ⋅ +
−
−
p
p
x
7
7 4 4 17
6
25 1
6
5 1
6
5 1
3 2 3 2
3 2 2 3 2
3
) ( ( ) ) ]
[( ) ] [( ) ]
[ ]
/ /
/ /
− − +
= − = −
= −
p p
p
=
= − = × =
p p p
6
125 1
6
124
62
3
[ ]
y
A
(−4, 0)
(2, 0)
x
O
y′ B′
B
x′
Fig. 6.40
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 97 5/19/2016 3:16:57 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-604-2048.jpg)


![6.100 ■ Engineering Mathematics
6.5.4 (b) Surface Area in Polar Coordinates
Let r f
= ( )
u be the equation of the curve.
Let A and B be two points on the curve with vectorial
angles a and b.
1. If the arc AB is revolved about the initial line
u = 0 (i.e., the x-axis) then the surface is generated.
The area of the surface is S y ds
= ∫2p with
limits for s.
∴ S y
ds
d
d
= ∫2p
u
u
a
b
= ∫2p u
u
u
a
b
r
ds
d
d
sin = +
⎛
⎝
⎜
⎞
⎠
⎟
∫2 2
2
p u
u
u
a
b
r r
dr
d
d
sin [ sin ]
{ y r
= u
2. If the arc AB is revolved about the line u
p
=
2
(i.e., about the y-axis, then a surface is generated)
The area of the surface is
S xds
= ∫2p within suitable limits
= ∫2p
u
u
a
b
x
ds
d
d = +
⎛
⎝
⎜
⎞
⎠
⎟
∫2 2
2
p u
u
u
a
b
r r
dr
d
d
cos [ cos ]
{ x r
= u
WORKED EXAMPLES
EXAMPLE 1
Find the area of the surface formed by revolving the lemniscate r a
2 2
2
5 u
cos about the polar
axis (polar axis is the initial line).
Solution.
Given the curve
r a r a
2 2
2 2
= ⇒ =
cos cos
u u
⇒
cos2 0
2
2
2
4 4
u
p
u
p
p
u
p
≥ ⇒ − ≤ ≤
− ≤ ≤
and
3
2
2
5
2
3
4
5
4
p
u
p p
u
p
≤ ≤ ⇒ ≤ ≤
The curve is symmetric about the initial line
A
B
O x
y
θ = 0
r = f(θ)
α
β
θ =
2
π
Fig. 6.42
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 100 5/19/2016 3:17:17 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-607-2048.jpg)
![Integral Calculus ■ 6.101
When u = 0, r a
= ± and when u
p
= =
2
0 0
, ,
r
We get the two loops of the curve as in Fig 6.43.
The required surface area is
S = area of the surface generated by revolving the two
loops about the initial line.
= 2[area of the surface generated by revolving the
arc OA] [{ the curve is symmetric]
= = +
⎛
⎝
⎜
⎞
⎠
⎟
∫ ∫
2 2 4
0
4
2
2
0
4
p
u
u p u
u
u
p p
y
ds
d
d r r
dr
d
d
/ /
sin
We have r a
= cos2u
∴
dr
d
a
u u
u
= −
1
2 2
2 2
cos
( sin )⋅ = −
asin
cos
2
2
u
u
∴
dr
d
a
u
u
u
⎛
⎝
⎜
⎞
⎠
⎟ =
2 2 2
2
2
sin
cos
∴ r
dr
d
a
a
2
2
2
2 2
2
2
2
+
⎛
⎝
⎜
⎞
⎠
⎟ = +
u
u
u
u
cos
sin
cos
=
+
=
+
⎡
⎣ ⎤
⎦ =
a a a a
2 2 2 2 2 2 2 2
2 2
2
2 2
2 2
cos sin
cos
cos sin
cos cos
u u
u
u u
u u
∴ r
dr
d
a
2
2
2
+
⎛
⎝
⎜
⎞
⎠
⎟ =
u u
cos
∴ S a
a
d
= ∫
4 2
2
0
4
p u u
u
u
p
cos sin
cos
/
= = −
∫
4 4
2
0
4
2
0
4
p u u p u
p
p
a d a
sin [ cos ]
/
/
= − −
⎡
⎣
⎢
⎤
⎦
⎥
= − −
⎡
⎣
⎢
⎤
⎦
⎥ = − −
⎡
⎣
⎢
⎤
⎦
⎥ = −
4
4
0
4
1
2
1 4
2
2
1 4
2
2 2
p
p
p p p
a
a a
cos cos
a
a a
2 2
2 2
2
2 2 2
−
⎡
⎣
⎢
⎤
⎦
⎥ = −
⎡
⎣
⎤
⎦
p
EXAMPLE 2
Find the area of the surface generated by revolving one branch of the lemniscates r a
5 u
cos 2
about the tangent at the origin.
y
O
x
θ =
2
π
θ =
4
π
A(a, 0)
B(−a, 0)
Fig. 6.43
M06_ENGINEERING_MATHEMATICS-I _CH06_PART B.indd 101 5/19/2016 3:17:24 PM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-608-2048.jpg)





![7.1 IMPROPER INTEGRALS
The definite integral f x dx
a
b
( )
∫ is defined as the limit of a sum under two conditions (i) the interval
[a, b] is of finite length and (ii) f is defined and bounded on [a, b]. Then f x dx
a
b
( )
∫ is called a proper
integral.
But there are many practical problems where f is unbounded on [a, b] or the interval is not finite.
Such integrals are known as improper integrals.
For example:
dx
x
dx
x
e x dx
x
, ,
0
1
2
0
2
1
∫ ∫ ∫
+
∞
−
−∞
∞
are improper integrals.
7.1.1 Kinds of Improper Integrals and Their Convergence
(a) Improper integrals of the first kind
If f is continuous and the interval is infinite, then the infinite integrals f x dx
a
( ) ,
∞
∫ f x dx
b
( ) ,
−∞
∫ f x
( )
−∞
∞
∫ dx
are called improper integrals of the first kind.
1. We define f x dx f x dx
a
b
a
b
( ) lim ( )
∞
→∞
∫ ∫
=
if (i) the proper integral f x dx
a
b
( )
∫ exists for every b a
(ii) the limit lim ( )
b
a
b
f x
→∞ ∫ exists with value equal to A, where A is finite.
Then f x dx
a
( )
∞
∫ is said to converge to A.
A is called the value of the integral and we write f x dx A
a
( ) .
∞
∫ =
Otherwise, f x dx
a
( )
∞
∫ is said to diverge.
2. We define f x dx f x dx
b
a
a
b
( ) lim ( )
−∞
→−∞
∫ ∫
=
if (i) the proper integral f x dx
a
b
( )
∫ exists for every a b
7
Improper Integrals
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 1 5/12/2016 9:52:30 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-614-2048.jpg)
![7.2 ■ Engineering Mathematics
(ii) the limit lim ( )
a
a
b
f x dx
→−∞ ∫ exists with value equal to B, where B is finite
Then f x dx
b
( )
−∞
∫ is said to converge to B.
B is called the value of the integral and we write f x dx B
b
( ) .
−∞
∫ =
Otherwise, f x dx
b
( )
−∞
∫ is said to diverge.
3. We define
f x dx f x dx f x dx
c
c
( ) ( ) ( )
−∞
∞
−∞
∞
∫ ∫ ∫
= + for some c,
if both the integrals on the R.H.S converge.
Then f x dx
( )
2∞
∞
∫ is said to converge to the sum of the values.
The integral f x dx
( )
−∞
∞
∫ is said to diverge if at least one of the integrals on the R.H.S diverges.
Note The integral f x dx
a
b
( )
∫ for every b ≥ a is analogus to “partial sum” in infinite series and so it may
be considered as “partial integral”.
(b) Improper integrals of the second kind
If the interval [a, b] is finite and f is unbounded at one or more points on [a, b], then f x dx
a
b
( )
∫ is called
an improper integral of the second kind.
1. If f is unbounded at a only (i.e., f has an infinite discontinuity at a), then we define
f x dx f x dx b a
a
b
a
b
( ) lim ( ) ,
∫ ∫
= ∈ −
∈→ +
+∈
0
0 ,
if (i) the proper integral f x dx
a
b
( )
+∈
∫ exists
(ii) the limit exists and is equal to A.
Then the integral f x dx
a
b
( )
∫ is said to converge to A.
A is called the value of the integral and we write f x dx A
a
b
( ) .
∫ =
Otherwise, f x dx
a
b
( )
∫ is said to diverge.
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 2 5/12/2016 9:52:36 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-615-2048.jpg)

![7.4 ■ Engineering Mathematics
WORKED EXAMPLES
Problems based on improper integral of the first kind
EXAMPLE 1
Evaluate the improper integral
dx
x
1 2
0 1
,
∞
∫ if it exists.
Solution.
Let I
dx
x
=
+
∞
∫1 2
0
=
+
→∞ ∫
lim
b
b
dx
x
1 2
0
=
= − = − = −
−
− − − −
lim[tan ]
lim[tan tan ] tan tan
b
b
b
x
b
→∞
→∞
∞
1
0
1 1 1 1
0 0
2
0
p
=
=
p
2
EXAMPLE 2
Evaluate
1
2
1 x
dx
∞
∫ if it exists.
Solution.
Let I
x
dx
=
∞
∫
1
2
1
=
→∞ ∫
lim
b
b
x
dx
1
2
1
=
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
→∞
→∞ →∞
lim
lim lim
b
b
b
b
b
x
x b
−
−
− − +
2 1
1
1
2 1
1 1
1
+
+
⎦
⎦
⎥ =
∞
⎡
⎣
⎢
⎤
⎦
⎥ =
− +
1
1 1
EXAMPLE 3
Evaluate xe dx
x
2
2
2
∞
∞
∫ if it exists.
Solution.
Let I xe dx xe dx xe dx I I
x x x
= = + = +
−
−∞
∞
−
−∞
−
∞
∫ ∫ ∫
2 2 2
0
0
1 2
where I xe dx xe dx
x
a
x
a
1
0 0
2 2
= =
−
−∞
→−∞
−
∫ ∫
lim
Put t = x2
∴ dt = 2xdx ⇒ xdx dt
=
1
2
When x = a, t = a2
and when x t
= =
0 0
,
∴ I e
dt
a
t
a
1
0
2
2
= ⋅
→−∞
−
∫
lim =
⎡
⎣
⎢
⎤
⎦
⎥ =
= =
1
2 1
1
2
1
2
1
1
2
2
0
0
lim lim [ ]
[ ]
a
t
a
a
a
e
e e
e
→−∞
−
→−∞
−
−∞
−
− −
− − −
2
2
1 0
1
2
[ ]
− −
=
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 4 5/12/2016 9:52:47 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-617-2048.jpg)
![Improper Integrals ■ 7.5
and I xe dx
x
2
0
2
= −
∞
∫ =
→∞
−
∫
lim
a
x
a
xe dx
2
0
=
→∞
−
∫
lim
a
t
a
e dt
1
2
0
2
=
⎡
⎣
⎢
⎤
⎦
⎥
= = = −
1
2 1
1
2
1
2
1
1
2
0
0
2
2
lim
lim [ ] [ ] [
a
t a
a
a
e
e e e
→∞
−
→∞
− −∞
−
− − − − 0
0 1
1
2
− =
]
∴ I xe dx
x
= = − + =
−
−∞
∞
∫
2 1
2
1
2
0
EXAMPLE 4
Evaluate
dx
a x
2 2
0
0
1
∞
∫
, a , if it exists.
Solution.
Let I
dx
a x
dx
a x
a
x
a
c
c
c
c
=
+
=
+
=
⎡
⎣
⎢
⎤
⎦
⎥
∞
→∞
→∞
∫ ∫
2 2
0
2 2
0
1
0
1
lim
lim tan−
=
⎡
⎣
⎢
⎤
⎦
⎥ = [ ] = =
lim tan tan tan
c a
c
a a a a
→∞
− − −
− ∞ − .
1
0
1
0
1
2 2
1 1 1 p p
EXAMPLE 5
Evaluate x xdx
sin ,
2∞
∫
0
if it exists.
Solution.
Let I x xdx
=
−∞
∫ sin
0
=
→−∞ ∫
lim sin
a
a
x xdx
0
=
=
lim [ ( cos ) ( sin )] [
lim
a
a
a
x x x
→ −∞
→
− − − 0
by Bernoulli’s formula,
−
−∞
→ −∞
−
− −
[ cos sin ] , sin ]
lim ( cos sin )
x x x u x v x
a a a
a
a
+ = =
= +
0
0
Here
[
[ ]= −
→ −∞
lim [ cos sin ]
a
a a a
But sin a and cos a oscillate finitely between −1 and +1.
Since a cos a → ∞ as a → ∞, limit is −∞
∴ the integral I x xdx
=
−∞
∫ sin
0
diverges to −∞.
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 5 5/12/2016 9:52:52 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-618-2048.jpg)
![7.6 ■ Engineering Mathematics
EXAMPLE 6
Evaluate
dx
x x
e
e (log )
,
3
∞
∫ if convergent.
Solution.
Let I
dx
x x
e
e
=
∞
∫ (log )3
=
→∞ ∫
lim
(log )
a
e
e
a
dx
x x 3
Put t = loge
x ∴ dt
x
dx
=
1
When x = e, t = loge
e = 1 and when x = a, t = loge
a
∴ I
dt
t
a
a
e
=
→∞ ∫
lim
log
3
1
=
→∞
−
∫
lim ( )
log
a
a
t dt
e
3
1
=
=
lim
lim
lim
log
log
a
a
a
a
a
t
t
e
e
→∞
→∞
→
−
−
−
−
⎡
⎣
⎢
⎤
⎦
⎥
⎡
⎣
⎢
⎤
⎦
⎥
=
2
1
2
1
2
1
2
1
1
2 ∞
∞
− −
∞
− − −
1
1
1
2
1
1
1
2
0 1
1
2
2
(log )
[ ]
e a
⎡
⎣
⎢
⎤
⎦
⎥ =
⎡
⎣
⎢
⎤
⎦
⎥ = =
EXAMPLE 7
Evaluate e xdx
x
2
sin ,
0
∞
∫ if it exists.
Solution.
Let I e xdx
x
= −
∞
∫ sin
0
=
→∞
−
∫
lim sin
b
x
b
e xdx
0
=
⎡
⎣
⎢
⎤
⎦
⎥
= +
lim ( sin cos )
lim [ (sin cos )]
b
x b
b
x
e
x x
e x x
→∞
−
→∞
−
− −
−
2
1
2
0
0
b
b
b
b
e b b e
e
= + +
= = =
− −
− − − −
→∞
−
−∞
1
2
0 1
1
2
1
1
2
0 1
1
0
lim [ (sin cos ) ( )]
[ ] [ ]
2
2
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 6 5/12/2016 9:52:57 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-619-2048.jpg)
![Improper Integrals ■ 7.7
EXAMPLE 8
Prove that
dx
x
a p
p
a
, ,
0 0
∞
∫ is convergent if p 1 and divergent if p ≤ 1.
Solution.
Let I
dx
x
x dx a p
p b
p
a
b
a
= =
→∞
−
∞
∫
∫ lim , ,
0 0
=
−
=
−
−
→∞
−
→∞
−
lim lim
b
p
a
b
b
p p
x
p
b a
p
+ − + +
+
⎡
⎣
⎢
⎤
⎦
⎥
+
⎡
⎣
⎢
⎤
⎦
⎥
1 1 1
1 1
If p 1,then −p + 1 0. ∴ as b → ∞, b−p + 1
→ 0
∴ I
a
p
a
p
p p
=
−
− +
= −
−
− + −
0
1 1
1 1
if p 0
If p 1, then −p + 1 0. ∴ as b → ∞, b−p + 1
→ ∞
∴ I = ∞ if p 1
When p = 1, I
x
dx
b
a
b
=
→∞ ∫
lim
1
=
= − = − =
∞
lim log
lim[log log ] log
b
e a
b
b
x
b a a
→
→∞
[ ]
∞ ∞
∴ I is convergent if p 1 and divergent if 0 1
≤
p
That is
dx
x p
a
∞
∫ is convergent if p 1 and divergent if 0 1
≤
p .
Note
1
2
1 x
dx
∞
∫ is convergent, since p =
2 1.
EXAMPLE 9
Evaluate
x
x x
dx
1
2 1
3
1 1
2
2 ( )( )
.
∞
∫
Solution.
Let I
x
x x
dx
=
+
− +
∞
∫
3
1 1
2
2 ( )( )
=
+
− +
→∞ ∫
lim
( )( )
b
b
x
x x
dx
3
1 1
2
2
Let
x
x x
A
x
Bx C
x
+
− +
=
−
+
+
+
3
1 1 1 1
2 2
( )( )
⇒ x + 3 = A(x2
+ 1) + (Bx + C)(x − 1)
Put x = 1, then 4 = A(1 + 1) ⇒ 2A = 4 ⇒ A = 2
Put x = 0, then 3 = A − C ⇒ C = A − 3 = 2 − 3 = −1
Equating coefficients of x2
, 0 = A + B ⇒ B = −A = −2
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 7 5/12/2016 9:53:04 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-620-2048.jpg)

![Improper Integrals ■ 7.9
Let I
dv
v v
b
1 2 1
0 1 1
=
+ + −
∫ ( )( tan )
Put t = tan−1
v ∴ dt
v
dv
=
+
1
1 2
When and when
v t v b t b
= = = = =
− −
0 0 0
1 1
, tan , tan
∴ I
dt
t
t
b
e
b
1
0
0
1
1
1
1
=
+
= +
[ ]
−
−
∫
tan
tan
log ( )
= + − = +
− −
log ( tan ) log log ( tan )
e e e
b b
1 1 1
1 1
∴ I b
b
e
= lim log ( tan )
→∞
−
1 1
+
⎡
⎣ ⎤
⎦ = + = +
⎛
⎝
⎜
⎞
⎠
⎟
log ( tan ) log
e e
1 1
2
1
−
∞
p
Problems based on improper integral of the second kind
EXAMPLE 11
Evaluate the improper integral
dx
x
9 2
0
3
2
,
∫ if it exists.
Solution.
Let I
dx
x
=
−
∫ 9 2
0
3
Here the integrand is f x
x
( ) =
−
1
9 2
When x f
= = = ∞
3 3
1
0
, ( ) . ∴ f(x) is unbounded when x = 3.
∴ the integrand is unbounded when x = 3 and the interval [0, 3] is finite.
So, it is an improper integral of the second kind.
∴ I
dx
x
=
−
∫ 9 2
0
3
=
−
∈→ +
−∈
∫
lim
0 2
0
3
9
dx
x
=
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥ =
+
+
lim sin
lim sin sin si
∈→
−
−∈
∈→
− −
− ∈
−
0
1
0
3
0
1 1
3
3
3
0
x
n
n [ , ]
−
− = ∈ − ∈
1
1 0
2
0 3 3
p
as → →
EXAMPLE 12
Evaluate the improper integral
dx
x
( )
,
/
21 2 3
0
2
∫ if it exists.
Solution.
Let I
dx
x
=
−
∫ ( ) /
1 2 3
0
2
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 9 5/12/2016 9:53:13 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-622-2048.jpg)
![7.10 ■ Engineering Mathematics
Here the integrand is f x
x
( )
( ) /
=
−
1
1 2 3
When x f
= = = ∞
1 1
1
0
, ( ) ∴ f(x) is unbounded at x = 1.
∴ the integrand is unbounded when x = 1 and the interval [0, 2] is finite.
Hence, it is an improper integral of the second kind.
∴ I
dx
x
=
−
∫ ( ) /
1 2 3
0
2
=
−
+
−
∫ ∫
dx
x
dx
x
( ) ( )
/ /
1 1
2 3
0
1
2 3
1
2
=
−
+
−
= −
∈→ +
−∈
→ +
+
∈→ +
∫ ∫
lim
( )
lim
( )
lim (
/ /
0 2 3
0
1
0 2 3
1
2
0
1 1
1
dx
x
dx
x
x
d
d
)
) lim ( )
/ /
−
−∈
→ +
−
+
∫ ∫
+ −
2 3
0
1
0
2 3
1
2
1
dx x dx
d
d
=
⎡
⎣
⎢
⎤
⎦
⎥ +
⎡
⎣
⎢
⎤
⎦
⎥
=
+
lim
( )
/
lim
( )
/
/ /
∈→
−∈
→
− −
0
1 3
0
1
0
1 3
1
2
1
1 3
1
1 3
3
x x
d
d
l
lim[( ) ( ) ] lim[ ( ) ]
lim
/ / / /
∈→ →
∈
− ∈− − − − −
0
1 3 1 3
0
1 3 1 3
1 1 1 3 1 1 1
3
+ +
=
d
d
→
→ →
− ∈ − − − − −
−
0
1 3
0
1 3 1 3
1 3 1 1 1
3 0 1 3 1
[( ) ( )] lim ( ) [ ( ) ]
[ ] [
/ / /
+ =
= + +
d
d {
0
0 6
] =
EXAMPLE 13
Evaluate the improper integral
dx
x x
2 2
0
2
2
,
∫ if it exists.
Solution.
Let I
dx
x x
dx
x x
=
−
=
−
∫ ∫
2 2
2
0
2
0
2
( )
Here the integrand is f x
x x
( )
( )
=
−
1
2
When x f x f
= = = ∞ = = = ∞
0 0
1
0
2 2
1
0
, ( ) , ( )
and when
∴ f(x) is unbounded at x = 0 and x = 2
∴ the integrand is unbounded and the interval [0, 2] is finite.
Hence, it is an improper integral of the second kind.
∴ I
dx
x x
dx
x x
dx
x x
dx
x x
=
−
=
−
+
−
=
−
+
∫ ∫ ∫
∫
∈→
+∈
( ) ( ) ( )
lim
( )
2 2 2
2
0
2
0
1
1
2
0
0
1
l
lim
( )
d
d
→
−
−
= +
∫
0
1
2
1 2
2
dx
x x
I I
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 10 5/12/2016 9:53:18 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-623-2048.jpg)
![Improper Integrals ■ 7.11
Let 1
2 2
x x
A
x
B
x
( )
−
= +
−
⇒ 1 2
= − +
A x Bx
( )
Putting x A A
= = =
0 1 2
1
2
, ⇒ and Putting x B B
= = =
2 1 2
1
2
, ⇒
∴
1
2
1
2
1 1
2
1
2
x x x x
( ) ( )
−
= ⋅ + ⋅
−
∴
dx
x x x x
dx
( ) ( )
2
1
2
1 1
2 2
−
= ⋅ +
−
⎛
⎝
⎜
⎞
⎠
⎟
∫ ∫
= − − =
−
⎛
⎝
⎜
⎞
⎠
⎟
1
2
1
2
2
1
2 2
log log ( ) log
e e e
x x
x
x
(1)
Now, I
dx
x x
1
0
0
1
2
=
−
∈→
+∈
∫
lim
( )
=
−
⎡
⎣
⎢
⎤
⎦
⎥
∈→
+∈
lim log
0
0
1
1
2 2
e
x
x
[using (1)]
= −
+ ∈
+ ∈
⎡
⎣
⎢
⎤
⎦
⎥
⎧
⎨
⎩
⎫
⎬
⎭
=
lim log log
( )
lim log
∈→
∈→
− −
0
0
1
2
1
2 1
0
2 0
1
2
1
e e
e −
− loge
∈
− ∈
⎡
⎣
⎢
⎤
⎦
⎥
⎧
⎨
⎩
⎫
⎬
⎭
2
= −
∈
− ∈
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎩
⎫
⎬
⎭
= − = ∞
∈→
1
2 2
1
2
0
0
lim log log
e e
and I
dx
x x
2
0
1
2
2
=
−
→
−
∫
lim
( )
d
d
=
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
lim log
d
d
→
−
−
0
1
2
1
2 2
e
x
x
[using (1)]
=
1
2
2
2 2
1
2 1
0
lim log
( )
log
d
d
d
→
−
− −
−
−
e e
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
=
−
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
1
2
2
1
0
lim log log
d
d
d
→
−
e e
= − = =
1
2
2
0
0
1
2
0
lim log log
d→
∞ ∞
e e
∴ I I I
= + =
1 2 ∞
i.e., the limit does not exist.
∴ the integral
dx
x x
( )
2
0
2
−
∫ is divergent.
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 11 5/12/2016 9:53:24 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-624-2048.jpg)
![7.12 ■ Engineering Mathematics
EXAMPLE 14
Evaluate the improper integral log | |
e x dx
21
1
∫ .
Solution.
Let I x dx
e
=
−
∫ log
1
1
= ⎡
⎣ ⎤
⎦
=
∫
2
2
0
1
log log
log
e e
e
x dx x is even
x
x dx x x x
0
1
0
∫ = ≥
⎡
⎣ ⎤
⎦
if
Here f x x
e
( ) log
=
As x x
e
→ →
0+ ∞
, log . So, f(x) is unbounded at x = 0.
∴ the integrand is unbounded and the interval [−1, 1] is fininte.
Hence, it is an improper integral of the second kind.
But I xdx x x
x
x dx
e e
= = ⋅
[ ] − ⋅
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
∈→ +
∈
∈→ + ∈
∈
∫ ∫
lim log lim log
0
1
0
1
1
1
=
= − ∈ ∈−
{ }
∈→ +
∈
lim log [ ]
0
1
0 e x
=
=
=
+
+
+
lim [ log ( )]
lim [ log ]
lim [ lo
∈→
∈→
∈→
− ∈ ∈− − ∈
− ∈ ∈− + ∈
− ∈
0
0
0
1
1
2
e
e
g
g ]
lim [ log ]
e
e
∈ −
− ∈ ∈
∈→
1 0
2 2
0
+
⎡
⎣
⎢
⎤
⎦
⎥
= −
+
∞
∞
form
⎡
⎣
⎢
⎤
⎦
⎥
Now lim ( log ) lim
log
/
lim
/
/
lim (
∈→ ∈→
∈→ ∈→
∈ ∈
∈
∈
∈
− ∈
− ∈
0 0
0 2 0
1
1
1
+ +
+
=
= =
e
e
+
)
) [ ]
= 0 by L-Hopital s rule
’
∴ I = =
2 0 2 2
[ ]− −
EXAMPLE 15
Evaluate
x
x
dx
1 2
0
1
2
∫ .
Solution.
Let I
x
x
dx
= ∫ 1 2
0
1
−
Hence, it is an improper integral of the second kind
Here f x
x
x
( ) =
−
1 2
When x = 1, f ( ) .
1
1
0
= = ∞ ∴ f(x) is unbounded at x = 1.
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 12 5/12/2016 9:53:29 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-625-2048.jpg)
![Improper Integrals ■ 7.13
∴ the integrand is unbounded and the interval is finite
∴ I
x
x
dx x x dx
=
−
= − − −
∈→ +
−∈
∈→ +
−∈
−
∫ ∫
lim lim ( ) ( )
0 2
0
1
0
2
0
1 1
2
1
1
2
1 2
= −
−
= − −
−
lim
( )
lim ( )
∈→ +
∈
∈→ +
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎤
⎦
⎥
0
2
1
2
0
1
0
2
1
2
1
2
1
1
2
1
x
x 0
0
1
0
2
1
2
1
2
1 1 1 1 1 1 0 1 1
−
= − − − − = − − − = − − =
∈
∈→ +
∈
⎡
⎣
⎢
⎤
⎦
⎥ { }
lim [ ( ) ] ( ) ( )
∴
x
x
dx
1
1
2
0
1
−
∫ =
EXERCISE 7.1
Test the convergence of the following improper integrals using definition. Find the value if convergent.
1.
dx
x2
1
∞
∫ 2.
1
0
1 x
dx p
p
,
∞
∫ 3. x dx
−
∞
∫
( / )
3 2
1
4.
x
x
dx
1 4
+
−∞
∞
∫ 5.
dx
x x
2
2 5
+ +
−∞
∞
∫ 6.
2
4
1 e
dx
x
+
∞
∫
7.
dx
x
4 2
0
2
−
∫ 8.
dx
x
( )
1 2
1
2
−
∫ 9. e dx p
px
−
∞
∫
0
0
,
10. tan xdx
−
∫p
p
2
2
11.
1
1
1
1
+
−
−
x
x
dx
∫ 12.
dx
x
p
p
,
∫ 0
0
1
13. x x dx
sin
0
∞
∫ 14.
x dx
x
( )
2 3
2 3
−
∞
∫
ANSWERS TO EXERCISE 7.1
1. 1 2.
1
1
p −
if p 1, divergent if p ≤ 1 3.
1
2
4. 0 5.
p
2
6. Divergent
7.
p
2
8. Divergent 9.
1
0
p
p
if
10. Divergent 11. p
12.
1
1
p −
if p 1, Divergent if p ≥ 1 13. Divergent 14. 1
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 13 5/12/2016 9:53:37 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-626-2048.jpg)


![7.16 ■ Engineering Mathematics
∴ lim
( )
( )
lim ( )
x x
f x
g x
x
→ →
∞ ∞
=
+
= ≠
1
1
1
1 0
∴ by the comparison test,
f x dx g x dx
( ) ( )
1 1
∞ ∞
∫ ∫
and behave alike.
But g x dx
dx
x
( ) /
1
3 2
1
∞ ∞
∫ ∫
= is convergent by p-integral, since p =
3
2
1.
∴ f x dx
dx
x x
( )
( )
1 1 1
∞ ∞
∫ ∫
=
+
is convergent.
EXAMPLE 3
Test the convergence of e dx
x
2 2
0
∞
∫ .
Solution.
Let I e dx
x
= −
∞
∫
2
0
= + = +
− −
∞
∫ ∫
e dx e dx I I
x x
2 2
0
1
1
1 2
where I e dx
x
1
0
1
2
= −
∫ is proper integral
and I e dx
x
2
1
2
= −
∞
∫ is an improper integral of the first kind
we shall test the convergent of I2
Here f x e x
( ) = − 2
. Consider g x
x
( ) =
1
2
∴ f x
g x
x e
x
e
x
x
( )
( )
= =
−
2
2
2
2
∴ lim
( )
( )
lim
x x x
f x
g x
x
e
→∞ →∞
=
∞
∞
⎡
⎣
⎢
⎤
⎦
⎥
2
2
form
=
⋅
= =
∞
=
→∞ →∞
lim lim
x x x x
x
e x e
2
2
1 1
0
2 2
[L-Hopital’s rule]
But
dx
x2
1
∞
∫ is convergent by p-integral, since p =
2 1. ∴ I e dx
x
2
1
2
= −
∞
∫ is convergent.
∴ I I I
= +
1 2 is convergent.
Hence, e dx
x
−
∞
∫
2
0
is convergent.
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 16 5/12/2016 9:54:20 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-629-2048.jpg)

![7.18 ■ Engineering Mathematics
= = =
∞
lim lim
x x
x
x
x
→∞ →
1
1
2
2
0 [by L’Hopital’s Rule]
But g x dx
dx
x
( ) /
1
3 2
1
∞ ∞
∫ ∫
= is convergent by p-integral, since p =
3
2
1.
∴ f x dx
x
x
dx
( )
log
1
2
1
∞ ∞
∫ ∫
= is convergent.
EXAMPLE 6
Test the convergence of
dx
x x
1 2
1 1
∞
∫ .
Solution.
Given
dx
x x
1 2
1 +
∞
∫ .
Here f x
x x
x
x
( ) .
=
+
=
+
1
1
1
1
1
2
2
2
Take g x
x
( ) =
1
2
∴ f x
g x
x
x
x
x
( )
( )
=
+
⋅ =
+
1
1
1
1
1
1
2
2
2
2
lim
( )
( )
lim ( )
x x
f x
g x
x
→ →
∞ ∞
=
+
= ≠
1
1
1
1 0
2
∴ by the comparison test,
f x dx g x dx
( ) ( )
and
1
1
∞
∞
∫
∫ behave alike.
But g x dx
x
dx
( )
1
2
1
1
∞ ∞
∫ ∫
= is convergent by p-integral, since p =
2 1.
∴ f x dx
dx
x x
( )
1
2
1 1
∞ ∞
∫ ∫
=
+
is convergent.
EXAMPLE 7
Test the convergence of
dx
ex
11
0
∞
∫ .
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 18 5/12/2016 9:54:34 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-631-2048.jpg)
![Improper Integrals ■ 7.19
Solution.
Given
dx
ex
+
∞
∫ 1
0
. Here f x
ex
( ) .
=
+
1
1
We know e e x
x x
+1 0
≥ ∀ ≥ ⇒
1
1
1
e e
x x
+
≤
∴
1
1
0 0
e
dx
dx
e
x x
+
≤
∞ ∞
∫ ∫
But
dx
e
e dx
x
x
0 0
∞
−
∞
∫ ∫
= is convergent, since a =
1 0.
∴
dx
ex
+
∞
∫ 1
0
is convergent, by comparison test.
EXAMPLE 8
Test the convergence of
cos
.
x
x
dx
1 2
0 1
∞
∫
Solution.
Given
cos
.
x
x
dx
1 2
0 +
∞
∫ Here f x
x
x
( )
cos
=
+
1 2
But
cos x
x x
x
1
1
1
0
2 2
+
≤
+
∀ ≥ ∴
cos x
x
dx
x
dx
1
1
1
2
0
2
0
+
≤
+
∞ ∞
∫ ∫
Now
dx
x
x
1 2
0
1
0
+
= [ ]
∞
− ∞
∫ tan = ∞ − = − =
− −
tan tan .
1 1
0
2
0
2
p p
∴ dx
x
1 2
0 +
∞
∫ is convergent. ⇒
cos x
x
dx
1 2
0 +
∞
∫ is convergent.
Hence,
cos x
x
dx
1 2
0 +
∞
∫ is absolutely convergent.
(b) Test of convergence of Improper Integrals of the second kind
We state the following theorems without proof.
Theorem 7.4 Let f(x) be positive and integrable in a x ≤ b and f(x) is unbounded at a. Then f x dx
a
b
( )
∫
will converge, if there exists a positive number M such that f x dx M
a
b
( ) ,
+∈
∫ ∀ ∈ where 0 ∈ −
b a.
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 19 5/12/2016 9:54:43 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-632-2048.jpg)


![7.22 ■ Engineering Mathematics
EXAMPLE 3
Test the convergence and evaluate the improper integral
x
x
dx
e
log
.
1
2
∫
Solution.
Given
x
x
dx
e
log
1
2
∫ . Here f x
x
x
x
e
( )
log
,
= ≥ 1
When x f x
e
= = = ∞
1
1
1
, ( )
log
∴ f(x) is unbounded when x = 1
Take g x
x x
e
( )
log
=
1
∴ f x
g x
x
x
x x x
e
e
( )
( ) log
log /
= ⋅ = 3 2
∴ lim
( )
( )
lim ( )
/
x x
f x
g x
x
→ →
1 1
3 2
1 0
= = ≠
∴ by the limits comparison test,
f x dx
( )
1
2
∫ and g x dx
( )
1
2
∫ behave alike.
But g x dx
x x
dx
e
( )
log
1
2
1
2
1
∫ ∫
=
= =
∈
+∈
∈
+∈
∫ ∫
lim
log
lim
log
→ →
0
1
2
0
1
2
1 1
x x
dx
x
x
dx
e e
/
= [ ]
= − +
[ ]
=
lim log (log )
lim log (log ) log (log )
∈→ +∈
∈→
∈
0 1
2
0
2 1
e e
e e e
x
l
log log log (log ) log log log
e e e e e
2 1 2 0
− = − = ∞
∴ g x dx
( )
1
2
∫ is divergent.
∴ f x dx
x
x
dx
e
( )
log
1
2
1
2
∫ ∫
= is divergent.
EXAMPLE 4
Test the convergence of the improper integral
dx
x2
1
1
2
∫ .
Solution.
Given
dx
x2
1
1
−
∫ . Here f x
x
( ) .
=
1
2
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 22 5/12/2016 9:55:25 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-635-2048.jpg)



![7.26 ■ Engineering Mathematics
Integrating by parts,
I x x
x
x x dx
e
= ⋅ −
[ ] − ⋅ −
⎧
⎨
∈ + ∈
∈
∫
lim log sin ( cos )
sin
cos ( cos )
/
/
→0
2
2
1
p
p
⎪
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
= −
[ ] +
−
⎧
⎨
⎪
∈ + ∈
∈
∫
lim cos log sin
sin
sin
/
/
→0
2
2
2
1
x x
x
x
dx
e
p
p
⎩
⎩
⎪
⎫
⎬
⎪
⎭
⎪
= − + ∈ ∈
⎡
⎣
⎢
⎤
⎦
⎥ + −
∈ +
lim cos log sin cos log sin
sin
s
→0 2 2
1
p p
e e
x
i
in
lim cos log sin s
/
x dx
x
e
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
= + ∈ ∈+ −
∈
∈ +
∫
p 2
0
0
→
cosec i
in
/
x dx
( )
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
∈
∫
p 2
=
⎛
⎝
⎜
⎞
⎠
⎟ + +
⎡
⎣
⎢
⎤
⎦
⎥
+
lim cos log sin cos log tan cos
/
∈→
∈
∈
∈ ∈
0
2
2
2 2 2
e e
x
x
p
⎧
⎧
⎨
⎩
⎫
⎬
⎭
= + +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎧
⎨
⎩
+
lim cos log log sin log cos log
∈→
∈
∈ ∈
0
2
2 2
e e e et
tan cos log tan cos
lim log cos cos
p p
4 2 2
2
0
+
⎡
⎣
⎢ − −
⎤
⎦
⎥
⎫
⎬
⎭
= ⋅
+
e
e
∈
∈
∈+
∈→
∈
∈
∈
∈
∈
+
∈
∈
∈
log sin cos log cos log
sin
cos
cos
e e e
2 2
0 2
2
+ − −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
= − ∈+ ∈
∈
+ ∈
∈
{ −
∈ +
lim (log )cos cos log sin cos log cos log sin
→0
2 1
2 2
e e e e
∈
∈
−
∈
⎛
⎝
⎜
⎞
⎠
⎟
⎫
⎬
⎭
= − ∈− − ∈
∈ +
2 2
2 1 1
0
log cos
lim (log )cos ( cos )log si
e
e e
→
n
n cos log cos log cos
∈
{ + ∈
∈
+
∈
}
2 2 2
e e
But ( cos )log sin sin log sin
1
2
2
2 2
2
− ∈
∈
=
∈ ∈
e e
∴ lim ( cos )log sin lim log , sin
∈ +
− ∈
∈
= =
∈
→ →
→
0 0
2
1
2
2
2
0
e
t
e
t t t
where as 0
∈→
=
∞
∞
⎛
⎝
⎜
⎞
⎠
⎟
lim
log
t
et
t
→0
2
2
1
form =
−
= − =
lim lim ( )
t t
t
t
t
→ →
0
3
0
2
2
2
0 [L-Hopital’s rule]
and log log as 0
e e e
cos cos log
∈
= =
2
0 1 0
→ ∈→
∴ I e
e
e e e e
= − = − =
(log )cos log log log .
2 1 0 2
2
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 26 5/20/2016 11:19:14 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-639-2048.jpg)

![7.28 ■ Engineering Mathematics
7.2.1 Leibnitz’s Rule—Differentiation Under Integral Sign for Variable limits
Theorem 7.7 If f(x, a), a(a) and b(a) are differentiable functions of a, where a is a parameter and
∂
∂
f
a
is continuous, then
d
d
f x dx
f x
dx f b
a
b
a
b
a
a
a
a
a
a
a
a
a
( , )
( , )
[ ( )
( )
( )
( )
( )
∫ ∫
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
=
∂
+
∂
,
, ] [ ( ), ] .
a
a
a a
a
db
d
f a
da
d
−
The proof of the theorem is beyond the scope of the book.
Corollary 1: If the limits a and b are constants (independent of the parameter a), then the Leibnitz’s
rule becomes
d
d
f x dx
f x
dx
a
b
a
b
a
a
a
a
( , )
( , )
∫ ∫
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
=
∂
∂
Corollary 2: If the limits are functions of a, a(a) and b(a), but f is independent of a, then the
Leibnitz’s rule becomes
d
d
f x dx f b
db
d
f a
da
d
a
b
a
a
a
a
a
a
a
( ) [ ( )] [ ( )]
( )
( )
∫
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
= −
Note
1. When f x dx
a
b
( , )
( )
( )
a
a
a
∫ is integrated and evaluated, it will be ultimately a function of a, say g(a). So,
differentiation of the integral w.r.to a is ordinary derivative
dg
da
.
But f(x, a) is a function two variables x and a. So, derivative of f w.r.to a is partial derivative
∂
∂
f
a
.
2. When f is independent of a, it is a function of x alone and so
∂
∂
=
f
a
0.
So, corollary 2 does not contain integral on the R.H.S.
3. Leibnitz’s rule can be used even if one of the limits of integration is infinite.
That is, the integral is of the form f x dx
a
( , )
a
∞
∫ or f x dx
a
( , ) .
( )
a
a
∞
∫
WORKED EXAMPLES
EXAMPLE 1
Evaluate
x
x
dx
e
a
2
a
1
0
0
1
log
, ,
≥
∫ using Leibnitz’s rule.
Solution.
Let F
x
x
dx
e
( )
log
a
a
=
−
∫
1
0
1
(1)
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 28 5/20/2016 11:19:45 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-641-2048.jpg)
![Improper Integrals ■ 7.29
[When the integral is evaluated, it will be a function of a].
Differentiating w.r.to a, using corollary (1) of Leibnitz’s rule, we get
dF
d
x
x
dx
x
x dx
x
e e
e
a a a
a
a
=
∂
∂
−
⎛
⎝
⎜
⎞
⎠
⎟ = ⋅
∂
∂
−
=
∫ ∫
0
1
0
1
0
1 1
1
1
log log
( )
log
1
1
0
1 1
0
1
1
1
1
∫
∫
⋅
= =
⎡
⎣
⎢
⎤
⎦
⎥ =
x x dx
x dx
x
e
a
a
a
a a
log
+
+ +
{
d
dx
a a a
x x
e
[ ] log
=
⎡
⎣
⎢
⎤
⎦
⎥
⇒ dF
da a
=
1
1
+
Integrating w.r.to a, we get
F d C
e
( ) log ( )
a
a
a a
=
+
= + +
∫
1
1
1 (2)
∴ F C F C
e
( ) log ( )
0 1 0
= + =
⇒
Put a = 0 in (1), we get
F
x
x
dx
x
dx C
e e
( )
log log
0
1 1 1
0 0
0
0
1
0
1
=
−
=
−
= =
∫ ∫ ⇒
∴ F e
( ) log ( )
a a
= +1 ⇒
x
x
dx
e
a
a
−
= +
∫
1
1
0
1
log
log ( )
EXAMPLE 2
Evaluate e
x
x
dx
x
2a
a
sin
,
0
0
∞
∫ ≥ and hence, show that
sin
.
x
x
dx
0
2
∞
∫ 5
p
Solution.
Let F e
x
x
dx
x
( )
sin
a a
= −
∞
∫
0
(1)
Differentiating w.r.to a, using cor (1) of Leibnitz’s rule, we get
dF
d
e
x
x
dx
x
x
e dx
x x
a a a
a a
=
∂
⎛
⎝
⎜
⎞
⎠
⎟ =
∂
∂
( )
∞
−
∞
−
∫ ∫
∂
0 0
sin sin
[{ the limits are constants]
= −
= −
−
∞
−
∞
∫
∫
sin
( )
sin
x
x
e x dx
e xdx
x
x
a
a
0
0
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 29 5/20/2016 11:19:52 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-642-2048.jpg)
![7.30 ■ Engineering Mathematics
= −
+
− −
( )
⎡
⎣
⎢
⎤
⎦
⎥
− ∞
e
x x
x
a
a
a
2
0
1
sin cos
{ e bxdx
e
a b
a bx b bx
ax
ax
sin [ sin cos ]
∫ =
+
−
⎡
⎣
⎢
⎤
⎦
⎥
2 2
∴ =
+
+
⎡
⎣ ⎤
⎦ =
+
− = −
+
− ∞
1
1
1
1
0 1
1
1
2 0 2 2
a
a
a a
a
e x x
x
( sin cos ) [ ]
Integrating w.r.to a, we get
F
d
( )
a
a
a
= −
+
∫ 2
1
⇒ F C
( ) tan
a a
= − +
−1
Put a
p
= ∞ ∴ ∞ = − ∞ + = − +
−
, ( ) tan
F C C
1
2
From (1), we get,
F e
x
x
dx dx
( )
sin
∞ = = =
−∞
∞ ∞
∫ ∫
0 0
0 0 ∴ 0
2 2
= − + =
p p
C C
⇒
∴ F( ) tan
a
p
a
= − −
2
1
⇒ e
x
x
dx
x
−
∞
−
∫ = −
a p
a
0
1
2
sin
tan = cot−1
a { tan cot
− −
⎡
⎣
⎢
⎤
⎦
⎥
1 1
2
a a
p
+ = (2)
To deduce the value of
sin
,
x
x
dx
0
0
∞
∫ =
put in (2)
a .
∴
sin
tan
x
x
dx
0
1
2
0
2
∞
−
∫ = − =
p p
EXAMPLE 3
Prove that
d
da
x
a
dx a a a
a
tan tan log ( ),
2 2
5 2 1
1
0
1 2
2
2
1
2
1
∫
⎛
⎝
⎜
⎞
⎠
⎟ using Leibnitz’s rule. Hence, evaluate
tan21
0
2
x
a
dx
a
∫ .
Solution.
Let F a
x
a
dx
a
( ) tan
= −
∫
1
0
2
(1)
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 30 5/20/2016 11:20:00 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-643-2048.jpg)
![Improper Integrals ■ 7.31
Differentiating w.r.to parameter a using Leibnitz’s rule, we get
dF
da a
x
a
dx
a
a
a
x
a
x
a
a
=
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ ⋅ −
=
+
−
− −
∫ tan tan
1
0
1
2
2
2
2
2 0
1
1
2
2
0
1
2 2
0
1
2
2
2
2
2
1
2
⎛
⎝
⎜
⎞
⎠
⎟ +
= −
+
+
= − +
∫
∫
−
−
dx a a
x
a x
dx a a
a
a
a
e
tan
tan
log ( x
x a a
f x
f x
dx f x
a
e
2
0
1
2
2
) tan
( )
( )
log ( )
⎡
⎣ ⎤
⎦ +
′
=
⎡
⎣
⎢
⎤
⎦
⎥
−
∫
{
= − + − +
= −
+
+
−
−
1
2
2
1
2
1
2
2 4 2 1
2 2
2
[log ( ) log ] tan
log
( )
tan
e e
e
a a a a a
a a
a
a 1
1 1 2
2
1
2
1
a a a a
e
= − +
−
tan log ( )
Integrating w.r.to a, we get
F a a a da a da
a
a
a
a
da
e
( ) tan log ( )
tan
= − +
= ⋅ −
+
⋅
⎡
−
−
∫ ∫
∫
2
1
2
1
2
2
1
1 2
1 2
1
2
2
2
⎣
⎣
⎢
⎤
⎦
⎥ − + ⋅ −
+
⋅ ⋅
⎡
⎣
⎢
⎤
⎦
⎥
= −
+
∫
−
1
2
1
1
1
2
1
2
2
2 1
2
2
log ( )
tan
e a a
a
a a da
a a
a
a
da
a
a
a
a
a
da
a a
a
a C
e
e
∫ ∫
− + +
+
= − + +
−
2
1
1
2
1
2
2
2
2 1 2
log ( )
tan log ( )
Putting a = 0, we get F C C
( )
0 0
= + =
Putting a = 0 in (1), we get F(0) = 0 ∴ C = 0
∴ F a a a
a
a
e
( ) tan log ( )
= − +
−
2 1 2
2
1
⇒ tan tan log ( )
− −
∫ = − +
1
0
2 1 2
2
2
1
x
a
dx a a
a
a
a
e
EXAMPLE 4
Let I e dx
x
a
x
5
2 2
2
2
0
⎛
⎝
⎜
⎞
⎠
⎟
∞
∫ , Prove that
dI
dx
I
522 . Hence, find the value of I.
Solution.
Given I e dx e e dx
x
a
x x
a
x
= =
− −
⎛
⎝
⎜
⎞
⎠
⎟
∞
−
−
∞
∫ ∫
2
2
2
2
2
0 0
(1)
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 31 5/20/2016 11:20:11 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-644-2048.jpg)
![7.32 ■ Engineering Mathematics
Differentiating (1) w.r.to a using Leibnitz’s rule, we get
dI
da a
e e dx
e
a
e dx e e
x
a
x
x
a
x x
=
∂
∂
⋅
( )
=
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟ =
∞
−
−
−
∞
−
−
−
∫
∫
0
0
2
2
2
2
2
2 2
a
a
x x
a
x
a
x
dx a e e
x
dx
2
2 2
2
2
2
2
2
0 2
0
−
⎛
⎝
⎜
⎞
⎠
⎟ = −
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
∞
−
∞
∫ ∫
−
Put y
a
x
x
a
y
dx
a
y
dy
= = = −
⇒ ∴ 2
When x y x y
= = ∞ = ∞ =
0 0
, ,
and when
∴ dI
da
a e e
y
a
a
y
dy
a
y y
= −
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
−
−
∞
∫
2
2
2 2
2
2 2
0
⇒
dI
da
e e dy
y
a
y
= −
∞
∫
2
2
2
2
0 −
= − = −
− −
∞
∫
2 2
2 2
0
e e dx I
x a x
( )
/
∴
dI
I
da
= −2
Integrating, we get
⇒
dI
I
da
∫ ∫
= −2
⇒ log I a C
= − +
2 ⇒ I e a C
= − +
2
e e
C a
= ⋅ −2
= Ke K e
a C
=
−2
, where
Putting then
a I Ke K
= = =
0 0
,
Putting a = 0 in (1), then
I e dx
x
( )
0
2
2
0
= =
−
∞
∫
p
⇒ K =
p
2
[Result]
∴ I e a
= −
p
2
2
EXAMPLE 5
Prove that
tan
( )
log ( ), .
2
1
5
p
1
1
2
0 1 2
1 0
ax
x x
dx a a
∞
∫ ≥
Solution.
Let F a
ax
x x
dx
( )
tan
( )
=
+
−
∞
∫
1
2
0 1
(1)
Differentiating (1) w.r.to a, using Leibnitz’s rule, we get
dF
da a
ax
x x
dx
x x a
ax d
=
∂
∂ +
⎛
⎝
⎜
⎞
⎠
⎟ =
+
∂
∂
∞ − ∞
−
∫ ∫
0
1
2 2
0
1
1
1
1
tan
( ) ( )
(tan ) x
x
x x a x
xdx
x a x
dx
=
+ +
⋅ =
+ +
∞ ∞
∫ ∫
1
1
1
1
1
1 1
2
0
2 2 2 2 2
0
( ) ( )( )
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 32 5/20/2016 11:20:25 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-645-2048.jpg)
![Improper Integrals ■ 7.33
We shall put
1
1 1
2 2 2
( )( )
+ +
x a x
into partial fractions.
Since it is a function of x2
, treating x2
as u, we write the special partial fraction
1
1 1 1 1
2 2
( )( ) ( ) ( )
+ +
=
+
+
+
u a u
A
u
B
a u
⇒ 1 1 1
2
= + + +
A a u B u
( ) ( )
Put u A a A
a
= − = − =
−
1 1 1
1
1
2
2
, ( )
then ⇒
Put u
a
B
a
B
a
a
B
a
a
= − = −
⎛
⎝
⎜
⎞
⎠
⎟
−
⎛
⎝
⎜
⎞
⎠
⎟ = = −
−
1
1 1
1 1
1
1
2 2
2
2
2
2
, then ⇒ ⇒
∴ 1
1 1
1
1
1
1 1
1
1
2 2
2
2 2
( )( )
+ +
=
−
⋅
+
−
−
⋅
+
u a u a u
a
a a u
⇒
1
1 1
1
1
1
1 1
1
1
2 2 2 2 2
2
2 2 2
( )( ) ( )
+ +
=
−
⋅
+
−
−
⋅
+
x a x a x
a
a a x
∴
dF
da a x
a
a a x
dx
=
−
⋅
+
−
−
⋅
+
⎡
⎣
⎢
⎤
⎦
⎥
∞
∫
1
1
1
1 1
1
1
2 2
2
2 2 2
0 ( )
=
− +
−
− +
=
−
[ ] −
−
∞
∞
− ∞
∫
∫
1
1 1 1
1
1
1
1 1
2 2
2
2 2 2
0
0
2
1
0
2
a
dx
x
a
a a x
dx
a
x
a
( )
tan
( a
a
dx
a
a
x
2
2
2
2
0
1
)
+
⎛
⎝
⎜
⎞
⎠
⎟
∞
∫
=
−
∞ −
[ ]−
−
⎡
⎣
⎢
⎤
⎦
⎥
=
−
− − −
1
1
0
1
1
1
1 1
1
1 2
2
1 1
2
1
0
2
a a a
x
a
a
tan tan
( )
tan
/ /
∞
p
−
−
⎡
⎣
⎢
⎤
⎦
⎥ −
−
∞ −
[ ]
=
−
−
−
−
⎡
⎣
⎢
⎤
− −
0
1
0
1
1 2 1 2
0
2
1 1
2 2
a
a
a
a
a
( )
tan tan
( ) ( )
p p
⎦
⎦
⎥ =
−
−
=
+
p p
2
1
1 2 1
2
( )
( ) ( )
a
a a
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 33 5/20/2016 11:20:33 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-646-2048.jpg)

![Improper Integrals ■ 7.35
Put then
x
a a
C
a
C
a
a a
= − − = +
⎛
⎝
⎜
⎞
⎠
⎟
+
= −
1 1
1
1 1 1
2
2
2
,
( )
⇒ ⇒ C
a
a
= −
+
1 2
Equating coefficients of x2
, we get
0
1
1
1
1
2 2
= ⇒
Aa C A
C
a a
a
a a
+ = − = − −
+
⎛
⎝
⎜
⎞
⎠
⎟ =
+
Equating constants, we get
0
1 2
= + = − =
+
B C B C
a
a
⇒
∴ x
x ax
a
x
a
a
x
a
a ax
( )( ) ( ) ( ) ( )
1 1
1
1 1
1 1
1
1
2
2 2
2 2
+ +
= +
+
+
+
−
+
⋅
+
=
+
⋅
+
+
−
+
⋅
+
=
+
⋅
+
+
+
1
1 1 1
1
1
1
1 1 1
2 2 2
2 2 2
( ) ( ) ( ) ( )
( ) ( ) ( )
a
x a
x
a
a ax
a
x
x
a
a
⋅
⋅
+
−
+
⋅
+
1
1 1
1
1
2 2
( ) ( ) ( )
x
a
a ax
∴
xdx
x ax a
xdx
x
a
a
dx
x
a a a
( )( ) ( ) ( ) ( ) ( )
1 1
1
1 1 1 1
2
0
2 2
0
2 2
0
+ +
=
+ +
+
+ +
−
∫ ∫ ∫
a
a
a
dx
ax
a
( ) ( )
1 1
2
0
+ +
∫
=
+
+
⎡
⎣ ⎤
⎦ +
+
[ ] −
+
−
1
1
1
2
1
1 1
1
2
2
0 2
1
0 2
( )
log ( )
( )
tan
( )
log
a
x
a
a
x
a
a a
e
a a
e (
( )
( )
log ( ) log
( )
tan tan
1
1
2 1
1 1
1
0
2
2
2
1
+
[ ]
=
+
+ −
⎡
⎣ ⎤
⎦ +
+
−
−
ax
a
a
a
a
a
a
e e
−
−
[ ]
−
+
+ −
⎡
⎣ ⎤
⎦
1
2
2
0
1
1
1 1
( )
log ( ) log
a
a
e e
∴
= −
+
+ +
+
= −
+
+
−
1
2 1
1
1
1
2 1
1
2
2
1
2
2
2
( )
log ( )
tan
( )
( )
log ( )
a
a
a a
a
dF
da a
a
e
e +
+
+
+
+
+
=
+
+
+
−
−
a a
a a
a
a
a
a
e
e
tan
( ) ( )
log ( )
log ( )
( )
tan
1
2 2
2
2
2
1
1
1
1
1
1
2 1
a
a
a
( )
1 2
+
Integrating w.r.to a, we get
F a
a
a
da
a a
a
da
a
e
e
( )
log ( )
( )
tan
( )
log ( )
=
+
+
+
+
= + ⋅
∫ ∫
−
1
2
1
1 1
1
2
1
1
2
2
1
2
2
(
( )
tan
( )
1 1
2
1
2
+
⎡
⎣
⎢
⎤
⎦
⎥ +
+
∫ ∫
−
a
da
a a
a
da
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 35 5/20/2016 11:20:45 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-648-2048.jpg)
![7.36 ■ Engineering Mathematics
= + ⋅ −
+
⋅
⎡
⎣
⎢
⎤
⎦
⎥ +
+
− −
−
∫
1
2
1
1
1
2
1
2 1
2
1
1
2
log ( ) tan tan
tan
( )
e a a
a
a a da
a a
a
d
da
a a
a a
a
da
a a
a
da
e
∫
∫ ∫
= + ⋅ −
+
+
+
−
− −
1
2
1
1 1
2 1
1
2
1
2
log ( ) tan
tan tan
⇒ F a a a C
e
( ) log ( ) tan
= + ⋅ +
−
1
2
1 2 1
Put a = 0, then F C C
e
( ) log ( ) tan
0
1
2
1 0 0
1
= + ⋅ + =
−
But from (1), we get F C
( )
0 0 0
= =
[
Hence, F a a a
e
( ) log ( ) tan
= + ⋅ −
1
2
1 2 1
⇒
log ( )
log ( ) tan
e
a
e
ax
x
dx a a
1
1
1
2
1
2
0
2 1
+
+
= + ⋅
∫
−
(2)
To deduce, put a 5 1 in (2).
∴
log ( )
log tan log log
e
e e e
x
x
dx
1
1
1
2
2 1
1
2
2
4 8
2
2
0
1
1
+
+
= ⋅ = ⋅ =
∫
− p p
EXAMPLE 7
Prove that
e
x
e dx a a
x
ax
e
2
2
2 5 1
( ) log ( ), .
1 1 0
0
∞
∫ ≥
Solution.
Let F a
e
x
e dx
x
ax
( ) ( )
= −
−
−
∞
∫ 1
0
(1)
Differentiating (1) w.r.to a, we get
dF
da a
e
x
e dx
e
x a
e dx
e
x
x
ax
x
ax
x
=
∂
∂
−
⎛
⎝
⎜
⎞
⎠
⎟ =
∂
∂
−
=
−
−
∞ −
−
∞
−
∫ ∫
( ) ( )
(
1 1
0 0
−
− −
−
∞
∫ e x dx
ax
)( )
0
= ⋅ =
− −
∞
− +
∞
∫ ∫
e e dx e dx
x ax a x
( )
0
1
0
=
− +
⎡
⎣
⎢
⎤
⎦
⎥ = −
+
− =
+
− + ∞
−∞
e
a a
e e
a
a x
( )
( )
[ ]
1
0
0
1
1
1
1
1
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 36 5/20/2016 11:20:51 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-649-2048.jpg)
![Improper Integrals ■ 7.37
Integrating w.r.to a,
⇒ F a
da
a
a C
e
( ) log ( )
=
+
= + +
∫1
1
Put a = 0, then F C C
e
( ) log
0 1
= + =
But from (1), we get F
e
x
dx C
x
( ) ( )
0 1 1 0 0
0
= − = =
−
∞
∫ [
Hence, F a a
e
( ) log ( )
= +
1
⇒ e
x
e dx a
x
ax
e
−
−
∞
− = +
∫ ( ) log ( )
1 1
0
EXAMPLE 8
Evaluate log( cos ) , .
1 0 1
0
1 a a
p
x dx
∫
Solution.
Let F x dx
( ) log( cos )
a a
p
= +
∫ 1
0
(1)
Differentiating w.r.to a, by Leibnitz’s rule, we get
dF
d
x dx
x
x dx
x
a a
a
a
a
a
a
p p
=
∂
∂
+ =
+
⋅
=
+
∫ ∫
0 0
1
1
1
1
1
[log ( cos )]
cos
cos
cos
co
os
cos
cos
cos
x
dx
x
x
dx
x
dx
0
0
0
1 1 1
1
1
1
1
1
p
p
p
a
a
a
a a
∫
∫
∫
=
+ −
+
= −
+
⎡
⎣
⎢
⎤
⎦
⎥
∴
= −
+
= −
+
∫ ∫
∫
1 1 1
1
1 1 1
1
0 0
0
0
a a a
a a a
p p
p
p
dx
x
dx
x
x
dx
cos
[ ]
cos x
dx
p
a a a
p
= −
+
∫
1 1
1
0
cos
(2)
Let I
x
dx
=
+
∫
1
1
0
a
p
cos
Put t
x
= tan .
2
dt
x
dx
⋅
sec
2
1
2
2
∴ =
⇒ dx
dt
x
dt
x
dt
t
= =
+
=
+
2
2
2
1
2
2
1
2 2
2
sec tan
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 37 5/20/2016 11:21:03 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-650-2048.jpg)
![7.38 ■ Engineering Mathematics
When x = 0, t = tan 0 = 0 and when x = p, t = = ∞
tan
p
2
∴ I
t
t
dt
t
=
+
−
+
⋅
+
∞
∫
1
1
1
1
2
1
2
2
2
0
a
=
=
=
2
1 1
2
1 1
2
1
1
1
2 2
0
2
0
2
dt
t t
dt
t
dt
t
+ + −
+ + −
−
+
−
+
⎡
⎣
⎢
∞
∞
∫
∫
a
a a
a
a
a
( )
( )
( )
⎤
⎤
⎦
⎥
∞
∫
0
{ cos
tan
tan
x
x
x
=
−
+
1
2
1
2
2
2
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
∴
=
−
⋅
+
−
+
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
− +
−
∞
2
1
1
1
1
1
1
0 1
2
1 1
1
0
a a
a
a
a
a
a a
tan ,
( )( )
tan
t
= −
− −
∞ −
[ ]
−
⋅
−
= − ⋅
−
1 1
2 2
2
0
2
1 2 1
1
1
tan
= =
a
p p
a
a
p
a a
p
a
dF
d
Integrating w.r.to a, we get
F d
d d d
( ) log
a
p
a
p
a a
a p
a
a
p
a
a a
p a p
a
a a
= −
−
⎡
⎣
⎢
⎤
⎦
⎥ = −
−
= −
−
∫ ∫ ∫ ∫
1 1 1
2 2 2
Let I
d
1 2
1
=
−
∫
a
a a
Put a u a u u
= =
sin cos
∴d d
I
d d d
1 2
1
=
−
= =
∫ ∫ ∫
cos
sin sin
cos
sin cos sin
u u
u u
u u
u u
u
u
=
= − +
∫cosec
cosec
u u
u u
d
e
log ( cot )
= − +
⎡
⎣
⎢
⎤
⎦
⎥
= −
+
⎡
⎣
⎢
⎤
⎦
⎥ = −
+ −
log
sin
cos
sin
log
cos
sin
log
e
e e
1
1 1 1
u
u
u
u
u
a
a
a
2
⎡
⎣
⎢
⎤
⎦
⎥
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 38 5/20/2016 11:21:14 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-651-2048.jpg)
![Improper Integrals ■ 7.39
∴ F C
e e
e e
( ) log log
log log
a p a p
a
a
p a
a
a
=
+ −
⎡
⎣
⎢
⎤
⎦
⎥ +
+ −
⎡
⎣
⎢
⎤
⎦
⎥
⎡
+
= +
1 1
1 1
2
2
⎣
⎣
⎢
⎤
⎦
⎥ +
⋅
+ −
⎡
⎣
⎢
⎤
⎦
⎥ + + +
C
C C
e e
= = −
p a
a
a
p a
log
( )
log ( )
1 1
1 1
2
2
Put a = 0, then F C
e
( ) log
0 2
= +
p
From (1), we get F dx
( ) log
0 1 0
0
= =
∫
p
∴ p p
log log
e e
C C
2 0 2
+ = = −
⇒
∴ F e e e
( ) log ( ) log log
a p a p p
a
= + − − =
+ −
⎡
⎣
⎢
⎤
⎦
⎥
1 1 2
1 1
2
2
2
∴ log ( cos ) log
1
1 1
2
0
2
+ =
+ −
⎡
⎣
⎢
⎤
⎦
⎥
∫ a p
a
p
x dx e
EXAMPLE 9
Show that
log ( sin )
sin
, .
/
e y x
x
dx y y
1
1 1 0
2
2
0
2
1
5p 1 2
p
⎡
⎣ ⎤
⎦
∫ ≥
Solution.
Let F y
y x
x
dx
e
( )
log ( sin )
sin
/
=
+
∫
1 2
2
0
2
p
(1)
Differentiating (1) w.r.to y, using Leibnitz’s rule, we get
dF
dy y
y x
x
dx
x y
y
=
∂
∂
+
⎡
⎣
⎢
⎤
⎦
⎥ =
∂
∂
+
∫
log ( sin )
sin sin
log ( si
/
1 1
1
2
2
0
2
2
p
n
n )
/
2
0
2
x dx
( )
⎡
⎣
⎢
⎤
⎦
⎥
∫
p
= ⋅
+
⋅
⎡
⎣
⎢
⎤
⎦
⎥
=
+
⎡
⎣
⎢
⎤
⎦
⎥
∫
1 1
1
1
1
2 2
2
0
2
2
0
2
sin ( sin )
sin
sin
/
/
x y x
x dx
y x
p
p
∫
∫
∫
=
+
⎡
⎣
⎢
⎤
⎦
⎥
dx
x
x y x
dx
sec
sec tan
[
/ 2
2 2
0
2
p
Multiplying Nr and Dr by
y sec ]
sec
tan tan
sec
( )tan
/
2
2
2 2
0
2 2
1 1 1
x
x
x y x
dx
x
y
=
+ +
⎡
⎣
⎢
⎤
⎦
⎥ =
+ +
∫
p
2
2
0
2
x
dx
⎡
⎣
⎢
⎤
⎦
⎥
∫
p/
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 39 5/20/2016 11:21:26 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-652-2048.jpg)
![7.40 ■ Engineering Mathematics
Put t x dt xdx
= =
tan . sec
[ 2
When and when
x t x t
= = = = = = ∞
0 0 0
2 2
, tan , tan
p p
∴
dF
dy
dt
y t y
dt
y
t
=
+ +
=
+
+
+
∞ ∞
∫ ∫
1 1
1
1 1
1
2
0 2
0
( ) ( )
( )
=
+
⋅
+ +
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
+
∞
−
∞
−
1
1
1
1
1
1
1
1
1
1
0
1
( )
( )
tan
( )
tan
y
y
t
y
y
−
−
[ ] =
+
−
⎡
⎣
⎢
⎤
⎦
⎥ =
+
−
tan 1
0
1
1 2
0
2 1
y y
p p
Integrating w.r.to y, we get
F y
y
dy y dy
y
C y C
( ) ( )
( )
/
/
=
+
⋅ = + =
+
+ = + +
∫ ∫
−
p p p
p
2 1 2
1
2
1
1 2
1
1 2
1 2
/
Put y = 0, then F C
( )
0 = +
p
But from (1), F
x
dx
( )
log
sin
/
0
1
0
2
0
2
= =
∫
p
∴ p p
+ = = −
C C
0 ⇒
∴ F y y
( ) = +
p p
1 − y
= +
⎡
⎣ ⎤
⎦
p 1 1
−
∴
log ( sin )
sin
/
1
1 1
2
2
0
2
+
= + −
{ }
∫
y x
x
dx y
p
p
EXAMPLE 10
Differentiating x dx
m
0
1
∫ w.r.to m successively, evaluate x x dx
m
e
n
(log )
0
1
∫ , where n N
∈ .
Solution.
Let F m x dx
m
( ) = ∫
0
1
Differentiating w.r.to m, using Leibnitz’s rule, we get
dF
dm m
x dx x x dx
m m
e
=
∂
∂
=
∫ ∫
0
1
0
1
( ) log
d
dx
a a a
x x
e
=
⎡
⎣
⎢
⎤
⎦
⎥
( ) log
{
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 40 5/20/2016 11:21:54 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-653-2048.jpg)
![Improper Integrals ■ 7.41
Differentiating again w.r.to m, using Leibnitz’s rule, we get
d F
dm m
x x dx
x
m
x dx
x x x dx
m
e
e
m
e
m
e
2
2
0
1
0
1
=
∂
∂
=
∂
∂
= ⋅
∫
∫
( log )
log ( )
log log
0
0
1
2
0
1
∫ ∫
= x x dx
m
e
(log )
Proceeding in the same way, differentiating n times w.r.to m, we get
d F
dm
x x dx
n
n
m
e
n
= ∫ (log )
0
1
(1)
But F m x dx
x
m m m
m
m
( ) [ ]
=
⎡
⎣
⎢
⎤
⎦
⎥ =
+
− =
+
∫
0
1 1
0
1
1
1
1
1 0
1
1
=
+
+
∴ dF
dm m
d F
dm m m
= −
+
= − − ⋅
+
= − ⋅
+
1
1
1 2
1
1
1
2
1
2
2
2 3
2
3
( )
( )( )
( )
( )
!
( )
and
d F
dm m m
3
3
2
4
3
4
1 2
3
1
1
3
1
= − ⋅
−
+
= −
+
( ) !
( )
( )
( )
!
( )
Proceeding in the same way, differentiating n times w.r.to m, we get
d F
dm
n
m
n
n
n
n
=
−
+ +
( ) !
( )
1
1 1
(2)
From (1) and (2), we get
x x dx
n
m
m
e
n n
n
(log ) ( )
!
( )
0
1
1
1
1
∫ = −
+ +
EXAMPLE 11
Evaluate
dx
a x
2 2
0 1
∞
∫ and then using the method of differentiation under the sign of integration
[i.e., Leibnitz’s rule] find the value of the integrals
dx
a x
( )
,
2 2 2
0 1
∞
∫
dx
a x
( )
2 2 3
0 1
∞
∫ and hence, obtain an
expression for
dx
a x n
( )
.
2 2 1
0 1 1
∞
∫
Solution.
Given
dx
a x
a
2 2
0
0
+
∞
∫ ,
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 41 5/20/2016 11:22:04 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-654-2048.jpg)
![7.42 ■ Engineering Mathematics
We know
dx
a x a
x
a a
2 2
0
1
0
1 1
1 1
0
+
=
⎡
⎣
⎢
⎤
⎦
⎥ = ∞ −
[ ]
∞
−
∞
− −
∫ tan tan tan = −
⎡
⎣
⎢
⎤
⎦
⎥
1
2
0
a
p
⇒
dx
a x a
2 2
0
2
+
=
∞
∫
p
(1)
Differentiating (1) w.r.to a, by Leibnitz’s rule, we get
d
da
dx
a x
d
da a
2 2
0
2
+
⎡
⎣
⎢
⎤
⎦
⎥ =
⎛
⎝
⎜
⎞
⎠
⎟
∞
∫
p
⇒
∂
∂ +
⎛
⎝
⎜
⎞
⎠
⎟ = −
⎛
⎝
⎜
⎞
⎠
⎟
∞
∫ a a x
dx
a
1
2
1
2 2
0
2
p
{ y
x
dy
dx x
= ⇒ = −
1 1
2
⎡
⎣
⎢
⎤
⎦
⎥
⇒ ∂
∂
+
⎡
⎣ ⎤
⎦ = −
−
∞
∫ a
a x dx
a
( )
2 2 1
0
2
2
p
⇒ ( )( )
− + = −
−
∞
∫ 1 2
2
2 2 2
0
2
a x a dx
a
p
⇒ −
+
= −
∞
∫
2
1
2
2 2 2
0
2
a
a x
dx
a
( )
p
⇒
1
4
2 2 2
0
3
( )
a x
dx
a
+
=
∞
∫
p
(2)
Differentiating (2) w.r.to a, by Leibnitz’s rule, we get
d
da a x
dx
d
da a
1
4
2 2 2
0
3
( )
+
=
⎛
⎝
⎜
⎞
⎠
⎟
∞
∫
p
⇒
∂
∂ +
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟
∞
−
∫ a a x
dx
d
da
a
1
4
2 2 2
0
3
( )
p
⇒ ∂
∂
+ = −
−
∞
−
∫ a
a x dx a
( ) ( )
2 2 2
0
4
4
3
p
⇒ ( )( )
− + = −
−
∞
−
∫ 2 2
3
4
2 2 3
0
4
a x adx a
p
⇒ −
+
= −
∞
∫
4
1 3
4
2 2 3
0
4
a
a x
dx
a
( )
p
⇒ dx
a x a
( )
2 2 3
0
5
3
16
+
=
∞
∫
p (3)
M07_ENGINEERING_MATHEMATICS-I _CH07_Part A.indd 42 5/20/2016 11:22:14 AM](https://image.slidesharecdn.com/p-240106174416-34a05fe0/75/P-Sivaramakrishna-Das-C-Vijayakumari-Engineering-Mathematics-Pearson-Education-2017-pdf-655-2048.jpg)