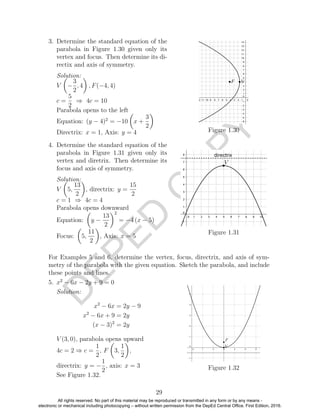
This document is the learner's material for precalculus developed by the Department of Education of the Philippines. It was collaboratively developed by educators from public and private schools. The document contains the copyright notice and details that it is the property of the Department of Education and may not be reproduced without their permission. It provides the table of contents that outlines the units and lessons covered in the material.






































































![D
EPED
C
O
PY
y = 7 =⇒ x = −1 and y = −1 =⇒ x = −1
Solutions: (−1, 7) and (−1, −1) 2
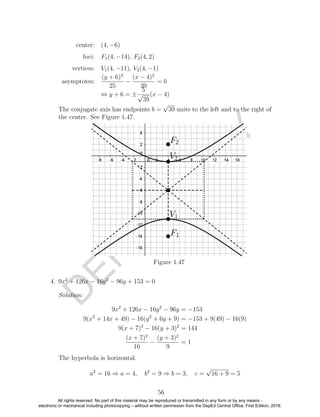
The graphs of the equations in the preceding example with the points of
intersection are shown below.
Usually, the general form is more convenient to use in solving systems of
equations. However, sometimes the solution can be simplified by writing the
equations in standard form. Moreover, the standard form is best for graphing.
Let us again solve the previous example in a different way.
Solution 2. By completing the square, we can change the first equation into stan-
dard form:
y2
− 4x − 6y = 11 =⇒ 4(x + 5) = (y − 3)2
.
4(x + 5) = (y − 3)2
4(3 − x) = (y − 3)2
Using substitution or the transitive property of equality, we get
4(x + 5) = 4(3 − x) =⇒ x = −1.
Substituting this value of x into the second equation, we have
4[3 − (−1)] = (y − 3)2
=⇒ 16 = (y − 3)2
=⇒ y = 7 or y = −1.
The solutions are (−1, 7) and (−1, −1), same as Solution 1. 2
71
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-77-320.jpg)









![D
EPED
C
O
PY
Example 2.1.1. Determine the first five terms of each defined sequence, and
give their associated series.
(1) {2 − n}
(2) {1 + 2n + 3n2
}
(3) {(−1)n
}
(4) {1 + 2 + 3 + · · · + n}
Solution. We denote the nth term of a sequence by an, and S = a1 + a2 + a3 +
a4 + a5.
(1) an = 2 − n
First five terms: a1 = 2 − 1 = 1, a2 = 2 − 2 = 0, a3 = −1, a4 = −2, a5 = −3
Associated series: S = a1 + a2 + a3 + a4 + a5 = 1 + 0 − 1 − 2 − 3 = −5
(2) an = 1 + 2n + 3n2
First five terms: a1 = 1 + 2 · 1 + 3 · 12
= 6, a2 = 17, a3 = 34, a4 = 57, a5 = 86
Associated series: S = 6 + 17 + 34 + 57 + 86 = 200
(3) an = (−1)n
First five terms: a1 = (−1)1
= −1, a2 = (−1)2
= 1, a3 = −1, a4 = 1,
a5 = −1
Associated series: S = −1 + 1 − 1 + 1 − 1 = −1
(4) an = 1 + 2 + 3 + · · · + n
First five terms: a1 = 1, a2 = 1+2 = 3, a3 = 1+2+3 = 6, a4 = 1+2+3+4 =
10, a5 = 1 + 2 + 3 + 4 + 5 = 15
Associated series: S = 1 + 3 + 6 + 10 + 15 = 35 2
The sequence {an} defined by an = an−1 + an−2 for n ≥ 3, where a1 =
a2 = 1, is called a Fibonacci sequence. It terms are 1, 1, 2, 3, 5, 8, 13, . . ..
An arithmetic sequence is a sequence in which each term after the first
is obtained by adding a constant (called the common difference) to the
preceding term.
If the nth term of an arithmetic sequence is an and the common difference is
d, then
an = a1 + (n − 1)d.
The associated arithmetic series with n terms is given by
Sn =
n(a1 + an)
2
=
n[2a1 + (n − 1)d]
2
.
82
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-88-320.jpg)


![D
EPED
C
O
PY
8. The 7th term of an arithmetic sequence is 25. Its first, third, and 21st term
form a geometric sequence. Find the first term and the common difference of
the sequence.
Solution: a7 = a1 + 6d = 25 ⇒ a1 = 25 − 6d
a3
a1
=
a21
a3
, or a1a21 = a2
3.
(25 − 6d) (25 − 6d + 20d) = (25 − 6d + 2d)2
d = 0 and an = 25 for all n, or d = 4 and a1 = 1.
9. Let {an} be an arithmetic sequence and {bn} an arithmetic sequence of positive
integers. Prove that the sequence with nth
term abn is arithmetic.
Solution: Let the common difference of {an} be d and of {bn} be c.
abn+1 − abn = [a1 + (bn+1 − 1) d] − [a1 + (bn − 1) d] = bn+1 − bn = c
This proves that the difference between any two consecutive terms of {abn } is
a constant independent of n.
10. Let {an} be a geometric sequence. Prove that {a3
n} is a geometric sequence.
Solution: Let r be the common ratio of {an}.
a3
n = (a1rn−1
)
3
= a3
1 (r3
)
n−1
.
Thus {a3
n} is a geometric sequence with first term a3
1 and common ratio r3
.
11. If {an} is a sequence such that its first three terms form both an arithmetic
and a geometric sequence, what can be concluded about {an}?
Solution: There is a real number r such that a2 = a1r and a3 = a1r2
.
Since a1, a2 and a3 form an arithmetic sequence, then a2 − a1 = a3 − a2, or
a3 − 2a2 + a1 = 0.
a3 − 2a2 + a1 = a1r2
− 2a1r + a1 = a1
(r − 1)2
= 0 ⇒ a1 = 0 or r = 1.
If a1 = 0, then a1 = a2 = a3 = 0. If r = 1, then a1 = a2 = a3.
In all cases, a1 = a2 = a3.
Supplementary Problems 2.1
1. Find the 5th term of the arithmetic sequence whose 3rd term is 35 and whose
10th term is 77.
2. Suppose that the fourth term of a geometric sequence is 2
9
and the sixth term
is 8
81
. Find the first term and the common ratio.
85
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-91-320.jpg)

![D
EPED
C
O
PY
(2) Evaluate sums written in sigma notation
(3) Properties of sigma notation
(4) Calculating sums using the properties of sigma notation
Introduction
The sigma notation is a shorthand for writing sums. In this lesson, we will
see the power of this notation in computing sums of numbers as well as algebraic
expressions.
2.2.1. Writing and Evaluating Sums in Sigma Notation
Mathematicians use the sigma notation to denote a sum. The uppercase Greek
letter Σ (sigma) is used to indicate a “sum.” The notation consists of several
components or parts.
Let f(i) be an expression involving an integer i. The expression
f(m) + f(m + 1) + f(m + 2) + · · · + f(n)
can be compactly written in sigma notation, and we write it as
n
i=m
f(i),
which is read “the summation of f(i) from i = m to n.” Here, m
and n are integers with m ≤ n, f(i) is a term (or summand) of the
summation, and the letter i is the index, m the lower bound, and n
the upper bound.
Example 2.2.1. Expand each summation, and simplify if possible.
(1)
4
i=2
(2i + 3)
(2)
5
i=0
2i
(3)
n
i=1
ai
(4)
6
n=1
√
n
n + 1
Solution. We apply the definition of sigma notation.
(1)
4
i=2
(2i + 3) = [2(2) + 3] + [2(3) + 3] + [2(4) + 3] = 27
87
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-93-320.jpg)


![D
EPED
C
O
PY
= c[f(m) + f(m + 1) + · · · + f(n)]
= c
n
i=m
f(i) 2
n
i=m
[f(i) + g(i)] =
n
i=m
f(i) +
n
i=m
g(i)
Proof.
n
i=m
[f(i) + g(i)]
= [f(m) + g(m)] + · · · + [f(n) + g(n)]
= [f(m) + · · · + f(n)] + [g(m) + · · · + g(n)]
=
n
i=m
f(i) +
n
i=m
g(i) 2
n
i=m
c = c(n − m + 1)
Proof.
n
i=m
c = c + c + c + · · · + c
n−m+1 terms
= c(n − m + 1) 2
A special case of the above result which you might encounter more often is
the following:
n
i=1
c = cn.
Telescoping Sum
n
i=m
[f(i + 1) − f(i)] = f(n + 1) − f(m)
90
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-96-320.jpg)
![D
EPED
C
O
PY
Proof.
n
i=m
f(i + 1) − f(i)
= [f(m + 1) − f(m)] + [f(m + 2) − f(m + 1)]
+ [f(m + 3) − f(m + 2)] + · · · + [f(n + 1) − f(n)]
Note that the terms, f(m+1), f(m+2), . . . , f(n), all cancel out. Hence, we have
n
i=m
[f(i + 1) − f(i)] = f(n + 1) − f(m). 2
Example 2.2.3. Evaluate:
30
i=1
(4i − 5).
Solution.
30
i=1
(4i − 5) =
30
i=1
4i −
30
i=1
5
= 4
30
i=1
i −
30
i=1
5
= 4
(30)(31)
2
− 5(30)
= 1710 2
Example 2.2.4. Evaluate:
1
1 · 2
+
1
2 · 3
+
1
3 · 4
+ · · · +
1
99 · 100
.
Solution.
1
1 · 2
+
1
2 · 3
+
1
3 · 4
+ · · · +
1
99 · 100
=
99
i=1
1
i(i + 1)
=
99
i=1
i + 1 − i
i(i + 1)
=
99
i=1
i + 1
i(i + 1)
−
i
i(i + 1)
91
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-97-320.jpg)

![D
EPED
C
O
PY
= 2n(n2
− 1) + 3n(n + 1)
= 2n(n − 1)(n + 1) + 3n(n + 1)
= n(n + 1)[2(n − 1) + 3]
= n(n + 1)(2n + 1).
Finally, after dividing both sides of the equation by 6, we obtain the desired
formula n
i=1
i2
=
n(n + 1)(2n + 1)
6
. 2
More Solved Examples
1. Expand the following sums and simplify if possible:
(a)
5
i=1
(i2
− i + 1)
(b)
6
i=3
i2 i + 1
2
2
(c)
5
i=0
x3i
y15−3i
(d)
9
i=1
x2i+1
(i + 1)2
(e)
∞
i=1
3−i+2
2i+1
Solution:
(a)
5
i=1
(i2
− i + 1) = (12
− 1 + 1) + (22
− 2 + 1) + . . . + (52
− 5 + 1) = 45 or
5(5 + 1)(2(5) + 1)
6
−
5(5 + 1)
2
+ 5 = 45
(b)
6
i=3
i2 i + 1
2
2
= 32 4
2
2
+ . . . + 62 7
2
2
= 802
(c)
5
i=0
x3i
y15−3i
= x3(0)
y15−3(0)
+ . . . + x3(5)
y15−3(5)
= xy15
+ x3
y12
+ x6
y9
+
x9
y6
+ x12
y3
+ x15
y
93
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-99-320.jpg)
![D
EPED
C
O
PY
(d)
9
i=1
x2i+1
(i + 1)2
=
x3
(1 + 1)2
+
x5
(2 + 1)2
+ . . . +
x19
(9 + 1)2
= 4x3
+ 9x5
+ 16x7
+
. . . + 100x19
(e)
∞
i=1
3−i+2
2i+1
= 27
∞
i=1
2
3
i+1
, which is an infinite geometric series with
|r| =
2
3
< 1 and a1 =
4
9
, giving us
∞
i=1
3−i+2
2i+1
= 27
4/9
1 − (2/3)
= 36.
2. Evaluate
20
i=1
[2(i − 1) + 2].
Solution:
20
i=1
(2(i − 1) + 2) =
20
i=1
2i = 4
(20)(21)
2
= 840.
3. Find a formula for
1
1(3)
+
1
2(4)
+
1
3(5)
+ · · · +
1
n(n + 2)
given any positive
integer n.
Solution: We have
1
1(3)
+
1
2(4)
+
1
3(5)
+· · ·+
1
n(n + 2)
=
n
i=1
1
i(i + 2)
. Rewriting
yields
1
i(i + 2)
=
(2 − 1) + (i − i)
i(i + 2)
=
1
i
−
1
i + 2
−
1
i(i + 2)
or equivalently
1
i + 2
=
1
2
1
i
−
1
i + 2
.
Expanding the sum term by term,
n
i=1
1
i(i + 2)
=
n
i=1
1
2
1
i
−
1
i + 2
= 1 −
1
3
+
1
2
−
1
4
+
1
3
−
1
5
· · ·
+
1
n − 2
−
1
n
+
1
n − 1
−
1
n + 1
+
1
n
−
1
n + 2
= 1 +
1
2
−
1
n + 1
−
1
n + 2
=
n(3n + 2)
2(n + 1)(n + 2)
.
94
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-100-320.jpg)




![D
EPED
C
O
PY
Part 2. Assume that the formula is true for n = k ≥ 1:
1 + 2 + 3 + · · · + k =
k(k + 1)
2
.
We want to show that the formula is true for n = k + 1; that is,
1 + 2 + 3 + · · · + k + (k + 1) =
(k + 1)(k + 1 + 1)
2
.
Using the formula for n = k and adding k + 1 to both sides of the equation,
we get
1 + 2 + 3 + · · · + k + (k + 1) =
k(k + 1)
2
+ (k + 1)
=
k(k + 1) + 2(k + 1)
2
=
(k + 1)(k + 2)
2
=
(k + 1) [(k + 1) + 1]
2
We have proven the two conditions required by the Principle of Mathematical
Induction. Therefore, the formula is true for all positive integers n. 2
Example 2.3.2. Use mathematical induction to prove the formula for the sum
of a geometric series with n terms:
Sn =
a1 (1 − rn
)
1 − r
, r = 1.
Solution. Let an be the nth term of a geometric series. From Lesson 2.1, we know
that an = a1rn−1
.
Part 1.
Prove that the formula is true for n = 1.
a1(1 − r1
)
1 − r
= a1 = S1
The formula is true for n = 1.
Part 2. Assume that the formula is true for n = k ≥ 1: Sk =
a1(1 − rk
)
1 − r
. We
want to prove that it is also true for n = k + 1; that is,
Sk+1 =
a1(1 − rk+1
)
1 − r
.
99
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-105-320.jpg)
![D
EPED
C
O
PY
We know that
Sk+1 = a1 + a2 + · · · + ak
Sk
+ak+1
= Sk + ak+1
=
a1 1 − rk
1 − r
+ a1rk
=
a1 1 − rk
+ a1rk
(1 − r)
1 − r
=
a1 1 − rk
+ rk
− rk+1
1 − r
=
a1 1 − rk+1
1 − r
By the Principle of Mathematical Induction, we have proven that
Sn =
a1(1 − rn
)
1 − r
for all positive integers n. 2
Example 2.3.3. Using mathematical induction, prove that
12
+ 22
+ 32
+ · · · + n2
=
n(n + 1)(2n + 1)
6
for all positive integers n.
Solution. We again establish the two conditions stated in the Principle of Math-
ematical Induction.
Part 1
1(1 + 1)(2 · 1 + 1)
6
=
1 · 2 · 3
6
= 1 = 12
The formula is true for n = 1.
Part 2
Assume: 12
+ 22
+ 32
+ · · · + k2
=
k(k + 1)(2k + 1)
6
.
Prove: 12
+ 22
+ 32
+ · · · + k2
+ (k + 1)2
=
(k + 1)(k + 2) [2(k + 1) + 1]
6
=
(k + 1)(k + 2)(2k + 3)
6
.
100
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-106-320.jpg)
![D
EPED
C
O
PY
12
+ 22
+ 32
+ · · · + k2
+ (k + 1)2
=
k(k + 1)(2k + 1)
6
+ (k + 1)2
=
k(k + 1)(2k + 1) + 6(k + 1)2
6
=
(k + 1) [k(2k + 1) + 6(k + 1)]
6
=
(k + 1) (2k2
+ 7k + 6)
6
=
(k + 1)(k + 2)(2k + 3)
6
Therefore, by the Principle of Mathematical Induction,
12
+ 22
+ 32
+ · · · + n2
=
n(n + 1)(2n + 1)
6
for all positive integers n. 2
2.3.2. Proving Divisibility Statements
We now prove some divisibility statements using mathematical induction.
Example 2.3.4. Use mathematical induction to prove that, for every positive
integer n, 7n
− 1 is divisible by 6.
Solution. Similar to what we did in the previous session, we establish the two
conditions stated in the Principle of Mathematical Induction.
Part 1
71
− 1 = 6 = 6 · 1
71
− 1 is divisible by 6.
Part 2
Assume: 7k
− 1 is divisible by 6.
To show: 7k+1
− 1 is divisible by 6.
7k+1
− 1 = 7 · 7k
− 1 = 6 · 7k
+ 7k
− 1 = 6 · 7k
+ (7k
− 1)
By definition of divisibility, 6 · 7k
is divisible by 6. Also, by the hypothesis
(assumption), 7k
− 1 is divisible by 6. Hence, their sum (which is equal to
7k+1
− 1) is also divisible by 6.
101
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-107-320.jpg)


![D
EPED
C
O
PY
that 0! = 1 and, for every positive integer n, n! = 1 · 2 · 3 · · · n. The factorial also
satisfies the property that (n + 1)! = (n + 1) · n!.
Example 2.3.7. Use mathematical induction to prove that 3n
< (n + 2)! for
every positive integer n. Can you refine or improve the result?
Solution. We proceed with the usual two-part proof.
Part 1
31
= 3 < 6 = 3! = (1 + 2)! =⇒ 31
< (1 + 2)!
Thus, the desired inequality is true for n = 1.
Part 2
Assume: 3k
< (k + 2)!
To show: 3k+1
< (k + 3)!
Given that 3k
< (k + 2)!, we multiply both sides of the inequality by 3 and
obtain
3 3k
< 3 [(k + 2)!] .
This implies that
3 3k
< 3 [(k + 2)!] < (k + 3) [(k + 2)!] , since k > 0,
and so
3k+1
< (k + 3)!.
Therefore, by the Principle of Math Induction, we conclude that 3n
< (n+2)!
for every positive integer n.
The left-hand side of the inequality is defined for any integer n. The right-
hand side makes sense only if n + 2 ≥ 0, or n ≥ −2.
When n = −2: 3−2
=
1
9
< 1 = 0! = (−2 + 2)!
When n = −1: 3−1
=
1
3
< 1 = 1! = (−1 + 2)!
When n = 0: 30
= 1 < 2 = 2! = (0 + 2)!
Therefore, 3n
< (n + 2)! for any integer n ≥ −2. 2
104
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-110-320.jpg)


![D
EPED
C
O
PY
5. n2
> 2n + 3 for n ≥ 4.
Solution:
Part 1.
24
= 16 > 7 = 2(2) + 3 The inequality is true for n = 4.
Part 2
Assume: k2
> 2k + 3
Prove: (k + 1)2
> 2(k + 1) + 3
We expand (k + 1)2
and use the inequality in the hypothesis to get
(k + 1)2
= k2
+ 2k + 1 > (2k + 3) + 2k + 1 = 4(k + 1) > 2(k + 1) + 3 if k > 0.
Therefore, by the principle of math induction, n2
> 2n + 3 for n ≥ 4.
6. Prove that 2n+3
< (n + 3)! for n ≥ 4.
Solution:
Part 1.
24+3
= 27
< 1 · 2 · 3 · · · 7 = (4 + 3)! The inequality is true for n = 1.
Part 2
Assume: 2k+3
< (k + 3)!
Prove: 2k+4
< (k + 4)!
Given that 2k+3
< (k + 3)!, we multiply both sides of the inequality by 2 and
obtain
2 2k+3
< 2 [(k + 3)!].
This implies that
2k+4
< 2 [(k + 3)!] < (k + 4) [(k + 3)!], if k > 0.
Therefore, by the principle of math induction, 2k+3
< (k+3)! for every positive
integer n.
107
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-113-320.jpg)






































![D
EPED
C
O
PY
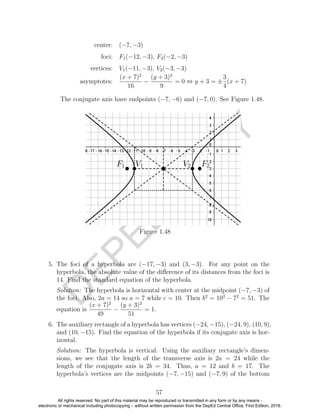
To sketch the graph of y = sin x, we plot the points presented in Table 3.16,
and join them with a smooth curve. See Figure 3.17. Since the graph repeats
every 2π units, Figure 3.18 shows periodic graph over a longer interval.
Figure 3.17
Figure 3.18
We can make observations about the cosine function that are similar to the
sine function.
• y = cos x has domain R and range [−1, 1].
• y = cos x is periodic with period 2π. The graph of y = cos x is shown in
Figure 3.19.
Figure 3.19
146
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-152-320.jpg)
![D
EPED
C
O
PY
From the graphs of y = sin x and y = cos x in Figures 3.18 and 3.19, re-
spectively, we observe that sin(−x) = − sin x and cos(−x) = cos x for any real
number x. In other words, the graphs of y = cos(−x) and y = cos x are the same,
while the graph of y = sin(−x) is the same as that of y = − sin x.
In general, if a function f satisfies the property that f(−x) = f(x) for all x
in its domain, we say that such function is even. On the other hand, we say that
a function f is odd if f(−x) = −f(x) for all x in its domain. For example, the
functions x2
and cos x are even, while the functions x3
− 3x and sin x are odd.
3.3.2. Graphs of y = a sin bx and y = a cos bx
Using a table of values from 0 to 2π, we can sketch the graph of y = 3 sin x, and
compare it to the graph of y = sin x. See Figure 3.20 wherein the solid curve
belongs to y = 3 sin x, while the dashed curve to y = sin x. For instance, if x = π
2
,
then y = 1 when y = sin x, and y = 3 when y = 3 sin x. The period, x-intercepts,
and domains are the same for both graphs, while they differ in the range. The
range of y = 3 sin x is [−3, 3].
Figure 3.20
In general, the graphs of y = a sin x and y = a cos x with a > 0 have the same
shape as the graphs of y = sin x and y = cos x, respectively. If a < 0, there is a
reflection across the x-axis.
In the graphs of y = a sin x and y = a cos x, the number |a| is called
its amplitude. It dictates the height of the curve. When |a| < 1,
the graphs are shrunk vertically, and when |a| > 1, the graphs are
stretched vertically.
Now, in Table 3.21, we consider the values of y = sin 2x on [0, 2π].
147
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-153-320.jpg)
![D
EPED
C
O
PY
x 0 π
6
π
4
π
3
π
2
2π
3
3π
4
5π
6
π
y 0
√
3
2
1
√
3
2
0 −
√
3
2
−1 −
√
3
2
0
0 0.87 1 0.87 0 −0.87 −1 −0.87 0
x 7π
6
5π
4
4π
3
3π
2
5π
3
7π
4
11π
6
2π
y
√
3
2
1
√
3
2
0 −
√
3
2
−1 −
√
3
2
0
0.87 1 0.87 0 −0.87 −1 −0.87 0
Table 3.21
Figure 3.22
Figure 3.22 shows the graphs of y = sin 2x (solid curve) and y = sin x (dashed
curve) over the interval [0, 2π]. Notice that, for sin 2x to generate periodic values
similar to [0, 2π] for y = sin x, we just need values of x from 0 to π. We then
expect the values of sin 2x to repeat every π units thereafter. The period of
y = sin 2x is π.
If b = 0, then both y = sin bx and y = cos bx have period given by
2π
|b|
.
If 0 < |b| < 1, the graphs are stretched horizontally, and if |b| > 1, the
graphs are shrunk horizontally.
To sketch the graphs of y = a sin bx and y = a cos bx, a, b = 0, we may proceed
with the following steps:
(1) Determine the amplitude |a|, and find the period 2π
|b|
. To draw one cycle
of the graph (that is, one complete graph for one period), we just need to
complete the graph from 0 to 2π
|b|
.
148
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-154-320.jpg)
![D
EPED
C
O
PY
(2) Divide the interval into four equal parts, and get five division points: x1 = 0,
x2, x3, x4, and x5 = 2π
|b|
, where x3 is the midpoint between x1 and x5 (that
is, 1
2
(x1 + x5) = x3), x2 is the midpoint between x1 and x3, and x4 is the
midpoint between x3 and x5.
(3) Evaluate the function at each of the five x-values identified in Step 2. The
points will correspond to the highest point, lowest point, and x-intercepts
of the graph.
(4) Plot the points found in Step 3, and join them with a smooth curve similar
to the graph of the basic sine curve.
(5) Extend the graph to the right and to the left, as needed.
Example 3.3.1. Sketch the graph of one cycle of y = 2 sin 4x.
Solution. (1) The period is 2π
4
= π
2
, and the amplitude is 2.
(2) Dividing the interval [0, π
2
] into 4 equal parts, we get the following x-
coordinates: 0, π
8
, π
4
, 3π
8
, and π
2
.
(3) When x = 0, π
4
, and π
2
, we get y = 0. On the other hand, when x = π
8
, we
have y = 2 (the amplitude), and y = −2 when x = 3π
8
.
(4) Draw a smooth curve by connecting the points. There is no need to proceed
to Step 5 because the problem only asks for one cycle.
Example 3.3.2. Sketch the graph of y = −3 cos x
2
.
Solution. (1) The amplitude is | − 3| = 3, and the period is
2π
1
2
= 4π.
(2) We divide the interval [0, 4π] into four equal parts, and we get the following
x-values: 0, π, 2π, 3π, and 4π.
149
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-155-320.jpg)
![D
EPED
C
O
PY
(3) We have y = 0 when x = π and 3π, y = −3 when x = 0 and 4π, and y = 3
when x = 2π.
(4) We trace the points in Step 3 by a smooth curve.
(5) We extend the pattern in Step 4 to the left and to the right.
Example 3.3.3. Sketch the graph of two cycles of y = 1
2
sin −2x
3
.
Solution. Since the sine function is odd, the graph of y = 1
2
sin −2x
3
is the same
as that of y = −1
2
sin 2x
3
.
(1) The amplitude is 1
2
, and the period is
2π
2
3
= 3π.
(2) Dividing the interval [0, 3π] into four equal parts, we get the x-coordinates
of the five important points:
0 + 3π
2
=
3π
2
,
0 + 3π
2
2
=
3π
4
,
3π
2
+ 3π
2
=
9π
4
.
(3) We get y = 0 when x = 0, 3π
2
, and 3π, y = −1
2
when 3π
4
, and y = 1
2
when
9π
4
.
(4) We trace the points in Step 3 by a smooth curve.
(5) We extend the pattern in Step 4 by one more period to the right.
150
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-156-320.jpg)
![D
EPED
C
O
PY
3.3.3. Graphs of y = a sin b(x − c) + d and y = a cos b(x − c) + d
We first compare the graphs of y = sin x and y = sin x − π
3
using a table of
values and the 5-step procedure discussed earlier.
As x runs from π
3
to 7π
3
, the value of the expression x− π
3
runs from 0 to 2π. So
for one cycle of the graph of y = sin x − π
3
, we then expect to have the graph of
y = sin x starting from x = π
3
. This is confirmed by the values in Table 3.23. We
then apply a similar procedure to complete one cycle of the graph; that is, divide
the interval [π
3
, 7π
3
] into four equal parts, and then determine the key values of
x in sketching the graphs as discussed earlier. The one-cycle graph of y = sin x
(dashed curve) and the corresponding one-cycle graph of y = sin x − π
3
(solid
curve) are shown in Figure 3.24.
x π
3
5π
6
4π
3
11π
6
7π
3
x − π
3
0 π
2
π 3π
2
2π
sin x − π
3
0 1 0 −1 0
Table 3.23
Figure 3.24
Observe that the graph of y = sin x − π
3
shifts π
3
units to the right of
y = sin x. Thus, they have the same period, amplitude, domain, and range.
The graphs of
y = a sin b(x − c) and y = a cos b(x − c)
have the same shape as y = a sin bx and y = a cos bx, respectively, but
shifted c units to the right when c > 0 and shifted |c| units to the left
if c < 0. The number c is called the phase shift of the sine or cosine
graph.
151
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-157-320.jpg)

![D
EPED
C
O
PY
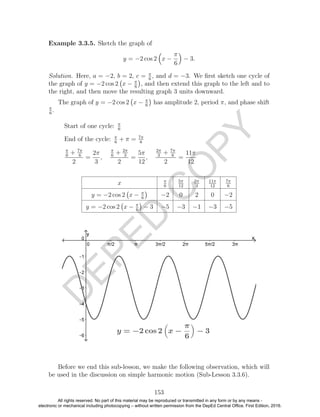
Different Equations, The Same Graph
1. The graphs of y = sin x and y = sin(x + 2πk), k any integer, are
the same.
2. The graphs of y = sin x, y = − sin(x + π), y = cos(x − π
2
), and
y = − cos(x + π
2
) are the same.
3. In general, the graphs of
y = a sin b(x − c) + d,
y = −a sin[b(x − c) + π + 2πk] + d,
y = a cos[b(x − c) − π
2
+ 2πk] + d,
and
y = −a cos[b(x − c) + π
2
+ 2πk] + d,
where k is any integer, are all the same.
Similar observations are true for cosine.
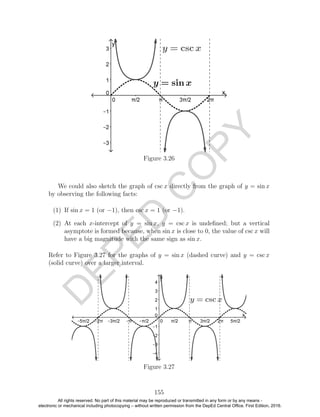
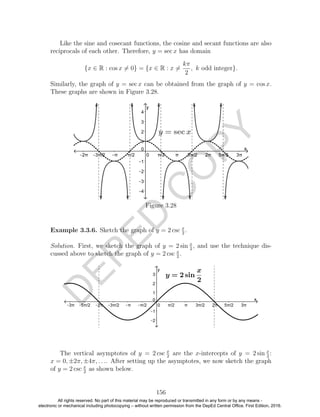
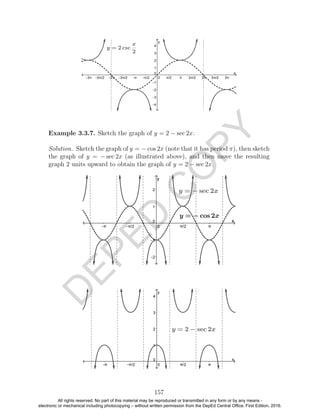
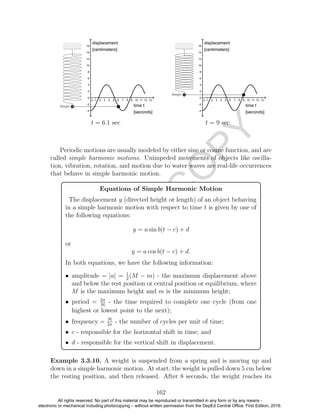
3.3.4. Graphs of Cosecant and Secant Functions
We know that csc x = 1
sin x
if sin x = 0. Using this relationship, we can sketch the
graph of y = csc x.
First, we observe that the domain of the cosecant function is
{x ∈ R : sin x = 0} = {x ∈ R : x = kπ, k ∈ Z}.
Table 3.25 shows the key numbers (that is, numbers where y = sin x crosses the
x-axis, attain its maximum and minimum values) and some neighboring points,
where “und” stands for “undefined,” while Figure 3.26 shows one cycle of the
graphs of y = sin x (dashed curve) and y = csc x (solid curve). Notice the
asymptotes of the graph y = csc x.
x 0 π
6
π
2
5π
6
π 7π
6
3π
2
11π
6
2π
y = sin x 0 1
2
1 1
2
0 −1
2
−1 −1
2
0
y = csc x und 2 1 2 und −2 −1 −2 und
Table 3.25
154
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-160-320.jpg)








![D
EPED
C
O
PY
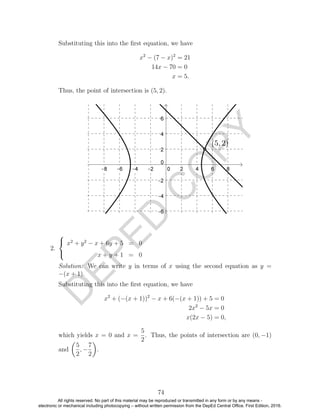
The domain of the given cosine function is R, and its range is [1, 5].
5. Sketch the graph of the function y = 1
4
tan x − π
4
over three periods. Find
the domain and range of the function.
Solution: The period of the function is π. One complete cycle may start at
x = π
4
and end at x = 5π
4
.
The domain of the function is {x|x = 3π
4
+ kπ, k ∈ Z}, and its range is R.
6. Sketch the graph of the function y = −3 cot 1
2
x + π
12
+ 2 over three periods.
Find the domain and range of the function.
Solution: y = −3 cot 1
2
x + π
12
+ 2 = −3 cot 1
2
x + π
6
+ 2 =⇒ P = 2π
One complete cycle may start at x = −π
6
and end at x = 11π
6
.
167
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-173-320.jpg)
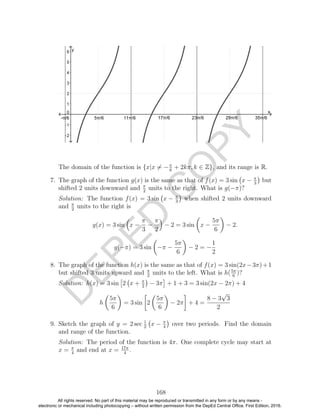
![D
EPED
C
O
PY
The domain of the function is {x|x = 5π
4
+ 2kπ, k ∈ Z}, and its range is
(−∞, −2] ∪ [2, ∞).
10. Sketch the graph of y = − csc x + π
3
+ 2 over two periods. Find the domain
and range of the function.
Solution: The period of the function is 2π. One complete cycle may start and
end at x = −π
3
and x = 5π
3
, respectively.
The domain of the function is {x|x = −π
3
+ kπ, k ∈ Z}, and its range is
(−∞, 1] ∪ [3, ∞).
169
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-175-320.jpg)


![D
EPED
C
O
PY
Here, for
√
x2 − 1 to be defined in R, x must be in (−∞, −1] ∪ [1, ∞).
In the third expression, the values of x that make the denominator zero make
the entire expression undefined.
x2
− 3x − 4 = (x − 4)(x + 1) = 0 ⇐⇒ x = 4 or x = −1
Hence, the expression
x
x2 − 3x − 4
is real when x = 4 and x = −1.
In the fourth expression, because the expression
√
x − 1 is in the denominator,
x must be greater than 1. Although the value of the entire expression is 0 when
x = 0, we do not include 0 as allowed value of x because part of the expression
is not real when x = 0.
In the expressions above, the allowed values of the variable x constitute the
domain of the expression.
The domain of an expression (or equation) is the set of all real values of
the variable for which every term (or part) of the expression (equation)
is defined in R.
In the expressions above, the domains of the first, second, third, and fourth
expressions are R, (−∞, −1] ∪ [1, ∞), R {−1, 4}, and (1, ∞), respectively.
Example 3.4.1. Determine the domain of the expression/equation.
(a)
x2
− 1
x3 + 2x2 − 8x
−
√
x + 1
1 − x
(b) tan θ − sin θ − cos 2θ
(c) x2
−
√
1 + x2 =
2
3
√
x2 − 1
(d) z −
cos2
z
1 + sin z
= 4 sin z − 1
Solution. (a) x3
+ 2x2
− 8x = x(x + 4)(x − 2) = 0 ⇐⇒ x = 0, x =
−4, or x = 2
√
x + 1 ∈ R ⇐⇒ x + 1 ≥ 0 ⇐⇒ x ≥ −1
1 − x = 0 ⇐⇒ x = 1
Domain = [−1, ∞) {−4, 0, 1, 2}
= [−1, 0) ∪ (0, 1) ∪ (1, 2) ∪ (2, ∞)
172
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-178-320.jpg)









![D
EPED
C
O
PY
Recall that P1 = P(u) = (cos u, sin u), P2 = P(v) = (cos v, sin v), and P3 =
P(u − v) = (cos(u − v), sin(u − v)), so that
P1P2 = (cos u − cos v)2 + (sin u − sin v)2,
while
AP3 = [cos(u − v) − 1]2 + [sin(u − v) − 0]2.
Equating these two expressions and expanding the squares, we get
(cos u − cos v)2
+ (sin u − sin v)2
= [cos(u − v) − 1]2
+ sin2
(u − v)
cos2
u − 2 cos u cos v + cos2
v + sin2
u − 2 sin u sin v + sin2
v
= cos2
(u − v) − 2 cos(u − v) + 1 + sin2
(u − v)
Applying the Pythagorean identity cos2
θ+sin2
θ = 1 and simplifying the resulting
equations, we obtain
(cos2
u + sin2
u) + (cos2
v + sin2
v) − 2 cos u cos v − 2 sin u sin v
= [cos2
(u − v) + sin2
(u − v)] − 2 cos(u − v) + 1
1 + 1 − 2 cos u cos v − 2 sin u sin v = 1 − 2 cos(u − v) + 1
cos(u − v) = cos u cos v + sin u sin v.
We have thus proved another identity.
Although we assumed at the start that 0 < v ≤ u < 2π, but because
cos(−θ) = cos θ (one of the even-odd identities), this new identity is true for
any real numbers u and v. As before, the variables can take any real values or
angle measures.
Cosine Difference Identity
cos(A − B) = cos A cos B + sin A sin B
Replacing B with −B, and applying the even-odd identities, we immediately
get another identity.
Cosine Sum Identity
cos(A + B) = cos A cos B − sin A sin B
Example 3.5.1. Find the exact values of cos 105◦
and cos π
12
.
182
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-188-320.jpg)

![D
EPED
C
O
PY
= (0) cos B + (1) sin B
= sin B.
From this identity, if we replace B with π
2
− B, we have
cos
π
2
−
π
2
− B = sin
π
2
− B
cos B = sin
π
2
− B .
As for the tangent function, we have
tan
π
2
− B =
sin π
2
− B
cos π
2
− B
=
cos B
sin B
= cot B.
We have just derived another set of identities.
Cofunction Identities
cos
π
2
− B = sin B sin
π
2
− B = cos B
tan
π
2
− B = cot B
Using the first two cofunction identities, we now derive the identity for sin(A+
B).
sin(A + B) = cos
π
2
− (A + B)
= cos
π
2
− A − B)
= cos
π
2
− A cos B + sin
π
2
− A sin B
= sin A cos B + cos A sin B
Sine Sum Identity
sin(A + B) = sin A cos B + cos A sin B
In the last identity, replacing B with −B and applying the even-odd identities
yield
sin(A − B) = sin[A + (−B)]
184
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-190-320.jpg)

![D
EPED
C
O
PY
Example 3.5.5. Prove:
sin(x + y) = (1 + cot x tan y) sin x cos y.
Solution.
(1 + cot x tan y) sin x cos y = sin x cos y + cot x tan y sin x cos y
= sin x cos y +
cos x
sin x
sin y
cos y
sin x cos y
= sin x cos y + cos x sin y = sin(x + y) 2
3.5.3. The Tangent Sum and Difference Identities
Recall that tan x is the ratio of sin x over cos x. When we replace x with A + B,
we obtain
tan(A + B) =
sin(A + B)
cos(A + B)
.
Using the sum identities for sine and cosine, and then dividing the numerator
and denominator by cos A cos B, we have
tan(A + B) =
sin A cos B + cos A sin B
cos A cos B − sin A sin B
=
sin A cos B
cos A cos B
+ cos A sin B
cos A cos B
cos A cos B
cos A cos B
− sin A sin B
cos A cos B
=
tan A + tan B
1 − tan A tan B
.
We have just established the tangent sum identity.
In the above identity, if we replace B with −B and use the even-odd identity
tan(−θ) = − tan θ, we get
tan(A − B) = tan[A + (−B)] =
tan A + tan(−B)
1 − tan A tan(−B)
=
tan A − tan B
1 + tan A tan B
.
This is the tangent difference identity.
Tangent Sum and Difference Identities
tan(A + B) =
tan A + tan B
1 − tan A tan B
tan(A − B) =
tan A − tan B
1 + tan A tan B
186
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-192-320.jpg)















![D
EPED
C
O
PY
works. Loosely speaking, a function that reverses what a given function f does
is called its inverse function, and is usually denoted by f−1
.
More formally, two functions f and g are inverse functions if
g(f(x)) = x for any x in the domain of f,
and
f(g(x)) = x for any x in the domain of g.
We denote the inverse function of a function f by f−1
. The graphs of a function
and its inverse function are symmetric with respect to the line y = x.
In this lesson, we first restrict the domain of each trigonometric function
because each of them is not one-to-one. We then define each respective inverse
function and evaluate the values of each inverse trigonometric function.
3.7.1. Inverse Sine Function
All the trigonometric functions that we consider are periodic over their entire
domains. This means that all trigonometric functions are not one-to-one if we
consider their whole domains, which implies that they have no inverses over those
sets. But there is a way to make each of the trigonometric functions one-to-one.
This is done by restricting their respective domains. The restrictions will give us
well-defined inverse trigonometric functions.
The domain of the sine function is the set R of real numbers, and its range is
the closed interval [−1, 1]. As observed in the previous lessons, the sine function
is not one-to-one, and the first step is to restrict its domain (by agreeing what the
convention is) with the following conditions: (1) the sine function is one-to-one
in that restricted domain, and (2) the range remains the same.
The inverse of the (restricted) sine function f(x) = sin x, where the
domain is restricted to the closed interval −π
2
, π
2
, is called the inverse
sine function or arcsine function, denoted by f−1
(x) = sin−1
x or
f−1
(x) = arcsin x. Here, the domain of f−1
(x) = arcsin x is [−1, 1],
and its range is −π
2
, π
2
. Thus,
y = sin−1
x or y = arcsin x
if and only if
sin y = x,
where −1 ≤ x ≤ 1 and −π
2
≤ y ≤ π
2
.
Throughout the lesson, we interchangeably use sin−1
x and arcsin x to mean
the inverse sine function.
202
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-208-320.jpg)
![D
EPED
C
O
PY
Example 3.7.1. Find the exact value of each expression.
(1) sin−1 1
2
(2) arcsin(−1)
(3) arcsin 0
(4) sin−1
−1
2
Solution. (1) Let θ = sin−1 1
2
. This is equivalent to sin θ = 1
2
. This means that
we are looking for the number θ in the closed interval −π
2
, π
2
whose sine is
1
2
. We get θ = π
6
. Thus, we have sin−1 1
2
= π
6
.
(2) arcsin(−1) = −π
2
because sin −π
2
= −1 and −π
2
∈ −π
2
, π
2
.
(3) arcsin 0 = 0
(4) sin−1
−1
2
= −π
6
2
As emphasized in the last example, as long as −1 ≤ x ≤ 1, sin−1
x is that
number y ∈ −π
2
, π
2
such that sin y = x. If |x| > 1, then sin−1
x is not defined in
R.
We can sometimes find the exact value of sin−1
x (that is, we can find a value
in terms of π), but if no such special value exists, then we leave it in the form
sin−1
x. For example, as shown above, sin−1 1
2
is equal to π
6
. However, as studied
in Lesson 3.2, no special number θ satisfies sin θ = 2
3
, so we leave sin−1 2
3
as is.
Example 3.7.2. Find the exact value of each expression.
(1) sin sin−1 1
2
(2) arcsin sin π
3
(3) arcsin(sin π)
(4) sin sin−1
−1
2
Solution. (1) sin sin−1 1
2
= sin π
6
= 1
2
(2) arcsin sin π
3
= arcsin
√
3
2
= π
3
(3) arcsin(sin π) = arcsin 0 = 0
(4) sin sin−1
−1
2
= sin −π
6
= −1
2
2
From the last example, we have the following observations:
1. sin(arcsin x) = x for any x ∈ [−1, 1]; and
2. arcsin(sin θ) = θ if and only if θ ∈ −π
2
, π
2
, and if θ ∈ −π
2
, π
2
, then
arcsin(sin θ) = ϕ, where ϕ ∈ −π
2
, π
2
such that sin ϕ = sin θ.
To sketch the graph of y = sin−1
x, Table 3.32 presents the tables of values
for y = sin x and y = sin−1
x. Recall that the graphs of y = sin x and y = sin−1
x
are symmetric with respect to the line y = x. This means that if a point (a, b) is
on y = sin x, then (b, a) is on y = sin−1
x.
203
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-209-320.jpg)
![D
EPED
C
O
PY
y = sin x
x −π
2
−π
3
−π
4
−π
6
0 π
6
π
4
π
3
π
2
y −1 −
√
3
2
−
√
2
2
−1
2
0 1
2
√
2
2
√
3
2
1
y = sin−1
x
x −1 −
√
3
2
−
√
2
2
−1
2
0 1
2
√
2
2
√
3
2
1
y −π
2
−π
3
−π
4
−π
6
0 π
6
π
4
π
3
π
2
Table 3.32
The graph (solid thick curve) of the restricted sine function y = sin x is shown
in Figure 3.33(a), while the graph of inverse sine function y = arcsin x is shown
in Figure 3.33(b).
(a) y = sin x (b) y = sin−1
x
Figure 3.33
Example 3.7.3. Sketch the graph of y = sin−1
(x + 1).
Solution 1. In this solution, we use translation of graphs.
Because y = sin−1
(x + 1) is equivalent to y = sin−1
[x − (−1)], the graph of
y = sin−1
(x + 1) is 1-unit to the left of y = sin−1
x. The graph below shows
y = sin−1
(x + 1) (solid line) and y = sin−1
x (dashed line).
204
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-210-320.jpg)

![D
EPED
C
O
PY
y = cos−1
x or y = arccos x
means
cos y = x,
where −1 ≤ x ≤ 1 and 0 ≤ y ≤ π.
The graph (solid thick curve) of the restricted cosine function y = cos x is
shown in Figure 3.34(a), while the graph of inverse cosine function y = arccos x
is shown in Figure 3.34(b).
(a) y = cos x (b) y = cos−1
x
Figure 3.34
Example 3.7.4. Find the exact value of each expression.
(1) cos−1
0
(2) arccos −
√
3
2
(3) cos cos−1
−
√
3
2
(4) cos−1
cos 3π
4
(5) arccos cos 7π
6
(6) sin cos−1
√
2
2
Solution. (1) cos−1
0 = π
2
because cos π
2
= 0 and π
2
∈ [0, π].
(2) arccos −
√
3
2
= 5π
6
(3) cos cos−1
−
√
3
2
= −
√
3
2
because −
√
3
2
∈ [−1, 1]
(4) cos−1
cos 3π
4
= 3π
4
because 3π
4
∈ [0, π].
206
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-212-320.jpg)
![D
EPED
C
O
PY
(5) arccos cos 7π
6
= arccos −
√
3
2
= 5π
6
(6) sin cos−1
√
2
2
=
√
2
2
2
Example 3.7.5. Simplify: sin arcsin 2
3
+ arccos 1
2
.
Solution. We know that arccos 1
2
= π
3
. Using the Sine Sum Identity, we have
sin arcsin 2
3
+ arccos 1
2
= sin arcsin 2
3
+ π
3
= sin arcsin 2
3
cos π
3
+ cos arcsin 2
3
sin π
3
= 2
3
· 1
2
+ cos arcsin 2
3
·
√
3
2
= 1
3
+
√
3
2
cos arcsin 2
3
.
We compute cos arcsin 2
3
. Let θ = arcsin 2
3
. By definition, sin θ = 2
3
, where
θ lies in QI. Using the Pythagorean identity, we have
cos arcsin 2
3
= cos θ = 1 − sin2
θ =
√
5
3
.
Going back to the original computations above, we have
sin arcsin 2
3
+ arccos 1
2
= 1
3
+
√
3
2
cos arcsin 2
3
= 1
3
+
√
3
2
·
√
5
3
= 2+
√
15
6
. 2
Example 3.7.6. Simplify: sin 2 cos−1
−4
5
.
Solution. Let θ = cos−1
−4
5
. Then cos θ = −4
5
. Because cos θ < 0 and range
of inverse cosine function is [0, π], we know that θ must be within the interval
π
2
, π . Using the Pythagorean Identity, we get sin θ = 3
5
.
Using the Sine Double-Angle Identity, we have
sin 2 cos−1
−4
5
= sin 2θ
= 2 sin θ cos θ
= 2 · 3
5
−4
5
= −24
25
. 2
Example 3.7.7. Sketch the graph of y = 1
4
cos−1
(2x).
Solution.
y =
1
4
cos−1
(2x) ⇐⇒ 4y = cos−1
(2x) ⇐⇒ x =
1
2
cos(4y)
207
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-213-320.jpg)




![D
EPED
C
O
PY
Define
cot−1
x =
π
2
− tan−1
x.
It follows that the domain of y = cot−1
x is R and its range is (0, π).
y = sec−1
x or y = arcsec x
means
sec y = x,
where |x| ≥ 1 and y ∈ 0, π
2
∪ π, 3π
2
.
Define
csc−1
x =
π
2
− sec−1
x.
This means that the domain of y = csc−1
x is (−∞, −1] ∪ [1, ∞) and
its range is −π, −π
2
∪ 0, π
2
.
The graphs of these last three inverse trigonometric functions are shown in
Figures 3.36, 3.37, and 3.38, respectively.
(a) y = cot x (b) y = cot−1
x
Figure 3.36
212
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-218-320.jpg)
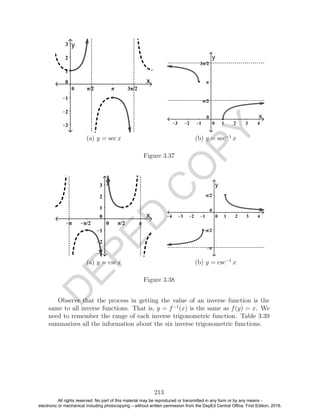
![D
EPED
C
O
PY
Function Domain Range Graph
sin−1
x [−1, 1] −π
2
, π
2
Figure
3.33(b)
cos−1
x [−1, 1] [0, π]
Figure
3.34(b)
tan−1
x R −π
2
, π
2
Figure
3.35(b)
cot−1
x R (0, π)
Figure
3.36(b)
sec−1
x {x : |x| ≥ 1} 0, π
2
∪ π, 3π
2
Figure
3.37(b)
csc−1
x {x : |x| ≥ 1} −π, −π
2
∪ 0, π
2
Figure
3.38(b)
Table 3.39
Example 3.7.11. Find the exact value of each expression.
(1) sec−1
(−2)
(2) csc−1
−2
√
3
3
(3) cot−1
−
√
3
(4) sin sec−1
−3
2
− csc−1
−2
√
3
3
Solution. (1) sec−1
(−2) = 4π
3
because sec 4π
3
= −2 and 4π
3
∈ π, 3π
2
(2) csc−1
−2
√
3
3
= −2π
3
(3) cot−1
−
√
3 = 5π
6
(4) From (2), we know that csc−1
−2
√
3
3
= −2π
3
. Let θ = sec−1
−3
2
. Then
sec θ = −3
2
. From defined range of inverse secant function and the notations
in Lesson 3.2, θ lies in QIII, and r = 3 and x = −2. Solving for y, we get
y = − 32 − (−2)2 = −
√
5. It follows that sin θ = −
√
5
3
and cos θ = −2
3
.
We now use the Sine Sum Identity.
sin sec−1
−
3
2
− csc−1
−
2
√
3
3
= sin θ − −
2π
3
= sin θ +
2π
3
214
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-220-320.jpg)
![D
EPED
C
O
PY
= sin θ cos
2π
3
+ cos θ sin
2π
3
= −
√
5
3
−
1
2
+ −
2
3
√
3
2
=
√
5 − 2
√
3
6
2
More Solved Examples
1. Find the exact values of the following, if they exist.
(a) sin−1
√
2
2
(b) arcsin −1
2
(c) sin−1
2
Solution: Note that the range of f(x) = sin−1
x is [−π
2
, π
2
]. Thus, if we let
y = sin−1
x, then we are looking for y ∈ [−π
2
, π
2
] such that sin y = x. Hence,
(a) sin−1
√
2
2
= π
4
,
(b) arcsin −1
2
= −π
6
, and
(c) sin−1
2 is undefined because sin y ≤ 1.
2. Find the exact value of each expression.
(a) sin sin−1
√
2
2
(b) cos arcsin −1
2
(c) sin−1
sin 11π
2
Solution:
(a) sin sin−1
√
2
2
= sin(π
4
) =
√
2
2
(b) cos arcsin −1
2
= cos(−π
6
) =
√
3
2
(c) sin−1
sin 11π
2
= sin−1
(−1) = −π
2
3. Answer the following.
(a) What is the domain of y = sin−1
2x?
(b) What is the range of y = sin−1
2x?
(c) What is the x−intercept of y = sin−1
2x?
Solution:
(a) Consider the function f(θ) = sin−1
θ. The domain of sin−1
θ is [−1, 1].
So, θ = 2x ∈ [−1, 1]. Therefore, the domain of sin−1
2x is [−1/2, 1/2].
215
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-221-320.jpg)
![D
EPED
C
O
PY
(b) [−π/2, π/2]
(c) (0, 0)
4. From the concept of projectile motion, if an object is directed at an angle θ
(with θ ∈ [0, π/2]), then the range will be R =
v2
0
g
sin 2θ (in feet) where v0 (in
ft/s) is the initial speed and g = 32 ft/s2
is the acceleration due to gravity.
At what angle shall the object be directed so that the range will be 100 ft,
given that the initial speed is v0 = 80 ft/s?
Solution: From the formula of the range, we get
100 =
802
32
sin 2θ =⇒
1
2
= sin 2θ
Since θ must be from 0 to π
2
(i.e. 0 ≤ 2θ ≤ π), this is equivalent to finding 2θ
such that 2θ = sin−1 1
2
. Hence,
2θ =
π
6
=⇒ θ =
π
12
.
Therefore, the object must be directed at an angle of π
12
rad (or 15◦
), to have
a projectile range of 100 ft.
5. Find the exact values of the following, if they exist.
(a) cos−1
√
2
2
(b) cos cos−1
−1
2
(c) arccos(cos π)
(d) arccos π
Solution:
(a) cos−1
√
2
2
= π
4
(b) cos cos−1
−1
2
= cos 2π
3
= −1
2
(c) arccos(cos π) = arccos(−1) = π
(d) Let y = arccos π. Since cos y ≤ 1, we have y is undefined because π > 3.
6. Simplify: (a) cos cos−1
√
3
2
− cos−1 1
3
Solution: We know that cos−1
√
3
2
= π
6
. Let θ = cos−1 1
3
. Which is equivalent
to cos θ = 1
3
with 0 ≤ θ ≤ π. Using the Cosine Difference Identity, we have
cos cos−1
√
3
2
− cos−1 1
3
= cos
π
6
− θ = cos
π
6
cos θ + sin
π
6
sin θ
=
√
3
2
·
1
3
+
1
2
· sin θ.
216
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-222-320.jpg)
![D
EPED
C
O
PY
Now, we solve for sin θ using the Pythagorean Identity which gives
sin2
θ = 1 − (1/3)2
= 1 − (1/9) = 8/9.
Thus, sin θ = 2
√
2
3
because θ ∈ [0, π]. Finally, we obtain
cos cos−1
√
3
2
− cos−1 1
3
=
√
3
2
·
1
3
+
1
2
·
2
√
2
3
=
√
3
6
+
2
√
2
6
=
√
3 + 2
√
2
6
.
7. Simplify: (a) cos 2 cos−1 2
5
; (b) sin cos−1 2
5
Solution: Let θ = cos−1 2
5
. Which is equivalent to cos θ = 2
5
with 0 ≤ θ ≤
π. Using the Double-Angle Identity for Cosine and one of the Fundamental
Idenity, we have
cos 2 cos−1 2
5
= cos(2θ) = 2 cos2
θ − 1 = 2
2
5
2
− 1 =
8
25
− 1 = −
17
25
and
sin cos−1 2
5
= sin θ =
√
1 − cos2 θ = 1 −
4
25
=
√
21
5
.
Here, sin θ ≥ 0 because θ ∈ [0, π].
8. Graph: y = 1 + cos−1
x
Solution: The graph can be obtained by translating the graph of the inverse
cosine function one unit upward.
217
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-223-320.jpg)

![D
EPED
C
O
PY
Supplementary Problems 3.7
1. Find the exact value of the following.
(a) sin[sin−1
(1/2)]
(b) cos[cos−1
(−
√
2/2)]
(c) tan[tan−1
(−
√
3)]
(d) sin[arctan(
√
3)]
(e) cos[arccos(
√
2)]
(f) tan[arcsin(1/4)]
(g) cos[sin−1
(
√
3/2)]
2. Find the exact value of the following.
(a) sin−1
[sin(25π/6)]
(b) arccos[cos(23π/4)]
(c) tan−1
[tan(−1)]
(d) arcsin[cos(13π/4)]
(e) cos−1
[sec(23π)]
(f) arctan[sin(−π/12)]
3. Solve the exact value of the following.
(a) sin[2 cos−1
(−4/5)]
(b) cos[2 sin−1
(5/13)]
(c) sin(sin−1
(3/5) + cos−1
(−5/13))
(d) cos[sin−1
(1/2) − cos−1
(8/17)]
4. Consider the function f(x) = tan−1
(x + 1). Do the following.
(a) Find the domain of f.
(b) Find the range of f.
(c) Find the x− and y−intercept of f, if there are any.
(d) Graph f.
5. Evaluate and simplify the following, if they exist.
(a) arcsec(−
√
2)
(b) arccsc(−2)
(c) arccot
√
3
(d) [sec−1
(−1)] · [cos−1
(−1)]
(e) 2 cot−1
√
3 + 3 csc−1
2
(f) csc−1
0
6. Evaluate and simplify the following, if they exist.
(a)
cos(sec−1
3 + tan−1
2)
cos(tan−1
2)
(b) tan(2 arcsin(1/6))
(c) cos2 sin−1(1/2)
2
(d) arcsec(sin(100π/3))
219
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-225-320.jpg)

![D
EPED
C
O
PY
values of the variable in the domain of the equation, while a conditional equation
is an equation that is not an identity.
In this lesson, we mostly study conditional trigonometric equations. Though
not explicitly, we have started it in the preceding lesson. For example, the equa-
tion sin x = 1
2
has the unique solution x = sin−1 1
2
= π
6
in the closed interval
−π
2
, π
2
. However, if we consider the entire domain (not the restricted domain)
of the sine function, which is the set R of real numbers, there are solutions (other
than π
6
) of the equation sin x = 1
2
. This current lesson explores the techniques of
solving (conditional) trigonometric equations.
We divide the lesson into two groups of equations: the ones using a basic way
of solving, and those using more advanced techniques.
3.8.1. Solutions of a Trigonometric Equation
Any equation that involves trigonometric expressions is called a trigonometric
equation. Recall that a solution or a root of an equation is a number in the domain
of the equation that, when substituted to the variable, makes the equation true.
The set of all solutions of an equation is called the solution set of the equation.
Technically, the basic method to show that a particular number is a solution
of an equation is to substitute the number to the variable and see if the equation
becomes true. However, we may use our knowledge gained from the previous
lessons to do a quicker verification process by not doing the manual substitution
and checking. We use this technique in the example.
Example 3.8.1. Which numbers in the set 0, π
6
, π
4
, π
3
, π
2
, 2π
3
, 3π
4
, 5π
6
, π, 2π are
solutions to the following equations?
(1) sin x = 1
2
(2) tan x = 1
(3) 3 sec x = −2
√
3
(4)
√
3| cot x| = 1
(5) sec2
x − tan2
x = 1
(6) sin x + cos x = 0
(7) cos2
x = cos 2x + sin2
x
(8) sin x + cos 2x = 0
(9) 2 sin x + tan x − 2 cos x = 2
(10) sin2
x + cos2
x = 2
(11) sin 2x = sin x
(12) 2 tan x + 4 sin x = 2 + sec x
Solution. Note that the choices (except 2π) are numbers within the interval [0, π].
To quickly determine which numbers among the choices are solutions to a par-
ticular equation, we use some distinctive properties of the possible solutions.
(1) The sine function is positive on (0, π). From Lesson 3.2, we recall that π
6
is
an obvious solution. We may imagine the graph of y = sin x. We may also
use the idea of reference angle. Thus, among the choices, only π
6
and 5π
6
are
the only solutions of sin x = 1
2
.
221
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-227-320.jpg)



![D
EPED
C
O
PY
(1) equivalent equations (that is, equations that have the same solutions as the
original equation);
(2) periodicity of the trigonometric function involved;
(3) inverse trigonometric function;
(4) values of the trigonometric function involved on the interval [0, π] or [0, 2π]
(depending on the periodicity of the function); and
(5) Zero-Factor Law: ab = 0 if and only if a = 0 or b = 0.
To “solve an equation” means to find all solutions of the equation. Here,
unless stated as angles measured in degrees, we mean solutions of the equation
that are real numbers (or equivalently, angles measured in radians).
Example 3.8.2. Solve the equation 2 cos x − 1 = 0.
Solution. The given equation is equivalent to
cos x =
1
2
.
On the interval [0, 2π], there are only two solutions of the last equation, and these
are x = π
3
(this is in QI) and x = 5π
3
(in QIV).
Because the period of cosine function is 2π, the complete solutions of the
equation are x = π
3
+ k(2π) and x = 5π
3
+ k(2π) for all integers k. 2
In the preceding example, by saying that the “complete solutions are x =
π
3
+ k(2π) and x = 5π
3
+ k(2π) for all integers k,” we mean that any integral
value of k will produce a solution to the given equation. For example, when
k = 3, x = π
3
+ 3(2π) = 19π
3
is a solution of the equation. When k = −2,
x = 5π
3
+ (−2)(2π) = −7π
3
is another solution of 2 cos x − 1 = 0. The family of
solutions x = π
3
+ k(2π) can be equivalently enumerated as x = 19π
3
+ 2kπ, while
the family x = 5π
3
+ k(2π) can also be stated as x = −7π
3
+ 2kπ.
Example 3.8.3. Solve: (1 + cos θ)(tan θ − 1) = 0.
Solution. By the Zero-Factor Law, the given equation is equivalent to
1 + cos θ = 0 or tan θ − 1 = 0
cos θ = −1 tan θ = 1
θ = π + 2kπ, k ∈ Z θ = π
4
+ kπ, k ∈ Z.
Therefore, the solutions of the equation are θ = π + 2kπ and θ = π
4
+ kπ for all
k ∈ Z. 2
225
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-231-320.jpg)
![D
EPED
C
O
PY
Example 3.8.4. Find all values of x in the interval [−2π, 2π] that satisfy the
equation (sin x − 1)(sin x + 1) = 0.
Solution.
sin x − 1 = 0 or sin x + 1 = 0
sin x = 1 sin x = −1
x = π
2
or − 3π
2
x = 3π
2
or − π
2
Solutions: π
2
, −3π
2
, 3π
2
, −π
2
2
Example 3.8.5. Solve: cos x = 0.1.
Solution. There is no special number whose cosine is 0.1. However, because
0.1 ∈ [−1, 1], there is a number whose cosine is 0.1. In fact, in any one-period
interval, with cos x = 0.1 > 0, we expect two solutions: one in QI and another in
QIV. We use the inverse cosine function.
From Lesson 3.7, one particular solution of cos x = 0.1 in QI is x = cos−1
0.1.
We can use this solution to get a particular solution in QIV, and this is x =
2π − cos−1
0.1, which is equivalent to x = − cos−1
0.1.
From the above particular solutions, we can produce all solutions of cos x =
0.1, and these are x = cos−1
0.1+2kπ and x = − cos−1
0.1+2kπ for all k ∈ Z. 2
Example 3.8.6. Solve: 3 tan θ + 5 = 0.
Solution.
3 tan θ + 5 = 0 =⇒ tan θ = −5
3
We expect only one solution in any one-period interval.
tan θ = −5
3
=⇒ θ = tan−1
−5
3
+ kπ, k ∈ Z 2
Example 3.8.7. The voltage V (in volts) coming from an electricity distribut-
ing company is fluctuating according to the function V (t) = 200 + 170 sin(120πt)
at time t in seconds.
(1) Determine the first time it takes to reach 300 volts.
(2) For what values of t does the voltage reach its maximum value?
Solution. (1) We solve for the least positive value of t such that V (t) = 300.
200 + 170 sin(120πt) = 300
sin(120πt) =
100
170
226
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-232-320.jpg)


![D
EPED
C
O
PY
2 sin2
x + sin x − 1 = 0
(2 sin x − 1)(sin x + 1) = 0 Factoring
2 sin x − 1 = 0 or sin x + 1 = 0
sin x = 1
2
sin x = −1
x = π
6
or x = 5π
6
x = 3π
2
Solutions: π
6
, 5π
6
, 3π
2
2
Example 3.8.11. Solve for x ∈ [0, 2π) in the equation 3 cos2
x + 2 sin x = 2.
Solution.
3 cos2
x + 2 sin x = 2
3(1 − sin2
x) + 2 sin x = 2 Pythagorean Identity
(3 sin x + 1)(sin x − 1) = 0 Factoring
3 sin x + 1 = 0 or sin x − 1 = 0
sin x = −1
3
sin x = 1
x = sin−1
(−1
3
) + 2π
or
x = π − sin−1
(−1
3
)
x = π
2
Solutions: 2π − sin−1
(1
3
)+, π + sin−1
(1
3
), π
2
2
One part of the last solution needs further explanation. In the equation
sin x = −1
3
, we expect two solutions in the interval [0, 2π): one in (π, 3π
2
) (which
is QIII), and another in (3π
2
, 2π) (which is QIV). Since no special number satisfies
sin x = −1
3
, we use inverse sine function. Because the range of sin−1
is [−π
2
, π
2
], we
know that −π
2
< sin−1
(−1
3
) < 0. From this value, to get the solution in (3π
2
, 2π),
we simply add 2π to this value, resulting to x = sin−1
(−1
3
) + 2π. On the other
hand, to get the solution in (π, 3π
2
), we simply add − sin−1
(−1
3
) to π, resulting to
x = π − sin−1
(−1
3
).
Example 3.8.12. Solve: sin2
x + 5 cos2 x
2
= 2.
Solution.
sin2
x + 5 cos2 x
2
= 2
sin2
x + 5 1+cos x
2
= 2 Cosine Half-Angle Identity
2 sin2
x + 5 cos x + 1 = 0
229
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-235-320.jpg)



![D
EPED
C
O
PY
3. Find the solution set of the trigonometric equation tan2
x + 1 = sec2
x.
Solution: Notice that this is a fundamental identity. Thus, the solution of
this equation is any number common to the domain of the tangent and secant
function. That is, the solution set is
{x ∈ R | cos x = 0} = {x ∈ R | x = ±π
2
, ±3π
2
, ±5π
2
, ...}
= {x ∈ R | x = (2k+1)π
2
, k ∈ Z}.
4. Find all solutions of
√
3 tan x + 1 = 0.
Solution: The equation is equivalent to tan x = − 1√
3
. This is true only if
x = 5π
6
+ kπ where k ∈ Z.
5. What are the solutions of
√
3 tan x + 1 = 0, where x ∈ [0, 2π].
Solution: The solutions are x = 5π
6
and x = 11π
6
.
6. Determine all solutions of 4 cos2
x − 1 = 0.
Solution: Note that the equation is quadratic in form, so we can apply tech-
niques in solving quadratic equations. For this case, we factor the expression
on the left and obtain, (2 cos x − 1)(2 cos x + 1) = 0. Consequently, we have
cos x = 1/2 or cos x = −1/2. The first equation have solutions of the form
(π/3 + 2kπ) or (5π/3 + 2kπ) where k ∈ Z, while the second equation have
solutions of the form (2π/3 + 2kπ) or (4π/3 + 2kπ). Combining the two solu-
tions, one observes that the solution set of the original equation may be given
by
π
3
,
2π
3
,
4π
3
,
5π
3
,
7π
3
, ... .
We can write this in a more compact form as
kπ
3
: k = 3j, where j ∈ Z .
7. Find the solutions of 4 cos2
x − 1 = 0 within the closed interval [0, 2π].
Solution: Similar to Example 6, the solution of the above equation is
kπ
3
: k = 3j, where j ∈ Z .
Since we are to find solutions in [0, 2π], we take k = 1, 2, 4, and 5 to obtain
the solutions π/3, 2π/3, 4π/3, and 5π/3.
233
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-239-320.jpg)






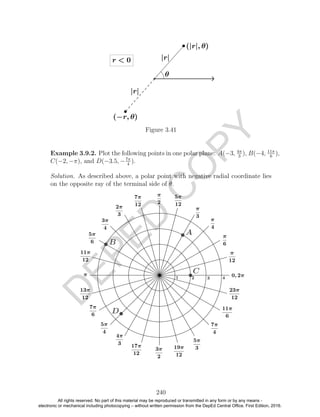






![D
EPED
C
O
PY
Example 3.9.9. The sound-pickup capability of a certain brand of microphone
is described by the polar equation r = −4 cos θ, where |r| gives the sensitivity of
the microphone to a sound coming from an angle θ (in radians).
(1) Identify and sketch the graph of the polar equation.
(2) Sound coming from what angle θ ∈ [0, π] is the microphone most sensitive
to? Least sensitive?
Solution. (1) r = −4 cos θ
r2
= −4r cos θ
x2
+ y2
= −4x
x2
+ 4x + y2
= 0
(x + 2)2
+ y2
= 4
This is a circle of radius 2 and with center at (2, π).
(2) We construct a table of values.
x 0 π
6
π
4
π
3
π
2
2π
3
3π
4
5π
6
π
r −4 −3.46 −2.83 −2 0 2 2.83 3.46 4
From the table, the microphone is most sensitive to sounds coming from
angles θ = 0 and θ = π, and least sensitive to sound coming from an angle
θ = π
2
. 2
247
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-253-320.jpg)


![D
EPED
C
O
PY
(b) Similarly, we use the conversion formulas to get
r = (−3)2 + (
√
3)2 =
√
12 = 2
√
3
and
θ = tan−1
[
√
3/(−3)] = −π/6.
Note that the point is in the second quadrant so we must use −pi
6
+ π. There-
fore, (−3,
√
3) in polar coordinate is (2
√
3, 5π/6).
(c) The point is in the third quadrant.
r = (−5
√
3)2 + (−15)2 =
√
300 = 10
√
3
and
tan θ = −15/(−5
√
3) ⇒ θ = 4π/3.
Therefore, (−5
√
3, −15) in polar coordinate is (10
√
3, 4π/3).
(d) Using the conversion formula, one can show that the point (8, 0) in polar
coordinate is also (8, 0).
5. Identify (and describe) the graph of the equation r = 4 sin θ. Using a graphing
software, graph the following equations.
(a) r = 2 sin θ
(b) r = −5
(c) θ = 2r
(d) r = 2 − 2 cos θ
Solution: (a) r = 2 sin θ is a circle with radius 1 centered at (1, π
2
).
(b) r = −5 is a standard circle with radius 5.
(c) Notice that as θ increases, the r also increases. The graph of θ = 2r is a
spiral rotating counter-clockwise from the pole.
(d) The graph of r = 2 − 2 cos θ is a cardioid.
(a) (b)
250
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-256-320.jpg)


![D
EPED
C
O
PY
Topic Test 3 for Unit 3
1. Let θ be an angle in QIII such that cos θ = −
12
13
. Find the values of the six
trigonometric functions of 2θ.
2. Prove that cot(2x) =
cot2
x − 1
2 cot x
.
3. Using half-angle identities to find the exact values of the following.
(a) tan 15◦
(b) tan 7.5◦
4. Find the exact value of the following.
(a) tan−1
cot
103π
6
(b) cos sin−1 40
41
5. Let y ∈ [0, 2π). Find the solutions of the equation
sin−1
(cos2
y − cos y − 1) = −π/2.
6. Let θ ∈ [0, 2π]. Find all the solutions of the equation
4 cos2
θ sin θ = 3 sin θ.
7. Let r = −2−2 sin θ. Complete the table and plot the points (r, θ) in the same
polar coordinates.
θ 0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 7π/6 5π/4 4π/3 3π/2
r
8. Transform the following points from Cartesian to polar coordinates.
(a) (−42, −56)
(b) (100, 100)
(c) (0, 7)
(d) (7, 0)
(e) (2π, 2π)
(f) (5, 12)
9. Transform the following points from polar to Cartesian coordinates.
(a) (3, π/3)
(b) (45, 7π/4)
(c) (−1, −π)
(d) (5, 0)
(e) (2π, 2π)
(f) (9, 17π/6)
253
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-259-320.jpg)
![D
EPED
C
O
PY
Topic Test 4 for Unit 3
1. Let θ be an angle in the 2nd quadrant such that cos θ = −
7
25
. Find the
following.
(a) cos(2θ) (b) sin(2θ) (c) tan(2θ)
2. Given that cos 48◦
≈ 0.6691. Find the approximate value of the following.
(a) cos2
24◦
(b) sin2
24◦
(c) tan2
24◦
3. Using half-angle identities to find the exact values of the following.
(a) tan(π/12) (b) tan(π/24)
4. Find the exact value of cos cos−1 1
7
+ cos−1 3
5
.
5. Let x ∈ [0, 2π). Find the solutions of the equation
4 sin2
x + (2
√
3 − 2
√
2) sin x −
√
6 = 0.
6. Let θ ∈ [0, 2π]. Find all the solutions of the equation
2 sin2
(2θ) − sin(2θ) − 1 = 0.
7. Let r = 2 + 2 cos θ. Complete the table and plot the points (r, θ) in the same
polar coordinates.
θ 0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 7π/6 5π/4 4π/3 3π/2
r
8. Transform the following points from Cartesian to polar coordinates.
(a) (21, −28)
(b) (−100, −100)
(c) (0, −5)
(d) (−5, 0)
(e) (π, π)
(f) (15, 8)
9. Transform the following points from polar to Cartesian coordinates.
(a) (4, π/6)
(b) (100, 5π/4)
(c) (1, π)
(d) (−5, 0)
(e) (π, π)
(f) (15, 8π/3)
254
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-260-320.jpg)

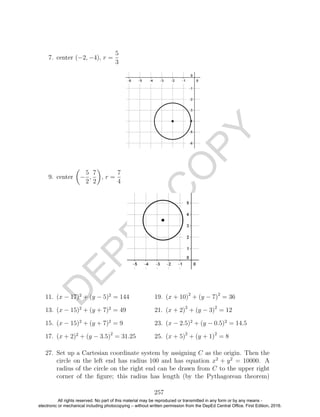


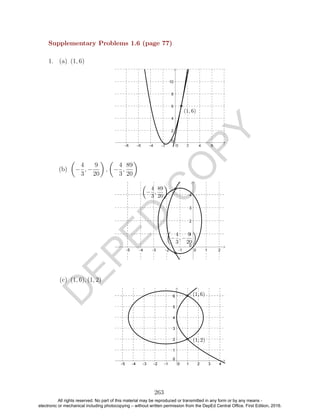
![D
EPED
C
O
PY
5. We have the system
x2
+ (y − 6)2
= 36
x2
= 4ky,
where the first equation is a circle above the x-axis, tangent to the x-axis at
x = 0, and the second equation is a parabola facing up/down, depending on
k.
Substituting the second equation in the first equation yields y2
+(4k−12)y = 0.
Note that y = 0 is already a root.
We now consider two cases.
If k > 0, the system might have one or two solutions. To ensure that the
solution is unique, we set the discriminant to be nonpositive: 4k − 12 ≤ 0 ⇒
k ≥ 3.
If k ≤ 0, the system will always have a unique solution.
Thus k ∈ (−∞, 0] ∪ (3, +∞).
1. (a) Since the coefficients of x2
and y2
are equal, the graph is a circle, a point,
or the empty set. Completing the squares, we see that the equation is
equivalent to
x −
1
2
2
+ y +
3
2
2
= 4.
Hence, the graph is a circle with center (0.5, −1.5) and radius 2.
(b) By inspection, the graph is a parabola. Completing the squares, we see
that the equation is equivalent to (x + 2)2
= 14(y + 4). Hence, the graph
has vertex at (−2, −4) and is opening upward.
(c) Since the coefficients of x2
and y2
are of opposite signs, the graph is a
hyperbola or a pair of intersecting lines. Completing the squares, we see
that the equation is equivalent to
(x − 7)2
4
−
(y + 3)2
3
= 1.
Hence, the graph is a horizontal hyperbola with center at (7, −3).
(d) Since the coefficients of x2
and y2
have the same sign and are unequal,
the graph is an ellipse, a point, or the empty set. Completing the squares,
we see that the equation is equivalent to
(x − 8)2
2
+
y2
7
= 0.
Hence, the graph is the point (8, 0).
265
Topic Test 1 for Unit 1 (page 78)
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-271-320.jpg)





![D
EPED
C
O
PY
1. Part 1.
1
2
= 2 −
1 + 2
21
The formula is true for n = 1.
Part 2.
Assume:
k
i=1
i
2i
= 2 −
k + 2
2k
.
To show:
k+1
i=1
i
2i
= 2 −
k + 3
2k+1
.
k+1
i=1
i
2i
=
k
i=1
i
2i
+
k + 1
2k+1
= 2 −
k + 2
2k
+
k + 3
2k+1
= 2 −
k + 3
2k+1
.
3. Part 1.
1(1!) = (1 + 1)! − 1
The formula is true for n = 1.
Part 2.
Assume:
k
i=1
i(i!) = (k + 1)! − 1.
To show:
k+1
i=1
i(i!) = (k + 2)! − 1.
k+1
i=1
i(i!) =
k
i=1
i(i!) + (k + 1)[(k + 1)!]
= (k + 1)! − 1 + (k + 1)[(k + 1)!]
= (k + 2)(k + 1)! − 1
= (k + 2)! − 1.
271
Supplementary Problems 2.3 (page 108)
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-277-320.jpg)





![D
EPED
C
O
PY
19. f(x) = sin 2x + cos 2x + sec 2x + csc 2x + tan 2x + cot 2x
f
7π
8
= −
√
2
2
+
√
2
2
+
√
2 −
√
2 − 1 − 1 = −2
1. P =
2π
1
4
= 8π
3.
π
4π
k
= 2 =⇒ k = 8
5. y = 3 sin 3
4
8π
9
+ 2π
3
− 5 = −13
2
7. domain = R; range = 4
3
, 8
3
9. y = 3 sec 2(x − π) − 3
11. Asymptotes: x = 3π
2
+ 2kπ, k ∈ Z
13. (a) P = 8π, phase shift = −π
4
, domain = R, range = [−3, 1]
(b) P = π, phase shift = −π
6
, domain = x|x = π
3
+ kπ, k ∈ Z , range = R
277
Supplementary Problems 3.3 (page 170)
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-283-320.jpg)
![D
EPED
C
O
PY
(c) P = 4π
3
, phase shift = π
2
, domain = x|x = π
2
+ 2kπ
3
, k ∈ Z , range =
−∞, −3
2
∪ −1
2
, ∞
(d) P = π, phase shift = −π
6
, domain = x|x = π
12
+ kπ
2
, k ∈ Z , range =
(−∞, 1] ∪ [3, ∞)
15. y = 8 cos 1
10
(t − 10π); at t = 10, y ≈ −4.32 (that is, the mass is located about
4.32 cm below the resting position)
278
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-284-320.jpg)



![D
EPED
C
O
PY
3. sin A =
12
13
, A is in QII =⇒ cos A = −
5
13
, tan A = −
12
5
cos B = −
5
3
, B is in QIV =⇒ sin B = −
3
5
, cos B =
4
5
, tan A = −
3
4
(a) cos(A − B) = cos A cos B + sin A sin B
= −
5
13
4
5
+
12
13
−
3
5
= −
56
65
(b) tan(A − B) =
tan A + tan B
1 + tan A tan B
=
−
12
5
+ −
3
4
1 + −
12
5
−
3
4
= −
33
56
4.
tan 57◦
+ tan 78◦
1 − tan 57◦ tan 78◦
= tan(57 + 78)◦
= tan 135◦
= −1
5.
cos x tan x + sin x
tan x
= cos x +
sin x
tan x
= 2 cos x = 2 1 − sin2
x = 2
√
1 − a2
6. cos6
x + sin6
x = (cos2
x)3
+ (sin2
x)3
= (cos2
x + sin2
x)(cos4
x − cos2
x sin2
x + sin4
x)
= cos4
x − cos2
x sin2
x + sin4
x
= cos4
x − cos2
x(1 − cos2
x) + (1 − cos2
x)2
= cos4
x − cos2
x + cos4
x + 1 − 2 cos2
x + cos4
x
= 3 cos4
x − 3 cos2
x − 1
7. Connect the three diagonals of the hexagon. In doing this, the hexagon is
divided into 6 equilateral triangles. Hence, B
1
2
,
√
3
2
. Same coordinates
for C, E and F, except that they will just vary in signs depending on the
quadrant.
8. y = 2 sin
x
2
+
π
3
− 1 =⇒ y = 2 sin
1
2
x +
2π
3
− 1
P = 4π, Phase Shift =
2π
3
, Amplitude = 2, Range = [−3, 1]
282
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-288-320.jpg)


![D
EPED
C
O
PY
13. (a) cos 105◦
=
√
2+
√
3
2
(b) tan 22.5◦
=
√
2 − 1
1. (a) sin[sin−1
(1/2)] = 1/2
(b) cos[cos−1
(−
√
2/2)] = −
√
2/2
(c) tan[tan−1
(−
√
3)] = −
√
3
(d) sin[arctan(
√
3)] = −
√
3/2
(e) cos[arccos(
√
2)] does not exist
(f) tan[arcsin(1/4)] =
√
15/15
(g) cos(sin−1
√
3/2) = 1/2
3. (a) sin[2 cos−1
(−4/5)] = −24/25
(b) cos[2 sin−1
(5/13)] = 119/169
(c) sin[sin−1
(3/5) + cos−1
(−5/13)] = 33/65
(d) cos[sin−1
(1/2) − cos−1
(8/17)] = (15 + 8
√
3)/34
5. (a) arcsec(−
√
2) = 3π/4
(b) arccsc(−2) = −π/6
(c) arccot
√
3 = π/6
(d) [sec−1
(−1)] · [cos−1
(−1)] = π · π = π2
(e) 2 cot−1
√
3 + 3 csc−1
2 = 2(π/6) + 3(π/6) = 5π/6
(f) csc−1
0 does not exist
7. Vertex angle θ should be π/3.
1. Solution set: {π/2, 3π/2, 5π/2, 7π/2, ...} = {(2k + 1)π/2 | k ∈ Z}
3. Solution set: {2kπ/3 | k ∈ Z}
5. Solution set: {π/8, 3π/8, 9π/8, 11π/8}
7. Solution set: {−π/2, π/6}
9. The bullet should be fired with an angle of θ = 60◦
.
285
Supplementary Problems 3.7 (page 219)
Supplementary Problems 3.8 (page 236)
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-291-320.jpg)


![D
EPED
C
O
PY
References
[1] R.N. Aufmann, V.C. Barker, and R.D. Nation, College Trigonometry, Houghton
Mifflin Company, 2008.
[2] E.A. Cabral, M.L.A.N. De Las Pe˜nas, E.P. De Lara-Tuprio, F.F. Francisco,
I.J.L. Garces, R.M. Marcelo, and J.F. Sarmiento, Precalculus, Ateneo de
Manila University Press, 2010.
[3] R. Larson, Precalculus with Limits, Brooks/Cole, Cengage Learning, 2014.
[4] L. Leithold, College Algebra and Trigonometry, Addison Wesley Longman
Inc., 1989, reprinted by Pearson Education Asia Pte. Ltd., 2002.
[5] M.L. Lial, J. Hornsby, and D.I. Schneider, College Algebra and Trigonometry
and Precalculus, Addison-Wesley Educational Publisher, Inc., 2001.
[6] J. Stewart, L. Redlin, and S. Watson, Precalculus: Mathematics for Calculus,
Brooks/Cole, Cengage Learning, 2012.
[7] M. Sullivan, Algebra & Trigonometry, Pearson Education, Inc., 2012.
[8] C. Young, Algebra and Trigonometry, John Wiley & Sons, Inc., 2013.
290
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2016.](https://image.slidesharecdn.com/deped-precalculus-lmv206012016-160830124826/85/Pre-calculus-Grade-11-Learner-s-Module-Senior-High-School-296-320.jpg)