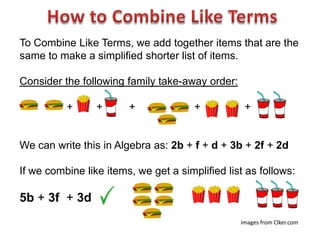
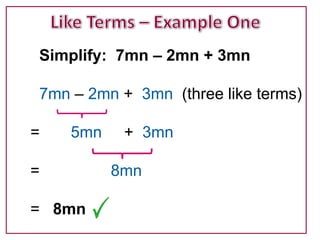
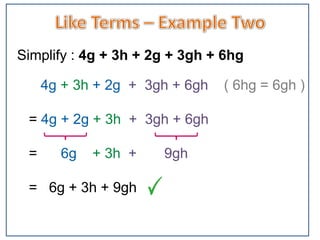
The document discusses like terms in algebra. It defines like terms as terms that have the same variables raised to the same powers. To combine like terms, you collect terms with the same variables and exponents together and add or subtract their coefficients. This simplifies expressions by reducing multiple terms into a single term. The document provides examples of combining like and unlike terms through addition, subtraction, and identifying whether terms can be combined.

1. Image Source: http://3.bp.blogspot.com

2. People who are twins are a “like pair” because
they have the exact same features.
An Algebra Equation we can write for this is :
T + T = 2T
Eg. One Twin + One Twin = 2 Twins.
In Algebra we call this “Combining Like Terms”.

3. A typical question is : Simplify 2a + 3b + 3a
2a + 3b + 3a
If we think of “a” being Apples and “b” being Bananas,
then we have the following situation:
We can see that by combining the like objects, the above
can be simplified to be 5 Apples and 3 Bananas, which in
Algebra is:
5a + 3b Images from Clker.com

4. "Like Terms" are terms that contain the same letter Variables
which are raised to the exact same Powers.
( Only the first number "Coefficients" of the terms are different )
3a and 2a are like terms, because although they have
different coefficient numbers, they have the exact same
letter "a" in them.
Some other examples of like terms are:
3d2y 12d2y - 2d2y d2y
bh 4bh -5bh -bh

5. Always remember that the Powers need to be the same.
P3 and P2 are NOT like terms
They have the same Variable letter “P” in them, but their
Exponent Index values are different.
Just as the Playstation PS-3
is different to the PS-2,
P3 is also different to P2 .
The items are not identical.

6. Just like checking two cars very carefully, make sure you
check every part of each pair of Algebraic Terms.
2 3 3 2 5 3
2x y z and 3x y z

7. Decide if the terms in each pair of items are “Like Terms”.
1) 4g and 4h ______
2) 3h and –h ______
3) 5x and 4xy ______
4) 2x2y3 and 2x2y5 ______
5) 5p2q3 and -4p2q3 ______

8. Decide if the terms in each pair of items are “Like Terms”.
1) 4g and 4h NO – letter variables are different.
2) 3h and –h YES – letters the same ( –h = -1h)
3) 5x and 4xy NO – letter variables are different.
4) 2x2y3 and 2x2y5 NO – y powers are different.
5) 5p2q3 and -4p2q3 YES – letters & powers same

9. Often in real life it is necessary to combine like items
together to create a shorter list of items we can deal with.
For example, imagine that a mathematics class is on an
excursion and need to order a take away food lunch.
It would be crazy to read out each individual order, one after
each other, at the counter of the fast food restaurant.
Instead we would total up how many burgers, how many
fries, how many drinks, etc that we need to order for the
whole group. We combine the items into a summarised list.
This type of summarizing process is exactly the same
as combining Algebraic Like Terms.

10. To Combine Like Terms, we add together items that are the
same to make a simplified shorter list of items.
Consider the following family take-away order:
+ + + + +
We can write this in Algebra as: 2b + f + d + 3b + 2f + 2d
If we combine like items, we get a simplified list as follows:
5b + 3f + 3d
Images from Clker.com

11. We can also Subtract Like Terms
Suppose that we have bought 5 apples and 6 bananas, but
we eat two bananas before putting our fruit into the bowl.
+ -
The Algebra is: 5a + 6b – 2b
= 5a + 6b – 2b (6 bananas take away 2 is 4)
= 5a + 4b
= 5a + 4b Images from Clker.com

12. WARNING: Like Terms are only used for
Adding and Subtracting algebraic terms.
We never use combining like terms for
Multiplying and Dividing !
Images from Clker.com

13. To Combine Like Terms, follow these steps:
 Identify the items which are “Like Terms”
 Rewrite the expression so that the like terms
are all next to each other
 Combine the groups of like terms together to
make a simplified shorter final answer
This last step involves adding
or subtracting the like terms

14. Simplify: 7mn – 2mn + 3mn
7mn – 2mn + 3mn (three like terms)
= 5mn + 3mn
= 8mn
= 8mn

15. Simplify : 4g + 3h + 2g + 3gh + 6hg
4g + 3h + 2g + 3gh + 6gh ( 6hg = 6gh )
= 4g + 2g + 3h + 3gh + 6gh
= 6g + 3h + 9gh
= 6g + 3h + 9gh

16. Simplify the expression: 4w + 3 + 2w - 1
4w + 3 + 2w – 1 (Now Group Like Terms)
= 4w + 2w + 3 – 1 (Combine Like Terms)
= 6w + 2
= 6w + 2

17. Simplify: 2a – 10ab + 3a – ab – 7
3 2 3 2
2a3 – 10ab2 + 3a3 – ab2 – 7
= 2a + 3a – 10ab – 1ab – 7
3 3 2 2
= 5a 3
– 11ab 2
–7
= 5a3 – 11ab2 – 7

18. Simplify the expression: 4a2 + 3a + 5a3 - 1
The expression contains terms that
are all different from each other.
The expression cannot be simplified
any further.
2 3
4a + 3a + 5a - 1

19. http://passyworldofmathematics.com
Visit our Site for Free Mathematics PowerPoints