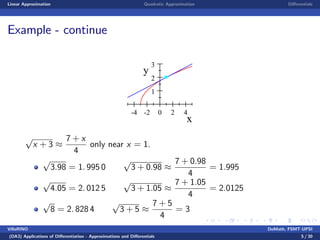
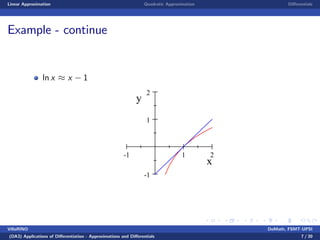
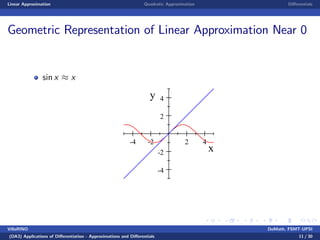
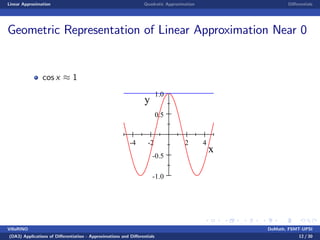
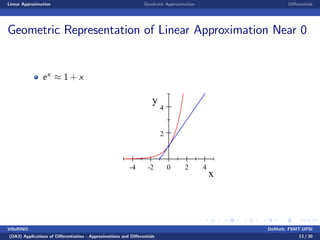
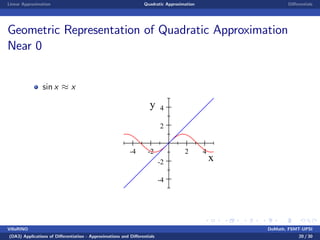
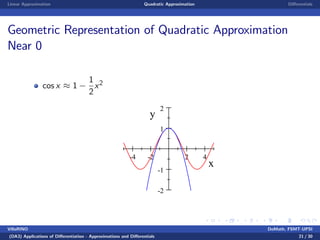
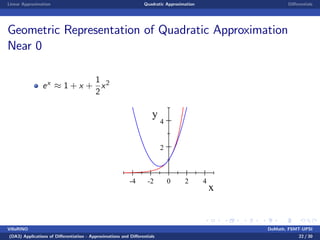
This document discusses linear and quadratic approximations using differentials. It begins by defining linear approximation as using the equation f(x) ≈ f(x0) + f'(x0)(x - x0), where f'(x0) is the derivative of the function f at the point x0. Examples of linear approximations are shown for functions like square root and logarithm. The document then introduces quadratic approximations, which add a second-order term involving the second derivative to improve accuracy. Graphs demonstrate the linear and quadratic approximations. Finally, differentials are defined using derivatives to estimate values like a cube root.