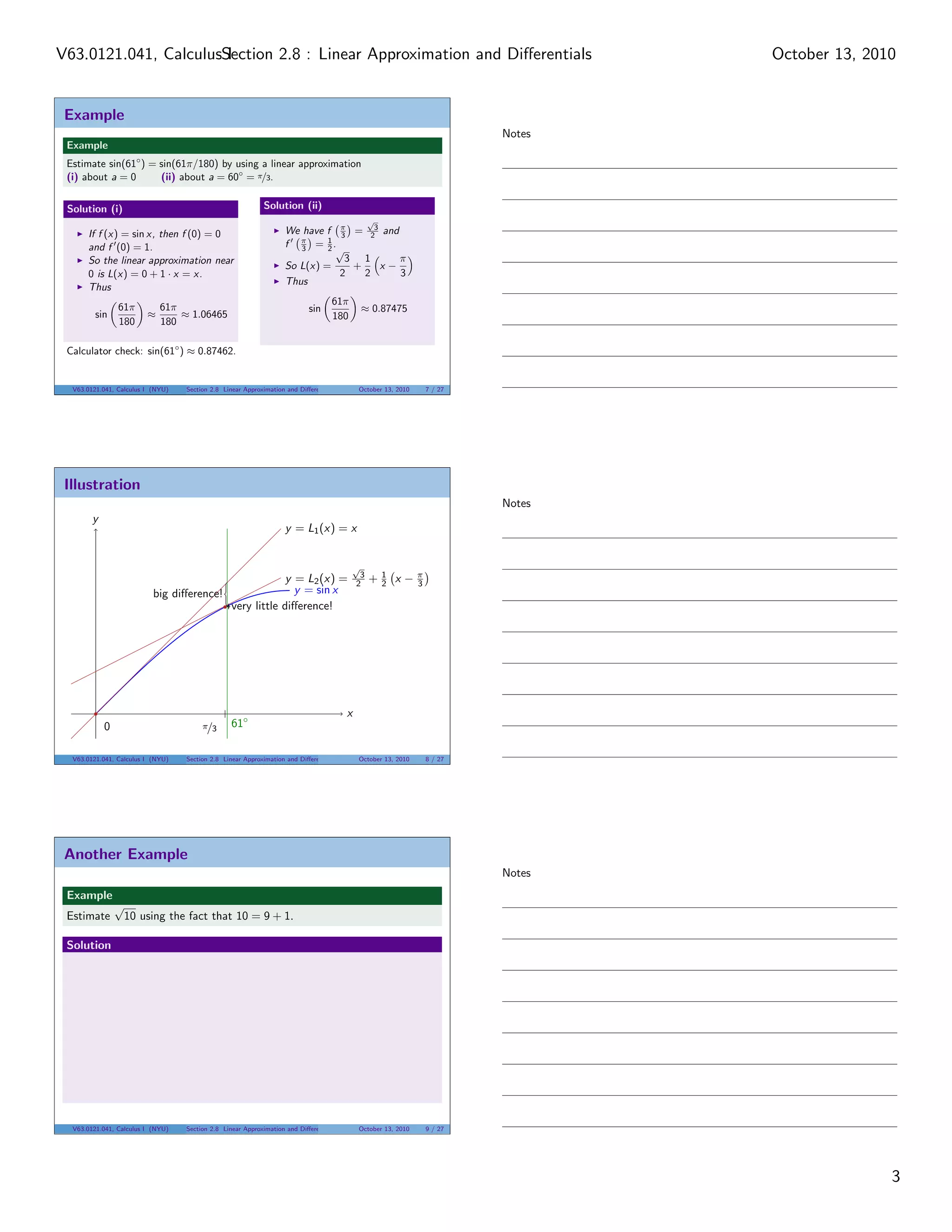
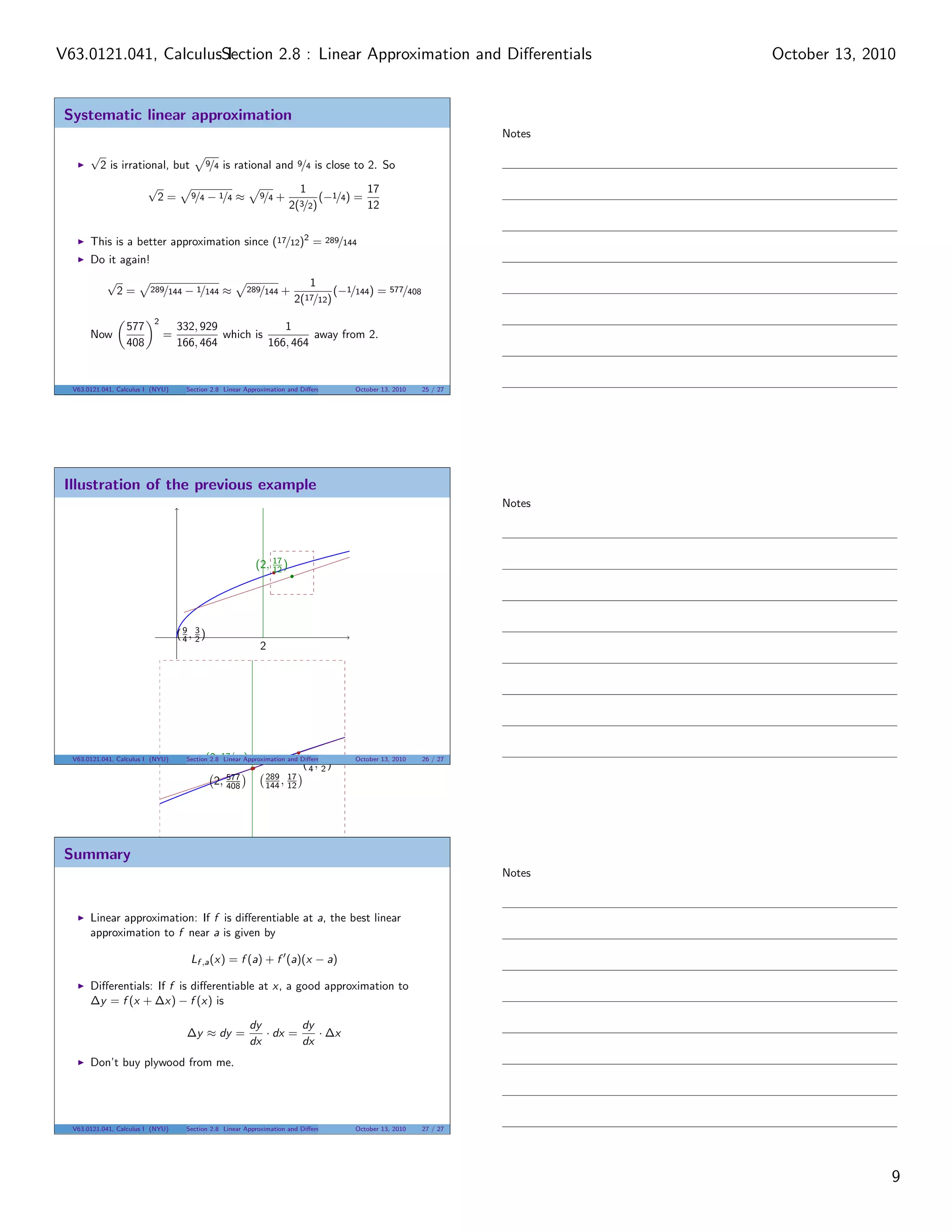
The document covers linear approximation and differentials in calculus, focusing on using tangent lines for approximating functions and calculating differentials to estimate errors. Key concepts include linearization, examples using trigonometric functions, and practical applications such as estimating distances and costs. It emphasizes the effectiveness of linear approximation methods for quick and reliable estimates in various scenarios.