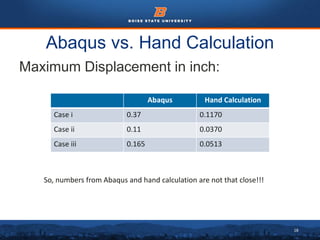
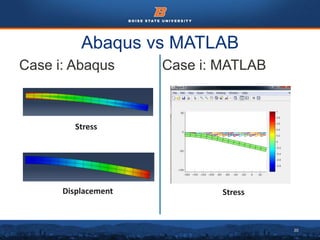
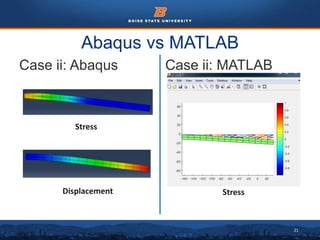
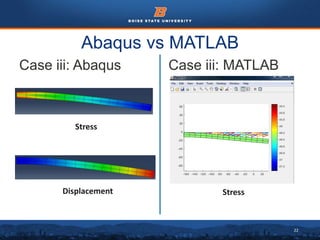
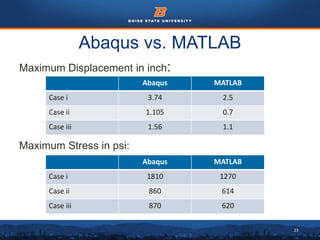
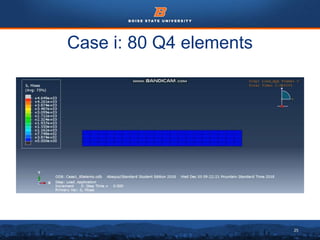
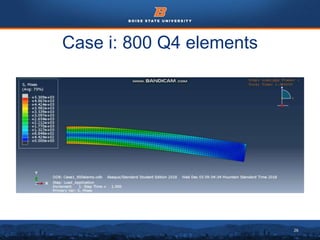
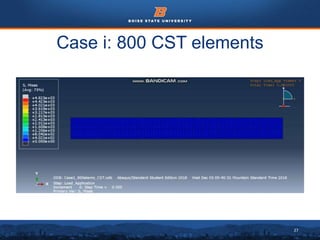
This document summarizes a finite element analysis of a cantilever beam using quadrilateral meshing elements. The beam is modeled and analyzed in Abaqus for three loading cases: a point load at the free end, a point load at the mid-section, and a distributed load along the length. Hand calculations are also performed and compared to Abaqus and MATLAB results. Increasing the number of elements improves accuracy of the models. Quadrilateral elements are preferred over triangular elements for beam bending problems. Maximum displacement occurs under a point load at the free end. The study concludes with recommendations for accurate beam modeling and design using finite element analysis.

1. © 2012 Boise State University 1
ME 570 - Finite Element
Methods

2. © 2012 Boise State University 2
Finite Element Based Structural
Analysis of a Cantilever Beam Using
Quadrilateral Meshing Elements.
MD ASIF RAHMAN
Graduate Student
Dept. of Civil Engineering
TITLE:

3. 3
Finite Element Method
Finite element methods are numerical methods for
approximating the solutions of mathematical
problems that are usually formulated so as to
precisely state an idea of some aspect of physical
reality.

4. 4
FEM, my point of interest!
• New focus: modeling works rather than
experimental tasks.
• Meso to micro-structure modeling of concrete
materials
• Basic understanding of finite element methods,
i.e. how FEA software like COMSOL or Abaqus
solve finite element problems.

5. 5
Cantilever Beam

6. 6
Cantilever Beam
• Structural beams are an integral part of
most structural projects. Cantilever beam
is of major concern because of it’s
overhanging concept.

7. 7
FEM for Cantilever Beam
• Importance:
• In real world beam is subjected to loading
conditions. So, stress and deflection
analysis is must for the accurate design.
• The element wise discretization in FEM
helps to effectively analyze structural
beam subjected to loading conditions.

8. 8
FEM for Cantilever Beam
Element Choice:
• Q4: Beam bends under load application
and for bending problems, quadratic
elements are preferred.
• Comparison with other element shape and
material property has been included in this
work.

9. 9
Problem Setup
A cantilever beam was considered with following
properties:
Length=120” Modulus of Elasticity: 1E6 psi
Depth=12” Poisson’s ratio: 0.3
Thickness=1” Mass density: 1lb/in^3

10. 10
Case Study
Applied load, P=1000lb
Case i: P as a point load applied at the free
end.
Case ii: P as a point load applied at the mid
section of beam.
Case iii: P distributed load applied along the
length of the beam.

11. 11
Hand Canculation

12. 12
Hand Canculation
Steps:
• Constitutive matrix, CM
• Strain displacement matrix
• Element stiffness matrix; Element 1 =Element 2
• Global stiffness matrix, K=k1+k2
• Application of load and BCs
• Displacement calculation

13. 13
Hand Calculation
Displacement values:
case i case ii case iii

14. 14
Abaqus
• To match with the hand calculation at first
beam was analyzed with only two Q4
elements for case i, ii and iii respectively.
Case i
Case ii
Case iii

15. 15
Abaqus
Displacement values:
case i

16. 16
Abaqus
Displacement values:
case ii

17. 17
Abaqus
Displacement values:
case iii

18. 18
Abaqus vs. Hand Calculation
Maximum Displacement in inch:
Abaqus Hand Calculation
Case i 0.37 0.1170
Case ii 0.11 0.0370
Case iii 0.165 0.0513
So, numbers from Abaqus and hand calculation are not that close!!!

19. 19
Then cantilever beam was analyzed with
increased element numbers (i.e. 30):
• To compare MATLAB and Abaqus results
• To predict result more accurately.

20. 20
Abaqus vs MATLAB
Case i: Abaqus Case i: MATLAB
Stress
Displacement Stress

21. 21
Abaqus vs MATLAB
Case ii: Abaqus Case ii: MATLAB
Stress
Displacement Stress

22. 22
Abaqus vs MATLAB
Case iii: Abaqus Case iii: MATLAB
Stress
Displacement Stress

23. 23
Abaqus vs. MATLAB
Maximum Displacement in inch:
Maximum Stress in psi:
Abaqus MATLAB
Case i 3.74 2.5
Case ii 1.105 0.7
Case iii 1.56 1.1
Abaqus MATLAB
Case i 1810 1270
Case ii 860 614
Case iii 870 620

24. 24
Then cantilever beam was with Q4 element
was further analyzed in Abaqus:
• To visualize the results
• To figure out how it behaves under different
element or material property.

25. 25
Case i: 80 Q4 elements

26. 26
Case i: 800 Q4 elements

27. 27
Case i: 800 CST elements

28. 28
Case i: 80 Q4 elements )
(Hyperfoam not Elastic)
mu=30pa-s, nu=0.3, alpha=0.03

29. 29
Conclusion
• Although triangular elements do not exhibit shear locking
behavior, they are usually too much stiff. They are thus
not really recommendable for beam problems.
• Q4 elements are preferred and effective for beams under
bending.
• Displacement and thus stress is maximum at case i So,
for cantilever beam most sensitive and challenging
scenario occur when load is applied at free end.
• As long as we move the load close to the support
condition displacement tends to decrease.
• Even in case of distributed load (case iii), the maximum
displacement is less than case i.

30. 30
Conclusion
• Triangular elements show less displacement than
quadratic elements since they are more stiff.
• Stress-strain curve will change significaltly if we change
material property based on inelastic analysis. For
example, hyperfoam material is very poor in terms of it’s
resistance to applied load as we saw in the video.
• So , to accurately design a beam with FEM we should be
aware of correct element choice, material behavior (i.e.
concrete shows non-linearity), material property,
meshing (i.e. no of elements, convergence issue) and
load & support conditions.

31. 31
References
 [1]. E. Monterrubio, Luis. Analytical solution, finite element
analysis, and experimental validation of a cantilever beam.
Robert Morris university.
 [2]. Belendez, Tarsicio et. Al. Large and small deflections of a
cantilever beam.
 [3]. Kumar, Sanjay. Comparison of deflection and slope of
cantilever beam with analytical and finite element method for
different loading conditions.
 [4]. Ghuku, Sushanta et. Al. A theoretical and experimental
study on geometric nonlinearity of initially curved cantilever
beams.
 [5]. Jadhao, V.B. et. Al. Investigation of stresses in cantilever
beam by FEM and its experimental verification.
 [6]. Samal, Ashis Kumar, et. Al. Analysis of stress and
deflection of cantilever beam and its validation using ANSYS

32. 32
THANK YOU
Md. Asif Rahman
Graduate Student
ID: 114084345
Email mdasifrahman@u.boisestate.edu