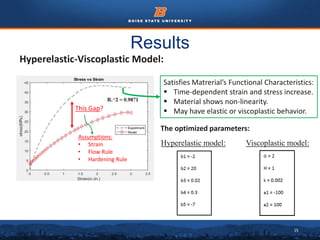
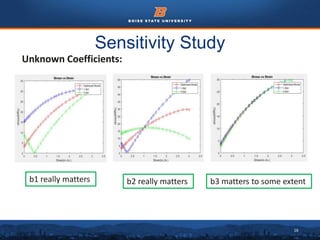
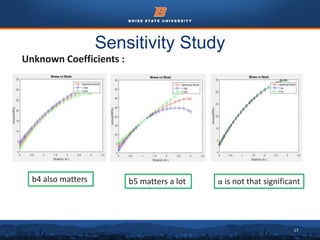
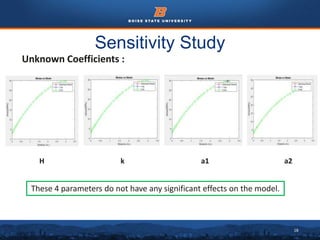
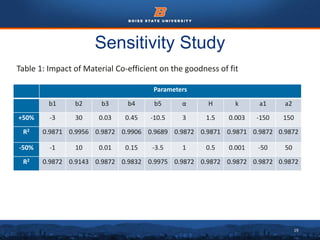
This document summarizes the development of a hyperelastic-viscoplastic model to model the behavior of concrete under uniaxial loading. It describes conducting a uniaxial compression test on a concrete cylinder specimen. A hyperelastic model and viscoplastic model were combined in a constitutive equation to model the material. Material coefficients for the models were optimized by fitting the model predictions to the experimental stress-strain data. A sensitivity study identified which coefficients most significantly affected the model fit. Other material models like Mooney-Rivlin and linear isotropic solid models were also tested but did not fit the experimental data as well. The model reasonably captured the nonlinear stress-strain behavior of concrete but had limitations and assumptions that could be

1. © 2012 Boise State University 1
ME 510 – Continuum
Mechanics

2. © 2012 Boise State University 2
Simplified Hyperelastic-Viscoplastic
Modeling of Concrete Subjected to
Uniaxial Loading.
MD ASIF RAHMAN
Graduate Student
Dept. of Civil Engineering
TITLE:

3. 3
Continuum Mechanics
My point of interest :
What is i, j, or k

4. 4
Material Selection: Concrete
Focus:
• Research Interest
• Modeling Purpose

5. 5
Concrete
What is Concrete:
Concrete = Aggregate + Cement Paste
Application:
 most frequently used construction material
 Concrete has environmental, social and
economic benefit
 Concrete is frequently used to build
skyscrapers, bridges, highways, houses,
dams, nuclear reactor and so on.
Picture Credit: free online resources

6. 6
Concrete
Classification:
 Composite Material
Composition:
 Portland Cement & Water
 Fine & Coarse Aggregate (i.e. Sand
and Brick Chips)
Organization:
 Anisotropy: Different aggregate
(CA) size.
 Isotropic: For simplicity
Function:
Qualitative:
 Time dependency
 Non-linearity
 Elasticity
 Plasticity
 Creep & Shrinkage
 Viscoelasticity
Quantitative1:
 Density: 2240-2400 kg/m3
 Compressive strength: 20-40 MPa
 Tensile strength: 2-5 MPa
 Modulus of Elasticity, E: 14-41 GPa
1.https://www.engineeringtoolbox.com/concrete-properties-d_1223.html

7. 7
Experimental Setup
 Concrete Cylinder
 Compression Test
 Confined Condition
 Uniaxial Loading Uniaxial Loading
Concrete Cylinder
Lab Setup

8. 8
Experimental Data
Concrete Type I; w/c = 0.4
Mean Strength: 43.5 Mpa
Mix: 1 : 1 : 2

9. 9
Modeling
Hyperelastic-Viscoplastic Model:
MODEL
Hyperelastic
Part
Viscoplastic
Part

10. 10
Constitutive Equation
+
Hyperelastic Part Viscoplastic Part

11. 11
Constitutive Equation
Hyperelastic Model:
Stress from Hyperelastic Model

12. 12
Constitutive Equation
Viscoplastic Model:
Loading Surface
where, a1 and a2 are parameters.
where, I1
c, I2
c and I3
c are the modified first, second and
third invariants.
w = damage variable =
Where, A0 is the initial area of undamaged section.
= Viscoplastic strain tensor
Stress from Viscoplastic Model

13. 13
Constitutive Equation
Assumptions:
1. Total strain,
2. Since, this is uniaxial loading there is only λ11.
Deformation gradient,
3. Infinitesimal Strain,
4. Effective stress =
final load at which concrete cracks
initial area of undamaged section
I assumed:

14. 14
Material Coefficients
Hyperelastic Model:
 α : This is a parameter.
 H: This is hardening parameter. Must be
positive to happen hardening.
 κ: This is the isotropic hardening
variable.
 a1 and a2:These two are parameters
which modify damage variable, w.
Viscoplastic Model:
 b1,b2,b3,b4, and b5: These five coefficients
are material constants.
 They form the second order hyperbolic
equation for strain energy function which
modify stress tensor.

15. 15
Results
Hyperelastic-Viscoplastic Model:
The optimized parameters:
Satisfies Matrerial’s Functional Characteristics:
 Time-dependent strain and stress increase.
 Material shows non-linearity.
 May have elastic or viscoplastic behavior.
Hyperelastic model: Viscoplastic model:
Assumptions:
• Strain
• Flow Rule
• Hardening Rule
This Gap?

16. 16
Sensitivity Study
Unknown Coefficients:
b1 really matters b2 really matters b3 matters to some extent

17. 17
Sensitivity Study
Unknown Coefficients :
b4 also matters b5 matters a lot α is not that significant

18. 18
Sensitivity Study
Unknown Coefficients :
These 4 parameters do not have any significant effects on the model.
H k a1 a2

19. 19
Sensitivity Study
Parameters
b1 b2 b3 b4 b5 α H k a1 a2
+50% -3 30 0.03 0.45 -10.5 3 1.5 0.003 -150 150
R2 0.9871 0.9956 0.9872 0.9906 0.9689 0.9872 0.9871 0.9871 0.9872 0.9872
-50% -1 10 0.01 0.15 -3.5 1 0.5 0.001 -50 50
R2 0.9872 0.9143 0.9872 0.9832 0.9975 0.9872 0.9872 0.9872 0.9872 0.9872
Table 1: Impact of Material Co-efficient on the goodness of fit

20. 20
Other Models
Mooney-Rivlin Model:
Optimized material coefficients:
C1 = 0.005
C2 = 10.9184
• limitations to represent non-linear
increase of stress with strain.
• Shows a good fit to experimental
data but goes with the different peak
value of strength.

21. 21
Other Models
Discrete Element Model (Voigt Model):
Optimized material coefficients:
k = 25
c = 2
• Time –dependent analysis
• Can show material non-linearity.
• Not that good fit to experimental
data and goes with the different peak
value of strength.

22. 22
Other Models
Linear Isotropic Solid:
Optimized material coefficients:
E=35.95
• Very poor fit
• Limitations to material non-linearity.

23. 23
Discussion
Interpretation of Results:
Pros: Cons:
• Can predict stress-strain behavior
• Can show material non-linearity
• Applicable to time-dependent
analysis
• Can simulate Concrete’s
hyperelastic/viscoplastic behavior to
some extent
• Linited to confined compression test
• Limited to uniaxial loading
• Valid for Concrete material
• Model works based on assumptions:

24. 24
Conclusion
• Though Model has some limitations, it can be used for
approximation/prediction of material behavior.
• Can be further developed using complete viscoplastic
model.
• Can be checked with other/realistic fraction of elastic and
viscoplastic strain.
• Can be validated by considering several experimental
data from different source/conditions.

25. 25
References
• [1]. Dinesh Panneerselvam and Vassilis P. Panoskaltsis, Numerical
Implementation of A Hyperelastic-Viscoplastic Damage Model for
Asphalt Concrete Materials and Pavements, ASCE journal, 2006.
DOI: 10.1061/40825(185)7
• [2]. Jianlian Cheng, Xudong Qian, Tieshuan Zhao, Rheological
Viscoplastic Models of Asphalt Concrete and Rate-Dependent
Numerical Implement, International Journal of Plasticity, 81 (2016)
209-230, http://dx.doi.org/10.1016/j.ijplas.2016.01.004
• [3]. T. Yu, J.G. Teng, Y.L. Wong, S.L. Dong, Finite Element Modeling
of Confined Concrete-II: Plastic-Damage Model, Engineering
Structures, 32 (2010) 680-691, doi:10.1016/j.engstruct.2009.11.013

26. 26
THANK YOU
Md. Asif Rahman
Graduate Student
ID: 114084345
Email mdasifrahman@u.boisestate.edu