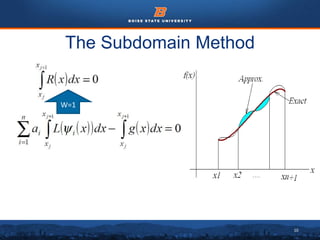
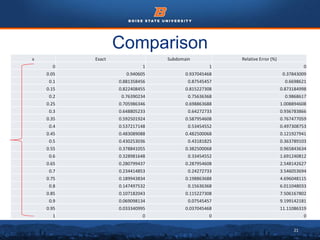
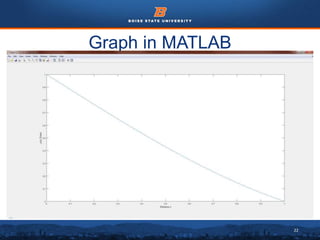
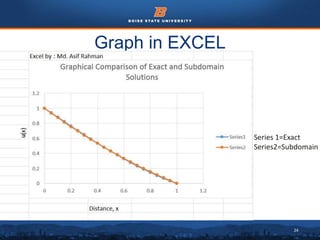
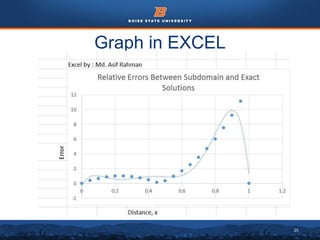
This document discusses the subdomain method for solving differential equations using finite element analysis. The subdomain method approximates solutions by forcing the integral of the residual to equal zero over subintervals, or subdomains, of the total domain. It provides an example problem of using the subdomain method to solve a second order differential equation. The exact solution is compared to the approximate subdomain solution, showing good accuracy with less than 12% relative error. The subdomain method is simple to formulate but works best for problems involving a single governing equation.

1. © 2012 Boise State University 1
CE 502 - Computational
Techniques

2. © 2012 Boise State University 2
The Subdomain Method
MD ASIF RAHMAN
Graduate Student

3. 3
Finite Element Method
• Finite element methods are numerical methods
for approximating the solutions of mathematical
problems that are usually formulated so as to
precisely state an idea of some aspect of
physical reality.
• We can solve differential equations with FEM.
• Approximations in two ways:
1. Variational and Raleigh-Ritz Procedures
2. Method of Weighted Residuals

4. 4
Raleigh-Ritz Procedures:
• A method of finding approximations to eigenvalue
equations that cannot be solved easily (or at all)
analytically
Method of Weighted Residuals
• An approximation technique for solving differential
equations.
• Here an error or residual will exist
• The notion in this method is to force the
residual to zero in some average

5. 5
Basic Concepts
• A linear differential equation may be written in
the form:
• Where L(.) is a linear differential operator.
• An approximate solution maybe of the form:

6. 6
Basic Concepts
• Applying the differential operator on the approximate
solution, we will get:

7. 7
Handling the Residue
• The weighted residual methods are all based on
minimizing the value of the residue.
• Since the residue can not be zero over the
whole domain, different techniques were
introduced:
1. Galerkin method.
2. Collocation method.
3. Sub-domain method.
4. Least Squares method.

8. 8
Subdomain Method

9. 9
What is Subdomain Method?
The idea behind the
subdomain method is
to force the integral
of the residue to be
equal to zero on an
subinterval of the
Domain.

10. 10
The Subdomain Method
W=1

11. 11
Example Problem 1
Physical Problem

12. 12
Structural Beam in Bending
Let’s consider the beam in Figure with constant modulus of elasticity and
Moment of inertia with respect to given boundary conditions.

13. 13
Developing a Solution

14. 14
Applying Subdomain Method

15. 15
Example Problem 2
Mathematical Problem

16. 16
Mathematical Problem
As an example, consider the solution of the
following mathematical problem. Find u(x) that
satisfies

17. 17
Exact Solution
From Basic Concepts we know,
Here,
The exact solution can be found and is, in general form,
u(x) = C1 sin x + C2 cos x + 1
For bounded conditions:
&
Exact Solution is

18. 18
Mathematical Problem
Using a polynomial function as a basis. The
approximating function be:
For bounded conditions:

19. 19
Applying Subdomain Method
Since we have one unknown constant, we choose a single
“subdomain” which covers the entire range of x.

20. 20
Now we can check how accurately
subdomain method represent this example
problem:
By considering result of Subdomain
method with the exact one

21. 21
Comparison
x Exact Subdomain Relative Error (%)
0 1 1 0
0.05 0.940605 0.937045468 0.37843009
0.1 0.881358456 0.87545457 0.6698621
0.15 0.822408455 0.815227308 0.873184998
0.2 0.76390234 0.75636368 0.9868617
0.25 0.705986346 0.698863688 1.008894608
0.3 0.648805233 0.64272733 0.936783866
0.35 0.592501924 0.587954608 0.767477059
0.4 0.537217148 0.53454552 0.497308753
0.45 0.483089088 0.482500068 0.121927941
0.5 0.430253036 0.43181825 0.363789103
0.55 0.378841055 0.382500068 0.965843634
0.6 0.328981648 0.33454552 1.691240812
0.65 0.280799437 0.287954608 2.548142627
0.7 0.234414853 0.24272733 3.546053694
0.75 0.189943834 0.198863688 4.696048115
0.8 0.147497532 0.15636368 6.011048033
0.85 0.107182043 0.115227308 7.506167802
0.9 0.069098134 0.07545457 9.199142181
0.95 0.033340995 0.037045468 11.11086319
1 0 0 0

22. 22
Graph in MATLAB

23. 23
Graph in MATLAB

24. 24
Graph in EXCEL
Series 1=Exact
Series2=Subdomain

25. 25
Graph in EXCEL

26. 26
The Subdomain Method
• Advantage:
 Simple to formulate.
 Provides satisfactory result.
 Used mostly for problems with only one governing
equation (axial bar, beam, heat etc.).
• Disadvantage:
 Complex situation for problems with more than
one governing equation.

27. 27
Summary on Subdomain Method
• This method doesn’t use weighting factors explicity,
so it is not, strictly speaking, a member of the
Weighted Residuals family.
• It can be considered as a modification of the
collocation method.
• The idea is to force the weighted residual to zero not
just at fixed points in the domain, but over various
subsections of the domain.
• The weight functions are set to unity, and the
integral over the entire domain is broken into a
number of subdomains sufficient to evaluate all
unknown parameters.

28. 28
References
 Approximate Methods in Structure Mechanics
----Mohammad Tawfik19 February 2014
 Fundamentals of the Finite Element Method,
Waveland Press, 1991
---- Grandin, H.

29. 29
THANK YOU
Md. Asif Rahman
Graduate Student
ID: 114084345
Email mdasifrahman@u.boisestate.edu