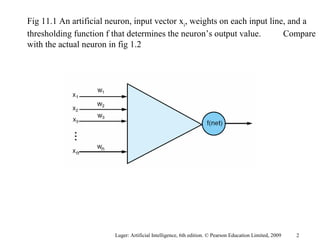
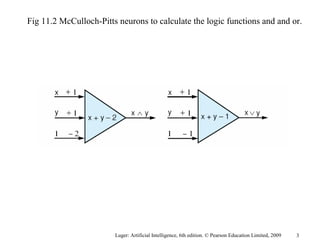
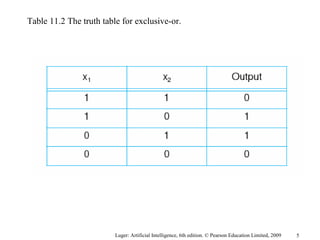
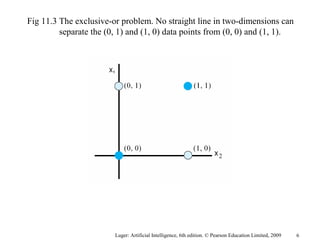
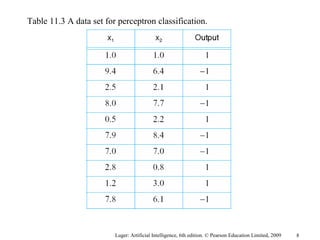
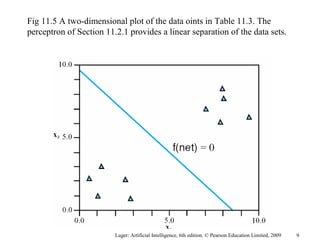
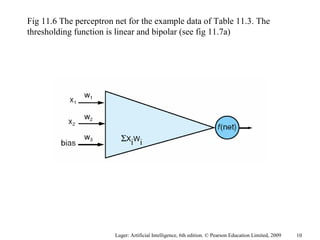
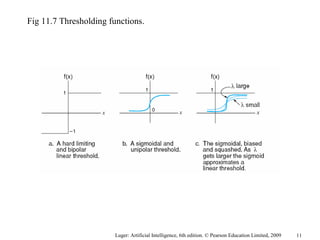
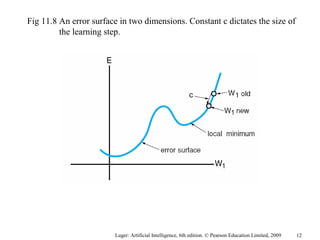
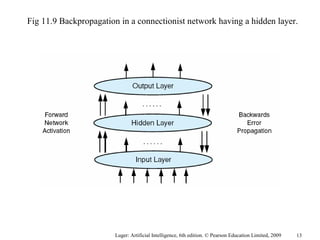
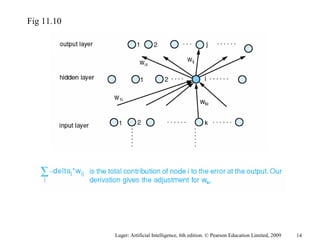
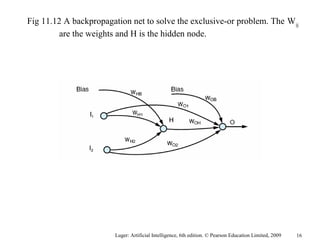
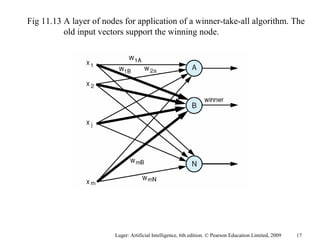
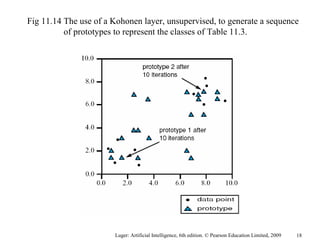
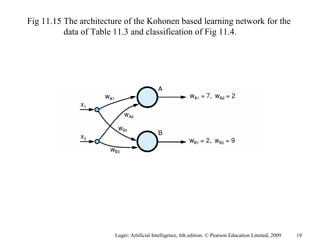
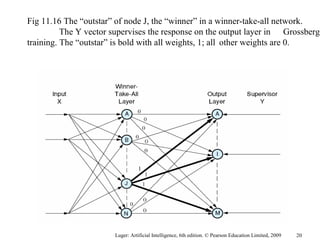
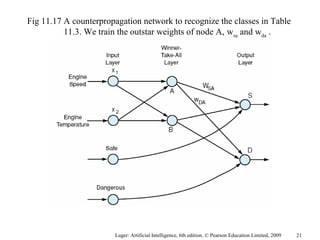
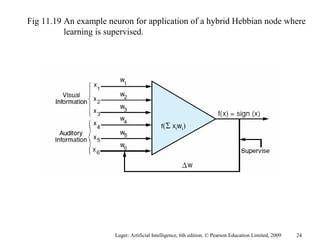
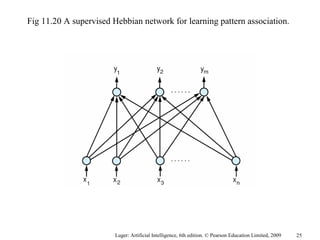
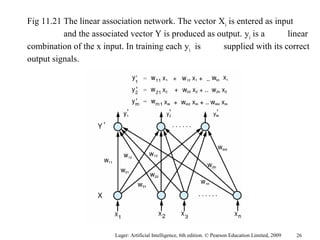
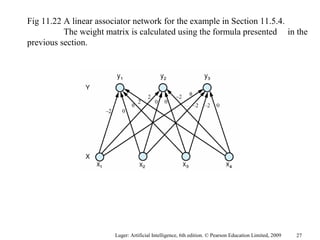
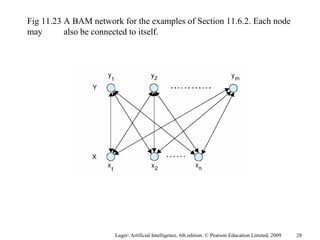
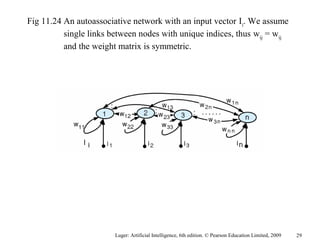
The document summarizes machine learning techniques in artificial neural networks, including perceptrons, backpropagation, competitive learning, Hebbian learning, and attractor networks. It includes figures and tables explaining concepts like artificial neurons, McCulloch-Pitts logic functions, perceptron classification of data, and network architectures for tasks like speech recognition.