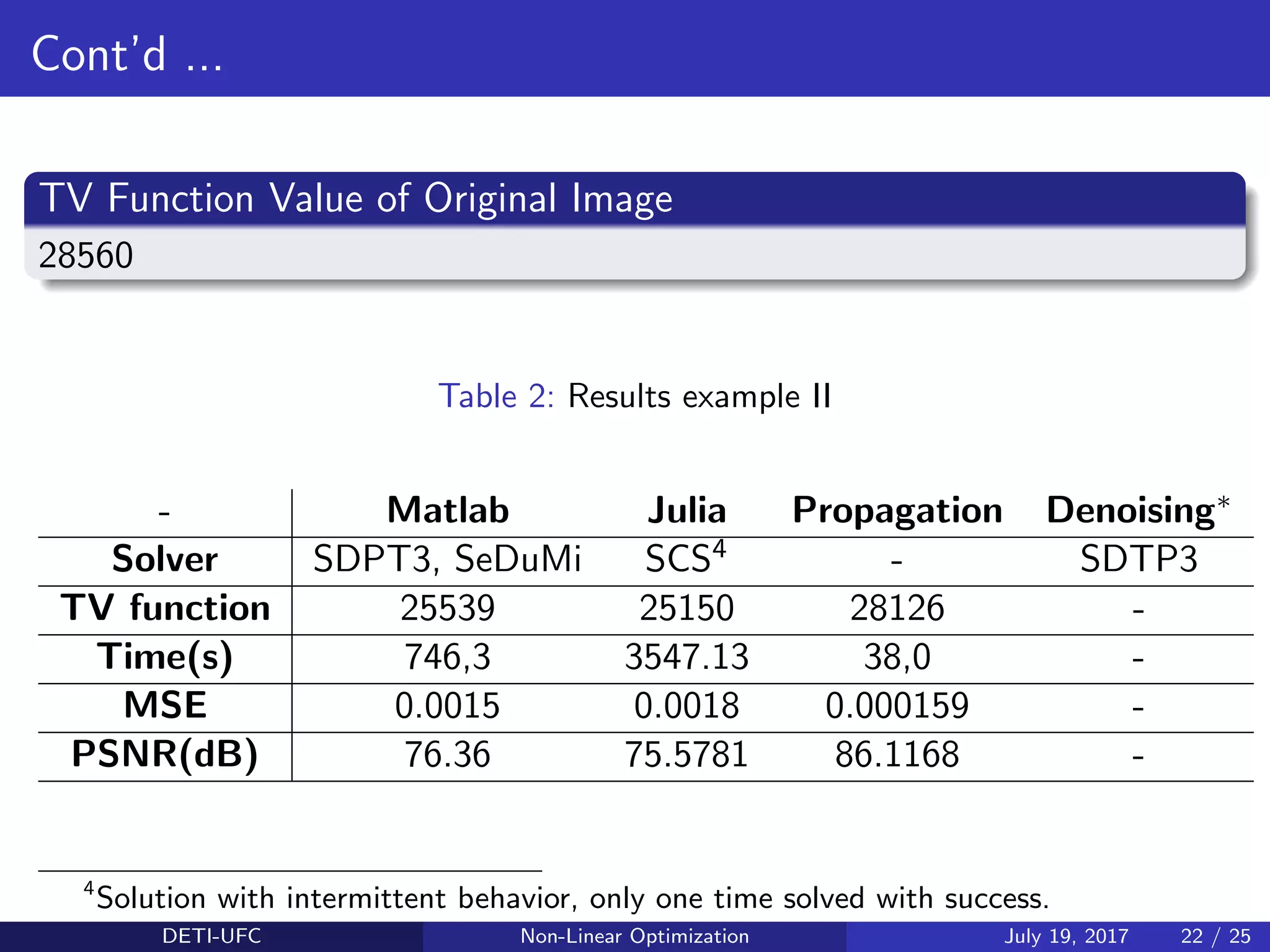
This document presents different methods for colorizing grayscale images, including total variation regularization, total variation denoising, and colorization by propagation. It outlines the problem statement, describes the various approaches, provides examples applying each method to images, and compares the results in terms of the total variation value, runtime, and image quality metrics. The propagation method achieved the best results with the lowest errors and highest PSNR values compared to other approaches like Boyd's method and total variation denoising.

1. Colorization with total variation regularization
J´ulio Peixoto da Silva J´unior
Fazal-E-Asim
Weskley Vinicius Fernandes Mauricio
Yosbel Rodrigues Ortega
Departamento de Teleinform´atica - UFC
Non-Linear Optimization
July 19, 2017
DETI-UFC Non-Linear Optimization July 19, 2017 1 / 25

2. Outlines
1 Problem Statement
2 Total Variation Regularization
3 Examples using Boyd’s method (CVX)
4 TV denoising solution.
5 Examples using TV denoising Solution (CVX)
6 Colorization by propagation method
7 Examples using propagation method
8 Comparison and Analysis
9 Conclusions
DETI-UFC Non-Linear Optimization July 19, 2017 2 / 25

3. Problem Statement
A color image (mxn) is represented as three matrices of intensities
R,G,B ∈ Rmxn with entries in [0,1] representing the red, green, and
blue pixel intensities, respectively.
A color image is converted to a monochrome image, represented as
one matrix M ∈ Rmxn using
M = 0.299R + 0.587G + 0.114B (1)
DETI-UFC Non-Linear Optimization July 19, 2017 3 / 25

4. Cont’d
In colorization, we are given M, the monochrome version of an image,
and the color values of some of the pixels. We are to guess its color
version,i.e.,the matrices R,G,B.
We have to minimize the total variation function, defined as:
tv(R, G, B) =
m−1
i=1
n−1
j=1








Rij − Ri,j+1
Gij − Gi,j+1
Bij − Bi,j+1
Rij − Ri+1,j
Gij − Gi+1,j
Bij − Bi+1,j








2
(2)
DETI-UFC Non-Linear Optimization July 19, 2017 4 / 25

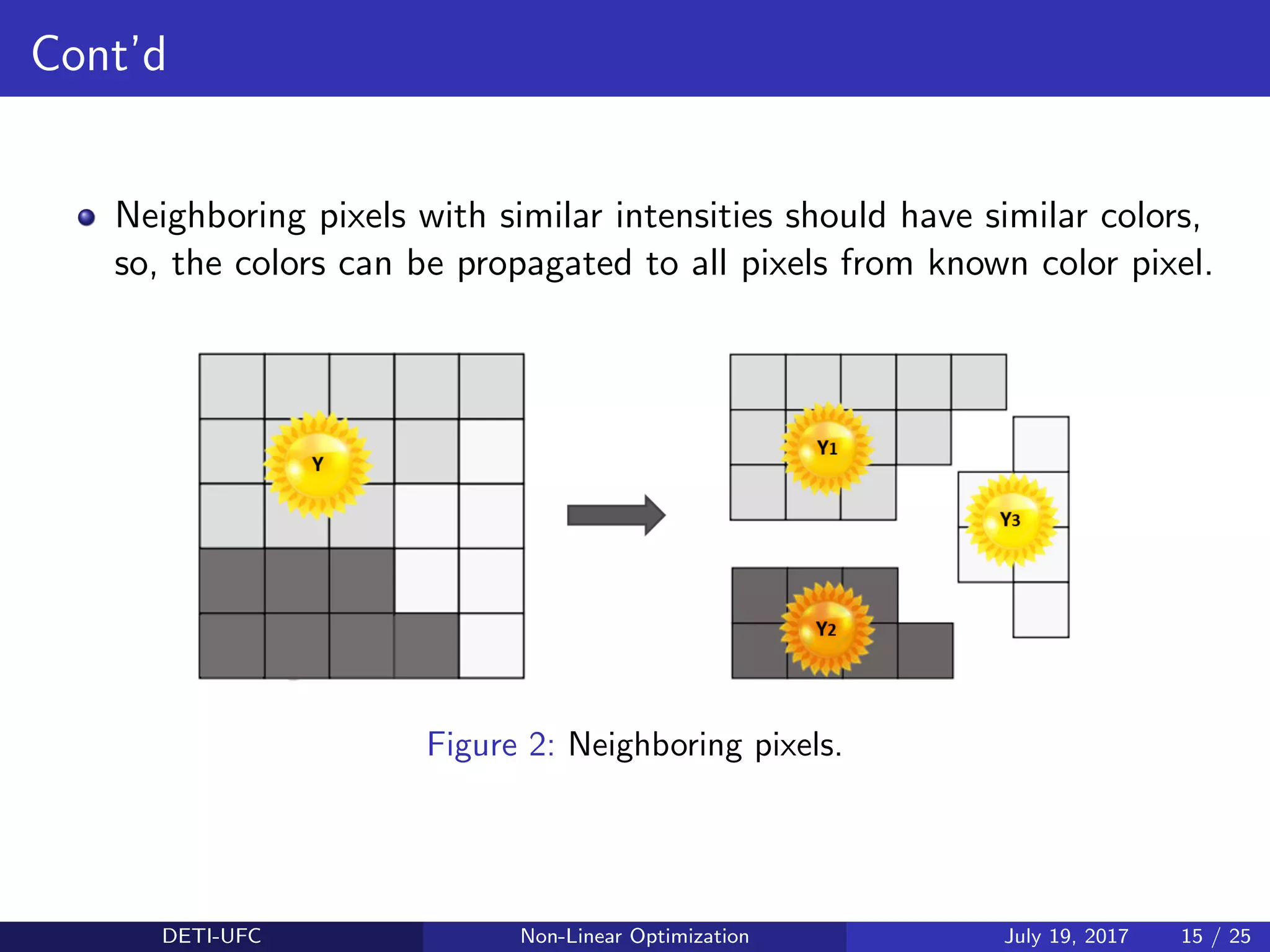
5. Cont’d
Subject to consistency with the given monochrome image M, the
knows ranges of the entries of (R,G,B) (i.e.,∈ [0,1]), and the given
color entries.
Monochrome version of the image, M, along with vectors of known
color intensities is given to us.
The tv function, invoked as tv(R,G,B), gives the total variation.
Report your optimal objective value and if you have access to a color
printer, attach your reconstructed image.
If you don’t have access to a color printer, it’s OK to just give the
optimal objective value.
DETI-UFC Non-Linear Optimization July 19, 2017 5 / 25

6. Cont’d
Convex Problem
Every norms on Rn is convex!
minimize tv(R, G, B)
subject to:
R(knom ind) == R know
G(knom ind) == G know
B(knom ind) == B know
0.229R + 0.587G + 0.114B == M
R, G and B ∈ [0, 1] (3)
DETI-UFC Non-Linear Optimization July 19, 2017 6 / 25

7. Examples using Boyd’s method (CVX)
Read the image
Read the image flower.png (50x50)
Grayscale Image
Apply M = 0.229R + 0.587G + 0.114 ∗ B to obtain grayscale image
Create Damage Image
known ind = find(rand(m, n) >= 0.90)
Solver
Using CVX for solve the problem
Reconstructed Image
Using the results of CVX for reconstructed the image.
DETI-UFC Non-Linear Optimization July 19, 2017 7 / 25

8. Results with CVX - Exampe I
(a) Original (b) Monochrome
(c) Given (d) Reconstructed
DETI-UFC Non-Linear Optimization July 19, 2017 8 / 25

9. Results with CVX - Exampe II
(e) Original (f) Monochrome
(g) Given (h) Reconstructed
DETI-UFC Non-Linear Optimization July 19, 2017 9 / 25

10. TV denoising solution
minimize ||X − Y || + λ · tv(R, G, B)
subject to:
R(knom ind) == R know
G(knom ind) == G know
B(knom ind) == B know
0.229R + 0.587G + 0.114B == M
R, G and B ∈ [0, 1] (4)
Definition of variables
where X is the concatenation of R, G and B and Y is the monochromatic
image, in vector form.
λ is a positive scale factor.
DETI-UFC Non-Linear Optimization July 19, 2017 10 / 25

11. Examples using TV denoising solution - Lambda = 0.1
(i) Original (j) Monochrome
(k) Given (l) Reconstructed
DETI-UFC Non-Linear Optimization July 19, 2017 11 / 25

12. Examples using TV denoising solution - Lambda = 1
(m) Original (n) Monochrome
(o) Given (p) Reconstructed
DETI-UFC Non-Linear Optimization July 19, 2017 12 / 25

13. Examples using TV denoising solution - Lambda = 10
(q) Original (r) Monochrome
(s) Given (t) Reconstructed
DETI-UFC Non-Linear Optimization July 19, 2017 13 / 25

14. Colorization by Propagation
YUV color space, is a model commonly used in video, where Y is the
monochromatic luminance channel (intensity), while U and V are the
chrominance channels, encoding the color.
The method called Propagation using Optimization, is given as input
an intensity volume Y (x; y; t) and outputs two color volumes U (x; y;
t) and V (x; y; t).
Figure 1: YUV color space
Thus, if Y(r) is the intensity of a particular pixel, then we wish to
impose the constraint that two neighboring pixels r, s should have
similar colors if their intensities are similar.
DETI-UFC Non-Linear Optimization July 19, 2017 14 / 25

15. Cont’d
Neighboring pixels with similar intensities should have similar colors,
so, the colors can be propagated to all pixels from known color pixel.
Figure 2: Neighboring pixels.
DETI-UFC Non-Linear Optimization July 19, 2017 15 / 25

16. Cont’d
The problem results in minimize the difference between the color U(r)
at pixel r and the affinity-weighted average of the colors at
neighboring pixels (s):
Objective Function
minimize J(U) =
r
U(r) −
s∈N(r)
wrsU(s) (5)
where wrs is a affinity-weighting function that sums to one, large
when Y(r) is similar to Y (s), and small when the two intensities are
different. The notation s ∈ N(r) denotes the fact that r and s are
neighboring pixels.
DETI-UFC Non-Linear Optimization July 19, 2017 16 / 25

17. Cont’d
There are in the literature different types of affinity-weighting
functions. The simplest one is commonly used by image segmentation
algorithms and is based on the squared difference between the two
intensities:
wrs ∝ exp −
(Y (r) − Y (s))2
2σ2
r
(6)
σ proportional to local variance.
Figure 3: Affinity-weighting functions.
DETI-UFC Non-Linear Optimization July 19, 2017 17 / 25

18. Results with Colorization by Propagation - Example I
(a) Original (b) Monochrome
(c) Given (d) Reconstructed
DETI-UFC Non-Linear Optimization July 19, 2017 18 / 25

19. Results with Colorization by Propagation - Exampe II
(e) Original (f) Monochrome
(g) Given (h) Reconstructed
DETI-UFC Non-Linear Optimization July 19, 2017 19 / 25

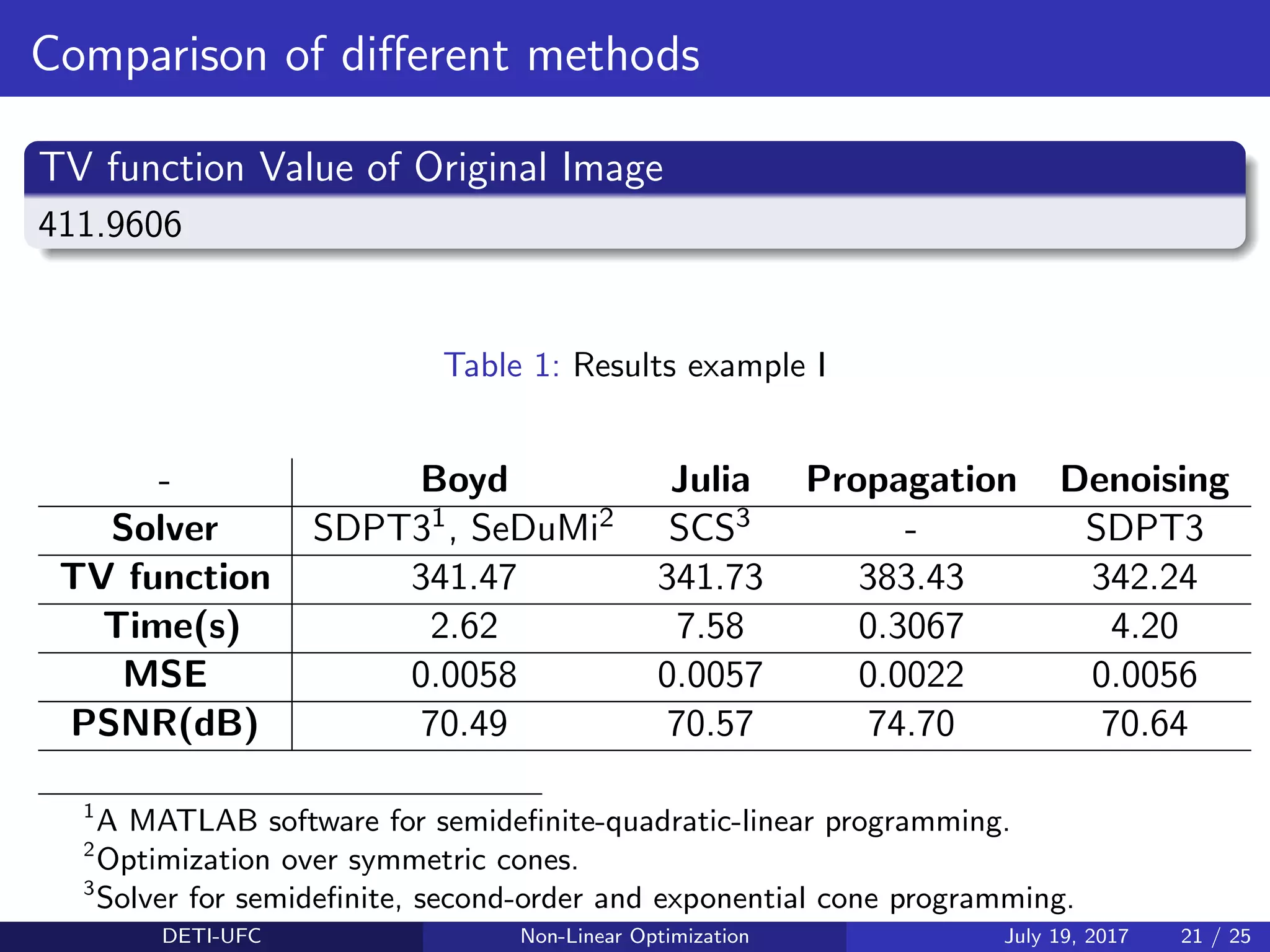
20. Metrics used for Comparison
Mean Square Error (MSE)
MSE =
1
MN
M
y=1
N
x=1
[I(x, y) − ˜I(x, y)]2
(7)
Peak Signal to Noise Ratio (PSNR)
PSNR = 20 ∗ log10
255
√
MSE
(8)
DETI-UFC Non-Linear Optimization July 19, 2017 20 / 25

21. Comparison of different methods
TV function Value of Original Image
411.9606
Table 1: Results example I
- Boyd Julia Propagation Denoising
Solver SDPT31, SeDuMi2 SCS3 - SDPT3
TV function 341.47 341.73 383.43 342.24
Time(s) 2.62 7.58 0.3067 4.20
MSE 0.0058 0.0057 0.0022 0.0056
PSNR(dB) 70.49 70.57 74.70 70.64
1
A MATLAB software for semidefinite-quadratic-linear programming.
2
Optimization over symmetric cones.
3
Solver for semidefinite, second-order and exponential cone programming.
DETI-UFC Non-Linear Optimization July 19, 2017 21 / 25

22. Cont’d ...
TV Function Value of Original Image
28560
Table 2: Results example II
- Matlab Julia Propagation Denoising∗
Solver SDPT3, SeDuMi SCS4 - SDTP3
TV function 25539 25150 28126 -
Time(s) 746,3 3547.13 38,0 -
MSE 0.0015 0.0018 0.000159 -
PSNR(dB) 76.36 75.5781 86.1168 -
4
Solution with intermittent behavior, only one time solved with success.
DETI-UFC Non-Linear Optimization July 19, 2017 22 / 25

23. Conclusions
We solved the problem using Boyd’s method using MATLAB and
JULIA.
We also used TV denoising and colorization by propagation methods
to solve the same problem in MATLAB.
The propagation method have the best solution as compared to other
methods.
The Boyd’s method shows least performance as compared to other
method..
DETI-UFC Non-Linear Optimization July 19, 2017 23 / 25

24. References
1 S. Boyd and L. Vandenberghe. Convex Optimization. Cambridge
University Press, 2004.
2 S. Boyd, Jenny Hong el al. Convex Optimization in Julia. HPTCDL
November 16-21, 2014, New Orleans, Louisiana, USA
3 Karanveer Mohan, Madeleine Udell, David Zeng, Jenny Hong.
Convex.jl Documentation. Jun 24, 2017.
4 Nonlinear total variation based noise removal algorithms, Rudin, L. I.;
Osher, S.; Fatemi, E. (1992). Physica D 60: 259–268.
5 A generalized vector-valued total variation algorithm., Rodriguez
Paul, and Brendt Wohlberg. Image Processing (ICIP), 2009 16th
IEEE International Conference on. IEEE, 2009.
6 R´emi Flamary. Avaliable at:
http://remi.flamary.com/demos/proxtv.html [Acessed - 07/16]
7 LEVIN, A., LISCHINSKI, D., AND WEISS, Y. 2004. Colorization
using optimization. ACM Trans. Graph. 23, 3 (Aug.), 689–694.
DETI-UFC Non-Linear Optimization July 19, 2017 24 / 25

25. The End
Thank you. Gracias. Obrigado
DETI-UFC Non-Linear Optimization July 19, 2017 25 / 25