This document describes the digital differential analyzer (DDA) algorithm for rasterizing lines, triangles, and polygons in computer graphics. It discusses implementing DDA using floating-point or integer arithmetic. The DDA line drawing algorithm works by incrementing either the x or y coordinate by 1 each step depending on whether the slope is less than or greater than 1. Pseudocode is provided to illustrate the algorithm. Potential drawbacks of DDA are also mentioned, such as the expense of rounding operations.

1. SUBJECT : COMPUTER AIDED DESIGN
(2161903 )
Gandhinagar Institute of
Technology
Active Learning assignment on:-
“Digital Differential Analyzer (DDA)
Algorithm ”
Prepared by:- Patel Yash (150123119039)

2. Introduction
In computer graphics, a digital differential analyzer
(DDA) is hardware or software used for interpolation of
variables over an interval between start and end point.
DDAs are used for rasterization of lines, triangles and
polygons. They can be extended to non linear functions,
such as perspective correct texture mapping, quadratic
curves, and traversing voxels.

3. The DDA method can be implemented using floating-
point or integer arithmetic. The native floating-point
implementation requires one addition and one rounding
operation per interpolated value (e.g. coordinate x, y,
depth, color component etc.) and output result.
This process is only efficient when an FPU with fast
add and rounding operation will be available.

4. The fixed-point integer operation requires two additions
per output cycle, and in case of fractional part overflow,
one additional increment and subtraction. The probability
of fractional part overflows is proportional to the ratio m
of the interpolated start/end values.
DDAs are well suited for hardware implementation and
can be pipelined for maximized throughput.

5. Digital Differential Analyzer (DDA): Line
Drawing Algorithm
Walk through the line, starting at (x0,y0)
Constrain x, y increments to values in [0,1] range
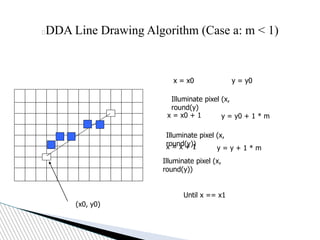
Case a: x is incrementing faster (m < 1)
Step in x=1 increments, compute and round y
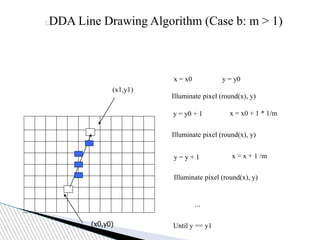
Case b: y is incrementing faster (m > 1)
Step in y=1 increments, compute and round x
(x0,y0)
(x1,y1)
dx
dy

6. DDA Line Drawing Algorithm (Case a: m < 1)
x = x0 y = y0x = x0 y = y0
Illuminate pixel (x,
round(y)
x = x0 + 1 y = y0 + 1 * m
Illuminate pixel (x,
round(y))x = x + 1 y = y + 1 * m
Illuminate pixel (x,
round(y))
Until x == x1
(x0, y0)

7. DDA Line Drawing Algorithm (Case b: m > 1)
y = y0 + 1 x = x0 + 1 * 1/m
Illuminate pixel (round(x), y)
y = y + 1 x = x + 1 /m
Illuminate pixel (round(x), y)
…
Until y == y1
x = x0 y = y0
Illuminate pixel (round(x), y)
(x1,y1)
(x0,y0)

8. DDA Line Drawing Algorithm Pseudocode
compute m;
if m < 1:
{
float y = y0; // initial value
for(int x = x0;x <= x1; x++, y += m)
setPixel(x, round(y));
}
else // m > 1
{
float x = x0; // initial value
for(int y = y0;y <= y1; y++, x += 1/m)
setPixel(round(x), y);
}
Note: setPixel(x, y) writes current color into pixel in column x and row y in frame buffer

9. DDA Line Drawing Algorithm Pseudocode
compute m;
if m < 1:
{
float y = y0; // initial value
for(int x = x0;x <= x1; x++, y += m)
setPixel(x, round(y));
}
else // m > 1
{
float x = x0; // initial value
for(int y = y0;y <= y1; y++, x += 1/m)
setPixel(round(x), y);
}
Note: setPixel(x, y) writes current color into pixel in column x and row y in frame buffer

10. Line Drawing Algorithm Drawbacks
DDA is the simplest line drawing algorithm
Not very efficient
Round operation is expensive
Optimized algorithms typically used.
Integer DDA
E.g.Bresenham algorithm (Hill, 10.4.1)
Bresenham algorithm
Incremental algorithm: current value uses previous
value
Integers only: avoid floating point arithmetic
Several versions of algorithm: we’ll describe midpoint
version of algorithm