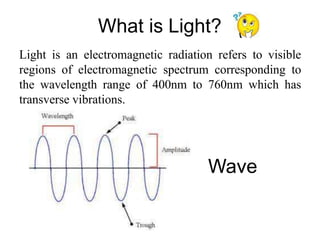
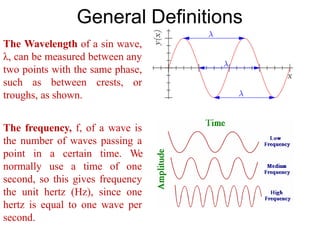
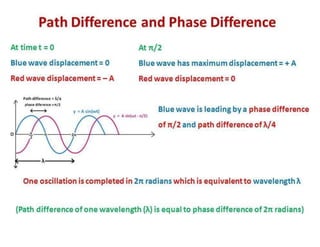
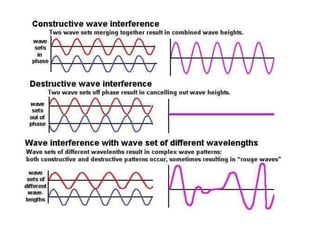
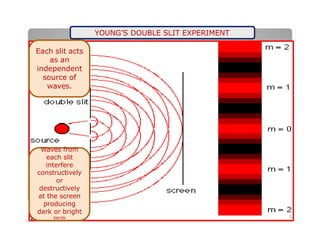
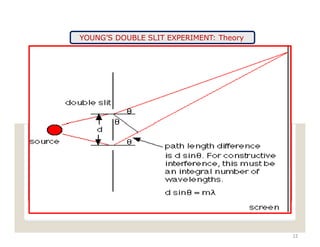
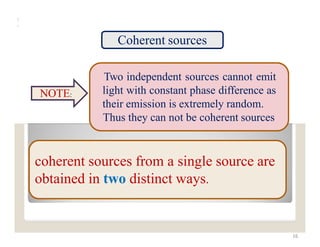
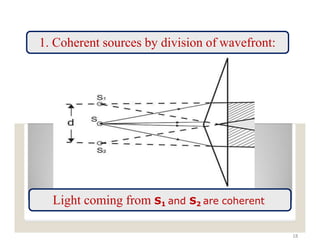
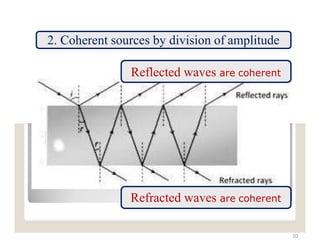
The document explains the nature of light as electromagnetic radiation and discusses the concepts of wave properties, including wavelength and frequency. It details the principles of superposition and interference, highlighting constructive and destructive interference, as well as the conditions necessary for sustained interference patterns. Additionally, it describes Young's double-slit experiment as a practical demonstration of interference and the requirement for coherent light sources.

1. Interference of light
1

2. What is Light?
Light is an electromagnetic radiation refers to visible
regions of electromagnetic spectrum corresponding to
the wavelength range of 400nm to 760nm which has
transverse vibrations.
Wave

3. General Definitions
The Wavelength of a sin wave,
λ, can be measured between any
two points with the same phase,
such as between crests, or
troughs, as shown.
The frequency, f, of a wave is
the number of waves passing a
point in a certain time. We
normally use a time of one
second, so this gives frequency
the unit hertz (Hz), since one
hertz is equal to one wave per
second.

5. Principle of Superposition
“Whenever two or more waves superimpose in a medium, the
total displacement at any point is equal to the vector sum of
individual displacement of waves at that point”
If Y1, Y2, Y3…are different
displacement vector due to
the waves 1,2,3 …acting
separately then according to
the principle of superposition
the resultant displacement is
given by
Y=Y1+Y2+Y3+……

6. INTERFERENCE is the process in which two or more
waves of the same frequency - be it light, sound, or other electromagnetic
waves - either reinforce or cancel each other, the amplitude of the resulting
wave being equal to the sum of the amplitudes of the combining waves.
For example, if at a given instant in time and location along the medium, the
crest of one wave meets the crest of a second wave, they will interfere in such
a manner as to produce a "super-crest." Similarly, the interference of a trough
and a trough interfere constructively to produce a "super-trough." This is called
constructive interference. If the two amplitudes have opposite signs, they will
subtract to form a combined wave with a lower amplitude. For example, the
interaction of a crest with a trough is an example of destructive interference.
Destructive interference has the tendency to decrease the resulting amount of
displacement of the medium. The bright bands show constructive interference
of light. The dark bands show destructive interference oflight.

8. Nature of Interference depends on the path
difference or phase difference between
the interfering waves.
8
constructive interference.
Path difference is
integral multiple of wavelength δ = nλ
(Phase difference φ= 2nπ)

9. Nature of Interference depends on the path
difference or phase difference between
the interfering waves.
9
destructive interference.
Path difference is
Odd integral multiple of half of the
wavelength δ = (2n+1)λ/2
(Phase difference φ= (2n+1)π)

10. Conditions for SUSTAINED
interference pattern.
1. Interfering light waves should be of same
frequency.
2. The two sources must be coherent.
3. Interfering light waves should travel
almost in the same direction.
4. Interfering light waves should be of almost
same amplitude.
5. The two sources producing the coherent
light must be narrow.
10

11. YOUNG’S DOUBLE SLIT EXPERIMENT
Each slit acts
as an
independent
source of
waves.
6
Waves from
each slit
interfere
constructively
or
destructively
at the screen
producing
dark or bright
bands

12. YOUNG’S DOUBLE SLIT EXPERIMENT: Theory
12

13. YOUNG’S DOUBLE SLIT EXPERIMENT: Theory
For P to be a bright point constructive
interference should take place.
d sin θ= n λ. since sin θ= x/D
xd/D= n λ or x= n λD/d
13
the next bright point is x′= (n+1) λD/d
distance between two successive bright
spots( fringes) is x′–x=β
width between two successive bright
fringes is β= λD/d

14. YOUNG’S DOUBLE SLIT EXPERIMENT: Theory
For P to be a dark point destructive
interference should take place.
d sin θ= (2n+1) λ/2. since sin θ= x/D
xd/D= (n+1/2) λ or x= (n+1/2) λD/d
next dark point is x′= (n+1+1/2) λD/d
distance between two successive bright
spots( fringes) is x′–x=β
14
width between two successive dark
fringes is β= λD/d

15. :
.
Coherent
sources
15
If two light sources emitting light waves with
the same phase or having a constant phase
difference are called coherent sources.
Two light sources are said to be coherent if they
emit light waves of the same frequency with
same phase or a constant phase difference.

16. :
.
Coherent sources
Two independent sources cannot emit
light with constant phase difference as
their emission is extremely random.
Thus they can not be coherent sources
NOTE:
coherent sources from a single source are
obtained in two distinct ways.
16

17. :
.
1. Coherent sources by division of wavefront:
In this method wavefront of a light source
is divided into two or more parts through
refraction.
Light passing through a biprism
can produce two virtual images.
The two virtual images act as
coherent sources.
Example:
17

18. 1. Coherent sources by division of wavefront:
Light coming from S1 and S2 are coherent
18

19. 2. Coherent sources by division of
amplitude
19
In this method wavefront of a light source
is subjected to partial reflection and partial
refraction.
:Light reflected by a thin film or
refracted through a transparent thin
film. We have here two sets of
wavefronts moving in the same
direction travelling in phase.
Example:

20. 2. Coherent sources by division of amplitude
Reflected waves are coherent
Refracted waves are coherent
20