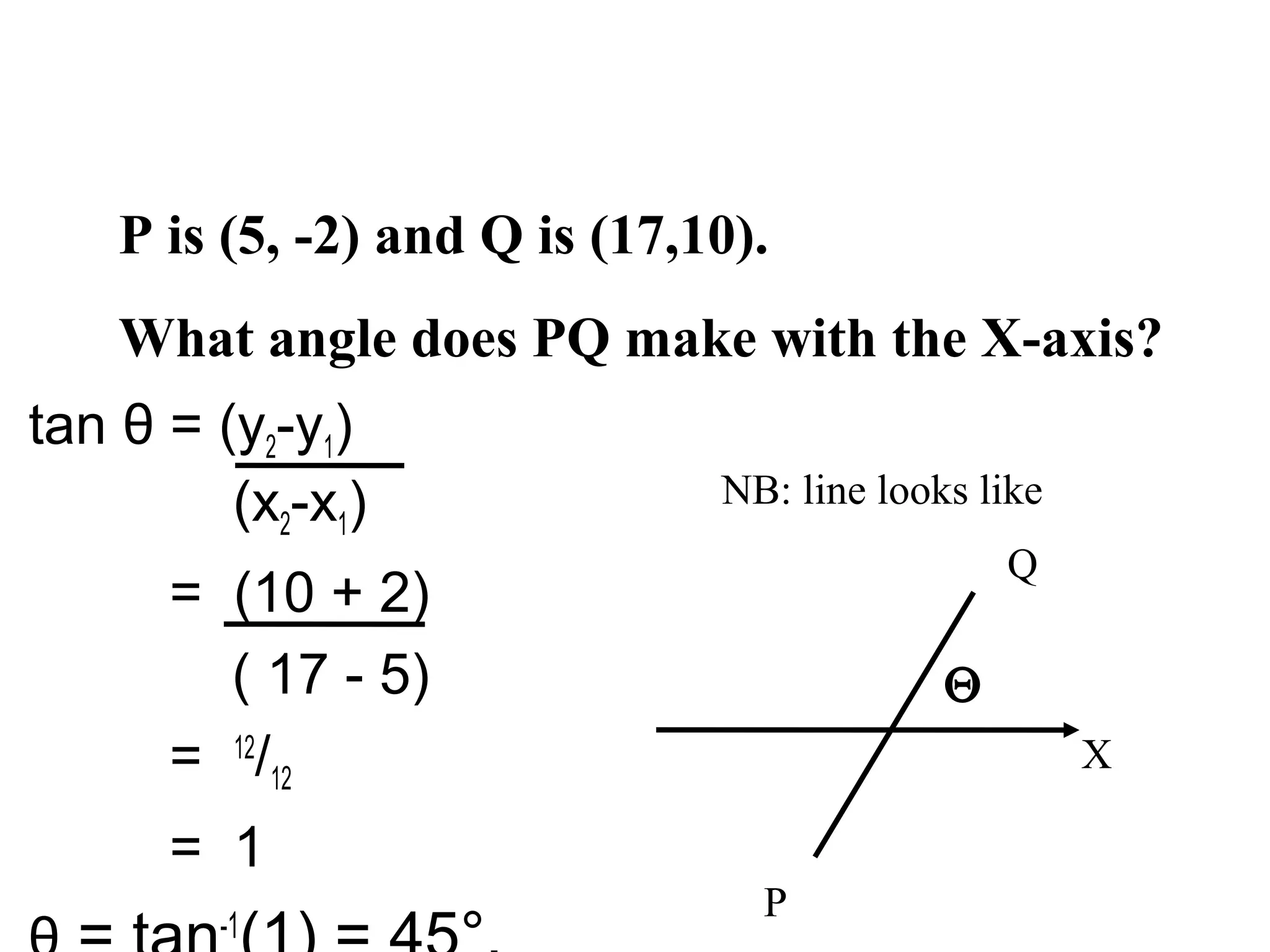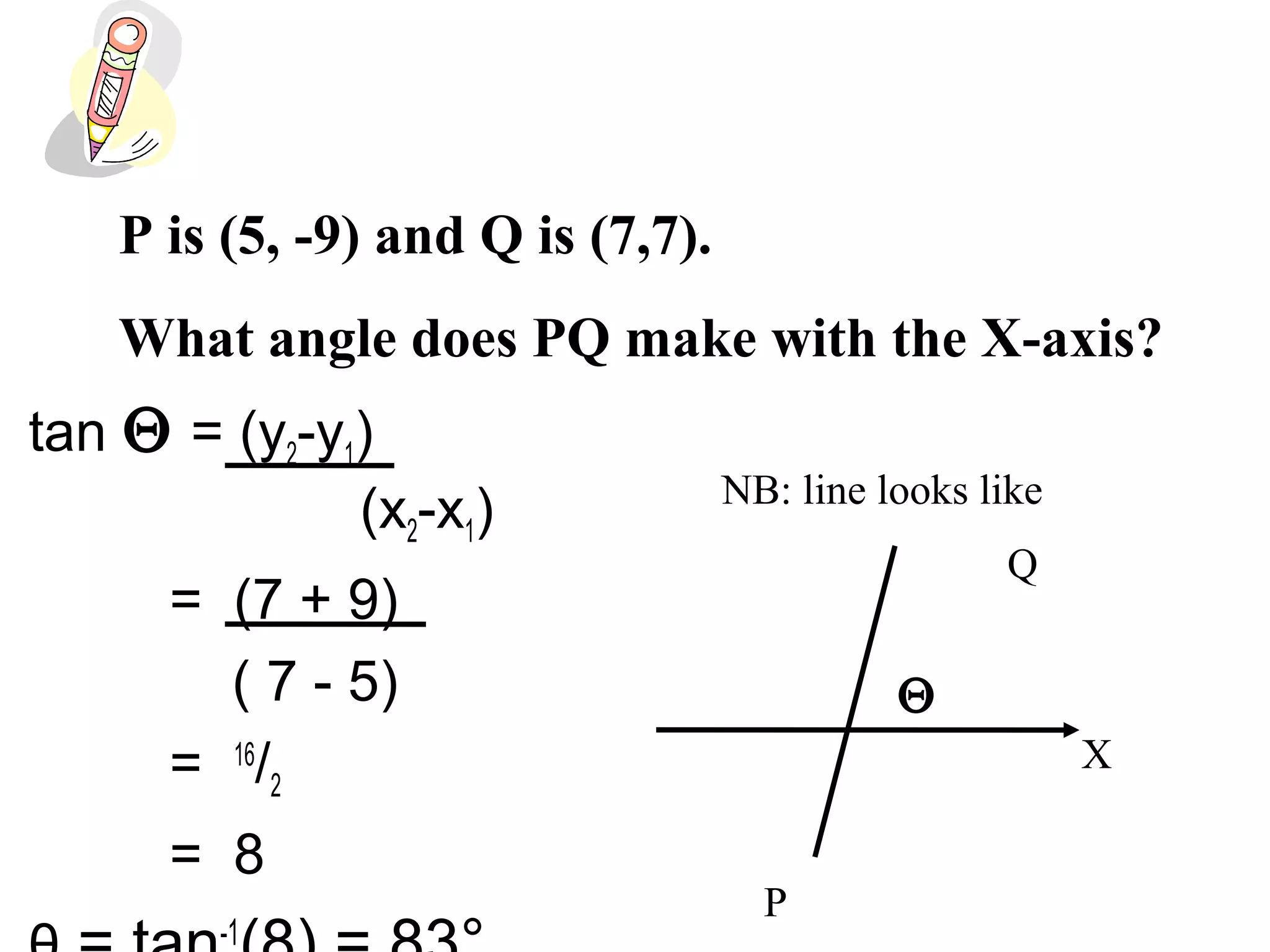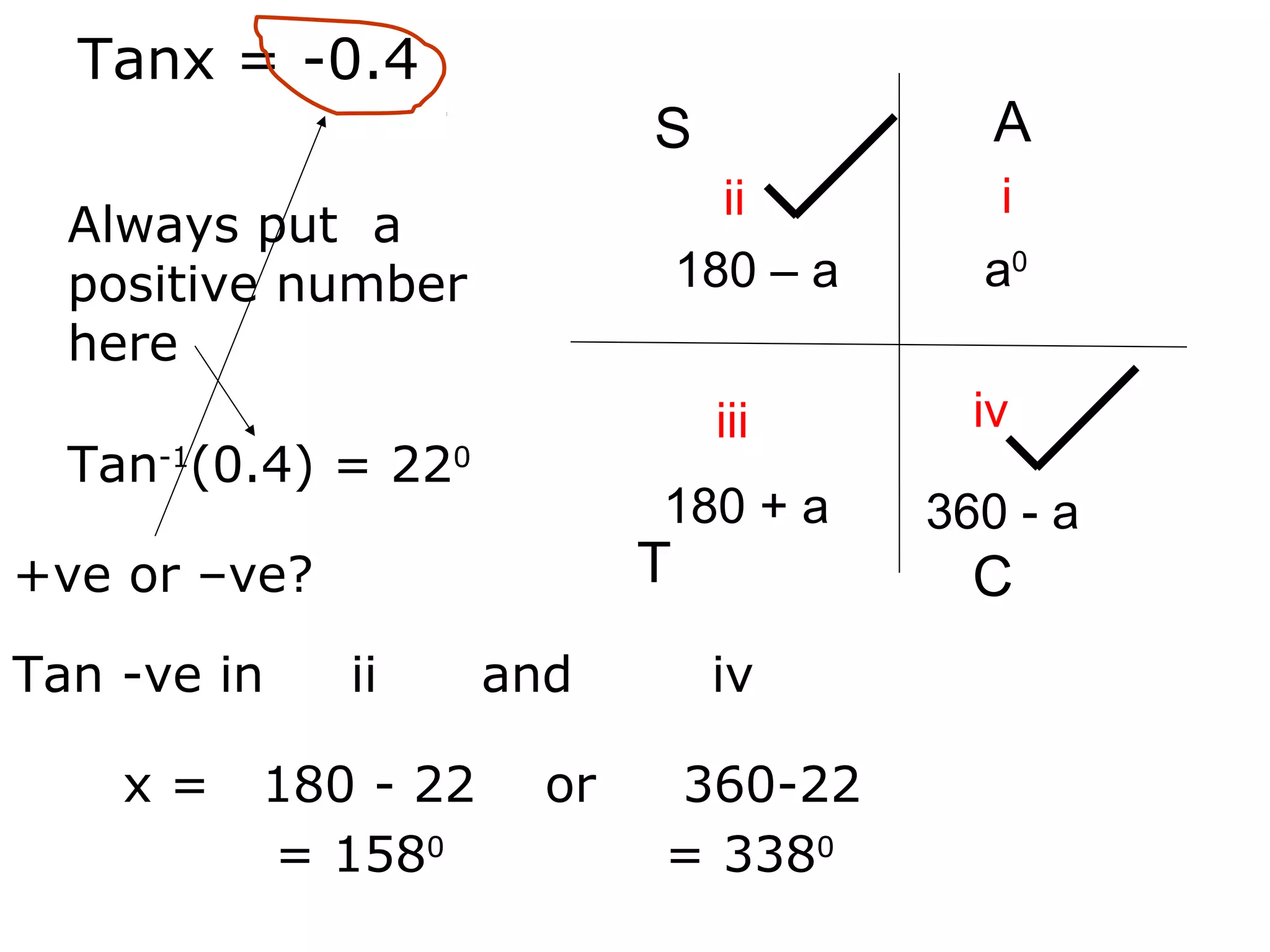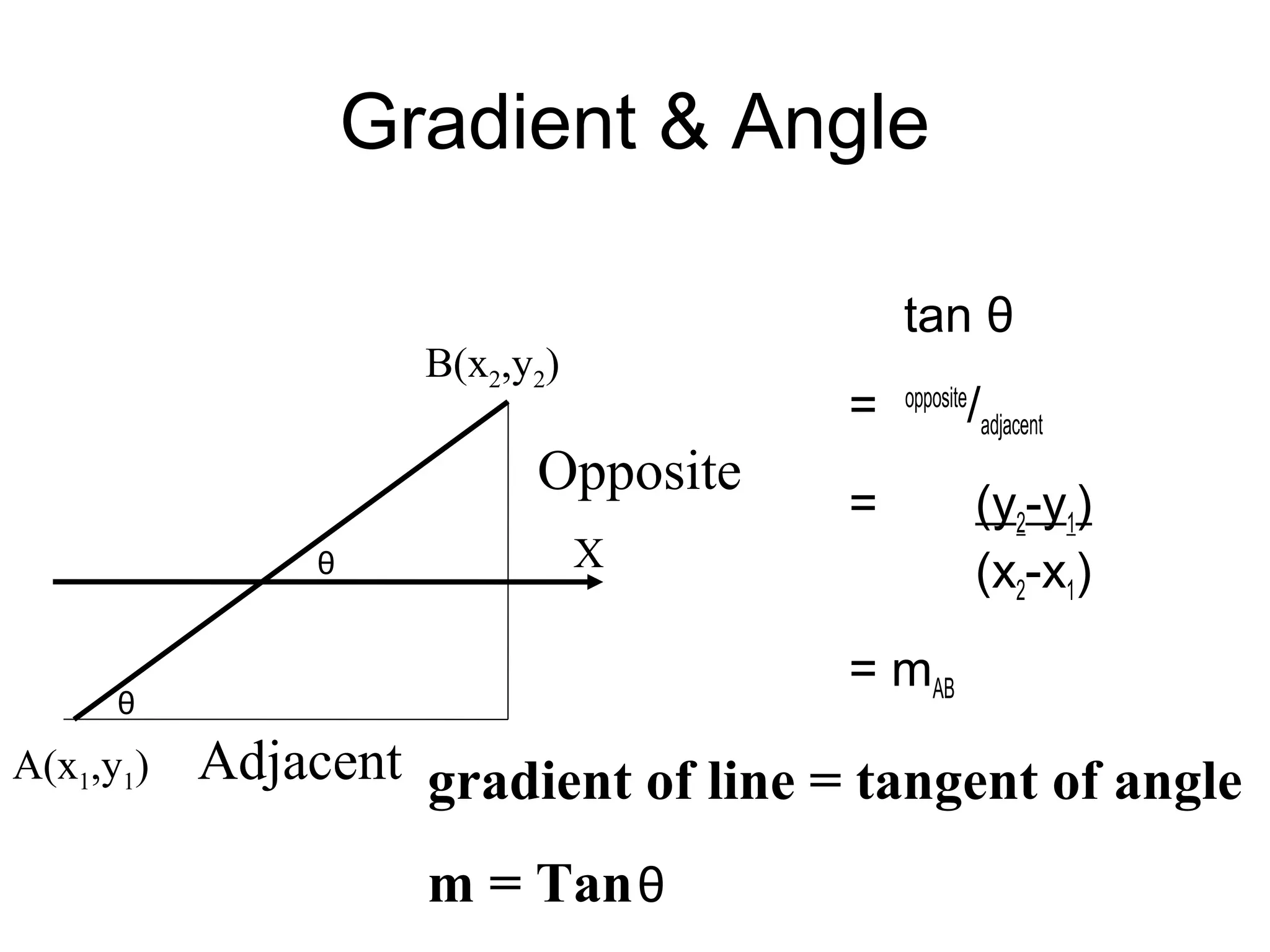
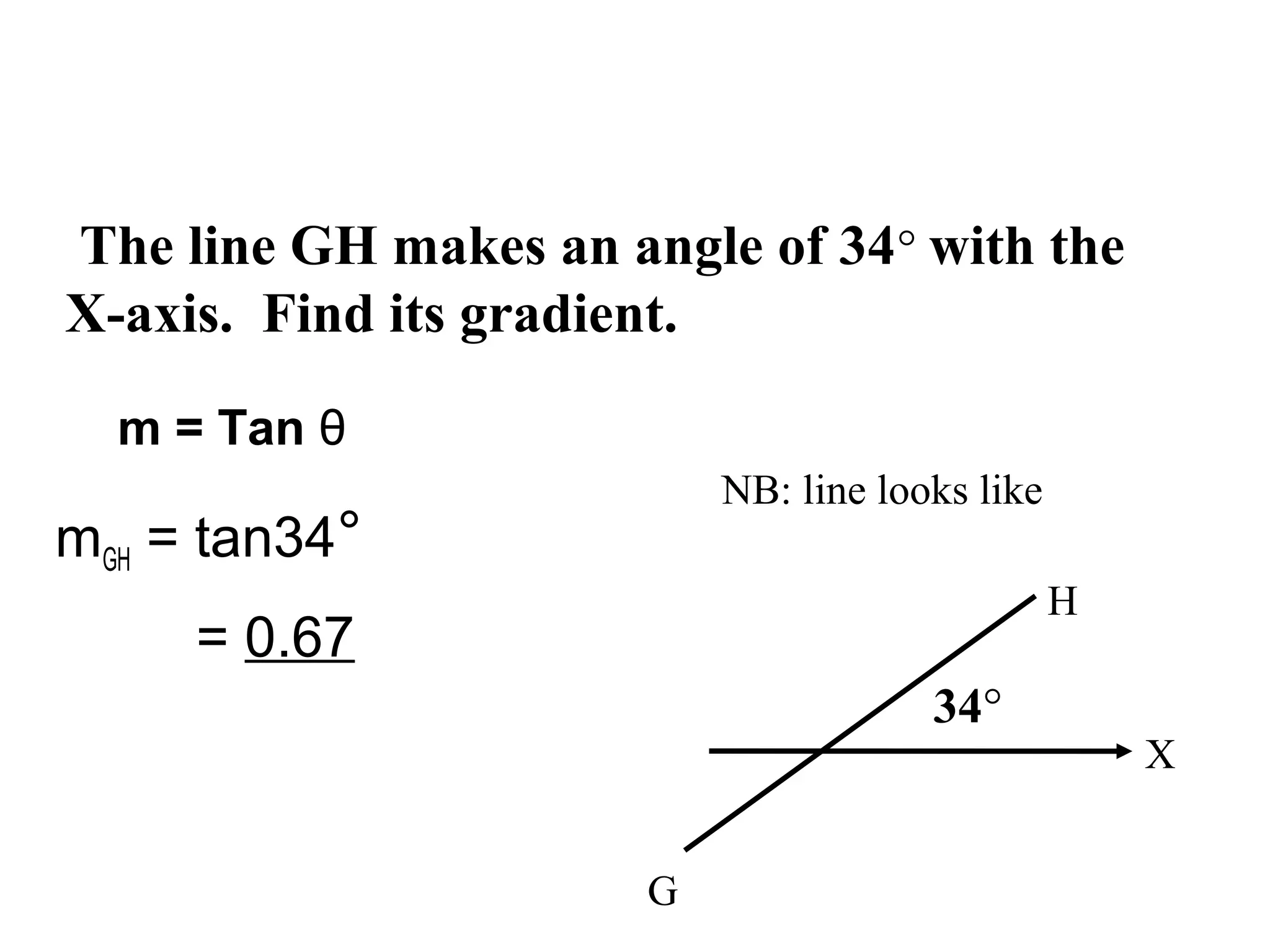
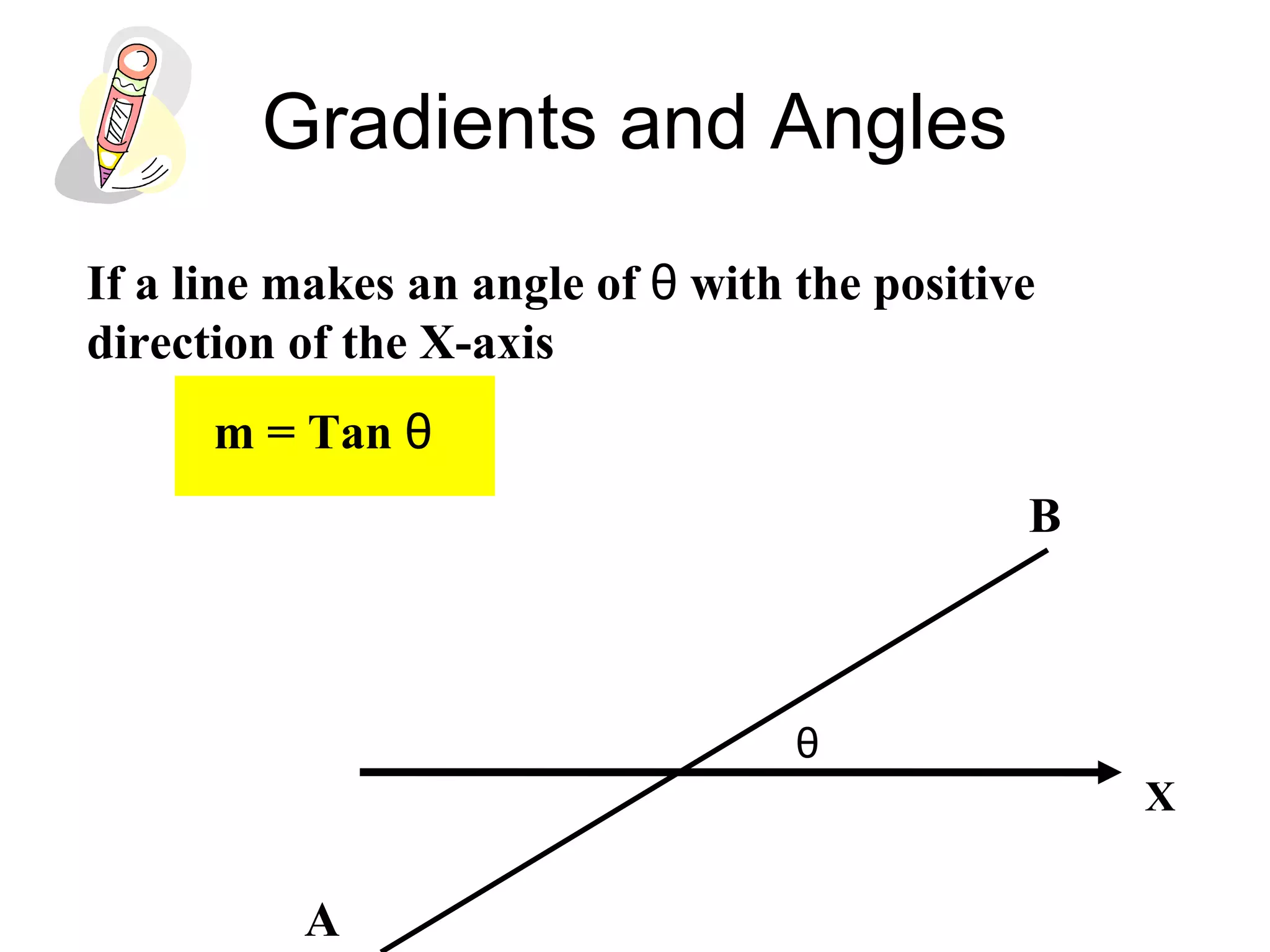
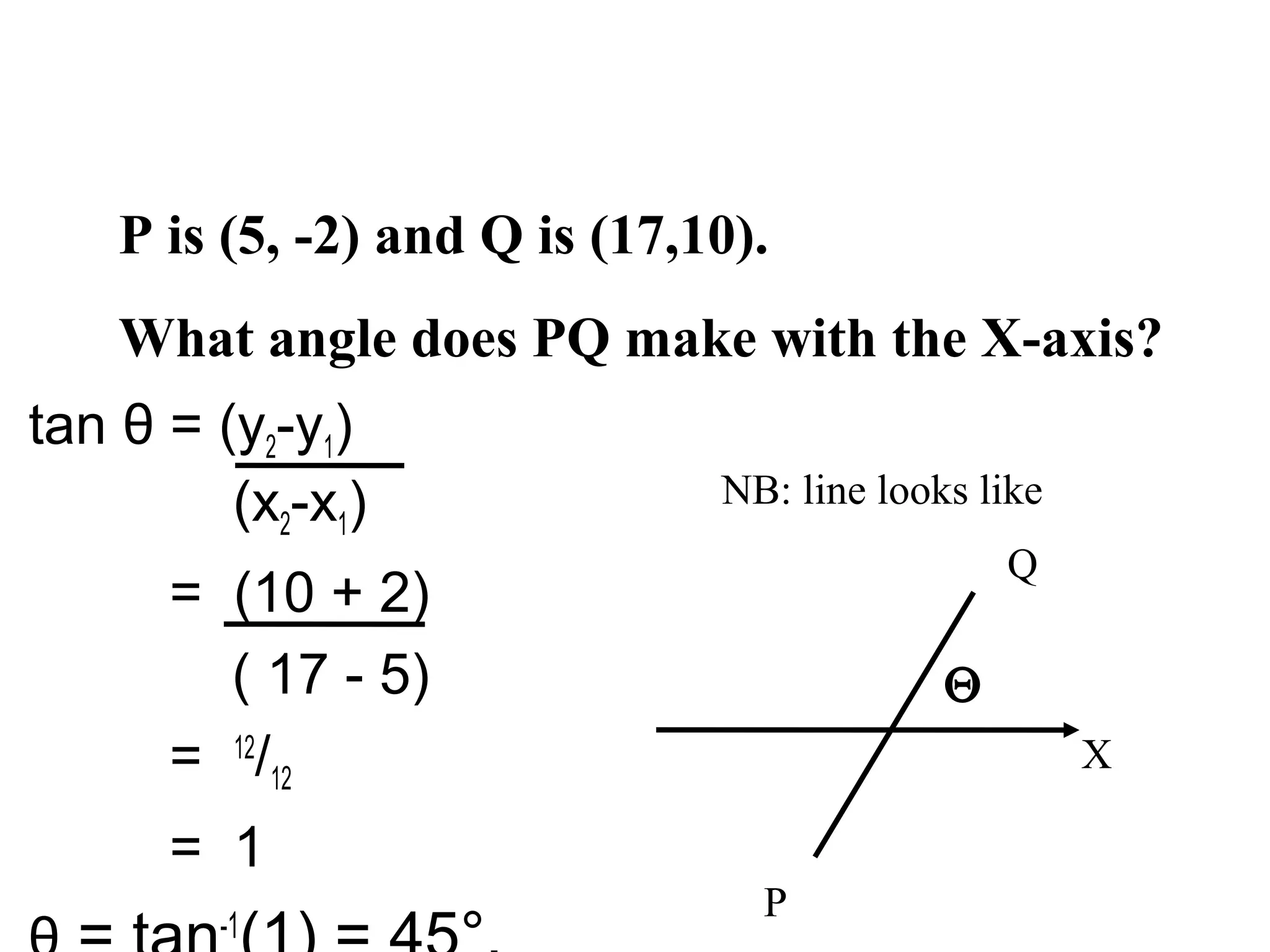
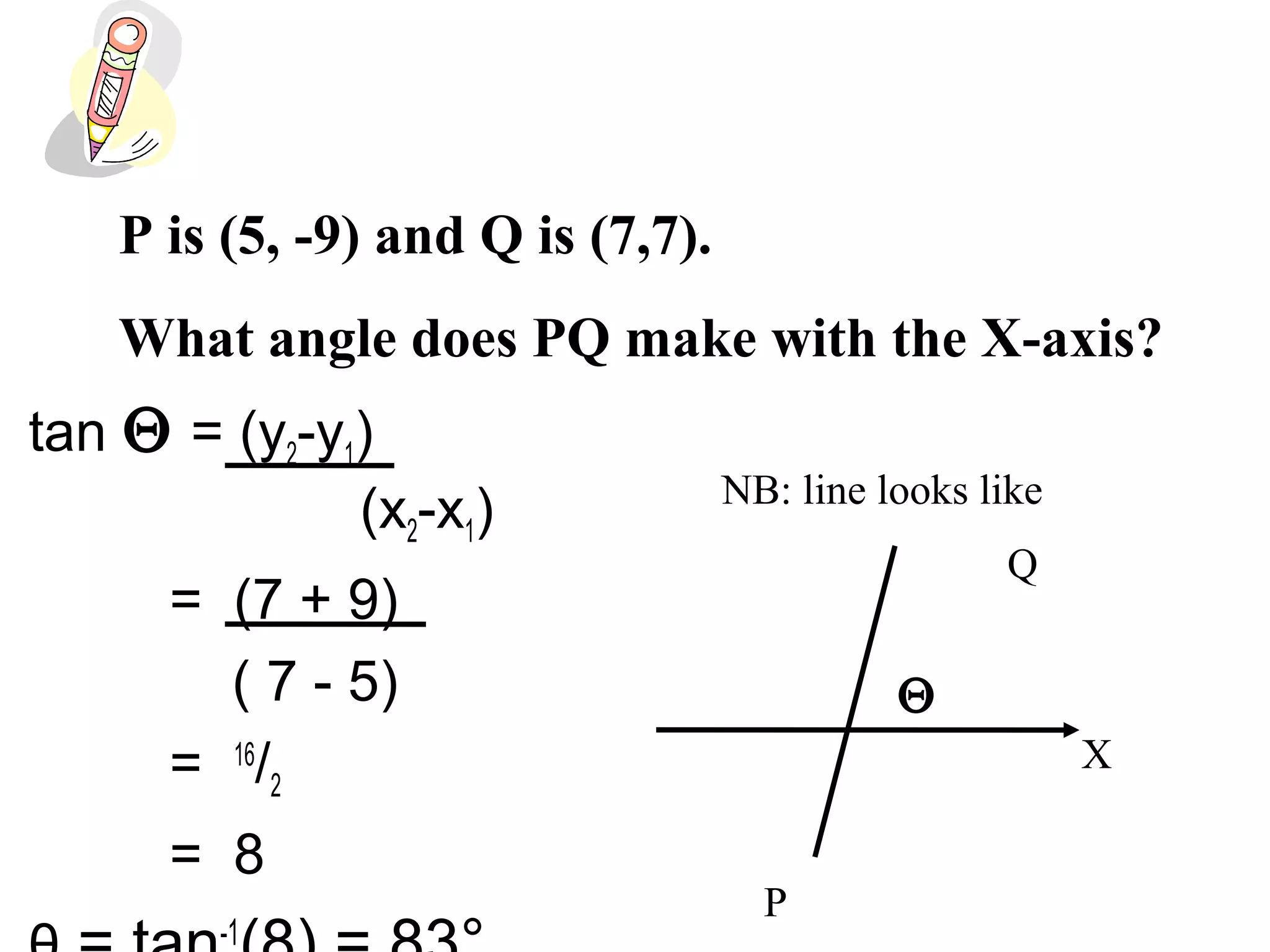
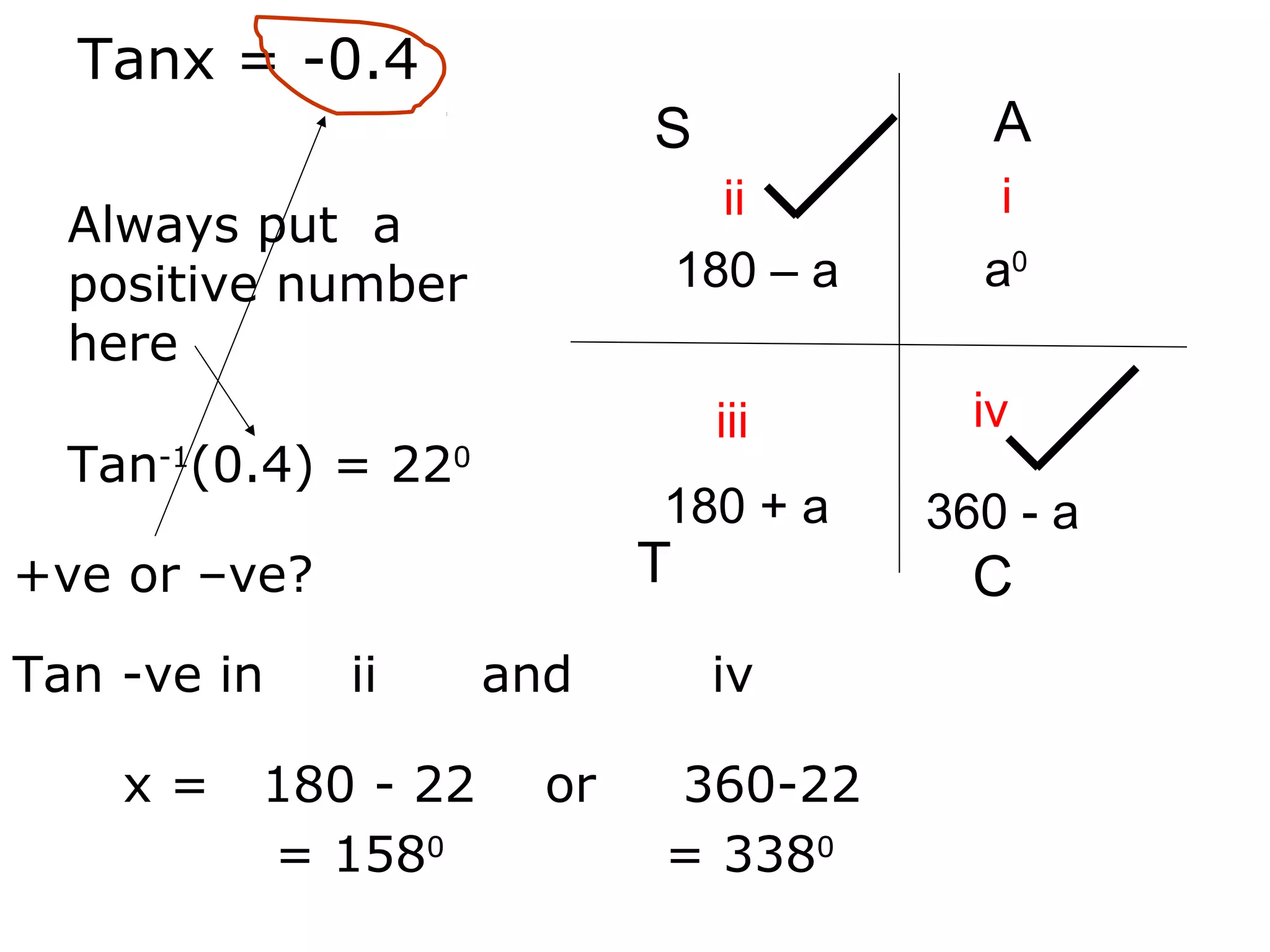
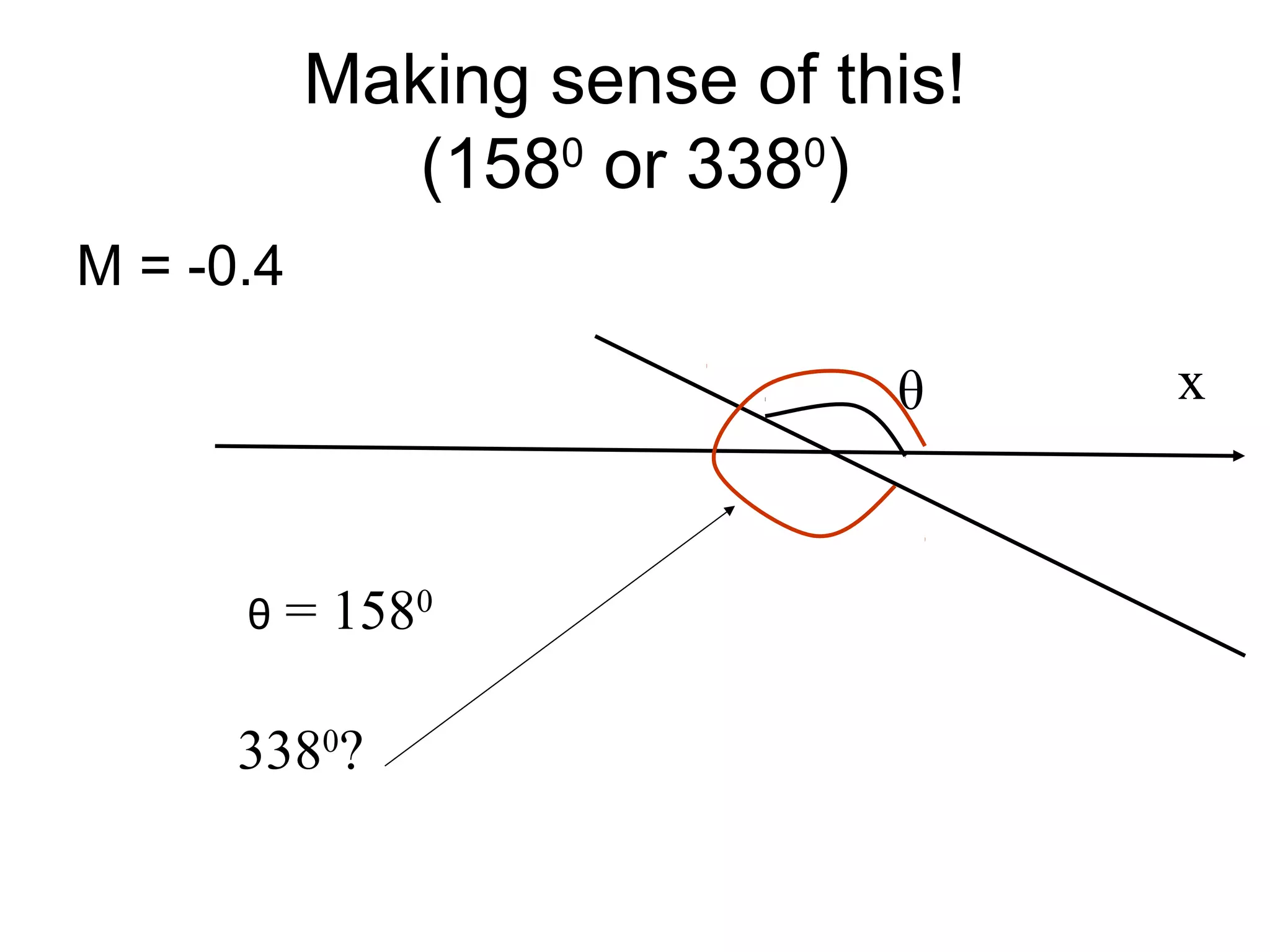
The document discusses the relationship between the gradient of a line and the angle it makes with the x-axis. Specifically: - The gradient (m) of a line is equal to the tangent of the angle (θ) it makes with the x-axis, or m = tanθ. - Examples are provided to demonstrate calculating the gradient given the angle, and calculating the angle given the gradient or two points on the line. - When taking the inverse tangent (tan-1) to find the angle from a negative gradient, there are two possible angles that are either in Quadrant II or Quadrant IV of the unit circle.

1. Block 1
Gradients and Angles

2. What is to be learned?
• A formula connecting gradient and angle

3. Gradient & Angle
tan θ
= opposite
/adjacent
= (y2-y1)
(x2-x1)
= mAB
B(x2,y2)
A(x1,y1)
Xθ
θ
Opposite
Adjacent gradient of line = tangent of angle
m = Tanθ

4. mGH = tan34°
= 0.67
NB: line looks like
G
H
The line GH makes an angle of 34° with the
X-axis. Find its gradient.
X
34°
m = Tan θ

5. mCD = tan110°
= -2.75
NB: line looks like
D
C
The line CD makes an angle of 110° with the
X-axis. Find its gradient.
X
110°
m = Tan θ

6. Gradients and Angles
If a line makes an angle of θ with the positive
direction of the X-axis
m = Tan θ
A
B
X
θ

7. mGH = tan116.6°
= -2.
NB: line looks like
G
H
The line GH makes an angle of 116.6° with
the X-axis. Find its gradient.
X
116.6°

8. tan θ = (y2-y1)
(x2-x1)
= (10 + 2)
( 17 - 5)
= 12
/12
= 1
-1
NB: line looks like
P
Q
P is (5, -2) and Q is (17,10).
What angle does PQ make with the X-axis?
X
Θ

9. tan Θ = (y2-y1)
(x2-x1)
= (7 + 9)
( 7 - 5)
= 16
/2
= 8
-1
NB: line looks like
P
Q
P is (5, -9) and Q is (7,7).
What angle does PQ make with the X-axis?
X
Θ

10. a0
180 – a
180 + a 360 - a
iii
iii iv
CT
AS
Tanx = -0.4
Tan-1
(0.4) = 220
+ve or –ve?
Tan -ve in ii and iv
x = 180 - 22 or 360-22
= 1580
Always put a
positive number
here
= 3380

11. Making sense of this!
(1580
or 3380
)
M = -0.4
xθ
θ = 1580
3380
?