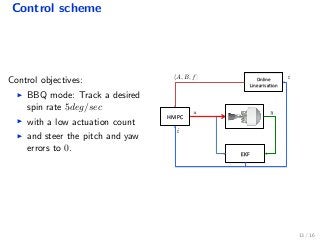
The document discusses a sloshing-aware dynamical model for attitude control of spacecraft utilizing impulsive actuators. It describes methods for state estimation, model linearization, and hybrid model predictive control, emphasizing the effects of sloshing dynamics and constraints of thruster activations. Simulation results demonstrate the control scheme's effectiveness in managing pitch and yaw errors while optimizing actuation counts.

1. Sloshing-aware attitude control of
impulsively actuated spacecraft
P. Sopasakisa, D. Bernardinia,c, H. Strauchb,
S. Bennanid and A. Bemporada,c
a Institute for Advanced Studies Lucca,
b Airbus DS, c ODYS Srl
d European Space Agency
July 14, 2015

2. CFD computations...
1 / 16

3. CFD computations...
Sloshing cannot be ignored!
1 / 16

4. Outline
1. Derivation of a sloshing-aware dynamical model
2. State estimation and model linearisation
3. Modelling of minimum impulse effect
4. Model predictive control & simulations
2 / 16

5. I. Modelling

6. Fixed Body Frame
3 / 16

7. Modelling sloshing
The concept of a rotating mass is used to
model the sloshing dynamics. Using
Lagrangian arguments we arrive at:
˙α = β,
˙β = κβ +
θ(α, ω)
mf r2
where θ is a nonlinear functiona which
depends of parameters p and r.
a
Given in the appendix
4 / 16

8. Modelling sloshing
The inertia tensor J of the upper stage is:
J(α) = J0 + Jmf
(α)
J0: diagonal inertia tensor without sloshing,
Jmf
(α) contribution of the moving mass given by
Jmf
(α)=mf


r2 pr cos α pr sin α
∗ p2 + r2 sin2
α − sin α cos α
∗ ∗ p2 + r2 cos2 α

 .
5 / 16

9. Modelling sloshing
The system dynamics is given by:
˙α = β,
˙β = κβ + θ(α,ω)
mf r2
Sloshing
˙ω = ψ(ω)ω + J−1
τext − J−1
J (α)βω
˙y = ωy + zωx,
˙z = ωz − yωx
Pitch and yaw errors
where ψ(ω) = J−1Ω(ω)J with
Ω(ω) =


0 ωz −ωy
−ωz 0 ωx
ωy −ωx 0

 .
6 / 16

10. System dynamics
The attitude dynamics is described by the state
vector z ∈ R7
z(t) = ( y, z, ωx, ωy, ωz, α, β)
with input u(t) = (τext,x, τext,y, τext,z) as follows
dz(t)
dt
= F(z(t), u(t)).
The above system is discretised with sampling
period h > 0:
zk+1 = zk + hF(zk, uk) =: fh(zk, uk)
* We measure only the five first coordinates of z,
that is yk = Czk.
7 / 16

11. II. State Estimation and
Linearisation

12. Ext. Kalman Filter
Using the EKF the estimates ˆzk are updated as
ˆzk+1 = (I − KkCfh(ˆzk, uk)) + Kkyk
where Kk is computed using first-order information of the system:
Fk =
∂fh
∂z (ˆzk,uk)
.
8 / 16

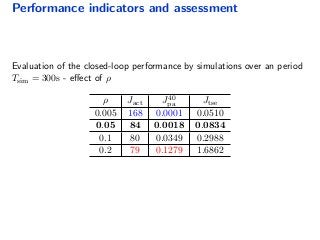
13. Ext. Kalman Filter
0 20 40 60 80 100
1
2
3
4
5
6
7
8
9
10
x 10
−4
Time [s]
Stateestimateionerror(norm)
9 / 16

14. Linearisation
At time kj we linearise the system around the current estimated state ˆzkj
and input ukj
:
zk+1 = Akj
zk + Bkj
uk + fkj
, for k > kj
where Akj
, Bkj
and fkj
are functions of ˆzkj
and ukj
as follows
Akj
= I + h
∂F
∂z (ˆzkj
,ukj
)
Bkj
= h
∂F
∂u (ˆzkj
,ukj
)
fkj
= fh(ˆzkj
, ukj
)
10 / 16

15. III. Minimum Impulse Effect

16. Minimum impulse effect
Minimum impulse effect: thrusters cannot produce arbitrarily small
torques, thus uk is constrained in
U = [−umax, −umin] ∪ {0} ∪ [umin, umax]
We introduce the binary vectors δ−
k and δ+
k so that1
δ−
k = [uk ≤ −umin],
δ+
k = [uk ≥ umin],
and the auxiliary variable ηk defined as
ηk,i = [δ−
k,i ∨ δ+
k,i] · uk,i
1
Here ≤ and ≥ are element-wise comparison operators.
11 / 16

17. Minimum impulse effect
To detect thruster activations we use the variable
vk = [δ−
k ∨ δ+
k ]
and we recast the system dynamics as
zk+1 = Azk + Bηk + f,
γk+1 = γk + [ 1 1 1 ] vk,
where γk is the total actuation count up to time k on which we impose:
γk ≤ γmax.
12 / 16

18. IV. Hybrid Model Predictive
Control

19. Control scheme
Control objectives:
BBQ mode: Track a desired
spin rate 5deg/sec
with a low actuation count
and steer the pitch and yaw
errors to 0.
HMPC
EKF
Online
Linearisa2on
(A, B, f)
ˆz
u y
ˆz
13 / 16

20. Hybrid Model Predictive Control
MPC problem2:
P(x0, γ0, A, B, f) : min
πN
VN (πN , γ0)
s.t. x(0) = x0, γ(0) = γ0,
Hybrid dynamics for k ∈ N[0,Nu−1],
Assume U = [−umax, umax] for k ∈ N[Nu,N−1],
where
VN (πN , γ0)= QN zN p + ρ(γN − γ0)
Penalises the tot.
actuation count along
the horizon
+
N−1
k=0
Qzk p + Rηk p
2
Optimisation with respect to the sequence of control actions uk, δk, vk and ηk.
14 / 16

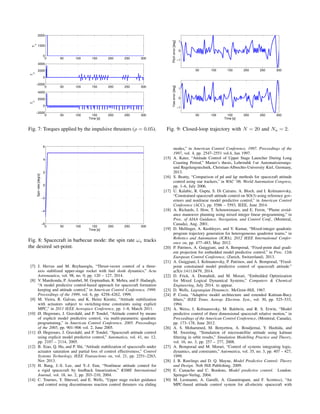
21. Simulation results3
−0.2 0 0.2 0.4 0.6 0.8 1 1.2
−0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Pitch error [deg]
Yawerror[deg]
50 100 150 200 250 300
0
0.2
0.4
0.6
0.8
Pitcherror[deg]
50 100 150 200 250 300
0
0.5
1
Yawerror[deg]
Time [s]
0 50 100 150 200 250 300
−6
−4
−2
0
2
4
6
Time [s]
Spinrate[deg/s]
0 50 100 150 200 250 300
0
1000
2000
T
x
0 50 100 150 200 250 300
−2000
0
2000
4000
T
y
0 50 100 150 200 250 300
−2000
0
2000
4000
T
z
Time [s]
3
Simulation parameters: Nu = 8, N = 20, ρ = 0.05
15 / 16

22. Simulation results
Choosing Nu = 2 we get:
50 100 150 200 250 300
−1
0
1Pitcherror[deg]
50 100 150 200 250 300
−1
0
1
Yawerror[deg]
Time [s]
16 / 16

23. Thank you for your attention

24. V. Appendix

25. Sloshing dynamics
The motion of the rotating mass is given by
d2α
dt2
= κ
dα
dt
+
θ(α, ω)
mf r2
,
And function θ is given by
θ(α, ω) = r2
(ω2
y − ω2
z) sin α cos α − prωxωy sin α
+ prωxωz cos α − r2
ωyωz cos(2α).

26. Attidute dynamics
The torque τ given by
τ = τext +


0 ωz −ωy
−ωz 0 ωx
ωy −ωx 0

 · l,
where l = Jω is the angular momentum and τext is the torque applied by
the thrusters. Differentiating l and by virtue of the above we have
˙l = ˙Jω + J ˙ω = J (α) ˙αω + J ˙ω,
and given that τ = ˙l, we have that
τ = J (α) ˙αω + J ˙ω.
The attitude dynamics is now described by
˙ω = J−1
ΩJω + J−1
τext − J−1
J (α)βω.

27. Performance indicators and assessment
Performance indicators: (i) the pointing-accuracy indicator
JK
pa =
Tsim
k=Tsim−K
2
y,k + 2
z,k,
Tsim: simulation time, K: parameter; (ii) the total squared error indicator
Jtse =
Tsim
k=0
2
y,k + 2
z,k,
(iii) the actuation count Jy
act and Jz
act along the y and z axes and (iv) the
total actuation count Jact.

28. Performance indicators and assessment
Evaluation of the closed-loop performance by simulations over an period
Tsim = 300s - effect of ρ
ρ Jact J40
pa Jtse
0.005 168 0.0001 0.0510
0.05 84 0.0018 0.0834
0.1 80 0.0349 0.2988
0.2 79 0.1279 1.6862

29. Extended Kalman Filter
The state estimates ˆzk are updated according to
ˆzk+1 = (I − KkCfh(ˆzk, uk)) + Kkyk,
where Kk is determined by
Kk = GkC (CGkC + R)−1
,
Pk+1 = (I − KkC)Pk,
with
Fk =
∂fh
∂z (ˆzk,uk)
,
Gk = FkPkFk + Q.