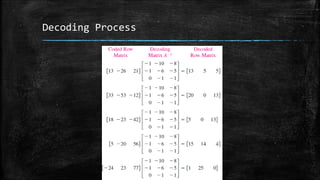
The document discusses the concept of matrices as rectangular arrangements of elements, highlighting their applications in various fields such as engineering, genetics, and cryptography. It explains how matrices can be used to encode and decode messages through a systematic process involving matrix multiplication. The encoding and decoding procedures require the use of an invertible matrix, where authorized receivers can easily decrypt messages by applying the inverse of the encoding matrix.

1. Application of Matrices
Presented By:
Mohammedi Limdiwala

2. Matrix
▪ A matrix is a rectangular arrangement of ‘mn’ elements.
▪ It consists of rows and columns arrangements.
▪ It is a systematic arrangement of elements and may represent
vectorial or scalar quantity.

3. Some of the applications of Matrix
▪ Engineering forces on a bridge or truss
▪ Electronics
▪ Genetics (working out selection process)
▪ Probability (finding quantities in a chemical reaction)
▪ Chemistry
▪ Economics (study of stock market, etc)
▪ Encryption And decryption messages –
Cryptography
(here we will discuss Cryptography)

4. Encryption and Decryption (Cryptography)
▪ A cryptogram is a message written according to a secret code (the Greek word kryptos
means “hidden”).The following describes a method of using matrix multiplication to encode
and decode messages.
▪ Then convert the message to numbers and partition it into
encoded row matrices, each having entries
 In the following example we take an example to
encode the Message “MEET ME MONDAY”

5. Encoding Process
▪ Partitioning the message (including blank spaces, but ignoring punctuation) into groups of
three produces the following uncoded row matrices.
▪ To encode a message, choose an invertible matrix and multiply the uncoded row matrices
(on the right) by to obtain coded row matrices.This inverted matrix will act as a password.
▪ For example here.

6. Encoding Process

7. Encoding Process
▪ The sequence of coded row matrices is
▪ Finally, removing the matrix notation produces the following cryptogram
▪ For those who do not know the encoding matrix A, decoding the cryptogram is possible.
▪ But for an authorized receiver who knows the encoding matrix decoding is relatively simple.
The receiver just needs to multiply the coded row matrices by A-1
to retrieve the uncoded row
matrices. In other words, if
▪ is an uncoded 1×n matrix, then Y=XA is the corresponding encoded matrix.The receiver of
the encoded matrix can decode by Y multiplying on the right by A-1
.

8. Decoding Process
▪ Begin by using Gauss-Jordan elimination to find A-1
▪ Now, to decode the message, partition the message into groups of three to form the coded
row matrices
▪ To obtain the decoded row matrices, multiply each coded row matrix by A-1

9. Decoding Process

10. Decoding Process
▪ The sequence of decoded row matrices is
▪ and the message is
▪ And the authorized person can easily decode the encoded message using the inverse of the
matrix A, which was the password during encoding.