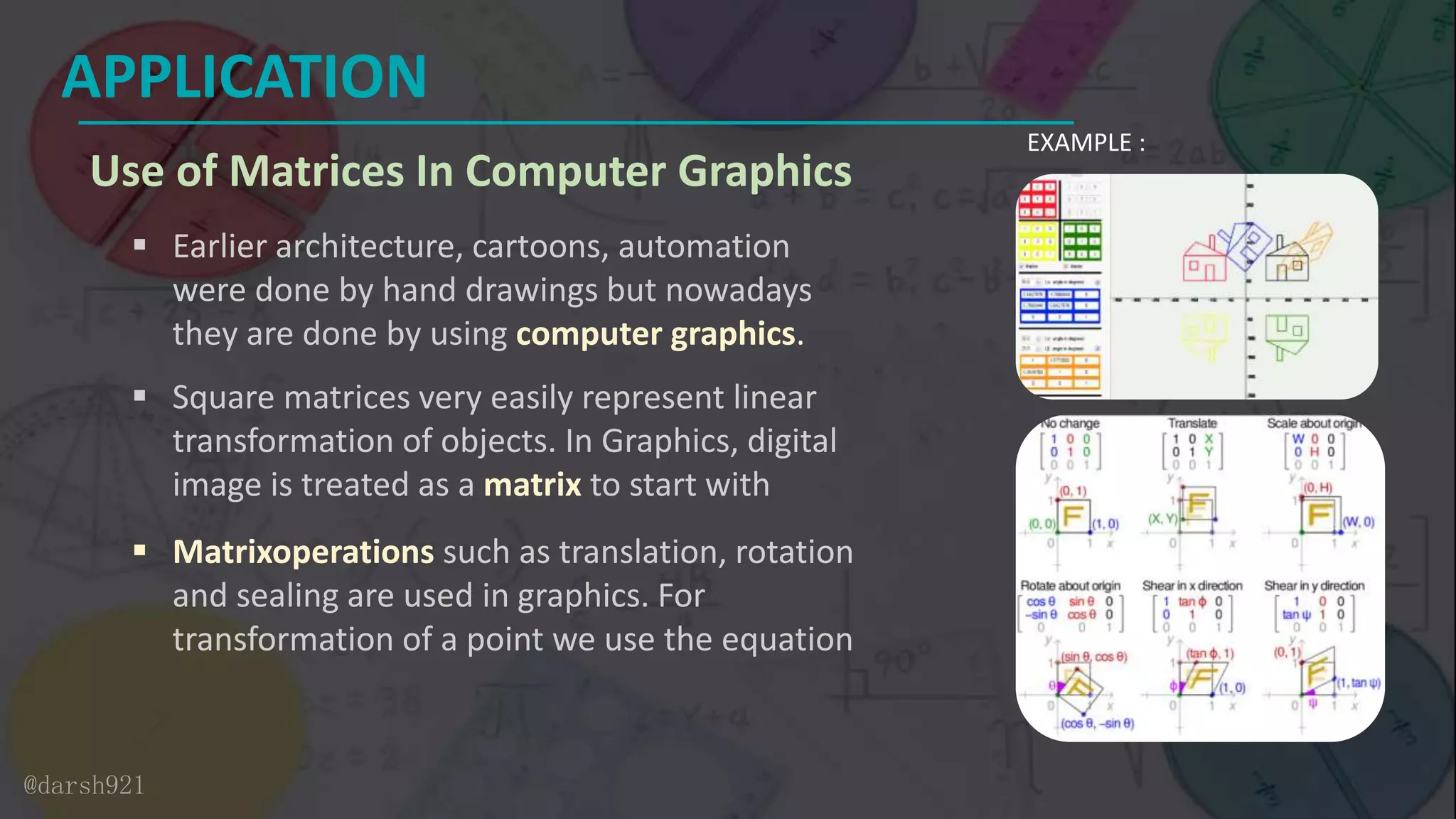
The document provides an overview of matrices, including: - A brief history of matrices dating back to ancient times. - Different types of matrices like row, column, null, square, diagonal, and more. - Applications of matrices in fields like computer graphics, cryptography, wireless communication, robotics, and chemistry. Matrices are used to represent transformations, encode/decode messages, model wireless signals, program robot movements, and balance chemical equations. - The document contains examples of matrix usage in graphics, cryptography, wireless communication, robotics, and chemistry.

1. MATRIX
Presentation by : DD MU
@darsh921
Prepared By: Darsh Patel
DD921921 B.tech 2n d Semester , MU UNIVERSITY

2. @darsh921

3. A LITTLE BIT OF HISTORY
 The history of matrices goes back to
ancient times , but the term
“Matrix” was not applied to the
concept till 1850
 Matrix is the Latin word for womb
and it retains that sense in English
 It can also mean more generally any
place where something is formed or
produced
A LITTLE BIT OF HISTORY
@darsh921

4. A LITTLE BIT OF HISTORY
 He was instrumental in proposing a
matrix concept independent of equation
systems. In 1858 Cayley published
his A memoir on the theory of matrices
 which he proposed and demonstrated
the Cayley-Hamilton theorem .
 In linear algebra, the Cayley–Hamilton
theorem states that every square
matrix over a commutative ring satisfies
its own characteristic equation.
@darsh921

5.  Row Matrix
 Column Matrix
 Null matrix
 Square Marix
 Diagonal Matrix
 Upper triangular matrix
 Lower triangular matrix
 Symmetric matrix
 Anti-Symmetric matrix
TYPE OF MATRIX

6. Use of Matrices In Computer Graphics
APPLICATION
 Earlier architecture, cartoons, automation
were done by hand drawings but nowadays
they are done by using computer graphics.
 Square matrices very easily represent linear
transformation of objects. In Graphics, digital
image is treated as a matrix to start with
 Matrixoperations such as translation, rotation
and sealing are used in graphics. For
transformation of a point we use the equation
EXAMPLE :
@darsh921

7. Use of Matrices in Cryptography
 Cryptography is the technique to encrypt data
so that only the relevant person can get the
data and relate information.
 One type of code, which is extremely difficult
to break, makes use of a large matrix to
encode a message.
 The receiver of the message decodes it using
the inverse of the matrix.
 This first matrix, used by the sender is called the
encoding matrix and its inverse is called the
decoding matrix, which is used by the receiver.
EXAMPLE :
@darsh921

8. A LITTLE BIT OF HISTORY
Use of Matrices in Wireless
 ommunication Matrices are used to model
the wireless signals and to optimize them.
 Matrices help in processing and representing
digital images.
 important part of the telecommunication
industry. Sensor array signal processing
focuses on signal enumeration and source
location applications and presents a huge
importance in many domains such as radar
signals and underwater surveillance.
EXAMPLE :
@darsh921

9. Use of Matrices in Robotics
 In robotics and automation, matrices are
the base elements for the robot
movements
 The movements of the robots are
programmed in MATLAB using matrix pencil
method.
 Matrices are used for movements in Robot
Arms. ROBOTICS
EXAMPLE :
@darsh921

10. Use of Matrices in Chemical
 In chemistry we use matrix methodology
to balance the chemical equations
 Initially we transform the chemical equations
into the matrices form.
 Then we apply Gauss Jordon method to
calculate the chemical reactions
aFeCl2 + bNa3(PO4) cFe3(PO4)2 + dNaCl
Fe: (1×a) + (0×b) –(3×c) = 0×d
Cl: (2 × a)+(0×b )+(0 × c) = 1 × d
Na: (0 × a)+(3 × b)+(0× c) = 1 × d
(PO4): (0×a)+(1×b)–(2 × c) = 0 × d
EX:
@darsh921

11. @darsh921