The document discusses several applications of matrices. It begins by explaining how matrices can be used to encrypt and decrypt messages by assigning numeric values to letters and performing matrix multiplication. It then discusses how geologists use matrices for seismic surveys to measure properties of the Earth. The document also notes that matrices are used in economics to calculate GDP and model industry output levels. Finally, it mentions that matrices are useful for computer graphics operations like scaling and rotation, and have various other uses in organizing data, engineering reports, and architecture.

1. Presentation On Application Of
Matrix
Prepared By:
Atikul Islam
162-33-3507

2.  Cryptography is the process of encrypting data so that third
party can’t read it and privacy can be maintained.
 It was started with the TV cable industries where even people
who were not the customer could watch the TV programs
 So, Videocipher encryption system was invented which would
convert signals into digital form i.e. encrypt it, and the data were
send over the satellite. The Videocipher box would decrypt the
signal and those satellite dish owner who had Videocipher box
would receive the decrypted signal i.e. the original signal before
encryption.
 In matrix same thing can be done.
Application of Matrix

3.  First, write a numerical value for each letter i.e. A=1,
B=2, and Z=26, and space=27.
 The data should be placed in matrix form i.e. in 2x1 or
3x1 matrix form.
 The data should be multiplied by given encoding
matrix.
 Then, write the answer (value after multiplying) in
linear form.
How to encrypt data?
Encryption Process

4.  The encoding matrix be
1 0 −1
0 1 0
0 −1 1
 Then, assign numeric value for “SUBMIT HER YOUR
PLANS” i.e. S=19, U=21, B=2, M=13, I=9, T=20,
space=27, H=8, E=5, R=18, space=27, Y=25, O=15, U=21,
R=18, space=27, P=16, L=12, A=1, N=14, S=19
Example: Let take the message
SUBMIT ME YOUR PLAN
S U B M I T H E R Y O U R P L A N S
19 21 2 13 9 20 27 8 5 18 27 25 15 21 18 27 16 12 1 14 19

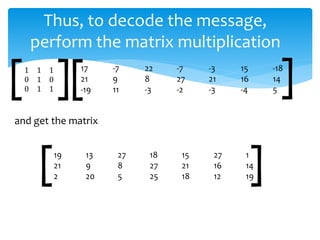
5.  Since we are using a 3 by 3 matrix, we break the
enumerated message above into a sequence of 3 by 1
vectors:
[ ] [ ] [ ] [ ] [ ] [ ] [ ]19
21
2
13
9
20
18
27
25
27
8
5
15
21
18
1
14
19
27
16
12

6.  The message should be encoded by multiplying the above
3x1 matrix by the given encoding matrix.
19 13 27 18 15 27 1
21 9 8 27 21 16 14
2 20 5 25 18 12 19
1 0 −1
0 1 0
0 −1 1
This gives,
17 -7 22 -7 -3 15 -18
21 9 8 27 21 16 14
-19 11 -3 -2 -3 -4 5

7.  The columns of this matrix give the encoded message. The
message is transmitted in the following linear form
17, 21, -21, -7, 9, -9, 22, 8, -8, -7, 27, -27, -
3, 21, -21, 15, 16, -16, -18, 14, -14

8.  The encrypted number should be written in matrix
form.
 The inverse of the encoding matrix should be found.
 Multiply the inverse encoding matrix, i.e. decoding
matrix with the encrypted number.
 Write the answer in linear form.
 Assign 1=A, 2=B and so on and also 27=space.
Decryption Process

9.  The inverse of the encoding matrix should be taken
out such as:
1 1 1
0 1 0
0 1 1

10. Thus, to decode the message,
perform the matrix multiplication
and get the matrix
1 1 1
0 1 0
0 1 1
17 -7 22 -7 -3 15 -18
21 9 8 27 21 16 14
-19 11 -3 -2 -3 -4 5
19 13 27 18 15 27 1
21 9 8 27 21 16 14
2 20 5 25 18 12 19

11.  The columns of this matrix, written in linear form,
give the original message:
S U B M I T H E R Y O U R P L A N S
19 21 2 13 9 20 27 8 5 18 27 25 15 21 18 27 16 12 1 14 19

12.  Many geologists make use certain types of matrices
for seismic surveys. The seismic survey is one form of
geophysical survey that aims at measuring the earth’s
(geo-) properties by means of physical (-physics)
principles such as magnetic, electric, gravitational,
thermal, and elastic theories.
Seismic Surveys

13.  Matrices are used to calculate gross domestic product
in economics, and help in calculation for producing
goods more efficiently. It is seen that through input-
output analysis that is used in matrix a researcher can
get information about what level of output should be
of each industry at the existing technology.
In economics

15.  Matrix transforms are very useful within the world of
computer graphics. Software and hardware graphics
processor uses matrices for performing operations
such as scaling, translation, reflection and rotation.
Computer Animations

16.  Matrices are very useful for organization, like for
scientists who have to record the data from their
experiments if it includes numbers.
 In engineering, math reports are recorded using
matrices.
 And in architecture, matrices are used with
computing. If needed, it will be very easy to add the
data together, like with matrices in mathematics.
Other uses…