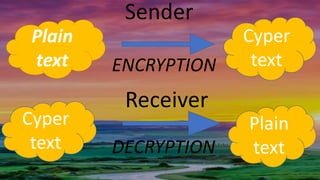
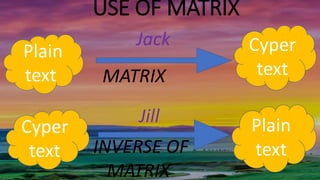
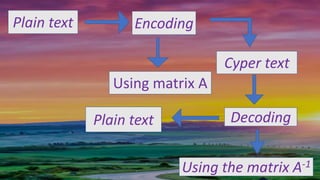
This document discusses how matrices can be used for encryption and decryption in cryptography. It explains that a plaintext message is first converted to numbers and arranged in a matrix. This matrix is then multiplied by a chosen encryption matrix to produce the ciphertext matrix. Decryption involves multiplying the ciphertext matrix by the inverse of the encryption matrix to recover the original plaintext matrix and message. An example is provided to illustrate the encryption of the message "ATTACK NOW" using a 2x2 matrix.

1. APPLICATIONS OF
MATRICES IN
CRYPTOGRAPHY

2. Cryptography
Keeping private Communication
ENCRYPTION and DECRYPTION

3. Sender
Plain
text
Cyper
text
ENCRYPTION
Receiver
Cyper
text DECRYPTION
Plain
text

4. USE OF MATRIX
Plain
text
Cyper
text
Jack
MATRIX
Cyper
text
Jill
INVERSE OF
MATRIX
Plain
text

5. 1. Convert the message in to numbers.
Ex:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
A B C D E F G H I J K L M N O P Q R S T U V
23 24 25 26
W X Y Z
2. Build the numbers in to Matrix.
3. Multiplying the matrix with our choice matrix.
4. We get a new matrix.
5. Convert the matrix in to string= cyber text encoded message.
RULES FOR ENCODING

6. RULES FOR DECODING
1. Convert the encoded message into matrix.
2. Multiplying the above matrix with the inverse of
our choice matrix.
3. We get another(plain text) matrix.
4. Convert Matrix into message(original message)

7. Plain text Encoding
Cyper text
Using matrix A
Decoding
Using the matrix A-1
Plain text

8. EXAMPLE:
Message to be Sent
ATTACK NOW Plain text
Encoding A = 1 2
1 3
AT=[1 20] 1 2 = [21 62]
1 3
TA=[20 1] 1 2 = [21 43]
1 3

9. CK =[3 11] 1 2 = [14 39]
1 3
_N =[27 14] 1 2 = [41 96]
1 3
OW=[15 23] 1 2 = [38 99]
1 3
Encoded
ATTACK NOW= 21 21 14 41 38
62 43 39
cyper text
DECODING A = 3 -2
-1 1

10. T=[21 62] 3 -2 =[1 20]
-1 1
A=[21 43] 3 -2 =[20 1] Decoded message:
-1 1 1 20 3 27 15
K=[14 29] 3 -2 =[3 11] 20 1 11 14 23
-1 1
N=[41 96] 3 -2 =[27 14]
-1 1
W=[38 99] 3 -2 =[15 23]

11. [1 20] [20 1] [3 11] [27 14] [15 23]
A T T A C K _ N O W
ATTACK NOW plain text