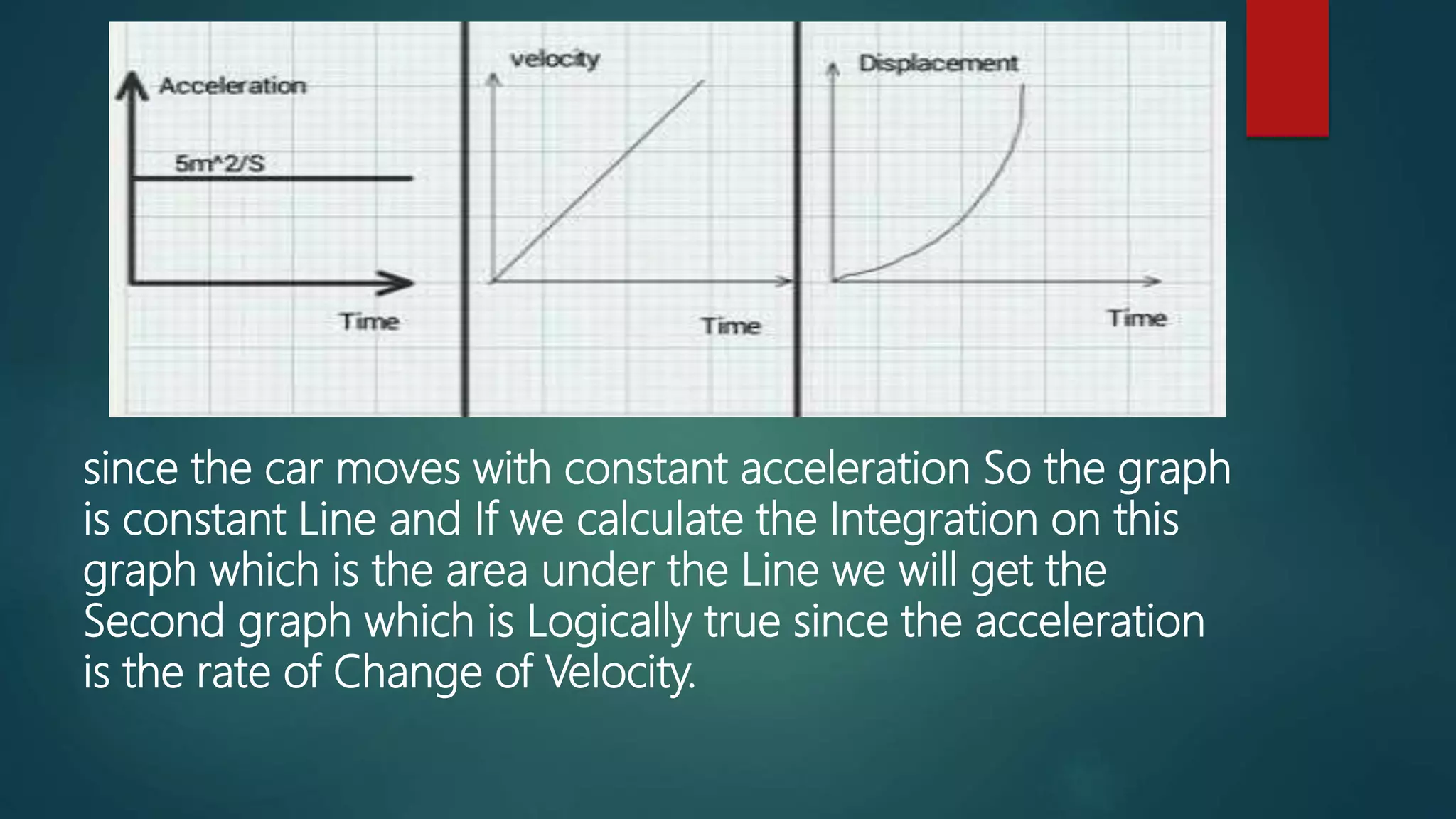
This presentation introduces engineering mathematics topics including matrix cryptography, mathematics in computer games, trigonometry, integration and differentiation applications, and Laplace transforms. It lists group members and their student IDs, describes how matrices are used to encrypt messages, and provides examples of how geometry, graphs, and pathfinding are applied in video games. Real-life applications of trigonometry, integration, differentiation, and Laplace transforms in fields like construction, surveying, electronics, signals, and physics are also outlined. The presentation emphasizes that engineering relies heavily on mathematical concepts and principles.

1. Welcome To Our
Presentation

2. Presentation Topics:
Engineering mathematics

3. Group members:
Md.Afzal Hossain
ID:171-15-1193
Md.Yusuf Khan
ID:171-15-1202
Md. Mahbobur Rahman
Salman
ID:171-15-1217
Md.Sarowar Zahan
ID:171-15-1221
Md.Rabbi Khan
ID:171-15-1427

4. APPLICATION OF MATRIX IN
CRYPTOGRAPHY:
 Cryptography is the process of encrypting
data so that third party can’t read it and
privacy can be maintained.
 It was started with the TV cable industries
where even people who were not the
customer could watch the TV programs.
 To prevent this, It was so much necessary to develop a system that can
keep the privacy unbroken
and only paid customers can watch the programs of corresponding TV
channels.

5. HOW MATRIX IS USED FOR
CRYPTOGRAPHY :
 Convert the text of the message into a stream of numerical values.
 Place the data into a matrix.
 Multiply the data by the encoding matrix.
 Convert the matrix into a stream of numerical values that contains
the encrypted message.
 Suppose the message is “SUBMIT HER YOUR PLANS”
 We assign a number for each letter of the alphabet. Such that A is 1, B is
2, and so on. Also, we assign the number
27 to space between two words.
Thus the message becomes:

6. MATHEMATICS IN COMPUTER
GAMES :
Examples of Computer Games

7. First Person Shooters:
 Geometric Figure: In this type of
games Geometry is the study of
shapes of various sort.
 3D graphics: The basic idea of 3D
graphics is to turn a mathematical
description of a world into a picture
of what that world would look like
to someone inside the world.

8. Strategy Games:
 Nodes , Edges and Graphs : To explain how the
computer works out the best route, We need to
know
what nodes , edges and graphs are.
 Path Finding : All the stuff about graphs help the
computer guide troops around levels are done by
it. Because.
It makes a graph where every interesting point is a
node on the graph, and every way of walking from
one node to another is an edge, then it solves the
problem We solved above to guide the troops

9. FIELDS OF TRIGONMETRY…
Plane Trigonometry
 In many applications of trigonometry the essential
problem is the solution of triangles. If enough sides
and angles are known, the remaining sides and
angles as well as the area can be calculated, and the
triangleis then said to be solved. Triangles can be
solved by the law of sines and the law of cosines.
 Surveyors apply the principles of geometry and
trigonometry in determining the shapes, measurements
and position of features on or beneath the surface of
the Earth. Such topographic surveys are useful in the
designof roads, tunnels, dams, and other structures.

10. Ancient Egypt and the Mediterranean
world…
 Several ancient civilizations in particular, the Egyptian,
Babylonian, Hindu, and Chinese possessed
considerable knowledge of practical geometry,
including some concepts of
trigonometry.
 A close analysis of the text, with its accompanying
figures, reveals that this word means the slope of an
incline, essential knowledge for huge construction
projects such as The pyramids. It shows that
the Egyptians had at least some knowledge of the
numerical
relations in a triangle, a kind of
“proto-trigonometry.”

11. Sine waves in nature:
 Sound waves are sine waves whenever we listen
to music, we are actually listening to sound waves.
 Light waves are also sine waves.
 Radio waves are sine waves.
 Simple harmonic motion of a spring when pulled
and released is a sine wave.
 Alternating current (AC) is a sine wave.
 Pendulum clock oscillations are sinusoidal in nature
 Waves of ocean are sinusoidal .
 The vibrations of guitar strings when played are
sinusoidal
in nature

12. some applications of integration and
differentiation in engineering sector…
 The best real life application that can be used to describe integration
and differentiation is the relation between the displacement , velocity
and acceleration and the explanation can be extended to Newton
laws.
 We can explain integration and differentiation by two ways
analytically, by equations, and graphically and Leave students to
figure out the relation between them.
 Imagine there is car start Moving from rest V= 0 , at position = 0 with
acceleration = 5 m/s^2

13. since the car moves with constant acceleration So the graph
is constant Line and If we calculate the Integration on this
graph which is the area under the Line we will get the
Second graph which is Logically true since the acceleration
is the rate of Change of Velocity.

14. REAL LIFE APPLICATION OF LAPELACE
TRANSFORM:
 1) System Modelling: Laplace transform is used to simplify
calculations in system modelling, where large differential equations
are used.
 2) Analysis of Electrical Circuits: In electrical circuits, a Laplace
transform is used for the analysis of linear time-invariant systems.
 3) Analysis of Electronic Circuits: Laplace transform is widely used by
Electronics engineers to quickly solve differential equations occurring
in the analysis of electronic circuits.

15. REAL LIFE APPLICATION OF LAPELACE
TRANSFORM
 4) Digital Signal Processing : One cannot imagine solving Digital Signal
processing problems without employing Laplace transform.
 5) Nuclear Physics: In order to get the true form of radioactive decay, a Laplace
transform is used. It makes studying analytic part of Nuclear Physics possible.
 6) Data mining: Data mining focuses on the discovery of unknown properties on
the data. Where Laplace equation is used to determine the prediction and to
analyses the step of knowledge in databases.

16. Conclusion:
Engineering + Maths = Everything
Enginnering – Maths = Nothing

17. Thank
You