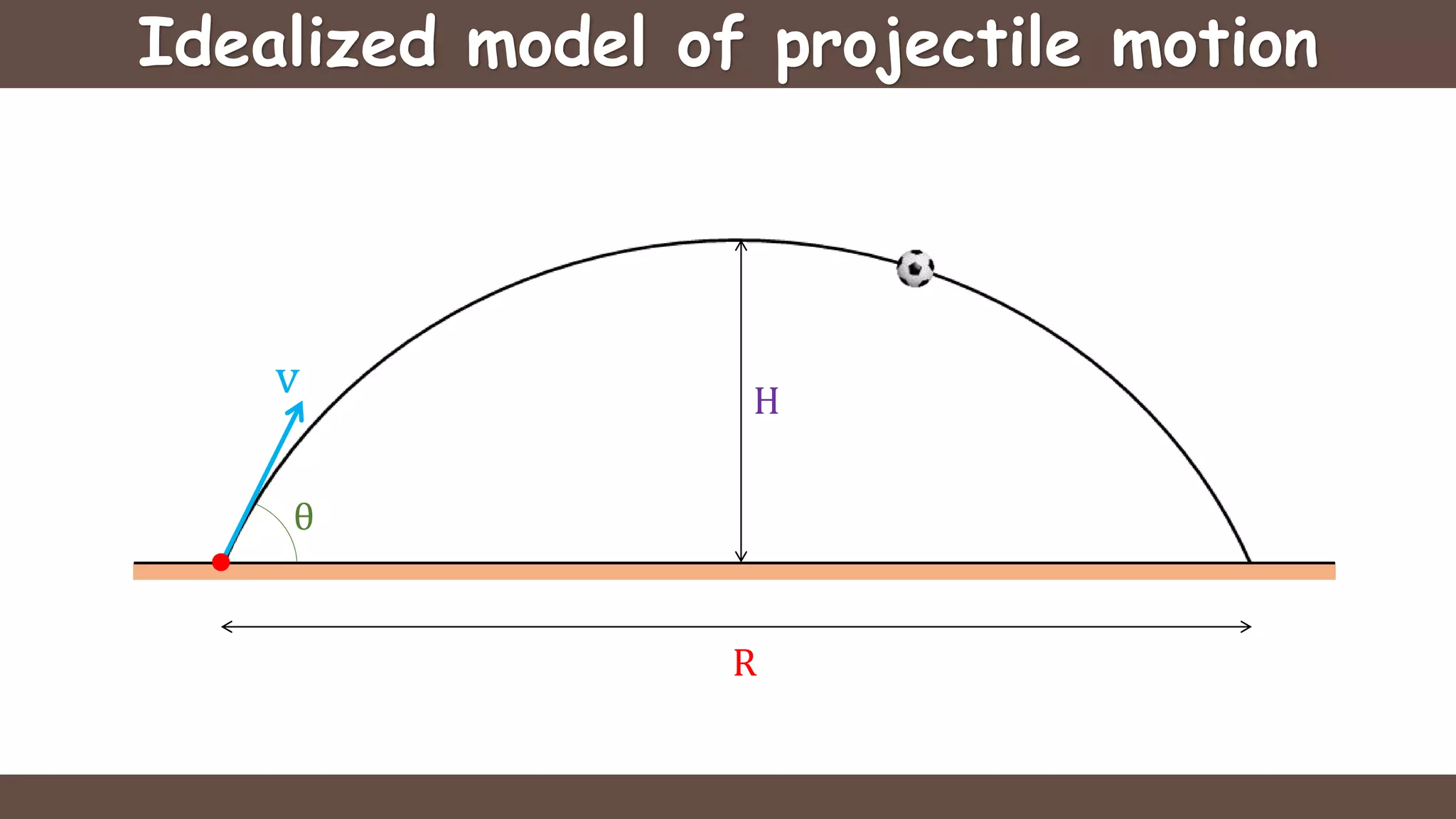
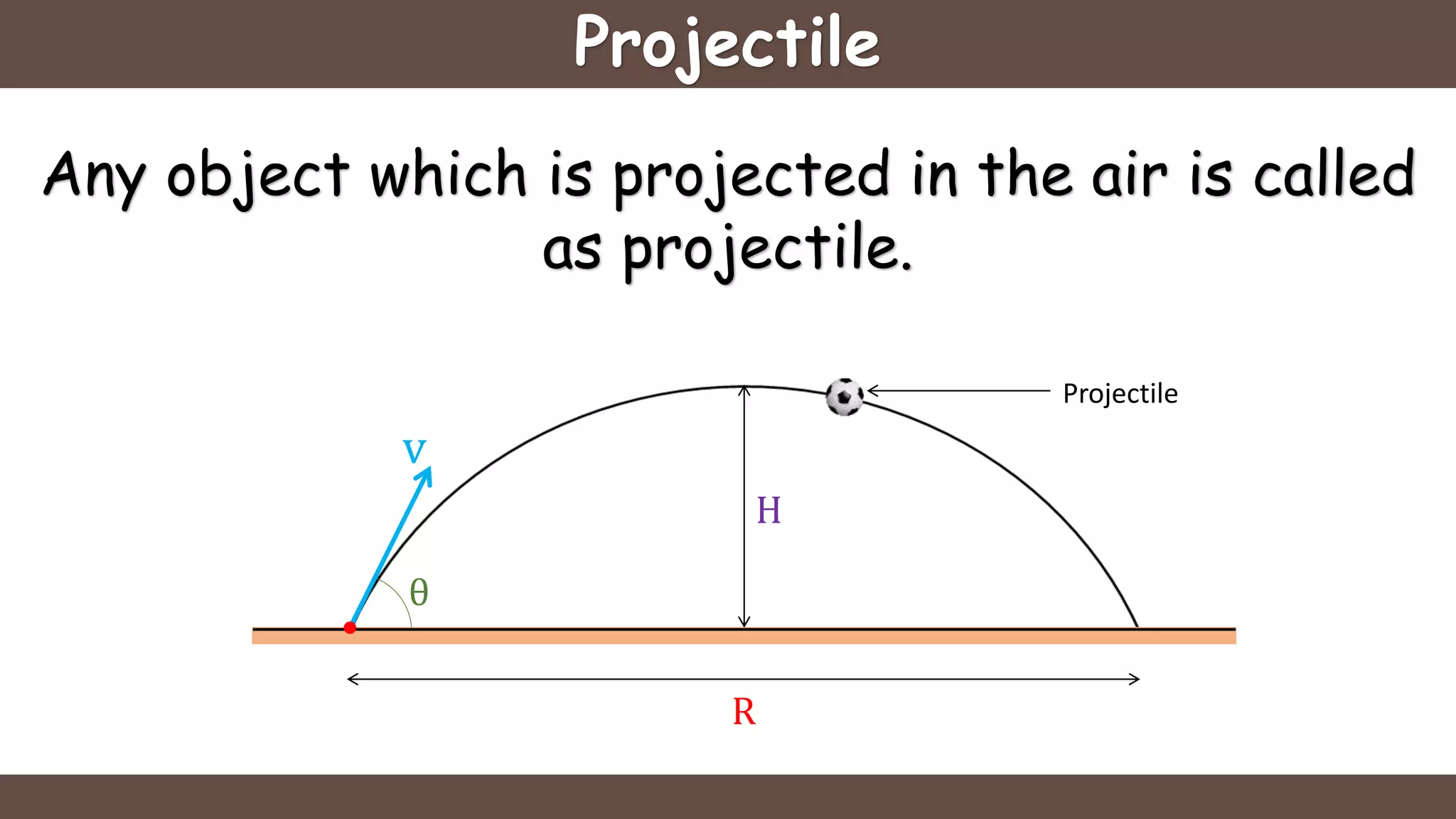
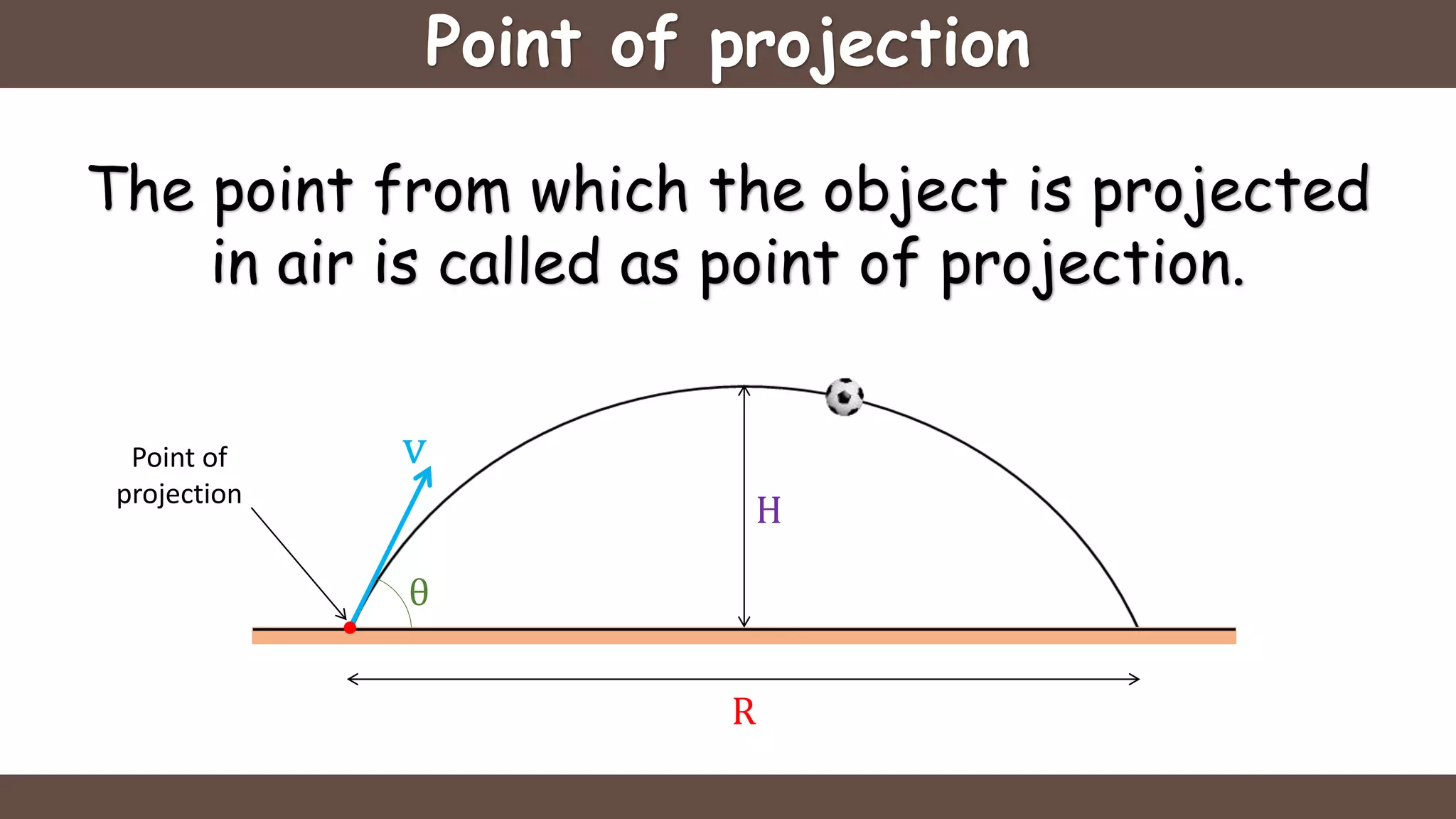
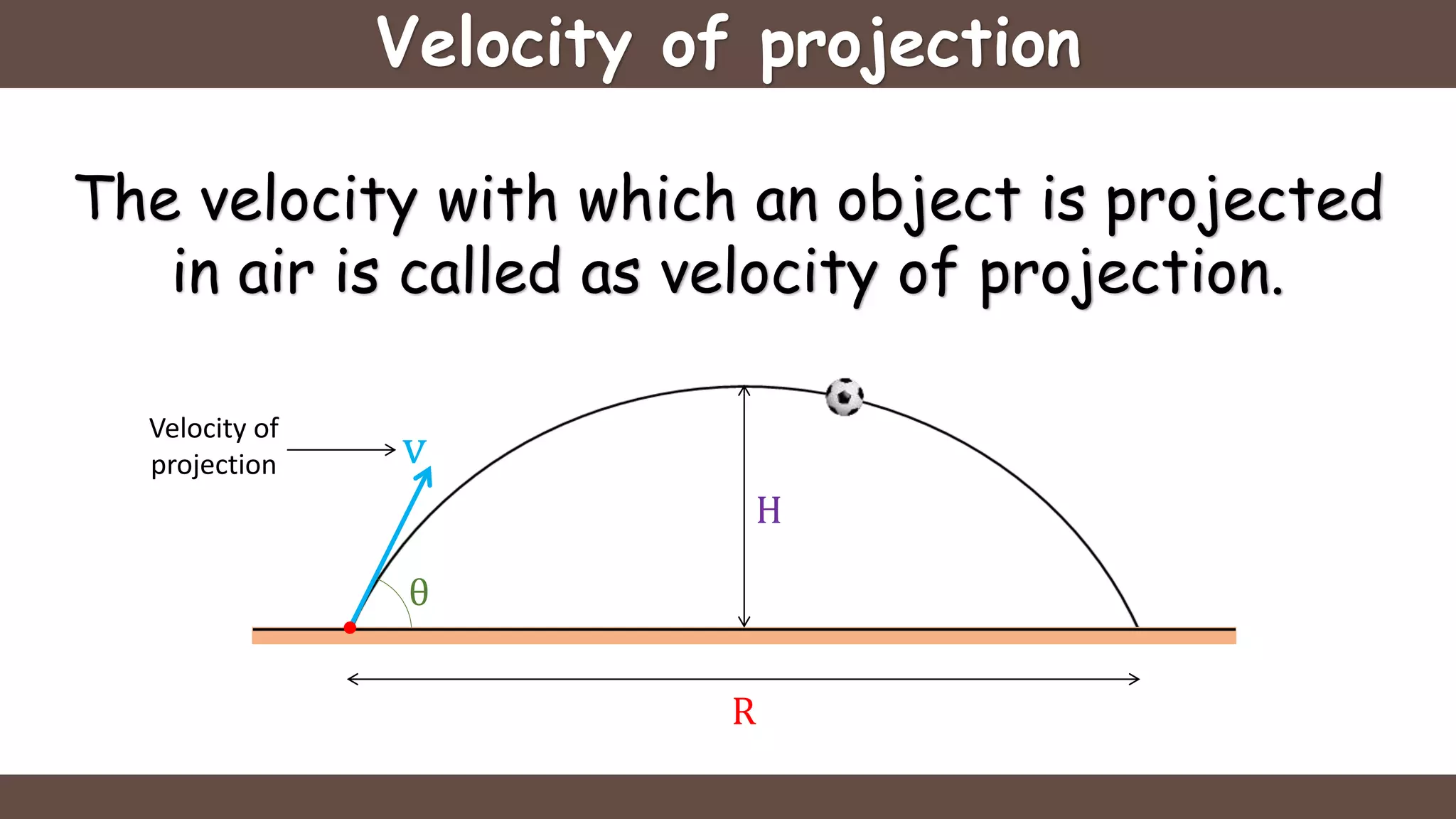
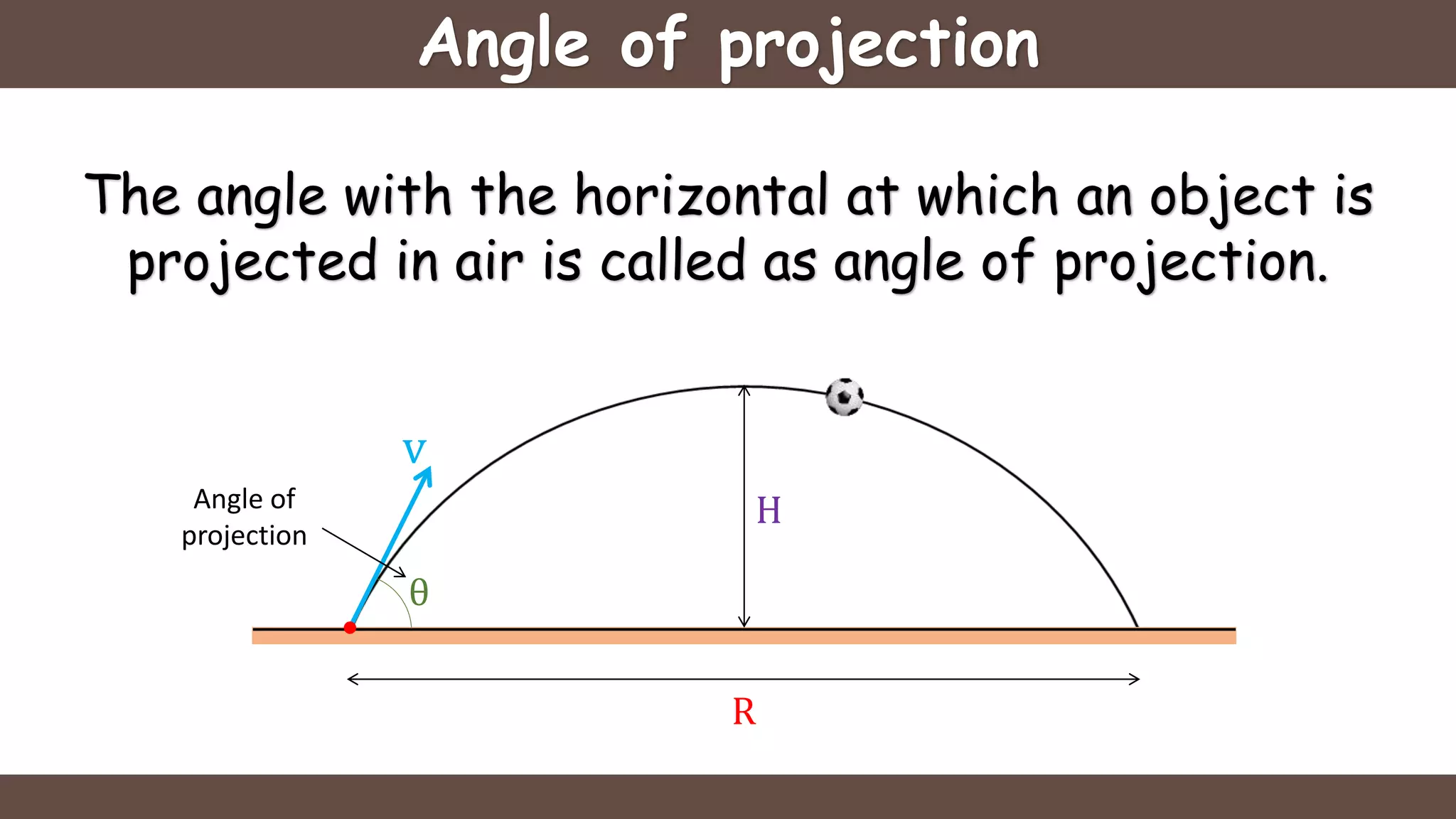
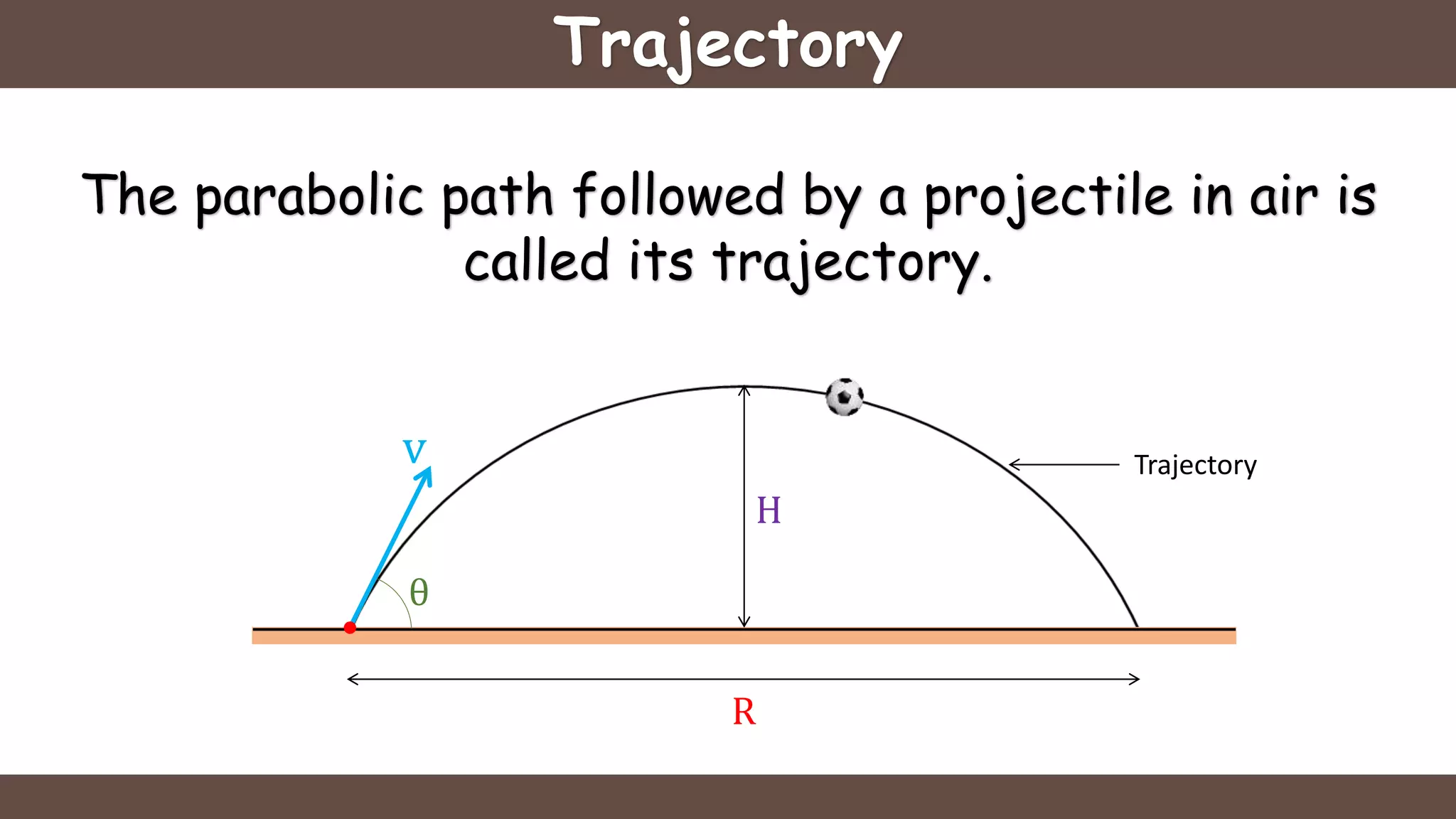
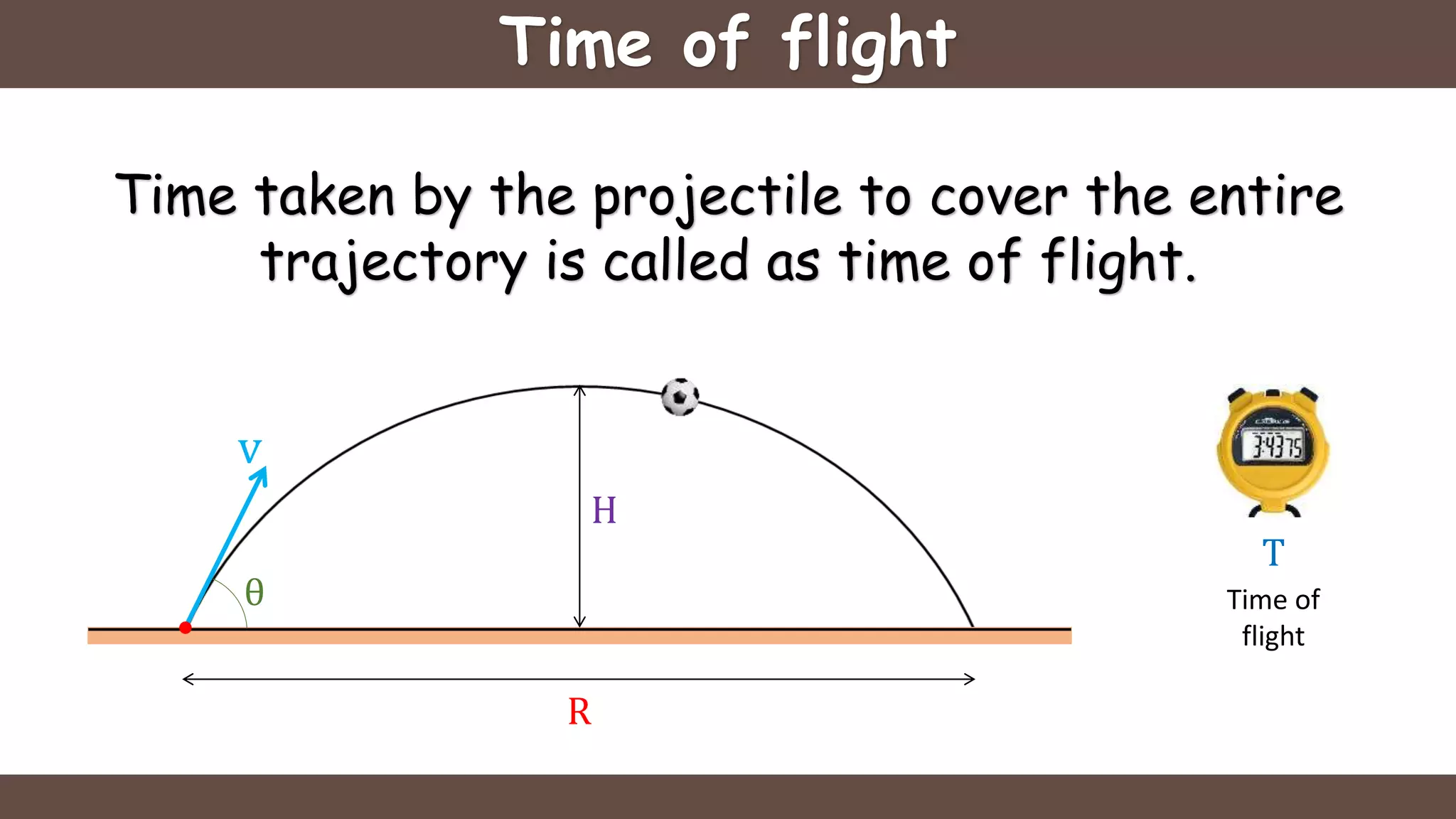
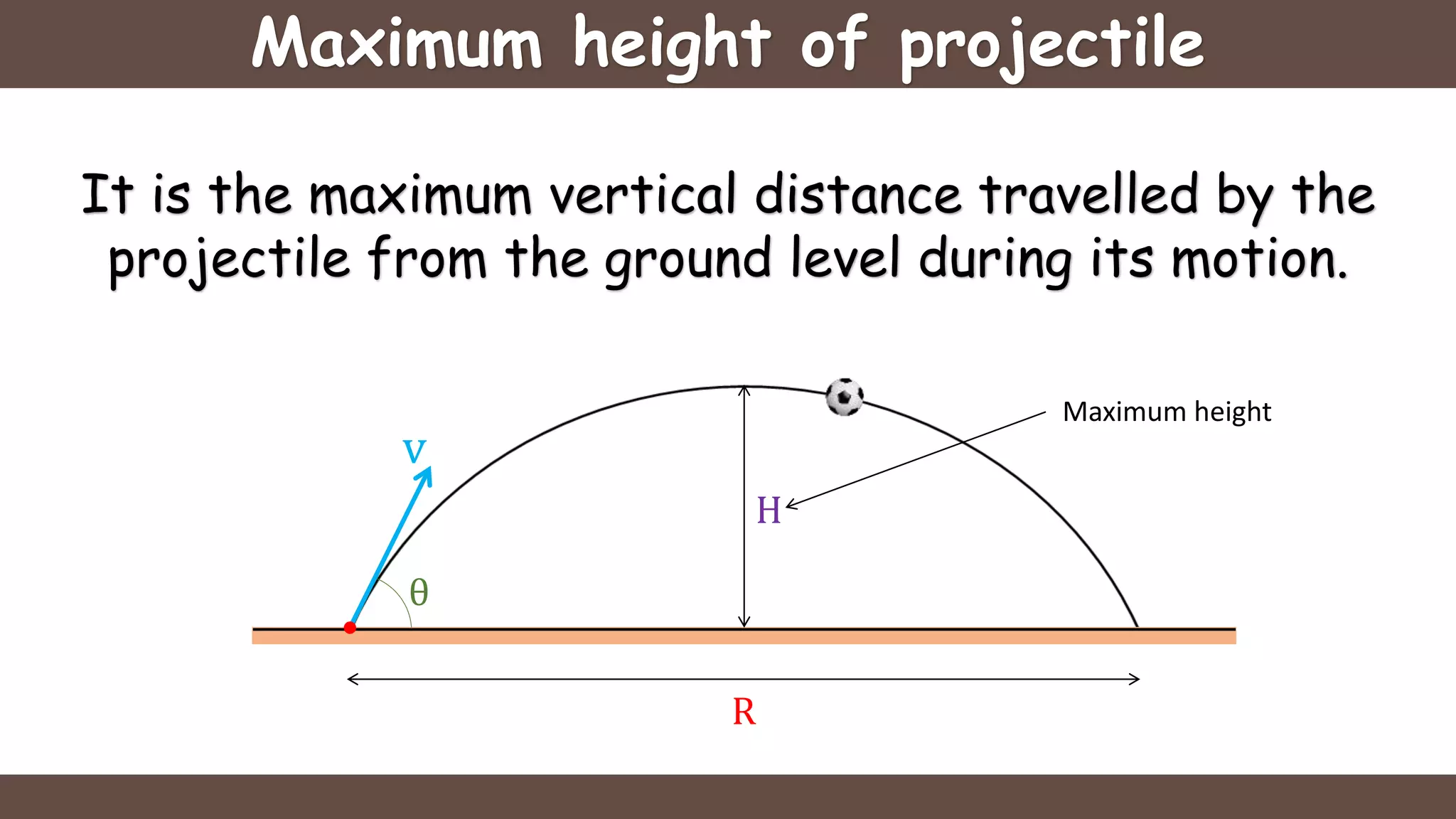
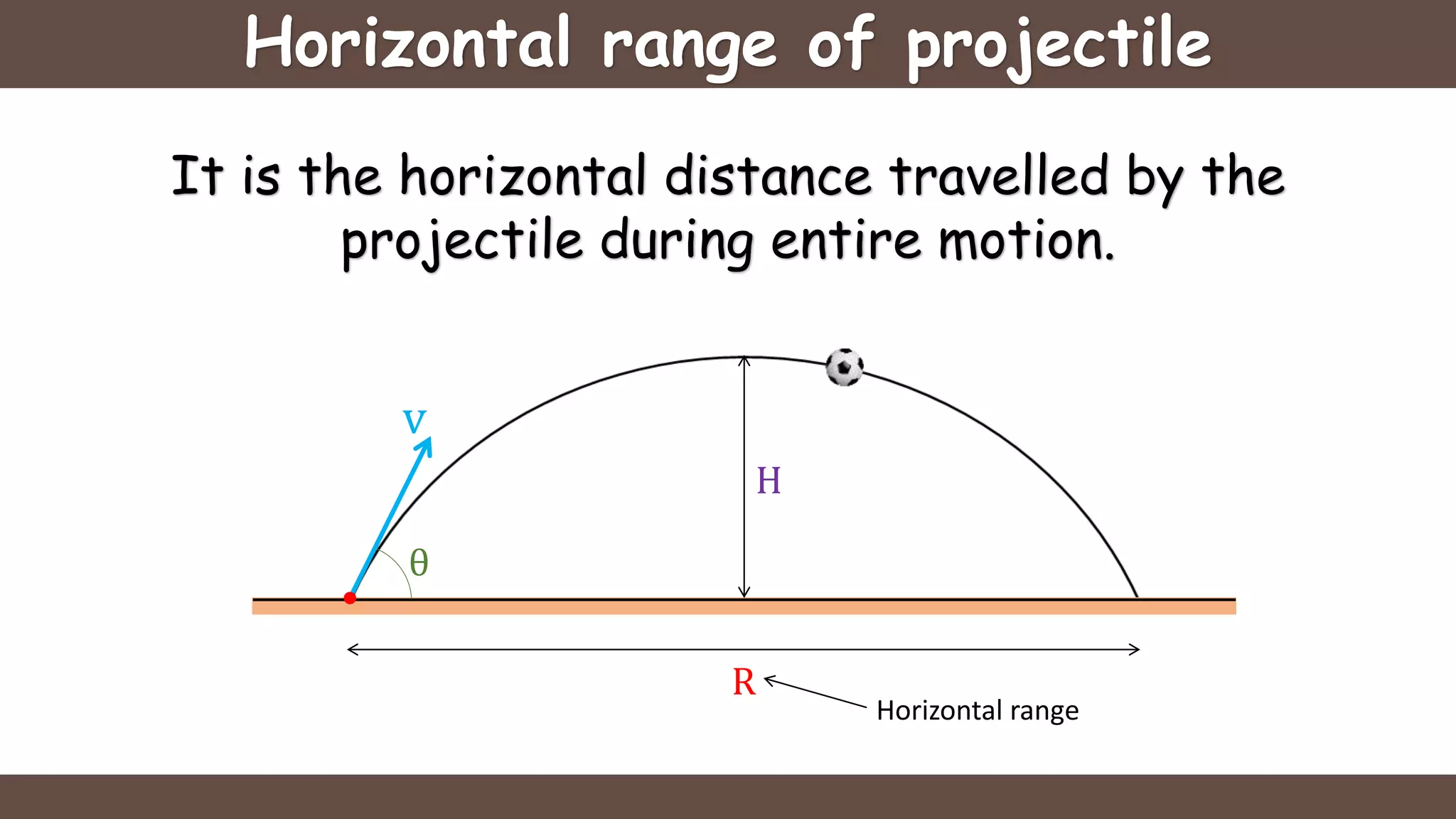
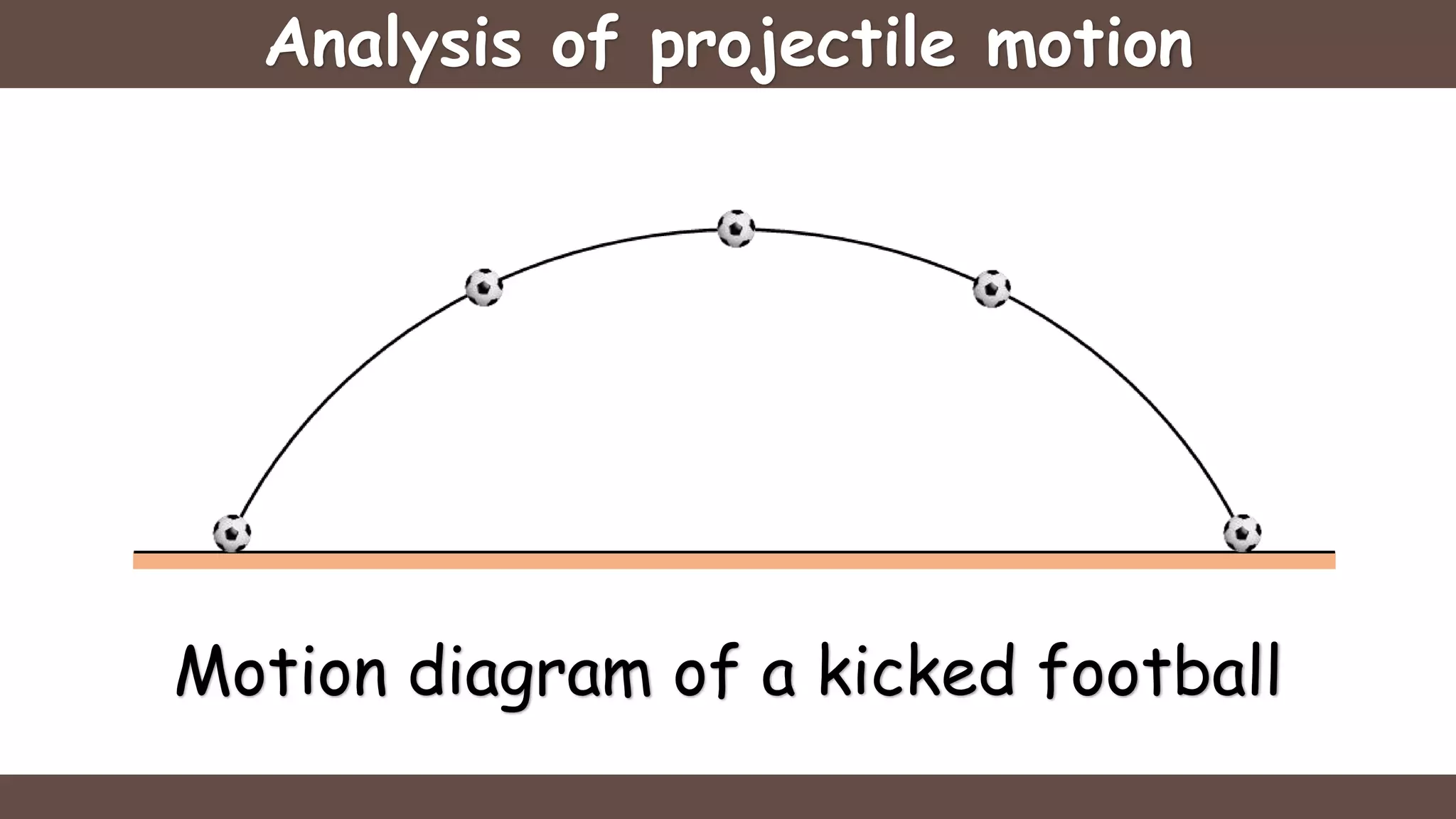
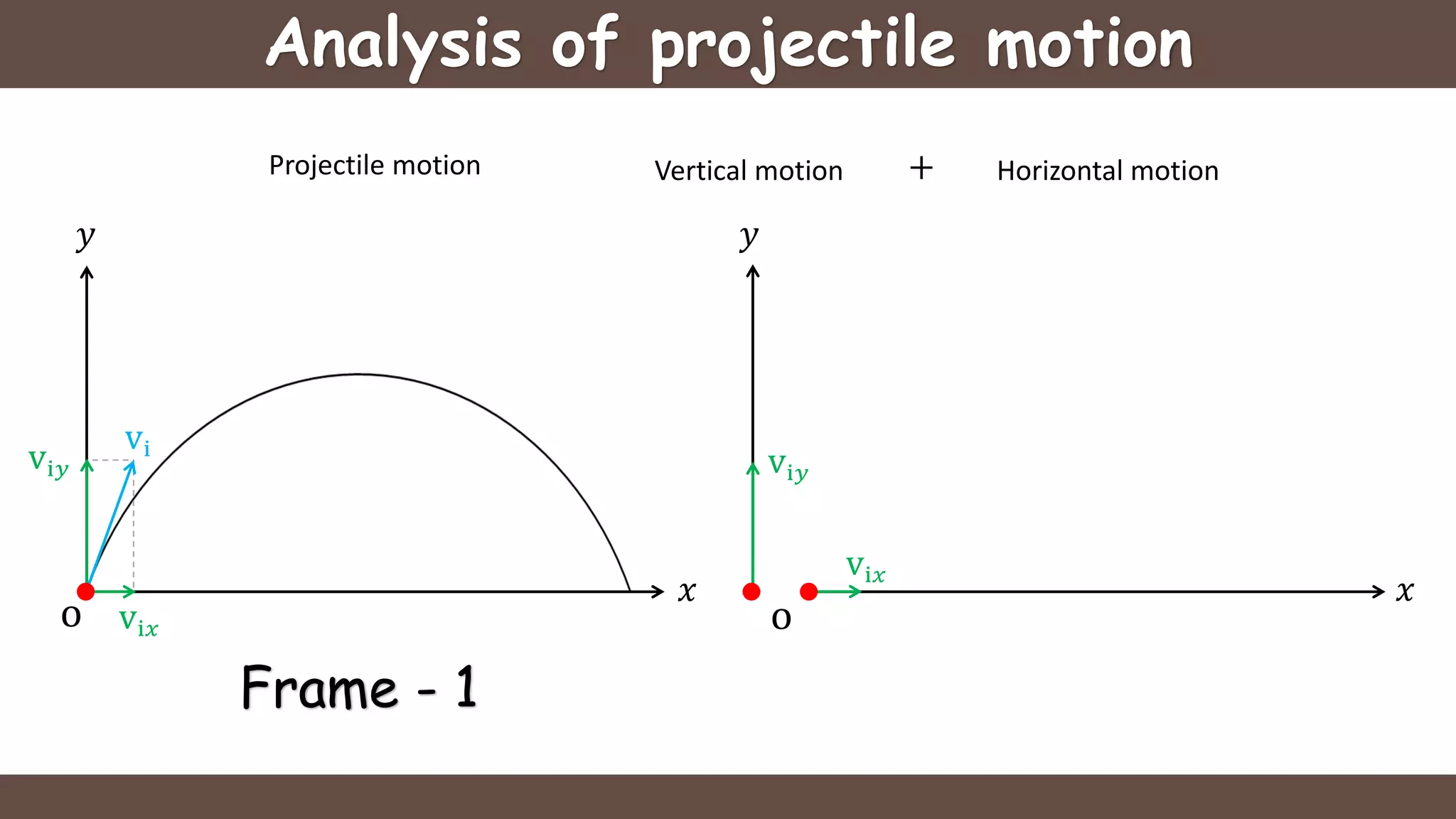
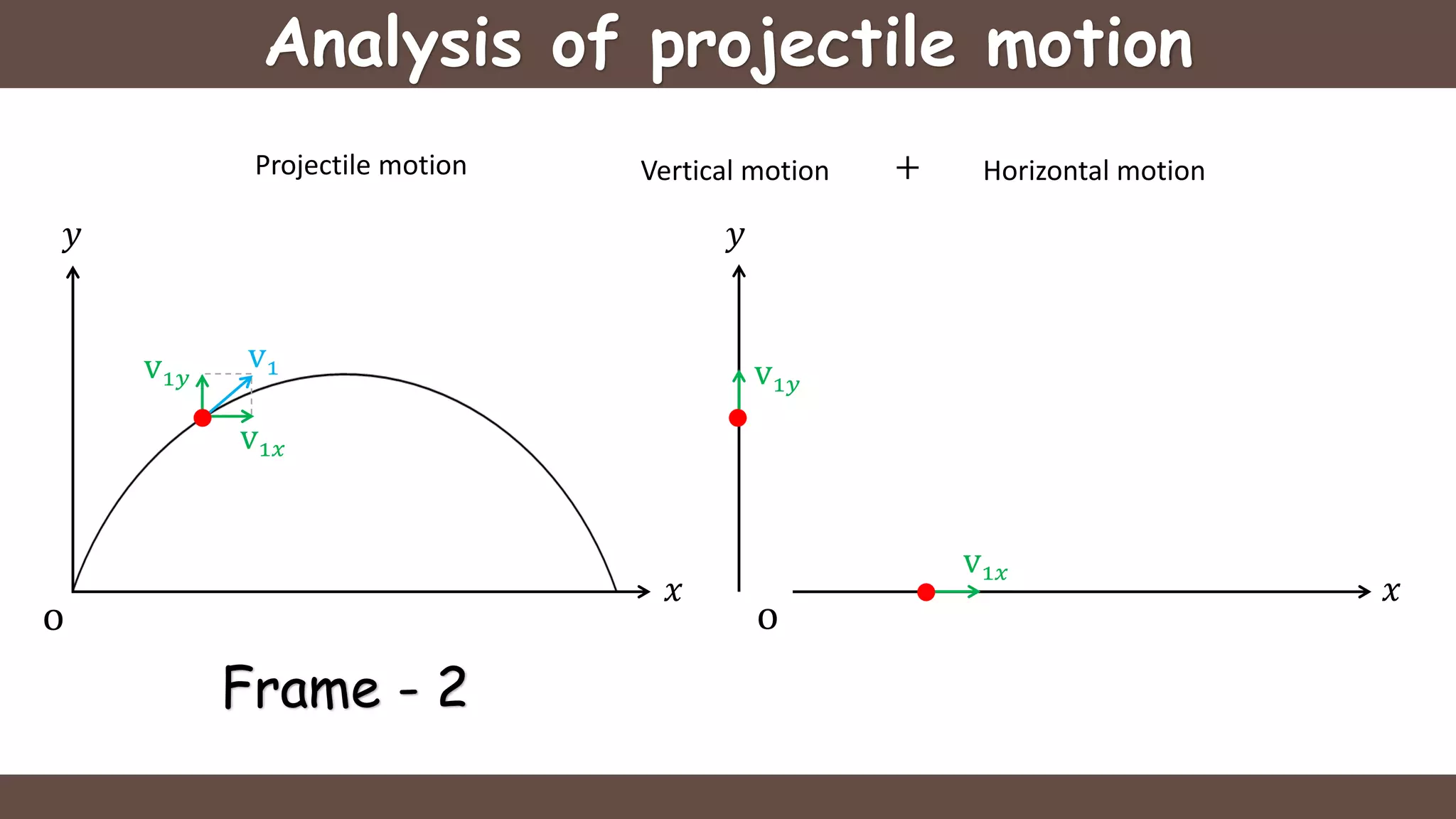
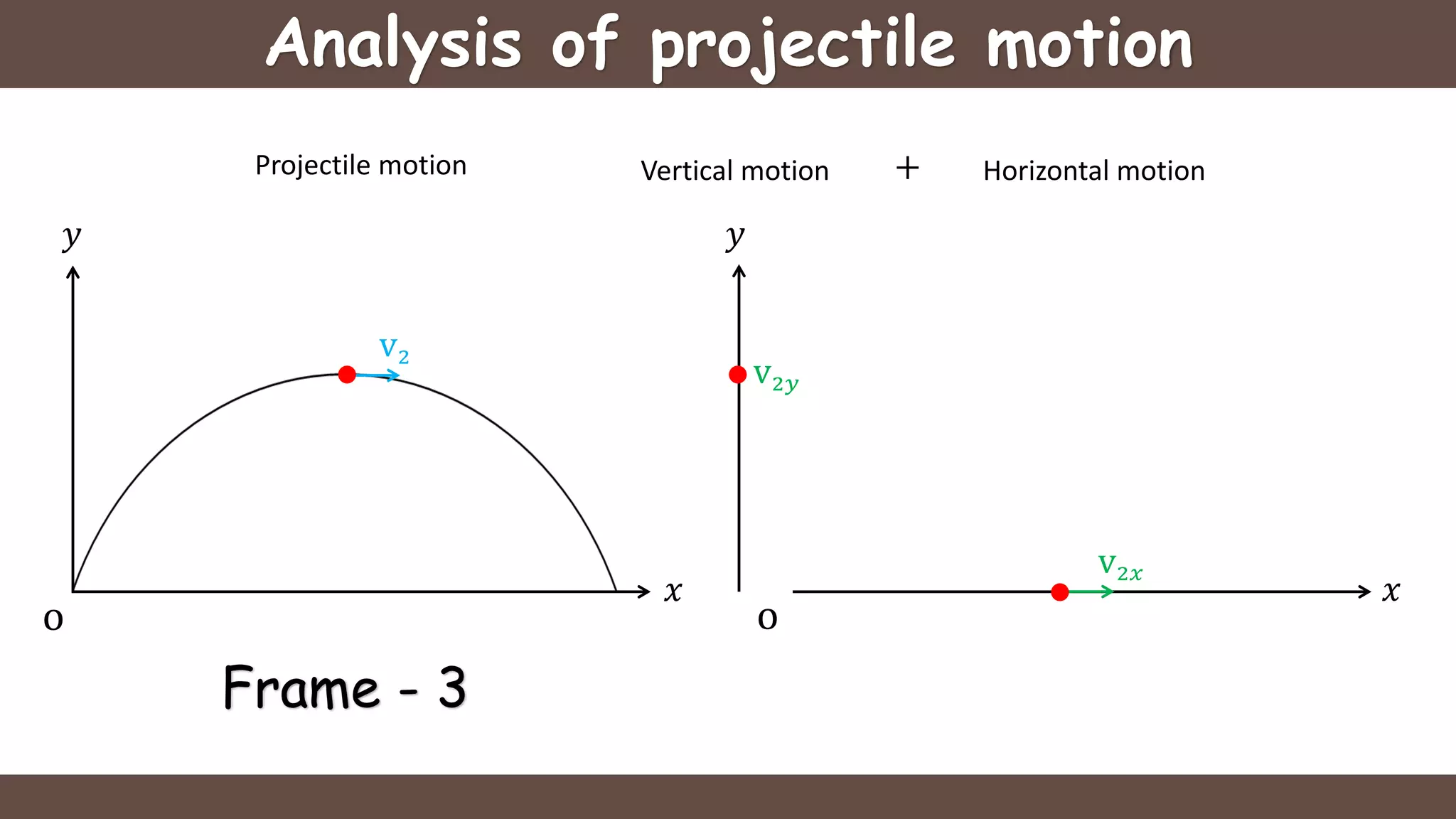
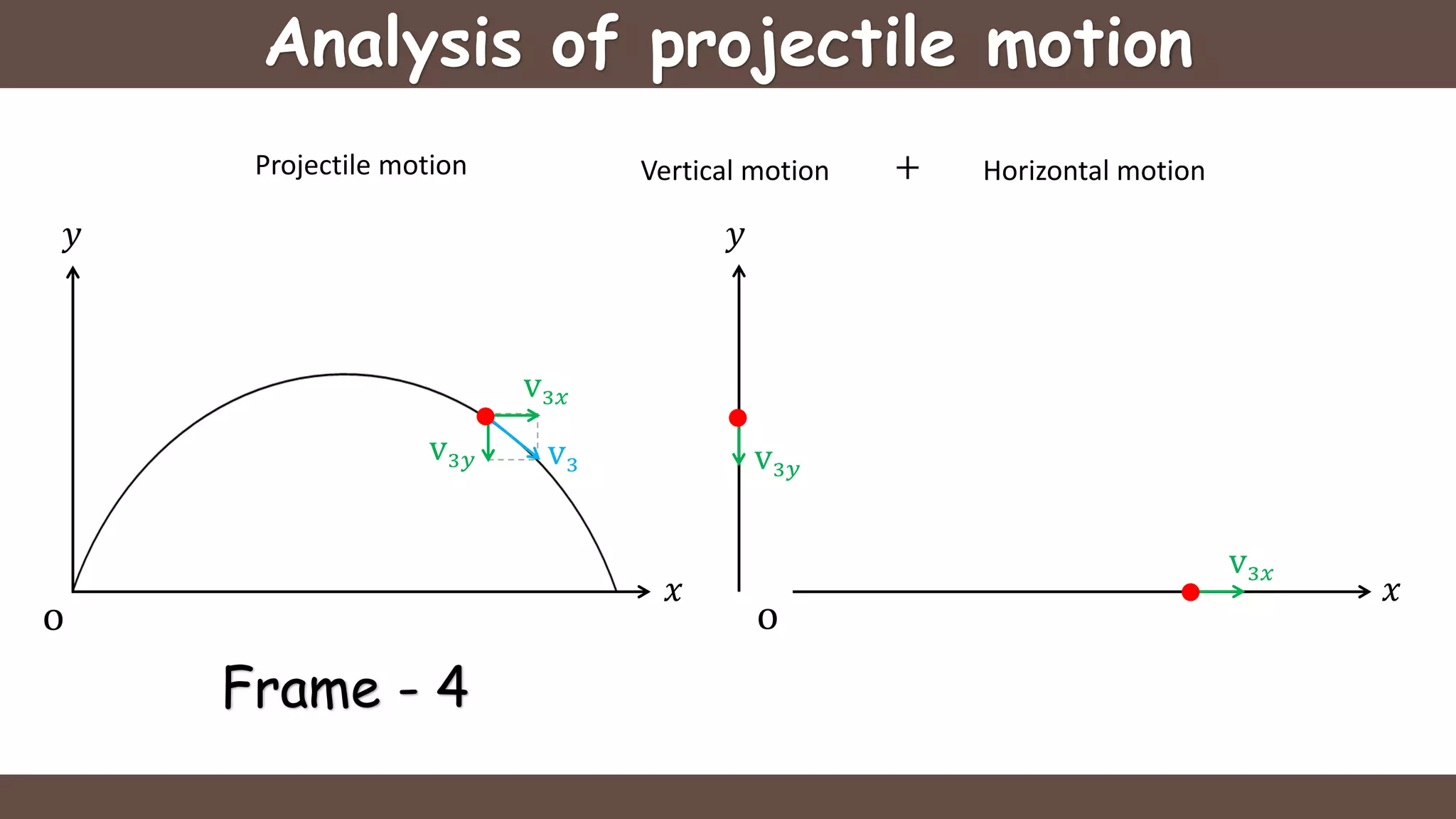
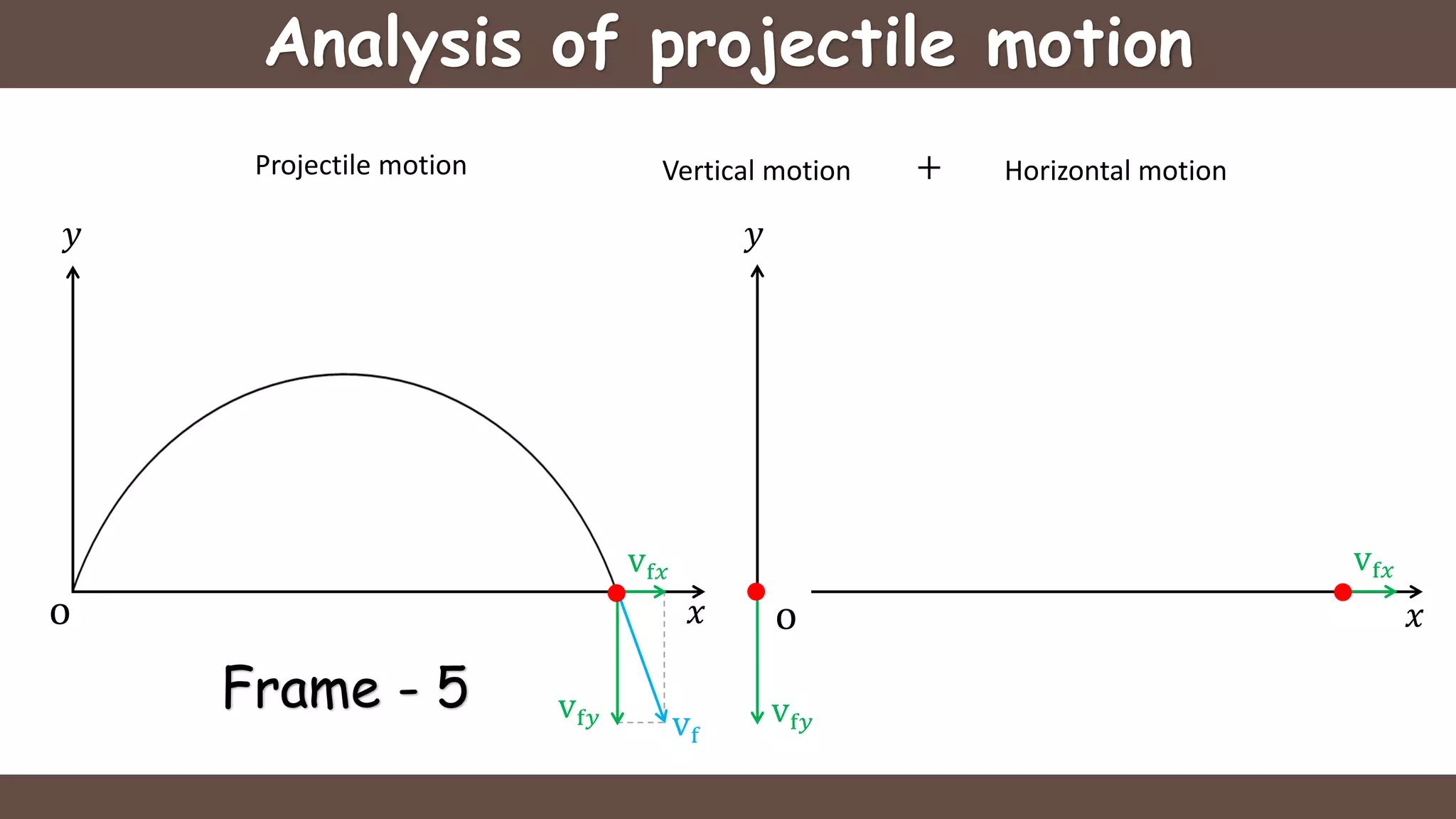
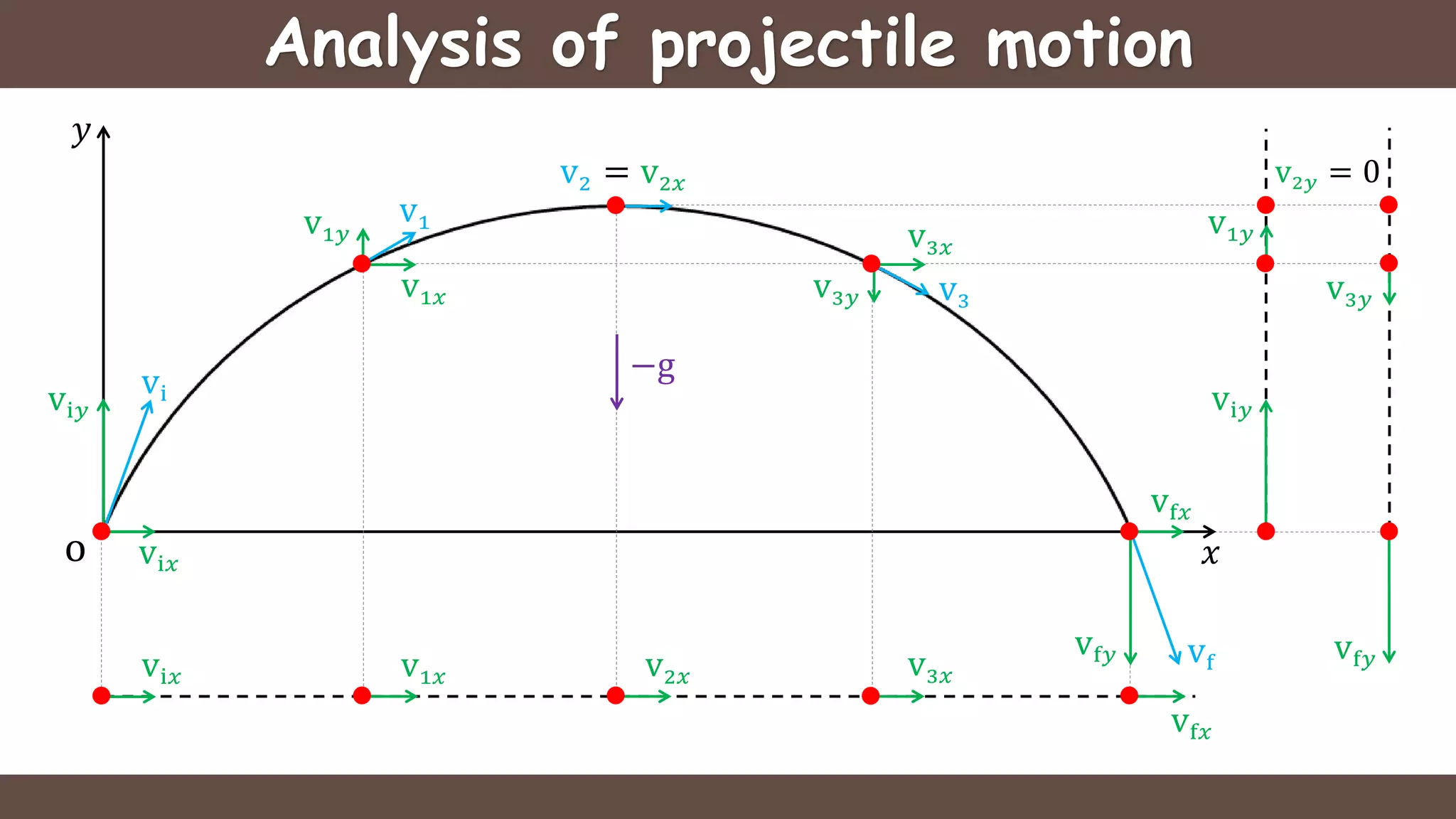
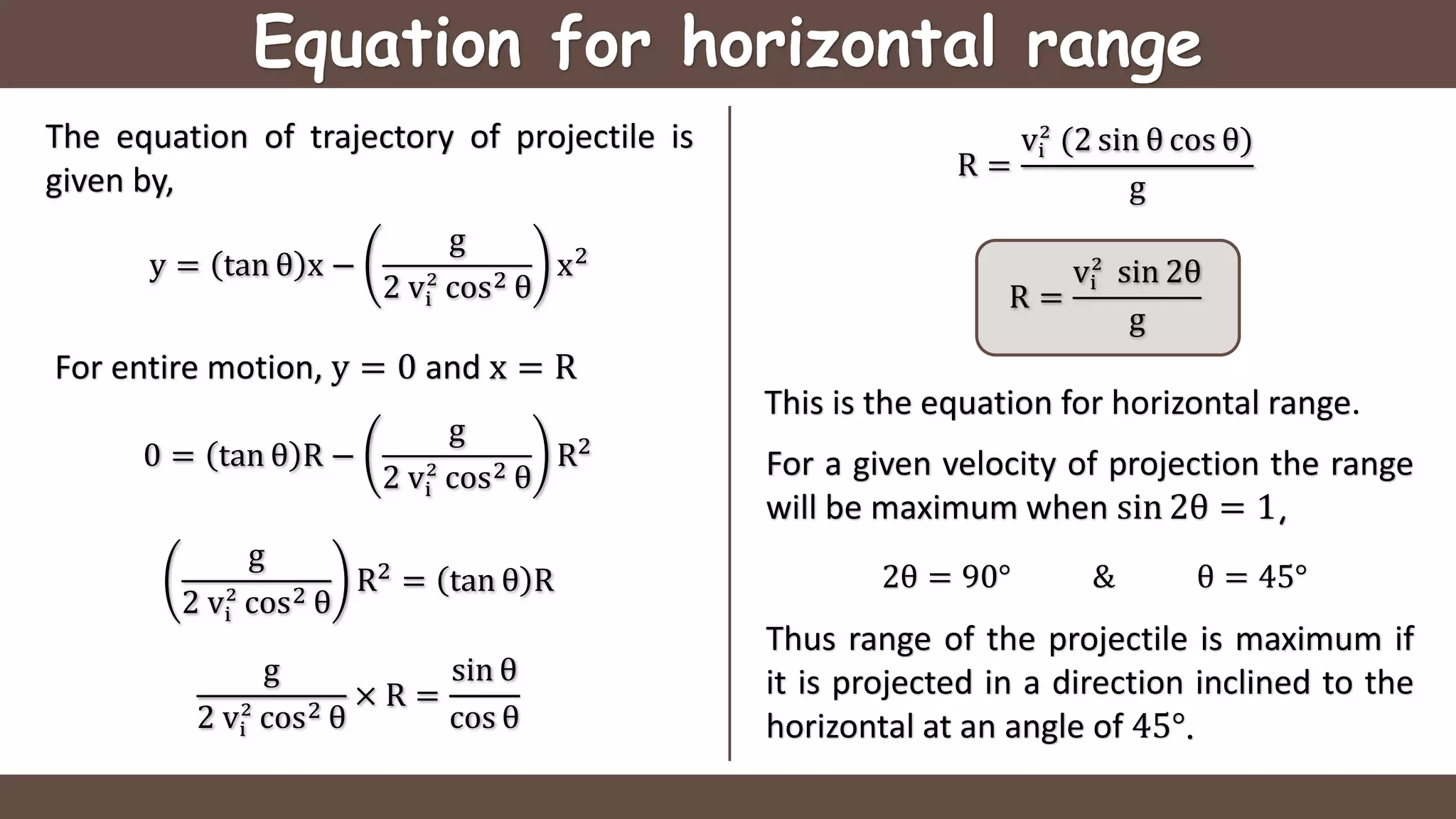
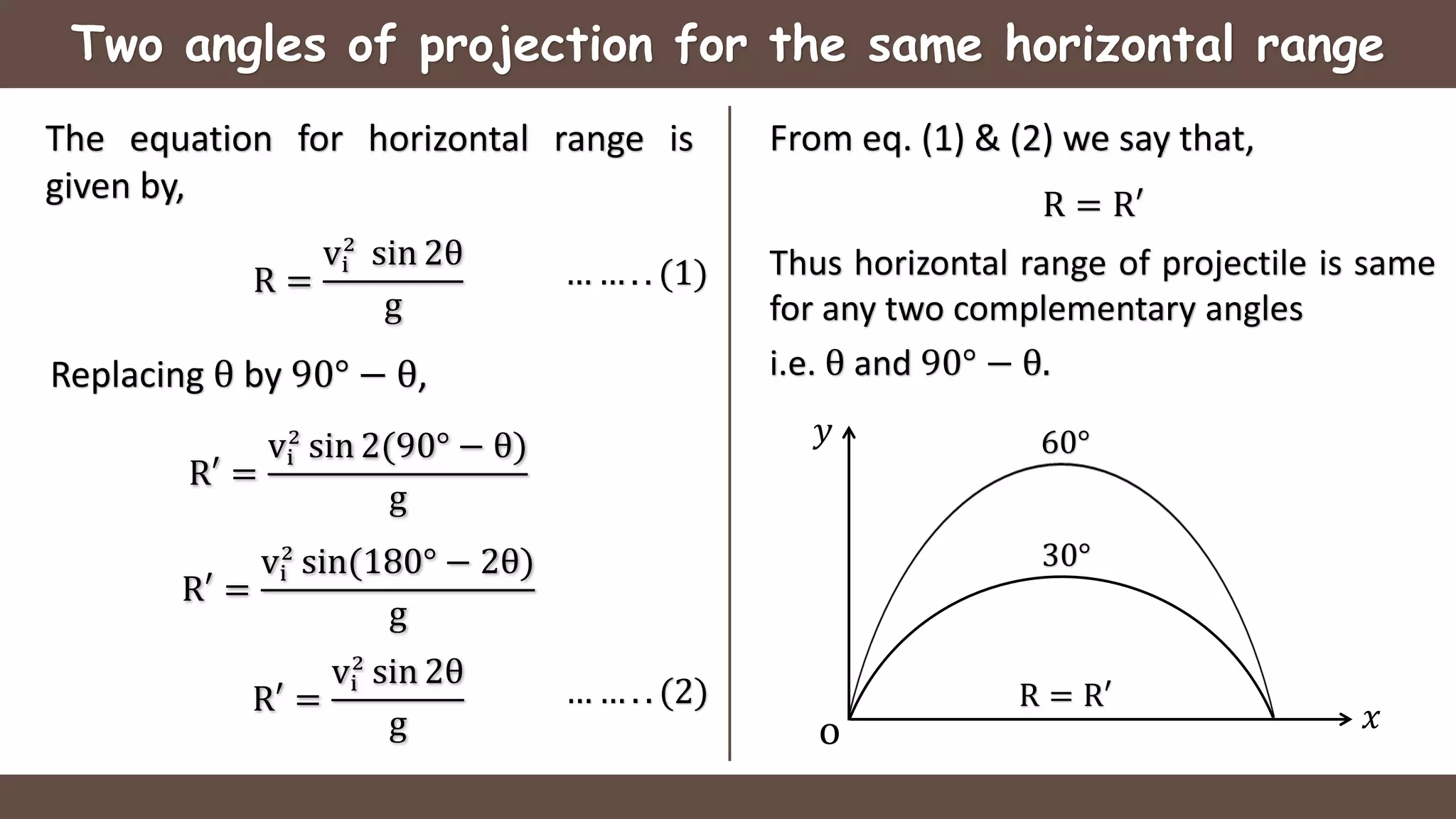
Projectile motion is the motion of an object thrown near the earth's surface, moving in a curved path under gravity with negligible air resistance and constant acceleration. It includes concepts like trajectory, velocity of projection, time of flight, maximum height, and horizontal range, with key formulas for calculating these parameters. The motion can be analyzed as a combination of horizontal motion at constant velocity and vertical motion with constant acceleration.

1. PROJECTILE MOTION

2. Projectile motion
Projectile motion is a motion in which an
object is thrown near the earth’s
surface, and it moves along the curved
path under the action of gravity only.

3. Motion of a snow boarder descending from a slope

4. Motion of a rider performing a bike stunt

5. Motion of water jets coming out from nozzles

6. Assumptions used in projectile motion
1. The effect due to air resistance is negligible.
2. The effect due to curvature of the earth is negligible.
3. The effect due to rotation of the earth is negligible.
4. The acceleration due to gravity is constant over the
range of motion.

7. Idealized model of projectile motion
θ
v H
R

8. Projectile
Any object which is projected in the air is called
as projectile.
Projectile
θ
v
H
R

9. Point of projection
The point from which the object is projected
in air is called as point of projection.
Point of
projection
θ
v
H
R

10. Velocity of projection
The velocity with which an object is projected
in air is called as velocity of projection.
Velocity of
projection
θ
v
H
R

11. Angle of projection
The angle with the horizontal at which an object is
projected in air is called as angle of projection.
Angle of
projection
θ
v
H
R

12. Trajectory
The parabolic path followed by a projectile in air is
called its trajectory.
Trajectory
θ
v
H
R

13. Time of flight
Time taken by the projectile to cover the entire
trajectory is called as time of flight.
Time of
flight
θ
v
H
R
T

14. Maximum height of projectile
It is the maximum vertical distance travelled by the
projectile from the ground level during its motion.
Maximum height
θ
v
H
R

15. Horizontal range of projectile
It is the horizontal distance travelled by the
projectile during entire motion.
Horizontal range
θ
v
H
R

16. Is horizontal and vertical motions are interdependent?
• Both pink and yellow balls are falling
at the same rate.
• Yellow ball is moving horizontally
while it is falling have no effect on
its vertical motion.
• It means horizontal and vertical
motions are independent of each
other.

17. Analysis of projectile motion
Motion diagram of a kicked football

18. Analysis of projectile motion
vi𝑥
vi𝑦
+Projectile motion Vertical motion Horizontal motion
𝑥
𝑦 𝑦
Frame - 1
o o
𝑥
vi
vi𝑦
vi𝑥

19. Analysis of projectile motion
v1𝑥
v1𝑦
+Projectile motion Vertical motion Horizontal motion
𝑥
𝑦 𝑦
Frame - 2
o o
𝑥
v1 v1𝑦
v1𝑥

20. Analysis of projectile motion
+Projectile motion Vertical motion Horizontal motion
𝑥
𝑦 𝑦
v2𝑦
v2𝑥
Frame - 3
o o
𝑥
v2

21. Analysis of projectile motion
v3𝑥
v3𝑦
+Projectile motion Vertical motion Horizontal motion
𝑥
𝑦 𝑦
v3𝑦
Frame - 4
o o
𝑥
v3𝑥
v3

22. Analysis of projectile motion
vf𝑥
vf𝑦
+Projectile motion Vertical motion Horizontal motion
𝑥
𝑦 𝑦
Frame - 5
o o 𝑥
vf
vf𝑥
vf𝑦

23. Analysis of projectile motion
vi𝑥
vi𝑦
vi
o
v1𝑥
v1𝑦
−g
v2 = v2𝑥
v3𝑥
v3v3𝑦
vf
vf𝑥
vf𝑦
vi𝑥 v1𝑥 v2𝑥 v3𝑥
vf𝑥
v1
vi𝑦
vf𝑦
v1𝑦
v2𝑦 = 0
v3𝑦
𝑦
𝑥

24. Important conclusion
Projectile motion is a combination of two
motions:
a) Horizontal motion with constant velocity
b) Vertical motion with constant acceleration

25. Equation of trajectory
The horizontal distance travelled by the
projectile in time ‘t’ along 𝑥-axis is,
x = vi𝑥 t
x = (vi cos θ)t
t =
x
vi cos θ
The vertical distance travelled by the projectile
in time ‘t’ along 𝑦-axis is,
y = vi𝑦t −
1
2
g t2
… … . . (1)
… … . . (2)
Substituting the value of ‘t’ from eq.(1) in eq.(2)
we get,
y = (vi sin θ)t −
1
2
g t2
y = vi sin θ ×
x
vi cos θ
−
1
2
g
x
vi cos θ
2
y = tan θ x −
g
2 vi
2
cos2 θ
x2
This is the equation of trajectory of a projectile.
y = αx − βx2
Thus y is a quadratic function of x. Hence the
trajectory of a projectile is a parabola.
As vi , θ and g are constant for a given
projectile, we can write
tan θ = α &
g
2 vi
2
cos2 θ
= β

26. Equation for time of flight
The vertical distance travelled by the
projectile in time ‘t’ along 𝑦-axis is,
y = viyt −
1
2
g t2
For symmetrical parabolic path, time
of ascent is equals to time of
descent.
For entire motion, t = T and y = 0
0 = (vi sin θ)T −
1
2
g T2
1
2
g T2
= (vi sin θ)T
T =
2 vi sin θ
g
TA = TD =
T
2
TA = TD =
vi sin θ
g
This is the equation for time of flight.

27. Equation for horizontal range
The equation of trajectory of projectile is
given by,
y = tan θ x −
g
2 vi
2
cos2 θ
x2
This is the equation for horizontal range.
For a given velocity of projection the range
will be maximum when sin 2θ = 1,
2θ = 90° & θ = 45°
For entire motion, y = 0 and x = R
0 = tan θ R −
g
2 vi
2
cos2 θ
R2
g
2 vi
2
cos2 θ
R2
= tan θ R
g
2 vi
2
cos2 θ
× R =
sin θ
cos θ
R =
vi
2
(2 sin θ cos θ)
g
R =
vi
2
sin 2θ
g
Thus range of the projectile is maximum if
it is projected in a direction inclined to the
horizontal at an angle of 45°.

28. Two angles of projection for the same horizontal range
The equation for horizontal range is
given by,
R =
vi
2
sin 2θ
g
R′ =
vi
2
sin 2(90° − θ)
g
Replacing θ by 90° − θ,
R′ =
vi
2
sin(180° − 2θ)
g
R′ =
vi
2
sin 2θ
g
… … . . (1)
… … . . (2)
From eq. (1) & (2) we say that,
R = R′
Thus horizontal range of projectile is same
for any two complementary angles
i.e. θ and 90° − θ.
𝑥
𝑦
o
30°
60°
R = R′

29. Equation for maximum height
The third kinematical equation for vertical
motion is,
vf𝑦
2
= viy
2
− 2 g y
At maximum height: vfy = 0 & 𝑦 = H
0 = vi sin θ 2
− 2 g H
2 g H = vi sin θ 2
H =
vi sin θ 2
2 g
This is the equation for maximum height.
Case-1: Angle of projection is 45°.
H =
vi sin 45° 2
2 g
H =
vi
2
1 2
2
2 g
⇒ Hmax =
vi
2
4 g
Case-2: Angle of projection is 90°.
H =
vi sin 90° 2
2 g
H =
vi
2
1 2
2 g
⇒ H =
vi
2
2g

30. Thank
you