Downloaded 40 times
Uploaded bysanjeev prajapati
Projecctile motion by sanjeev
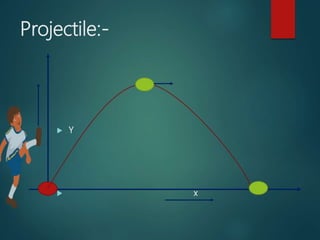
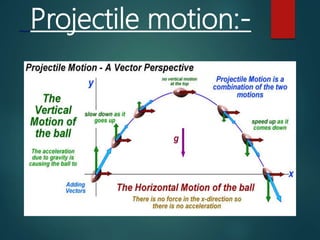
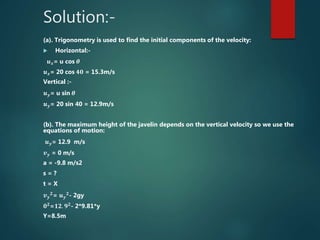
The document describes projectile motion and the key concepts involved. It defines a projectile as a particle thrown obliquely near the earth's surface that moves along a curved path. It discusses the trajectory, components of velocity and acceleration, equations of motion, time of flight, range, maximum height, and velocity of a projectile at any instant. Examples of projectile motion calculations are provided to illustrate how to determine initial velocities, maximum height, range, and the time and distance required for a bomb to hit a target from an airplane.
More Related Content
Similar to Projecctile motion by sanjeev
Projecctile motion by sanjeev
- 1.
- 2. PROJECTILE MOTION:- Whena particle is thrown obliquely near the earth’s surface it moves along a curved path, such particle is called projectile and it motion is said to be projectile motion.
- 3.
- 4. Terminology:- Point of projection:-the point on the earth from where particle is thrown . Angle of projection (𝜽):- the angle made by the velocity with x-axis is called as angle of projection. Trajectory:- the path followed by the particle is called as the trajectory.
- 5.
- 6. Sign convention:- Thevertically upward direction is taken as the positive direction of the y-axis. The vertically downward motion is taken as the negative direction of the y- axis.
- 7. Terminology:- u - initialvelocity 𝜃 − 𝑎𝑛𝑔𝑙𝑒 𝑜𝑓 𝑝𝑟𝑜𝑗𝑒𝑐𝑡𝑖𝑜𝑛 ux - horizontal velocity(m/s) uy - vertical velocity (m/s) ax-acceleration in horizontal direction ay – acceleration in vertical direction t – time in second (s) x – horizontal displacement y- vertical displacement
- 8. Component of velocityand acceleration:- 𝒖 𝒙= u cos 𝜽 𝒖 𝒚= u sin 𝜽 𝒂 𝒙= 0 m/s2 𝒂 𝒚= -g m/s2
- 9. Equation of motionfor horizontal direction:- 𝒂 𝒙= 0 m/s2 1. 𝒗 𝒙 = 𝒖 𝒙 + 𝒂 𝒙t 𝒗 𝒙 = 𝒖 𝒙=u cos 𝜽 2. x = 𝒖 𝒙t + 𝟏 𝟐 a𝒕 𝟐 x = u t cos 𝜽 t = 𝒙 𝒖𝒄𝒐𝒔𝜽 …………(1)
- 10. Equation of motionfor Vertical direction:- 𝒖 𝒚= u sin𝜽 & 𝒂 𝒚= -g m/𝒔 𝟐 1. 𝒗 𝒚= 𝒖 𝒚- gt 2. y = 𝒖 𝒚 𝒕 - 𝟏 𝟐 g𝒕 𝟐 3 𝒗 𝒚 𝟐 = 𝒖 𝒚 𝟐 - 2gy
- 11. Time of flight:- It is the total time taken for which the projectile remains in its flight. (T) y = 𝒖 𝒚 𝒕 - 𝟏 𝟐 g𝒕 𝟐 As we know that displacement along the y-axis is zero ( y = 0 ). y = ut sin𝜽 − 𝟏 𝟐 g𝒕 𝟐 => 0 => usin𝜽 = 𝟏 𝟐 gt …… (2) T= 𝟐 𝒖 𝒔𝒊𝒏𝜽 𝒈
- 12. Horizontal Range:- Itis the horizontal distance travelled by the particle during its time of flight. So, range = horizontal velocity* time of flight R = u cos𝜽 * T From equation no (1) T= 𝟐 𝒖 𝒔𝒊𝒏𝜽 𝒈 R= u cos𝜽 * 𝟐 𝐮 𝐬𝐢𝐧𝛉 𝐠 ….(3) R = 𝒖 𝟐 𝐬𝐢𝐧𝟐𝜽 𝒈
- 13. Maximum height :- It is the maximum vertical distance attained by the projectile above the horizontal plane of projection. Vertical velocity become zero at the maximum height. 𝑣 𝑦= 𝑢 𝑦- gt => 𝑣 𝑦= usin𝜃 – gt = 0 t = usin 𝜃 𝑔 ….(3) Max height= H = 𝑢 𝑦 𝑡 - 1 2 g𝑡2 Putting value of t from equation no (3) H= usin𝜃 * usin 𝜃 𝑔 - 1 2 g( usin 𝜃 𝑔 ∗ usin 𝜃 𝑔 ) ….(4) H = 𝐮 𝟐 𝐬𝐢𝐧 𝟐 𝛉 𝟐𝐠
- 14. Equation of trajectory:- We know that displacement along y-axis is Y = 𝒖 𝒚 𝒕 - 𝟏 𝟐 g𝒕 𝟐 => u sin𝜽 t - 𝟏 𝟐 g𝒕 𝟐 From equation no 1 :- t = 𝒙 𝒖𝒄𝒐𝒔𝜽 Put the value of t in above equation we get, y = u sin𝜽 ∗ 𝒙 𝒖𝒄𝒐𝒔𝜽 - 𝟏 𝟐 g( 𝒙 𝒖𝒄𝒐𝒔𝜽 ) 𝟐 On solving we get :- y = x tan𝜽 − 𝟏 𝟐 ( 𝒈 𝒖 𝟐𝒄𝒐𝒔 𝟐 𝜽 )𝒙 𝟐 ……..(5)
- 15. Velocity of theprojectile at any instant:- In projectile motion, vertical component of velocity changes but horizontal component of velocity remains always constant. Horizontal component of velocity=> 𝒖 𝒙= u cos 𝜽 Vertical component of velocity => . 𝒗 𝒚=usin𝜽 – gt The resultant velocity will be:- V= (u cos 𝜽) 𝟐+(usin𝜽 – gt ) 𝟐 Direction:- tan𝜷 = 𝒗 𝒚 𝒗 𝒙 = usin 𝜽 – gt u cos 𝜽
- 16. Numerical:- Q(1). A javelinthrower launches his javelin with an initial velocity of 20 m/s at an angle of 40 above the horizontal. a) Calculate: i. The initial horizontal velocity ii. The initial vertical velocity b) What is the maximum height the javelin will reach? c) What is the range of the javelin?
- 17. Solution:- (a). Trigonometry isused to find the initial components of the velocity: Horizontal:- 𝒖 𝒙= u cos 𝜽 𝒖 𝒙= 20 cos 𝟒𝟎 = 15.3m/s Vertical :- 𝒖 𝒚= u sin 𝜽 𝒖 𝒚= 20 sin 40 = 12.9m/s (b). The maximum height of the javelin depends on the vertical velocity so we use the equations of motion: 𝒖 𝒚= 12.9 m/s 𝒗 𝒚 = 0 m/s a = -9.8 m/s2 s = ? t = X 𝒗 𝒚 𝟐 = 𝒖 𝒚 𝟐 - 2gy 𝟎 𝟐 =𝟏𝟐. 𝟗 𝟐 - 2*9.81*y Y=8.5m
- 18. c) Therange of a projectile will depend on the time of flight. The time of flight is controlled by the vertical velocity:- Y = 𝑢 𝑦 𝑡 - 1 2 g𝑡2 0=12.9t- 1 2 *9.81*𝑡2 t=2.6sec The range of the projectile is then given by: X=v*t X=15.30*2.6 X=39.8m ….this will range of the projectile.
- 19. Question 2 The trajectoryof a projectile is represented by Y= 3𝑥 - 𝑔𝑥2 2 . then the angle of projection is (a) 30 (b) 45 (c) 60 (d) None of these
- 20. solution By comparing thecoefficient of x in given equation with standard equation y =x tan𝜃 − 1 2 ( 𝑔 𝑢2𝑐𝑜𝑠2 𝜃 )𝑥2 tan𝜃 = 3 𝜃 = 60.
- 21. Projectile given inhorizontal direction:-
- 22.
- 23. Trajectory of theprojectile:- The horizontal displacement x is governed by the equation x = ut t = 𝒙 𝒖 Vertical distance travelled by the body in time t :- y = 𝒖 𝒚 𝒕 + 𝟏 𝟐 g𝒕 𝟐 𝒖 𝒚 =0 (only horizontal velocity will be given) Y = 𝟏 𝟐 g𝒕 𝟐 = 𝟏 𝟐 g ( 𝒙 𝒖 ) 𝟐 Y=k𝒙 𝟐 ……….this also equation of parabola
- 24. Time of flight:- For vertical downward motion of the body h = 𝒖 𝒚 𝒕 + 𝟏 𝟐 g𝒕 𝟐 𝒖 𝒚 = 0 Then , T = √ 𝟐𝒉 𝒈 …… this is the time of flight.
- 25. Horizontal range:- R=horizontalvelocity* time of flight R = u*t R = u*√ 𝟐𝒉 𝒈 ….. This is the range
- 26. Questions 3 Abody is projected horizontally from the top of a tower with initial velocity 18 ms–1. It hits the ground at angle 45o. What is the vertical component of velocity when it strikes the ground (a) 9 m/s (b) 9 √2 m/s (c) 18 m/s (d) 18√ 2 m/s
- 27. solution When the bodystrikes the ground tan45 = 𝑣 𝑦 𝑣 𝑥 = 𝑣 𝑦 18 𝑣 𝑦 = 18m/s Correct answer :- (c)
- 28. Question 4 Anaeroplane is flying at a height of 1960 m in horizontal direction with a velocity of 360 km/hr. When it is vertically above the point. A on the ground, it drops a bomb. The bomb strikes a point B on the ground, then the time taken by the bomb to reach the ground is (a) 2√20 sec (b) 20 sec (c) 2 √10 sec (d) 10 sec
- 29. solution We knowthat Time of flight:- T = √ 2ℎ 𝑔 = T = √ 2∗1960 9.8 T= 20sec Correct answer :- (b)
- 30. Question 5 Abomb is dropped on an enemy post by an aeroplane flying with a horizontal velocity of 60 km/hr and at a height of 490 m. How far the aeroplane must be from the enemy post at time of dropping the bomb, so that it may directly hit the target. (g = 9.8 m/s2) (a) 100 3 m (b) 500 3 m (c) 200 3 m (d) 400 3 m
- 31. solution S= u*t S=u*√ 2ℎ 𝑔 S=60* 5 18 ∗ √ 2∗490 9.8 On solving we get, S= 500 3 m Correct answer :- (b)