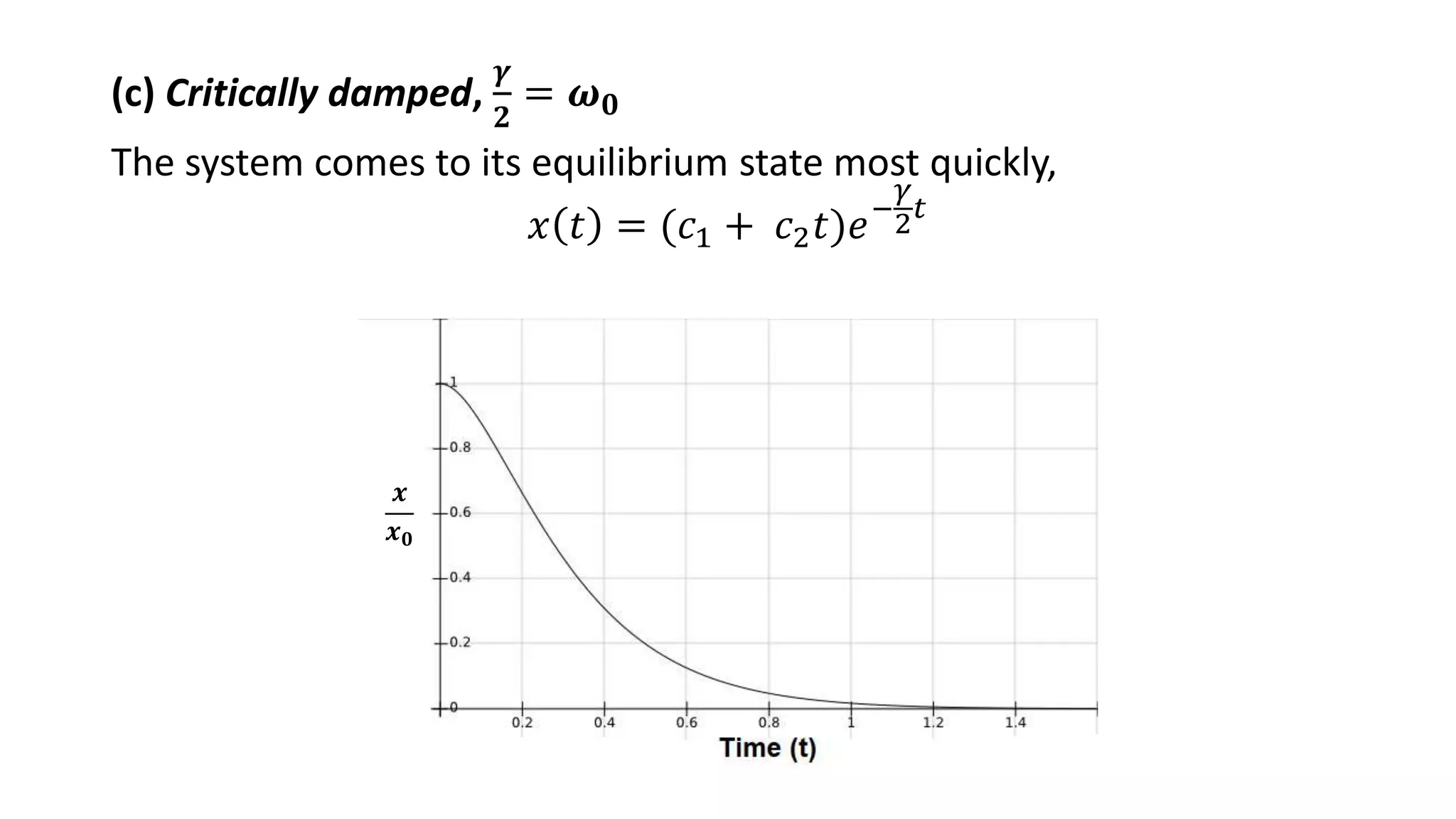
The document discusses the concepts of simple and damped harmonic oscillators, detailing their equations of motion and solutions. It categorizes damped oscillators into three types: overdamped, underdamped, and critically damped, each with distinct behavior in relation to equilibrium states. Additionally, it highlights the application of damped oscillators in systems such as car suspension.

1. Damped Harmonic
Oscillator
Kamran Ansari02–01-2018

2. Content
• Simple harmonic oscillator (SHM),
• Damped harmonic oscillator
• Over damped,
• Under damped,
• Critical damped
• Application of damped oscillator.

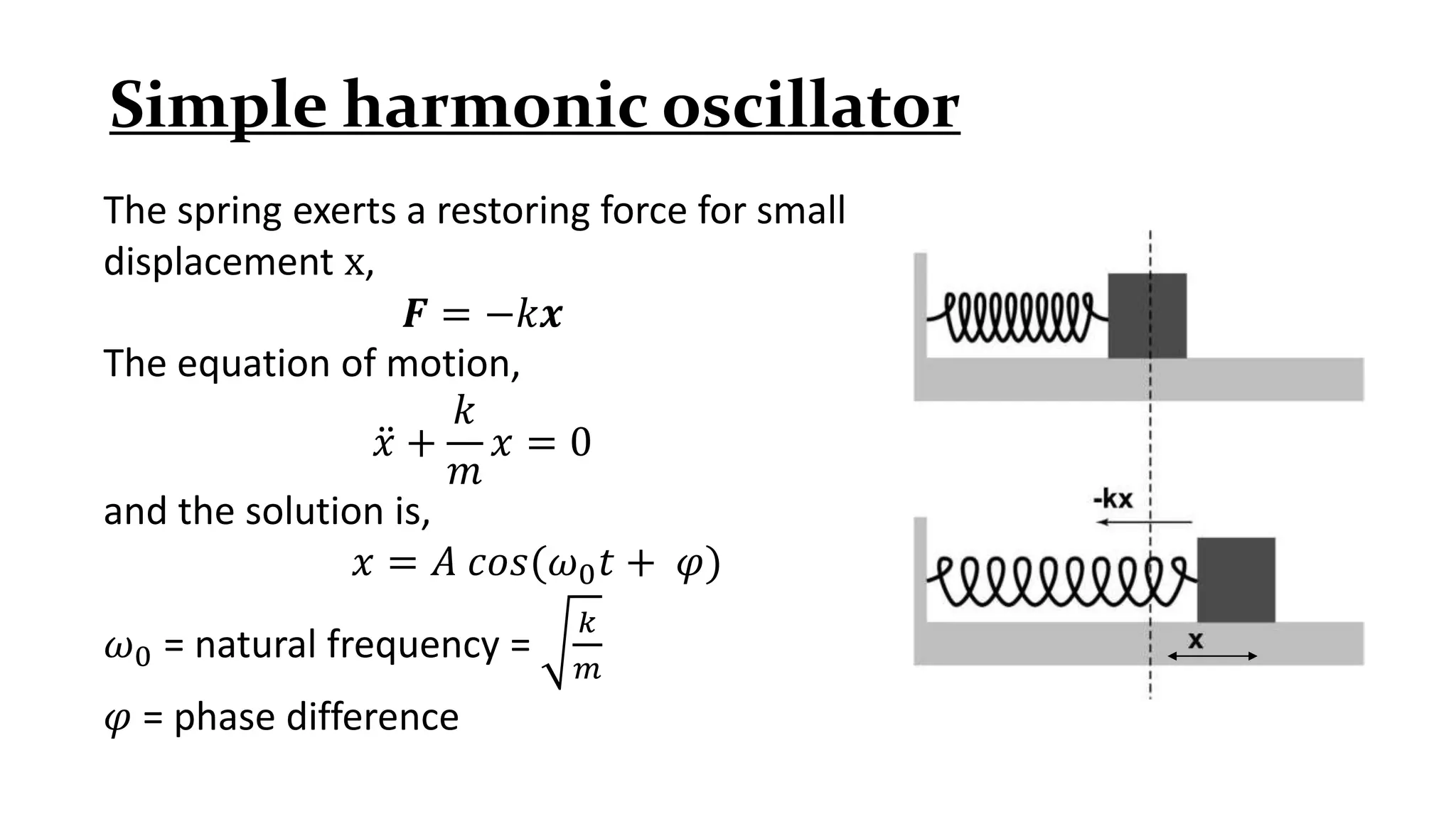
3. Simple harmonic oscillator
The spring exerts a restoring force for small
displacement x,
𝑭 = −𝑘𝒙
The equation of motion,
𝑥 +
𝑘
𝑚
𝑥 = 0
and the solution is,
𝑥 = 𝐴 𝑐𝑜𝑠(𝜔0 𝑡 + 𝜑)
𝜔0 = natural frequency =
𝑘
𝑚
𝜑 = phase difference

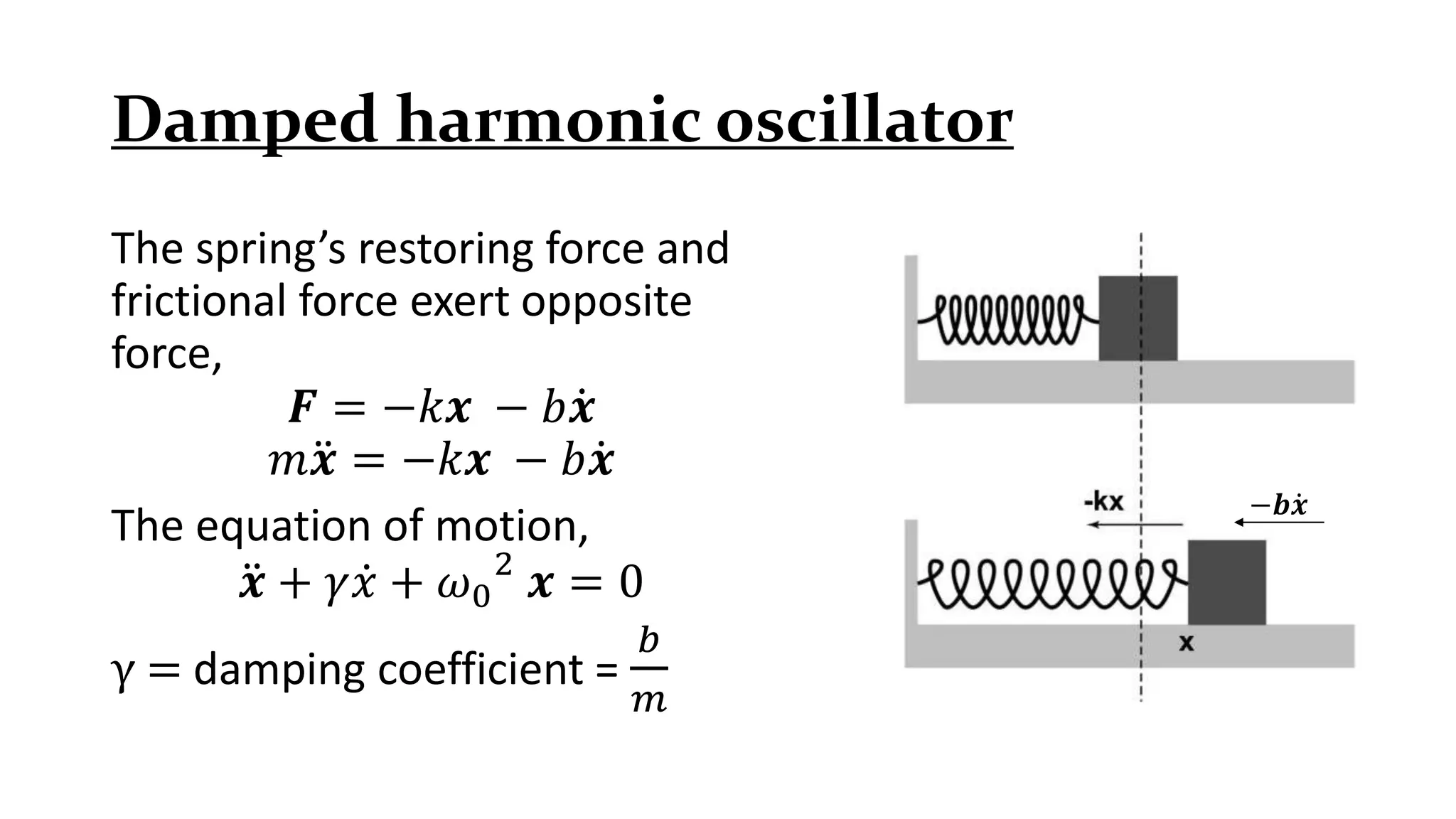
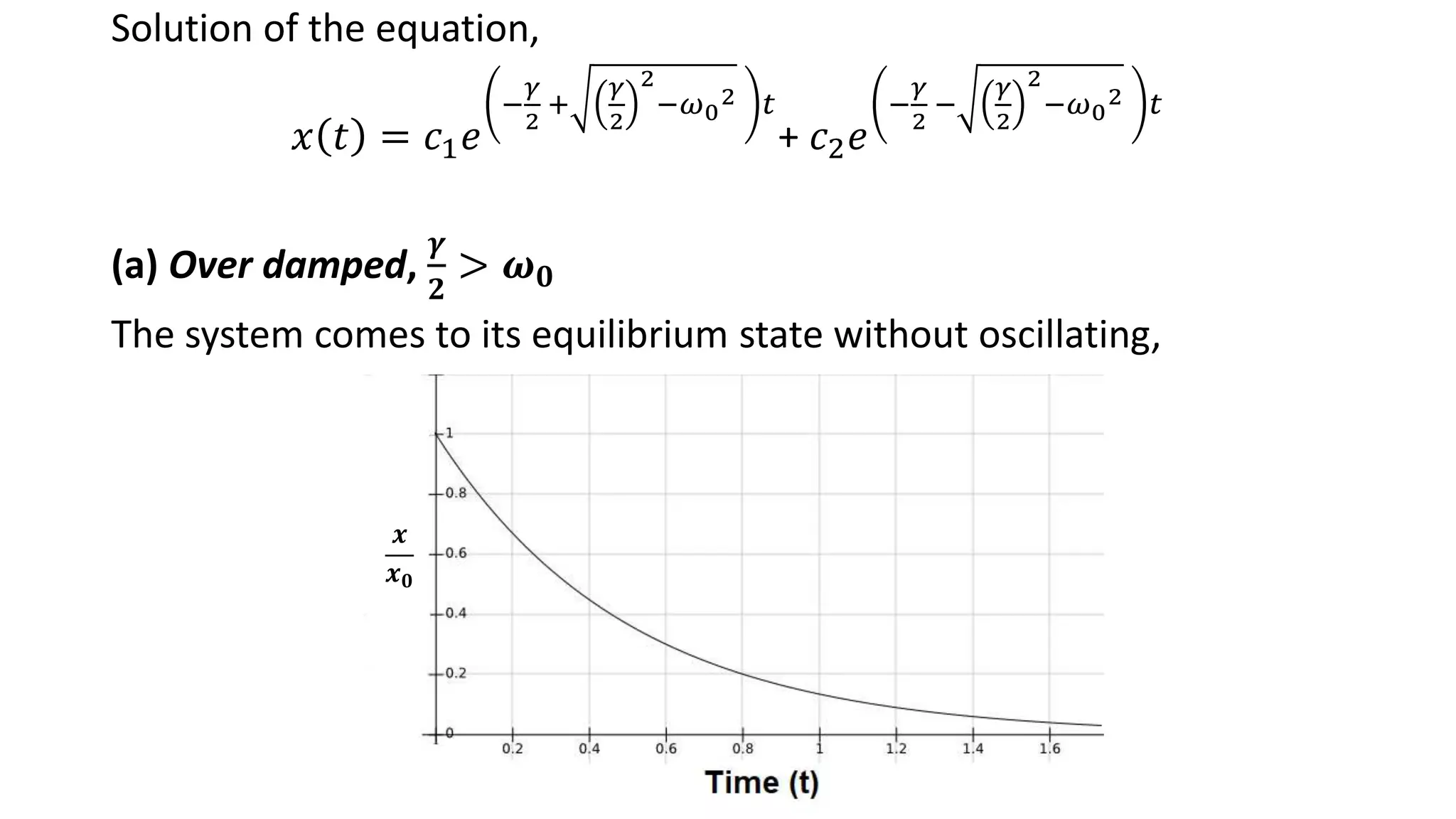
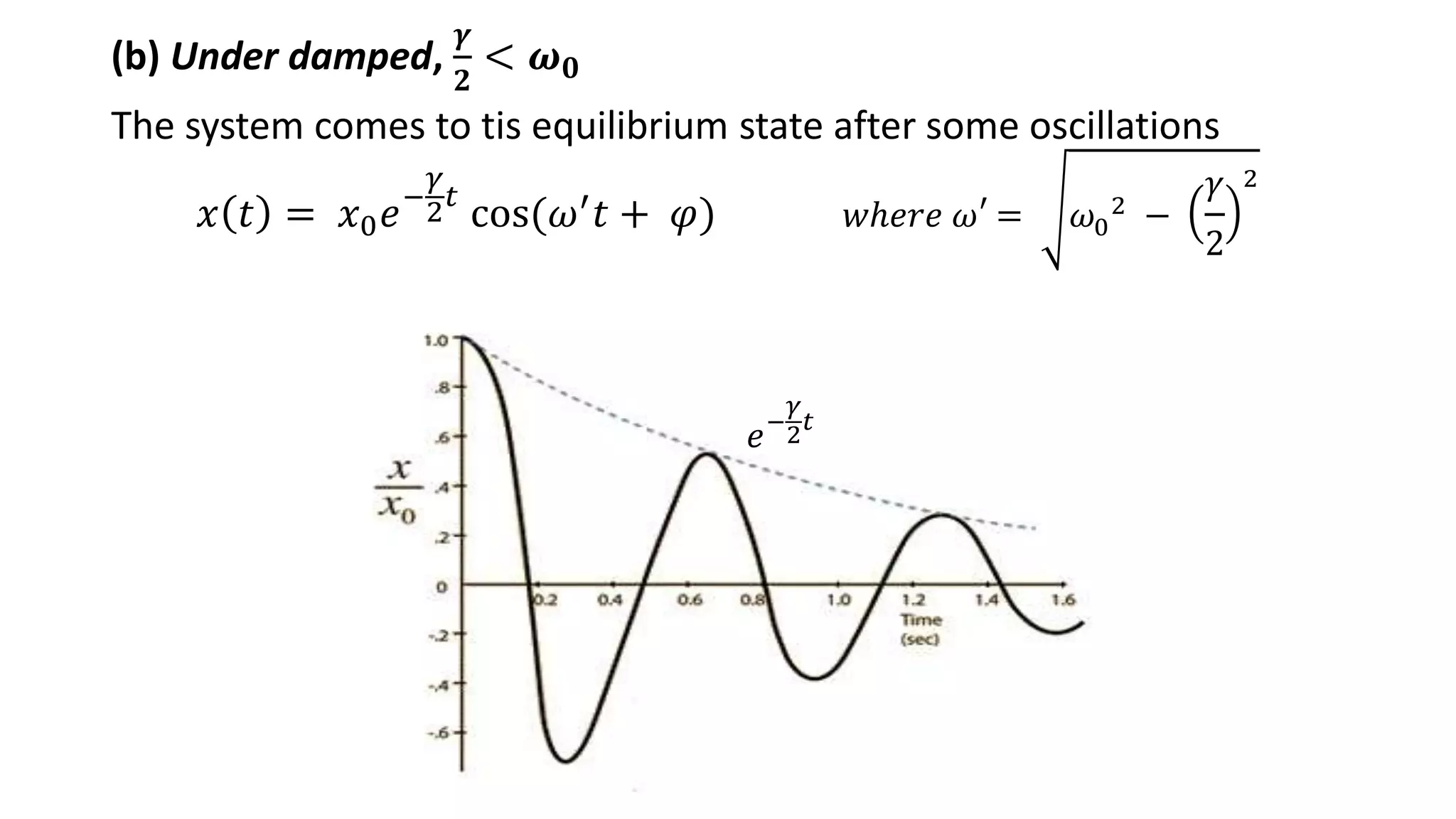
4. Damped harmonic oscillator
The spring’s restoring force and
frictional force exert opposite
force,
𝑭 = −𝑘𝒙 − 𝑏 𝒙
𝑚 𝒙 = −𝑘𝒙 − 𝑏 𝒙
The equation of motion,
𝒙 + 𝛾 𝑥 + 𝜔0
2
𝒙 = 0
γ = damping coefficient =
𝑏
𝑚
−𝒃 𝒙

5. Solution of the equation,
𝑥 𝑡 = 𝑐1 𝑒
−
𝛾
2
+
𝛾
2
2
−𝜔0
2 𝑡
+ 𝑐2 𝑒
−
𝛾
2
−
𝛾
2
2
−𝜔0
2 𝑡
(a) Over damped,
𝜸
𝟐
> 𝝎 𝟎
The system comes to its equilibrium state without oscillating,
𝒙
𝒙 𝟎

6. (b) Under damped,
𝜸
𝟐
< 𝝎 𝟎
The system comes to tis equilibrium state after some oscillations
𝑥 𝑡 = 𝑥0 𝑒−
𝛾
2
𝑡
cos(𝜔′ 𝑡 + 𝜑) 𝑤ℎ𝑒𝑟𝑒 𝜔′
= 𝜔0
2 −
𝛾
2
2
𝑒−
𝛾
2 𝑡

7. (c) Critically damped,
𝜸
𝟐
= 𝝎 𝟎
The system comes to its equilibrium state most quickly,
𝑥 𝑡 = (𝑐1 + 𝑐2 𝑡)𝑒−
𝛾
2 𝑡
𝒙
𝒙 𝟎

9. Application of Damped harmonic
oscillator
• Car suspension system

11. Thank you