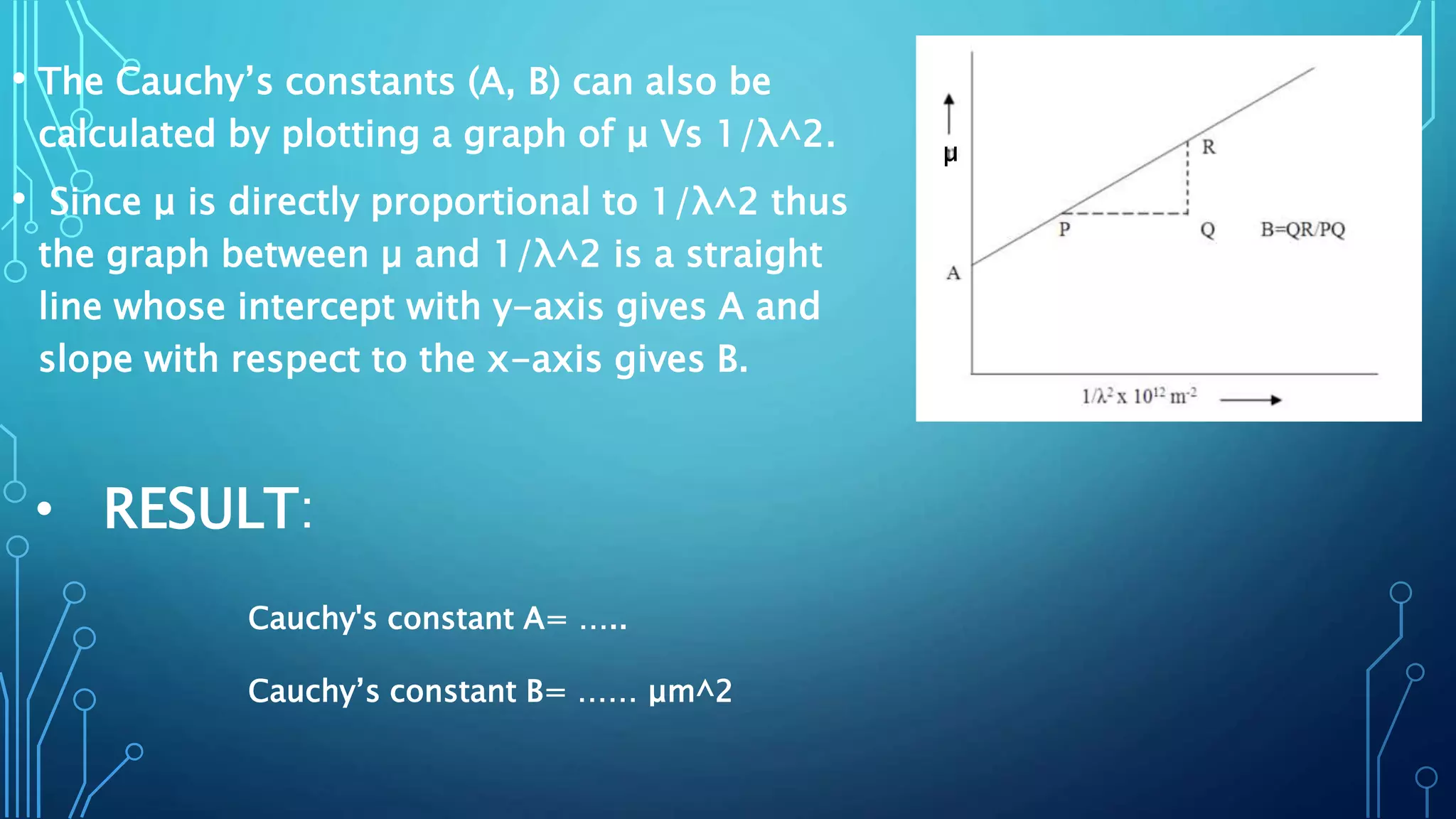
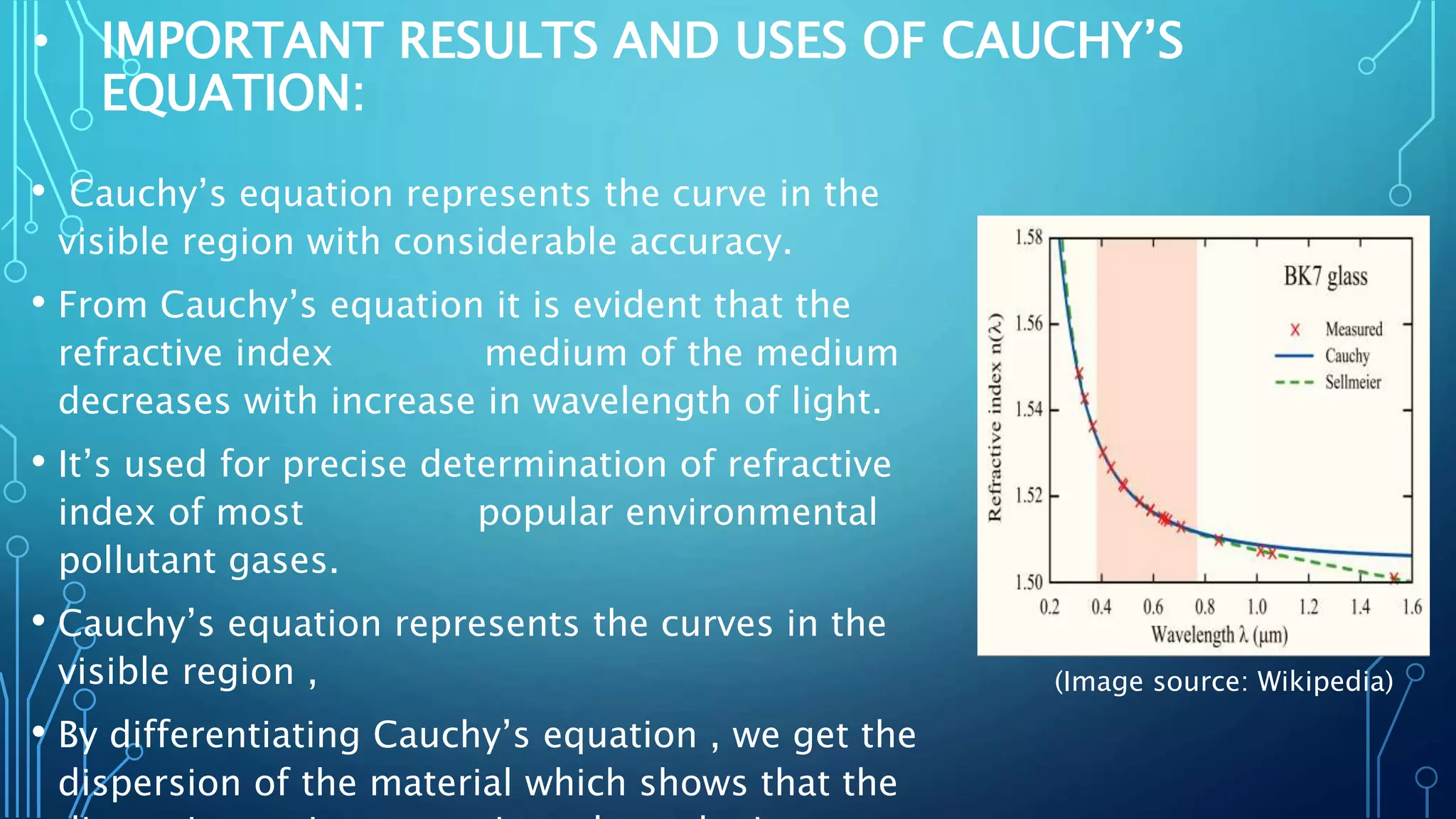
The document discusses Cauchy's constant, introduced by Augustin-Louis Cauchy, focusing on the determination of these constants through the refractive index of spectral lines using a prism spectrometer. It outlines the procedure, including the use of specific formulas and parameters, along with the results showing that Cauchy's equation accurately represents the refractive index in the visible spectrum. Limitations are noted, such as its empirical nature and inapplicability to metals and regions of anomalous dispersion.

1. CAUCHY’S CONSTANT
By- Diksha Tripathi
B.Sc (Hons)Physics
6th Semester

2. HISTORY:
• Augustin-Louis Cauchy was born on August 21,1789
in Paris.
• He was a French Mathematician ,Engineer , and
Physicist.
• He published 789 research papers.
• He defined Cauchy’s Equation in his work on spectral
theory i.e. “Cauchy Memoire” in 1836.
(Source: Wikipedia)

3. AIM: TO FIND THE VALUE OF CAUCHY’S CONSTANTS
BY DETERMINING THE REFRACTIVE INDEX OF SPECTRAL
LINES OF MERCURY SOURCE
• Apparatus:
1. Prism Spectrometer
2. Prism
3. Prism Clamp
4. Reading lens
5. Spectral lamp with spectral power supply (Prism spectrometer)

4. • FORMULA USED:
1.The most general form of Cauchy's equation is,
μ(λ)=A + B/λ^2 ​+ C/​λ^4......
• Here A, B, C, etc are material-dependent Cauchy’s constants.
• The constants have physical meaning i.e. 0< |C| < |B| <1 <A.
• To find the values of the constants, it is necessary to know values of μ for
different λ’s.
• Then equation may be set up which , when solved as simultaneous equations ,
give A,B and C.
• Since, wavelength is a very small number of the order of few hundred nano
meter we omit the higher powers of .
Thus,
Where, μ= refractive index of the material of the prism
λ =wavelength of incident light
μ(λ)=A + B​/λ^2

5. μ= Sin( (A+Dm)/2)
sin(A/2)
Where, A=angle of prism
Dm=angle of minimum deviation for different colour
of light
• Parameters of Cauchy's constant:
1. A is a dimensionless parameter: when λ  ∞
then μ  A.
2. B(μm^2) affects the curvature and the
amplitude of the refractive index for medium
wavelength in the visible region.
3. C (μm^4) affects the curvature.
(Source: Wikipedia)

6. • PROCEDURE:
1. Setting of Prism table by using spirit-level and method
of optical alignment.
2. Using Schuster’s method of focusing a spectrometer for
parallel light.
3. Measurements of angle of minimum deviation Dm and
prism angle A.
4. Using values of δm and A calculate refractive index for
different wavelengths of light.
5. Then by using Cauchy’s equation, µ and λ we can
calculate Cauchy’s constant A and B.

7. • RESULT:
• The Cauchy’s constants (A, B) can also be
calculated by plotting a graph of μ Vs 1/λ^2.
• Since μ is directly proportional to 1/λ^2 thus
the graph between µ and 1/λ^2 is a straight
line whose intercept with y-axis gives A and
slope with respect to the x-axis gives B.
Cauchy's constant A= …..
Cauchy’s constant B= …… μm^2
µ

8. • PRECAUTIONS:
1.The turn table should be properly levelled.
2.The eye piece should be focused on cross wire.
3.Both the telescope and collimator should be
focused for parallel ray.

9. • IMPORTANT RESULTS AND USES OF CAUCHY’S
EQUATION:
• Cauchy’s equation represents the curve in the
visible region with considerable accuracy.
• From Cauchy’s equation it is evident that the
refractive index medium of the medium
decreases with increase in wavelength of light.
• It’s used for precise determination of refractive
index of most popular environmental
pollutant gases.
• Cauchy’s equation represents the curves in the
visible region ,
• By differentiating Cauchy’s equation , we get the
dispersion of the material which shows that the
(Image source: Wikipedia)

10. • LIMITATIONS:
• The theoretical reasoning on which Cauchy based his equation was
later shown to be false , so that it is to be considered essentially as an
empirical equation.
• Cauchy’s formulation can not be easily applied to metals and
semiconductors.
• The equation is only valid for regions of normal dispersion in
the visible wavelength region. In the infrared, the equation becomes
inaccurate, and it cannot represent regions of anomalous dispersion.

11. • CONCLUSION:
• It’s mathematical simplicity makes it useful in some
applications.
• The “Sellmeier equation” is a later developed of Cauchy’s work
that handles anomalously dispersive region i.e.
where n is the refractive index, λ is the
wavelength, and Bi and Ci are experimentally
determined Sellmeier coefficients.

12. Thank
You!