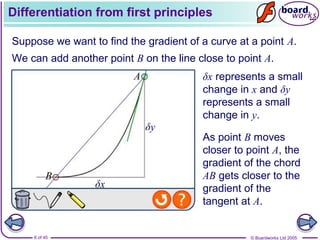
This document introduces calculus concepts like differentiation and gradients. It discusses: - Calculating the gradient of a curve at a point from two given points on the curve. - Using limits to find the gradient of a tangent line as another point on the curve approaches the point of tangency. - Differentiating polynomials from first principles by considering small changes in x and y. - Noting that the derivative of x^n is nx^{n-1} and the derivative of ax^n is anx^{n-1}. 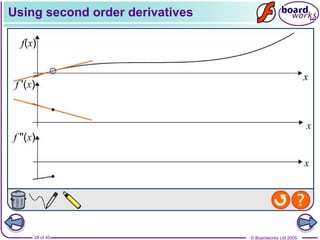- Introducing concepts like the second derivative and using derivatives to find equations of tangents and normals to curves.

1. Gradients and differentiation an
introduction to calculus
LEARNING OBJECTIVES

To work out the gradient of a curve at a given
point

To differentiate from first principles
Esbolov Baurzhan

2. CALCULUS(исчисление)

3. © Boardworks Ltd 20053 of 45
Rates of change
This graph shows the distance that a car travels over a period
of 5 seconds.
The gradient of the graph tells us the
rate at which the distance changes
with respect to time.
In other words, the gradient tells us
the speed of the car.
Gradient=градиент
change in distance
gradient = =
change in time
40
=
5
8 m/s
The car in this example is travelling at a constant speed since
the gradient is the same at every point on the graph.
time (s)
distance(m)
0 5
40

4. © Boardworks Ltd 20054 of 45
x
y
(x1, y1)
(x2, y2)
0
Finding the gradient from two given points
If we are given any two points (x1, y1) and (x2, y2) on a
line we can calculate the gradient of the line as follows:
the gradient =
change in y
change in x
x2 – x1
y2 – y1
Draw a right-angled
triangle between the two
points on the line as
follows:
y y
m
x x
−
−
2 1
2 1
the gradient, =

5. © Boardworks Ltd 20055 of 45

6. © Boardworks Ltd 20056 of 45
Differentiation from first principles
Suppose we want to find the gradient of a curve at a point A.
We can add another point B on the line close to point A.
As point B moves
closer to point A, the
gradient of the chord
AB gets closer to the
gradient of the
tangent at A.
δx represents a small
change in x and δy
represents a small
change in y.

7. © Boardworks Ltd 20057 of 45
Differentiation from first principles
We can write the gradient of the chord AB as:
change in
=
change in
y
x
y
x
δ
δ
As B gets closer to A, δx gets closer to 0 and gets closer
y
x
δ
δ
to the value of the gradient of the tangent at A.
δx can’t actually be equal to 0 because we would then have
division by 0 and the gradient would then be undefined.
Instead we must consider the limit as δx tends to 0.
This means that δx becomes infinitesimal without actually
becoming 0.

8. © Boardworks Ltd 20058 of 45
Differentiation from first principles
Let’s apply this method to a general point on the curve y = x2
.
If we let the x-coordinate of a general point A on the curve
y = x2
be x, then the y-coordinate will be x2
.
So, A is the point (x, x2
).
If B is another point close to A(x, x2
) on the curve, we can
write the coordinates of B as (x + δx, (x + δx)2
).

9. © Boardworks Ltd 20059 of 45
Differentiation from first principles
The gradient of chord AB is:
2 2
( )
=
( )
y x x x
x x x x
δ δ
δ δ
+ −
+ −
δx
δy
2 2 2
2 ( )
=
x x x x x
x
δ δ
δ
+ + −
2
2 ( )
=
x x x
x
δ δ
δ
+
(2 )
=
x x x
x
δ δ
δ
+
2
0
So for = , lim = 2
x
y
y x x
xδ
δ
δ→
= 2 +x xδ
A(x, x2
)
B(x + δx, (x + δx)2
)

10. © Boardworks Ltd 200510 of 45
The gradient function
So the gradient of the tangent to the curve y = x2
at the general
point (x, y) is 2x.
2x is often called the derived function(полученные
функции) of y = x2
.
If the curve is written using function notation as y = f(x), then
the derived function can be written as f ′(x).
So, if: f(x) = x2
This notation is useful if we want to find the gradient of f(x) at a
particular point.
For example, the gradient of f(x) = x2
at the point (5, 25) is:
f ′(5) = 2 × 5 = 10
f ′(x) = 2xThen:

11. © Boardworks Ltd 200511 of 45
Differentiating y = x3
from first principles
For the curve y = x3
, we can consider the general point A (x, x3
)
and the point B (x + δx, (x + δx)3
) a small distance away from A.
The gradient of chord AB is then:
3 3
( )
=
( )
y x x x
x x x x
δ δ
δ δ
+ −
+ −
3 2 2 3 3
3 3 ( ) ( )
=
x x x x x x x
x
δ δ δ
δ
+ + + −
2 2 3
3 3 ( ) ( )
=
x x x x x
x
δ δ δ
δ
+ +
2 2
(3 3 ( ) )
=
x x x x x
x
δ δ δ
δ
+ +
2 2
= 3 3 ( )x x x xδ δ+ +
3 2
0
So for = , lim = 3
x
y
y x x
xδ
δ
δ→

12. © Boardworks Ltd 200512 of 45
The gradient of y = x3
So, the gradient of the tangent to the curve y = x3
at the
general point (x, y) is 3x2
.
So if, f(x) = x3
What is the gradient of the tangent to the
curve f(x) = x3
at the point (–2, –8)?
f ′(x) = 3x2
f ′(–2) = 3(–2)2
= 12
Explain why the gradient of f(x) = x3
will always be positive.
f ′(x) = 3x2
Then:

13. © Boardworks Ltd 200513 of 45
Using the notation
We have shown that for y = x3
dy
dx
represents the derivative of y with respect to x.
dy
dx
2
0
lim = 3
x
y
x
xδ
δ
δ→
0
lim
x
y
xδ
δ
δ→
is usually written as .
dy
dx
So if y = x3
of the tangent.
Remember, is the gradient of a chord, while is the gradient
y
x
δ
δ
dy
dx
2
= 3
dy
x
dx
then:

14. © Boardworks Ltd 200514 of 45
Using the notation dy
dx
This notation can be adapted for other variables so, for
example:
Also, if we want to differentiate 2x4
with respect to x, for
example, we can write:
represents the derivative of s with respect to t.
ds
dt
We could work this out by differentiating from first principles,
but in practice this is unusual.
4
(2 )
d
x
dx
If s is distance and t is time then we can interpret this as the
rate of change in distance with respect to time. In other words,
the speed.

15. © Boardworks Ltd 200515 of 45
Contents
© Boardworks Ltd 200515 of 45
Rates of change
The gradient of the tangent at a point
The gradient of the tangent as a limit
Differentiation of polynomials
Second order derivatives
Tangents and normals
Examination-style questions
Differentiation of polynomials

16. © Boardworks Ltd 200516 of 45
Differentiation
If we continued the process of differentiating from first
principles we would obtain the following results:
y
dy
dx
x x2
x3
x4
x5
x6
What pattern do you notice?
In general:
1
If thenn ndy
y x nx
dx
−
= =
and when xn
is preceded by a constant multiplier a we have:
1 2x 3x2
4x3
5x4
6x5
1
If = then =n ndy
y ax anx
dx
−

17. © Boardworks Ltd 200517 of 45
y
x0
Differentiation
For example, if y = 2x4
4 1
= 2×4 =
dy
x
dx
− 3
8x
Suppose we have a function of the form y = c, where c is a
constant number.
This corresponds to a horizontal line through the point (0, c).
c
The gradient of this line is always
equal to 0.
∴ If y = c
= 0
dy
dx

18. © Boardworks Ltd 200518 of 45
Differentiation
Find the gradient of the curve
y = 3x4
at the point (–2, 48).
Differentiating:
3
=12
dy
x
dx
At the point (–2, 48) x = –2 so:
3
=12( 2)
dy
dx
−
=12 × 8−
= 96−
The gradient of the curve y = 3x4
at the point (–2, 48) is –96.

19. © Boardworks Ltd 200519 of 45
Differentiating polynomials
Suppose we want to differentiate a polynomial function.
For example:
If = ( )± ( ) then = '( )± '( )
dy
y f x g x f x g x
dx
Differentiate y = x4
+ 3x2
– 5x + 2 with respect to x.
In general, if y is made up of the sum or difference of any given
number of functions, its derivative will be made up of the
derivative of each of the functions.
We can differentiate each term in the function to give .
dy
dx
4x3
+ 6x – 5=
dy
dx
So:

20. © Boardworks Ltd 200520 of 45
Differentiating polynomials
Find the point on y = 4x2
– x – 5 where the gradient is 15.
= 8 1
dy
x
dx
−
=15
dy
dx
when 8x – 1 = 15
8x = 16
x = 2
We now substitute this value into the equation y = 4x2
– x – 5
to find the value of y when x = 2
y = 4(2)2
– 2 – 5
The gradient of y = 4x2
– x – 5 is 15 at the point (2, 9).
= 9

21. © Boardworks Ltd 200521 of 45
Differentiating polynomials
In some cases, a function will have to be written as separate
terms containing powers of x before differentiating.
For example:
Given that f(x) = (2x – 3)(x2
– 5) find f ′(x).
Expanding: f(x) = 2x3
– 3x2
– 10x + 15
f ′(x) = 6x2
– 6x –10
Find the gradient of f(x) at the point (–3, –36).
When x = –3 we have f ′(–3) = 6(–3)2
– 6(–3) –10
= 54 + 18 – 10
= 62

22. © Boardworks Ltd 200522 of 45
Differentiating polynomials
312
2= + 2
dy
x
dx
= 6x3
+ 2
5 2
3 + 4 8
Differentiate = with respect to .
2
x x x
y x
x
−
5 2
3 4 8
= +
2 2 2
x x x
y
x x x
−
43
2= + 2 4y x x −
We can now differentiate:
= 2(3x3
+ 1)

23. © Boardworks Ltd 200523 of 45
Differentiating axn
for all rational n
This is true for all negative or fractional values of n.
For example:
1
If = then =n ndy
y ax anx
dx
−
2
Differentiate = with respect to .y x
x
Start by writing this as y = 2x–1
So:
1 1
= 1 × 2
dy
x
dx
− −
−
2
= 2x−
−
2
=
2
x
−

24. © Boardworks Ltd 200524 of 45
Differentiating axn
for all rational n
Differentiate = 4 with respect to .y x x
So:
1
2
11
2= × 4
dy
x
dx
−
1
2
= 2x
−
=
2
x
Start by writing this as
1
2
= 4y x
Remember, in some cases, a function will have to be written as
separate terms containing powers of x before differentiating.

25. © Boardworks Ltd 200525 of 45
Differentiating axn
for all rational n
2
Given that ( ) = (1+ ) find '( ).f x x f x
( ) = (1+ )(1+ )f x x x
=1+ 2 +x x
1
2
=1+ 2 +x x
1
2
'( ) = +1f x x
−
=
1
+1
x

26. © Boardworks Ltd 200526 of 45
Contents
© Boardworks Ltd 200526 of 45
Rates of change
The gradient of the tangent at a point
The gradient of the tangent as a limit
Differentiation of polynomials
Second order derivatives
Tangents and normals
Examination-style questions
Second order derivatives

27. © Boardworks Ltd 200527 of 45
Second order derivatives
Differentiating a function y = f(x) gives us the derivative
dy
dx
or f ′(x)
Differentiating the function a second time gives us the second
order derivative. This can be written as
2
2
d y
dx
or f ′′(x)
The second order derivative gives us the rate of change of the
gradient of a function.
We can think of it as the gradient of the gradient.

28. © Boardworks Ltd 200528 of 45
Using second order derivatives

29. © Boardworks Ltd 200529 of 45
Contents
© Boardworks Ltd 200529 of 45
Rates of change
The gradient of the tangent at a point
The gradient of the tangent as a limit
Differentiation of polynomials
Second order derivatives
Tangents and normals
Examination-style questions
Tangents and normals

30. © Boardworks Ltd 200530 of 45
Tangents and normals
Remember, the tangent to a curve at a point is a straight line
that just touches the curve at that point.
The normal to a curve at a point is a straight line that is
perpendicular to the tangent at that point.
We can use differentiation to find the equation of the tangent
or the normal to a curve at a given point. For example:
Find the equation of the tangent and the normal
to the curve y = x2
– 5x + 8 at the point P(3, 2).

31. © Boardworks Ltd 200531 of 45
Tangents and normals
y = x2
– 5x + 8
= 2 5
dy
x
dx
−
At the point P(3, 2) x = 3 so:
= 2(3) 5 =
dy
dx
− 1
The gradient of the tangent at P is therefore 1.
Using y – y1 = m(x – x1), give the equation of the tangent at the
point P(3, 2):
y – 2 = x – 3
y = x – 1

32. © Boardworks Ltd 200532 of 45
Tangents and normals
The normal to the curve at the point P(3, 2) is perpendicular to
the tangent at that point.
Using y – y1 = m(x – x1) give the equation of the tangent at the
point P(3, 2):
The gradient of the tangent at P is 1 and so the gradient of the
normal is –1.
2 = ( 3)y x− − −
+ 5 = 0y x −

33. © Boardworks Ltd 200533 of 45
Contents
© Boardworks Ltd 200533 of 45
Rates of change
The gradient of the tangent at a point
The gradient of the tangent as a limit
Differentiation of polynomials
Second order derivatives
Tangents and normals
Examination-style questions
Examination-style questions

34. © Boardworks Ltd 200534 of 45
Examination-style question
The curve f(x) = x2
+ 2x – 8 cuts the x-axes at the points A(–a,
0) and B(b, 0) where a and b are positive integers.
a) Find the coordinates of points A and B.
b) Find the gradient function of the curve.
c) Find the equations of the normals to the curve at points A
and B.
d) Given that these normals intersect at the point C, find the
coordinates of C.
a) The equation of the curve can be written in factorized form
as y = (x + 4)(x – 2) so the coordinates of A are (–4, 0) and
the coordinates of B are (2, 0).

35. © Boardworks Ltd 200535 of 45
Examination-style question
b) f(x) = x2
+ 2x – 8 ⇒ f’(x) = 2x + 2
c) At (–4, 0) the gradient of the curve is –8 + 2 = –6
Using y – y1 = m(x – x1), the equation of the normal at (–4, 0) is:
∴ The gradient of the normal at (–4, 0) is .1
6
y – 0 = (x + 4)
1
6
16y = x + 4
At (2, 0) the gradient of the curve is 4 + 2 = 6
Using y – y1 = m(x – x1), the equation of the normal at (2, 0) is:
∴ The gradient of the normal at (2, 0) is – .1
6
y – 0 = – (x – 2)1
6
26y = 2 – x

36. © Boardworks Ltd 200536 of 45
Examination-style question
x + 4 = 2 – x
d) Equating and :1 2
2x = –2
x = 1
When x = –1, y = . So the coordinates of C are (–1, ).
1
2
1
2