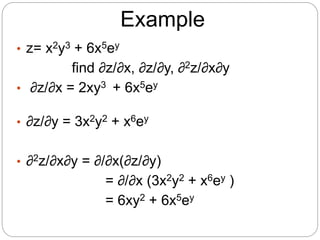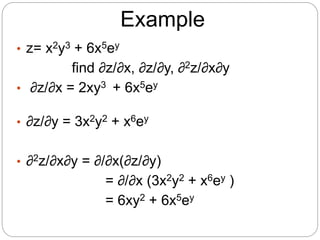
Partial derivatives are used to calculate the rate of change of a function of two or more variables with respect to one variable, while holding the other variables constant. The partial derivative of z with respect to x, denoted ∂z/∂x, is defined as the limit of the difference quotient as Δx approaches 0, while holding y constant. Similarly, the partial derivative of z with respect to y, denoted ∂z/∂y, is defined as the limit of the difference quotient as Δy approaches 0, while holding x constant. Notations for higher order partial derivatives are also introduced. An example problem finds the first and second order partial derivatives of the function z=x^2y^3+6

2. Partial Derivatives
BY:- Aman Singh
R.no. 3
1st Sem Mechanical

3. What is Partial Derivative
 Let z = f(x,y) be function of two individual
variables x and y the derivative with respect
to x keeping y constant is called Partial
derivative of z with respect to x.
 It is denoted by ∂z/∂x, ∂f/∂x, fx………
 It is defined as
∂z/∂x = lim f(x+ ∂x ,y)- f(x,y)/ ∂x
∂x→0
x f

4. Contd……
 Similarly the Partial Derivative of z w.r.t y
keeping x as a constant is denoted by
∂z/∂y, ∂f/∂y, fy………. and it is
defined as
∂z/∂y = lim f(x, y+ ∂y) – f(x, y)/
∂y
∂y→0

5. Meaning of ∂f/∂x
 Partial Derivative of f w.r.t x provided
that f is function of two or more than two
variable.
f




( ) ( )
xx yy
f
f
f




xy yx
y x
x
y
f
f




x y
f
f
y


x
f
y
f
y
y
f
x
f
x
x

 



 












2 2
2
2
2
2
( ) ( )

6. Notations
• ∂z/∂x = p ∂z/ ∂x = q
• ∂2z/∂x2 = r ∂2z/∂x∂y = s
• ∂2z/∂y2 = t

7. Example
• z= x2y3 + 6x5ey
find ∂z/∂x, ∂z/∂y, ∂2z/∂x∂y
• ∂z/∂x = 2xy3 + 6x5ey
• ∂z/∂y = 3x2y2 + x6ey
• ∂2z/∂x∂y = ∂/∂x(∂z/∂y)
= ∂/∂x (3x2y2 + x6ey )
= 6xy2 + 6x5ey