This document discusses Galois theory and provides illustrations of the main theorem of Galois theory. It begins with an outline and introduction. The main theorem of Galois theory establishes a one-to-one correspondence between subgroups of the Galois group of a finite normal extension and intermediate fields. The document then provides examples illustrating this theorem for various polynomials and extensions. It concludes with problems related to Galois groups and extensions.

1. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
GALOIS THEORY
Shinoj K.M.
Department of Mathematics
St.Joseph’s College,Devagiri
Kozhikode-8
shinusaraswathy@gmail.com
26 June 2019, Wednesday
Shinoj K.M. Department of MathematicsGALOIS THEORY

2. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Plan of Action
1 RESUME
2 MAIN THEOREM OF GALOIS THEORY
3 ILLUSTRATIONS
4 MORE ILLUSTRATIONS
5 CYCLOTOMIC EXTENSION
Shinoj K.M. Department of MathematicsGALOIS THEORY

3. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Let F ≤ E ≤ F, α ∈ E, and let β be a conjugate of α over
F. Then there is an isomorphism ψα,β mapping F(α) onto
F(β) that leaves F fixed and maps α onto β.
If F ≤ E ≤ F, α ∈ E, then an automorphism σ of F that
leaves F fixed must map α onto some conjugate of α over
F.
If F ≤ E,the collection of all automorphisms of E leaving
F fixed forms a group G(E/F). For any subset S of
G(E/F),the set of all elements of E left fixed by all
elements of S is a field ES. Also, F ≤ EG(E/F)
Shinoj K.M. Department of MathematicsGALOIS THEORY

4. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
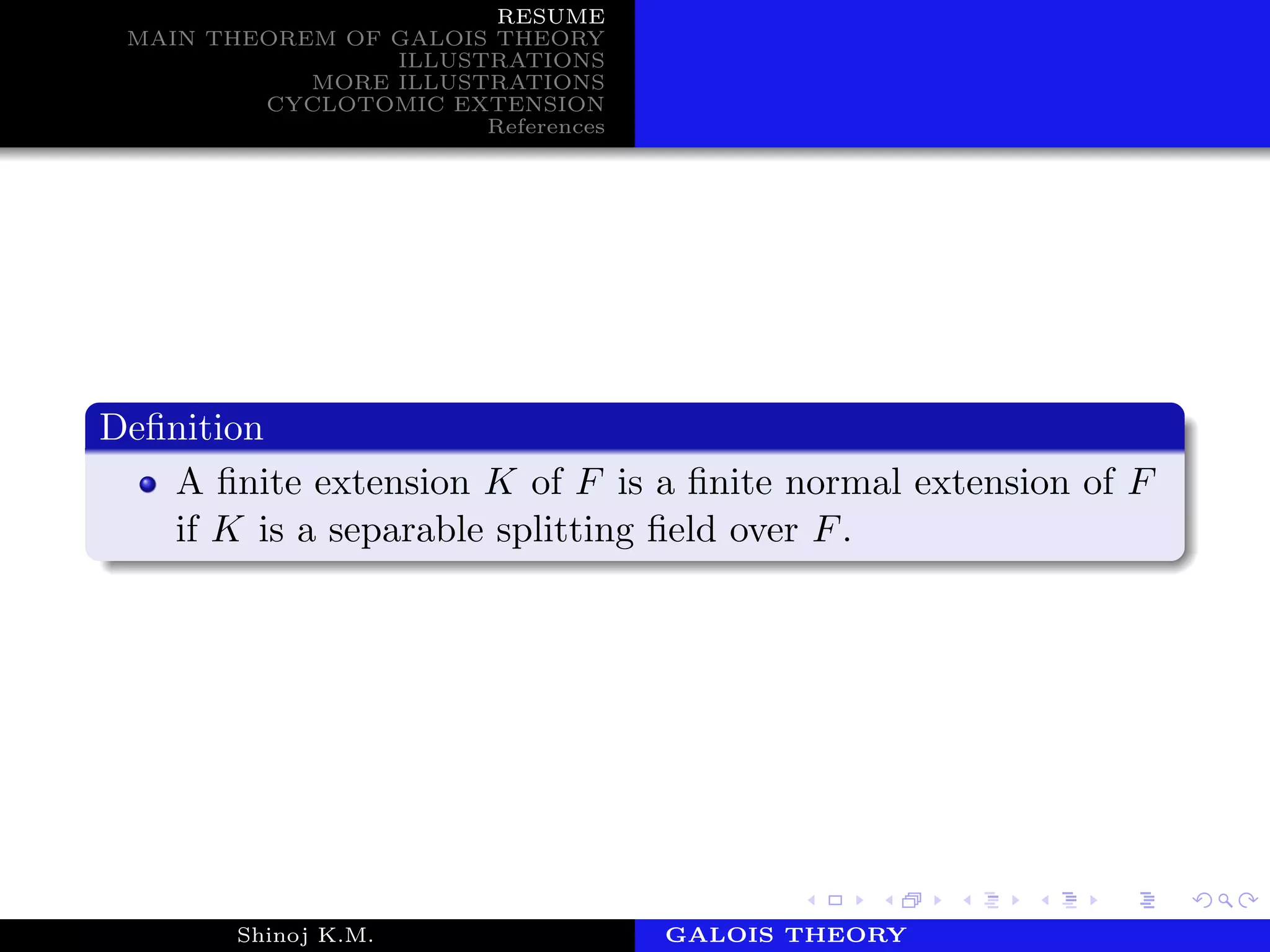
A field E, F ≤ E ≤ F, is a splitting field over F if and only
if every isomorphism of E onto a subfield of F leaving F
fixed is an automorphism on E.
If E is a finite extension and a splitting field over F, then
|G(E/F)| = {E : F}
If E is a finite extension of F,then {E : F} divides [E : F].
If E is also separable over F,then {E : F} = [E : F]
Also, E is separable over F if and only if irr(α, F) has all
zeros of multiplicity 1 for every α ∈ E.
If E is a finite extension of F and is a separable splitting
field over F,then |G(E/F)| = {E : F} = [E : F].
Shinoj K.M. Department of MathematicsGALOIS THEORY

5. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Definition
A finite extension K of F is a finite normal extension of F
if K is a separable splitting field over F.
Shinoj K.M. Department of MathematicsGALOIS THEORY

6. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Definition
If K is a finite normal extension of F then G(K/F)is the
Galois group of K over F.
Shinoj K.M. Department of MathematicsGALOIS THEORY

7. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Main Theorem of Galois Theory
Let K be a finite normal extension of a field F, with Galois
group G(K/F). For a field E,where F ≤ E ≤ K,let λ(E) be the
subgroup of G(K/F) leaving E fixed. Then λ is a one-to-one
map of the set of all such intermediate fields E onto the set of
all subgroups of G(K/F). The following properties hold for λ:
E = KG(K/E) = Kλ(E)
For H ≤ G(K/F), λ(KH) = H
[K : E] = |λ(E)|, [E : F] = {G(K/F) : λ(E)}, the number
of left cosets of λ(E) in G(K/F)
E is a normal extension of F if and only if λ(E) is a
normal subgroup of G(K/F) . When λ(E) is a normal
subgroup of G(K/F), then G(E/F) G(K/F)/G(K/E).
The diagram of subgroups of G(K/F) is the inverted
diagram of intermediate fields of K over F.
Shinoj K.M. Department of MathematicsGALOIS THEORY

8. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
What is the moral of the story?
For a finite normal extension K of a field F, there is a
one-to-one correspondence between the subgroups of
G(K/F) and the intermediate fields E, where F ≤ E ≤ K.
This correspondence associates with each intermediate field
E the subgroup G(K/E).
We associate each subgroup H of G(K/F) its fixed field
KH.
Shinoj K.M. Department of MathematicsGALOIS THEORY

9. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Galois group over finite fields are cyclic.
Let K be a finite extension of degree n of a finite field F of
pr elements.Then G(K/F) is cyclic of degree n and is
generated by σpr , where for α ∈ K, σpr (α) = αpr
Shinoj K.M. Department of MathematicsGALOIS THEORY

10. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Group of a polynomial
If f(x) ∈ F[x] is such that every irreducible factor of f(x)
is separable over F, then the splitting field K of f(x) over
F is a normal extension of F. The Galois grup G(K/F) is
the group of the polynomial f(x) over F.
Shinoj K.M. Department of MathematicsGALOIS THEORY

11. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Illustrations
Illustrate the main theorem of Galois theory with F = Q
and K = Q(
√
2).
Illustrate the main theorem of Galois theory with F = Q
and K = Q(
√
2,
√
3).
Illustrate the main theorem of Galois theory with F = Q
and K = the splitting field of x3 − 2 over Q.
Illustrate the main theorem of Galois theory with F = Zp
and K = GF(p12).
Shinoj K.M. Department of MathematicsGALOIS THEORY

12. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Problems
Describe the group of the polynomial x4 − 1 ∈ Q[x] over Q.
Give the order and describe a generator of the group
G(GF(729)/GF(9))
Describe the group of the polynomial x4 − 5x2 + 6 ∈ Q[x]
over Q.
Describe the group of the polynomial x3 − 1 ∈ Q[x] over Q.
Give an example of two finite normal extensions K1 and
K2 of the same field F such that K1 and K2 are not
isomorphic fields, but G(K1/F) ≡ G(K2/F).
Shinoj K.M. Department of MathematicsGALOIS THEORY

13. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Example 1
Consider the splitting field in C of x4 + 1 over Q. Now x4 + 1 is
irreducible over Q. The zeros of x4 + 1 are (1 ± i)/
√
2 and
(−1 ± i)/
√
2. If α = 1+i√
2
, then α3 = −1+i√
2
, α5 = −1−i√
2
, α7 = 1−i√
2
.
Thus the splitting field K of x4 + 1 over Q is Q(α) and
[K : Q] = 4
Shinoj K.M. Department of MathematicsGALOIS THEORY

14. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Since there exist automorphisms of Kmapping α onto each
conjugate of α, and since an automorphism σ of Q(α) is
completely determined by σ(α), we see that the four
automorphisms of G(K/Q) are as follows.
σ1 σ3 σ5 σ7
α → α α3 α5 α7
G(K/Q) is isomorphic to the Klein 4-group.
Shinoj K.M. Department of MathematicsGALOIS THEORY

15. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
To find K{σ1,σ3}, it is only necessary to find an element of K
not in Q left fixed by {σ1, σ3}, since [K{σ1,σ3} : Q] = 2
Clearly σ1(α) + σ3(α) is left fixed by both σ1 and σ3,since
{σ1, σ3} is a group.
We have σ1(α) + σ3(α) = α + α3 = i
√
2
So K{σ1,σ3} = Q(i
√
2)
Shinoj K.M. Department of MathematicsGALOIS THEORY

16. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
To find K{σ1,σ7}, it is only necessary to find an element of K
not in Q left fixed by {σ1, σ7}, since [K{σ1,σ7} : Q] = 2
Clearly σ1(α) + σ7(α) is left fixed by both σ1 and σ7,since
{σ1, σ7} is a group.
We have σ1(α) + σ7(α) = α + α7 =
√
2
So K{σ1,σ7} = Q(
√
2)
Shinoj K.M. Department of MathematicsGALOIS THEORY

17. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
To find K{σ1,σ5}, it is only necessary to find an element of K
not in Q left fixed by {σ1, σ5}, since [K{σ1,σ5} : Q] = 2
Clearly σ1(α).σ5(α) is left fixed by both σ1 and σ5, since
{σ1, σ5} is a group.
We have σ1(α).σ5(α) = α.α5 = −i
So K{σ1,σ5} = Q(−i) = Q(i)
Shinoj K.M. Department of MathematicsGALOIS THEORY

18. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Example 2
Consider the splitting field in C of x4 − 2 over Q. Now x4 − 2 is
irreducible over Q, by Eisenstein’s criterion, with p = 2.Let
α = 4
√
2be the real positive zero of x4 − 2. Then the four zeros
of x4 − 2 in C are α, −α, iα and −iα. The splitting field K of
x4 − 2 over Q thus contains (iα)/α = i. Since α is a real
number,Q(α) ≤ R,so Q(α) = K. However, since Q(α, i)
contains all zeros of x4 − 2, we see that Q(α, i) = K.
Shinoj K.M. Department of MathematicsGALOIS THEORY

19. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Let E = Q(α). Now,{1, α, α2, α3} is a basis for E over Q and
{1, i} is a basis K over E. Thus {1, α, α2, α3, i, iα, iα2, iα3} is a
basis for K over Q.
Shinoj K.M. Department of MathematicsGALOIS THEORY

20. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
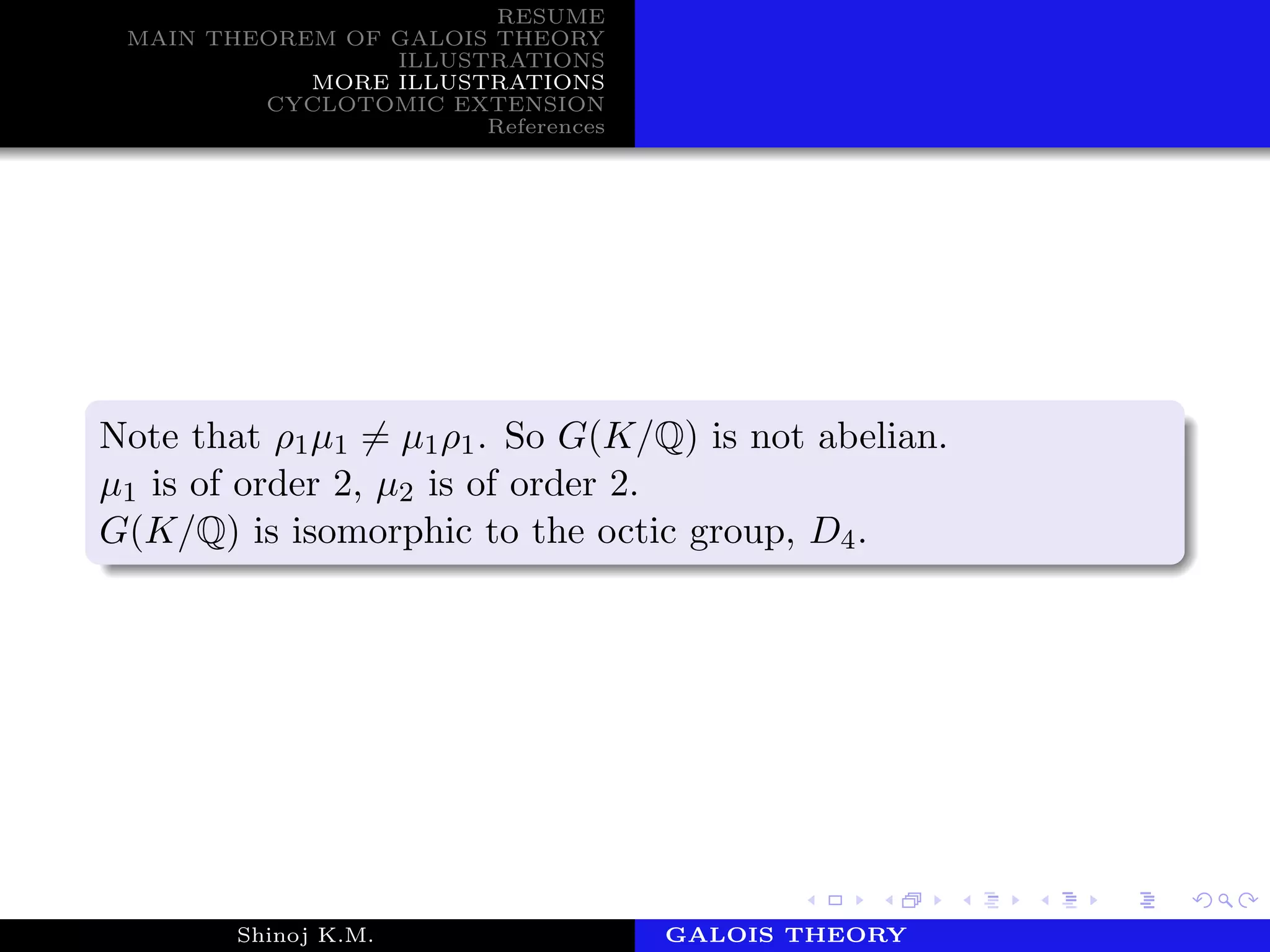
Since [K : Q] = 8, we must have G(K/Q) = 8, so we need to
find eight automorphisms of K leaving Q fixed. Any such
automorphism σ is completely determined by its values on
elements of the basis {1, α, α2, α3, i, iα, iα2, iα3}, and these
values are in turn determined by σ(α) and σ(i).
Shinoj K.M. Department of MathematicsGALOIS THEORY

21. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
But σ(α) must always be a conjugate of α over Q,that is, one of
the four zeros of irr(α, Q) = x4 − 2. Likewise, σ(i) must be a
zero of irr(i, Q) = x2 + 1. The the four possibilities for
σ(α),combined with the two possibilities for σ(i), must give all
eight automorphisms.
Shinoj K.M. Department of MathematicsGALOIS THEORY

22. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
The eight automorphisms of G(K/Q)
ρ0 ρ1 ρ2 ρ3 µ1 δ1 µ2 δ2
α → α iα −α −iα α iα −α −iα
i → i i i i −i −i −i −i
Shinoj K.M. Department of MathematicsGALOIS THEORY

23. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Note that ρ1µ1 = µ1ρ1. So G(K/Q) is not abelian.
µ1 is of order 2, µ2 is of order 2.
G(K/Q) is isomorphic to the octic group, D4.
Shinoj K.M. Department of MathematicsGALOIS THEORY

24. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Definition
The splitting field of xn − 1 over F is the nth cyclotomic
extension of F.
Shinoj K.M. Department of MathematicsGALOIS THEORY

25. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Definition
The polynomial Φn(x) = Π (x − αi) where the αi are the
primitive nth roots of unity in F, is the nth cyclotomic
polynomial over F.
Shinoj K.M. Department of MathematicsGALOIS THEORY

26. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Theorem
The Galois group of the nth cyclotomic extension of Q has
φ(n) elements and is isomorphic to the group Gn of all
positive integers less than n and relatively prime to n under
multiplication modulo n.
Shinoj K.M. Department of MathematicsGALOIS THEORY

27. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Corollary
The Galois group of the pth cyclotomic extension of Q for
prime p is cyclic of order p − 1.
Shinoj K.M. Department of MathematicsGALOIS THEORY

28. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Problems
Find the cyclotomic polynomials
Φ1(x), Φ2(x).Φ3(x), Φ4(x), Φ5(x), Φ6(x), Φ7(x), and Φ8(x)
over Q.
Find Φ3(x) over Z2.
Find Φ8(x) over Z3.
Shinoj K.M. Department of MathematicsGALOIS THEORY

29. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
Problems
Classify the group of the polynomial x10 − 1 ∈ Q[x] over Q
according to the fundamental theorem on finitely generated
abelian groups.
Classify the group of the polynomial x20 − 1 ∈ Q[x] over Q
according to the fundamental theorem on finitely generated
abelian groups.
Classify the group of the polynomial x12 − 1 ∈ Q[x] over Q
according to the fundamental theorem on finitely generated
abelian groups.
Shinoj K.M. Department of MathematicsGALOIS THEORY

30. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
References
[1] Joseph A. Gallian ,”Contemporary Abstract Algebra” ,
Narosa Publishing House.
[2] John.B.Fraleigh, ”A First Course in Abstract Algebra”.
[3] Thomas V.Hungerford, ”Abstract Algebra”
Shinoj K.M. Department of MathematicsGALOIS THEORY

31. RESUME
MAIN THEOREM OF GALOIS THEORY
ILLUSTRATIONS
MORE ILLUSTRATIONS
CYCLOTOMIC EXTENSION
References
THANK YOU
Shinoj K.M. Department of MathematicsGALOIS THEORY