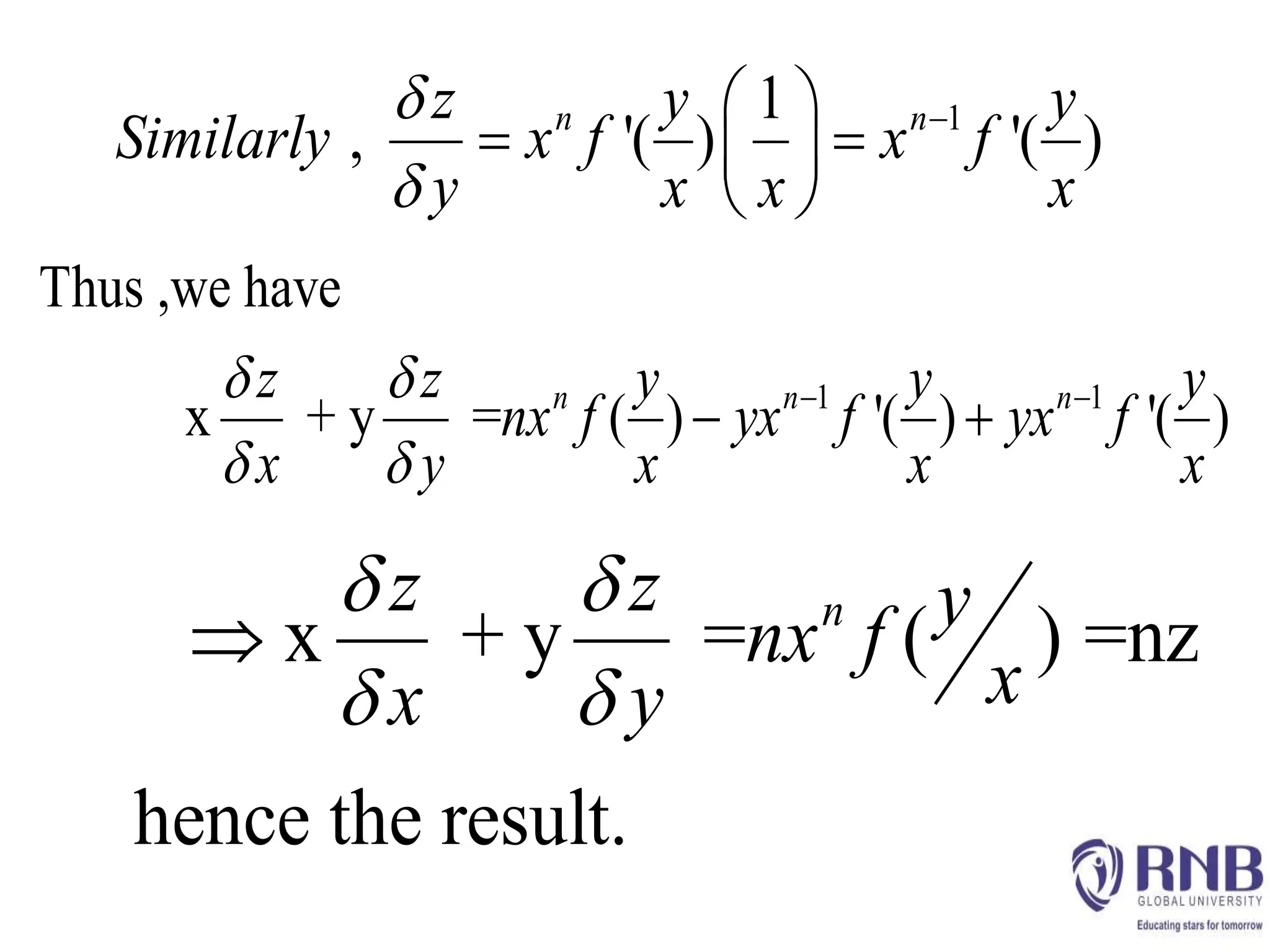1) Partial differentiation allows a function of two variables to be differentiated with respect to one variable while keeping the other constant. This produces partial derivatives that show the rate of change. 2) Second-order partial derivatives take the partial derivative of a first-order partial derivative, producing four possible second-order partial derivatives. 3) Euler's theorem states that if a function is homogeneous of degree n, the sum of its variables multiplied by the function value will equal n times the function value. This can be used to prove properties of homogeneous functions.

1. Subject:- BUSINESS MATHEMATICS
GROUP PRESENTATION – 02
B.Com(Hons.) IVth sem
SUBMITTED TO: SUBMITTED BY:
Mr. SUNIL BHARDWAJ SIR K.Devika
Jaishree chauhan

2. PARTIAL
DIFFERENTIATION
• When we write u = f(x , y), we are saying that
we have a function, u, which depends on two
independent variables: x and y. We can
consider the change in u with respect to either
of these two independent variables by using
the partial derivative.

3. The partial derivative of u with respect to x is
written as:
the partial of u with respect to y. It is written as:
* The rule for partial derivatives is that we
differentiate with respect to one variable while
keeping all the other variables constant.
= f(x , y)
= f(x , y)

4. Taking the Partial Derivative of a Partial
Derivative
• So far we have defined and given examples for
first-order partial derivatives. Second-order
partial derivatives are simply the partial
derivative of a first-order partial derivative.
We can have four second-order partial
derivatives:

7. • Homogeneous Function
• An important property of homogeneous
functions is given by Euler’s Theorem.
),,,(
0wherenumberanyfor
if,degreeofshomogeneouisfunctionA
21
21
n
k
n
sxsxsxfYs
ss
k),x,,xf(xy





Euler’s Theorem on Homogeneous
Function

8. If z = F (x,y) be a homogenious function of x,y of degree n
then x + y = nz for all x,y
z z
x y
 
 
Proof: We have
z is a homogenious function of degree n.
1
2
1 2
( ) '( )
( ) '( )
n n
n n
z y y y
nx f x f
x x x x
y y
nx f yx f
x x



 
 
    
 
 
so that z = xn y
x

 
 
 
f
EXAMPLE

9. 11
, '( ) '( )n nz y y
Similarly x f x f
y x x x


 
  
 
1 1
Thus ,we have
x + y = ( ) '( ) '( )n n nz z y y y
nx f yx f yx f
x y x x x
 
 
 
 
x + y = ( ) =nz
hence the result.
nz z ynx f
xx y
 
 


10. Maxima and Minima of Functions of
Two Variables
Let f be a function with two variables with continuous second
order partial derivatives fxx, fyy and fxy at a critical point (a,b).
Let D = fxx(a,b) fyy(a,b) - fxy
2(a,b)
• If D > 0 and fxx(a,b) > 0, then f has a relative minimum at (a,b).
• If D > 0 and fxx(a,b) < 0, then f has a relative maximum at (a,b).
• If D < 0, then f has a saddle point at (a,b).
• If D = 0, then no conclusion can be drawn.