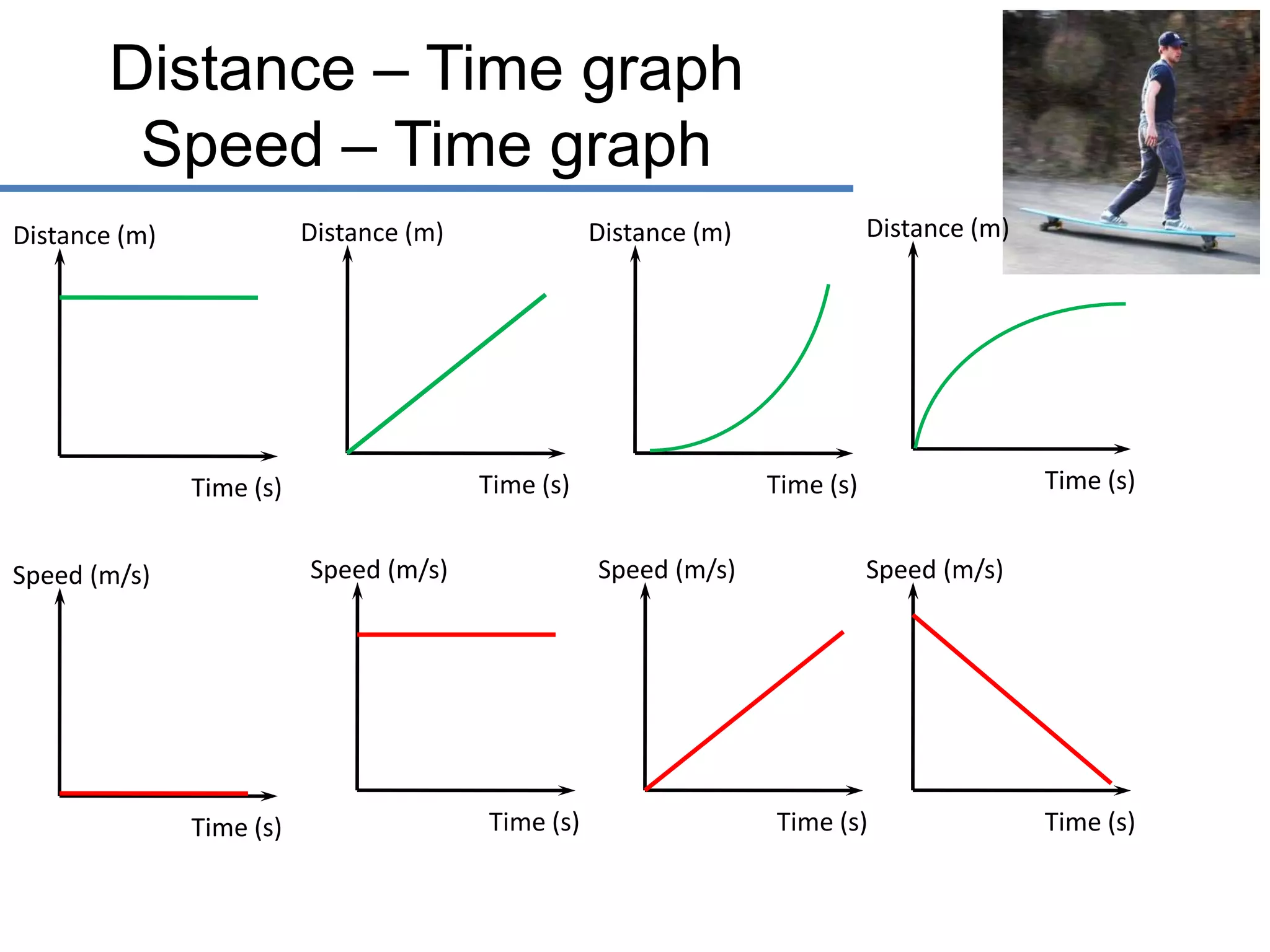
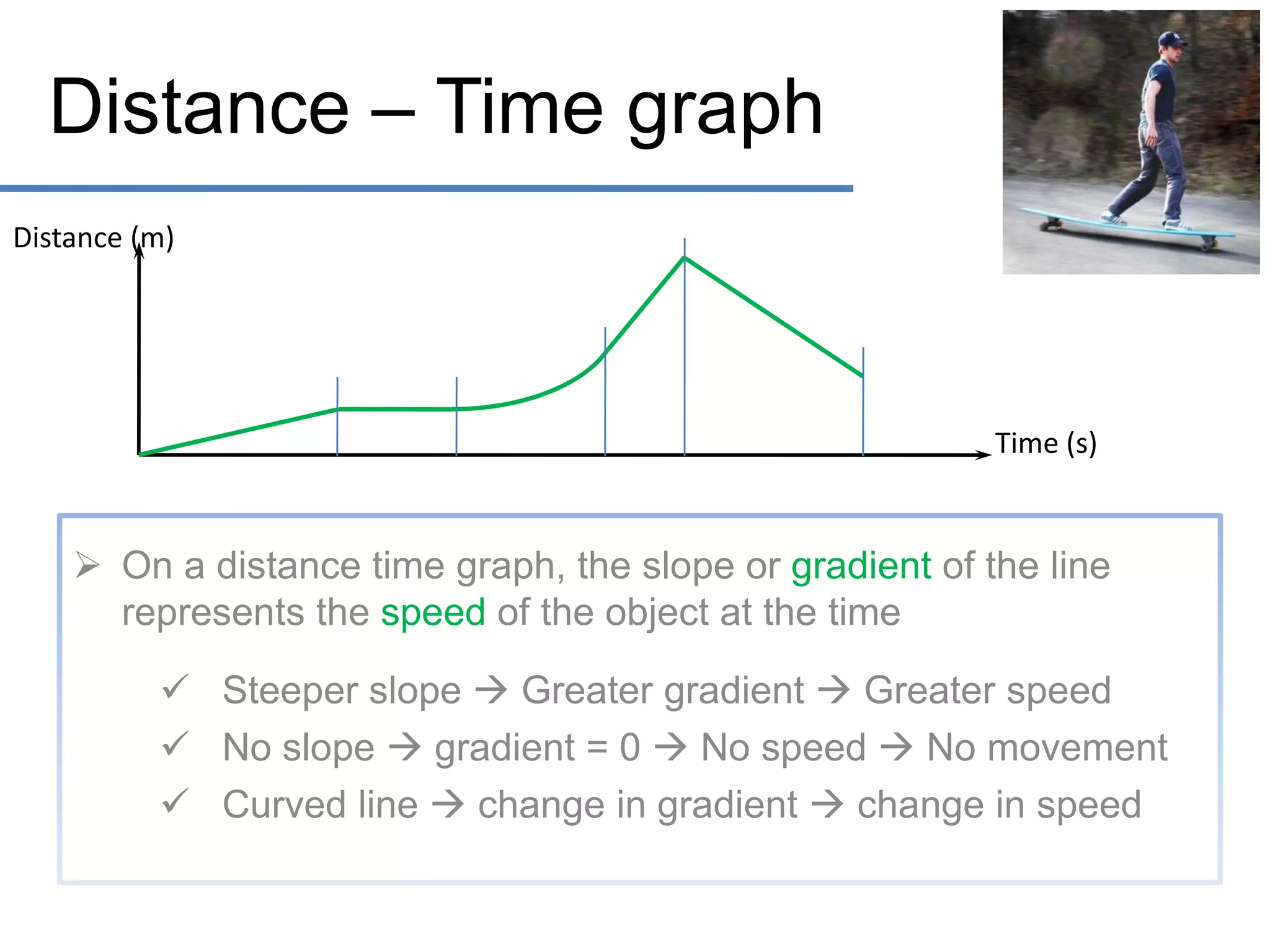
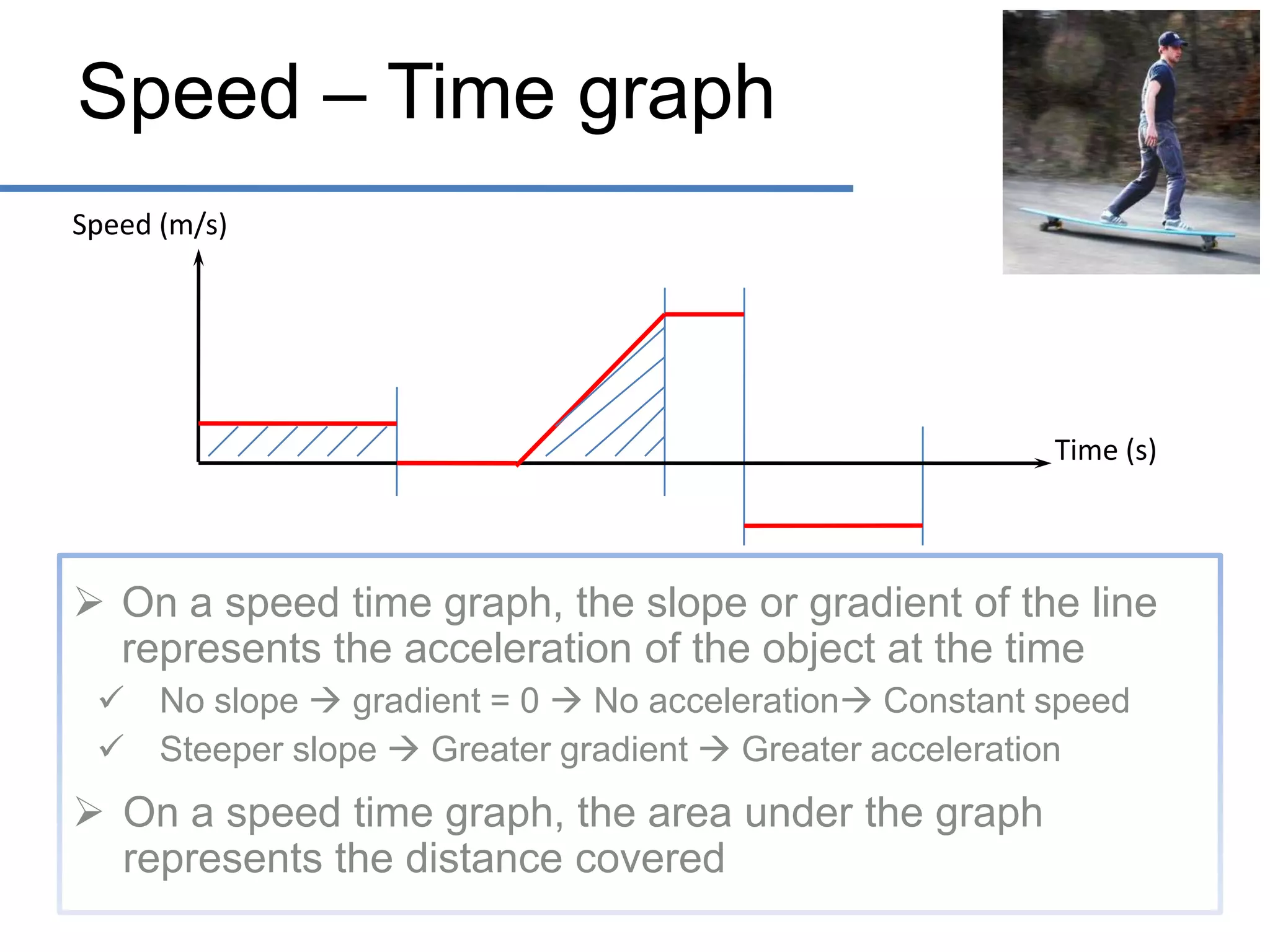
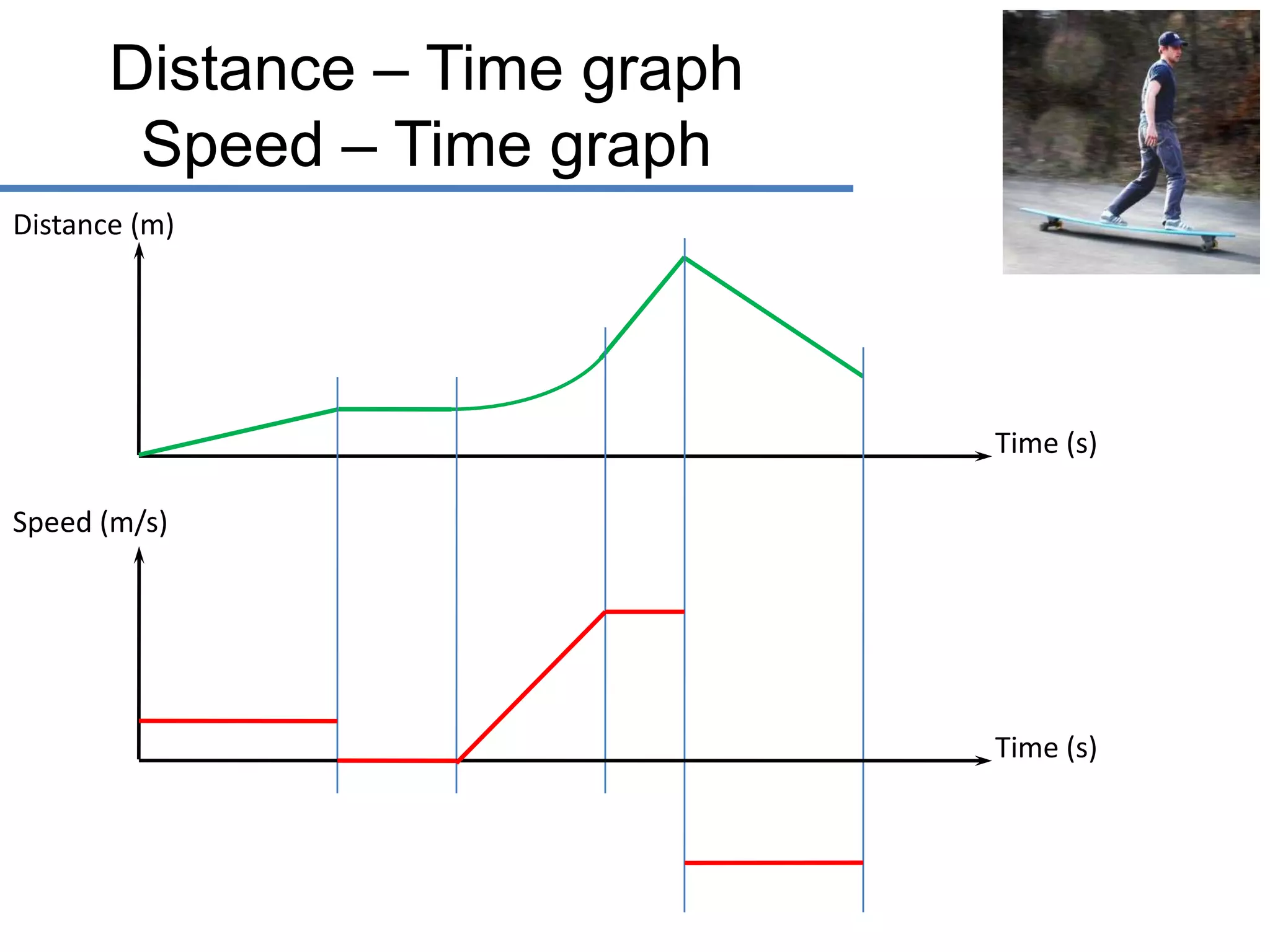
This document discusses key concepts related to motion, including: - Distance is a scalar quantity that measures the total length of an object's path, while displacement is a vector quantity that measures the change in an object's position. - Speed is the rate of change of distance and is a scalar, while velocity is the rate of change of displacement and is a vector. - Graphs can show the relationship between distance, speed, time, and other motion variables. The slope of a distance-time graph represents speed, while the slope of a speed-time graph represents acceleration.

1. Motion
By Nico Vaunois 2011

2. Distance and
Displacement
 Distance is the measure of the total length of the path
taken during the change of position of an object
 Distance is a scalar quantity
 Displacement is the measure of the change of position
of an object
 Displacement is a vector quantity

3. Speed and Velocity
 Speed is the measure of rate of the distance covered
 Speed is a scalar quantity
Distance covered
Speed (m/s) =
(m)
Time taken (s)
 Velocity is the measure of rate of displacement of an
object
 Velocity is a vector quantity
Displacement
Velocity
Time taken
=

4. Scalars and Vectors
 Scalars are quantities that have a size (or magnitude)
only
 Vectors are quantities that have a size and a direction

5. d
Speed Distance Time
s
t
 We can calculate the speed of a moving
object using the equation :
Average Speed
=
Distance covered
Time taken
s
=
d
t
 Because distance is measured in metres (m) and time in
seconds (s), the S.I. unit for speed is metres per second
(m/s or m s-1)
Distance covered
Speed (m/s) =
(m)
Time taken (s)

6. Acceleration
Δv
a
Δt
 Acceleration is the rate of change of speed
Acceleration =
Change in
Velocity
Change in Time
Δv
a
= Δt
 Because speed is measured in metres per second (m s1) and time in seconds (s), the S.I. unit for acceleration is :
 metres per second squared (m/s/s or m s-2)
Change in velocity (m
Acceleration (m s-2)
s-1)
Change in time
=
(s)

7. Distance – Time graph
Speed – Time graph
Distance (m)
Distance (m)
Time (s)
Time (s)
Speed (m/s)
Speed (m/s)
Time (s)
Distance (m)
Distance (m)
Speed (m/s)
Time (s)
Time (s)
Time (s)
Speed (m/s)
Time (s)
Time (s)

8. Distance – Time graph
Distance (m)
Time (s)
 On a distance time graph, the slope or gradient of the line
represents the speed of the object at the time
 Steeper slope  Greater gradient  Greater speed
 No slope  gradient = 0  No speed  No movement
 Curved line  change in gradient  change in speed

9. Speed – Time graph
Speed (m/s)
Time (s)
 On a speed time graph, the slope or gradient of the line
represents the acceleration of the object at the time
 No slope  gradient = 0  No acceleration Constant speed
 Steeper slope  Greater gradient  Greater acceleration
 On a speed time graph, the area under the graph
represents the distance covered

10. Velocity - time graphs
• Distance and displacement can be found from a velocity
- time graph by
velocity
+
Area 1


Area 1 + Area 2 = Distance
Area 1 – Area 2 = Displacement
Area 2
time

11. Distance – Time graph
Speed – Time graph
Distance (m)
Time (s)
Speed (m/s)
Time (s)

12. d
Speed Distance Time
s
t
 We can calculate the speed of a moving
object using the equation :
Average Speed
=
Distance covered
Time taken
s
=
d
t
 Because distance is measured in meters (m) and time in
seconds (s), the S.I. unit for speed is meters per second
(m/s or m s-1)
Distance covered
Speed (m/s) =
(m)
Time taken (s)

13. Δv
Acceleration
a
Δt
 Acceleration is the rate of change of speed
Acceleration =
Change in
Speed
Change in
Time
Δv
a
= Δt
 Because speed is measured in meters per second (m s1) and time in seconds (s), the S.I. unit for acceleration is :
 meters per second squared (m s-1 /s or m s-2)
Change in speed (m
Acceleration (m s-2)
s-1)
Change in time
=
(s)