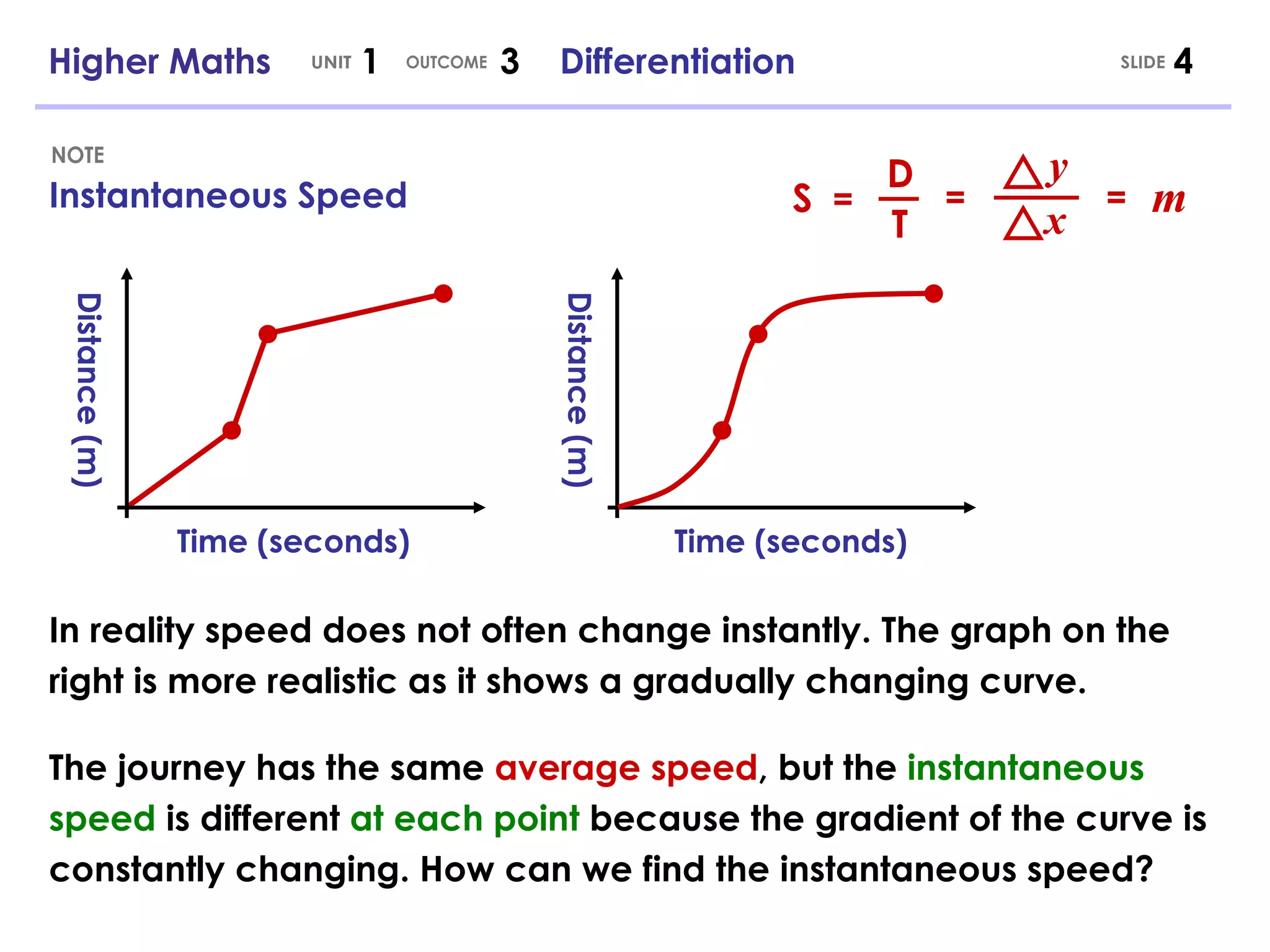
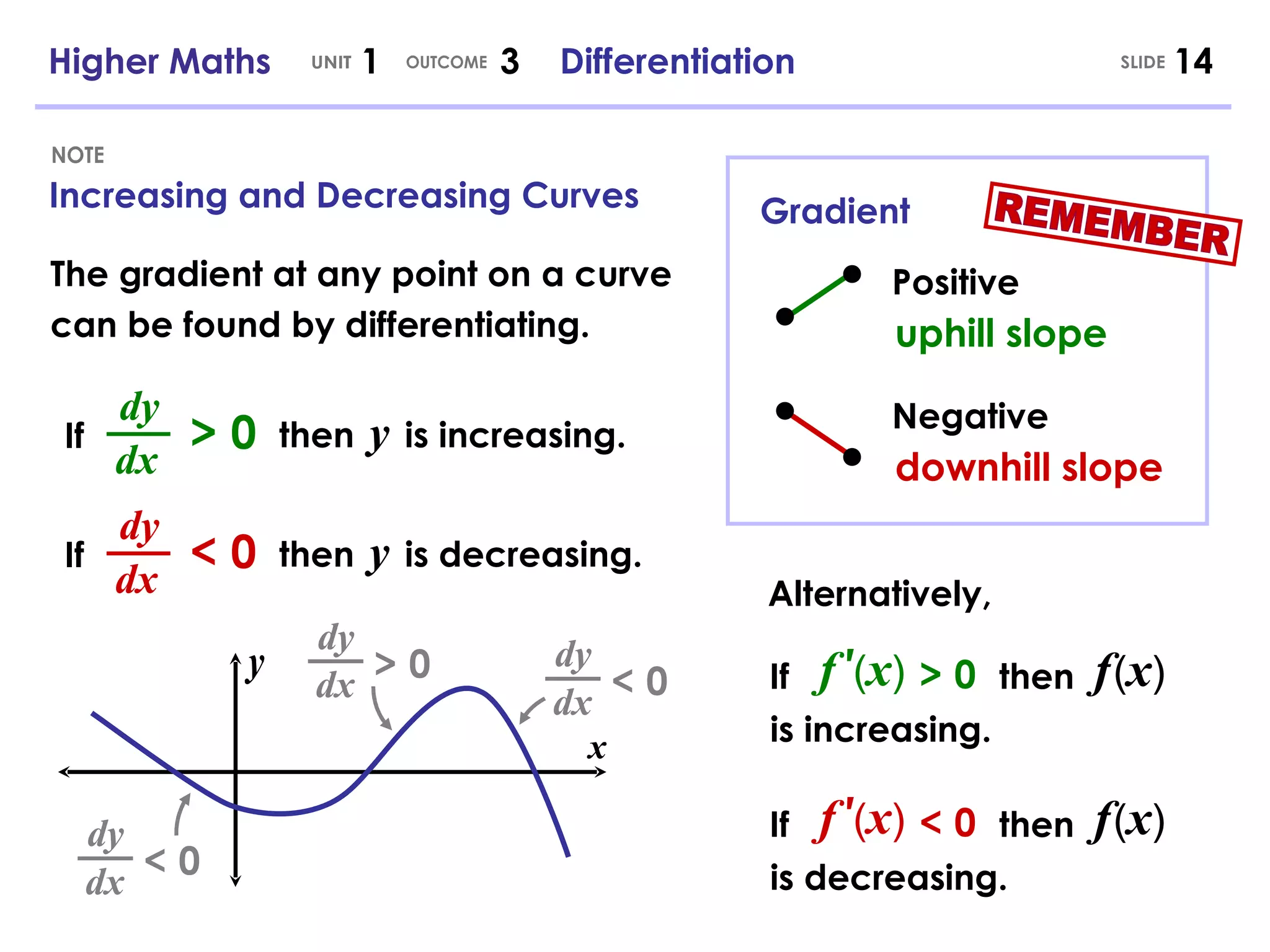
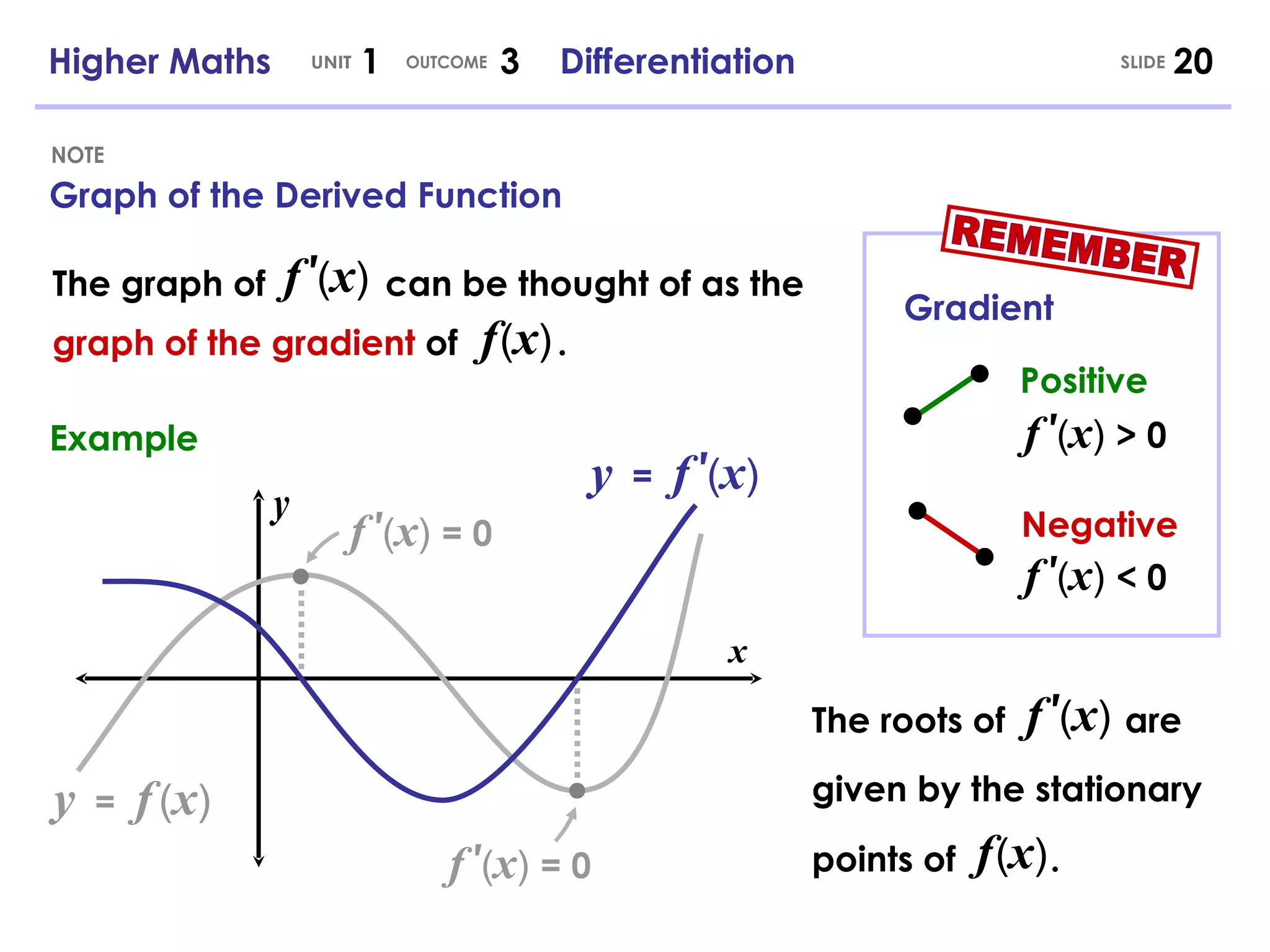
The document discusses differentiation and its history. It was independently developed in the 17th century by Isaac Newton and Gottfried Leibniz. Differentiation allows the calculation of instantaneous rates of change and is used in many areas including mathematics, physics, engineering and more. Key concepts covered include calculating speed, estimating instantaneous rates of change, the rules for differentiation, and differentiation of expressions with multiple terms.

1. Higher Maths 1 3 Differentiation UNIT OUTCOME SLIDE

2. Higher Maths 1 3 Differentiation UNIT OUTCOME The History of Differentiation NOTE Differentiation is part of the science of Calculus , and was first developed in the 17 th century by two different Mathematicians. Gottfried Leibniz (1646-1716) Germany Sir Isaac Newton (1642-1727) England SLIDE Differentiation, or finding the instantaneous rate of change , is an essential part of: • Mathematics and Physics • Chemistry • Biology • Computer Science • Engineering • Navigation and Astronomy

3. Higher Maths 1 3 Differentiation Calculating Speed UNIT OUTCOME NOTE 2 4 6 8 4 8 2 6 10 0 0 Time (seconds) Distance (m) Example Calculate the speed for each section of the journey opposite. A B C speed in A = 4 3 speed in B = 5 1 5 m/s = speed in C = 2 5 0.4 m/s = average speed = 9 1.22 m/s ≈ ≈ 1.33 m/s Notice the following things: • the speed at each instant is not the same as the average • speed is the same as gradient D T S = y x = m = SLIDE D S T × ÷ ÷ 1 1

4. Instantaneous Speed NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME Time (seconds) Distance (m) Time (seconds) Distance (m) In reality speed does not often change instantly. The graph on the right is more realistic as it shows a gradually changing curve. The journey has the same average speed , but the instantaneous speed is different at each point because the gradient of the curve is constantly changing. How can we find the instantaneous speed? D T S = y x = m = SLIDE

5. Introduction to Differentiation NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME Differentiate means D T speed = ‘ rate of change of distance with respect to time ’ S T acceleration = ‘ find out how fast something is changing in comparison with something else at any one instant ’. gradient = y x ‘ rate of change of speed with respect to time ’ ‘ rate of change of -coordinate with respect to -coordinate ’ y x SLIDE

6. Estimating the Instantaneous Rate of Change NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME The diagrams below show attempts to estimate the instantaneous gradient (the rate of change of with respect to ) at the point A . x y A x y A y A Notice that the accuracy improves as gets closer to zero. x y x The instantaneous rate of change is written as: y x dy dx = as approaches 0. x SLIDE y x x y y x

7. Basic Differentiation NOTE The instant rate of change of y with respect to x is written as . Higher Maths 1 3 Differentiation UNIT OUTCOME dy dx By long experimentation, it is possible to prove the following: dy dx = y = x n n x n – 1 If then • multiply by the power • reduce the power by one How to Differentiate: Note that describes both the rate of change and the gradient . dy dx SLIDE

8. Differentiation of Expressions with Multiple Terms NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME y = ax m + bx n + … • multiply every x -term by the power How to Differentiate: dy dx = • reduce the power of every x -term by one The basic process of differentiation can be applied to every x -term in an algebraic expession. Important Expressions must be written as the sum of individual terms before differentiating. SLIDE a m x m + b n x n + … – 1 – 1

9. Examples of Basic Differentiation NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME Find for dy dx y = 3 x 4 – 5 x 3 + + 9 7 x 2 y = 3 x 4 – 5 x 3 + 7 x -2 + 9 dy dx = 12 x 3 – 15 x 2 – 14 x -3 9 = 9 x 0 this disappears because = 12 x 3 – 15 x 2 – 14 x 3 SLIDE (multiply by zero) Example 1

10. Examples of Basic Differentiation NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME Find the gradient of the curve Example 2 SLIDE y = ( x + 3 ) ( x – 5 ) y = x ² – 2 x – 15 x 2 = 1 2 x – 15 x 2 x 2 – = 1 – 2 x - 1 – 15 x - 2 dy dx = 2 x - 2 + 30 x - 3 disappears (multiply by zero) = 2 + 30 x 3 x 2 At x = 5 , at the point (5,0) . dy dx = 2 + 30 25 125 = 8 25

11. The Derived Function NOTE The word ‘ derived ’ means ‘produced from’, for example orange juice is derived from oranges. Higher Maths 1 3 Differentiation UNIT OUTCOME It is also possible to express differentiation using function notation. = f ( x ) nx n – 1 If then f ′ ( x ) = x n f ′ ( x ) dy dx and mean exactly the same thing written in different ways. Leibniz Newton The derived function is the rate of change of the function with respect to . f ′ ( x ) f ( x ) x SLIDE

12. A tangent to a function is a straight line which intersects the function in only one place, with the same gradient as the function. Tangents to Functions NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME SLIDE The gradient of any tangent to the function can be found by substituting the x -coordinate of intersection into . f ( x ) A B f ′ ( x ) f ( x ) m AB = f ′ ( x )

13. f ′ ( x ) Equations of Tangents NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME SLIDE y – b = m ( x – a ) REMEMBER To find the equation of a tangent: • substitute gradient and point of intersection into y – b = m ( x – a ) • substitute -coordinate to find gradient at point of intersection x • differentiate Straight Line Equation Example Find the equation of the tangent to the function at the point ( 2,4 ) . f ( x ) = x 3 1 2 = x 2 3 2 f ′ ( 2 ) = × ( 2 ) 2 3 2 = 6 m = y – 4 = 6 ( x – 2 ) 6 x – y – 8 = 0 substitute:

14. Increasing and Decreasing Curves NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME The gradient at any point on a curve can be found by differentiating. SLIDE uphill slope Positive downhill slope Negative Gradient REMEMBER If dy dx > 0 then y is increasing. If dy dx < 0 then y is decreasing. Alternatively, If > 0 f ′ ( x ) is increasing. f ( x ) then If < 0 f ′ ( x ) is decreasing. f ( x ) then x y dy dx < 0 dy dx > 0 dy dx < 0

15. If a function is neither increasing or decreasing, the gradient is zero and the function can be described as stationary . Stationary Points NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME SLIDE There are two main types of stationary point. Minimum Maximum Turning Points Points of Inflection At any stationary point, or alternatively dy dx = 0 f ′ ( x ) = 0 Rising Falling

16. Investigating Stationary Points NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME SLIDE Example Find the stationary point of f ( x ) = x 2 – 8 x + 3 Stationary point given by f ′ ( x ) = 2 x – 8 2 x – 8 = 0 and determine its nature. x = 4 f ′ ( x ) = 0 x 4 – 4 + 4 slope The stationary point at is a minimum turning point. – 0 + f ′ ( x ) x = 4 Use a nature table to reduce the amount of working. ‘ slightly less than four ’ ‘ slightly more ’ gradient is positive

17. Investigating Stationary Points NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME SLIDE Example 2 Investigate the stationary points of y = 4 x 3 – x 4 dy dx = 12 x 2 – 4 x 3 = 0 4 x 2 ( 3 – x ) = 0 4 x 2 = 0 x = 0 3 – x = 0 x = 3 or y = 0 y = 27 x 0 – 0 + 0 slope dy dx rising point of inflection + 0 + stationary point at ( 0,0 ) : x 3 – 3 + 3 slope dy dx maximum turning point + 0 – stationary point at ( 3, 27 ) :

18. Positive and Negative Infinity NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME SLIDE Example ∞ The symbol is used for infinity. + ∞ – ∞ ‘ positive infinity’ ‘ negative infinity’ The symbol means approaches’. y = 5 x 3 + 7 x 2 For very large , the value of becomes insignificant compared with the value of . 5 x 3 ± x as x , ∞ y 5 x 3 5× ( ) 3 + ∞ = + ∞ 5× ( ) 3 – ∞ = – ∞ REMEMBER as x + ∞ ∞ +1 = ∞ y + ∞ and as x – ∞ y – ∞ 7 x 2

19. Higher Maths 1 3 Differentiation UNIT OUTCOME SLIDE x 7 – 7 + 7 slope – 0 + dy dx Curve Sketching NOTE To sketch the graph of any function, the following basic information is required: • the stationary points and their nature • the x -intercept ( s ) and y -intercept • the value of y as x approaches positive and negative infinity solve for y = 0 and x = 0 solve for = 0 and use nature table dy dx y = x 3 – 2 x 4 – ∞ y + ∞ as x ∞ y -2 x 4 + ∞ y – ∞ as x and as x Example

20. Graph of the Derived Function NOTE Higher Maths 1 3 Differentiation UNIT OUTCOME SLIDE x y Example y = f ( x ) y = f ′ ( x ) f ′ ( x ) = 0 f ′ ( x ) = 0 Positive Negative Gradient f ′ ( x ) > 0 f ′ ( x ) < 0 f ′ ( x ) f ( x ) The graph of can be thought of as the graph of the gradient of . REMEMBER The roots of are f ( x ) f ′ ( x ) given by the stationary points of .