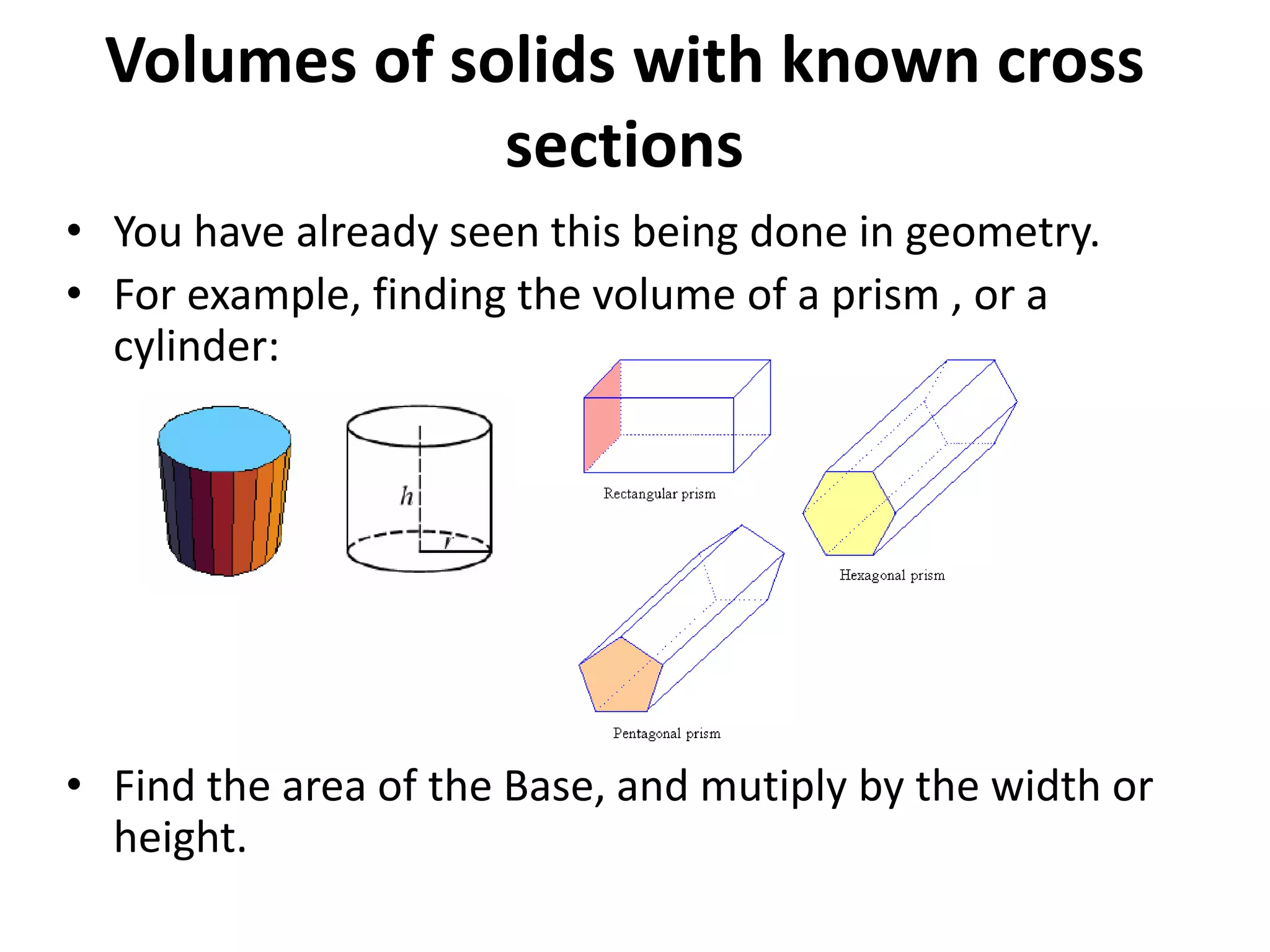
This document discusses several methods for calculating the volume of solids with known cross-sectional areas: calculating the volume of prisms and cylinders by multiplying the area of their circular or rectangular base by the height; using the disk method for solids of revolution by multiplying the circular cross-sectional areas by the width; and applying this method to solids with any shaped cross-section, such as squares, triangles, or ellipses, by multiplying the varying cross-sectional area by the width. Formulas for calculating volume by integrating the cross-sectional area with respect to x or y are also provided, along with an example problem.

1. Volumes of solids with known cross
sections
• You have already seen this being done in geometry.
• For example, finding the volume of a prism , or a
cylinder:
• Find the area of the Base, and mutiply by the width or
height.

2. The disk and washer method
• We have also seen this in our study of Calculus
via Solids of revolution
• The disk and washer method use Circular
cross sections
• We multiply the cross sections times the
width to get the actual volume.

3. It can really be ANY cross section
• It doesn’t necessarily have to be circular.
• It can be a square, triangle, ellipse, etc..
• If we can find the Area of the cross
section, then we can multiple it times the
width (just like before) to get the entire
volume.
• ANIMATION

4. Formulas
• When the cross section is perpendicular to the
x-axis, integrate with respect to x:
b
V
A ( x ) dx
a
• When the cross section is perpendicular to the
y-axis, integrate with respect to y:
b
V
A ( y ) dy
a

5. Example:
• A solid is formed with a base bounded by the graphs of:
f ( x)
1
x
2
x
0
g ( x)
1
x
2
Find the volume of the solid using equilateral triangle cross –
sections taken perpendicular to the x-axis.

6. Practice