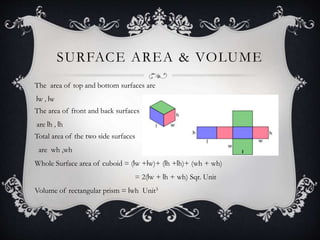
The document discusses cuboids and cubes. It defines a cuboid as a three-dimensional structure with six rectangular faces where parallel edges are equal length and faces meet perpendicularly. Bricks are given as examples of cuboids. A cube is defined as a special cuboid where all sides have equal length. The document provides formulas for calculating the surface area and volume of cuboids and cubes. It derives formulas showing that the diagonal of a cuboid is the square root of the sum of the squares of its dimensions, and the diagonal of a cube is three times the length of one side.

1. CUBOID
Presented By:-
Subhajit Manna

2. AIMS & OBJECTIVES
 Students can get a brief concept about Cuboid.
 After the lesson Students can easily evaluate the Area, Volume of
a Cuboid .
 Students can find the length of diagonals of not only a Cuboid
but also a Cube.
 Students can overcome the Real-Life problems including the
objects similar to Cuboid.

3. CONCEPT
FORMING A CUBOID
At first we know how to form a
RECTANGULAR PARALLELOPIPED
Or,
CUBOID.

4. FORMATION
At first we take a
Rectangular piece
ABCD ,shown
In R.H.S.
A D
B C

5. FORMATION
Then we add two
Rectangular pieces D
Similar length of AB
And CD in both sides
AB , CD Of the
rectangle ABCD. B
C
A

6. FORMATION
A
Next, we repeat the same
Process i.e, we add two rectangular D
Pieces Similar length of AD
And CB in both sides
AD , CB Of the
rectangle ABCD.
B
C

7. FORMATION
A
 Then we add a rectangular E
piece EFGH whose length and D H
width are equivalent to the
face ABCD.
B C
F G
Such a figure is Called Rectangular Parallelepiped Or, Cuboid.

8. DEFINITIONS
Rectangular Parallelepiped /Cuboid is a three-dimensional
structure whose all the six faces possess a rectangular shape, in which
the lengths of all the parallel edges are equal and consecutive faces are
perpendicular to each other.
The face, vertex and edges of a
Cuboid are shown in R.H.S.
Bricks are the examples of Cuboid.

9. CUBE
Cube is a special type of Cuboid ,
Whose length ,width and height
of the sides are equal.
The easy example of a Cube in real –life
is a Dice .(Shown in R.H.S.)

10. SURFACE AREA & VOLUME
 Since the Cuboid has Six faces,
So ,
Whole surface area of a Cuboid is
= Sum of the area of 6 faces

11. SURFACE AREA & VOLUME
The area of top and bottom surfaces are
lw , lw
The area of front and back surfaces
are lh , lh
Total area of the two side surfaces
are wh ,wh
Whole Surface area of cuboid = (lw +lw)+ (lh +lh)+ (wh + wh)
= 2(lw + lh + wh) Sqr. Unit
Volume of rectangular prism = lwh Unit3

12. SURFACE AREA & VOLUME
 Since the equal length , height , width of the faces of a cuboid are
called a Cube
So putting , l =w=h in the previous case
We get, The whole surface area of a Cube as
=Sum of the area of 6 equal faces
= 2( l.l + l.l + l.l)=6l2 Sqr Unit
Similarly , the volume of the Cube is
= l . l . l = l3 Unit3
l
l
l

13. DIAGONAL OF A CUBOID
Now , we find the length of a diagonal of a Cuboid.
From the R.H.S. figure ,we see
length=HG= l unit
width=GF= b unit
height=BF= h unit
From the Right-Angled Triangle HGF
the hypotenuse , HF=√(l2 +b2 ) unit
Also , from the Right-Angled Triangle HBF
the hypotenuse , HB=√(l2 +b2+h2 ) unit
Which (HB) is nothing but one of the Diagonals of the
Cuboid ABCDHEFG.
Hence , The length of Diagonal of a Cuboid = √(length2 + width2 +height2)

14. DIAGONAL OF A CUBE
 Since the equal length , height , width of the faces of a cuboid are
called a Cube.
So putting , l = b =h in the previous case
we get one of the Diagonals of a cube as
d =√(l2 + l2+ l2 ) unit
= 3 l unit
Hence , The length of Diagonal of a Cube = 3 x (length of a side)